Aerodynamic System Machine Learning Modeling with Gray Wolf Optimization Support Vector Regression and Instability Identification Strategy of Wavelet Singular Spectrum
Abstract
:1. Introduction
2. Data Acquisition and Phase Space Processing
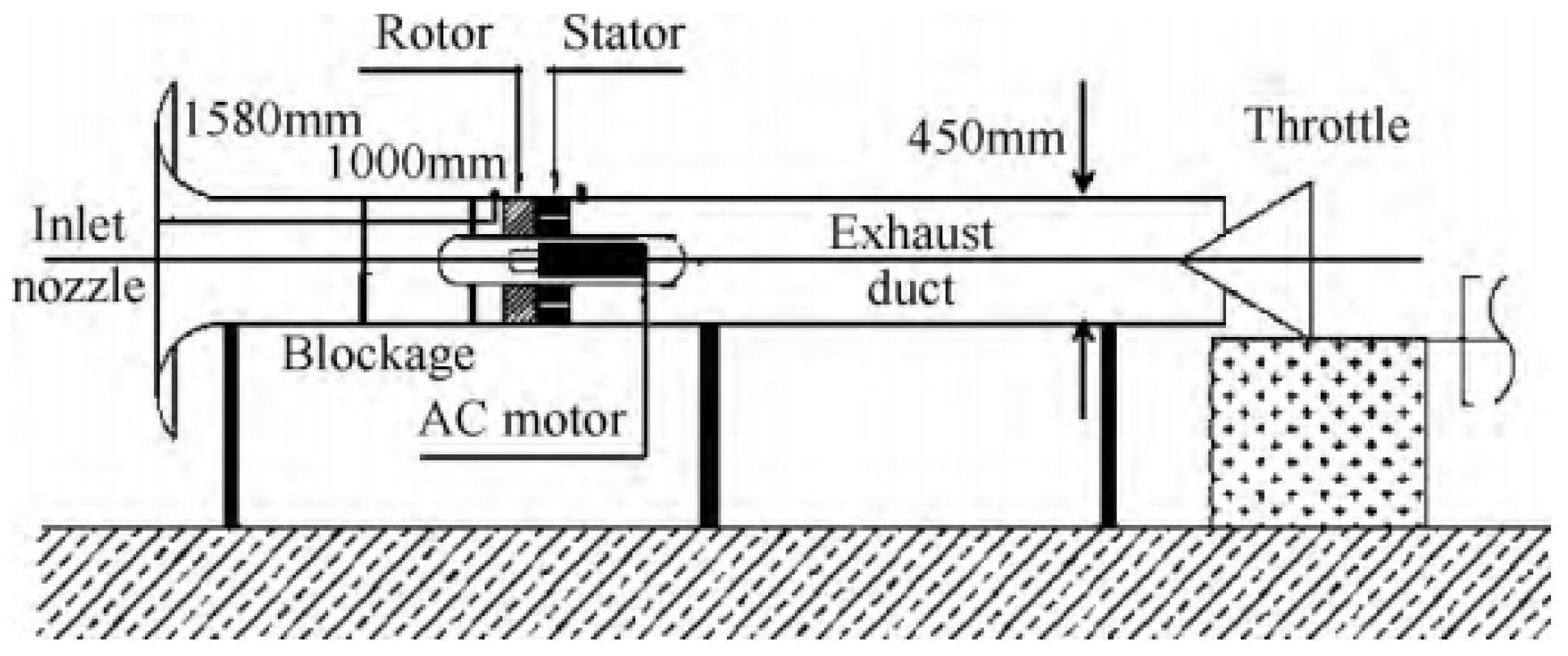
2.1. Introduction to Experimental Data Collection
2.2. Evolution of the Spatial Mode in Flow Field
2.3. Phase Space Reconstruction of Spatial Mode
3. Modeling Methodology with Support Vector Regression
3.1. Basic Theory of Support Vector Regression Algorithm
3.2. Support Vector Regression Prediction Model Based on Gray Wolf Optimization Algorithm
3.3. Gray Wolf Algorithm Optimized Support Vector Regression Model Combined with Wavelet Transform
4. Identification Strategy on the Aerodynamic System Instability
4.1. Instability Identification Design with Single Step Based on Wavelet Singular Spectrum Entropy Algorithm
4.2. Foregleam with Multi-Step Prediction by Wavelet Singular Spectrum Entropy Identification Strategy
5. Discussion
6. Conclusions
- (1)
- In the processing of the feature correlation, the spatial modes are extracted according to the pressure data of multiple measuring points. The sudden increase in the amplitude of the modal energy is implied accurately as the verification of the rotating stall in the system. From the view of the system identification, the information contained in the spatial mode can be selected as the key parameter for the occurrence of the instability quantitatively. Because of the chaotic characteristic represented by the sequence of the spatial modal, the solutions of the WT and CC algorithm are adopted to decompose and reconstruct the phase space in the field. The local signal components are obtained with different frequency information, associated with the characteristic the stall precursor.
- (2)
- On the premise of finding out the local laws of the system, the SVR method is used to model each reconstructed frequency component. With the determination of the embedding dimension and the delay time of the sequence optimized by the GWO algorithm, the mathematical correlation between the aerodynamic parameters and the instability index is effectively built up by the WT-GWO-SVR hybrid model. Taking cluster analysis and gradient optimization as the way, the data modeling process is established based on data fusion and feature association. It is indicated that the established the SVR hybrid model in this research reflects an outstanding performance for the nonlinear dynamic system prediction. In order to achieve a longer forecast margin, the research on the multi-step prediction is continued to carry out on the hybrid modeling for the system information. It has still achieved an acceptable accuracy for the prediction with multi-timesteps.
- (3)
- In order to effectively identify the sign of the instability in the modeling system, a information entropy algorithm is proposed to detect the stall inception. Focusing on the time-frequency analysis, the wavelet singular spectrum is introduced to describe the instability process of the dynamic system. According to the obvious difference between the entropy weights under the normal and stall conditions of the compressor, the instability boundary can be well distinguished in the modal space of system. By designing the three sigma criteria to design the recognition threshold strategy, the warning location of the stall precursor can be suggested about 102r in advance with the multi-step prediction, showing a good accuracy and application prospect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Epstein, A.H.; Williams, J.E.F.; Greitzer, E.M. Active suppression of aerodynamic instabilities in turbomachines. J. Propuls. Power 1989, 5, 204–211. [Google Scholar] [CrossRef]
- Day, I.J.; Breuer, T.; Escuret, J.; Cherrett, M.; Wilson, A. Stall inception and the prospects for active control in four high-speed compressors. J. Turbomach. 1999, 12, 18–27. [Google Scholar] [CrossRef]
- Inoue, M.; Kuroumaru, M.; Tanino, T.; Furukawa, M. Propagation of Multiple Short-Length-Scale Stall Cells in an Axial Compressor Rotor. J. Turbomach. 2000, 122, 45–53. [Google Scholar] [CrossRef]
- Christensen, D.; Cantin, P.; Gutz, D.A.; Szucs, P.N.; Wadia, A.R.; Armor, J.B.; Dhingra, M.; Neumeier, Y.; Prasad, J.V. Development and demonstration of a stability management system for gas turbine engines. J. Turbomach. 2008, 130, 165–174. [Google Scholar] [CrossRef]
- Liu, B.; Lei, Y. Design and implementation of aerodynamic instability embedded early warning system for compressor. Meas. Control Technol. 2010, 29, 68–71. [Google Scholar]
- Salunkhe, P.B.; Pradeep, A.M. Theoretical analysis of rotating stall under static inflow distortion including effect of tip injection. Int. J. Turbo Jet Engines 2010, 27, 39–50. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Du, J. Application of fast wavelet analysis on early stall warning in axial compressors. J. Therm. Sci. 2019, 28, 837–849. [Google Scholar] [CrossRef]
- Qiu, X.; Liu, Z. Stall Warning of Axial Compressor Using Spatial FFT and Combined Analysis of Multiple Statistical Parameters. J. Phys. Conf. Ser. 2021, 2033, 012105. [Google Scholar] [CrossRef]
- Ping, X.; Bin, L. Study on Multi-Resolution Singular-Spectrum Entropy and Its Usage in Vibration Signal Monitoring. J. Trans. Technol. 2004, 17, 547–550. [Google Scholar]
- He, Z.; Fu, L.; Lin, S. Fault detection and classification in EHV transmission line based on wavelet singular entropy. IEEE Trans. Power Deliv. 2010, 25, 2156–2163. [Google Scholar] [CrossRef]
- Zhang, M.; Kong, P.; Hou, A. Identification Strategy Design with the Solution of Wavelet Singular Spectral Entropy Algorithm for the Aerodynamic System Instability. Aerospace 2022, 9, 320. [Google Scholar] [CrossRef]
- Gan, X.S.; Gao, H.L. Research on Longitudinal Aerodynamics Modeling Method for Aircraft Stall Based on Wavelet Neural Network from Flight Data. Appl. Mech. Mater. 2014, 602, 3144–3147. [Google Scholar] [CrossRef]
- Lin, P.; Wang, C.; Wang, M. Bifurcation predication in axial compressors with nonuniform inflow via deterministic learning. Int. J. Bifurc. Chaos 2017, 27, 1750159. [Google Scholar] [CrossRef]
- Hipple, S.M.; Bonilla-Alvarado, H.; Pezzini, P. Using machine learning tools to predict compressor stall. J. Energy Resour. Technol. 2020, 142, 070915. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J.; Hou, A. Dynamic System Modeling of a Hybrid Neural Network with Phase Space Reconstruction and a Stability Identification Strategy. Machines 2022, 10, 122. [Google Scholar] [CrossRef]
- Longley, J.P. Inlet Distortion and Compressor Stability. Ph.D. Thesis, Cambridge University, Cambridge, UK, 1988. [Google Scholar]
- Kugiumtzis, D. State space reconstruction parameters in the analysis of chaotic time series—The role of the time window length. Phys. D Nonlinear Phenom. 1996, 95, 13–28. [Google Scholar] [CrossRef] [Green Version]
- Ge, T.; He, K.; Ke, Q. Optimized product quantization for approximate nearest neighbor search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 2946–2953. [Google Scholar]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Luo, Z.; Hasanipanah, M.; Amnieh, H.B. GA-SVR: A novel hybrid data-driven model to simulate vertical load capacity of driven piles. Eng. Comput. 2021, 37, 823–831. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems. Appl. Soft Comput. 2020, 97, 106761. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. Mtv-mfo: Multi-trial vector-based moth-flame optimization algorithm. Symmetry 2021, 13, 2388. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. Ewoa-opf: Effective whale optimization algorithm to solve optimal power flow problem. Electronics 2021, 10, 2975. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Su, X.; Cao, C.; Zeng, X. Application of DBN and GWO-SVM in analog circuit fault diagnosis. Sci. Rep. 2021, 11, 7969. [Google Scholar] [CrossRef]
- Chen, W.; Wu, J.J.; Duan, W.J. Model of Urban Air Pollution Concentration Forecast Based on Wavelet Decomposition and Support Vector Machine. Mod. Electron. Technol. 2011, 34, 145–148. [Google Scholar]
- Safty, S.; Zonkoly, A. Applying wavelet entropy principle in fault classification. Int. J. Electr. Power 2009, 31, 604–607. [Google Scholar] [CrossRef] [Green Version]
- Kaushal, P.; Mudhalwadkar, R. Stationary wavelet singular entropy based electronic tongue for classification of milk. Trans. Inst. Meas. Control 2020, 42, 870–879. [Google Scholar] [CrossRef]











| Parameter | Value |
|---|---|
| Design speed n (rpm) | 3000 |
| Outer diameter D (mm) | 450 |
| Blade height h (mm) | 56 |
| Tip speed (m/s) | 70.7 |
| Hub-tip ratio | 0.75 |
| Rotor blade number | 19 |
| Stator blade number | 13 |
| Model Type | MAE × 10−4 | RMSE × 10−4 | R2 × 10−4 |
|---|---|---|---|
| WT-GWO-SVR | 3.5753 | 6.6172 | 0.9923 |
| GWO-SVR | 4.8937 | 8.4660 | 0.9874 |
| DE-SVR | 7.9318 | 9.9174 | 0.9827 |
| PSO-SVR | 5.7468 | 8.8422 | 0.9863 |
| Chaos-K-means-GD-RBF [17] | 12.01 | 26.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Kong, P.; Xia, A.; Tuo, W.; Lv, Y.; Wang, S. Aerodynamic System Machine Learning Modeling with Gray Wolf Optimization Support Vector Regression and Instability Identification Strategy of Wavelet Singular Spectrum. Biomimetics 2023, 8, 132. https://doi.org/10.3390/biomimetics8020132
Zhang M, Kong P, Xia A, Tuo W, Lv Y, Wang S. Aerodynamic System Machine Learning Modeling with Gray Wolf Optimization Support Vector Regression and Instability Identification Strategy of Wavelet Singular Spectrum. Biomimetics. 2023; 8(2):132. https://doi.org/10.3390/biomimetics8020132
Chicago/Turabian StyleZhang, Mingming, Pan Kong, Aiguo Xia, Wei Tuo, Yongzhao Lv, and Shaohong Wang. 2023. "Aerodynamic System Machine Learning Modeling with Gray Wolf Optimization Support Vector Regression and Instability Identification Strategy of Wavelet Singular Spectrum" Biomimetics 8, no. 2: 132. https://doi.org/10.3390/biomimetics8020132
APA StyleZhang, M., Kong, P., Xia, A., Tuo, W., Lv, Y., & Wang, S. (2023). Aerodynamic System Machine Learning Modeling with Gray Wolf Optimization Support Vector Regression and Instability Identification Strategy of Wavelet Singular Spectrum. Biomimetics, 8(2), 132. https://doi.org/10.3390/biomimetics8020132






