Aerodynamic Evaluation of Flapping Wings with Leading-Edge Twisting
Abstract
:1. Introduction
2. Materials and Methods
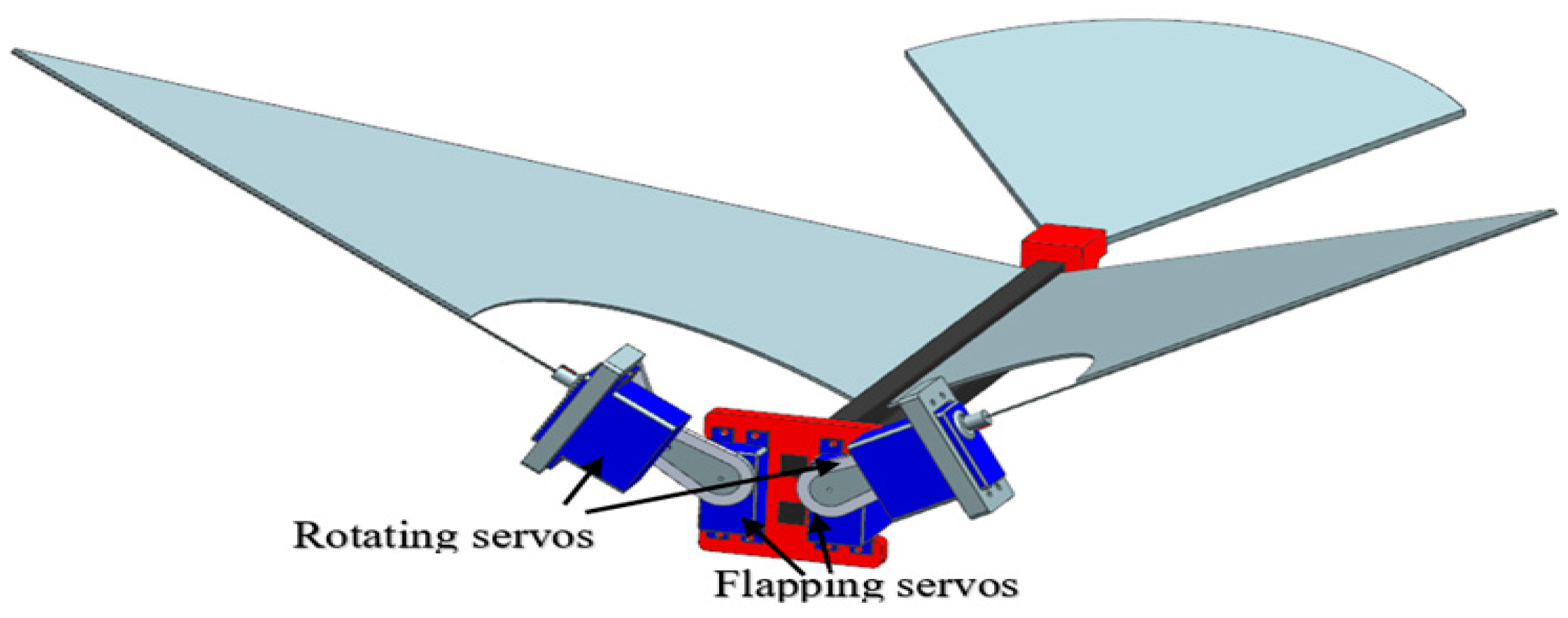
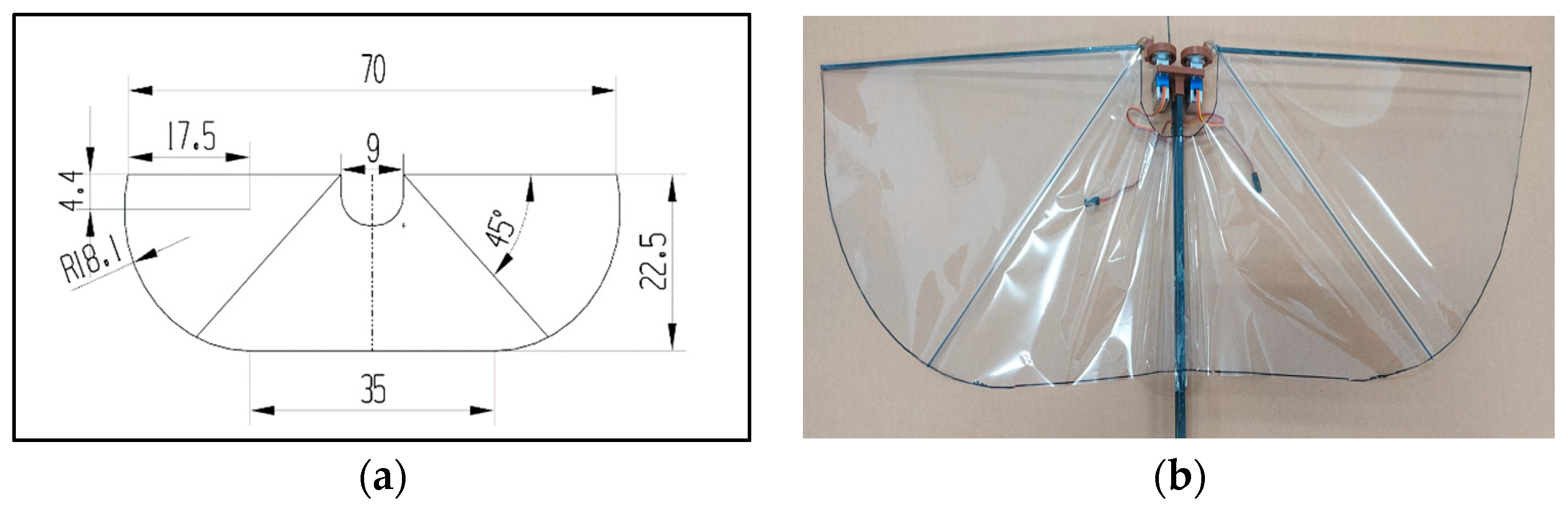
2.1. Type-A: All Servo Mechanism
2.2. Type-A1: Normal Servo Mechanism
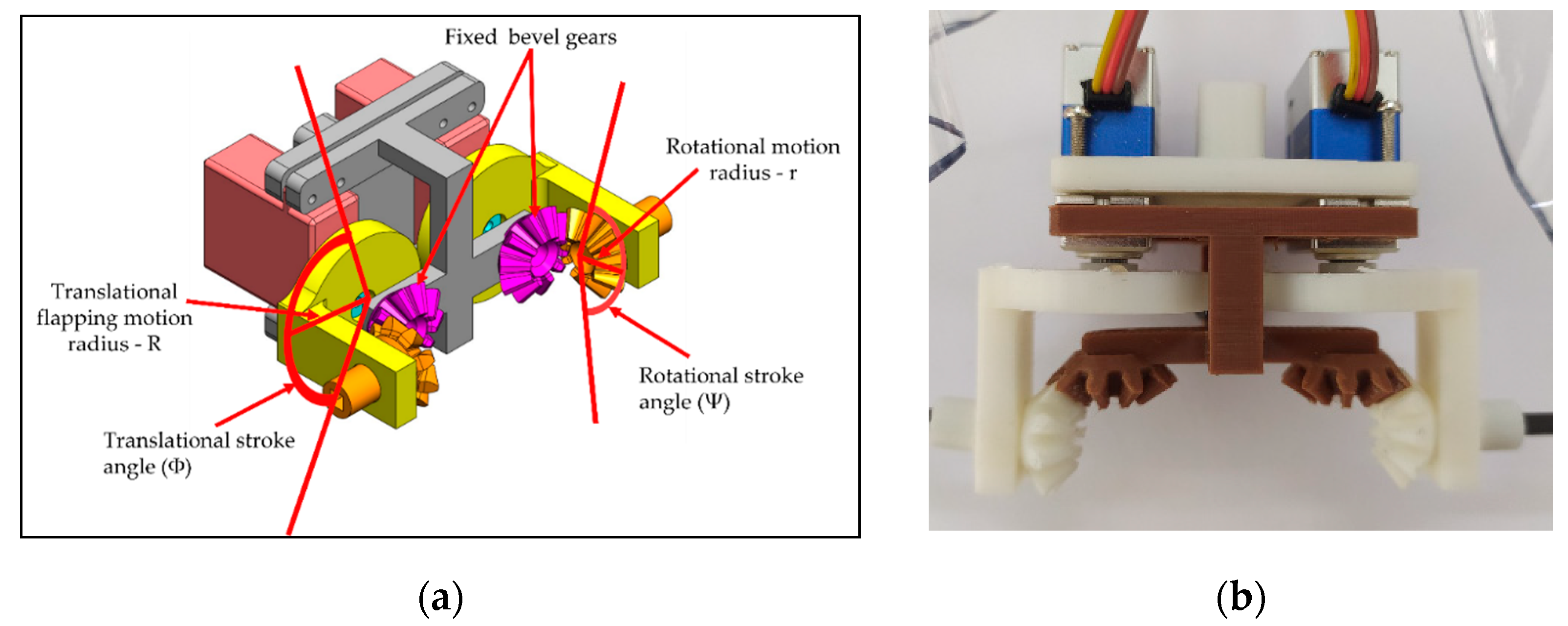
2.3. Type-B: Servo-Bevel Gear Mechanism
2.4. Type-B1: Servo-Bevel Gear Mechanism with Adjustable Mechanical Stopper
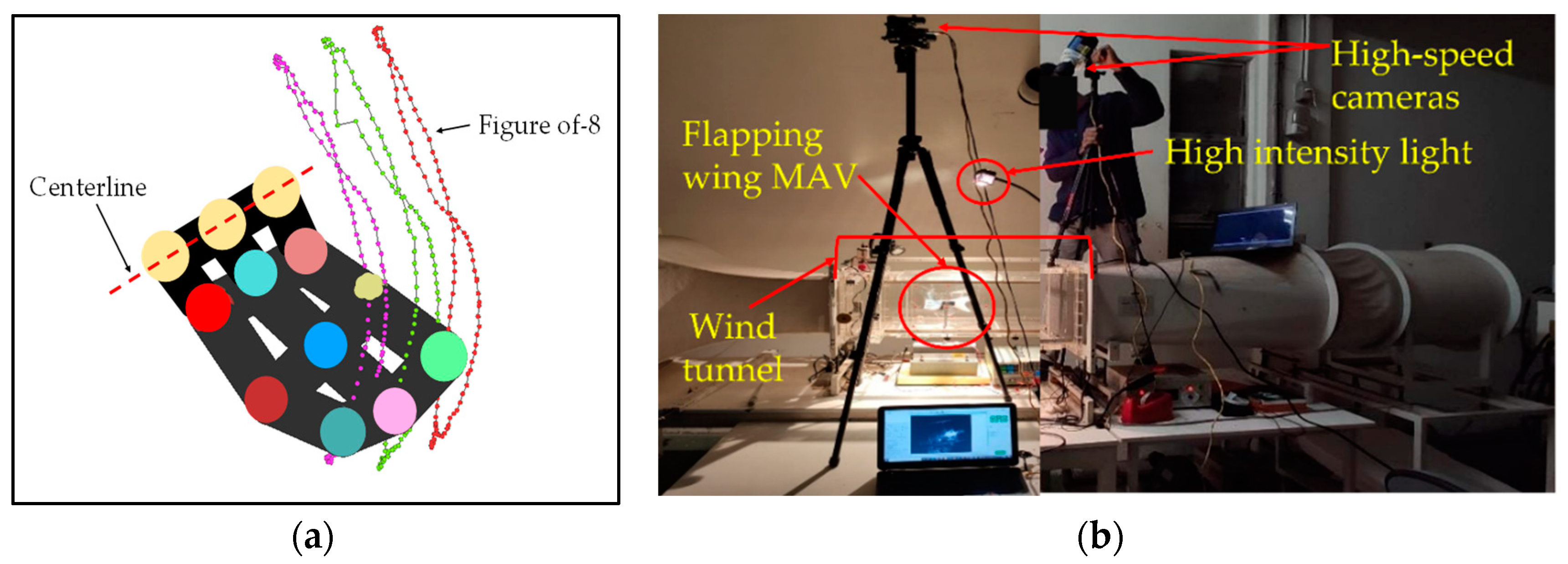
2.5. Testing Methodology
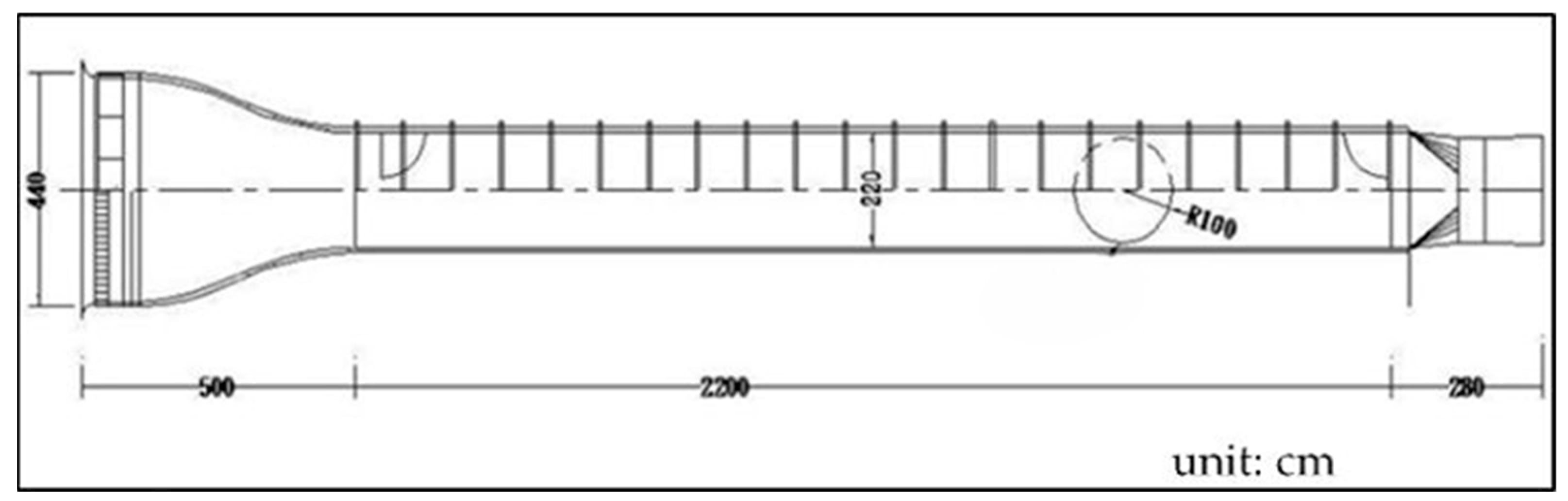
- Wind tunnel testing
- Kwon3D analysis
3. Results and Discussion
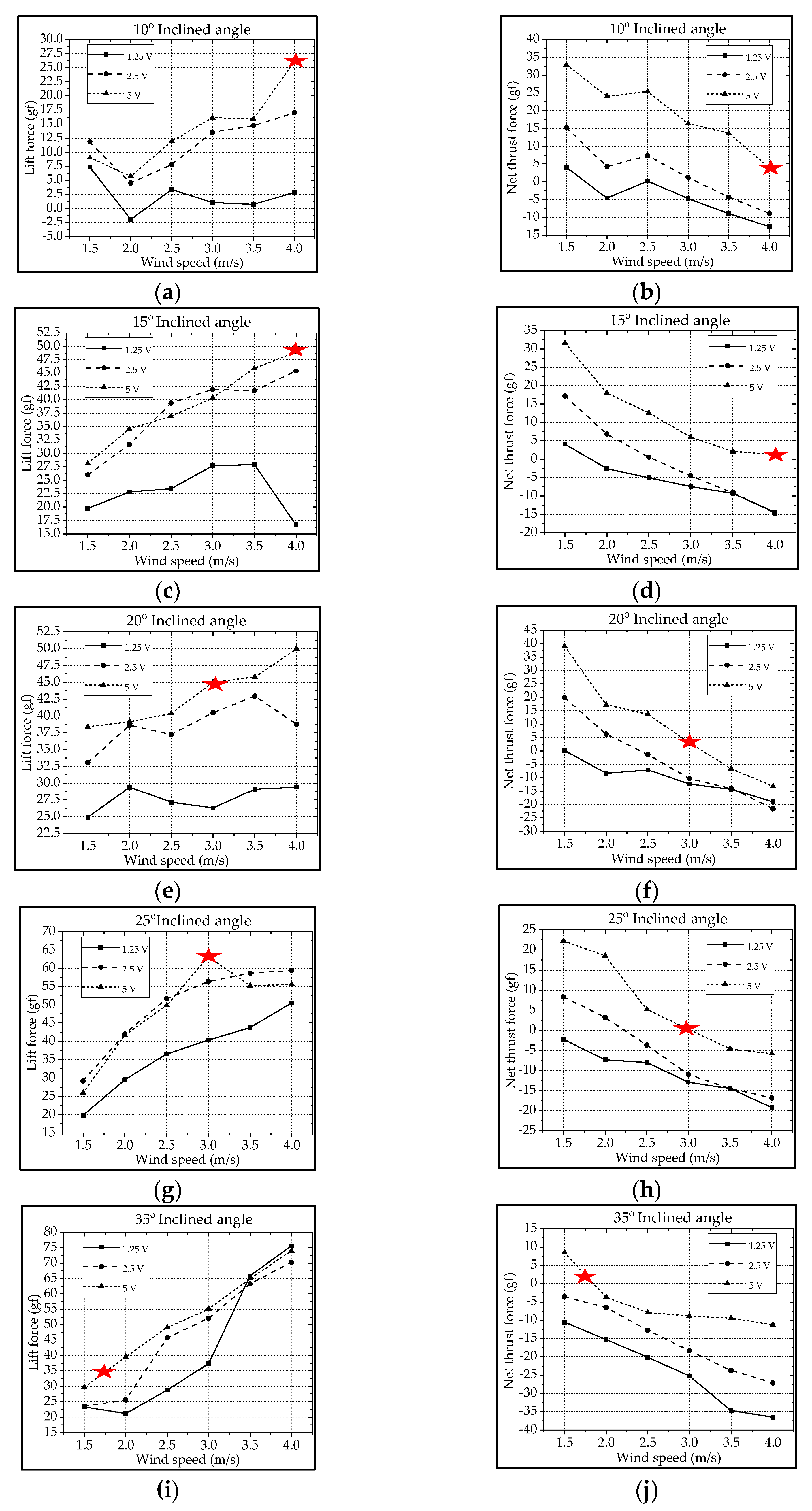
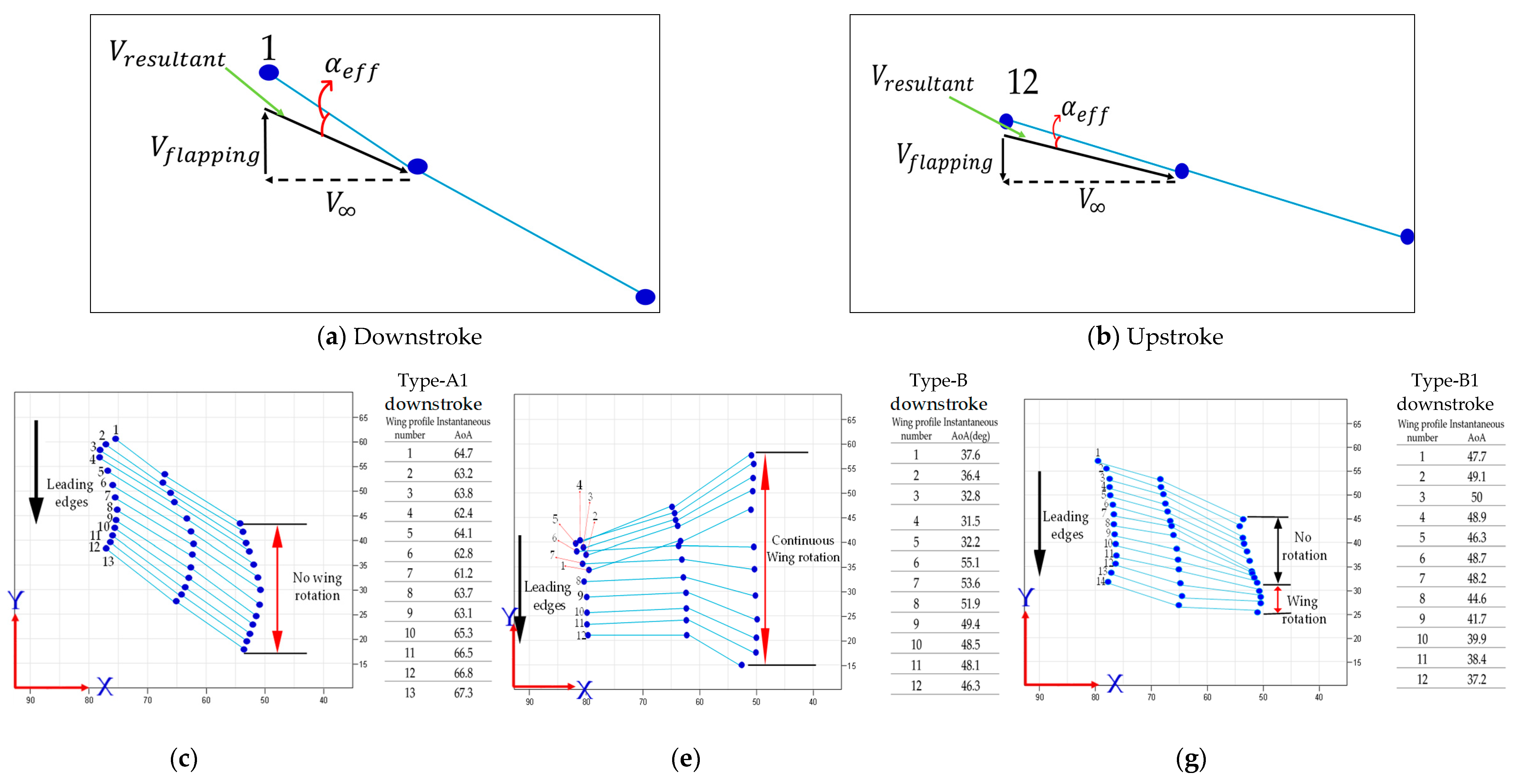
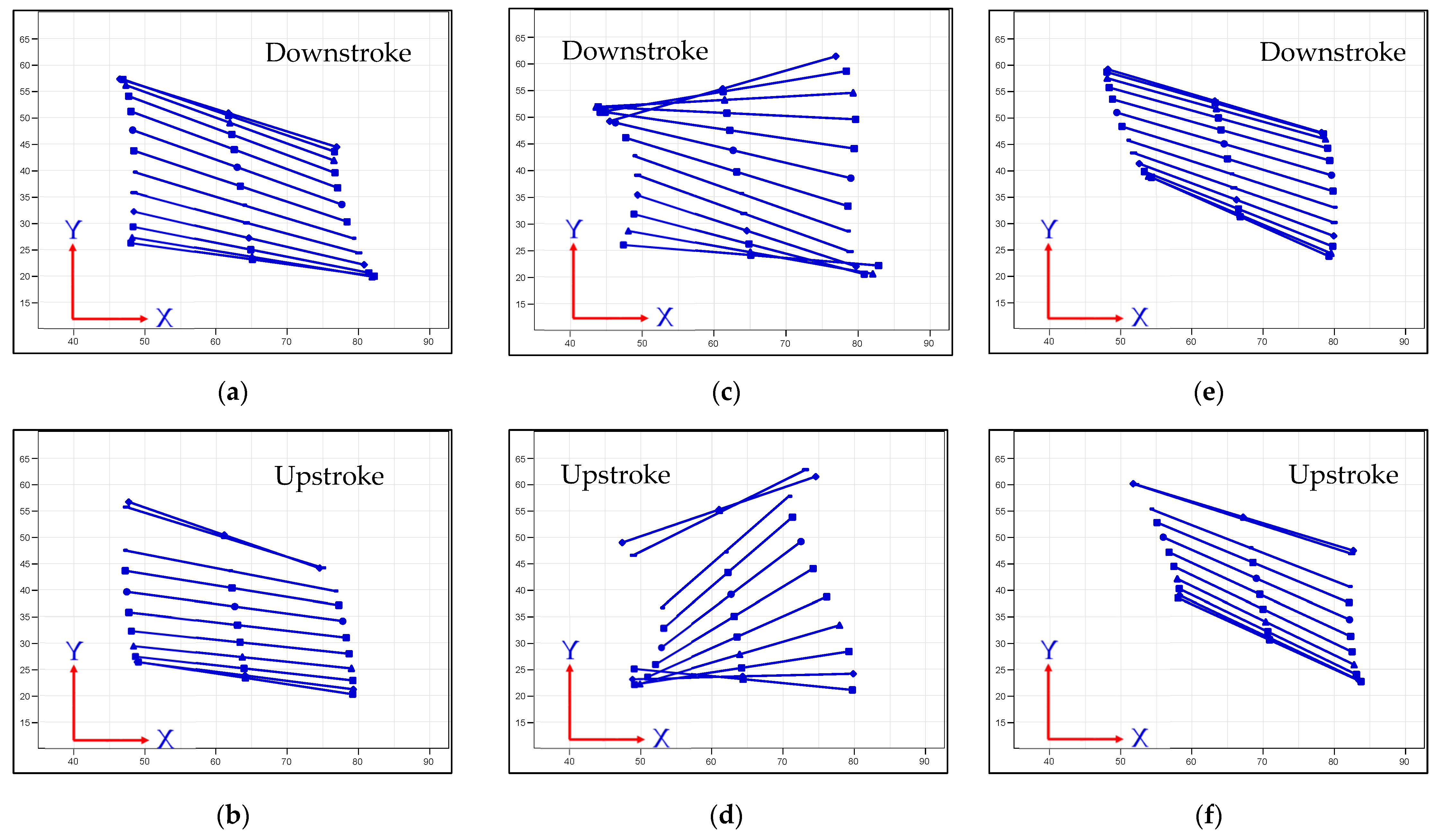
3.1. Type-A1: Normal Servo Mechanism
 ) [13,46].
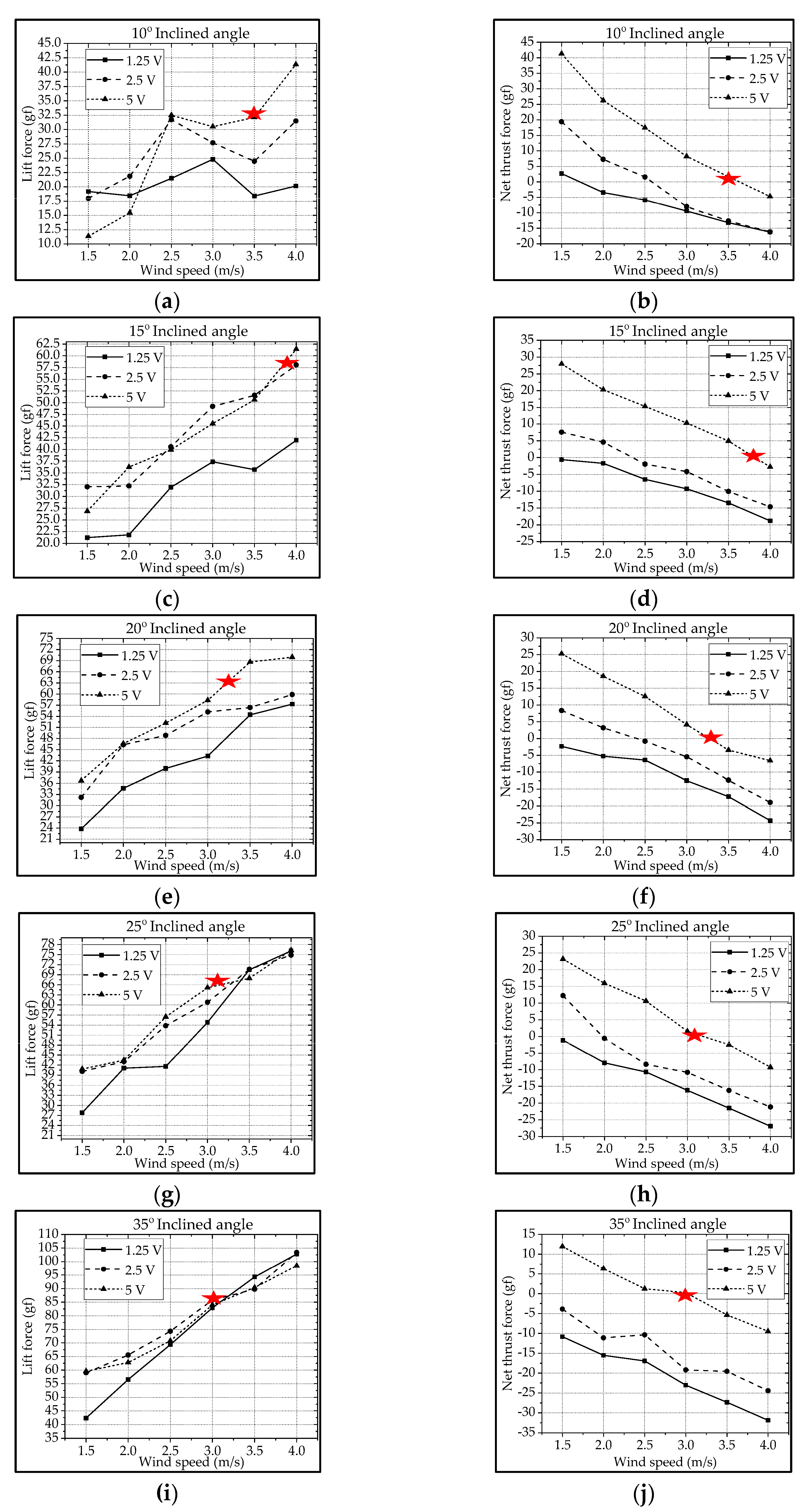
) [13,46].3.2. Type-B: Bevel Gear Mechanism
3.3. Type-B1: Bevel Gear Mechanism with Adjustable Mechanical Stopper
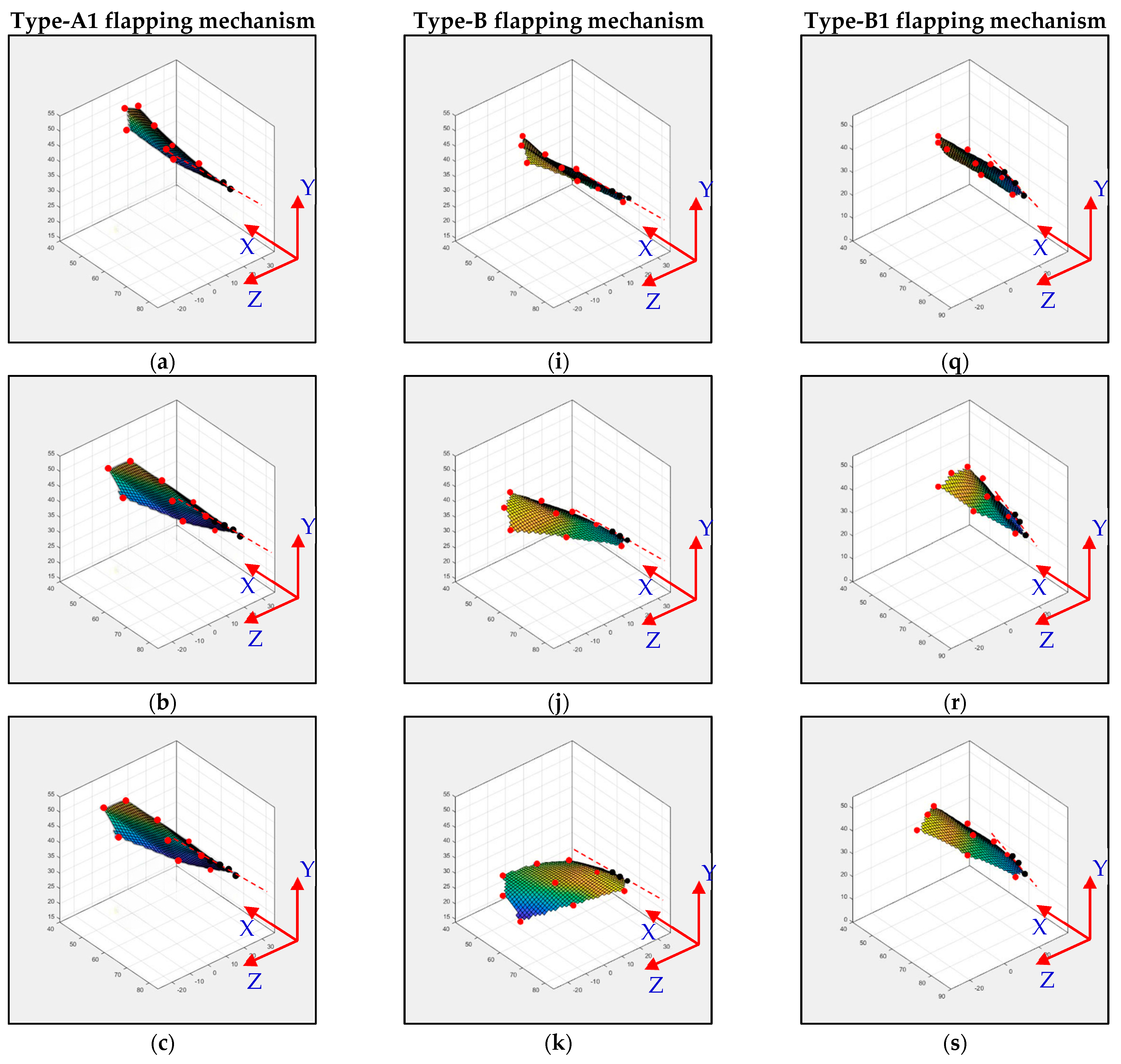
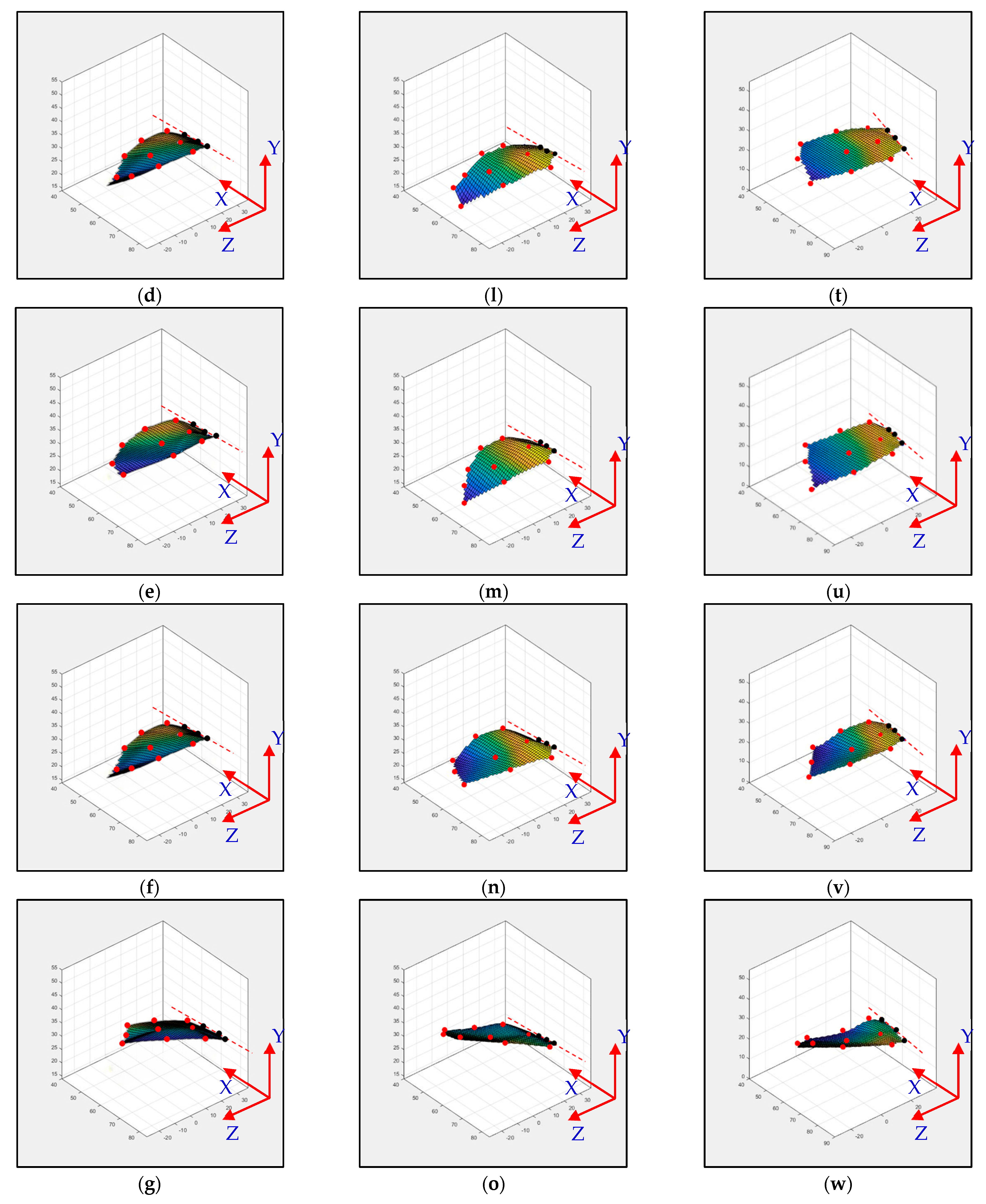
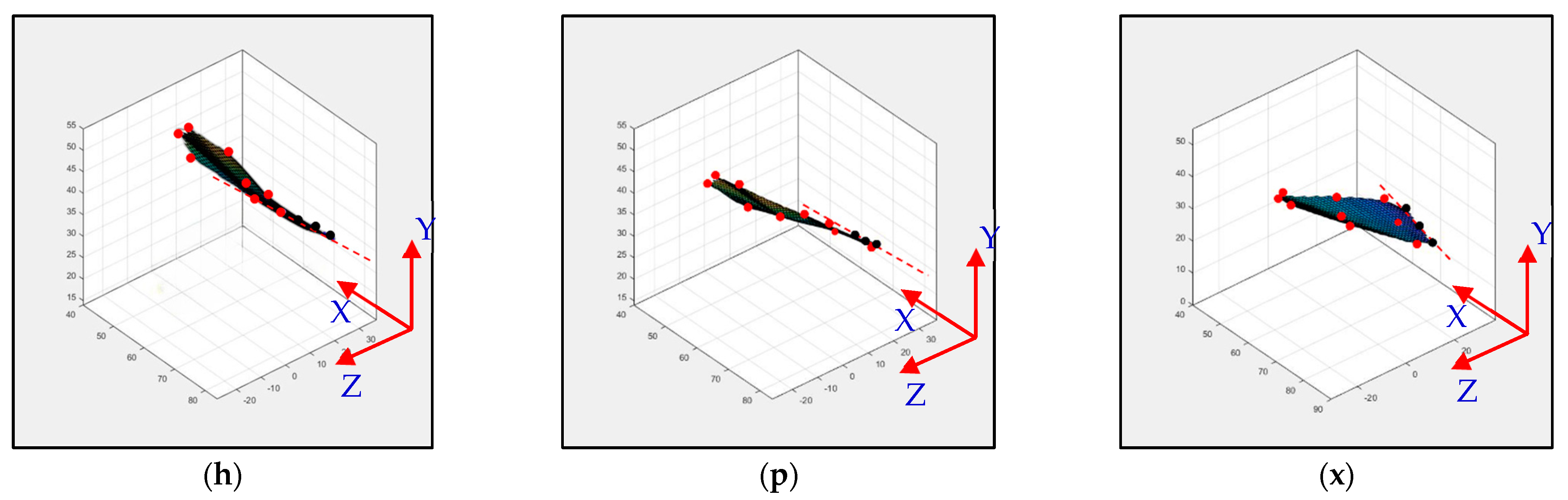
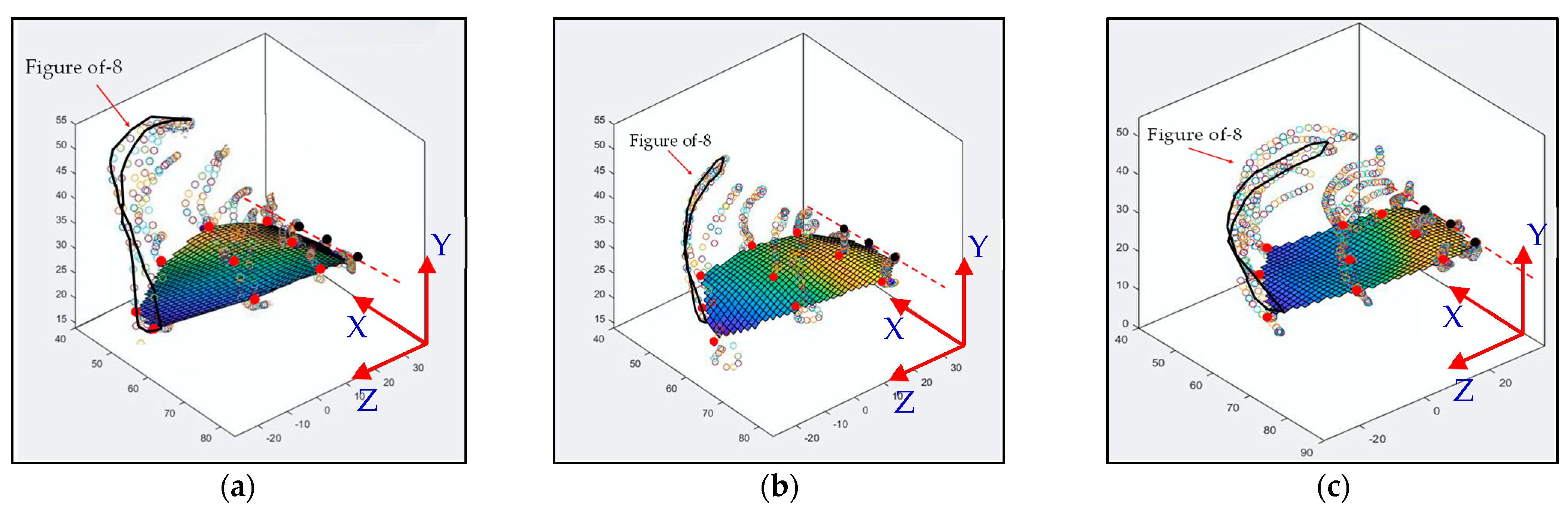
3.4. Flapping Trajectory of Rigid-Body Model Fitting to the Kwon3D/MATLAB Visual Motion Data
4. Conclusions
5. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dickinson, M.H. Unsteady mechanisms of force generation in aquatic and aerial locomotion. Am. Zool. 1996, 36, 537–554. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.-O.; Sane, S.P. Leading-edge twisting and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef]
- Maxworthy, T. Fluid dynamics of insect flight. Annu. Rev. Fluid Mech. 1981, 13, 329–350. [Google Scholar] [CrossRef]
- Van Den Berg, C.; Ellington, C.P. The vortex wake of a hovering model hawkmoth. Philos. Trans. R. Soc. London. Ser. B Biol. Sci. 1997, 352, 317–328. [Google Scholar] [CrossRef] [Green Version]
- Ellington, C.P.; Van Den Berg, C.; Willmott, A.P.; Thomas, A.L. Leading-edge vortices in insect flight. Nature 1996, 384, 626–630. [Google Scholar] [CrossRef]
- Kompala, S. Leading-edge twisting Mechanisms Using Bevel Gears for Ornithopters. Master’s Thesis, Tamkang University, Department of Mechanical and Electro-Mechanical Engineering, Taipei City, Taiwan, 2020. [Google Scholar]
- Singh, S.; Zuber, M.; Hamidon, M.N.; Mazlan, N.; Basri, A.A.; Ahmad, K.A. Classification of actuation mechanism designs with structural block diagrams for flapping-wing drones: A comprehensive review. Prog. Aerosp. Sci. 2022, 132, 100833. [Google Scholar] [CrossRef]
- George, R.B.; Colton, M.B.; Mattson, C.A.; Thomson, S.L. A differentially driven flapping wing mechanism for force analysis and trajectory optimization. Int. J. Micro Air Veh. 2012, 4, 31–49. [Google Scholar] [CrossRef]
- Yang, L.-J. The micro-air-vehicle Golden Snitch and its figure-of-8 flapping. J. Appl. Sci. Eng. 2012, 15, 197–212. [Google Scholar]
- Yang, L.-J.; Hsiao, F.-Y.; Tang, W.-T.; Huang, I.-C. 3D flapping trajectory of a micro-air-vehicle and its application to unsteady flow simulation. Int. J. Adv. Robot. Syst. 2013, 10, 264. [Google Scholar] [CrossRef]
- Yang, L.-J.; Kao, A.-F.; Hsu, C.-K. Wing stiffness on light flapping micro aerial vehicles. J. Aircr. 2012, 49, 423–431. [Google Scholar] [CrossRef]
- Yang, L.-J.; Esakki, B.; Chandrasekhar, U.; Hung, K.-C.; Cheng, C.-M. Practical flapping mechanisms for 20 cm-span micro air vehicles. Int. J. Micro Air Veh. 2015, 7, 181–202. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.-J.; Esakki, B. Flapping Wing Vehicles: Numerical and Experimental Approach; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Yan, J.; Wood, R.J.; Avadhanula, S.; Sitti, M.; Fearing, R.S. Towards flapping wing control for a micromechanical flying insect. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; pp. 3901–3908. [Google Scholar]
- Avadhanula, S.; Wood, R.J.; Steltz, E.; Yan, J.; Fearing, R.S. Lift force improvements for the micromechanical flying insect. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), Las Vegas, NV, USA, 27–31 October 2003; pp. 1350–1356. [Google Scholar]
- Lai, W.; Yan, J.; Motamed, M.; Green, S. Force measurements on a scaled mechanical model of dragonfly in forward flight. In Proceedings of the 12th International Conference on Advanced Robotics (ICAR’05), Virtual, 18–20 July 2005; pp. 595–600. [Google Scholar]
- Z˙bikowski, R.; Galin´ ski, C.; Pedersen, C.B. Four-bar linkage mechanism for insectlike flapping wings in hover: Concept and an outline of its realization. J. Mech. Des. 2005, 127, 817–824. [Google Scholar] [CrossRef]
- Finio, B.M.; Eum, B.; Oland, C.; Wood, R.J. Asymmetric flapping for a robotic fly using a hybrid power-control actuator. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 2755–2762. [Google Scholar]
- Tanaka, H.; Hoshino, K.; Matsumoto, K.; Shimoyama, I. Flight dynamics of a butterfly-type ornithopter. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 2706–2711. [Google Scholar]
- Banala, S.K.; Agrawal, S.K. Design and optimization of a mechanism for out-of-plane insect winglike motion with twist. J. Mech. Des. 2005, 127, 841–844. [Google Scholar] [CrossRef]
- Syaifuddin, M.; Park, H.C.; Goo, N.S. Design and evaluation of a LIPCA-actuated flapping device. Smart Mater. Struct. 2006, 15, 1225–1230. [Google Scholar]
- Isaac, K.M.; Colozza, A.; Rolwes, J. Force measurements on a flapping and pitching wing at low Reynolds numbers. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 450. [Google Scholar]
- Han, J.-s.; Chang, J.-W.; Kang, I.-M.; Kim, S.-T. Flow visualization and force measurement of an insect-based flapping wing. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 66. [Google Scholar]
- Fujikawa, T.; Hirakawa, K.; Sato, Y.; Makata, Y.; Kikuchi, K. Motion analysis of small flapping robot for various design and control parameters. In Proceedings of the 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 15–28 December 2007; pp. 13–18. [Google Scholar]
- Madangopal, R.; Khan, Z.A.; Agrawal, S.K. Energetics-based design of small flapping-wing micro air vehicles. IEEE/ASME Trans. Mechatron. 2006, 11, 433–438. [Google Scholar] [CrossRef]
- DiLeo, C.; Deng, X. Experimental testbed and prototype development for a dragonfly-inspired robot. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1594–1599. [Google Scholar]
- Fenelon, M.A.; Furukawa, T. Design of an active flapping wing mechanism and a micro aerial vehicle using a rotary actuator. Mech. Mach. Theory 2010, 45, 137–146. [Google Scholar] [CrossRef]
- Wang, P.L.; Michael McCarthy, J. Design of a flapping wing mechanism to coordinate both wing swing and wing pitch. J. Mech. Robot. 2018, 10, 025003. [Google Scholar] [CrossRef] [Green Version]
- Wu, P.; S¨ allstr¨ om, E.; Bou, J.; Ukeiley, L.; Ifju, P. Active rotation and vibration during the flapping stroke of a micro elastic wing for thrust production. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 12–15 April 2010; p. 2885. [Google Scholar]
- Balta, M.; Ahmed, K.A.; Wang, P.L.; McCarthy, J.M.; Taha, H.E. Design and manufacturing of flapping wing mechanisms for micro air vehicles. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017; p. 0509. [Google Scholar]
- Moses, K.C.; Prigg, D.; Weisfeld, M.; Bachmann, R.J.; Willis, M.; Quinn, R.D. Simulating flapping wing mechanisms inspired by the Manduca sexta hawkmoth. In Proceedings of the Conference on Biomimetic and Biohybrid Systems, Paris, France, 17–20 July 2018; pp. 326–337. [Google Scholar]
- Jeon, J.; Cho, H.; Kim, Y.; Lee, J.; Gong, D.; Shin, S.; Kim, C. Design and analysis of the link mechanism for the flapping wing MAV using flexible multi-body dynamic analysis. Int. J. Micro Air Veh. 2017, 9, 253–269. [Google Scholar] [CrossRef]
- Jang, J.H.; Yang, G.-H. Design of wing root rotation mechanism for dragonfly-inspired micro air vehicle. Appl. Sci. 2018, 8, 1868. [Google Scholar] [CrossRef] [Green Version]
- Conn, A.; Burgess, S.; Ling, C. Design of a parallel crank-rocker flapping mechanism for insect-inspired micro air vehicles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 1211–1222. [Google Scholar] [CrossRef]
- Khatait, J.; Mukherjee, S.; Seth, B. Compliant design for flapping mechanism: A minimum torque approach. Mech. Mach. Theory 2006, 41, 3–16. [Google Scholar] [CrossRef]
- Wood, R.J. Design, fabrication, and analysis of a 3DOF, 3cm flapping-wing MAV. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1576–1581. [Google Scholar]
- Hubel, T.Y.; Tropea, C. Experimental investigation of a flapping wing model. In Animal Locomotion; Springer: Berlin/Heidelberg, Germany, 2010; pp. 383–399. [Google Scholar]
- Park, J.-H.; Yang, E.P.; Zhang, C.; Agrawal, S.K. Kinematic design of an asymmetric in-phase flapping mechanism for MAVs. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 5099–5104. [Google Scholar]
- Teoh, Z.E.; Wood, R.J. A flapping-wing microrobot with a differential angle-of-attack mechanism. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 1381–1388. [Google Scholar]
- Yang, W.; Wang, L.; Song, B. Dove: A biomimetic flapping-wing micro air vehicle. Int. J. Micro Air Veh. 2018, 10, 70–84. [Google Scholar] [CrossRef] [Green Version]
- Panchal, N. Wing Rotation Effect on an Ornithopter Using Servo Control. Master Thesis, Tamkang University, Department of Mechanical and Electro-Mechanical Engineering, Taipei City, Taiwan, 2019. [Google Scholar]
- Lim, I.-S.; Kwon, O.; Park, J.H. Gait optimization of biped robots based on human motion analysis. Robot. Auton. Syst. 2014, 62, 229–240. [Google Scholar] [CrossRef]
- Lim, B.-O.; Lee, Y.S.; Kim, J.G.; An, K.O.; Yoo, J.; Kwon, Y.H. Effects of sports injury prevention training on the biomechanical risk factors of anterior cruciate ligament injury in high school female basketball players. Am. J. Sport. Med. 2009, 37, 1728–1734. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.-T.; Zhang, W.-Y.; Huang, C.-C.; Young, M.-S.; Hwang, I.-S. Postural tremor and control of the upper limb in air pistol shooters. J. Sport. Sci. 2008, 26, 1579–1587. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.-T.; Liao, W.-C.; Lee, H.-M. Contribution of upper limb muscles to two different gripping styles in elite indoor tug of war athletes. Sport. Biomech. 2018, 17, 322–335. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.-J.; Waikhom, R.; Wang, W.-C.; Jabaraj Joseph, V.; Esakki, B.; Kumar Unnam, N.; Li, X.-H.; Lee, C.-Y. Check-valve design in enhancing aerodynamic performance of flapping wings. Appl. Sci. 2021, 11, 3416. [Google Scholar] [CrossRef]
- Chuang, S.-W.; Lih, F.-L.; Miao, J.-M. Effects of Reynolds number and inclined angle of stroke plane on aerodynamic characteristics of flapping corrugated airfoil. J. Appl. Sci. Eng. 2012, 15, 247–256. [Google Scholar]
- Yang, L.-J.; Huang, H.-L.; Liou, J.-C.; Esakki, B.; Chandrasekhar, U. 2D quasi-steady flow simulation of an actual flapping wing. J. Unmanned Syst. Technol. 2014, 2, 10–16. [Google Scholar]









| Parameters | Metric |
|---|---|
| Length | 15 m |
| Width | 2.2 m |
| Height | 1.8 m |
| Wind speed range | 1–28 m/s |
| Lowest turbulence intensity | 0.5% |
| Inclined Angle | Flapping Frequency | Driving Voltage | Cruising Speed | Cruising Lift |
|---|---|---|---|---|
| 10° | 2.5 Hz | 5V | 4.0 m/s | 26 gf |
| 15° | 2.5 Hz | 5V | 4.0 m/s | 49 gf |
| 20° | 2.5 Hz | 5V | 3.0 m/s | 45 gf |
| 25° | 2.5 Hz | 5V | 3.0 m/s | 63.2 gf |
| 35° | 2.5 Hz | 5V | 1.7 m/s | 35 gf |
| Inclined Angle | Flapping Frequency | Driving Voltage | Cruising Speed | Cruising Lift |
|---|---|---|---|---|
| 10° | 2.5 Hz | 5V | 3.0 m/s | 28 gf |
| 15° | 2.5 Hz | 5V | 2.5 m/s | 40.3 gf |
| 20° | 2.5 Hz | 5V | 2.2 m/s | 47 gf |
| 25° | 2.5 Hz | 5V | 1.6 m/s | 45.5 gf |
| 35° | 2.5 Hz | 5V | 1.5 m/s | 51.1 gf |
| Inclined Angle | Flapping Frequency | Driving Voltage | Cruising Speed | Cruising Lift |
|---|---|---|---|---|
| 10° | 2.5 Hz | 5V | 3.6 m/s | 34 gf |
| 15° | 2.5 Hz | 5V | 3.8 m/s | 57 gf |
| 20° | 2.5 Hz | 5V | 3.25 m/s | 64 gf |
| 25° | 2.5 Hz | 5V | 3.1 m/s | 66 gf |
| 35° | 2.5 Hz | 5V | 3.0 m/s | 84 gf |
| Mechanism Type | R (mm) | Φ (deg) Stroke Angle | r (mm) | Ψ (deg) Leading-Edge Twisting Angle | |
|---|---|---|---|---|---|
| Design | Measured | ||||
| Type-A1: Servo mechanism | 14.6 | 75 | Nil | Nil | Nil |
| Type-B: Servo + bevel gear | 14.6 | 96 | 8.63 | 162 | 144 |
| Type-B1: Servo + bevel gear + stopper | 14.6 | 87 | 6.62 | 143 | 108 |
| Mechanism Type | Wake Capture | 2nd Peak Due to Delayed Stall | FSI Effect/ Figure-of-8 | Negative AOA at Stroke Reversal | |
|---|---|---|---|---|---|
| 1st Peak | 3rd Peak | ||||
| Type-A1: Servo mechanism | Medium | Medium | Medium | Medium | None |
| Type-B: Servo + bevel gear | Medium | Weak | Weak | Weak | Yes |
| Type-B1: Servo + bevel gear + stopper | Strong | Strong | Strong | Strong | None |
| Mechanism Type | Measured Stroke Angle Φ (deg) | Stroke Angle by Kwon3D Φ (deg) | Measured Leading-Edge Twisting Angle Ψ(deg) | Leading-Edge Twisting Angle by Kwon3D Ψ(deg) |
|---|---|---|---|---|
| Type-A1: Servo mechanism | 75 | 71.5 | Nil | Nil |
| Type-B: Servo + bevel gear | 96 | 92.4 (96.3%) | 144 | 134.3 (93.3%) |
| Type-B1: Servo + bevel gear + stopper | 87 | 80.6 (92.6%) | 108 | 101.8 (94.3%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.-J.; Joseph, V.J.; Lo, Y.-L.; Tang, W.-T.; Esakki, B.; Kompala, S.; Veeranjaneyulu, P. Aerodynamic Evaluation of Flapping Wings with Leading-Edge Twisting. Biomimetics 2023, 8, 134. https://doi.org/10.3390/biomimetics8020134
Yang L-J, Joseph VJ, Lo Y-L, Tang W-T, Esakki B, Kompala S, Veeranjaneyulu P. Aerodynamic Evaluation of Flapping Wings with Leading-Edge Twisting. Biomimetics. 2023; 8(2):134. https://doi.org/10.3390/biomimetics8020134
Chicago/Turabian StyleYang, Lung-Jieh, Vivek Jabaraj Joseph, Yuan-Lung Lo, Wen-Tzu Tang, Balasubramanian Esakki, Saravana Kompala, and Paritala Veeranjaneyulu. 2023. "Aerodynamic Evaluation of Flapping Wings with Leading-Edge Twisting" Biomimetics 8, no. 2: 134. https://doi.org/10.3390/biomimetics8020134
APA StyleYang, L.-J., Joseph, V. J., Lo, Y.-L., Tang, W.-T., Esakki, B., Kompala, S., & Veeranjaneyulu, P. (2023). Aerodynamic Evaluation of Flapping Wings with Leading-Edge Twisting. Biomimetics, 8(2), 134. https://doi.org/10.3390/biomimetics8020134






