Continuum Robots: From Conventional to Customized Performance Indicators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Defining Requirements
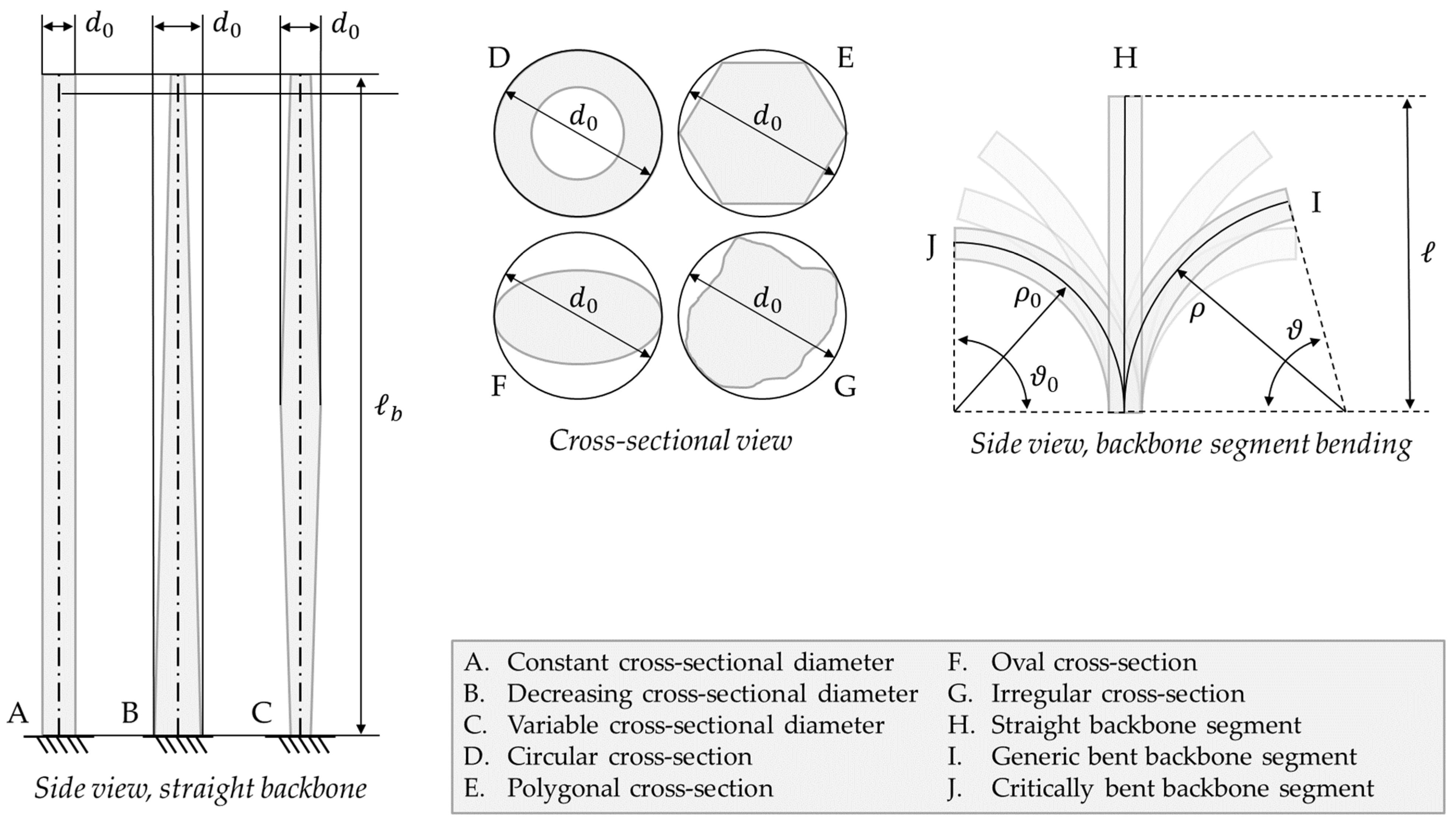
- The distance from the entrance or access port * (i.e., the insertion point of the continuum robot) to the desired workspace determines the appropriate length of the backbone of the continuum robot. This dimension must take into account the curvature of the shortest path that the robot can access, plus collision risks and other constraints.
- The cross-section of the robot must fit the narrowest passage along the navigation path. As such, for a circular cross-section, the external diameter must be smaller than the width of the strictest choke point in the path. In the case of non-circular cross-sections, the diameter of the circle circumscribed to the outer edge can be used instead as a conservative estimation.
- The geometry of the sharpest bend along the navigation path defines the minimum bending radius that the backbone must achieve.
- Local parameters. Whereas backbone length is a fixed parameter, diameter and bending radius are local variables that can have different values at different backbone lengths; payload is similarly evaluated at the tip but does not properly characterize the behavior of different backbone segments.
- Absolute metrics. The proposed specifications are not suited to compare different continuum robot designs. When evaluating the form factor of a continuum robot, we favor a smaller diameter and bending radius, and a longer backbone. Absolute values, however, can complicate comparison of designs at different scales. For example, is a smaller but shorter continuum robot with a 10 mm diameter and bending radius and a 50 mm length better than a larger but longer one with 20 mm diameter and bending radius, but 1000 mm length?
2.2. Slenderness
2.3. Flexibility
2.4. Stiffness
2.5. Remarks
3. Results and Discussion
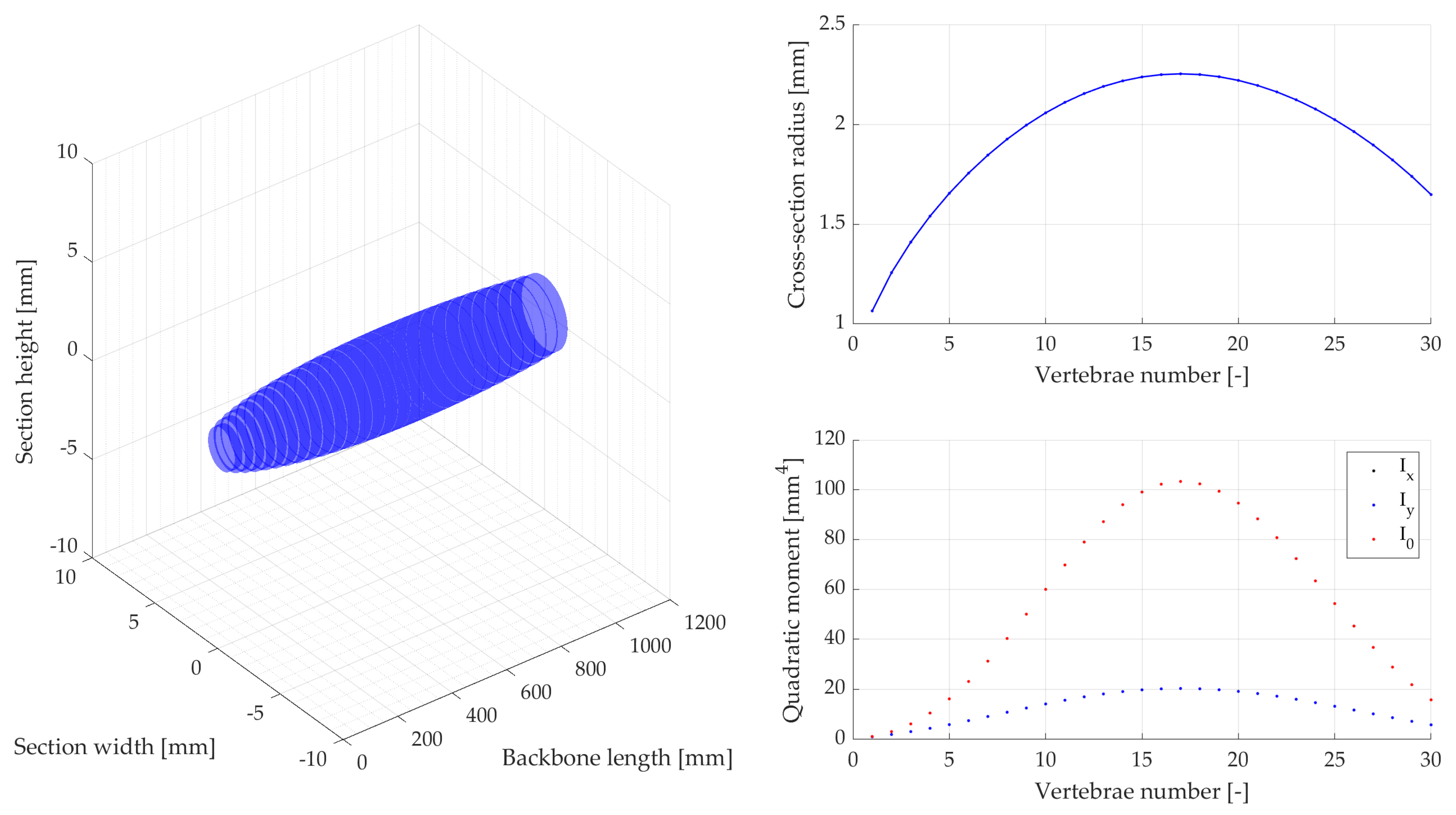
3.1. Performance Metrics as Design Tools: A Bioinspired Example
3.2. Performance Metrics for Design Evaluation: Comparing Existing Continuum Robots
4. Conclusions
- Slenderness, defined as the ratio between the length of the backbone of the robot and the maximum cross-section diameter.
- Flexibility, defined as the ratio between the length of the backbone of the robot and the minimum bending radius of the backbone.
- Stiffness, defined as the ratio between an applied load at the tip of a backbone segment and the corresponding deflection.
- The design requirements for continuum robots were discussed with respect to their operational environment and task.
- Tailored metrics for continuum robots were defined to describe their shape factor (slenderness), motion range (flexibility), and dynamic behavior (stiffness).
- A numerical example of bioinspired design has been reported as an example of the proposed metrics as design tools.
- A review of a wide variety of designs further extends the usefulness of the proposed metrics to compare different systems at different scales.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Backbone Stiffness
| Segment | Stiffness | Segment | Stiffness | Segment | Stiffness | Segment | Stiffness | Segment | Stiffness |
|---|---|---|---|---|---|---|---|---|---|
| i [-] | [N/mm] | i [-] | [N/mm] | i [-] | [N/mm] | i [-] | [N/mm] | i [-] | [N/mm] |
| 1 | 0.0697 | 7 | 0.6302 | 13 | 1.2498 | 19 | 1.3640 | 25 | 0.9105 |
| 2 | 0.1352 | 8 | 0.7468 | 14 | 1.3140 | 20 | 1.3200 | 26 | 0.8069 |
| 3 | 0.2142 | 9 | 0.8624 | 15 | 1.3611 | 21 | 1.2605 | 27 | 0.7019 |
| 4 | 0.3052 | 10 | 0.9735 | 16 | 1.3899 | 22 | 1.1875 | 28 | 0.5977 |
| 5 | 0.4065 | 11 | 1.0771 | 17 | 1.3998 | 23 | 1.1033 | 29 | 0.4965 |
| 6 | 0.5158 | 12 | 1.1701 | 18 | 1.3910 | 24 | 1.0101 | 30 | 0.4002 |
References
- Walker, I.D.; Choset, H.; Chirikjian, G.S. Snake-like and continuum robots. In Springer Handbook of Robotics; Springer: Cham, Switzerland, 2016; pp. 481–498. [Google Scholar]
- Russo, M.; Sadati, S.M.H.; Dong, X.; Mohammad, A.; Walker, I.D.; Bergeles, C.; Xu, K.; Axinte, D.A. Continuum Robots: An Overview. Adv. Intell. Syst. 2023, 2200367. [Google Scholar] [CrossRef]
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abil-ities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Wang, M.; Mohammad, A.; Ba, W.; Russo, M.; Norton, A.; Kell, J.; Axinte, D. Continuum Robots Collaborate for Safe Manipulation of High-Temperature Flame to Enable Repairs in Challenging Environments. IEEE/ASME Trans. Mechatron. 2022, 27, 4217–4220. [Google Scholar] [CrossRef]
- Troncoso, D.A.; Robles-Linares, J.A.; Russo, M.; Elbanna, M.A.; Wild, S.; Dong, X.; Mohammad, A.; Kell, J.; Norton, A.D.; Axinte, D. A Continuum Robot for Remote Applications: From Industrial to Medical Surgery With Slender Continuum Robots. IEEE Robot. Autom. Mag. 2022, 2–13. [Google Scholar] [CrossRef]
- Burgner-Kahrs, J.; Rucker, D.C.; Choset, H. Continuum Robots for Medical Applications: A Survey. IEEE Trans. Robot. 2015, 31, 1261–1280. [Google Scholar] [CrossRef]
- Dupont, P.E.; Simaan, N.; Choset, H.; Rucker, C. Continuum Robots for Medical Interventions. Proc. IEEE 2022, 110, 847–870. [Google Scholar] [CrossRef]
- Walker, I.D. Continuous backbone “continuum” robot manipulators. Int. Sch. Res. Not. 2013, 2013, 726506. [Google Scholar] [CrossRef]
- Amanov, E.; Nguyen, T.D.; Burgner-Kahrs, J. Tendon-driven continuum robots with extensible sections—A model-based evaluation of path-following motions. Int. J. Robot. Res. 2021, 40, 7–23. [Google Scholar] [CrossRef]
- Kim, Y.; Cheng, S.S.; Diakite, M.; Gullapalli, R.P.; Simard, J.M.; Desai, J.P. Toward the Development of a Flexible Mesoscale MRI-Compatible Neurosurgical Continuum Robot. IEEE Trans. Robot. 2017, 33, 1386–1397. [Google Scholar] [CrossRef]
- Li, M.; Kang, R.; Geng, S.; Guglielmino, E. Design and control of a tendon-driven continuum robot. Trans. Inst. Meas. Control. 2018, 40, 3263–3272. [Google Scholar] [CrossRef]
- Bishop, C.; Russo, M.; Dong, X.; Axinte, D. A Novel Underactuated Continuum Robot with Shape Memory Alloy Clutches. IEEE/ASME Trans. Mechatron. 2022, 27, 5339–5350. [Google Scholar] [CrossRef]
- Mahoney, A.W.; Gilbert, H.B.; Webster, R.J., III. A review of concentric tube robots: Modeling, control, design, planning, and sensing. In The Encyclopedia of Medical Robotics: Volume 1 Minimally Invasive Surgical Robotics; World Scientific: Singapore, 2019; pp. 181–202. [Google Scholar]
- Mitros, Z.; Sadati, S.H.; Henry, R.; Da Cruz, L.; Bergeles, C. From Theoretical Work to Clinical Translation: Progress in Concentric Tube Robots. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 335–359. [Google Scholar] [CrossRef]
- Murphy, R.J.; Kutzer, M.D.M.; Segreti, S.M.; Lucas, B.C.; Armand, M. Design and kinematic characterization of a surgical manipulator with a focus on treating osteolysis. Robotica 2013, 32, 835–850. [Google Scholar] [CrossRef]
- Hawkes, E.W.; Blumenschein, L.H.; Greer, J.D.; Okamura, A.M. A soft robot that navigates its environment through growth. Sci. Robot. 2017, 2, aan3028. [Google Scholar] [CrossRef] [PubMed]
- Talas, S.K.; Baydere, B.A.; Altinsoy, T.; Tutcu, C.; Samur, E. Design and Development of a Growing Pneumatic Soft Robot. Soft Robot. 2020, 7, 521–533. [Google Scholar] [CrossRef]
- Grazioso, S.; Tedesco, A.; Sabella, R.; Fusco, S.; Selvaggio, M.; Duraccio, L.; De Benedetto, E.; Lanzotti, A.; Dallet, D.; Angrisani, L. Soft Growing Robot to Enable Monitoring Applications in Remote Constrained Environments. In Proceedings of the 2022 6th International Symposium on Instrumentation Systems, Circuits and Transducers (INSCIT), Porto Alegre, Brazil, 22–26 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Laribi, M.A.; Carbone, G.; Zeghloul, S. Robot Design: Optimization Methods and Task-Based Design. In Robot Design; Springer: Cham, Switzerland, 2023; pp. 97–115. [Google Scholar]
- Russo, M. Measuring Performance: Metrics for Manipulator Design, Control, and Optimization. Robotics 2022, 12, 4. [Google Scholar] [CrossRef]
- Rao, P.; Peyron, Q.; Lilge, S.; Burgner-Kahrs, J. How to Model Tendon-Driven Continuum Robots and Benchmark Modelling Performance. Front. Robot. AI 2021, 7, 630245. [Google Scholar] [CrossRef]
- Russo, M.; Raimondi, L.; Dong, X.; Axinte, D.; Kell, J. Task-oriented optimal dimensional synthesis of robotic manip-ulators with limited mobility. Robot. Comput. Integr. Manuf. 2021, 69, 102096. [Google Scholar] [CrossRef]
- Campisano, F.; Caló, S.; Remirez, A.A.; Chandler, J.H.; Obstein, K.L.; Webster III, R.J.; Valdastri, P. Closed-loop control of soft continuum manipulators under tip follower actuation. Int. J. Robot. Res. 2021, 40, 923–938. [Google Scholar] [CrossRef]
- Mohammad, A.; Russo, M.; Fang, Y.; Dong, X.; Axinte, D.; Kell, J. An Efficient Follow-the-Leader Strategy for Continuum Robot Navigation and Coiling. IEEE Robot. Autom. Lett. 2021, 6, 7493–7500. [Google Scholar] [CrossRef]
- Shi, C.; Luo, X.; Qi, P.; Li, T.; Song, S.; Najdovski, Z.; Fukuda, T.; Ren, H. Shape Sensing Techniques for Continuum Robots in Minimally Invasive Surgery: A Survey. IEEE Trans. Biomed. Eng. 2016, 64, 1665–1678. [Google Scholar] [CrossRef] [PubMed]
- Gao, A.; Liu, H.; Zhou, Y.; Yang, Z.; Wang, Z.; Li, H. A cross-helical tendons actuated dexterous continuum manipulator. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September 2015–2 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2012–2017. [Google Scholar]
- Russo, M.; Sriratanasak, N.; Ba, W.; Dong, X.; Mohammad, A.; Axinte, D. Cooperative Continuum Robots: Enhancing Individual Continuum Arms by Reconfiguring into a Parallel Manipulator. IEEE Robot. Autom. Lett. 2021, 7, 1558–1565. [Google Scholar] [CrossRef]
- Wu, L.; Crawford, R.; Roberts, J. Dexterity Analysis of Three 6-DOF Continuum Robots Combining Concentric Tube Mechanisms and Cable-Driven Mechanisms. IEEE Robot. Autom. Lett. 2016, 2, 514–521. [Google Scholar] [CrossRef]
- Wang, J.; Lau, H.Y.K. Dexterity Analysis based on Jacobian and Performance Optimization for Multi-segment Continuum Robots. J. Mech. Robot. 2021, 13, 061012. [Google Scholar] [CrossRef]
- Zhang, G.; Du, F.; Xue, S.; Cheng, H.; Zhang, X.; Song, R.; Li, Y. Design and Modeling of a Bio-Inspired Compound Continuum Robot for Minimally Invasive Surgery. Machines 2022, 10, 468. [Google Scholar] [CrossRef]
- Xu, K.; Simaan, N. Intrinsic Wrench Estimation and Its Performance Index for Multisegment Continuum Robots. IEEE Trans. Robot. 2010, 26, 555–561. [Google Scholar] [CrossRef]
- Zhang, H.J.; Lilge, S.; Chikhaoui, M.T.; Burgner-Kahrs, J. Cooperative Control of Dual-Arm Concentric Tube Continuum Robots. In Proceedings of the 2022 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Toronto, Canada, 25–29 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, C.; Angeles, J. Generalized transmission index and transmission quality for spatial linkages. Mech. Mach. Theory 2007, 42, 1225–1237. [Google Scholar] [CrossRef]
- Liljebäck, P.; Stavdahl, Ø.; Pettersen, K.Y.; Gravdahl, J.T. Mamba-A waterproof snake robot with tactile sensing. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 294–301. [Google Scholar]
- Romano, D.; Wahi, A.; Miraglia, M.; Stefanini, C. Development of a Novel Underactuated Robotic Fish with Magnetic Transmission System. Machines 2022, 10, 755. [Google Scholar] [CrossRef]
- Katzschmann, R.K.; DelPreto, J.; MacCurdy, R.; Rus, D. Exploration of underwater life with an acoustically controlled soft robotic fish. Sci. Robot. 2018, 3, aar3449. [Google Scholar] [CrossRef]
- Gautreau, E.; Sandoval, J.; Bonnet, X.; Arsicault, M.; Zeghloul, S.; Laribi, M.A. A new bio-inspired Hybrid Ca-ble-Driven Robot (HCDR) to design more realistic snakebots. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2134–2140. [Google Scholar]
- Zhong, Y.; Li, Z.; Du, R. A Novel Robot Fish with Wire-Driven Active Body and Compliant Tail. IEEE/ASME Trans. Mechatronics 2017, 22, 1633–1643. [Google Scholar] [CrossRef]
- Armanini, C.; Boyer, F.; Mathew, A.T.; Duriez, C.; Renda, F. Soft Robots Modeling: A Structured Overview. IEEE Trans. Robot. 2023, 1–21. [Google Scholar] [CrossRef]
- Janabi-Sharifi, F.; Jalali, A.; Walker, I.D. Cosserat Rod-Based Dynamic Modeling of Tendon-Driven Continuum Robots: A Tutorial. IEEE Access 2021, 9, 68703–68719. [Google Scholar] [CrossRef]
- Hirose, S.; Mori, M. Biologically inspired snake-like robots. In Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetics, Shenyang, China, 22–26 August 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 1–7. [Google Scholar]
- Immega, G.; Antonelli, K. The KSI tentacle manipulator. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 3, pp. 3149–3154. [Google Scholar]
- Walker, I.D.; Hannan, M.W. A novel ‘elephant’s trunk’ robot. In Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (Cat. No. 99TH8399), Atlanta, GA, USA, 19–23 September 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 410–415. [Google Scholar]
- Gautreau, E.; Sandoval, J.; Arsicault, M.; Bonnet, X.; Zeghloul, S.; Laribi, M.A. Kinematic Modelling of a Bioinspired Two Sections Serial Continuum Robot (SCR). In Proceedings of the International Conference on Robotics in Alpe-Adria Danube Region, Klagenfurt, Austria, 8–10 June 2022; Springer: Cham, Switzerland, 2022; pp. 247–255. [Google Scholar] [CrossRef]
- Jiang, Z.; Luo, Y.; Jin, Y. New cable-driven continuun robot with only one actuator. In Proceedings of the 2017 IEEE Interna-tional Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Ningbo, China, 19–21 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 693–698. [Google Scholar]
- Nguyen, P.L.; Do, V.P.; Lee, B.R. Dynamic Modeling of a Non-Uniform Flexible Tail for a Robotic Fish. J. Bionic Eng. 2013, 10, 201–209. [Google Scholar] [CrossRef]
- Gautreau, E.; Bonnet, X.; Fox, T.; Fosseries, G.; Valle, V.; Herrel, A.; Laribi, M.A. Complementary Methods to Acquire the Kinematics of Swimming Snakes: A Basis to Design Bio-inspired Robots. J. Bionic Eng. 2022, 20, 668–682. [Google Scholar] [CrossRef]
- Gautreau, E.; Bonnet, X.; Sandoval, J.; Fosseries, G.; Herrel, A.; Arsicault, M.; Zeghloul, S.; Laribi, M.A. A Biomimetic Method to Replicate the Natural Fluid Movements of Swimming Snakes to Design Aquatic Robots. Biomimetics 2022, 7, 223. [Google Scholar] [CrossRef]
- Vázquez-Leal, H.; Khan, Y.; Herrera-May, A.L.; Filobello-Nino, U.; Sarmiento-Reyes, A.; Jiménez-Fernández, V.M.; Pereyra-Díaz, D.; Perez-Sesma, A.; Castaneda-Sheissa, R.; Díaz-Sanchez, A.; et al. Approximations for Large Deflection of a Cantilever Beam under a Terminal Follower Force and Nonlinear Pendulum. Math. Probl. Eng. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Cianchetti, M.; Ranzani, T.; Gerboni, G.; Nanayakkara, T.; Althoefer, K.; Dasgupta, P.; Menciassi, A. Soft robotics technologies to address shortcomings in today’s minimally invasive surgery: The STIFF-FLOP approach. Soft Robot. 2014, 1, 122–131. [Google Scholar] [CrossRef]
- Kang, R.; Guo, Y.; Chen, L.; Branson, D.T.; Dai, J.S. Design of a pneumatic muscle based continuum robot with em-bedded tendons. IEEE/ASME Trans. Mechatron. 2016, 22, 751–761. [Google Scholar] [CrossRef]
- Elena, G. Novel design of a soft lightweight pneumatic continuum robot arm with decoupled variable stiffness and positioning. Soft Robot. 2018, 5, 54–70. [Google Scholar]
- Carmichael, H.; D’Andrea, A.P.; Skancke, M.; Obias, V.; Sylla, P. Feasibility of transanal total mesorectal excision (taTME) using the Medrobotics Flex® System. Surg. Endosc. 2019, 34, 485–491. [Google Scholar] [CrossRef]
- Berthet-Rayne, P.; Gras, G.; Leibrandt, K.; Wisanuvej, P.; Schmitz, A.; Seneci, C.A.; Yang, G.-Z. The i2Snake Robotic Platform for Endoscopic Surgery. Ann. Biomed. Eng. 2018, 46, 1663–1675. [Google Scholar] [CrossRef] [PubMed]
- Degani, A.; Choset, H.; Wolf, A.; Ota, T.; Zenati, M.A. Percutaneous intrapericardial interventions using a highly articulated robotic probe. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, BioRob 2006, Pisa, Italy, 20–22 February 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 7–12. [Google Scholar]
- Ding, J.; Goldman, R.E.; Xu, K.; Allen, P.K.; Fowler, D.L.; Simaan, N. Design and coordination kinematics of an in-sertable robotic effectors platform for single-port access surgery. IEEE/ASME Trans. Mechatron. 2012, 18, 1612–1624. [Google Scholar] [CrossRef]
- Simaan, N.; Xu, K.; Wei, W.; Kapoor, A.; Kazanzides, P.; Taylor, R.; Flint, P. Design and Integration of a Telerobotic System for Minimally Invasive Surgery of the Throat. Int. J. Robot. Res. 2009, 28, 1134–1153. [Google Scholar] [CrossRef]
- Burgner, J.; Rucker, D.C.; Gilbert, H.B.; Swaney, P.J.; Russell, P.T.; Weaver, K.D.; Webster, R.J. A Telerobotic System for Transnasal Surgery. IEEE/ASME Trans. Mechatronics 2013, 19, 996–1006. [Google Scholar] [CrossRef] [PubMed]
- Fagogenis, G.; Mencattelli, M.; Machaidze, Z.; Rosa, B.; Price, K.; Wu, F.; Weixler, V.; Saeed, M.; Mayer, J.E.; Dupont, P.E. Autonomous robotic intracardiac catheter navigation using haptic vision. Sci. Robot. 2019, 4, eaaw1977. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Symbol | Formulation | Description | Type |
|---|---|---|---|---|
| Average stiffness | Equations (5) or (6) | Average stiffness of the backbone | Index (global) | |
| Backbone coordinate | Backbone curvilinear coordinate | Design | ||
| Backbone length | - | Max length of robot centerline (base to tip) | Design | |
| Bending angle | - | Bending angle of a segment | Variable | |
| Bending radius | Bending radius of a segment | Variable | ||
| Cross-section diameter | - | Cross-section width at length | Design | |
| Deflection | - | Deflection caused by external force | Variable | |
| Desired stiffness | - | Stiffness of the biological equivalent | Requirement | |
| External force | - | Load on a generic segment | Variable | |
| Flexibility | Ratio of backbone length and minimum bending radius | Index (global) | ||
| Flexibility | Max angle subtended by coiled backbone | Index (global) | ||
| Local min bending radius | - | Minimum bending radius at length | Design | |
| Max. cross-section diameter | Largest cross-section width of the robot | Design | ||
| Maximum bending angle | - | Maximum bending angle of a segment | Design | |
| Maximum payload | - | Maximum payload at the end-effector | Index (global) | |
| Minimum bending radius | Minimum bending radius of the robot | Design | ||
| Narrowest passage width | Width of choke point along the path | Requirement | ||
| Required reach | Length of longest desired path | Requirement | ||
| Segment length | - | Length of a generic backbone segment | Design | |
| Sharpest bending radius | Smallest bending radius along the path | Requirement | ||
| Slenderness | Ratio of backbone length and maximum cross-section diameter | Index (global) | ||
| Stiffness | Stiffness of a segment | Index (local) |
| Robot | Ref. | Type | [mm] | [mm] | [mm] | [N/m] | [N] | [-] | [-] |
|---|---|---|---|---|---|---|---|---|---|
| STIFF-FLOP | [50] | Pneumatic | 100 | 32 | 36 | - | 47.1 | 3 | 2.8 |
| TEPM | [51] | Pneumatic | 200 | - | 176 | 290 | - | - | 1.13 |
| Pneumatic robot | [52] | Pneumatic | 380 | 150 | 200 | 1.1 | 50 | 2.5 | 1.9 |
| FLARE | [4] | Tendon-driven | 715 | 12 | 55 | 11.2 | - | 60 | 13 |
| COBRA | [5] | Tendon-driven | 5500 | 9 | 60 | - | - | 610 | 91.7 |
| Extensible robot | [9] | Tendon-driven | 165 | 7 | 7 | - | - | 24 | 24 |
| RAIN | [27] | Tendon-driven | 1015 | 20 | - | 14.7 | 0.2 | 50 | - |
| Medrobotics Flex | [53] | Tendon-driven | 170 | 28 | 113 | - | - | 9 | 1.5 |
| I2 Snake Robot | [54] | Tendon-driven | 366 | 16 | - | - | 2 | 23 | - |
| HARP | [55] | Tendon-driven | 300 | 12 | 75 | - | 5 | 25 | 4.0 |
| IREP | [56] | Push-pull | 60 | 6.4 | 19 | - | 2 | 30 | 3.1 |
| MIS Robot | [57] | Push-pull | 37 | 4.2 | 12 | - | 1 | 8.8 | 3.1 |
| Surgical Robot | [58] | Concentric tube | 420 | 2.3 | - | - | - | 182 | - |
| Robotic Catheter | [59] | Concentric tube | 830 | 4.5 | - | - | - | 184 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, M.; Gautreau, E.; Bonnet, X.; Laribi, M.A. Continuum Robots: From Conventional to Customized Performance Indicators. Biomimetics 2023, 8, 147. https://doi.org/10.3390/biomimetics8020147
Russo M, Gautreau E, Bonnet X, Laribi MA. Continuum Robots: From Conventional to Customized Performance Indicators. Biomimetics. 2023; 8(2):147. https://doi.org/10.3390/biomimetics8020147
Chicago/Turabian StyleRusso, Matteo, Elie Gautreau, Xavier Bonnet, and Med Amine Laribi. 2023. "Continuum Robots: From Conventional to Customized Performance Indicators" Biomimetics 8, no. 2: 147. https://doi.org/10.3390/biomimetics8020147
APA StyleRusso, M., Gautreau, E., Bonnet, X., & Laribi, M. A. (2023). Continuum Robots: From Conventional to Customized Performance Indicators. Biomimetics, 8(2), 147. https://doi.org/10.3390/biomimetics8020147









