Deep-Learning-Based Reduced-Order Model for Power Generation Capacity of Flapping Foils
Abstract
:1. Introduction
2. Numerical Methodology
2.1. Governing Formulations for Incompressible Fluid Flows
2.2. Prescribed Flapping Kinematics
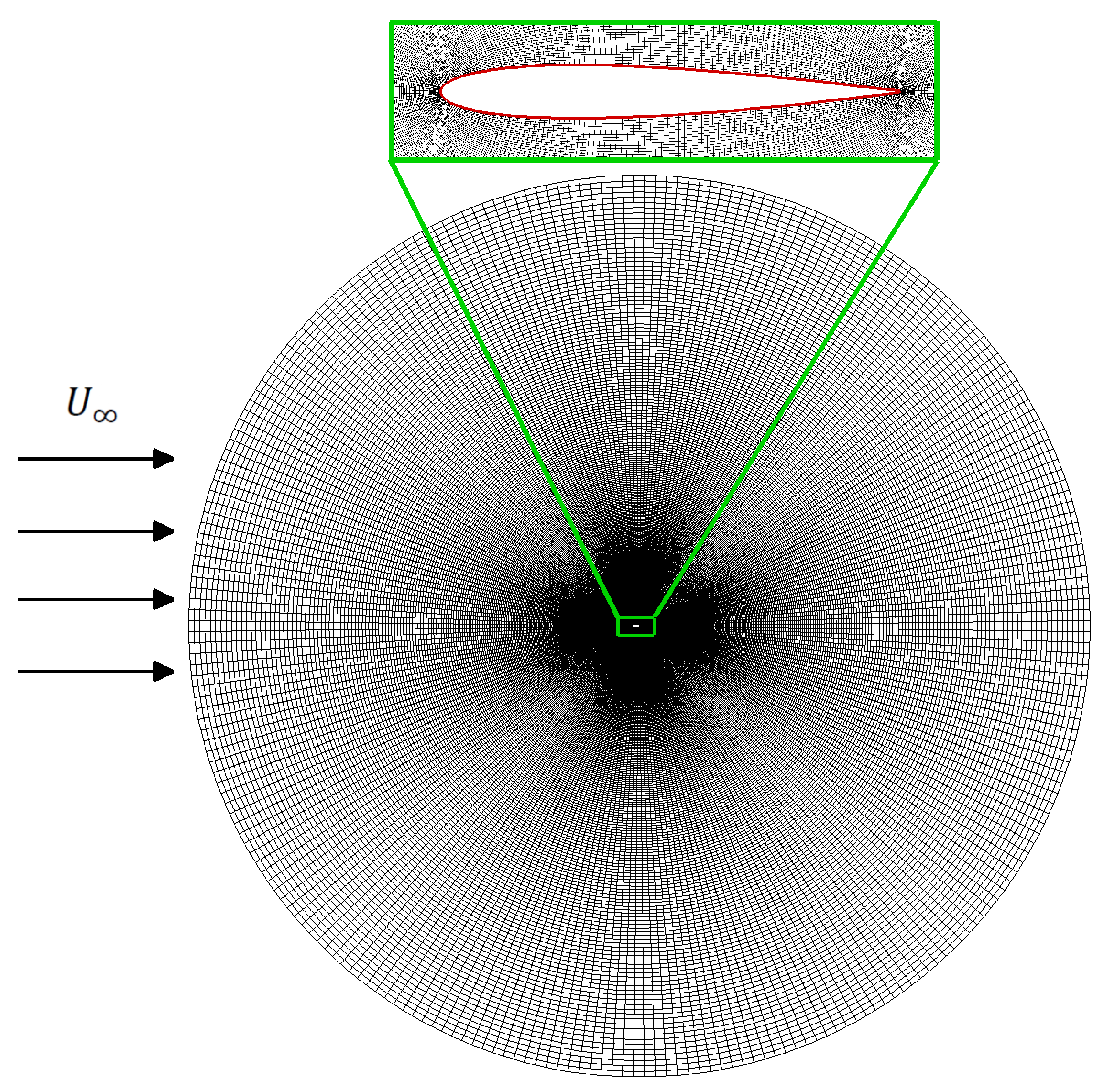
2.3. Discretization Strategy
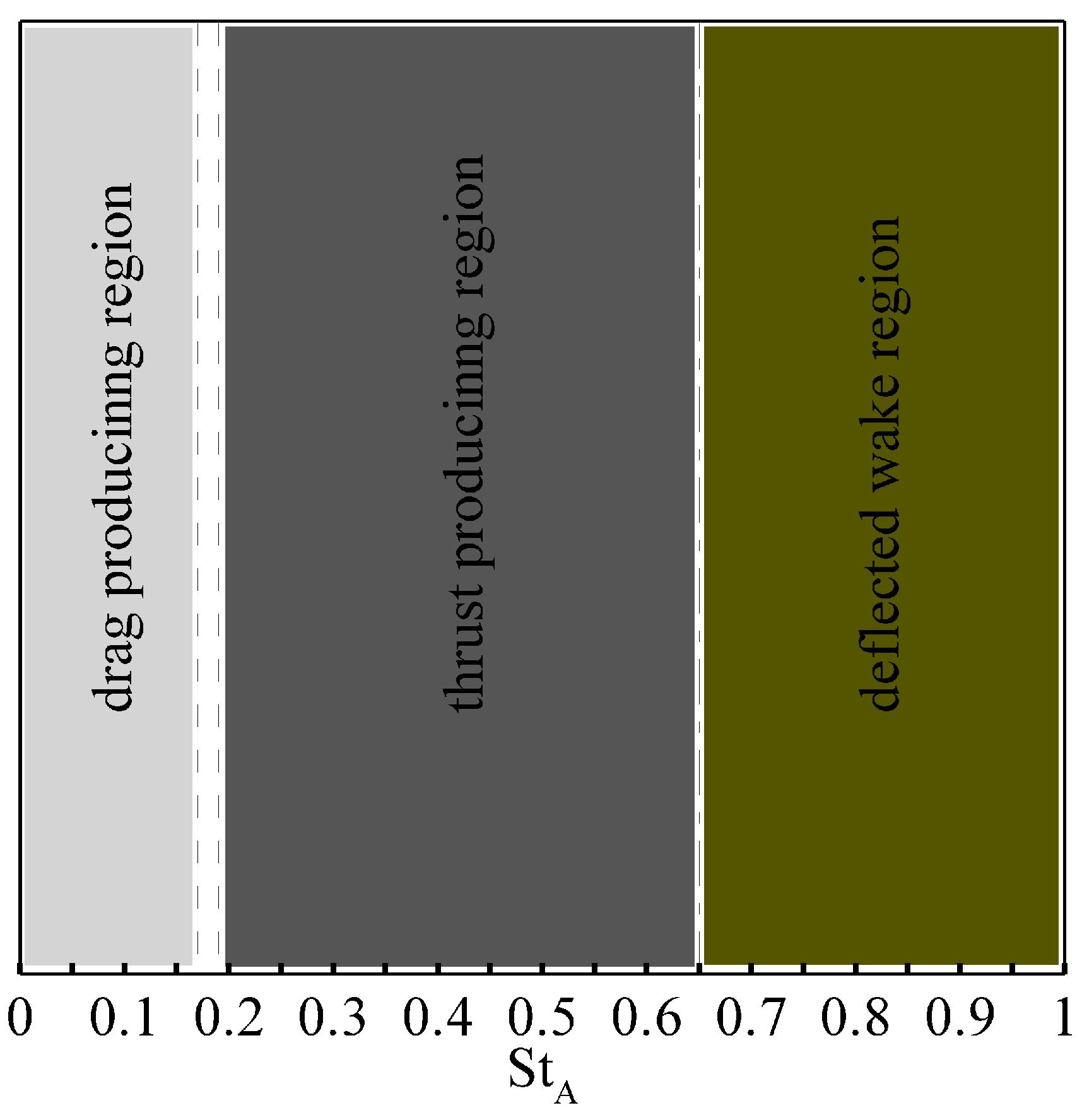
3. Hydrodynamic Performance Metrics
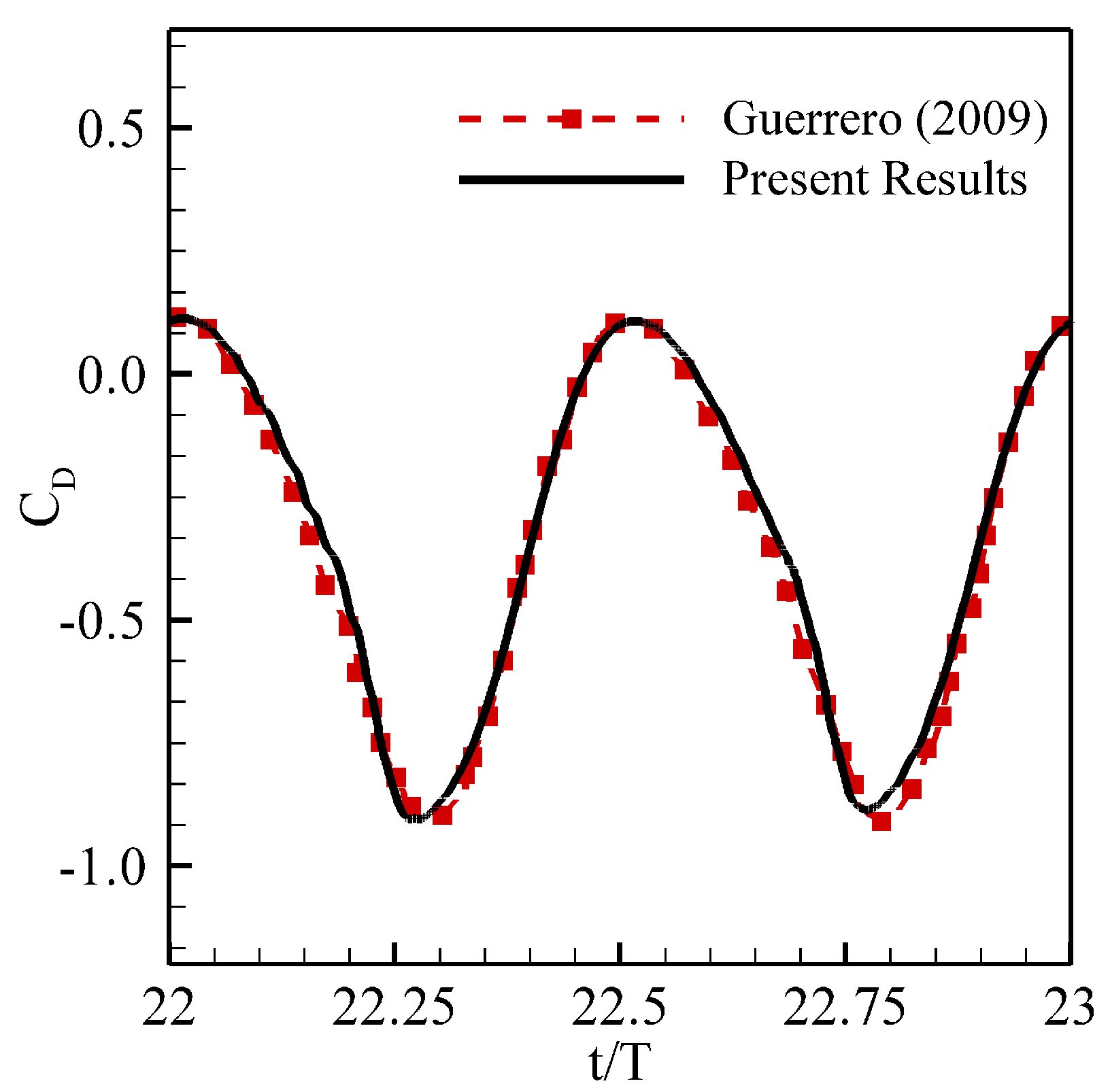
4. Validation
5. Results and Discussions
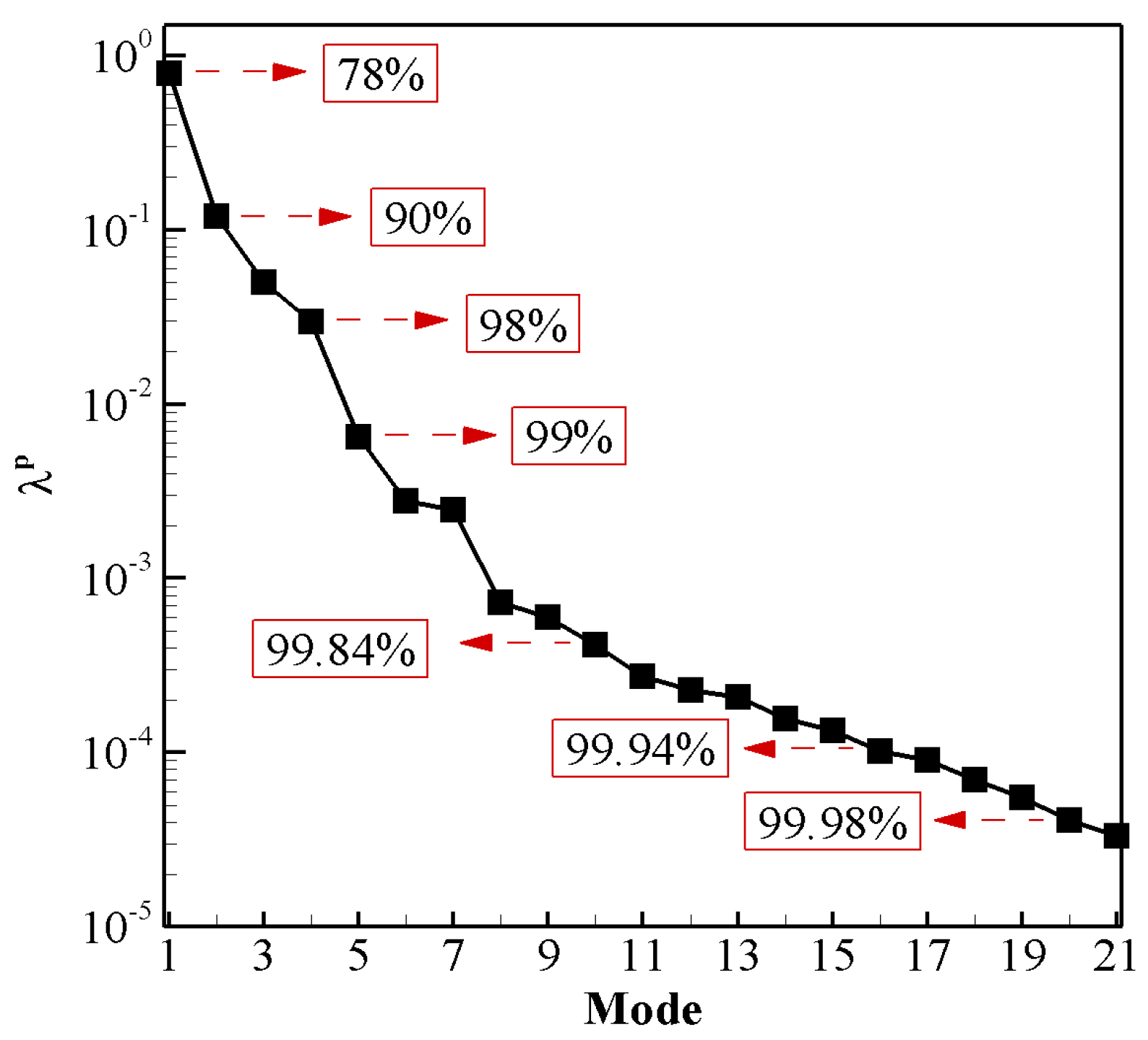
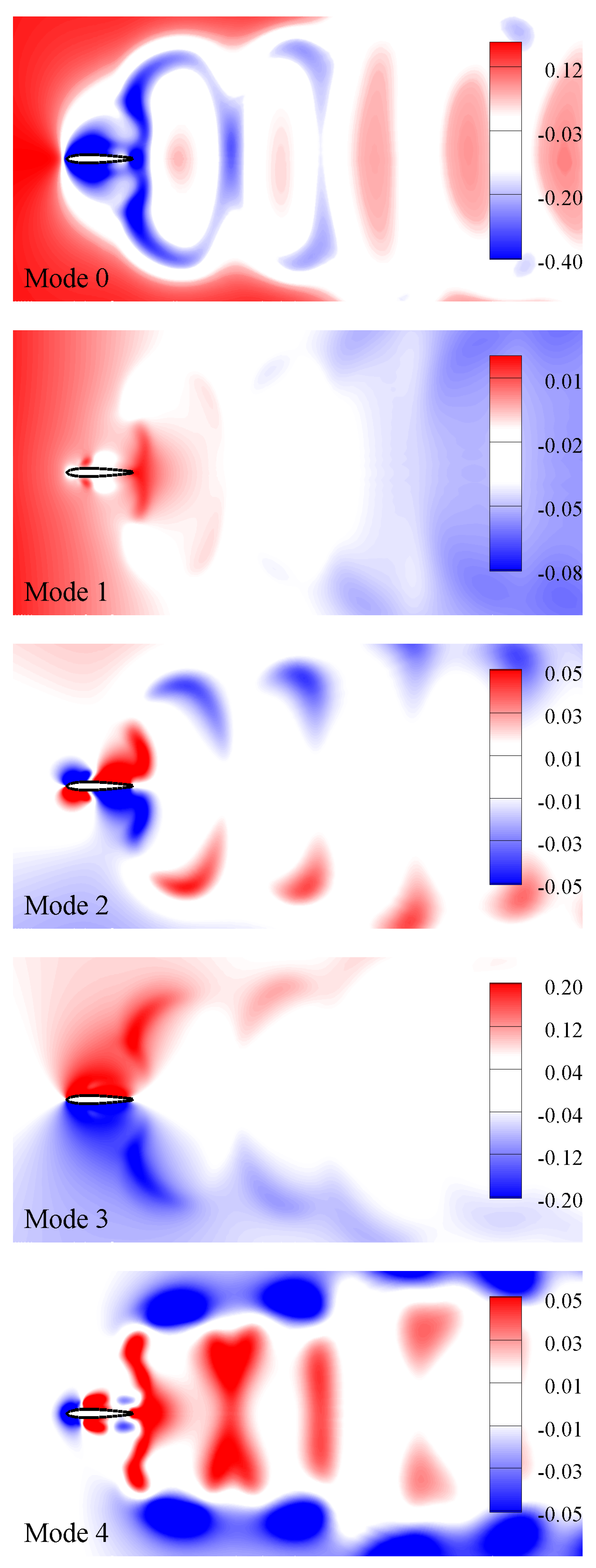
5.1. Proper Orthogonal Decomposition
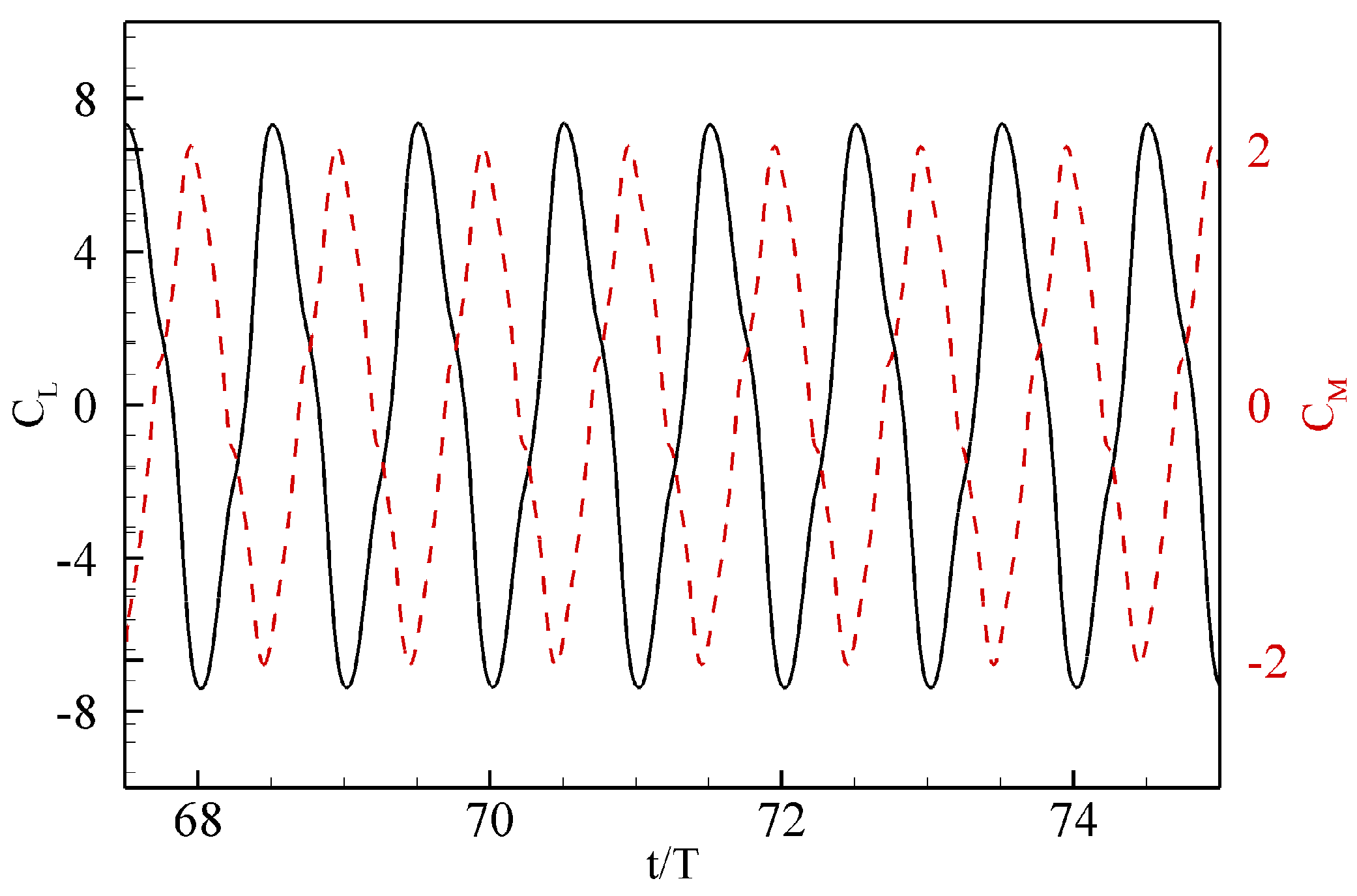
5.2. Models of Hydrodynamic Forces and Moment
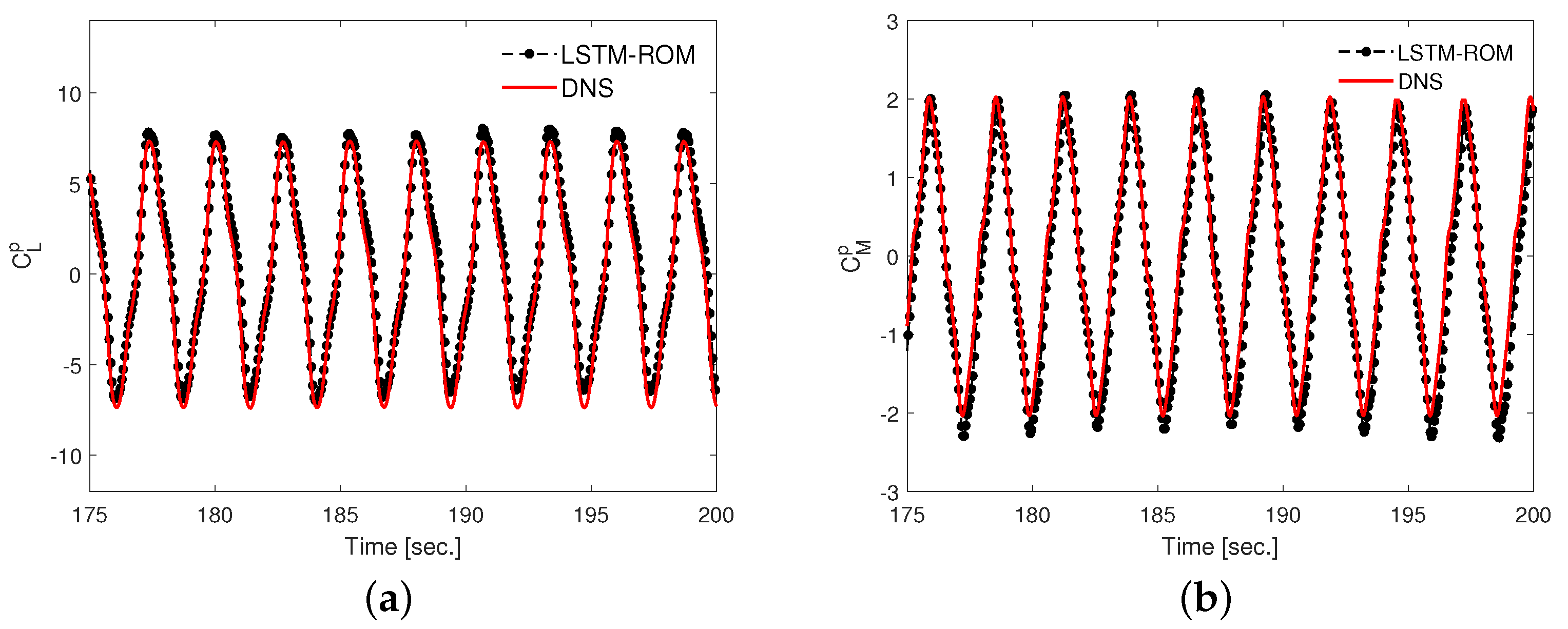
5.3. Long-Short-Term Neural Network
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akhtar, I.; Borggaard, J.; Burns, J.A.; Imtiaz, H.; Zietsman, L. Using functional gains for effective sensor location in flow control: A reduced-order modelling approach. J. Fluid Mech. 2015, 781, 622–656. [Google Scholar] [CrossRef]
- Buffoni, M.; Camarri, S.; Iollo, A.; Salvetti, M. Low-dimensional modelling of a conned three-dimensional wake ow. J. Fluid Mech. 2006, 569, 141150. [Google Scholar] [CrossRef]
- Fang, F.; Pain, C.; Navon, I.; Gorman, G.; Piggott, M.; Allison, P.; Farrell, P.; Goddard, A. A POD reduced order unstructured mesh ocean modelling method for moderate Reynolds number flows. Ocean. Model. 2009, 28, 127–136. [Google Scholar] [CrossRef]
- Fortuna, L.; Nunnari, G.; Gallo, A. Model Order Reduction Techniques with Applications in Electrical Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Noack, B.R.; Morzynski, M.; Tadmor, G. Reduced-Order Modelling for Flow Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 528. [Google Scholar]
- Bakewell, H.P.; Lumley, J.L. Viscous sublayer and adjacent wall region in turbulent pipe flow. Phys. Fluids 1967, 10, 1880–1889. [Google Scholar] [CrossRef]
- Deane, A.; Kevrekidis, I.; Karniadakis, G.E.; Orszag, S. Low-dimensional models for complex geometry flows: Application to grooved channels and circular cylinders. Phys. Fluids Fluid Dyn. 1991, 3, 2337–2354. [Google Scholar] [CrossRef] [Green Version]
- Shirovich, L. Turbulence and the Dynamics of Coherent Structures; Part I: Coherent Structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Noack, B.R.; Schlegel, M.; Ahlborn, B.; Mutschke, G.; Morzyński, M.; Comte, P. A finite-time thermodynamics of unsteady fluid flows. J. Non-Equilib. Thermodyn. 2008, 33, 103–148. [Google Scholar] [CrossRef] [Green Version]
- Graham, W.R.; Peraire, J.; Tang, K.Y. Optimal control of vortex shedding using low order models. Part I: Open-loop model development. Int. J. Numer. Methods Eng. 1999, 44, 945–972. [Google Scholar] [CrossRef]
- Graham, W.R.; Peraire, J.; Tang, K.Y. Optimal control of vortex shedding using low order models. Part II: Model-based control. Int. J. Numer. Methods Eng. 1999, 44, 973–990. [Google Scholar] [CrossRef]
- Akhtar, I.; Nayfeh, A.H. Model based control of laminar wake using fluidic actuation. J. Comput. Nonlinear Dyn. 2010, 5, 041015. [Google Scholar] [CrossRef]
- Kunisch, K.; Volkwein, S. Control of the Burgers equation by a reduced-order approach using proper orthogonal decomposition. J. Optim. Theory Appl. 1999, 102, 345–371. [Google Scholar] [CrossRef]
- Yue, Y. The Use of Model Order Reduction in Design Optimization Algorithms. Ph.D. Thesis, Katholieke Univerisiteit, Leuven, Belgium, 2012. [Google Scholar]
- Imtiaz, H.; Akhtar, I. Nonlinear closure modeling in reduced order models for turbulent flows: A dynamical system approach. Nonlinear Dyn. 2020, 99, 479–494. [Google Scholar] [CrossRef]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Two-Level Discretizations of Nonlinear Closure Models for Proper Orthogonal Decomposition. J. Comput. Phys. 2011, 230, 126–146. [Google Scholar] [CrossRef]
- Wang, Z. Reduced-order modeling of complex engineering and geophysical flows: Analysis and computations. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2012. [Google Scholar]
- Östh, J.; Noack, B.R.; Krajnović, S.; Barros, D.; Borée, J. On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body. J. Fluid Mech. 2014, 747, 518–544. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Fang, F.; Buchan, A.G.; Pain, C.C.; Navon, I.M.; Du, J.; Hu, G. Non-linear model reduction for the Navier–Stokes equations using residual DEIM method. J. Comput. Phys. 2014, 263, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Sabetghadam, F.; Jafarpour, A. α regularization of the POD-Galerkin dynamical systems of the Kuramoto–Sivashinsky equation. Appl. Math. Comput. 2012, 218, 6012–6026. [Google Scholar] [CrossRef]
- Akhtar, I.; Nayfeh, A.H.; Ribbens, C.J. On the stability and extension of reduced-order Galerkin models in incompressible flows. Theor. Comput. Fluid Dyn. 2009, 23, 213–237. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Schlegel, M.; Noack, B.R. On long-term boundedness of Galerkin models. J. Fluid Mech. 2015, 765, 325–352. [Google Scholar] [CrossRef] [Green Version]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef] [Green Version]
- Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine learning–accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef] [PubMed]
- Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Hesthaven, J.S. Data-driven reduced order modeling for time-dependent problems. Comput. Methods Appl. Mech. Eng. 2019, 345, 75–99. [Google Scholar] [CrossRef]
- Han, J.; Jentzen, A.; Weinan, E. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hesthaven, J.S.; Ubbiali, S. Non-intrusive reduced order modeling of nonlinear problems using neural networks. J. Comput. Phys. 2018, 363, 55–78. [Google Scholar] [CrossRef] [Green Version]
- Noack, B.R.; Papas, P.; Monkewitz, P.A. The need for a pressure-term representation in empirical Galerkin models of incompressible shear flows. J. Fluid Mech. 2005, 523, 339–365. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.F.; Farooq, H.; Akhtar, I.; Bangash, Z. Machine learning–based reduced-order modeling of hydrodynamic forces using pressure mode decomposition. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2021, 235, 2517–2528. [Google Scholar] [CrossRef]
- Farooq, H.; Saeed, A.; Akhtar, I.; Bangash, Z. Neural Network-Based Model Reduction of Hydrodynamics Forces on an Airfoil. Fluids 2021, 6, 332. [Google Scholar] [CrossRef]
- Fish, F.; Lauder, G. Passive and active flow control by swimming fishes and mammals. Annu. Rev. Fluid Mech. 2006, 38, 193–224. [Google Scholar] [CrossRef] [Green Version]
- Rozhdestvensky, K.V.; Ryzhov, V.A. Aerohydrodynamics of flapping-wing propulsors. Prog. Aerosp. Sci. 2003, 39, 585–633. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Techet, A.H.; Hover, F.S. Review of experimental work in biomimetic foils. IEEE J. Ocean. Eng. 2004, 29, 585–594. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.J. Dissecting insect flight. Annu. Rev. Fluid Mech. 2005, 37, 183–210. [Google Scholar] [CrossRef] [Green Version]
- Guerrero, J. Numerical simulation of the unsteady aerodynamics of flapping flight. Ph.D. Thesis, Department of Civil, Environmental, Architectural Engineering Universita degli Studi di Genova, Genoa, Italy, 2009. [Google Scholar]
- Xiao, Q.; Zhu, Q. A review on flow energy harvesters based on flapping foils. J. Fluids Struct. 2014, 46, 174–191. [Google Scholar] [CrossRef]
- Young, J.; Lai, J.C.; Platzer, M.F. A review of progress and challenges in flapping foil power generation. Prog. Aerosp. Sci. 2014, 67, 2–28. [Google Scholar] [CrossRef]
- Farooq, H.; Ghommem, M.; Khalid, M.S.U.; Akhtar, I. Numerical investigation of hydrodynamic performance of flapping foils for energy harvesting. Ocean. Eng. 2022, 260, 112005. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Parametric study of an oscillating airfoil in a power-extraction regime. AIAA J. 2008, 46, 1318–1330. [Google Scholar] [CrossRef]
- Platzer, M.; Ashraf, M.; Young, J.; Lai, J. Extracting power in jet streams: Pushing the performance of flapping wing technology. In Proceedings of the 27th Congress of the International Council of the Aeronautical Sciences, International Council of the Aeronautical Sciences Paper, Nice, France, 19–24 September 2010; Volume 2. [Google Scholar]
- Ashraf, M.; Young, J.; Lai, J.; Platzer, M. Numerical analysis of an oscillating-wing wind and hydropower generator. AIAA J. 2011, 49, 1374–1386. [Google Scholar] [CrossRef]
- Zhu, Q. Energy harvesting by a purely passive flapping foil from shear flows. J. Fluids Struct. 2012, 34, 157–169. [Google Scholar] [CrossRef]
- Shimizu, E.; Isogai, K.; Obayashi, S. Multiobjective design study of a flapping wing power generator. J. Fluids Eng. 2008, 130. [Google Scholar] [CrossRef]
- Zhu, Q.; Haase, M.; Wu, C.H. Modeling the capacity of a novel flow-energy harvester. Appl. Math. Model. 2009, 33, 2207–2217. [Google Scholar] [CrossRef]
- Zhu, Q.; Peng, Z. Mode coupling and flow energy harvesting by a flapping foil. Phys. Fluids 2009, 21, 033601. [Google Scholar] [CrossRef] [Green Version]
- Abiru, H.; Yoshitake, A. Study on a flapping wing hydroelectric power generation system. J. Environ. Eng. 2011, 6, 178–186. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Chen, Y.; Zhao, N. Role of induced vortex interaction in a semi-active flapping foil based energy harvester. Phys. Fluids 2015, 27, 093601. [Google Scholar] [CrossRef]
- Deng, J.; Teng, L.; Pan, D.; Shao, X. Inertial effects of the semi-passive flapping foil on its energy extraction efficiency. Phys. Fluids 2015, 27, 053103. [Google Scholar] [CrossRef]
- Farooq, H.; Khalid, M.S.U.; Akhtar, I.; Hemmati, A. Nonlinear response of passively flapping foils. Ocean. Eng. 2022, 261, 112071. [Google Scholar] [CrossRef]
- Young, J.; Ashraf, M.A.; Lai, J.C.; Platzer, M.F. Numerical simulation of fully passive flapping foil power generation. AIAA J. 2013, 51, 2727–2739. [Google Scholar] [CrossRef]
- Veilleux, J.C.; Dumas, G. Numerical optimization of a fully-passive flapping-airfoil turbine. J. Fluids Struct. 2017, 70, 102–130. [Google Scholar] [CrossRef]
- Wang, Z.; Du, L.; Zhao, J.; Sun, X. Structural response and energy extraction of a fully passive flapping foil. J. Fluids Struct. 2017, 72, 96–113. [Google Scholar] [CrossRef]
- Ashraf, M.A. Numerical simulation of the flow over flapping airfoils in propulsion and power extraction regimes. Ph.D. Thesis, University of New South Wales, Sydney, Australia, 2010. [Google Scholar]
- Daqaq, M.F.; Bibo, A.; Akhtar, I.; Alhadidi, A.H.; Panyam, M.; Caldwell, B.; Noel, J. Micropower generation using cross-flow instabilities: A review of the literature and its implications. J. Vib. Acoust. 2019, 141, 030801. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Maulik, R.; Ahmed, M. An artificial neural network framework for reduced order modeling of transient flows. Commun. Nonlinear Sci. Numer. Simul. 2019, 77, 271–287. [Google Scholar] [CrossRef] [Green Version]
- Saeed, A.; Farooq, H.; Akhtar, I.; Bangash, Z. Deep learning-based reduced-order model for turbulent flows. In Proceedings of the 2022 19th International Bhurban Conference on Applied Sciences and Technology (IBCAST), IEEE, Islamabad, Pakistan, 16–20 August 2022; pp. 821–829. [Google Scholar]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Gupta, R.; Jaiman, R. Three-dimensional deep learning-based reduced order model for unsteady flow dynamics with variable Reynolds number. Phys. Fluids 2022, 34, 033612. [Google Scholar] [CrossRef]
- Pawar, S.; Ahmed, S.E.; San, O.; Rasheed, A. Data-driven recovery of hidden physics in reduced order modeling of fluid flows. Phys. Fluids 2020, 32, 036602. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ji, T.; Xie, F.; Zheng, H.; Zheng, Y. Unsteady flow prediction from sparse measurements by compressed sensing reduced order modeling. Comput. Methods Appl. Mech. Eng. 2022, 393, 114800. [Google Scholar] [CrossRef]
- de Boer, A.; van der Schoot, M.; Bijl, H. Mesh deformation based on radial basis function interpolation. Comput. Struct. 2007, 85, 784–795. [Google Scholar] [CrossRef]
- Bos, F.M.; van Oudheusden, B.W.; Bijl, H. Radial basis function based mesh deformation applied to simulation of flow around flapping wings. Comput. Fluids 2013, 79, 167–177. [Google Scholar] [CrossRef]
- Akhtar, I. Parallel simulations, reduced-order modeling, and feedback control of vortex shedding using fluidic actuators. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2008. [Google Scholar]
- Leonard, B.P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Methods Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. III. Dynamics and scaling. Q. Appl. Math. 1987, 45, 583–590. [Google Scholar] [CrossRef] [Green Version]
- Sirovich, L.; Kirby, M. Low-dimensional procedure for the characterization of human faces. JOSA A 1987, 4, 519–524. [Google Scholar] [CrossRef] [Green Version]
- Imtiaz, H.; Akhtar, I. On lift and drag decomposition coefficients in a model reduction framework using pressure-mode decomposition (PMD) analysis. J. Fluids Struct. 2017, 75, 174–192. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Tallet, A.; Allery, C.; Leblond, C.; Liberge, E. A minimum residual projection to build coupled velocity–pressure POD–ROM for incompressible Navier–Stokes equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 909–932. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeed, A.; Farooq, H.; Akhtar, I.; Tariq, M.A.; Khalid, M.S.U. Deep-Learning-Based Reduced-Order Model for Power Generation Capacity of Flapping Foils. Biomimetics 2023, 8, 237. https://doi.org/10.3390/biomimetics8020237
Saeed A, Farooq H, Akhtar I, Tariq MA, Khalid MSU. Deep-Learning-Based Reduced-Order Model for Power Generation Capacity of Flapping Foils. Biomimetics. 2023; 8(2):237. https://doi.org/10.3390/biomimetics8020237
Chicago/Turabian StyleSaeed, Ahmad, Hamayun Farooq, Imran Akhtar, Muhammad Awais Tariq, and Muhammad Saif Ullah Khalid. 2023. "Deep-Learning-Based Reduced-Order Model for Power Generation Capacity of Flapping Foils" Biomimetics 8, no. 2: 237. https://doi.org/10.3390/biomimetics8020237
APA StyleSaeed, A., Farooq, H., Akhtar, I., Tariq, M. A., & Khalid, M. S. U. (2023). Deep-Learning-Based Reduced-Order Model for Power Generation Capacity of Flapping Foils. Biomimetics, 8(2), 237. https://doi.org/10.3390/biomimetics8020237







