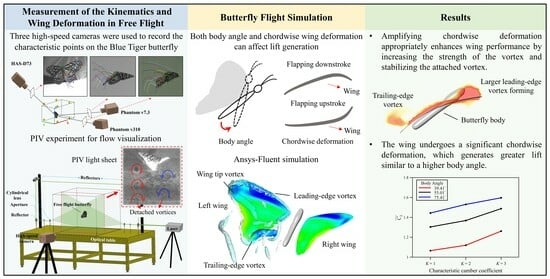
The Lift Effects of Chordwise Wing Deformation and Body Angle on Low-Speed Flying Butterflies
Abstract
:1. Introduction
2. Materials and Methods
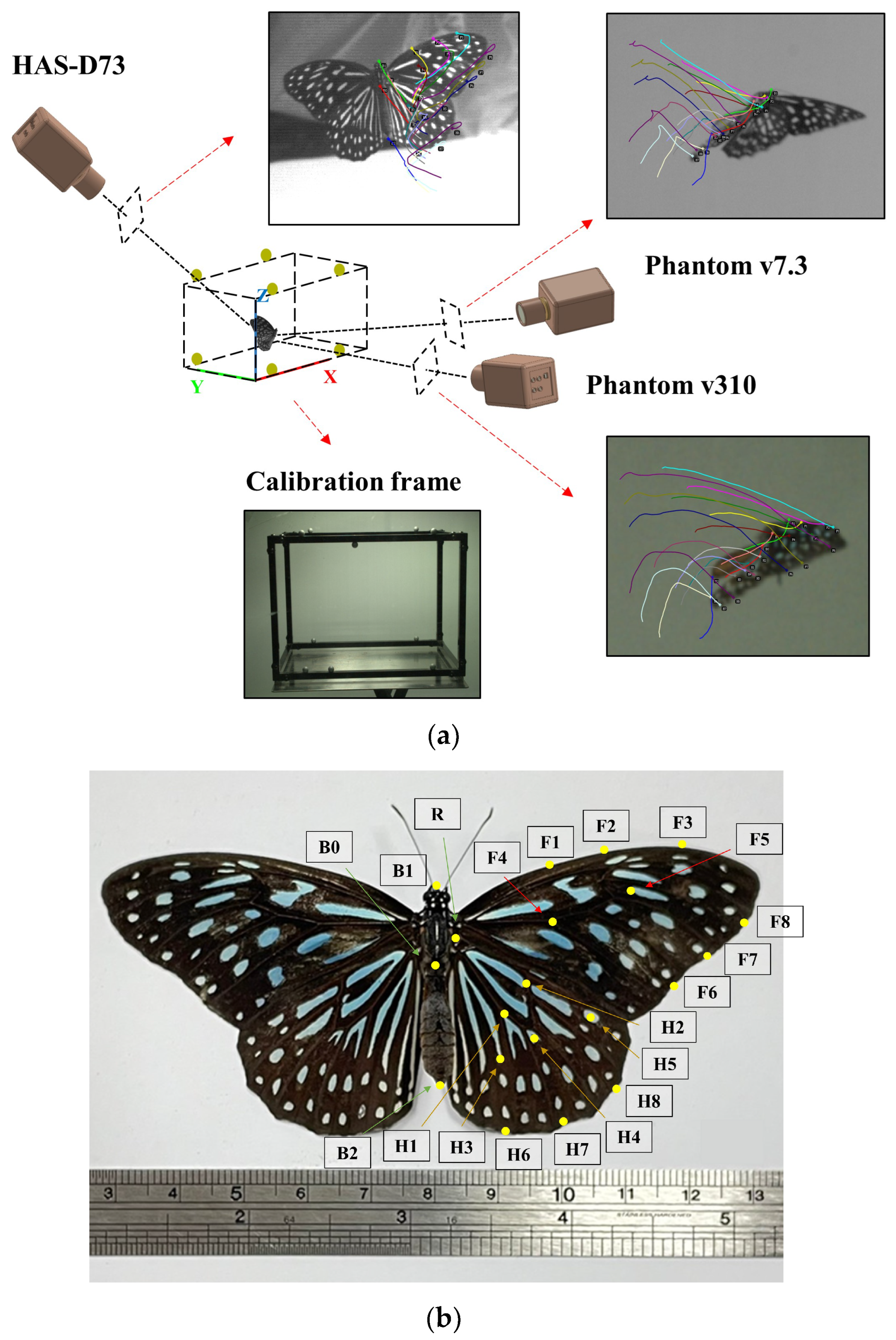
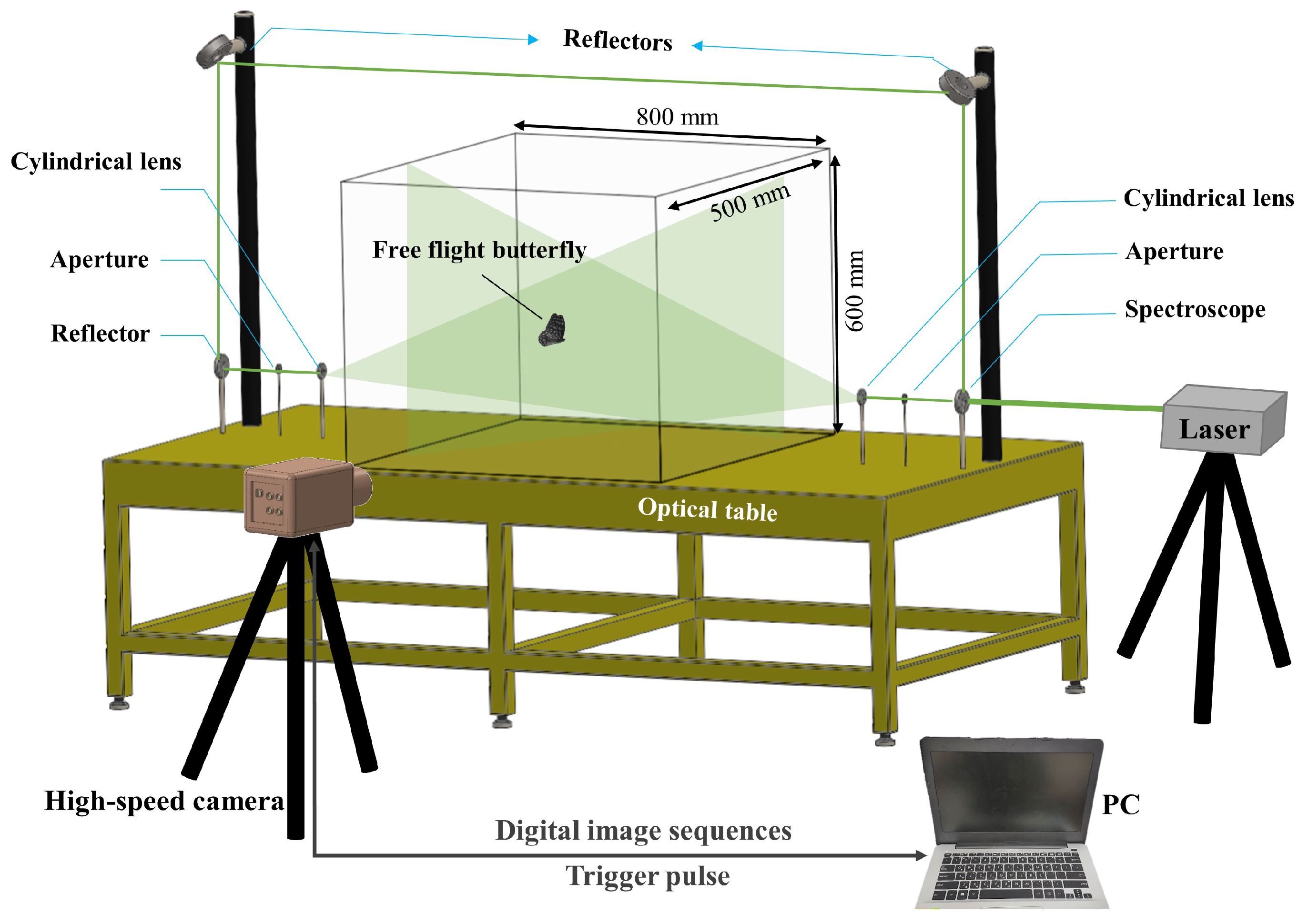
2.1. Experimental Setup
2.2. Flow Visualization
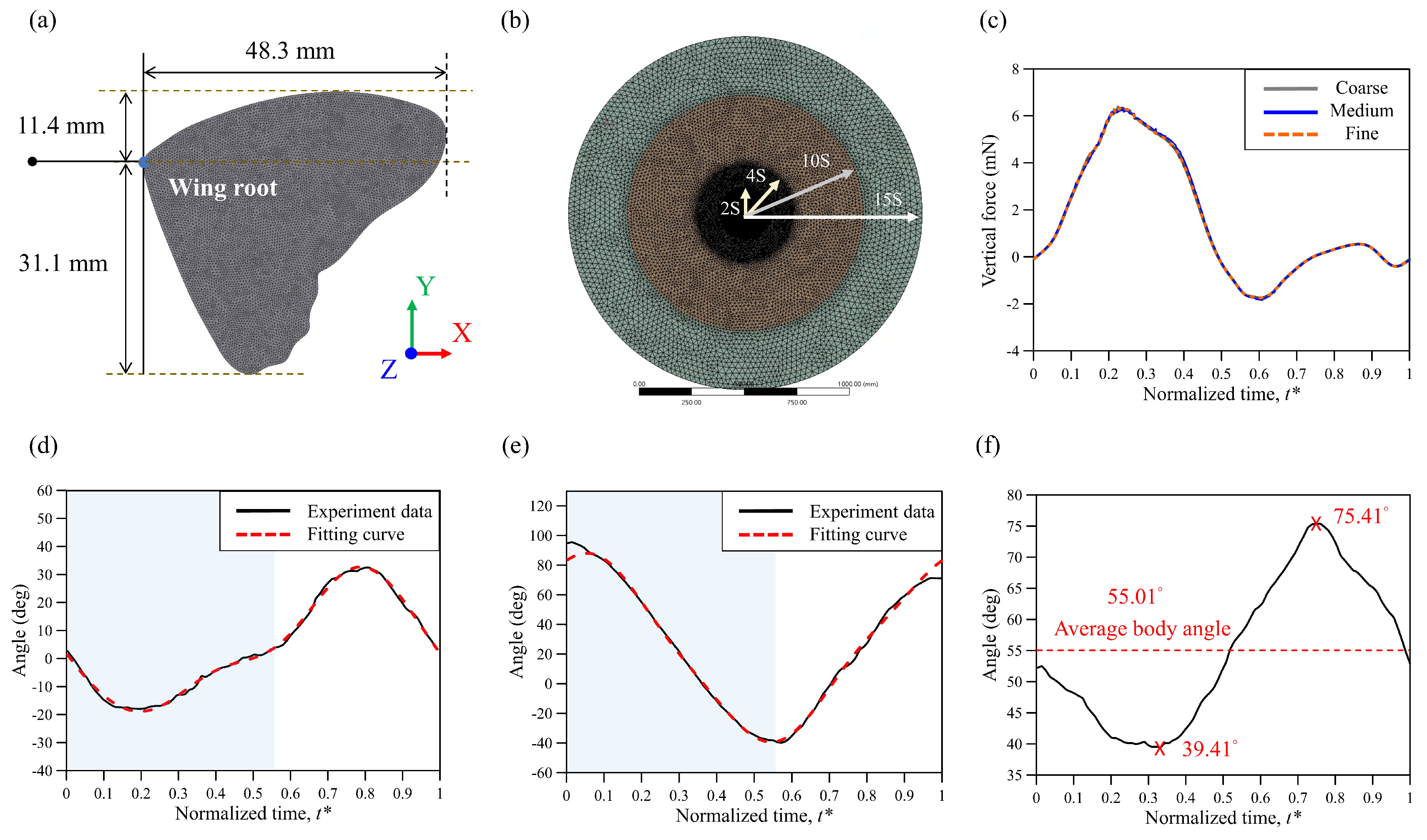
2.3. Simulation Scheme and Wing Model
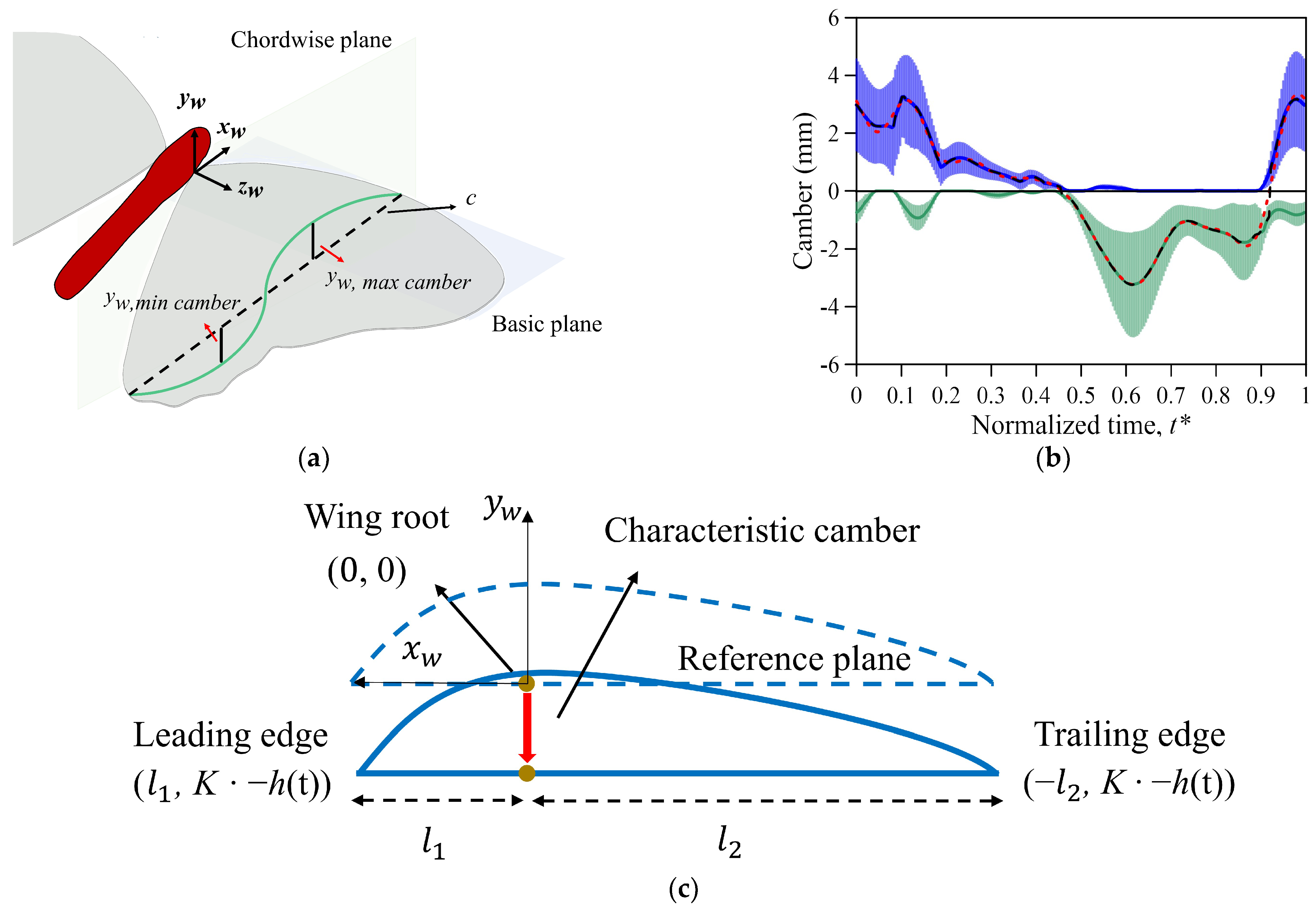
2.4. Kinematics and Deformation of the Wing Model
3. Results and Discussion
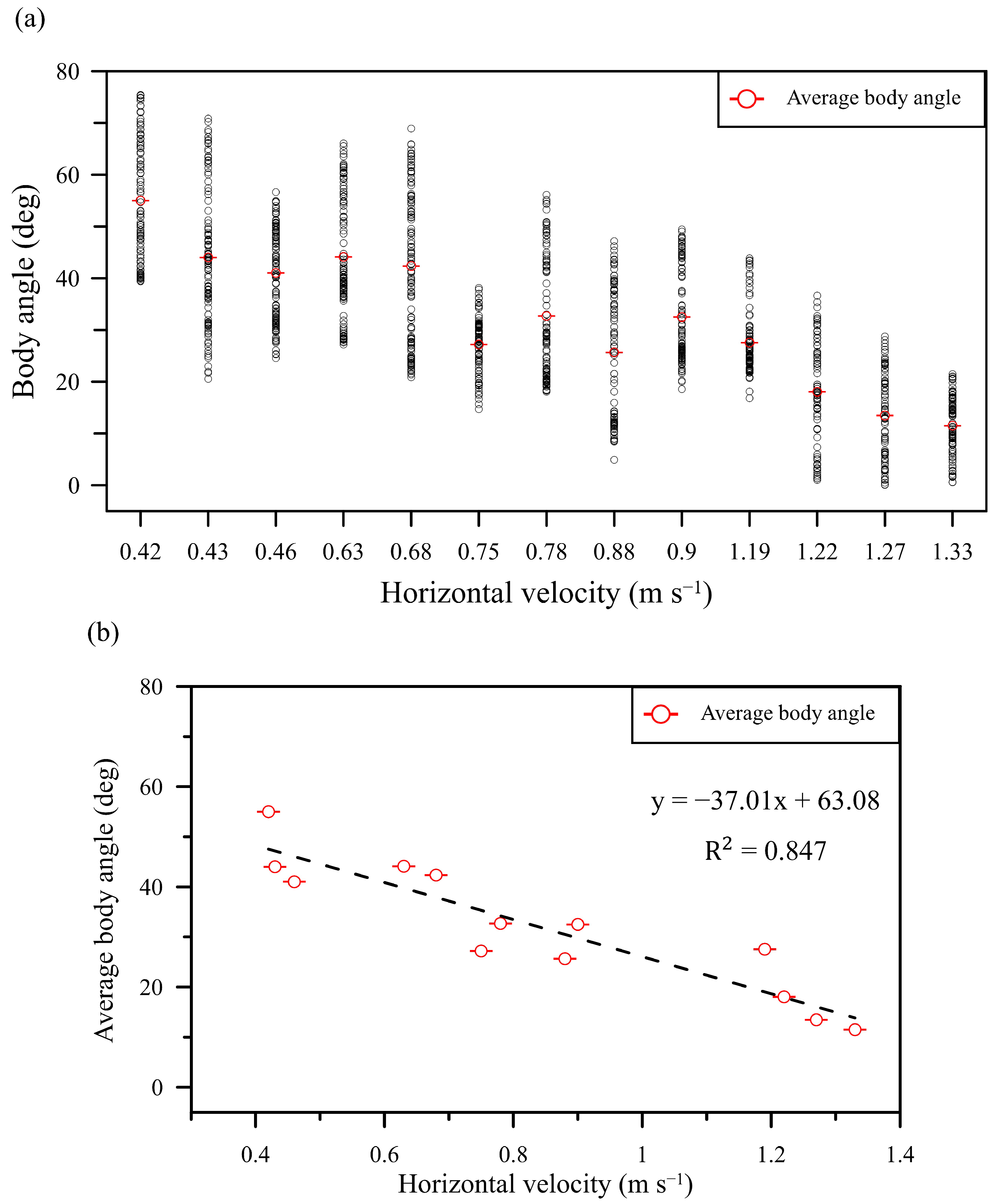
3.1. Biological Observation
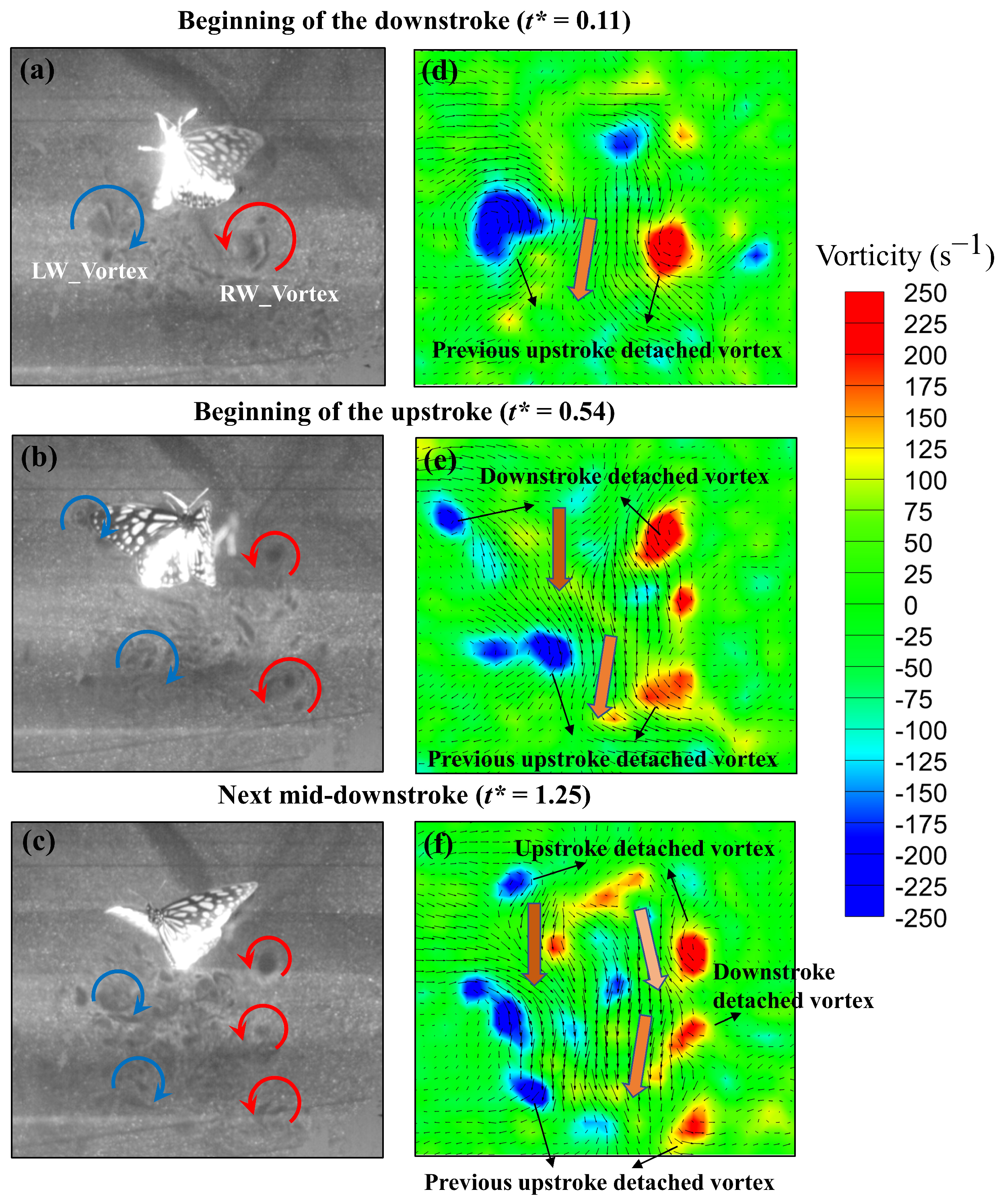
3.2. Experimental Results of Particle-Image Velocimetry on a Low-Speed Butterfly
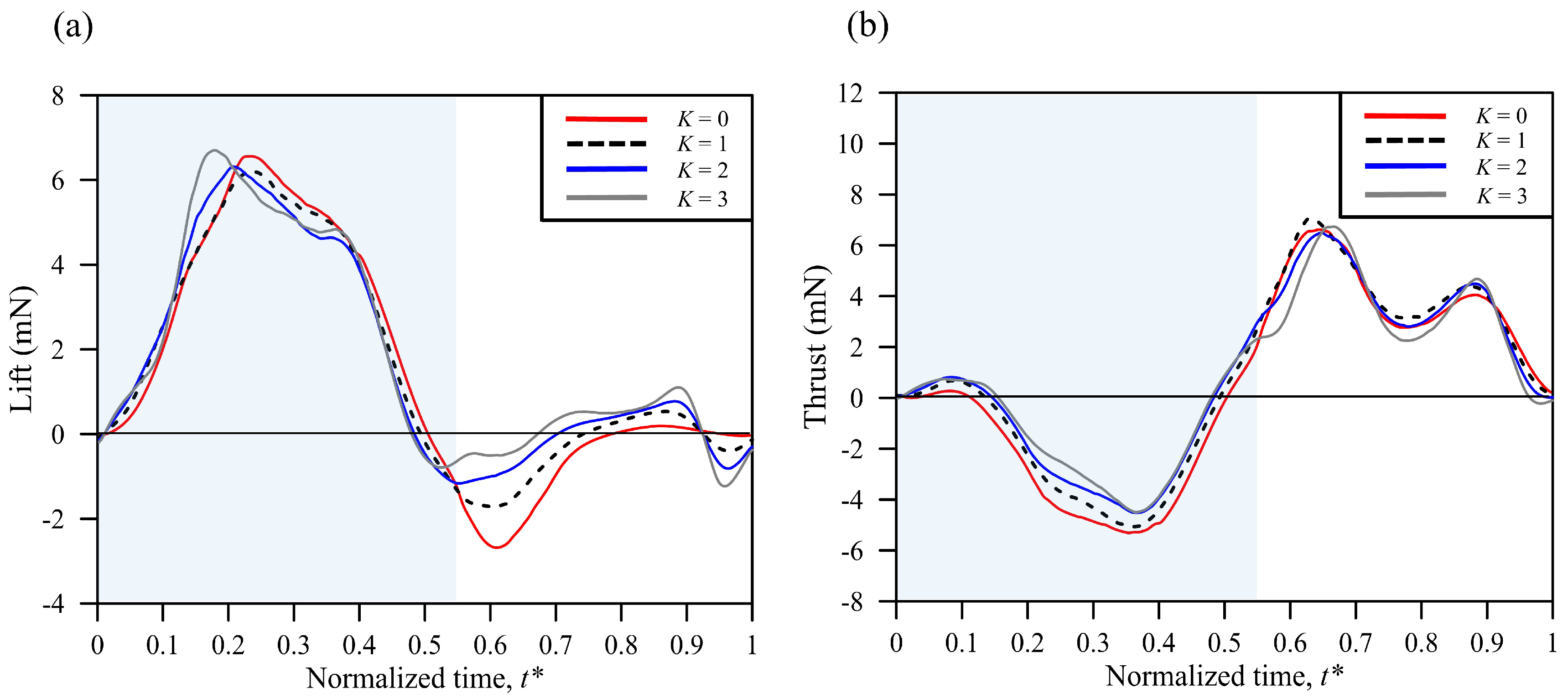
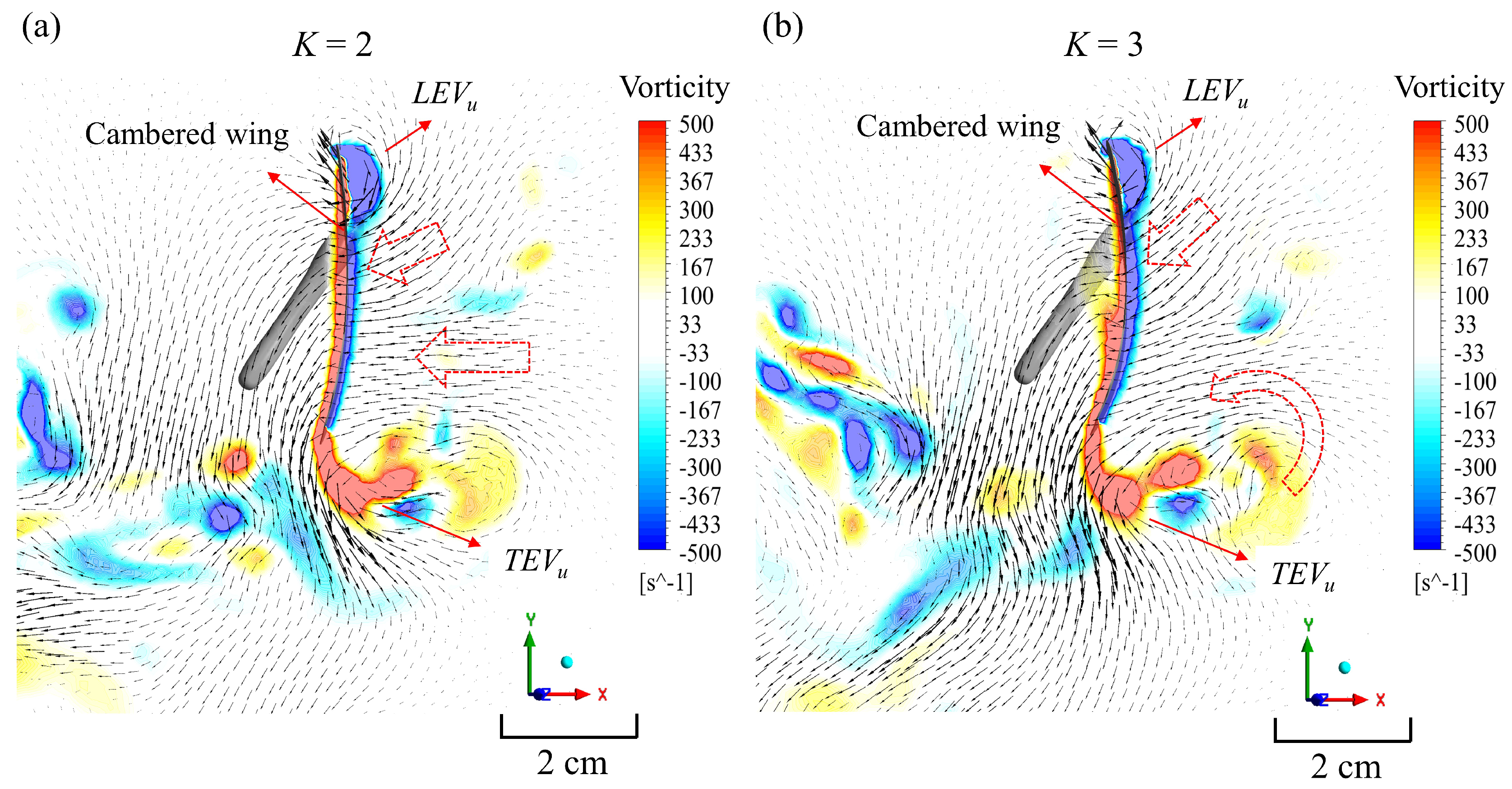
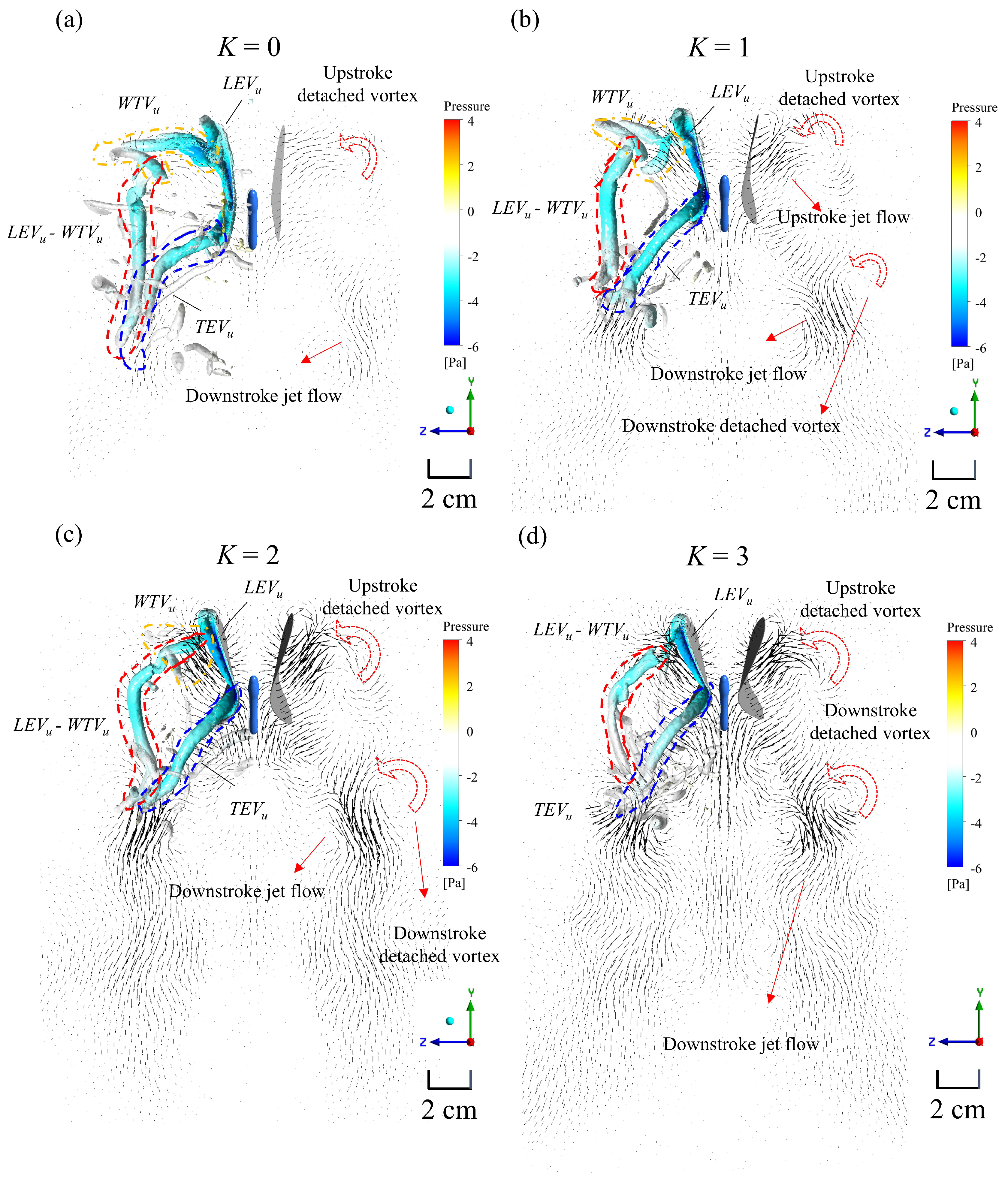
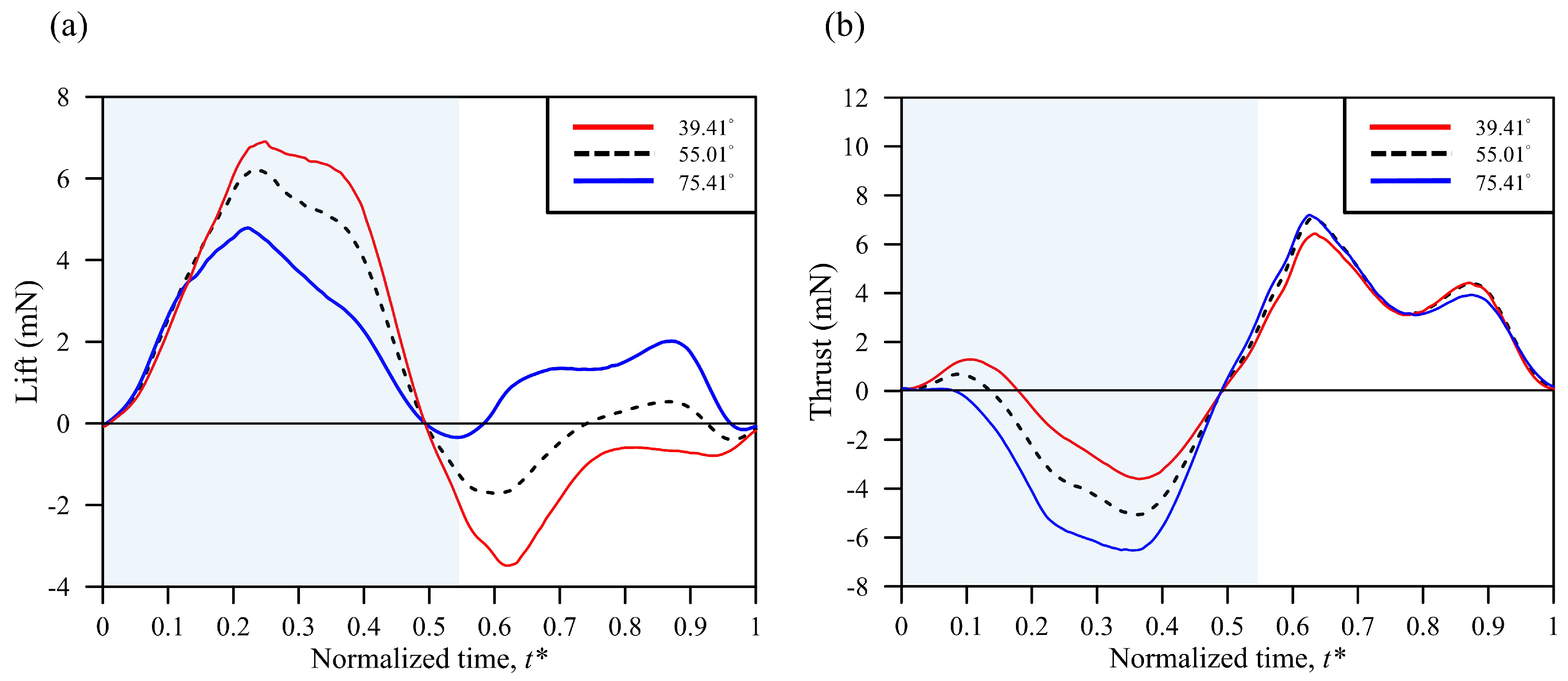
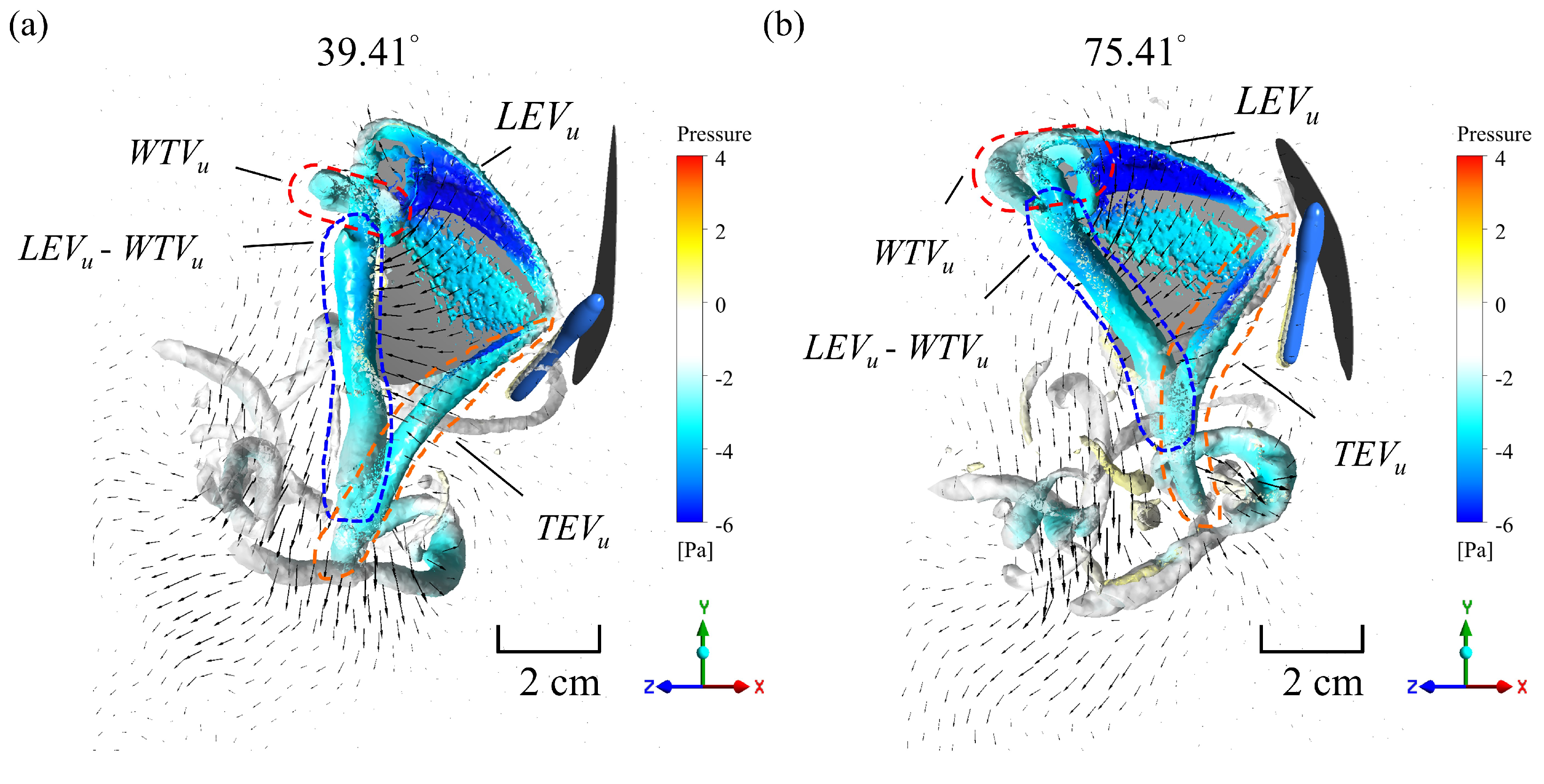
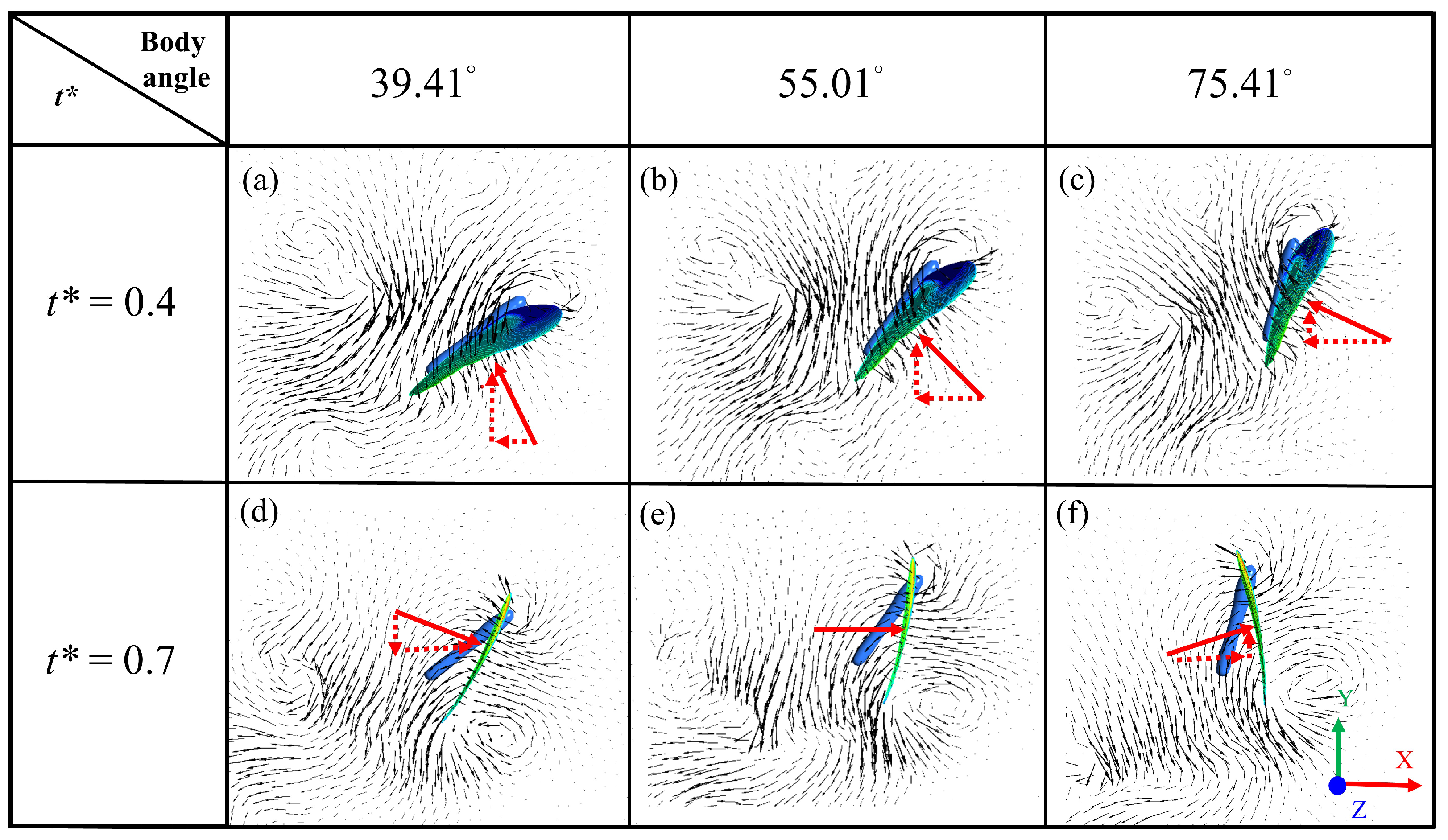
3.3. Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lai, Y.H.; Lin, Y.J.; Chang, S.K.; Yang, J.T. Effect of wing-wing interaction coupled with morphology and kinematic features of damselflies. Bioinspir. Biomim. 2020, 16, 016017. [Google Scholar] [CrossRef] [PubMed]
- Lai, Y.H.; Chang, S.K.; Lan, B.; Hsu, K.L.; Yang, J.-T. Optimal thrust efficiency for a tandem wing in forward flight using varied hindwing kinematics of a damselfly. Phys. Fluids 2022, 34, 061909. [Google Scholar] [CrossRef]
- Su, J.Y.; Ting, S.C.; Chang, Y.H.; Yang, J.T. A passerine spreads its tail to facilitate a rapid recovery of its body posture during hovering. J. R. Soc. Interface 2012, 9, 1674–1684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, J.S.; Kim, H.Y.; Han, J.H. Interactions of the wakes of two flapping wings in hover. Phys. Fluids 2019, 31, 021901. [Google Scholar]
- Henningsson, P.; Johansson, L.C. Downstroke and upstroke conflict during banked turns in butterflies. J. R. Soc. Interface 2021, 18, 20210779. [Google Scholar] [CrossRef]
- Li, C.; Dong, H. Wing kinematics measurement and aerodynamics of a dragonfly in turning flight. Bioinspir. Biomim. 2017, 12, 026001. [Google Scholar] [CrossRef]
- Bode-Oke, A.T.; Zeyghami, S.; Dong, H. Flying in reverse: Kinematics and aerodynamics of a dragonfly in backward free flight. J. R. Soc. Interface 2018, 15, 20180102. [Google Scholar] [CrossRef] [Green Version]
- Kang, C.-K.; Cranford, J.; Sridhar, M.K.; Kodali, D.; Landrum, D.B.; Slegers, N. Experimental Characterization of a Butterfly in Climbing Flight. AIAA J. 2018, 56, 15–24. [Google Scholar] [CrossRef]
- Nakata, T.; Liu, H. Aerodynamic performance of a hovering hawkmoth with flexible wings: A computational approach. Proc. R. Soc. B. 2012, 279, 722–731. [Google Scholar] [CrossRef]
- Dudley, R. Biomechanics of flight in neotropical butterflies: Morphometrics and kinematics. J. Exp. Biol. 1990, 150, 37–53. [Google Scholar] [CrossRef]
- Fei, Y.H.; Yang, J.T. Importance of body rotation during the flight of a butterfly. Phys. Rev. E 2016, 93, 033124. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.K.; Lin, Y.J.; Hsu, K.L.; Yang, J.T. Decoupling wing-shape effects of wing-swept angle and aspect ratio on a forward-flying butterfly. Phys. Rev. E 2023, 107, 065105. [Google Scholar] [CrossRef]
- Engels, T.; Kolomenskiy, D.; Schneider, K.; Farge, M.; Lehmann, F.-O.; Sesterhenn, J. Impact of turbulence on flying insects in tethered and free flight: High-resolution numerical experiments. Phys. Rev. Fluids 2019, 4, 013103. [Google Scholar] [CrossRef] [Green Version]
- Bomphrey, R.J.; Nakata, T.; Phillips, N.; Walker, S.M. Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight. Nature 2017, 544, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Zou, P.Y.; Lai, Y.H.; Yang, J.T. Effects of phase lag on the hovering flight of damselfly and dragonfly. Phys. Rev. E 2019, 100, 063102. [Google Scholar] [CrossRef]
- Liu, G.; Dong, H.; Li, C. Vortex dynamics and new lift enhancement mechanism of wing–body interaction in insect forward flight. J. Fluid Mech. 2016, 795, 634–651. [Google Scholar] [CrossRef]
- Tanaka, H.; Shimoyama, I. Forward flight of swallowtail butterfly with simple flapping motion. Bioinspir. Biomim. 2010, 5, 026003. [Google Scholar] [CrossRef]
- Senda, K.; Obara, T.; Kitamura, M.; Yokoyama, N.; Hirai, N.; Iima, M. Effects of structural flexibility of wings in flapping flight of butterfly. Bioinspir. Biomim. 2012, 7, 025002. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.K.; Lai, Y.H.; Lin, Y.J.; Yang, J.T. Enhanced lift and thrust via the translational motion between the thorax-abdomen node and the center of mass of a butterfly with a constructive abdominal oscillation. Phys. Rev. E 2020, 102, 062407. [Google Scholar] [CrossRef]
- Fuchiwaki, M.; Kuroki, T.; Tanaka, K.; Tababa, T. Dynamic behavior of the vortex ring formed on a butterfly wing. Exp. Fluids 2013, 54, 10–14. [Google Scholar] [CrossRef] [Green Version]
- Yokoyama, N.; Senda, K.; Iima, M.; Hirai, N. Aerodynamic forces and vortical structures in flapping butterfly’s forward flight. Phys. Fluids 2013, 25, 021902. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.J.; Chang, S.K.; Lai, Y.H.; Yang, J.T. Beneficial wake-capture effect for forward propulsion with a restrained wing-pitch motion of a butterfly. R. Soc. Open Sci. 2021, 8, 202172. [Google Scholar] [CrossRef]
- Sunada, S.; Kawachi, K.; Watanabe, I.; Azuma, A. Performance of a Butterfly in Take-Off Flight. J. Exp. Biol. 1993, 183, 249–277. [Google Scholar] [CrossRef]
- Wilson, T.; Albertani, R. Wing-flapping and abdomen actuation optimization for hovering in the butterfly Idea leuconoe. In Proceedings of the 52th Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Mountcastle, A.M.; Daniel, T.L. Aerodynamic and functional consequences of wing compliance. Exp. Fluids 2009, 46, 873–882. [Google Scholar] [CrossRef]
- Zheng, L.; Hedrick, T.L.; Mittal, R. Time-varying wing-twist improves aerodynamic efficiency of forward flight in butterflies. PLoS ONE 2013, 8, e53060. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K.; Aoki, T.; Yoshino, M. Effect of chordwise wing flexibility on flapping flight of a butterfly model using immersed-boundary lattice Boltzmann simulations. Phys. Rev. E 2019, 100, 013104. [Google Scholar] [CrossRef] [PubMed]
- Gehrke, A.; Richeux, J.; Uksul, E.; Mulleners, K. Aeroelastic characterisation of a bio-inspired flapping membrane wing. Bioinspir. Biomim. 2022, 17, 065004. [Google Scholar] [CrossRef] [PubMed]
- Nakata, T.; Liu, H.; Tanaka, Y.; Nishihashi, N.; Wang, X.; Sato, A. Aerodynamics of a bio-inspired flexible flapping-wing micro air vehicle. Bioinspir. Biomim. 2011, 6, 045002. [Google Scholar] [CrossRef]
- Du, G.; Sun, M. Effects of wing deformation on aerodynamic forces in hovering hoverflies. J. Exp. Biol. 2010, 213, 2273–2283. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.; Liu, X.; Shyy, W.; Qiu, H. Effects of flexibility and aspect ratio on the aerodynamic performance of flapping wings. Bioinspir. Biomim. 2018, 13, 036001. [Google Scholar] [CrossRef]
- Lua, K.B.; Lai, K.C.; Lim, T.T.; Yeo, K.S. On the aerodynamic characteristics of hovering rigid and flexible hawkmoth-like wings. Exp. Fluids 2010, 49, 1263–1291. [Google Scholar] [CrossRef]
- Young, J.; Walker, S.M.; Bomphrey, R.J.; Taylor, G.K.; Thomas, A.L. Details of Insect Wing Design and Deformation Enhance Aerodynamic Function and Flight Efficiency. Science 2009, 325, 1549–1552. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.K.; Shyy, W. Scaling law and enhancement of lift generation of an insect-size hovering flexible wing. J. R. Soc. Interface 2013, 10, 20130361. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, L.-J.; Joseph, V.J.; Lo, Y.-L.; Tang, W.-T.; Esakki, B.; Kompala, S.; Veeranjaneyulu, P. Aerodynamic Evaluation of Flapping Wings with Leading-Edge Twisting. Biomimetics 2023, 8, 134. [Google Scholar] [CrossRef] [PubMed]
- Abas, M.F.B.; Singh, B.; Ahmad, K.A.; Ng, E.Y.K.; Khan, T.; Sebaey, T.A. Dwarf Kingfisher-Inspired Bionic Flapping Wing and Its Aerodynamic Performance at Lowest Flight Speed. Biomimetics 2022, 7, 123. [Google Scholar] [CrossRef]
- Srygley, R.B.; Thomas, A.L.R. Unconventional lift-generating mechanisms in free-flying butterflies. Nature 2002, 420, 660–664. [Google Scholar] [CrossRef]
- Prasad, A.K. Stereoscopic particle image velocimetry. Curr. Sci. 2000, 79, 51–60. [Google Scholar] [CrossRef]
- Lua, K.B.; Lim, T.T.; Yeo, K.S. Scaling of Aerodynamic Forces of Three-Dimensional Flapping Wings. AIAA J. 2014, 52, 1095–1101. [Google Scholar] [CrossRef]
- Lee, Y.J.; Lua, K.B.; Lim, T.T. Aspect ratio effects on revolving wings with Rossby number consideration. Bioinspir. Biomim. 2016, 11, 056013. [Google Scholar] [CrossRef]
- Fei, Y.H.; Yang, J.T. Enhanced thrust and speed revealed in the forward flight of a butterfly with transient body translation. Phys. Rev. E 2015, 92, 033004. [Google Scholar] [CrossRef]
- Bode-Oke, A.T.; Dong, H. The reverse flight of a monarch butterfly (Danaus plexippus) is characterized by a weight-supporting upstroke and postural changes. J. R. Soc. Interface 2020, 17, 20200268. [Google Scholar] [CrossRef] [PubMed]
- Shyy, W.; Aono, H.; Chimakurthi, S.K.; Trizila, P.; Kang, C.K.; Cesnik, C.E.S.; Liu, H. Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2010, 46, 284–327. [Google Scholar] [CrossRef]
- Huang, H.; Sun, M. Forward flight of a model butterfly: Simulation by equations of motion coupled with the Navier-Stokes equations. Acta Mech. Solida Sin. 2012, 28, 1590–1601. [Google Scholar] [CrossRef]


| Simulation | Experiment (Average ± SEM) | |
|---|---|---|
| Total mass (g) | 0.35 | 0.36 ± 0.04 |
| Flapping frequency (Hz) | 11.00 | 10.77 ± 0.38 |
| Wingspan (mm) | 48.00 | 47.50 ± 0.63 |
| Mean wing chord (mm) | 20.11 | 19.79 ± 0.14 |
| Aspect ratio | 2.4 | 2.40 ± 0.03 |
| Wing Flexibility | Mean Lift (mN) | Mean Thrust (mN) | Total Force (mN) | Power (mW) | L/P (N/W) | T/P (N/W) | F/P (N/W) |
|---|---|---|---|---|---|---|---|
| K = 0 | 1.48 | 0.449 | 5.73 | 7.44 | 0.198 | 0.060 | 0.770 |
| (−6.9%) | (−45.6%) | (4.2%) | (6.6%) | (−13.2%) | (−49.2%) | (−2.3%) | |
| K = 1 | 1.59 | 0.825 | 5.50 | 6.98 | 0.228 | 0.118 | 0.788 |
| K = 2 | 1.67 | 0.892 | 5.22 | 6.30 | 0.265 | 0.141 | 0.829 |
| (5.0%) | (8.1%) | (−5.1%) | (−9.7%) | (16.2%) | (19.5%) | (5.2%) | |
| K = 3 | 1.81 | 0.839 | 4.92 | 5.90 | 0.307 | 0.142 | 0.834 |
| (13.8%) | (1.7%) | (−10.5%) | (−15.5%) | (34.6%) | (20.3%) | (5.8%) |
| Body Angle | Mean Lift (mN) | Mean Thrust (mN) | Total Force (mN) | Power (mW) | L/P (N/W) | T/P (N/W) | F/P (N/W) |
|---|---|---|---|---|---|---|---|
| 39.41° | 1.30 | 1.19 | 5.56 | 6.92 | 0.188 | 0.172 | 0.305 |
| (−18.2%) | (44.2%) | (1.1%) | (−0.9%) | (−17.5%) | (45.8%) | (0.3%) | |
| 55.01° | 1.59 | 0.825 | 5.50 | 6.98 | 0.228 | 0.118 | 0.304 |
| 75.41° | 1.77 | 0.224 | 5.59 | 6.94 | 0.255 | 0.032 | 0.307 |
| (11.3%) | (−72.9%) | (1.6%) | (−0.6%) | (11.8%) | (−72.9%) | (1.0%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.-H.; Tang, C.-H.; Lin, Y.-J.; Yeh, S.-I.; Yang, J.-T. The Lift Effects of Chordwise Wing Deformation and Body Angle on Low-Speed Flying Butterflies. Biomimetics 2023, 8, 287. https://doi.org/10.3390/biomimetics8030287
Fang Y-H, Tang C-H, Lin Y-J, Yeh S-I, Yang J-T. The Lift Effects of Chordwise Wing Deformation and Body Angle on Low-Speed Flying Butterflies. Biomimetics. 2023; 8(3):287. https://doi.org/10.3390/biomimetics8030287
Chicago/Turabian StyleFang, Yan-Hung, Chia-Hung Tang, You-Jun Lin, Szu-I Yeh, and Jing-Tang Yang. 2023. "The Lift Effects of Chordwise Wing Deformation and Body Angle on Low-Speed Flying Butterflies" Biomimetics 8, no. 3: 287. https://doi.org/10.3390/biomimetics8030287
APA StyleFang, Y.-H., Tang, C.-H., Lin, Y.-J., Yeh, S.-I., & Yang, J.-T. (2023). The Lift Effects of Chordwise Wing Deformation and Body Angle on Low-Speed Flying Butterflies. Biomimetics, 8(3), 287. https://doi.org/10.3390/biomimetics8030287