A Comparative and Collaborative Study of the Hydrodynamics of Two Swimming Modes Applicable to Dolphins
Abstract
:1. Introduction
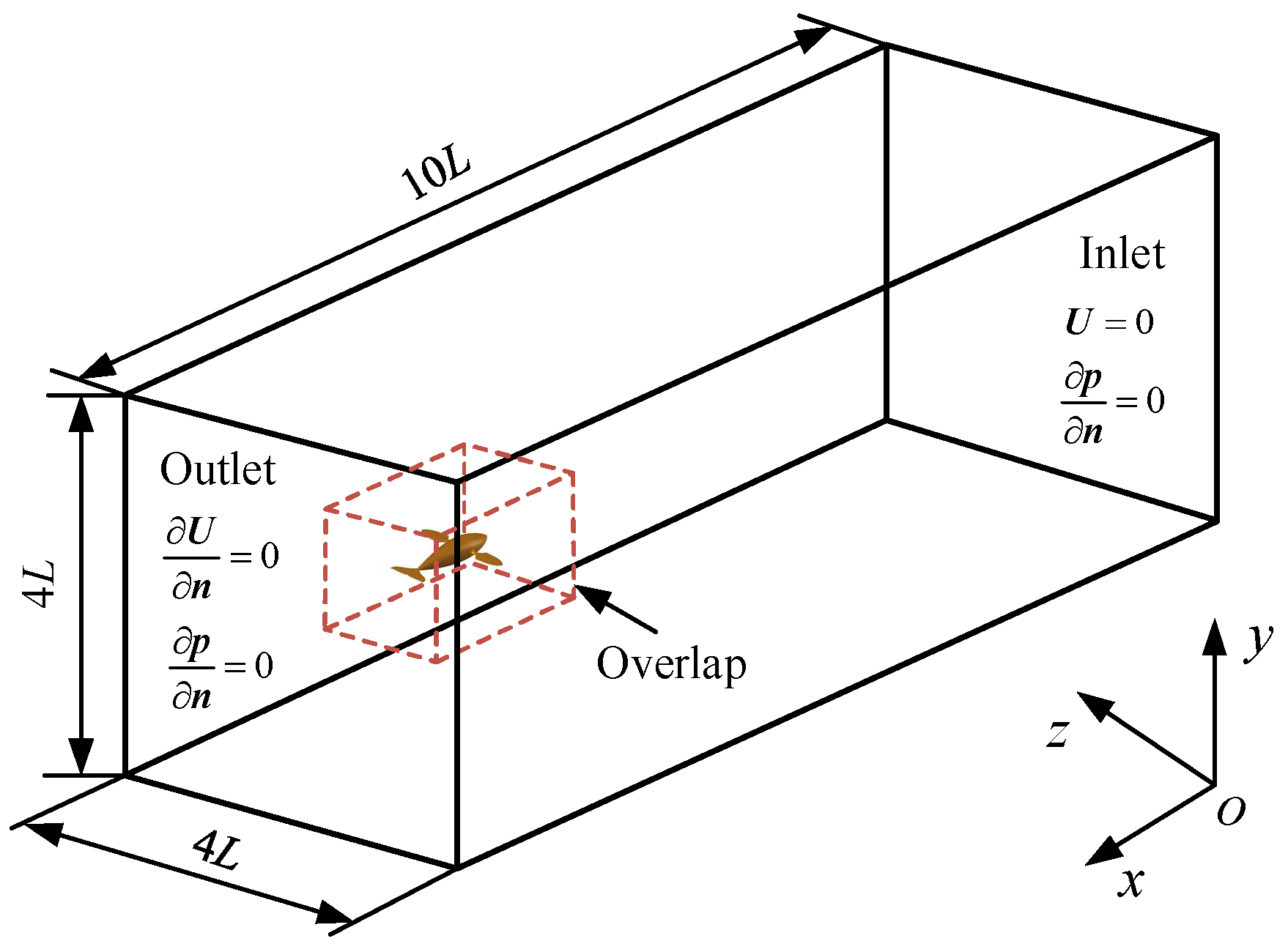
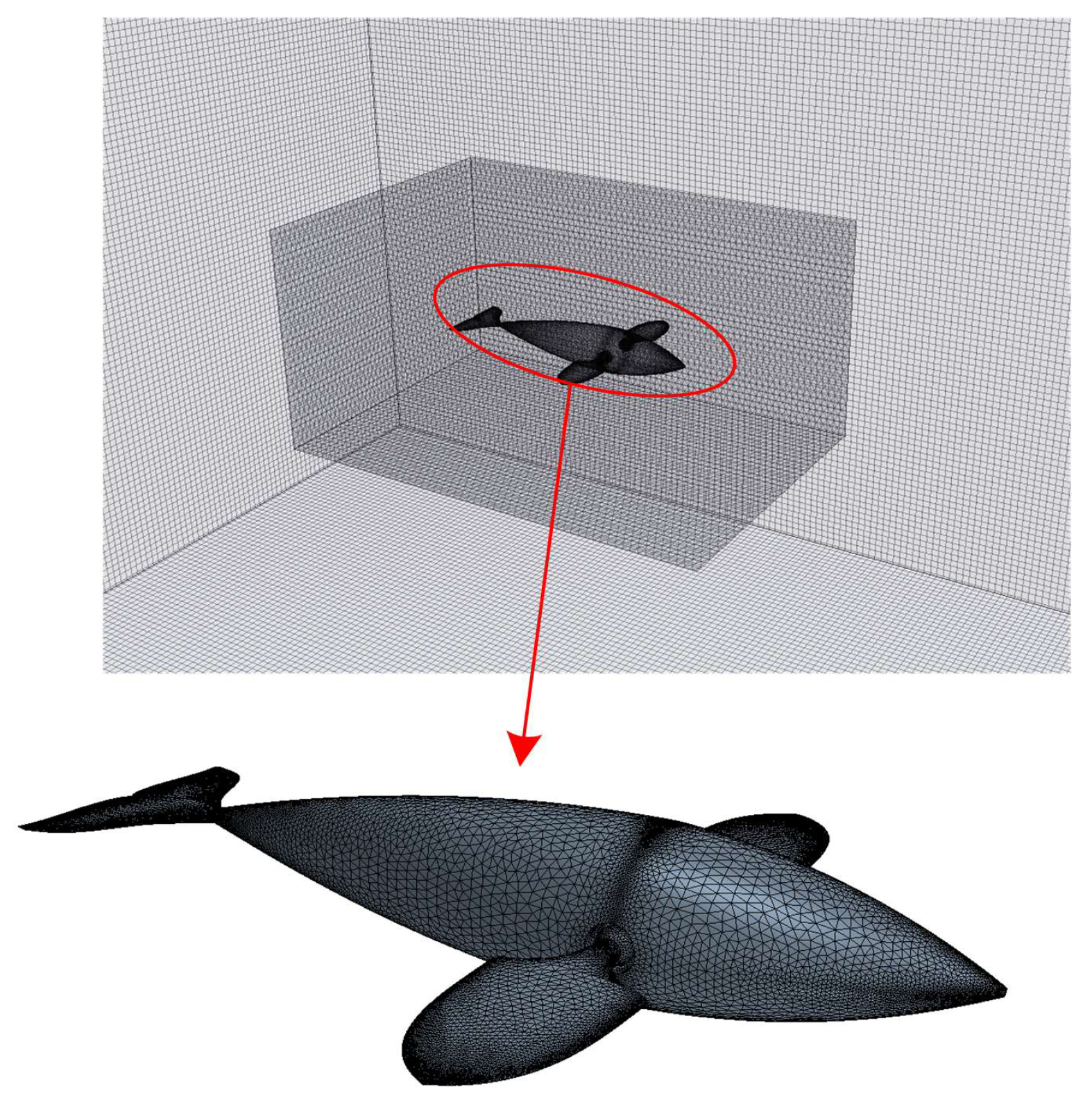
2. Materials and Methods
2.1. Physical Model
2.2. Kinematics
2.3. Kinematics
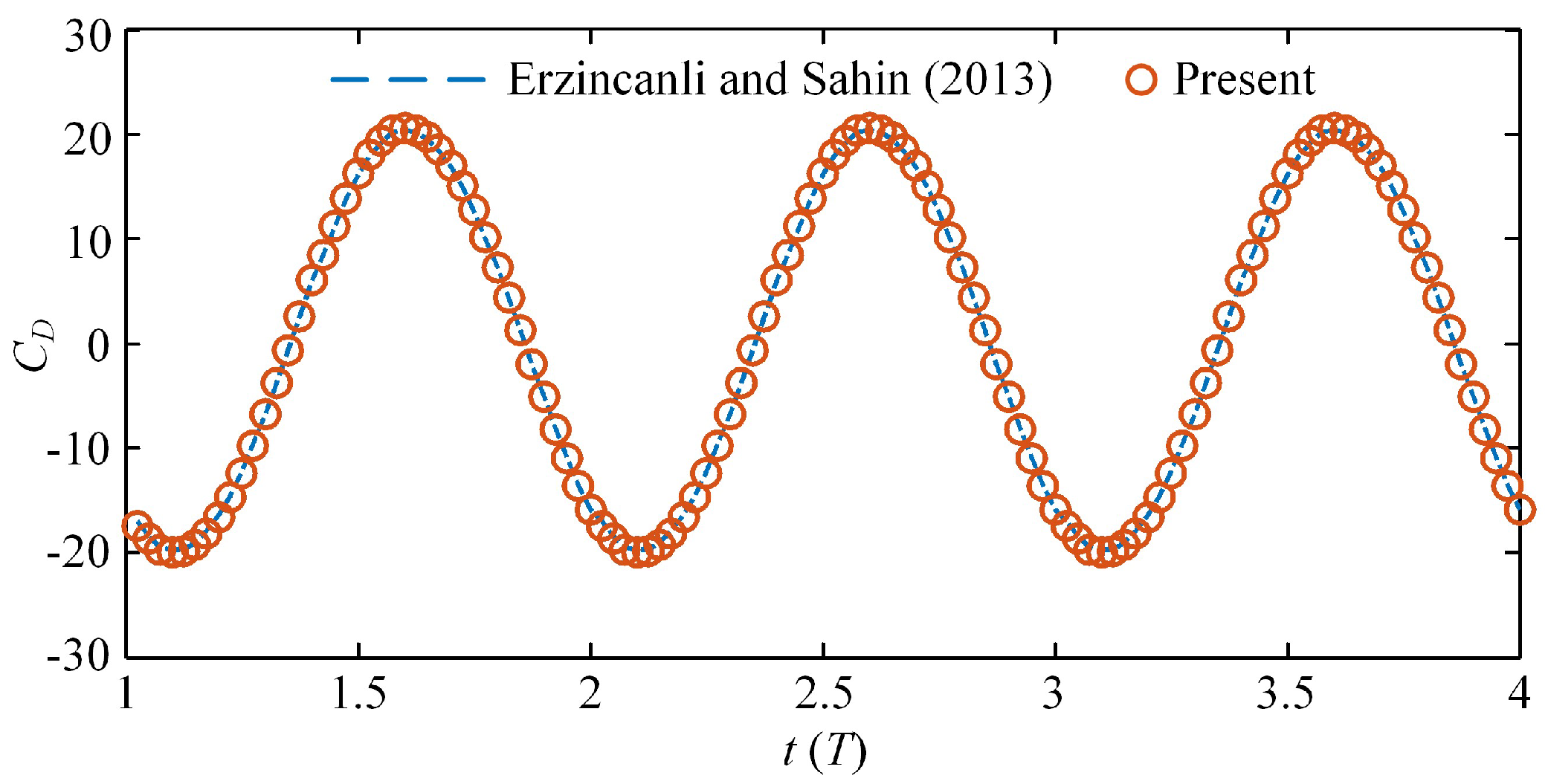
2.4. Numerical Method and Validation Test
2.5. Calculation of Performance Parameters
3. Results and Discussion
3.1. Time History Variations of Performance Parameters
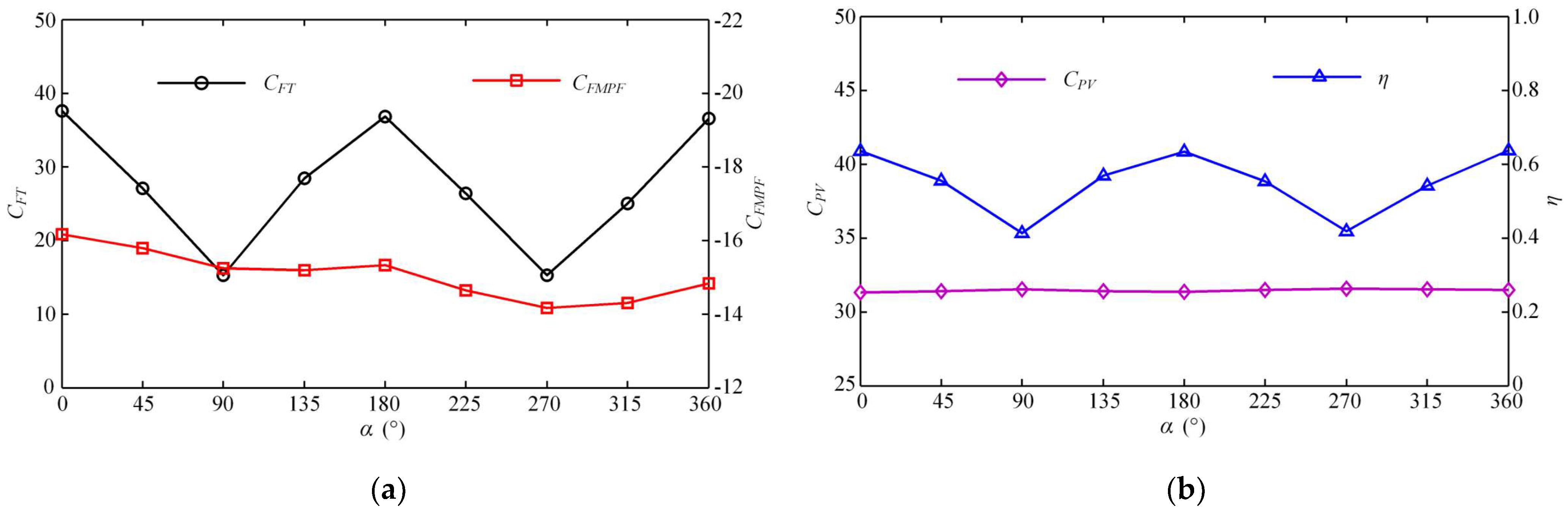
3.2. Effect of Starting Phase Difference on Self-Propelled Performance
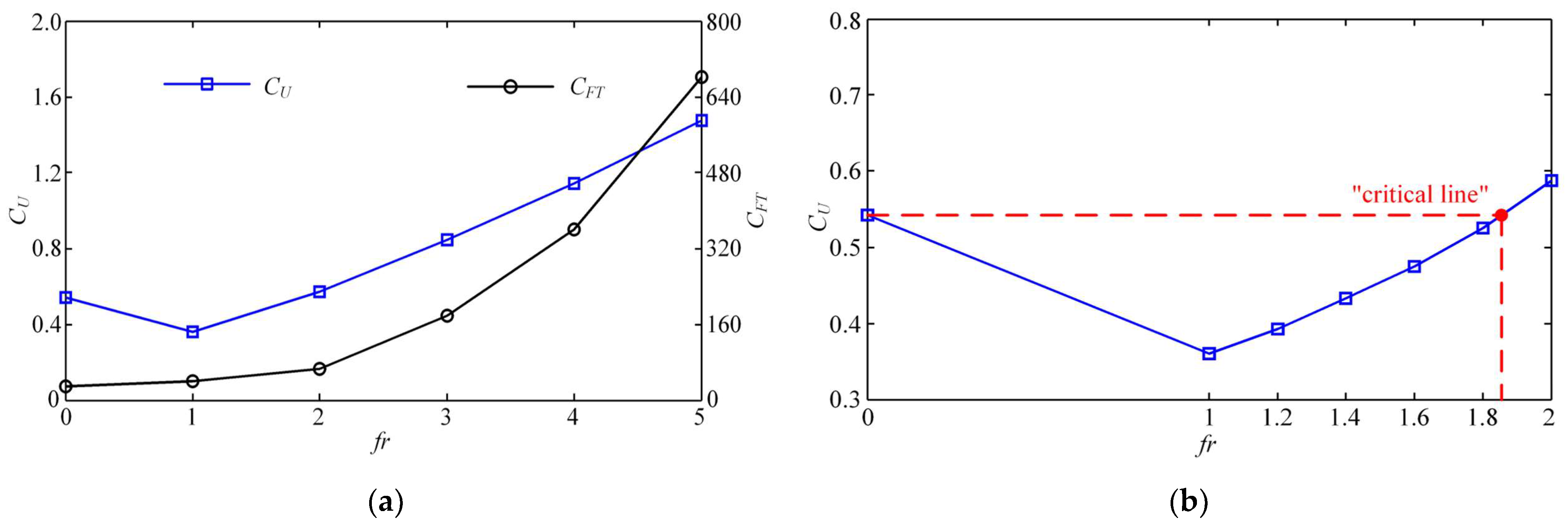
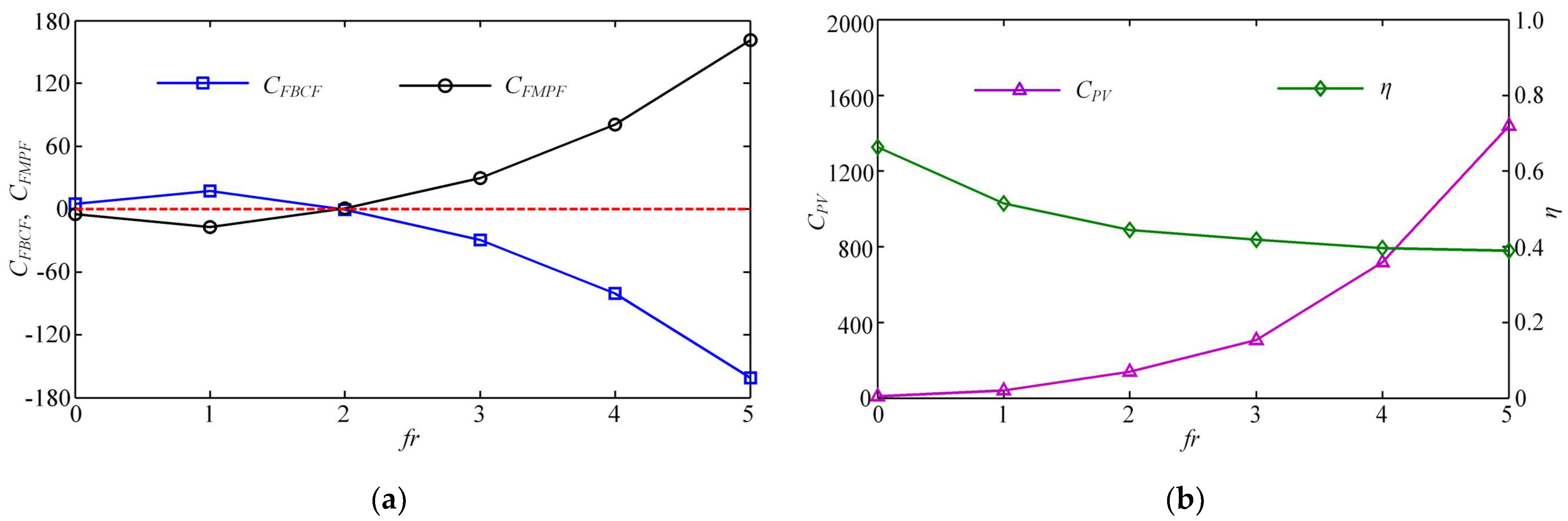
3.3. Effect of Frequency Ratio on Self-Propelled Performance
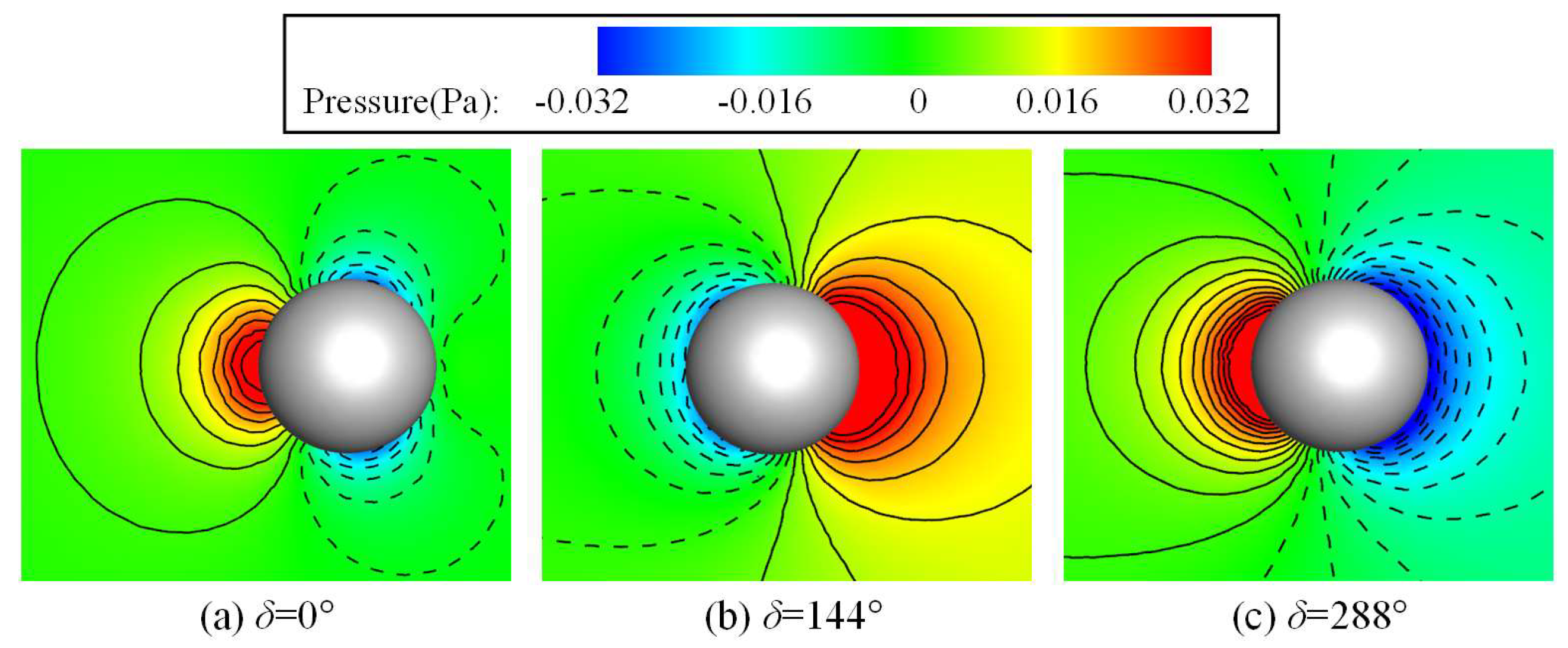
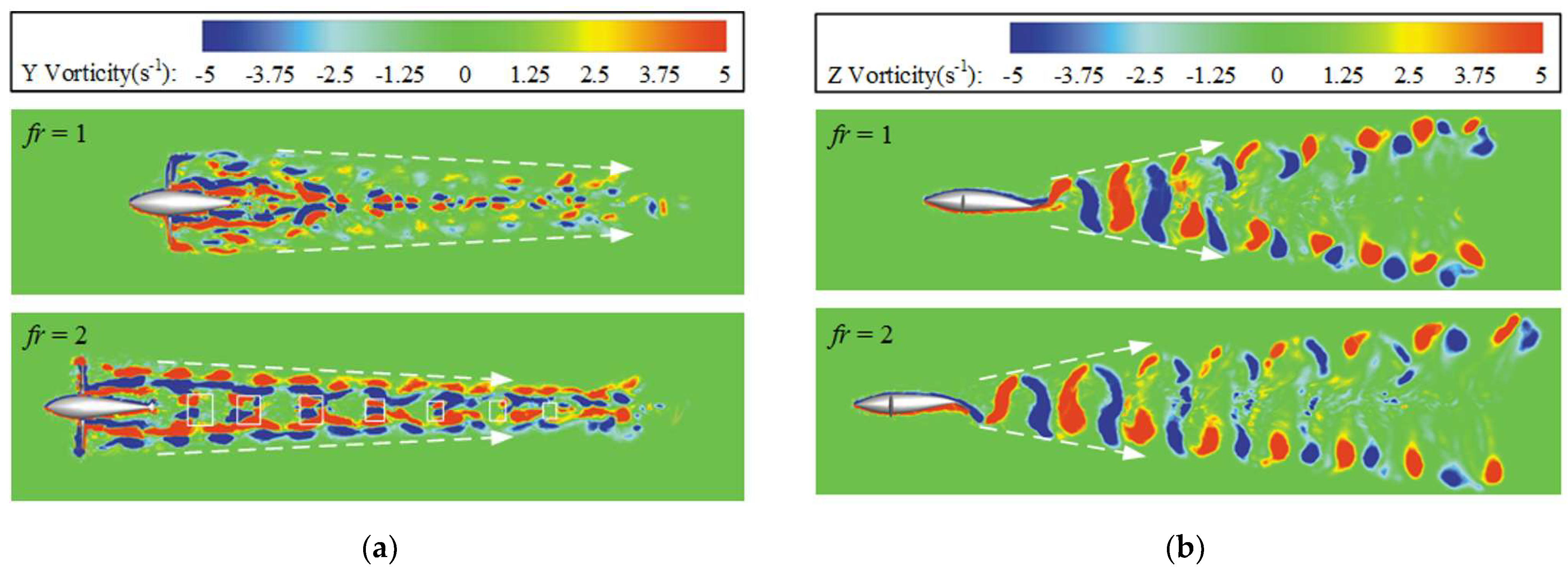
3.4. Three-Dimensional Flow Structure
4. Conclusions
- (1)
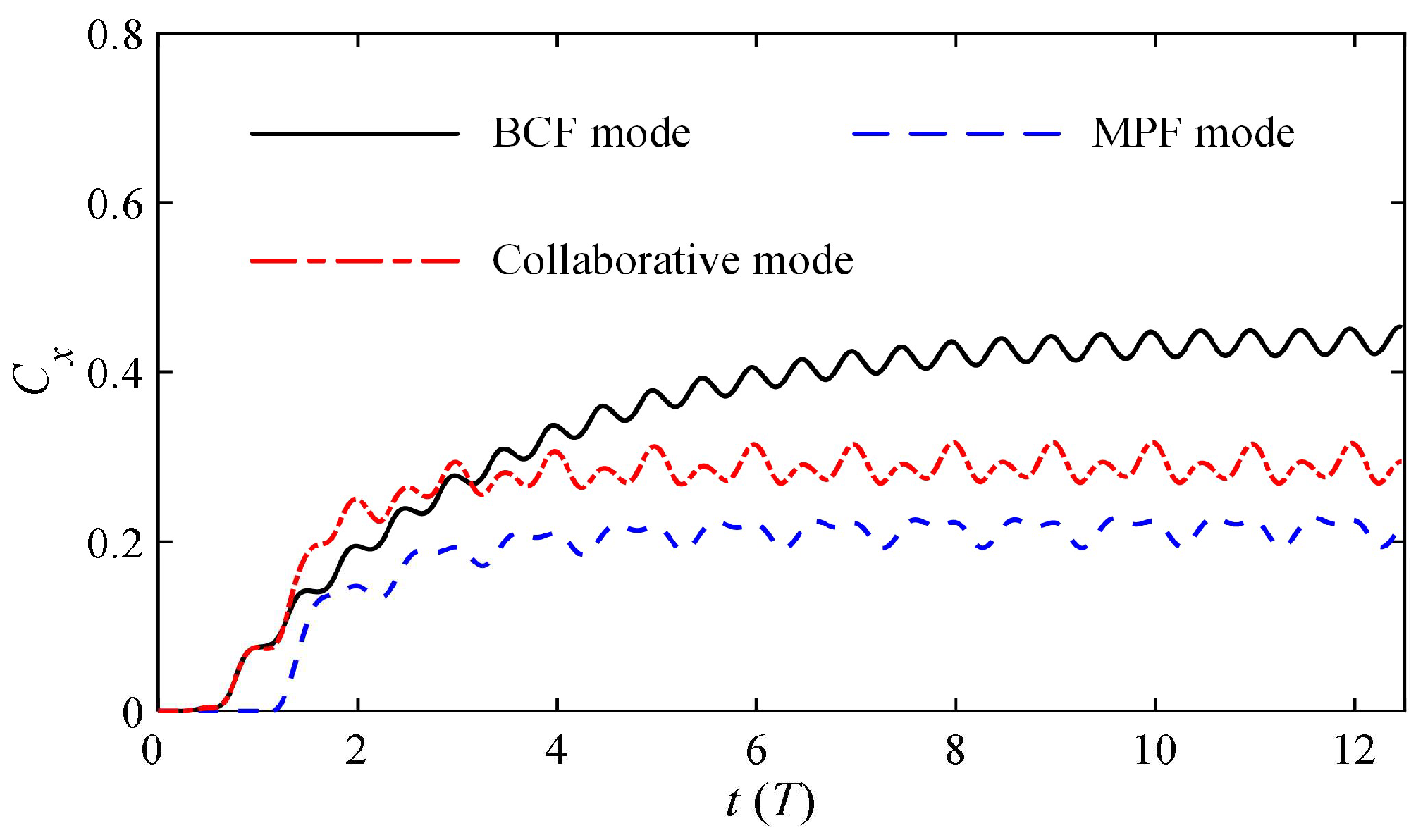
- Given the same frequency, the swimming process gradually converges, and the propulsion effect of the swimmer in the BCF mode is better than that in the MPF mode and the collaborative mode, which is mainly reflected in the value of the final steady-state swimming velocity and the related thrust force. It was found that the participation of the MPF module does not promote the acceleration of the swimming, but plays a cumbersome role. Fortunately, it was found in this work that there are two ways to improve their collaborative performance; one is to adjust the phase difference between the two modes, and the other is to optimize the frequency ratio between the two modes.
- (2)
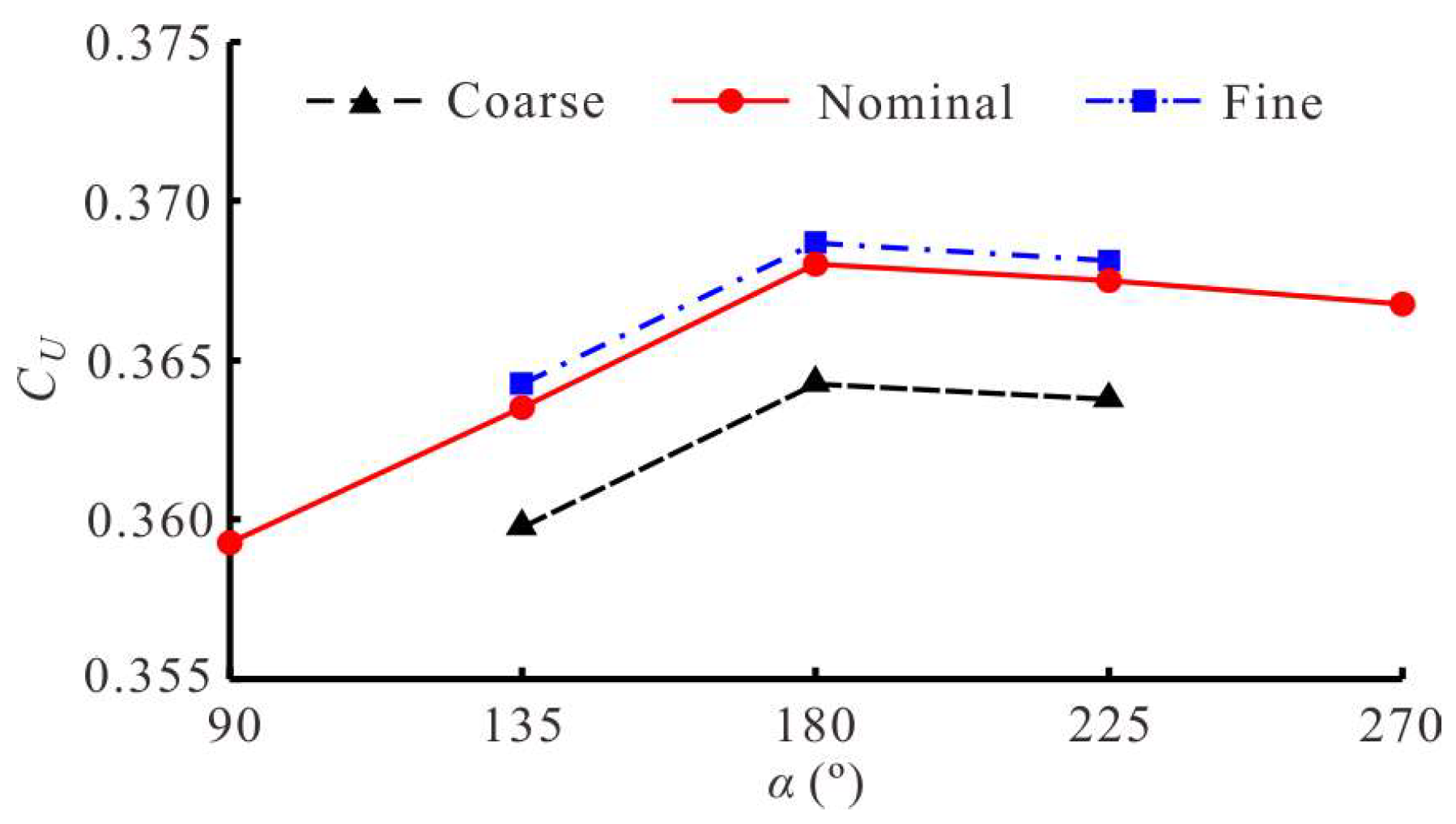
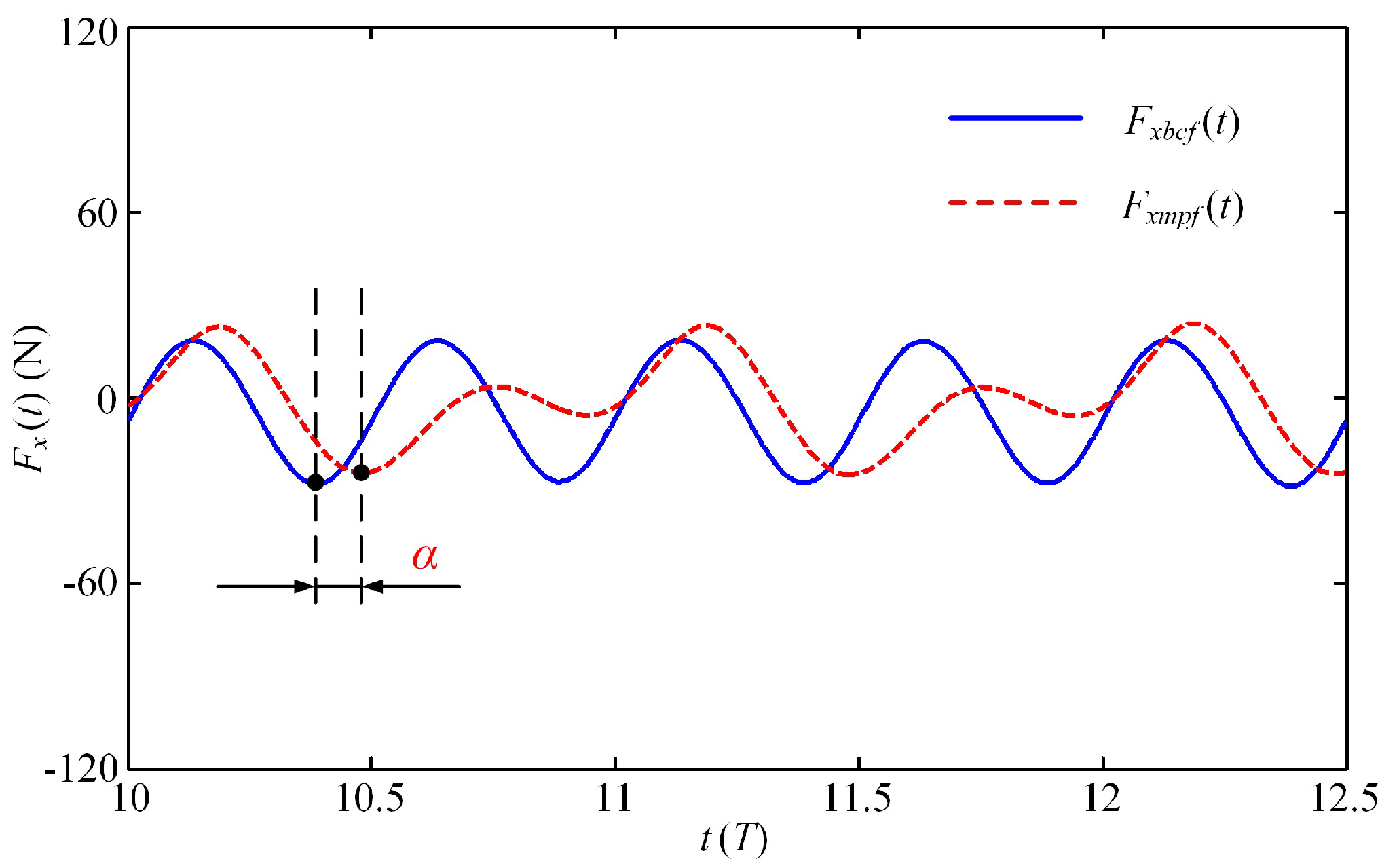
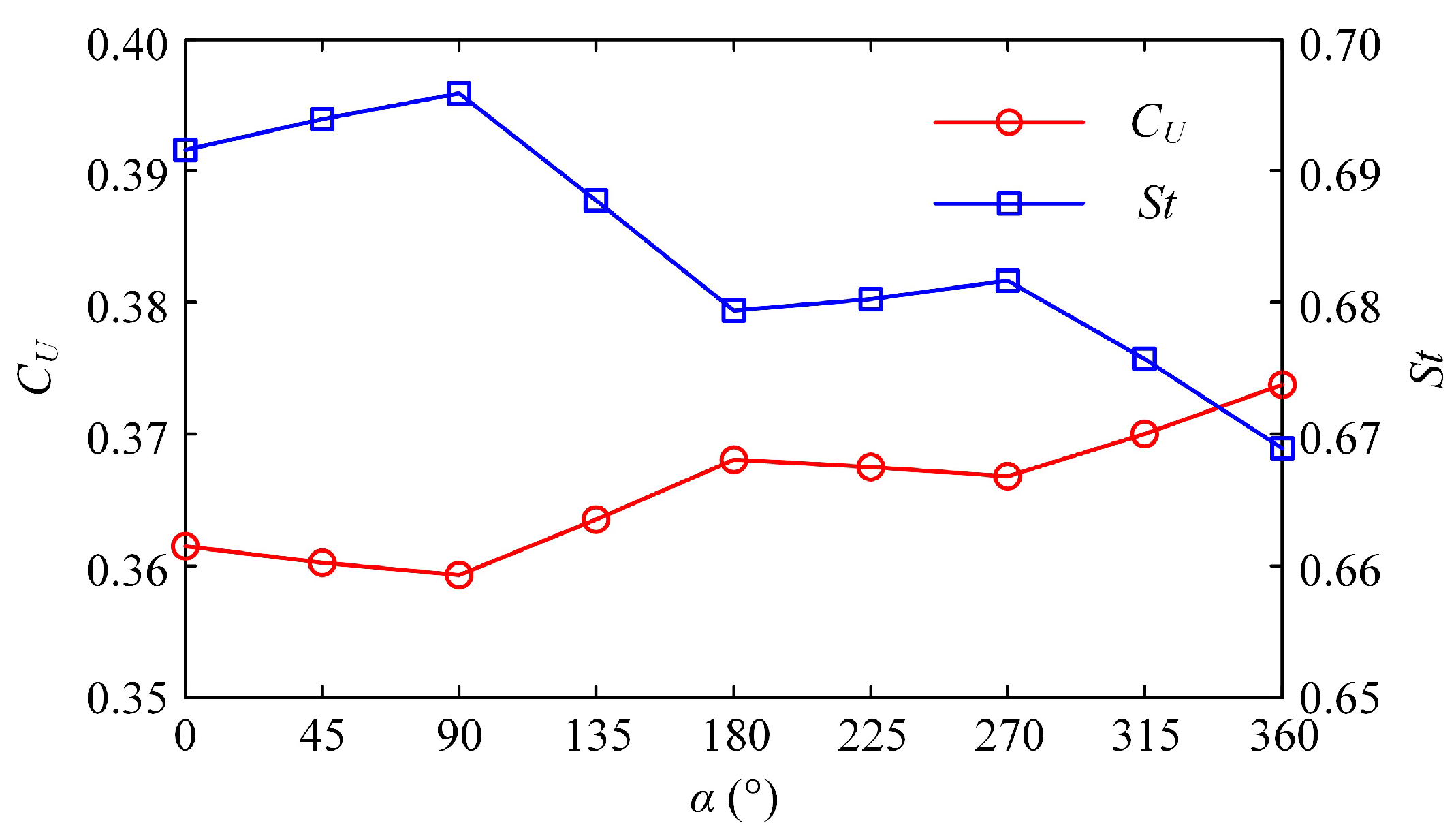
- The definition of the starting phase difference α is helpful to analyze the superposition effect of the two modules in the collaborative mode. When α is a multiple of 180°, the final steady-state velocity reaches the maximum. When α is a multiple of 90°, the resistance generated by the MPF mode is relatively large, and the collaborative effect of the two modes is not ideal at this time. The starting phase difference α is perhaps the most direct variable to adjust the collaboration of the two modes, and analyzing its quantitative impact is an effective way to explore the contribution of each module to propulsion in the collaborative mode.
- (3)
- It was confirmed that the increase of the frequency ratio β can effectively improve the propulsion effect of the MPF mode. When β is taken as a critical value between 1.8 and 2, the final steady-state velocity of the swimmer in collaboration mode can reach the value of the swimmer with single BCF propulsion. As β further increases, the effect of the MPF mode is more obvious and the value of CFMPF increases with a steeper growth trend. When the swimmer reaches the high-frequency ratio, the steady-state velocity increases, while decreases somewhat and is not as good as the low-frequency ratio. These findings suggest that each module of the swimmer contributes unequally to propulsion when multiple modules work together. Therefore, in a sense, it is possible to rationally allocate their contributions to the entire swimmer by adjusting the parameters between the modules, so as to achieve the best collaborative performance, such as the fastest steady-state swimming velocity, the largest thrust or the highest propulsion efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, J. Maneuvering and Control of a Biomimetic Autonomous Underwater Vehicle. Auton. Robot. 2009, 26, 241–249. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Lapierre, L.; Zhang, J.; Zhang, Q. Jialei Survey on Fuzzy-Logic-Based Guidance and Control of Marine Surface Vehicles and Underwater Vehicles. Int. J. Fuzzy Syst. 2018, 20, 572–586. [Google Scholar] [CrossRef]
- Roper, D.T.; Sharma, S.; Sutton, R.; Culverhouse, P. A Review of Developments towards Biologically Inspired Propulsion Systems for Autonomous Underwater Vehicles. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2011, 225, 77–96. [Google Scholar] [CrossRef]
- Wen, L.; Wang, T.; Wu, G.; Liang, J. Quantitative Thrust Efficiency of a Self-Propulsive Robotic Fish: Experimental Method and Hydrodynamic Investigation. IEEE/ASME Trans. Mechatron. 2013, 18, 1027–1038. [Google Scholar] [CrossRef]
- Liu, L.; Chen, M.; Yu, J.; Zhang, Z.; Wang, X. Full-Scale Simulation of Self-Propulsion for a Free-Running Submarine. Phys. Fluids 2021, 33, 047103. [Google Scholar] [CrossRef]
- Posa, A.; Balaras, E. Large-Eddy Simulations of a Notional Submarine in Towed and Self-Propelled Configurations. Comput. Fluids 2018, 165, 116–126. [Google Scholar] [CrossRef]
- Lauder, G.V.; Tytell, E.D. Hydrodynamics of Undulatory Propulsion. Fish Physiol. 2005, 23, 425–468. [Google Scholar] [CrossRef]
- Chen, Z.; Shatara, S.; Tan, X. Modeling of Biomimetic Robotic Fish Propelled by an Ionic Polymermetal Composite Caudal Fin. IEEE/ASME Trans. Mechatron. 2010, 15, 448–459. [Google Scholar] [CrossRef]
- Park, Y.J.; Jeong, U.; Lee, J.; Kwon, S.R.; Kim, H.Y.; Cho, K.J. Kinematic Condition for Maximizing the Thrust of a Robotic Fish Using a Compliant Caudal Fin. IEEE Trans. Robot. 2012, 28, 1216–1227. [Google Scholar] [CrossRef]
- Hu, Y.; Liang, J.; Wang, T. Mechatronic Design and Locomotion Control of a Robotic Thunniform Swimmer for Fast Cruising. Bioinspiration Biomim. 2015, 10, 026006. [Google Scholar] [CrossRef]
- Feilich, K.L.; Lauder, G.V. Passive Mechanical Models of Fish Caudal Fins: Effects of Shape and Stiffness on Self-Propulsion. Bioinspiration Biomim. 2015, 10, 036002. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Xia, D.; Yang, G.; Wang, X.; Shi, Y. Hydrodynamics of the Self-Diving Function of Thunniform Swimmer Relying on Switching the Caudal Fin Shape. J. Mar. Sci. Technol. 2023, 28, 326–340. [Google Scholar] [CrossRef]
- Chung, H.; Cao, S.; Philen, M.; Beran, P.S.; Wang, K.G. CFD-CSD Coupled Analysis of Underwater Propulsion Using a Biomimetic Fin-and-Joint System. Comput. Fluids 2018, 172, 54–66. [Google Scholar] [CrossRef]
- Shi, G.; Xiao, Q.; Zhu, Q.; Liao, W. Fluid-Structure Interaction Modeling on a 3D Ray-Strengthened Caudal Fin. Bioinspiration Biomim. 2019, 14, 036012. [Google Scholar] [CrossRef] [PubMed]
- Krishnadas, A.; Ravichandran, S.; Rajagopal, P. Analysis of Biomimetic Caudal Fin Shapes for Optimum Propulsive Efficiency. Ocean Eng. 2018, 153, 132–142. [Google Scholar] [CrossRef]
- Yu, J.; Su, Z.; Wu, Z.; Tan, M. Development of a Fast-Swimming Dolphin Robot Capable of Leaping. IEEE/ASME Trans. Mechatron. 2016, 21, 2307–2316. [Google Scholar] [CrossRef]
- Liu, H.; Wassersug, R.J.; Kawachi, K. A Computational Fluid Dynamics Study of Tadpole Swimming. J. Exp. Biol. 1996, 199, 1245–1260. [Google Scholar] [CrossRef]
- Xia, D.; Chen, W.S.; Liu, J.K.; Luo, X. The Energy-Saving Advantages of Burst-and-Glide Mode for Thunniform Swimming. J. Hydrodyn. 2018, 30, 1072–1082. [Google Scholar] [CrossRef]
- Singh, N.; Gupta, A.; Mukherjee, S. A Dynamic Model for Underwater Robotic Fish with a Servo Actuated Pectoral Fin. SN Appl. Sci. 2019, 1, 659. [Google Scholar] [CrossRef]
- Arastehfar, S.; Chew, C.M.; Jalalian, A.; Gunawan, G.; Yeo, K.S. A Relationship between Sweep Angle of Flapping Pectoral Fins and Thrust Generation. J. Mech. Robot. 2019, 11, 011014. [Google Scholar] [CrossRef]
- Di Santo, V.; Blevins, E.L.; Lauder, G.V. Batoid Locomotion: Effects of Speed on Pectoral Fin Deformation in the Little Skate, Leucoraja Erinacea. J. Exp. Biol. 2017, 220, 705–712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, C.L.; Ting, S.C.; Yeh, M.K.; Yang, J.T. Three-Dimensional Numerical Simulation of Hydrodynamic Interactions between Pectoral-Fin Vortices and Body Undulation in a Swimming Fish. Phys. Fluids 2011, 23, 091901. [Google Scholar] [CrossRef]
- Weng, J.; Zhu, Y.; Du, X.; Yang, G.; Hu, D. Theoretical and Numerical Studies on a Five-Ray Flexible Pectoral Fin during Labriform Swimming. Bioinspiration Biomim. 2020, 15, 016007. [Google Scholar] [CrossRef] [PubMed]
- Sampath, K.; Geder, J.D.; Ramamurti, R.; Pruessner, M.D.; Koehler, R. Hydrodynamics of Tandem Flapping Pectoral Fins with Varying Stroke Phase Offsets. Phys. Rev. Fluids 2020, 5, 094101. [Google Scholar] [CrossRef]
- Behbahani, S.B.; Tan, X. Design and Modeling of Flexible Passive Rowing Joint for Robotic Fish Pectoral Fins. IEEE Trans. Robot. 2016, 32, 1119–1132. [Google Scholar] [CrossRef]
- Xu, Y.G.; Wan, D.C. Numerical Simulation of Fish Swimming with Rigid Pectoral Fins. J. Hydrodyn. 2012, 24, 263–272. [Google Scholar] [CrossRef]
- Bianchi, G.; Cinquemani, S.; Schito, P.; Resta, F. A Numerical Model for the Analysis of the Locomotion of a Cownose Ray. J. Fluids Eng. Trans. ASME 2022, 144, 031203. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Z. Numerical Investigation on Novel Conceptual Design of Hybrid-Driven Autonomous Underwater Glider with Active Twin Flapping Foils. Ocean Eng. 2020, 214, 107867. [Google Scholar] [CrossRef]
- Li, Z.; Xia, D.; Zhou, X.; Cao, J.; Chen, W.; Wang, X. The Hydrodynamics of Self-Rolling Locomotion Driven by the Flexible Pectoral Fins of 3-D Bionic Dolphin. J. Ocean Eng. Sci. 2021, 7, 29–40. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, Z.; Yu, J.; Tan, M. Sliding Mode Observer-Based Heading Control for a Gliding Robotic Dolphin. IEEE Trans. Ind. Electron. 2017, 64, 6815–6824. [Google Scholar] [CrossRef]
- Dong, H.; Mittal, R.; Najjar, F. Wake Topology and Hydrodynamic Performance of Low-Aspect-Ratio Flapping Foils By. Fluid Mech. 2006, 566, 309–343. [Google Scholar] [CrossRef] [Green Version]
- Barrett, D.; Grosenbaugh, M.; Triantafyllou, M. Optimal Control of a Flexible Hull Robotic Undersea Vehicle Propelled by an Oscillating FoilIn. In Proceedings of the Symposium on Autonomous Underwater Vehicle Technology, Monterey, CA, USA, 2–6 June 1996; pp. 1–9. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Triantafyllou, G.S.; Yue, D.K.P. Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 2000, 32, 33–53. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, C.; Zhang, Z.; Tian, Q.; Sun, A.; Yuan, L.; Zhang, L. Review of Multi-Fin Propulsion and Functional Materials of Underwater Bionic Robotic Fish. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 7350–7367. [Google Scholar] [CrossRef]
- Tytell, E.D. Median Fin Function in Bluegill Sunfish Lepomis Macrochirus: Streamwise Vortex Structure during Steady Swimming. J. Exp. Biol. 2006, 209, 1516–1534. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Li, G.; Li, R.; Xiao, Q.; Liu, H. Multi-Fin Kinematics and Hydrodynamics in Pufferfish Steady Swimming. Ocean Eng. 2018, 158, 111–122. [Google Scholar] [CrossRef] [Green Version]
- Berlinger, F.; Saadat, M.; Haj-Hariri, H.; Lauder, G.V.; Nagpal, R. Fish-like Three-Dimensional Swimming with an Autonomous, Multi-Fin, and Biomimetic Robot. Bioinspiration Biomim. 2021, 16, 026018. [Google Scholar] [CrossRef]
- Castano, M.L.; Tan, X. Trajectory Tracking Control of Rowing Pectoral Fin-Actuated Robotic Fish. IEEE/ASME Trans. Mechatron. 2022, 27, 2007–2015. [Google Scholar] [CrossRef]
- De Silva, L.W.A.; Yamaguchi, H. Numerical Study on Active Wave Devouring Propulsion. J. Mar. Sci. Technol. 2012, 17, 261–275. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.K.; Liu, H.X.; Su, Y.Y.; Su, Y.M. Numerical Study on the Hydrodynamics of C-Turn Maneuvering of a Tuna-like Fish Body under Self-Propulsion. J. Fluids Struct. 2020, 94, 102954. [Google Scholar] [CrossRef]
- Erzincanli, B.; Sahin, M. An Arbitrary Lagrangian-Eulerian Formulation for Solving Moving Boundary Problems with Large Displacements and Rotations. J. Comput. Phys. 2013, 255, 660–679. [Google Scholar] [CrossRef]
- Lee, J.; You, D. An Implicit Ghost-Cell Immersed Boundary Method for Simulations of Moving Body Problems with Control of Spurious Force Oscillations. J. Comput. Phys. 2013, 233, 295–314. [Google Scholar] [CrossRef]
- Wu, Z.; Yu, J.; Yuan, J.; Tan, M.; Qi, S. Gliding Motion Regulation of a Robotic Dolphin Based on a Controllable Fluke. IEEE Trans. Ind. Electron. 2020, 67, 2945–2953. [Google Scholar] [CrossRef]
- Tytell, E.D.; Lauder, G.V. The Hydrodynamics of Eel Swimming: I. Wake Structure. J. Exp. Biol. 2004, 207, 1825–1841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borazjani, I.; Sotiropoulos, F. Numerical Investigation of the Hydrodynamics of Carangiform Swimming in the Transitional and Inertial Flow Regimes. J. Exp. Biol. 2008, 211, 1541–1558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Xia, D.; Cao, J.; Chen, W.; Wang, X. Hydrodynamics Study of Dolphin’s Self-Yaw Motion Realized by Spanwise Flexibility of Caudal Fin. J. Ocean Eng. Sci. 2022, 7, 213–224. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, D.; Li, Z.; Lei, M.; Yan, H.; Zhou, Z. A Comparative and Collaborative Study of the Hydrodynamics of Two Swimming Modes Applicable to Dolphins. Biomimetics 2023, 8, 311. https://doi.org/10.3390/biomimetics8030311
Xia D, Li Z, Lei M, Yan H, Zhou Z. A Comparative and Collaborative Study of the Hydrodynamics of Two Swimming Modes Applicable to Dolphins. Biomimetics. 2023; 8(3):311. https://doi.org/10.3390/biomimetics8030311
Chicago/Turabian StyleXia, Dan, Zhihan Li, Ming Lei, Han Yan, and Zilong Zhou. 2023. "A Comparative and Collaborative Study of the Hydrodynamics of Two Swimming Modes Applicable to Dolphins" Biomimetics 8, no. 3: 311. https://doi.org/10.3390/biomimetics8030311
APA StyleXia, D., Li, Z., Lei, M., Yan, H., & Zhou, Z. (2023). A Comparative and Collaborative Study of the Hydrodynamics of Two Swimming Modes Applicable to Dolphins. Biomimetics, 8(3), 311. https://doi.org/10.3390/biomimetics8030311





