Teaching–Learning Optimization Algorithm Based on the Cadre–Mass Relationship with Tutor Mechanism for Solving Complex Optimization Problems
Abstract
:1. Introduction
2. Related Work
2.1. Teacher Phase
2.2. Learner Phase
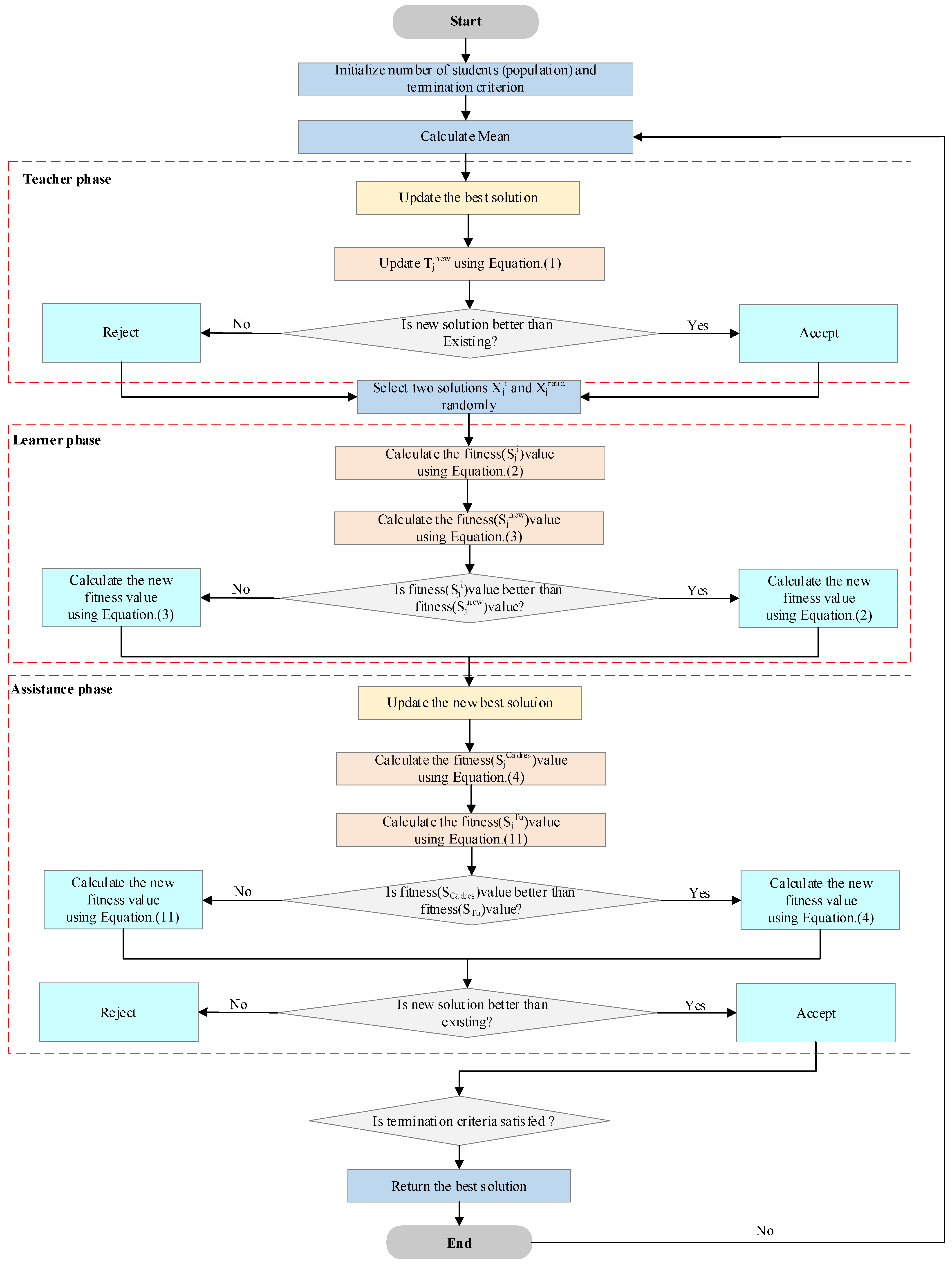
3. The Proposed TLOCTO
3.1. Inspiration
3.2. New Learner Strategy
3.3. Assistance Phase
3.3.1. Cadre–Mass Relationship Strategy
3.3.2. Tutor Mechanism
| Algorithm 1: The framework of the TLOCTO algorithm |
| 1: Initialize the solution’s positions of population N randomly; 2: Set the maximum number of iterations (Tmax) and other parameters; 3: For t = 1 to Tmax do; 4: Calculate the average of the population; 5: Select the teacher; 6: Calculate the fitness function for the given solutions using Equation (1); 7: Find the best solution position and fitness value so far; 8: For i = 1 to N do; 9: Update the individual position using Equation (2); 10: Update the individual position using Equation (3); 11: Compare and select the one that generates the smaller value as the update position; 12: For i = 1 to N do; 13: Update the individual position using Equation (4); 14: Update the individual position using Equation (11); 15: Calculate the fitness values Fitness () and Fitness (); 16: If Fitness () < Fitness (), then 17: Obtain the best position and the best fitness value of the current iteration using Equation (4); 18: else; 19: Obtain the best position and the best fitness value of the current iteration using Equation (11); 20: end if; 21: end for; 22: end for; 23: Return the best solution. |
3.4. Computational Complexity Analysis
4. Experimental Results and Detailed Analyses
4.1. Qualitative Evaluation
4.1.1. Convergence Behavior Analysis
4.1.2. Population Diversity Analysis
4.1.3. Exploration and Exploitation Analysis
4.2. Performance Indicators
4.3. TLOCTO’s Performance on the Benchmark Test Functions
4.3.1. Comparison Using the Benchmark Test Functions
4.3.2. Analysis of Convergence Behavior
4.4. TLOCTO’s Performance on CEC 2020 Test Functions
4.4.1. Analysis of CEC 2020 Test Function
4.4.2. Analysis of Convergence Behavior
4.4.3. Analysis of Scalability
5. Mechanical Engineering Application Problems
5.1. Planetary Gear Train Design Optimization Problem
5.2. Robot Gripper Problem
5.3. Speed Reducer Design Problem
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Function | Dimensions | Range | fmin |
|---|---|---|---|
| 30/50/100 | [−100, 100] | 0 | |
| 30/50/100 | [−10, 10] | 0 | |
| 30/50/100 | [−100, 100] | 0 | |
| 30/50/100 | [−100, 100] | 0 | |
| 30/50/100 | [−30, 30] | 0 | |
| 30/50/100 | [−100, 100] | 0 | |
| 30/50/100 | [−1.28, −1.28] | 0 |
| Function | Dimensions | Range | fmin |
|---|---|---|---|
| 30/50/100 | [−500, 500] | −418.9829 d | |
| 30/50/100 | [−5.12, 5.12] | 0 | |
| 30/50/100 | [−32, 32] | 0 | |
| 30/50/100 | [−600, 600] | 0 | |
| 30/50/100 | [−50, 50] | 0 | |
| 30/50/100 | [−50, 50] | 0 |
| Function | Dimensions | Range | fmin |
|---|---|---|---|
| 2 | [−65.536, 65.536] | 0.998 | |
| 4 | [−5, 5] | 0.0003 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−5, 5] | 0.398 | |
| 2 | [−2, 2] | 3 | |
| 3 | [0, 1] | −3.86 | |
| [0, 1] | −3.32 | ||
| 4 | [0, 10] | −10.1532 | |
| 4 | [0, 10] | −10.4028 | |
| 4 | [0, 10] | −10.5364 |
| Objective Functions | Constraints | Diagram |
|---|---|---|
| Minimize: where With bounds: | Subject to: where, . | 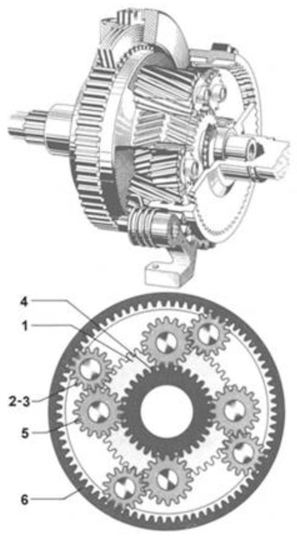 Structure of the planetary gear train design [43]. |
| Objective Functions | Constraints | Diagram |
|---|---|---|
| Minimize: With bounds: . | Subject to: . Where, | 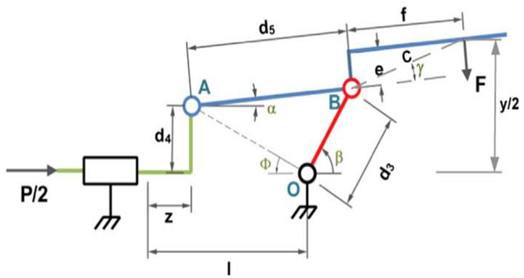 Force distribution and geometrical variables of the gripper mechanism [44]. |
| Objective Functions | Constraints | Diagram |
|---|---|---|
| Minimize: With bounds: . | Subject to: . | 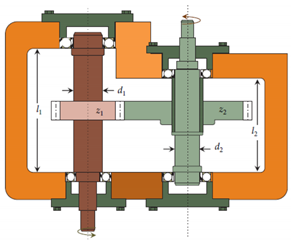 Speed reducer design problem [45]. |
References
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Dhiman, G. SSC: A Hybrid Nature-Inspired Meta-Heuristic Optimization Algorithm for Engineering Applications. Knowl.-Based Syst. 2021, 222, 106926. [Google Scholar] [CrossRef]
- Yuan, Y.; Ren, J.; Wang, S.; Wang, Z.; Mu, X.; Zhao, W. Alpine Skiing Optimization: A New Bio-Inspired Optimization Algorithm. Adv. Eng. Softw. 2022, 170, 103158. [Google Scholar] [CrossRef]
- Meidani, K.; Mirjalili, S.; Barati Farimani, A. Online Metaheuristic Algorithm Selection. Expert Syst. Appl. 2022, 201, 117058. [Google Scholar] [CrossRef]
- Shen, Y.X.; Zeng, C.H.; Wang, X.Y. A Novel Sine Cosine Algorithm for Global Optimization. In Proceedings of the 2021 5th International Conference on Computer Science and Artificial Intelligence, Beijing, China, 4–6 December 2021; pp. 202–208. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Ewees, A.A.; Neggaz, N.; Ibrahim, R.A.; Al-Qaness, M.A.A.; Lu, S. Cooperative Meta-Heuristic Algorithms for Global Optimization Problems. Expert Syst. Appl. 2021, 176, 114788. [Google Scholar] [CrossRef]
- Audet, C.; Hare, W. Genetic Algorithms. In Springer Series in Operations Research and Financial Engineering; Springer: Berlin/Heidelberg, Germany, 2017; pp. 57–73. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Xiang, Y.; Gong, X.G. Efficiency of Generalized Simulated Annealing. Phys. Rev. E 2000, 62, 4473–4476. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the MHS’95, Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 39–43. [Google Scholar]
- Trojovský, P.; Dehghani, M.; Trojovská, E.; Milkova, E. Green Anaconda Optimization: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Comput. Model. Eng. Sci. 2023, 136, 1527–1573. [Google Scholar] [CrossRef]
- Chen, Z.; Francis, A.; Li, S.; Liao, B.; Xiao, D.; Ha, T.T.; Li, J.; Ding, L.; Cao, X. Egret Swarm Optimization Algorithm: An Evolutionary Computation Approach for Model Free Optimization. Biomimetics 2022, 7, 144. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. Comput. Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: An Optimization Method for Continuous Non-Linear Large Scale Problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Balic, J. Teaching-Learning-Based Optimization Algorithm for Unconstrained and Constrained Real-Parameter Optimization Problems. Eng. Optim. 2012, 44, 1447–1462. [Google Scholar] [CrossRef]
- Toĝan, V. Design of Planar Steel Frames Using Teaching-Learning Based Optimization. Eng. Struct. 2012, 34, 225–232. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, H.; Huang, C.; Han, B. An Improved TLBO with Logarithmic Spiral and Triangular Mutation for Global Optimization. Neural Comput. Appl. 2019, 31, 4435–4450. [Google Scholar] [CrossRef]
- Zhang, M.; Pan, Y.; Zhu, J.; Chen, G. ABC-TLBO: A Hybrid Algorithm Based on Artificial Bee Colony and Teaching-Learning-Based Optimization. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 2410–2417. [Google Scholar] [CrossRef]
- Kumar, Y.; Singh, P.K. A Chaotic Teaching Learning Based Optimization Algorithm for Clustering Problems. Appl. Intell. 2019, 49, 1036–1062. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Hashim, F.A.; Shaban, H.; Hassaballah, M. Lévy Flight Distribution: A New Metaheuristic Algorithm for Solving Engineering Optimization Problems. Eng. Appl. Artif. Intell. 2020, 94, 103731. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary Programming Made Faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Bolufe-Rohler, A.; Chen, S. A Multi-Population Exploration-Only Exploitation-Only Hybrid on CEC-2020 Single Objective Bound Constrained Problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020. [Google Scholar] [CrossRef]
- Yu, X.; Chen, W.; Zhang, X. An Artificial Bee Colony Algorithm for Solving Constrained Optimization Problems. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 2663–2666. [Google Scholar] [CrossRef]
- Agarwal, A.; Chandra, A.; Shalivahan, S.; Singh, R.K. Grey Wolf Optimizer: A New Strategy to Invert Geophysical Data Sets. Geophys. Prospect. 2018, 66, 1215–1226. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Knowl. Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-Heuristic Algorithm for Global Optimization; Springer: New York, NY, USA, 2022; ISBN 0123456789. [Google Scholar]
- Mann, H.B.; Whitney, D.R. On a Test of Whether One of Two Random Variables Is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization. Comput. Res. Repos. 2017, 12, 73–87. [Google Scholar]
- Nadimi-Shahraki, M.H.; Zamani, H. DMDE: Diversity-Maintained Multi-Trial Vector Differential Evolution Algorithm for Non-Decomposition Large-Scale Global Optimization. Expert Syst. Appl. 2022, 198, 116895. [Google Scholar] [CrossRef]
- Morales-Castañeda, B.; Zaldívar, D.; Cuevas, E.; Fausto, F.; Rodríguez, A. A Better Balance in Metaheuristic Algorithms: Does It Exist? Swarm Evol. Comput. 2020, 54, 100671. [Google Scholar] [CrossRef]
- Lee, D.K.; In, J.; Lee, S. Standard Deviation and Standard Error of the Mean. Korean J. Anesthesiol. 2015, 68, 220–223. [Google Scholar] [CrossRef]
- Ge, F.; Hong, L.; Shi, L. An Autonomous Teaching-Learning Based Optimization Algorithm for Single Objective Global Optimization. Int. J. Comput. Intell. Syst. 2016, 9, 506–524. [Google Scholar] [CrossRef]
- Ji, X.; Ye, H.; Zhou, J.; Yin, Y.; Shen, X. An Improved Teaching-Learning-Based Optimization Algorithm and Its Application to a Combinatorial Optimization Problem in Foundry Industry. Appl. Soft Comput. J. 2017, 57, 504–516. [Google Scholar] [CrossRef]
- Akbari, E.; Ghasemi, M.; Gil, M.; Rahimnejad, A.; Andrew Gadsden, S. Optimal Power Flow via Teaching-Learning-Studying-Based Optimization Algorithm. Electr. Power Compon. Syst. 2022, 49, 584–601. [Google Scholar] [CrossRef]
- Kumar, A.; Das, S.; Zelinka, I. A Self-Adaptive Spherical Search Algorithm for Real-World Constrained Optimization Problems. In Proceedings of the GECCO’20: Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 13–14. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Ali, M.Z.; Wu, G.; Liang, J.J.; Qu, B.Y. Special Session & Competitions on Real World Single Objective Constrained Optimization. In Proceedings of the CEC-2020, Glasgow, UK, 19–24 July 2020; Volume 2017. [Google Scholar]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H.; Talatahari, S. Bat Algorithm for Constrained Optimization Tasks. Neural Comput. Appl. 2013, 22, 1239–1255. [Google Scholar] [CrossRef]
- Li, Y.; Yu, X.; Liu, J. An Opposition-Based Butterfly Optimization Algorithm with Adaptive Elite Mutation in Solving Complex High-Dimensional Optimization Problems. Math. Comput. Simul. 2023, 204, 498–528. [Google Scholar] [CrossRef]
- Wan, W.; Zhang, S.; Meng, X. Study on Reliability-Based Optimal Design of Multi-Stage Planetary Gear Train in Wind Power Yaw Reducer. Appl. Mech. Mater. 2012, 215–216, 867–872. [Google Scholar] [CrossRef]
- Kumar, A.; Wu, G.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A Test-Suite of Non-Convex Constrained Optimization Problems from the Real-World and Some Baseline Results. Swarm Evol. Comput. 2020, 56, 100693. [Google Scholar] [CrossRef]
- Dörterler, M.; Atila, U.; Durgut, R.; Sahin, I. Analyzing the Performances of Evolutionary Multi-Objective Optimizers on Design Optimization of Robot Gripper Configurations. Turkish J. Electr. Eng. Comput. Sci. 2021, 29, 349–369. [Google Scholar] [CrossRef]
- Bayzidi, H.; Talatahari, S.; Saraee, M.; Lamarche, C.P. Social Network Search for Solving Engineering Optimization Problems. Comput. Intell. Neurosci. 2021, 2021, 8548639. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Kaur, J. Hybridizing Sine–cosine Algorithm with Harmony Search Strategy for Optimization Design Problems. Soft Comput. 2021, 25, 11053–11075. [Google Scholar] [CrossRef]
- Hassan, A.; Abomoharam, M. Modeling and Design Optimization of a Robot Gripper Mechanism. Robot. Comput. Integr. Manuf. 2017, 46, 94–103. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, J.; Li, S.; Lv, D.; Li, M. An Enhanced Differential Evolution Algorithm with Bernstein Operator and Refracted Oppositional-Mutual Learning Strategy. Entropy 2022, 24, 1205. [Google Scholar] [CrossRef]
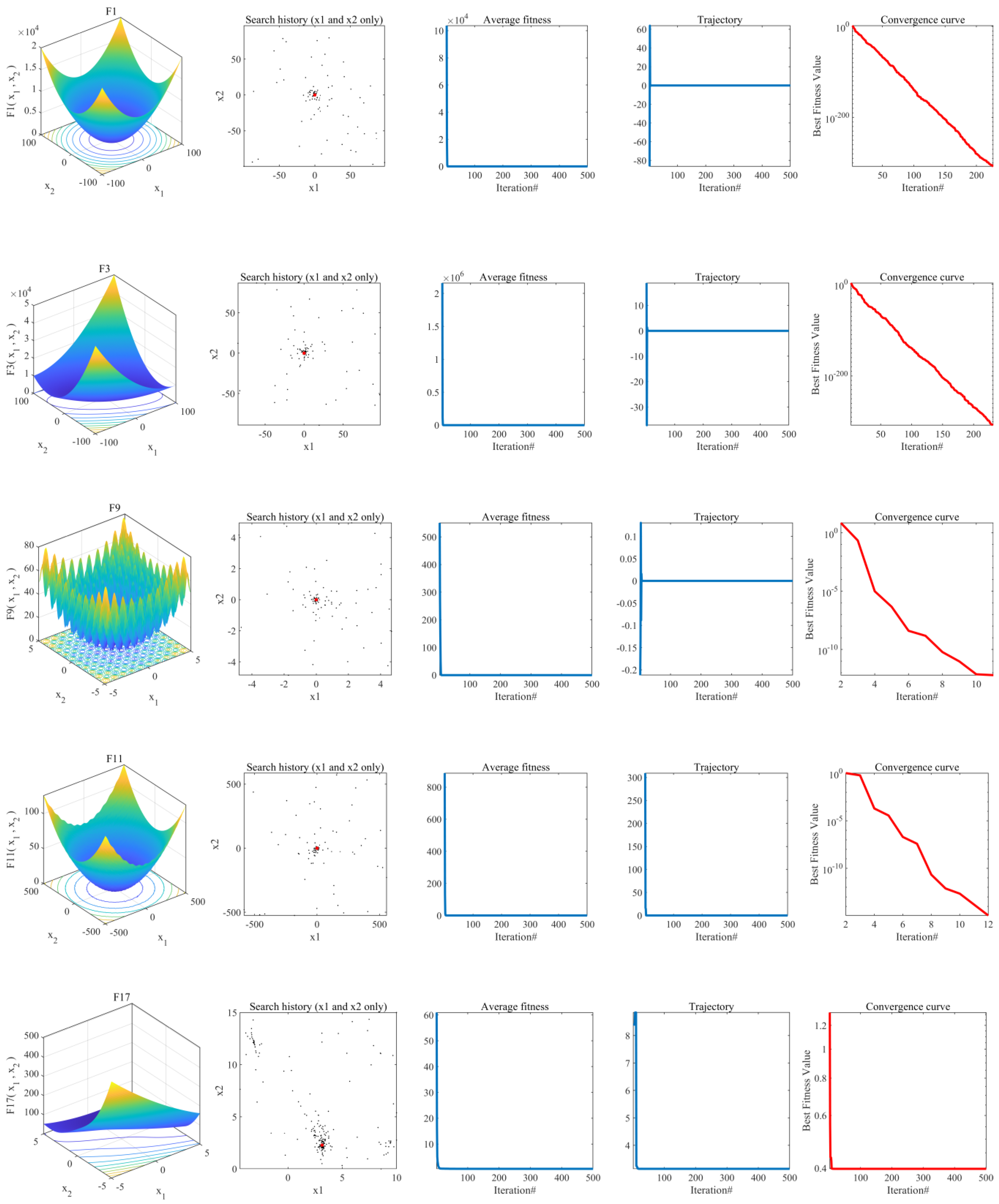

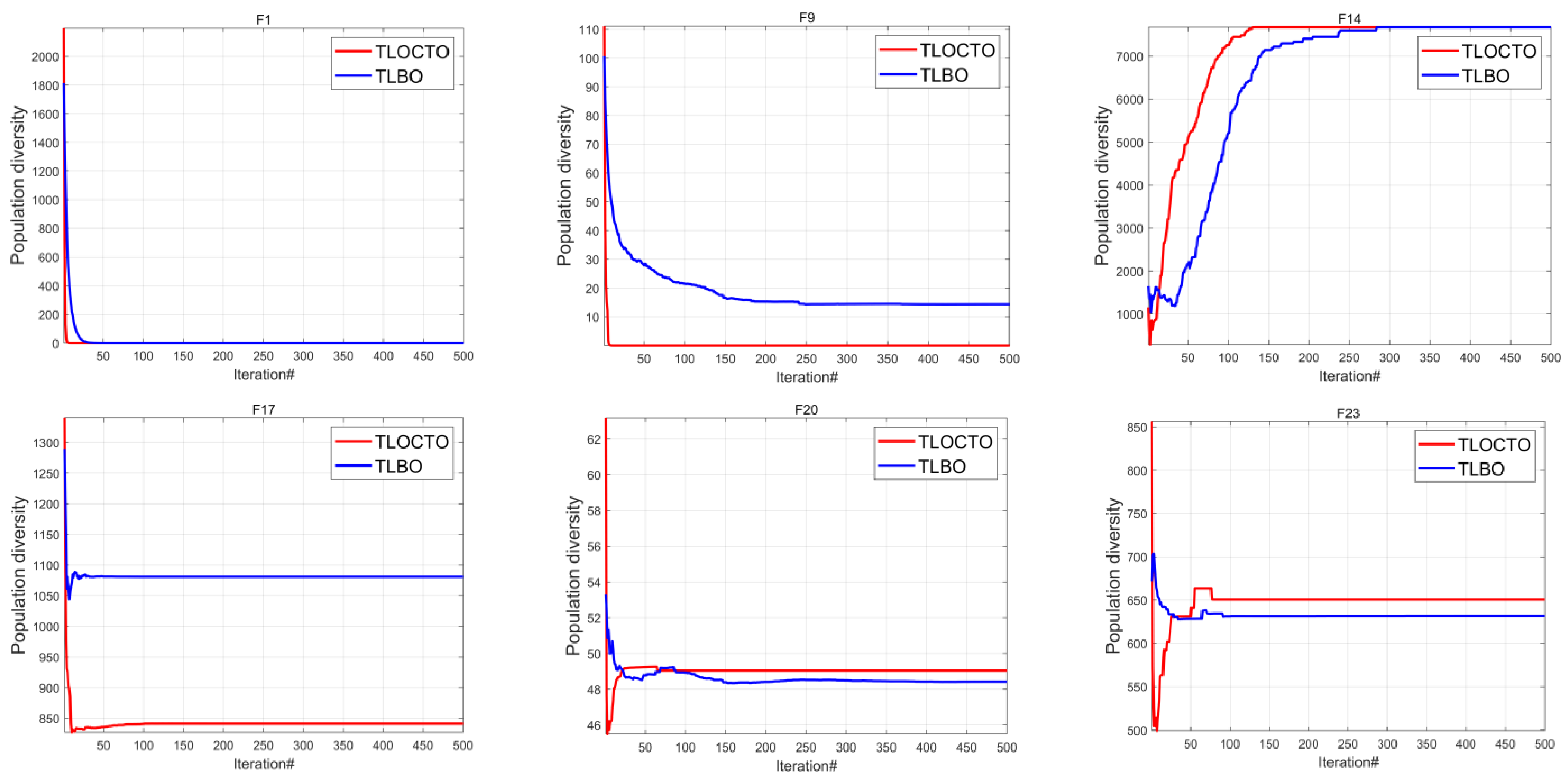
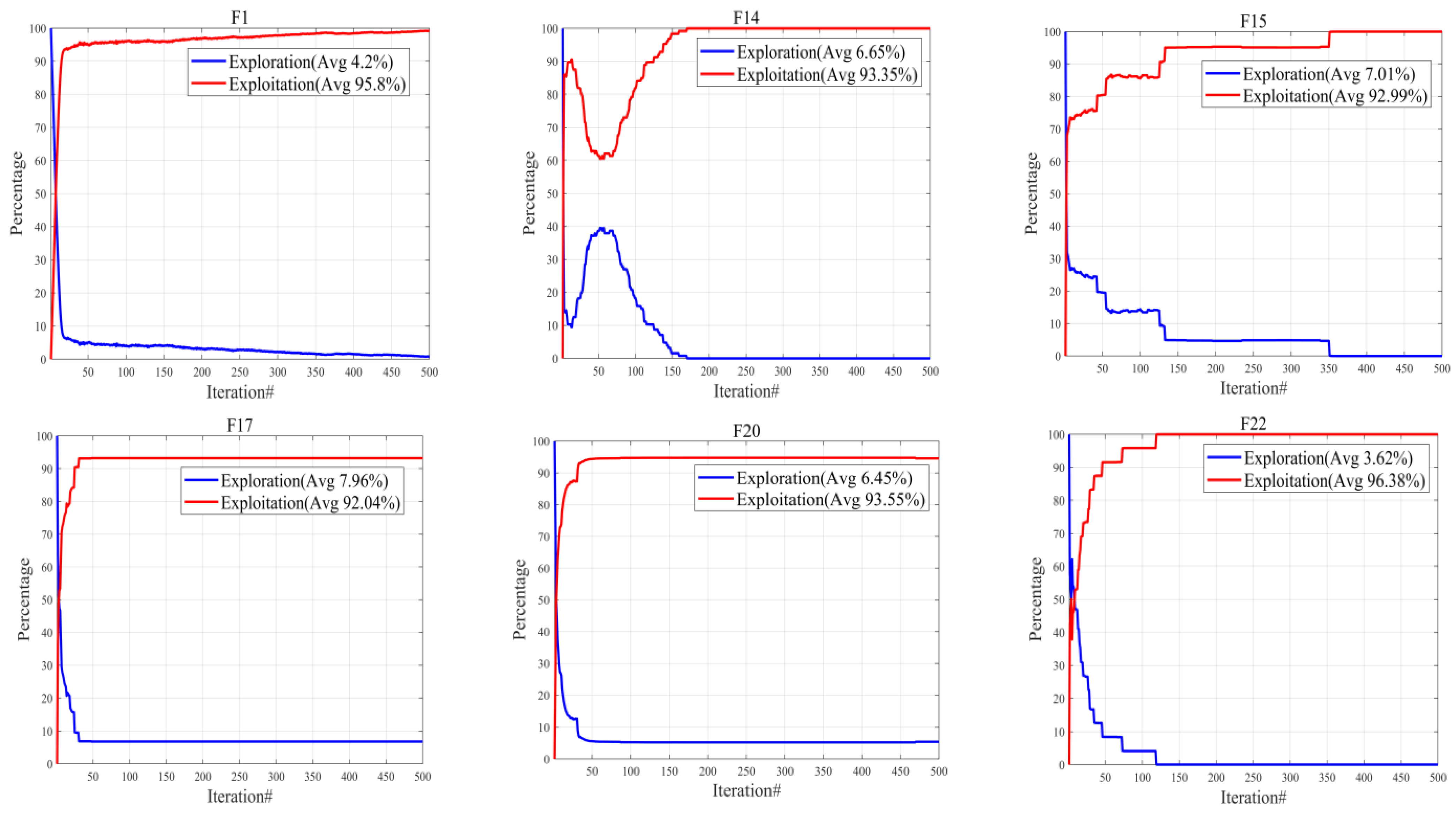
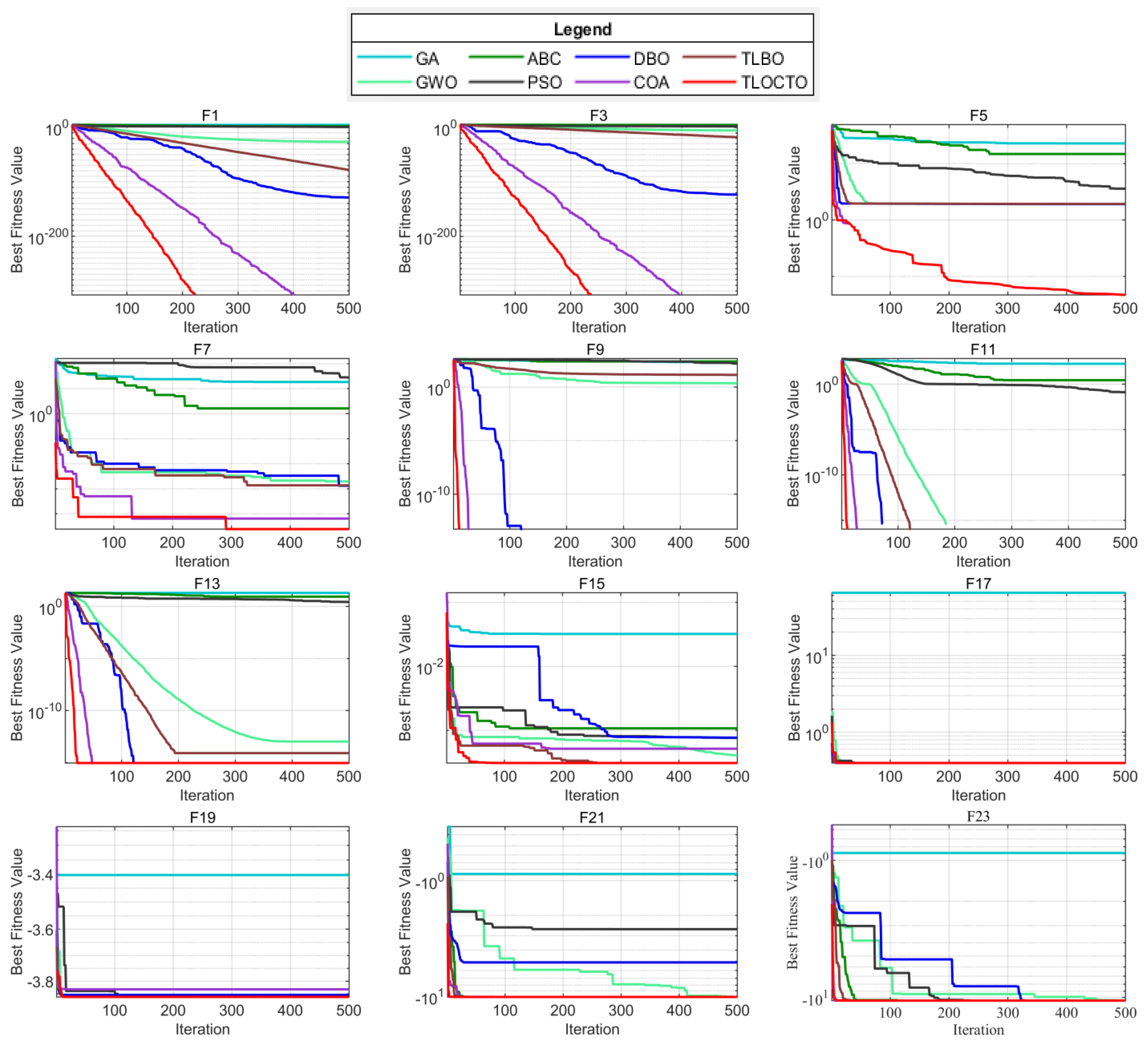
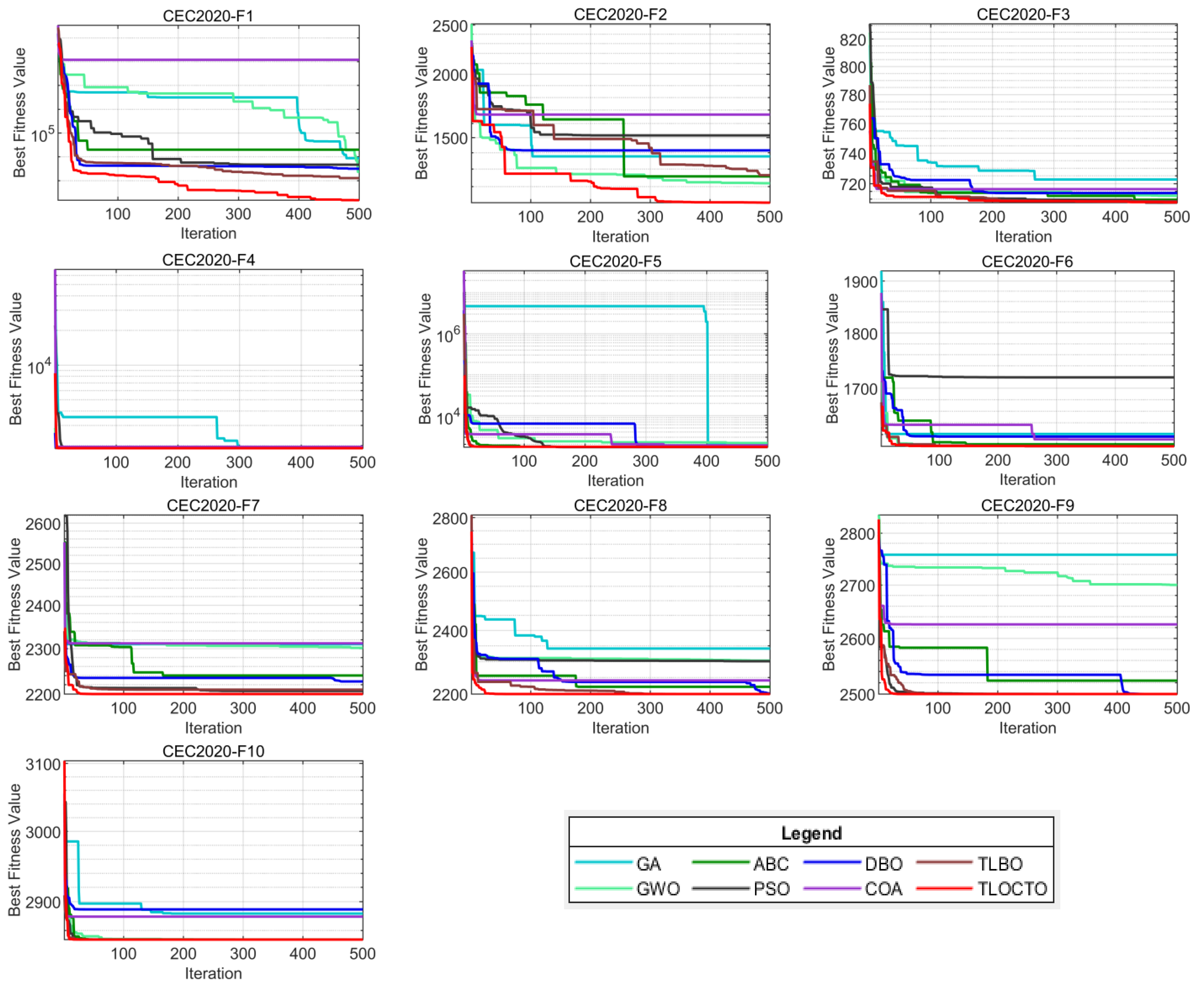
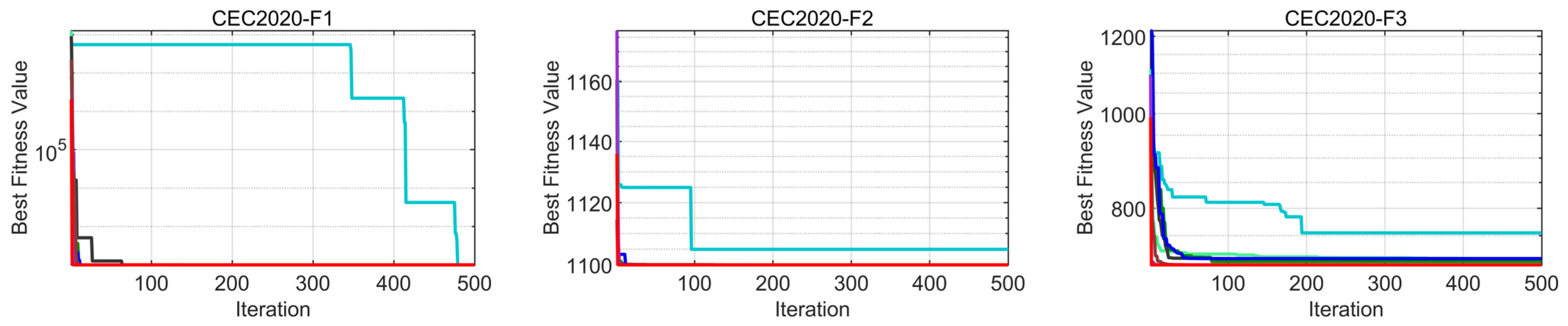
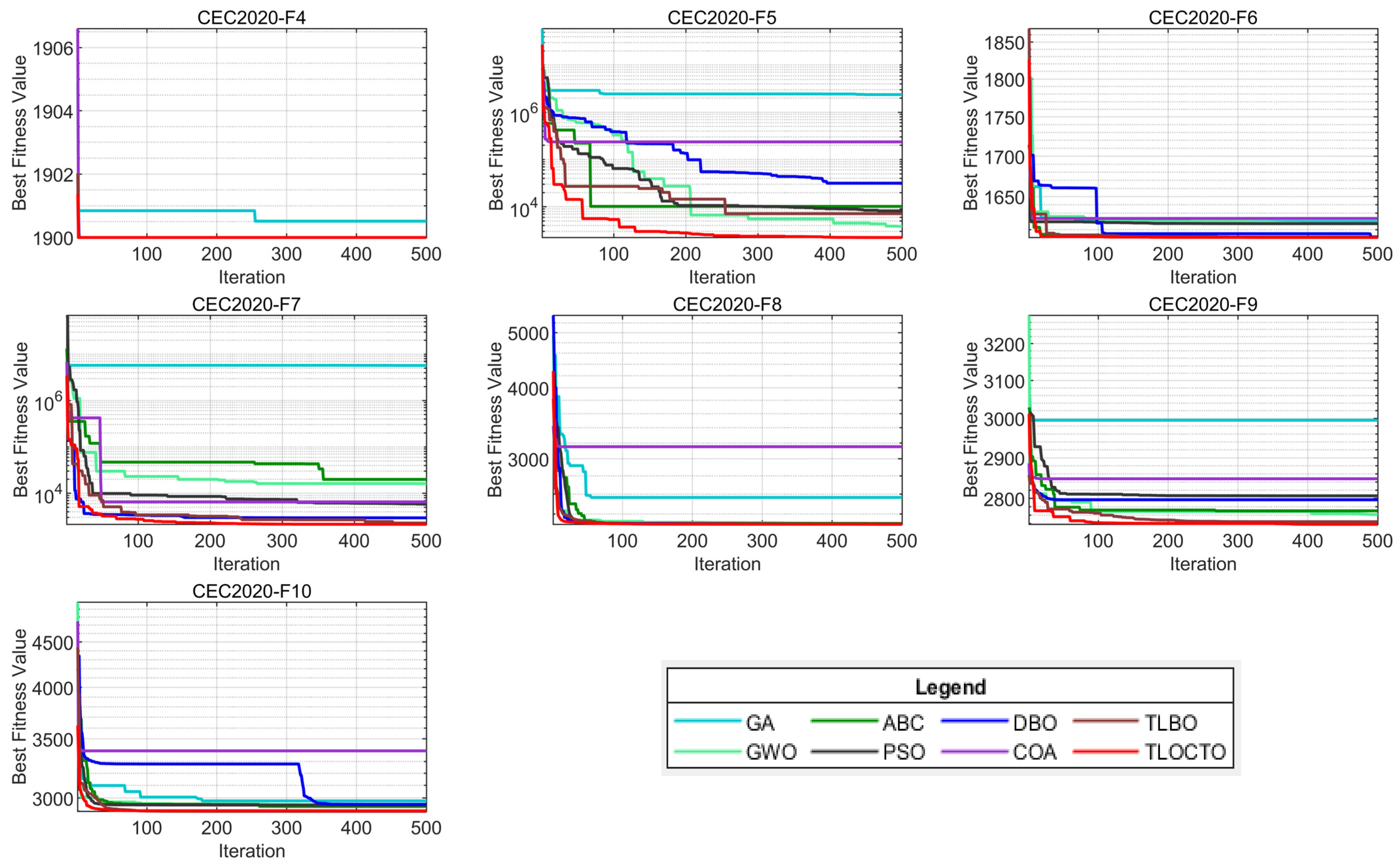
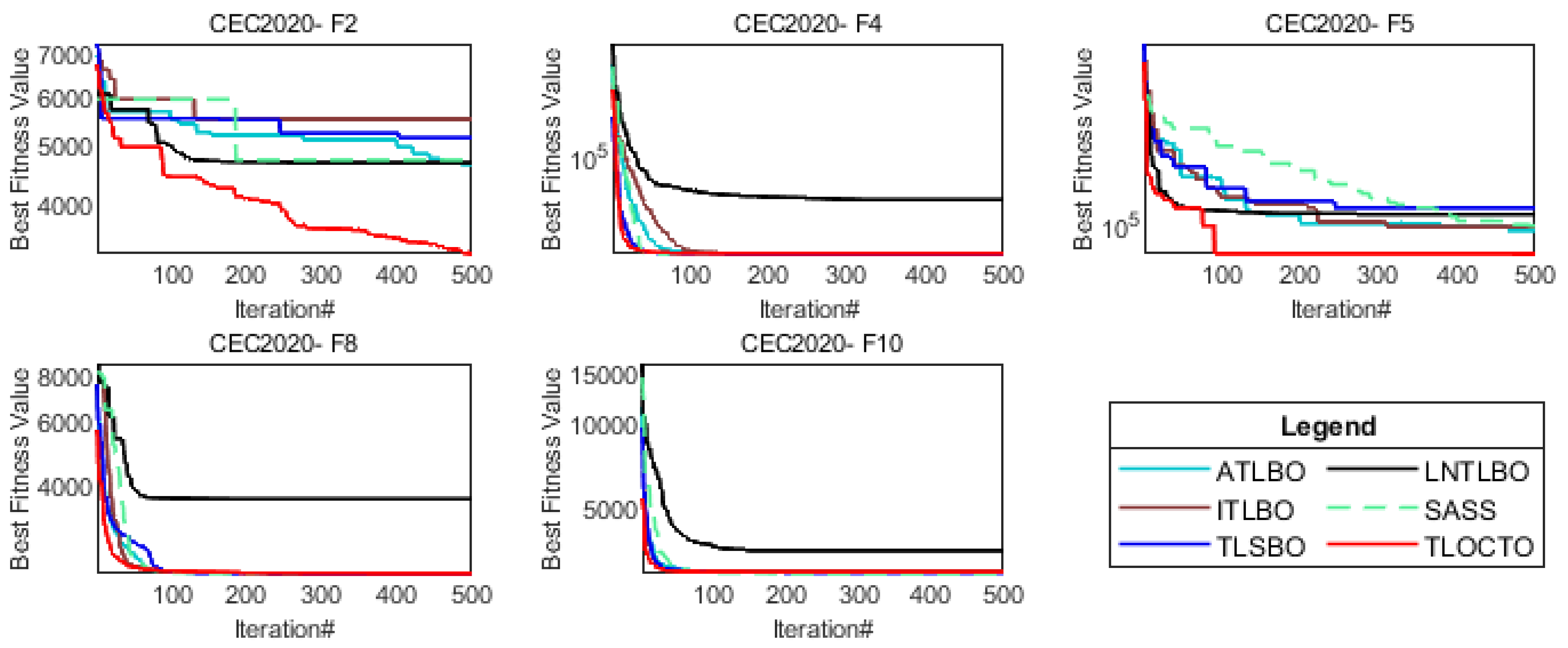
| Problem | Metric | TLOCTO | ABC | GWO | PSO | GA | COA | DBO | TLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | AVG STD | 0.0000 × 100 0.00 × 100 | 8.3930 × 100 6.86 × 100 | 8.6133 × 10−38 1.40 × 10−37 | 2.6801 × 100 1.0384 × 100 | 1.1609 × 100 4.16 × 10−2 | 0.0000 × 100 0.00 × 100 | 6.0286 × 104 6.84 × 103 | 3.3163 × 10−78 1.10 × 10−77 |
| F2 | AVG STD | 0.0000 × 100 0.00 × 100 | 8.9866 × 10−1 4.11 × 10−1 | 1.5131 × 10−22 1.53 × 10−22 | 4.0965 × 100 1.0268 × 100 | 5.8101 × 10−1 1.24 × 10−2 | 1.2046 × 10−184 0.00 × 100 | 4.3274 × 106 1.97 × 107 | 6.1081 × 10−40 5.10 × 10−40 |
| F3 | AVG STD | 0.0000 × 100 0.00 × 100 | 2.8314 × 104 8.30 × 103 | 1.6118 × 10−1 6.14 × 10−1 | 1.8046 × 102 5.52 × 101 | 1.6834 × 100 6.02 × 10−1 | 0.0000 × 100 0.00 × 100 | 1.5840 × 100 6.36 × 100 | 3.5098 × 10−17 1.06 × 10−16 |
| F4 | AVG STD | 0.0000 × 100 0.00 × 100 | 8.6368 × 101 4.76 × 100 | 2.4439 × 10−9 4.91 × 10−9 | 2.0328 × 100 2.45 × 10−1 | 2.0040 × 10−1 0.00 × 100 | 1.2709 × 10−181 0.00 × 100 | 8.5609 × 101 4.36 × 100 | 3.5091 × 10−33 3.01 × 10−33 |
| F5 | AVG STD | 1.8890 × 10−4 4.30 × 10−4 | 4.0777 × 103 5.00 × 103 | 2.8415 × 101 7.62 × 10−1 | 9.3311 × 102 5.27 × 102 | 4.2570 × 102 7.91 × 102 | 0.0000 × 100 0.00 × 100 | 2.5716 × 101 1.78 × 10−1 | 2.6539 × 101 4.3 × 10−1 |
| F6 | AVG STD | 0.0000 × 100 0.00 × 100 | 1.4700 × 101 1.12 × 101 | 6.6667 × 10−2 2.54 × 10−1 | 2.2603 × 100 1.03 × 100 | 3.3333 × 10−2 1.83 × 10−1 | 0.0000 × 100 0.00 × 100 | 0.0000 × 100 0.00 × 100 | 9.7384 × 10−3 4.1 × 10−1 |
| F7 | AVG STD | 3.6988 × 10−2 3.12 × 10−2 | 2.9306 × 10−1 9.01 × 10−2 | 9.1929 × 10−2 5.26 × 10−2 | 1.7808 × 101 1.78 × 101 | 4.8093 × 10−2 1.50 × 10−2 | 4.8764 × 10−5 3.76 × 10−5 | 6.0628 × 10−2 5.11 × 10−2 | 1.1936 × 10−3 4.26 × 10−4 |
| F8 | AVG STD | −1.1790 × 104 9.13 × 102 | −9.1626 × 103 6.99 × 102 | −1.5991 × 103 3.64 × 102 | −6.1198 × 103 1.44 × 103 | −1.1152 × 104 3.29 × 102 | −1.2569 × 103 5.85 × 10−2 | −8.5886 × 103 2.12 × 103 | −7.4077 × 103 1.02 × 103 |
| F9 | AVG STD | 0.0000 × 100 0.00 × 100 | 1.6257 × 102 6.13 × 101 | 0.0000 × 100 0.00 × 100 | 1.7389 × 102 3.71 × 101 | 2.0327 × 100 1.21 × 100 | 0.0000 × 100 0.00 × 100 | 2.9850 × 10−1 1.63 × 100 | 1.6721 × 101 6.23 × 100 |
| F10 | AVG STD | 8.8818 × 10−16 0.00 × 100 | 2.6192 × 100 5.65 × 10−1 | 7.9936 × 10−15 1.32 × 10−15 | 2.6744 × 100 5.02 × 10−1 | 1.7871 × 10−1 4.16 × 10−2 | 8.8818 × 10−16 0.00 × 100 | 8.8818 × 10−16 0.00 × 100 | 6.9278 × 10−15 1.66 × 10−5 |
| F11 | AVG STD | 0.0000 × 100 0.00 × 100 | 1.0966 × 100 9.41 × 10−2 | 0.0000 × 100 0.00 × 100 | 1.1093 × 10−1 3.73 × 10−2 | 4.5412 × 10−1 1.20 × 10−1 | 0.0000 × 100 0.00 × 100 | 0.0000 × 100 0.00 × 100 | 3.0152 × 10−6 1.65 × 10−5 |
| F12 | AVG STD | 7.2295 × 10−7 1.13 × 10−6 | 4.0123 × 102 3.29 × 102 | 3.1208 × 100 1.51 × 10−1 | 4.4793 × 10−2 5.51 × 10−2 | 4.1303 × 10−2 3.04 × 10−2 | 1.5705 × 10−32 5.57 × 10−48 | 2.4235 × 100 6.86 × 10−1 | 8.6770 × 10−5 3.01 × 10−4 |
| F13 | AVG STD | 1.8164 × 10−7 2.62 × 10−7 | 1.6327 × 103 3.62 × 103 | 2.1180 × 100 2.40 × 10−1 | 6.3050 × 10−1 2.37 × 10−1 | 2.3183 × 10−2 8.76 × 10−3 | 1.3498 × 10−32 5.57 × 10−48 | 6.0204 × 10−1 4.36 × 10−1 | 1.9071 × 10−1 1.48 × 10−1 |
| F14 | AVG STD | 2.0458 × 100 2.50 × 100 | 1.6202 × 100 1.42 × 100 | 1.2198 × 101 1.86 × 100 | 3.0027 × 100 2.51 × 100 | 9.9800 × 10−1 2.15 × 10−11 | 9.9800 × 10−1 8.67 × 10−11 | 1.5218 × 100 1.87 × 100 | 9.9800 × 10−1 0.00 × 100 |
| F15 | AVG STD | 3.0979 × 10−4 8.72 × 10−6 | 1.4522 × 10−3 3.58 × 10−3 | 7.3193 × 10−3 8.39 × 10−3 | 9.2132 × 10−4 2.69 × 10−4 | 4.5409 × 10−3 7.62 × 10−3 | 4.4093 × 10−4 1.20 × 10−4 | 7.7156 × 10−4 2.74 × 10−4 | 3.5310 × 10−4 0.00 × 100 |
| F16 | AVG STD | −1.0316 × 100 6.65 × 10−16 | −1.0316 × 100 5.53 × 10−16 | −1.0235 × 100 7.84 × 10−3 | −1.0316 × 100 4.88 × 10−16 | −1.0316 × 100 4.94 × 10−7 | −1.0316 × 100 1.23 × 10−4 | −1.0316 × 100 4.44 × 10−16 | −1.0316 × 100 6.71 × 10−15 |
| F17 | AVG STD | 3.9789 × 10−1 0.00 × 100 | 3.9789 × 10−1 0.00 × 100 | 8.1189 × 10−1 4.91 × 10−9 | 3.9789 × 10−1 0.00 × 100 | 3.9789 × 10−1 8.38 × 10−7 | 3.9831 × 10−1 8.62 × 10−4 | 3.9789 × 10−1 3.24 × 10−16 | 3.9789 × 10−1 0.00 × 100 |
| F18 | AVG STD | 3.0000 × 100 1.28 × 10−15 | 3.0000 × 100 4.24 × 10−15 | 3.2919 × 100 4.89 × 10−1 | 3.0000 × 100 6.24 × 10−14 | 3.0000 × 100 4.84 × 10−6 | 3.0459 × 100 6.34 × 10−2 | 3.0000 × 100 1.85 × 10−14 | 3.0000 × 100 1.39 × 10−15 |
| F19 | AVG STD | −3.8628 × 100 2.71 × 10−15 | −3.8628 × 100 2.46 × 10−15 | −3.5047 × 100 3.57 × 10−1 | −3.8628 × 100 1.92 × 10−15 | −3.8628 × 100 1.74 × 10−7 | −3.8002 × 100 7.97 × 10−2 | −3.8615 × 100 2.99 × 10−3 | −3.8628 × 100 2.71 × 10−15 |
| F20 | AVG STD | −3.3146 × 100 2.79 × 10−2 | −3.2744 × 100 5.92 × 10−2 | −2.4044 × 100 2.82 × 10−1 | −3.2586 × 100 6.03 × 10−3 | −3.2744 × 100 5.92 × 10−2 | −2.6194 × 100 3.88 × 10−1 | −3.2998 × 100 5.17 × 10−2 | −3.3100 × 100 3.62 × 10−2 |
| F21 | AVG STD | −1.0153 × 101 7.01 × 10−15 | −6.8147 × 100 3.68 × 100 | −2.4730 × 100 1.12 × 100 | −7.056 × 100 3.269 × 100 | −6.1443 × 100 3.45 × 100 | −1.0153 × 101 7.07 × 10−5 | −6.2541 × 100 2.19 × 100 | −1.0153 × 101 2.92 × 10−14 |
| F22 | AVG STD | −1.0403 × 101 1.32 × 10−15 | −7.6146 × 100 3.54 × 100 | −1.3810 × 100 1.01 × 100 | −8.3590 × 100 3.01 × 100 | −7.5984 × 100 3.31 × 100 | −1.0403 × 101 4.24 × 10−4 | −7.5244 × 100 2.77 × 100 | −1.0183 × 101 1.22 × 100 |
| F23 | AVG STD | −1.0536 × 101 1.89 × 10−15 | −8.5397 × 100 3.38 × 100 | −1.3328 × 100 9.82 × 10−1 | −9.7550 × 100 2.17 × 100 | −6.0831 × 100 3.76 × 100 | −1.0536 × 101 8.51 × 10−5 | −8.0278 × 100 2.73 × 100 | −1.0536 × 101 3.75 × 10−3 |
| (+/−/=) | ~ | ~ | 0/18/5 | 0/20/3 | 0/23/0 | 1/21/1 | 4/12/7 | 0/16/7 | 1/22/0 |
| Function | Name | Range | fmin |
|---|---|---|---|
| F1 (CEC_01) | Shifted and rotated bent cigar function | [−100, 100]Dim | 100 |
| F2 (CEC_02) | Shifted and rotated schwefel’s function | [−100, 100]Dim | 1100 |
| F3 (CEC_03) | Shifted and rotated lunacek bi-rastrigin function | [−100, 100]Dim | 700 |
| F4 (CEC_04) | Expanded rosenbrock’s plus griewangk’s function | [−100, 100]Dim | 1900 |
| F5 (CEC_05) | Hybrid function 1 (N = 3) | [−100, 100]Dim | 1700 |
| F6 (CEC_06) | Hybrid function 1 (N = 4) | [−100, 100]Dim | 1600 |
| F7 (CEC_07) | Hybrid function 1 (N = 5) | [−100, 100]Dim | 2100 |
| F8 (CEC_08) | Composition function 1 (N = 3) | [−100, 100]Dim | 2200 |
| F9 (CEC_09) | Composition function 1 (N = 4) | [−100, 100]Dim | 2400 |
| F10 (CEC_10) | Composition function 1 (N = 5) | [−100, 100]Dim | 2500 |
| Problem | Metric | TLOCTO | ABC | GWO | PSO | GA | COA | DBO | TLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | AVG STD | 3.9393 × 102 3.16 × 102 | 3.9926 × 103 4.21 × 103 | 1.0928 × 108 8.11 × 107 | 1.1321 × 108 1.88 × 108 | 4.2118 × 103 4.17 × 103 | 9.5389 × 108 6.45 × 108 | 3.0308 × 103 3.67 × 103 | 3.0856 × 105 2.95 × 105 |
| F2 | AVG STD | 1.1942 × 103 6.82 × 101 | 1.2459 × 103 1.37 × 102 | 1.8413 × 103 2.24 × 102 | 1.5817 × 103 1.66 × 102 | 1.2611 × 103 1.37 × 102 | 2.1665 × 103 2.07 × 102 | 1.3873 × 103 1.49 × 102 | 1.3663 × 103 1.11 × 102 |
| F3 | AVG STD | 7.0722 × 102 1.44 × 100 | 7.0849 × 102 3.20 × 100 | 7.3054 × 102 6.96 × 100 | 7.1652 × 102 6.43 × 100 | 7.0796 × 102 2.22 × 100 | 7.5890 × 102 7.34 × 100 | 7.1223 × 102 3.56 × 100 | 7.1670 × 102 4.33 × 100 |
| F4 | AVG STD | 1.9002 × 103 1.02 × 10−1 | 1.9006 × 103 3.04 × 10−1 | 1.9083 × 103 3.92 × 100 | 3.1673 × 103 5.93 × 103 | 1.9003 × 103 1.92 × 10−1 | 1.3707 × 104 1.38 × 104 | 1.9013 × 103 1.15 × 100 | 1.9008 × 103 3.40 × 10−1 |
| F5 | AVG STD | 1.7051 × 103 7.07 × 100 | 1.7364 × 103 4.72 × 101 | 6.5142 × 105 6.29 × 105 | 7.8483 × 103 6.66 × 103 | 1.7394 × 103 5.00 × 101 | 3.3860 × 106 3.96 × 106 | 2.0135 × 103 7.92 × 102 | 1.8101 × 103 4.17 × 101 |
| F6 | AVG STD | 1.6008 × 103 4.29 × 10−1 | 1.6025 × 103 7.38 × 100 | 1.6927 × 103 8.03 × 101 | 1.6455 × 103 5.27 × 101 | 1.6115 × 103 3.07 × 101 | 1.8093 × 103 1.04 × 102 | 1.6055 × 103 1.19 × 101 | 1.6067 × 103 6.44 × 100 |
| F7 | AVG STD | 2.1002 × 103 3.13 × 10−1 | 2.1004 × 103 3.01 × 10−1 | 2.1816 × 103 7.25 × 101 | 2.1225 × 103 2.68 × 101 | 2.1034 × 103 1.02 × 101 | 2.2411 × 103 8.05 × 101 | 2.1017 × 103 6.02 × 100 | 2.1008 × 103 1.96 × 10−1 |
| F8 | AVG STD | 2.2461 × 103 5.25 × 101 | 2.2390 × 103 4.70 × 101 | 2.3204 × 103 3.27 × 101 | 2.2856 × 103 6.46 × 101 | 2.2748 × 103 5.00 × 101 | 2.4921 × 103 1.53 × 102 | 2.2433 × 103 4.45 × 101 | 2.2358 × 103 2.72 × 101 |
| F9 | AVG STD | 2.5181 × 103 5.58 × 101 | 2.5520 × 103 8.72 × 101 | 2.7130 × 103 8.62 × 101 | 2.6786 × 103 9.23 × 101 | 2.5883 × 103 1.13 × 102 | 2.7258 × 103 6.49 × 101 | 2.5000 × 103 2.65 × 10−4 | 2.5357 × 103 6.33 × 100 |
| F10 | AVG STD | 2.8391 × 103 3.78 × 101 | 2.8458 × 103 8.65 × 100 | 2.8575 × 103 7.03 × 100 | 2.8736 × 103 2.68 × 101 | 2.8394 × 103 2.14 × 101 | 2.9488 × 103 5.51 × 101 | 2.8500 × 103 2.01 × 101 | 2.8247 × 103 1.18 × 101 |
| (+/−/=) | ~ | ~ | 0/7/3 | 0/10/0 | 0/10/0 | 0/8/2 | 0/10/0 | 1/7/2 | 2/7/1 |
| Problem | Metric | TLOCTO | ABC | GWO | PSO | GA | COA | DBO | TLBO |
| F1 | AVG STD | 2.6402 × 103 2.96 × 103 | 3.9681 × 103 3.59 × 103 | 2.0448 × 109 6.82 × 108 | 6.0622 × 109 3.51 × 109 | 1.7744 × 104 1.73 × 104 | 1.5653 × 1010 6.10 × 109 | 1.2644 × 106 4.50 × 106 | 1.9777 × 108 9.19 × 107 |
| F2 | AVG STD | 1.5719 × 103 2.81 × 102 | 2.4585 × 103 6.75 × 102 | 3.0011 × 103 3.01 × 102 | 2.2721 × 103 3.37 × 102 | 1.5736 × 103 2.25 × 102 | 3.6023 × 103 3.34 × 102 | 2.0814 × 103 3.09 × 102 | 2.4658 × 103 2.50 × 102 |
| F3 | AVG STD | 7.2975 × 102 7.97 × 100 | 7.4313 × 102 2.08 × 101 | 8.0923 × 102 1.42 × 101 | 7.8781 × 102 3.24 × 101 | 7.2642 × 102 7.30 × 100 | 9.0337 × 102 2.78 × 101 | 7.5004 × 102 1.86 × 101 | 8.0925 × 102 2.81 × 101 |
| F4 | AVG STD | 1.9018 × 103 8.77 × 10−1 | 1.9031 × 103 1.67 × 100 | 2.2790 × 103 4.16 × 102 | 7.2218 × 104 8.19 × 104 | 1.9023 × 103 1.03 × 100 | 5.2207 × 105 4.34 × 105 | 1.9053 × 103 2.68 × 100 | 1.9102 × 103 8.24 × 100 |
| F5 | AVG STD | 2.7587 × 103 9.63 × 102 | 3.0432 × 105 4.52 × 105 | 6.2118 × 105 1.33 × 105 | 7.9091 × 105 8.38 × 105 | 4.5979 × 105 5.39 × 105 | 7.3010 × 106 7.23 × 106 | 1.9503 × 104 2.02 × 104 | 1.1536 × 104 5.47 × 103 |
| F6 | AVG STD | 1.6706 × 103 7.49 × 101 | 1.7373 × 103 1.10 × 102 | 2.0147 × 103 9.65 × 101 | 2.1041 × 103 1.70 × 102 | 1.7671 × 103 1.27 × 102 | 2.8130 × 103 2.95 × 102 | 1.8091 × 103 1.29 × 102 | 1.7854 × 103 7.64 × 101 |
| F7 | AVG STD | 2.4853 × 103 1.66 × 102 | 1.1205 × 104 9.80 × 103 | 3.0861 × 106 4.62 × 106 | 6.6925 × 105 1.30 × 106 | 1.4839 × 105 3.55 × 105 | 4.0225 × 106 5.47 × 106 | 7.8715 × 103 9.06 × 103 | 4.9133 × 103 1.50 × 103 |
| F8 | AVG STD | 2.3051 × 103 1.88 × 101 | 2.3073 × 103 1.48 × 101 | 2.4639 × 103 5.96 × 101 | 2.7308 × 103 3.94 × 102 | 2.3100 × 103 8.25 × 10−3 | 3.6911 × 103 5.98 × 102 | 2.3115 × 103 2.22 × 100 | 2.4274 × 103 1.59 × 102 |
| F9 | AVG STD | 2.7129 × 103 8.25 × 101 | 2.7553 × 103 1.70 × 101 | 2.8194 × 103 1.20 × 101 | 2.8307 × 103 1.02 × 102 | 2.7581 × 103 1.50 × 101 | 2.9661 × 103 1.08 × 102 | 2.7751 × 103 3.88 × 101 | 2.7689 × 103 4.82 × 101 |
| F10 | AVG STD | 2.9279 × 103 2.32 × 101 | 2.9359 × 103 2.07 × 101 | 3.0253 × 103 4.66 × 101 | 3.1485 × 103 1.31 × 102 | 2.9399 × 103 2.73 × 101 | 3.9653 × 103 3.73 × 102 | 2.9379 × 103 6.66 × 101 | 2.9490 × 103 1.21 × 101 |
| (+/−/=) | ~ | ~ | 0/7/3 | 0/10/0 | 0/9/1 | 1/6/3 | 0/10/0 | 0/10/0 | 0/10/0 |
| Problem | Metric | TLOCTO | ATLBO | ITLBO | TLSBO | LNTLBO | SASS |
|---|---|---|---|---|---|---|---|
| F1 | Ave | 1.5872 × 105 | 1.5285 × 106 | 4.2403 × 103 | 1.7599 × 103 | 8.3267 × 109 | 1.6100 × 103 |
| Std | 3.79 × 105 | 3.25 × 106 | 3.95 × 103 | 2.24 × 103 | 2.71 × 109 | 2.26 × 103 | |
| F2 | Ave | 3.2654 × 103 | 4.7114 × 103 | 5.1045 × 103 | 5.3031 × 103 | 4.4598 × 103 | 5.4914 × 103 |
| Std | 1.52 × 102 | 6.72 × 102 | 4.15 × 102 | 2.20 × 102 | 5.89 × 102 | 2.63 × 102 | |
| F3 | Ave | 8.6336 × 102 | 8.5826 × 102 | 8.4488 × 102 | 8.2675 × 102 | 1.0341 × 103 | 8.2943 × 102 |
| Std | 4.33 × 101 | 3.80 × 101 | 2.88 × 101 | 3.89 × 101 | 6.54 × 101 | 8.71 × 100 | |
| F4 | Ave | 1.9353 × 103 | 1.9204 × 103 | 1.9163 × 103 | 1.9117 × 103 | 1.7668 × 104 | 1.9088 × 103 |
| Std | 1.85 × 101 | 9.98 × 100 | 6.88 × 100 | 3.14 × 100 | 1.45 × 104 | 1.40 × 100 | |
| F5 | Ave | 4.4176 × 104 | 7.2356 × 104 | 1.3859 × 105 | 1.7059 × 105 | 1.6930 × 105 | 4.7068 × 104 |
| Std | 3.71 × 104 | 5.66 × 104 | 1.01 × 105 | 1.29 × 105 | 2.16 × 105 | 4.50 × 104 | |
| F6 | Ave | 1.6291 × 103 | 1.7099 × 103 | 1.8043 × 103 | 1.9356 × 103 | 1.7243 × 103 | 2.2605 × 103 |
| Std | 2.31 × 10−13 | 1.16 × 10−12 | 1.16 × 10−12 | 1.16 × 10−12 | 1.16 × 10−12 | 1.85 × 10−12 | |
| F7 | Ave | 1.6466 × 104 | 2.0766 × 104 | 5.2183 × 104 | 2.7900 × 104 | 8.8333 × 104 | 2.1520 × 104 |
| Std | 9.40 × 103 | 1.51 × 104 | 4.76 × 104 | 1.71 × 104 | 1.47 × 105 | 1.30 × 104 | |
| F8 | Ave | 2.3061 × 103 | 2.3098 × 103 | 2.4348 × 103 | 2.3072 × 103 | 3.8601 × 103 | 2.3069 × 103 |
| Std | 3.74 × 100 | 9.77 × 100 | 7.25 × 102 | 1.30 × 100 | 8.36 × 102 | 9.61 × 101 | |
| F9 | Ave | 2.8775 × 103 | 2.8706 × 103 | 2.8565 × 103 | 2.8418 × 103 | 3.0211 × 103 | 2.8633 × 103 |
| Std | 3.13 × 101 | 2.41 × 101 | 2.78 × 101 | 1.52 × 101 | 5.75 × 101 | 4.19 × 101 | |
| F10 | Ave | 2.9981 × 103 | 3.0151 × 103 | 2.9992 × 103 | 3.0768 × 103 | 3.4933 × 103 | 3.0328 × 103 |
| Std | 3.10 × 101 | 4.33 × 101 | 3.31 × 101 | 3.28 × 101 | 2.77 × 102 | 3.87 × 101 | |
| (+/−/=) | ~ | ~ | 0/6/4 | 1/6/3 | 1/5/4 | 0/7/3 | 1/5/4 |
| Algorithm | Best | Mean | Worst | Std | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TLOCTO | 0.52325 | 0.53592 | 0.53706 | 0.00364 | 32 | 18 | 15 | 19 | 15 | 69 | 4 | 2 | 2 |
| TLBO | 0.53706 | 0.53877 | 0.55667 | 0.00494 | 22 | 14 | 15 | 17 | 15 | 62 | 3 | 2 | 2 |
| DBO | 0.54846 | 1.8 × 1020 | 0.77667 | 3.66 × 1020 | 26 | 14 | 14 | 19 | 14 | 69 | 3 | 1.75 | 1.75 |
| COA | 0.55706 | 7.00 × 1019 | 0.86074 | 1.44 × 1020 | 17 | 14 | 20 | 17 | 14 | 62 | 3 | 1.75 | 1.75 |
| GWO | 0.52967 | 0.55229 | 0.71000 | 0.03423 | 47 | 24 | 15 | 21 | 14 | 76 | 3 | 2 | 2 |
| PSO | 0.52624 | 0.54632 | 0.80573 | 0.04942 | 26 | 17 | 22 | 24 | 14 | 87 | 3 | 2.75 | 1.75 |
| ABC | 0.59312 | 0.93813 | 1.76841 | 0.28424 | 56 | 26 | 19 | 28 | 28 | 103 | 3 | 2 | 1.75 |
| Algorithm | Constraints | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TLOCTO | −77 | −80 | −118 | −4 | −14.8553 | −20.6838 | −6.54163 | −1165.89 | −15 | −15 |
| TLBO | −91 | −116 | −122 | −18 | −14.6769 | −23.2032 | −10.2128 | −1698.90 | −91 | −116 |
| DBO | −77 | −108 | −122 | −26 | −18.141 | −31.1314 | −12.0788 | −3597.35 | −17 | −17 |
| COA | −91 | −126 | −126 | −18 | −10.3468 | −13.8731 | −10.3468 | −377.447 | −91 | −126 |
| GWO | −63 | −26 | −118 | −16 | −34.9878 | −35.3275 | −13.8109 | −4988.21 | −63 | −26 |
| PSO | −41 | −34 | −112 | −4 | −17.7391 | −31.7917 | −16.4090 | −4383.19 | −41 | −34 |
| ABC | −9 | 0 | −48 | 0 | −42.5141 | −51.2461 | −17.9974 | −7422.03 | −9 | 0 |
| Algorithm | Best | Mean | Worst | Std | a | b | c | e | f | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| TLOCTO | 2.77479 | 3.09241 | 3.31269 | 0.15419 | 149.2512 | 132.6060 | 200.0000 | 16.4597 | 149.9069 | 104.6298 | 2.4493 |
| TLBO | 3.01791 | 3.59001 | 5.98043 | 0.59922 | 143.5842 | 133.7948 | 200.0000 | 9.58430 | 149.9702 | 106.9715 | 2.4607 |
| DBO | 3.31432 | 5.82827 | 9.34913 | 1.43645 | 150.0000 | 149.4977 | 198.8000 | 0.0306 | 17.01180 | 124.6755 | 1.7178 |
| COA | 3.79460 | 2.94 × 1022 | 3.56 × 1023 | 7.68 × 1022 | 147.8050 | 139.9458 | 153.5251 | 7.4652 | 147.8050 | 115.7780 | 2.6540 |
| GWO | 3.32379 | 3.77367 | 4.54004 | 0.30097 | 150.0000 | 140.7627 | 176.0328 | 8.7721 | 149.1059 | 118.9015 | 2.5634 |
| PSO | 3.44092 | 4.16993 | 9.54223 | 1.07760 | 150.0000 | 111.7020 | 199.5793 | 37.1027 | 144.0012 | 129.4336 | 2.7289 |
| ABC | 4.39851 | 8.21286 | 13.19273 | 2.44974 | 147.5731 | 138.0619 | 197.6639 | 6.5379 | 148.0575 | 160.0094 | 2.6131 |
| Algorithm | Constraints | ||||||
|---|---|---|---|---|---|---|---|
| TLOCTO | −32.4842 | −17.5158 | −45.1971 | −4.8029 | −68225.1644 | −70.6672 | −4.6299 |
| TLBO | −43.0799 | −6.9201 | −31.3405 | −18.6595 | −65404.3490 | −103.5279 | −6.9716 |
| DBO | −49.1101 | −0.8899 | −43.5540 | −6.4460 | −74154.8911 | −750.1439 | −24.6756 |
| COA | −6.3163 | −43.6837 | −20.6581 | −29.3419 | −69340.2484 | −359.3810 | −15.7781 |
| GWO | −21.0329 | −28.9671 | −26.2605 | −23.7395 | −70328.4313 | −488.4525 | −18.9016 |
| PSO | −40.5933 | −9.4067 | −34.8365 | −15.1635 | −50358.2696 | −1134.8062 | −29.4337 |
| ABC | −45.0324 | −4.9676 | −34.9849 | −15.0151 | −55941.6010 | −4430.9795 | −60.0095 |
| Algorithm | Best | Mean | Worst | Std | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| TLOCTO | 2994.424 | 2994.424 | 2994.424 | 1.85 × 10−12 | 3.50000 | 0.70000 | 17.0000 | 7.30000 | 7.71532 | 3.35054 | 5.28665 |
| TLBO | 2994.424 | 2994.492 | 2994.870 | 0.096 | 3.50000 | 0.700002 | 17.0000 | 7.30006 | 7.71532 | 3.35054 | 5.28666 |
| DBO | 3032.779 | 3406.531 | 5735.099 | 782.939 | 3.50264 | 0.70000 | 17.0000 | 7.30000 | 7.77305 | 3.35332 | 5.28696 |
| COA | 3060.413 | 4.57 × 1017 | 1.31 × 1019 | 2.38 × 1018 | 3.50022 | 0.70000 | 17.0000 | 7.30000 | 7.89676 | 3.35155 | 5.28631 |
| GWO | 3003.825 | 3011.045 | 3018.471 | 3.854 | 3.50122 | 0.70002 | 17.0001 | 7.77206 | 7.82642 | 3.35226 | 5.28846 |
| PSO | 3007.437 | 3160.023 | 3363.736 | 120.986 | 3.50000 | 0.70001 | 17.0000 | 7.30000 | 8.30215 | 3.35054 | 5.28686 |
| ABC | 2549.639 | 2597.282 | 2635.205 | 20.995 | 5.99485 | 0.70402 | 14.4866 | 7.30748 | 7.90121 | 3.49492 | 5.29177 |
| Algorithm | Constraints | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| TLOCTO | −2.16 × 100 | −9.81 × 101 | −1.93 × 100 | −1.83 × 101 | −9.35 × 10−4 | −2.15 × 10−3 | −2.81 × 101 | 0.00 × 100 | −7.00 × 100 | −3.74 × 10−1 | −5.00 × 10−6 |
| TLBO | −2.16 × 100 | −9.81 × 101 | −1.93 × 100 | −1.83 × 101 | −1.01 × 10−3 | −2.67 × 10−3 | −2.81 × 101 | −1.43 × 10−5 | −7.00 × 100 | −3.74 × 10−1 | −6.00 × 10−6 |
| DBO | −2.18 × 100 | −9.85 × 101 | −1.94 × 100 | −1.79 × 101 | −2.73 × 100 | −1.38 × 10−1 | −2.81 × 101 | −3.77 × 10−3 | −7.00 × 100 | −3.70 × 10−1 | −5.74 × 10−2 |
| COA | −2.16 × 100 | −9.82 × 101 | −1.93 × 100 | −1.69 × 101 | −9.93 × 10−1 | −1.96 × 10−1 | −2.81 × 101 | −3.14 × 10−4 | −7.00 × 100 | −3.73 × 10−1 | −1.82 × 10−1 |
| GWO | −2.17 × 100 | −9.83 × 101 | −1.27 × 100 | −1.75 × 101 | −7.98 × 10−1 | −8.52 × 10−1 | −2.81 × 101 | −1.60 × 10−3 | −7.00 × 100 | −8.44 × 10−1 | −1.09 × 10−1 |
| PSO | −2.16 × 100 | −9.81 × 101 | −1.93 × 100 | −1.43 × 101 | −7.43 × 10−4 | −9.41 × 10−5 | −2.81 × 101 | −7.14 × 10−5 | −7.00 × 100 | −3.74 × 10−1 | −5.87 × 10−1 |
| ABC | −1.60 × 101 | −2.26 × 102 | −1.97 × 100 | −1.43 × 101 | −1.29 × 102 | −2.19 × 100 | −2.98 × 101 | −3.52 × 100 | −3.48 × 100 | −1.65 × 10−1 | −1.80 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Li, S.; Wu, F.; Jiang, X. Teaching–Learning Optimization Algorithm Based on the Cadre–Mass Relationship with Tutor Mechanism for Solving Complex Optimization Problems. Biomimetics 2023, 8, 462. https://doi.org/10.3390/biomimetics8060462
Wu X, Li S, Wu F, Jiang X. Teaching–Learning Optimization Algorithm Based on the Cadre–Mass Relationship with Tutor Mechanism for Solving Complex Optimization Problems. Biomimetics. 2023; 8(6):462. https://doi.org/10.3390/biomimetics8060462
Chicago/Turabian StyleWu, Xiao, Shaobo Li, Fengbin Wu, and Xinghe Jiang. 2023. "Teaching–Learning Optimization Algorithm Based on the Cadre–Mass Relationship with Tutor Mechanism for Solving Complex Optimization Problems" Biomimetics 8, no. 6: 462. https://doi.org/10.3390/biomimetics8060462
APA StyleWu, X., Li, S., Wu, F., & Jiang, X. (2023). Teaching–Learning Optimization Algorithm Based on the Cadre–Mass Relationship with Tutor Mechanism for Solving Complex Optimization Problems. Biomimetics, 8(6), 462. https://doi.org/10.3390/biomimetics8060462







