Optimization of Butterworth and Bessel Filter Parameters with Improved Tree-Seed Algorithm
Abstract
:1. Introduction
2. Tree Seed Algorithm
| Algorithm 1 TSA pseudo-code |
| Step 1: The initialization of the algorithm Randomly generate tree locations on the D-dimensional search space using Equation (3). Evaluate the tree locations by the fitness function. Select the best location using Equation (4). Step 2: Search with seeds FOR all trees Decide the number of seeds produced for this tree. FOR all seeds FOR all dimensions IF (rand < ST) Update this dimension using Equation (1). ELSE Update this dimension using Equation (2). END IF END FOR END FOR Select the best seed and compare it with the tree. If the seed location is better than the tree location, the seed substitutes for this tree. END FOR Step 3: Selection of the best solution Select the best solution of the population. If new best solution is better than the previous best solution, new best solution substi-tutes for the previous best solution. Step 4: Testing the termination condition |
3. Improved Tree Seed Algorithm
4. Filter Design Problem
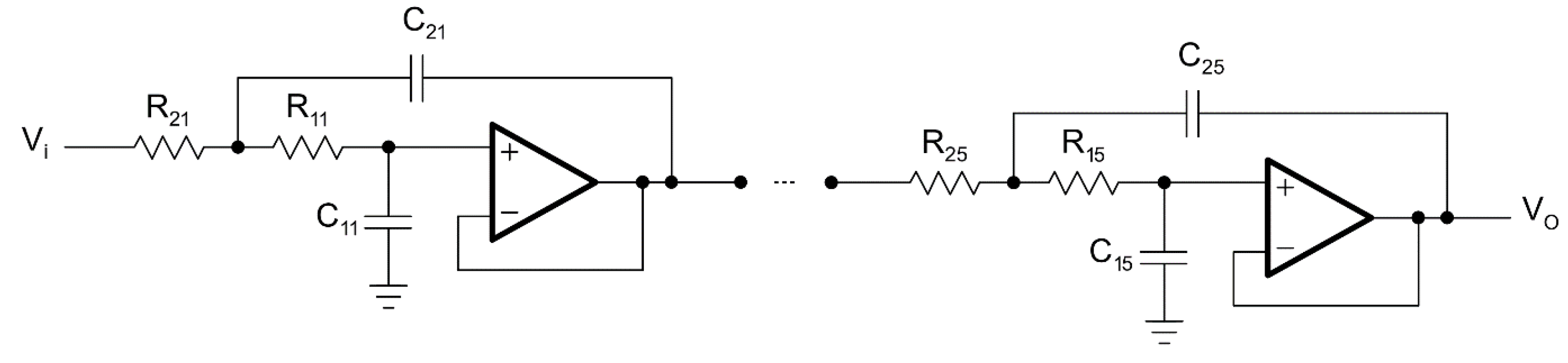
4.1. Design and Equations of LPAF
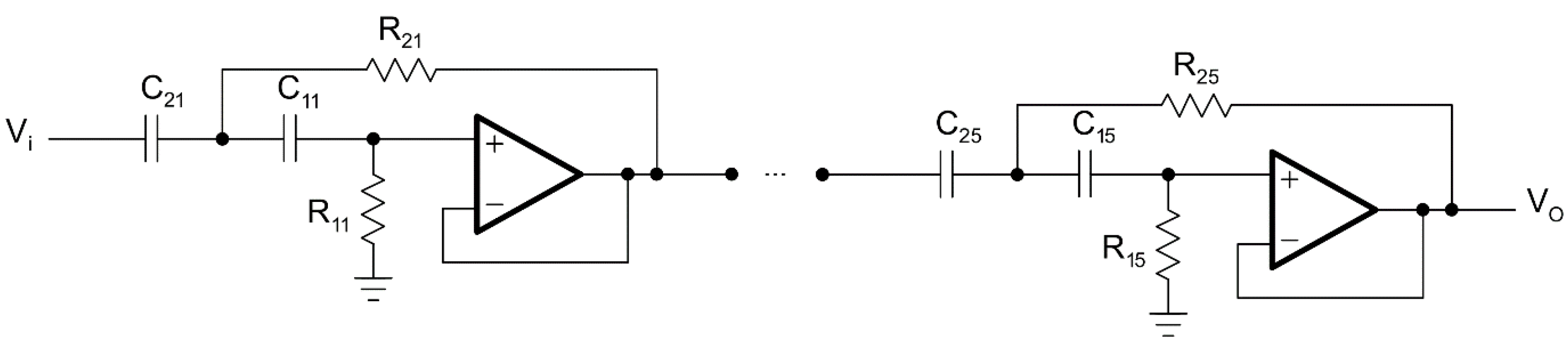
4.2. Design and Equations of HPAF
4.3. Cost Function Errors
5. Experimental Results
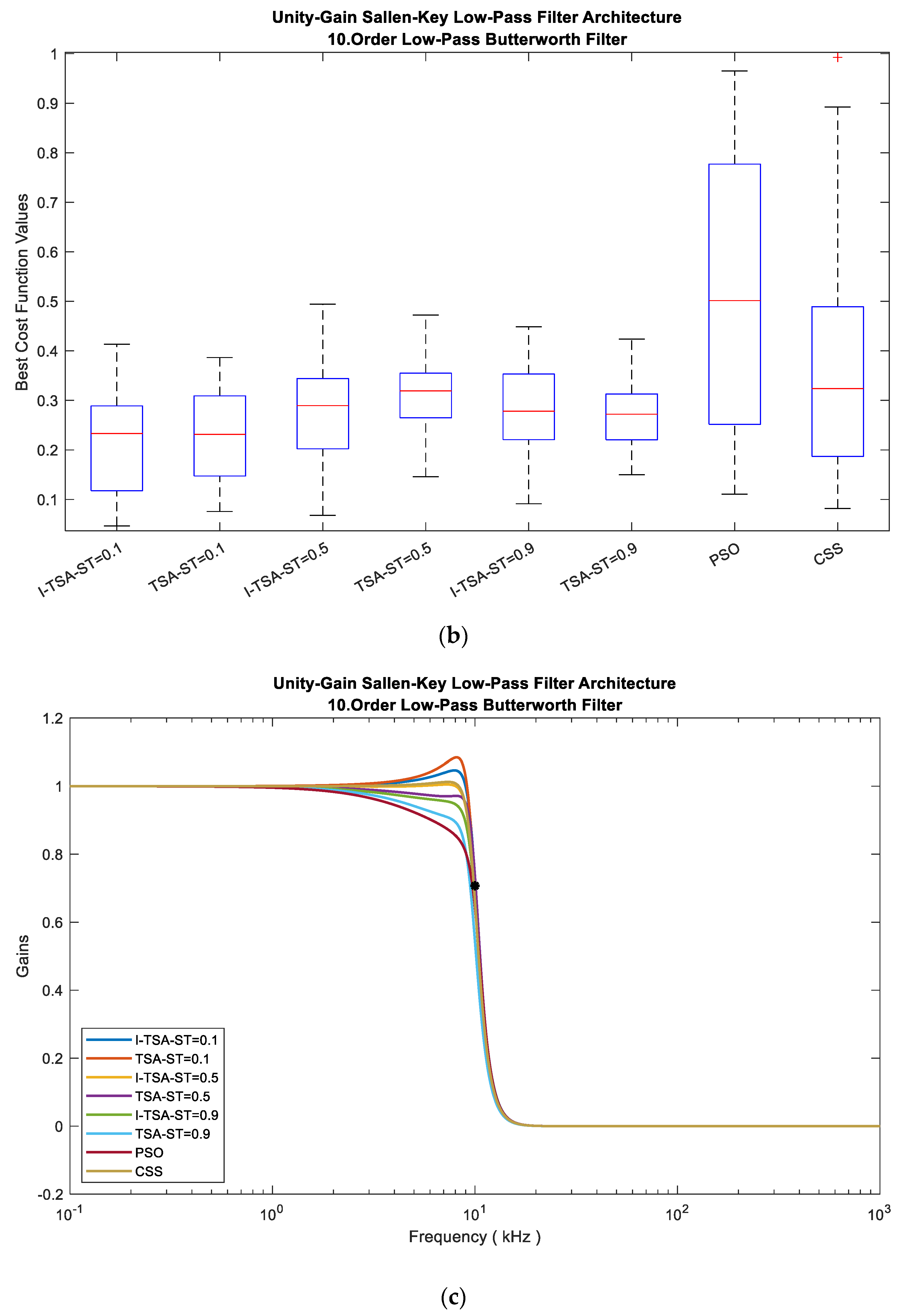
5.1. Butterworth Filter (BWF) Results
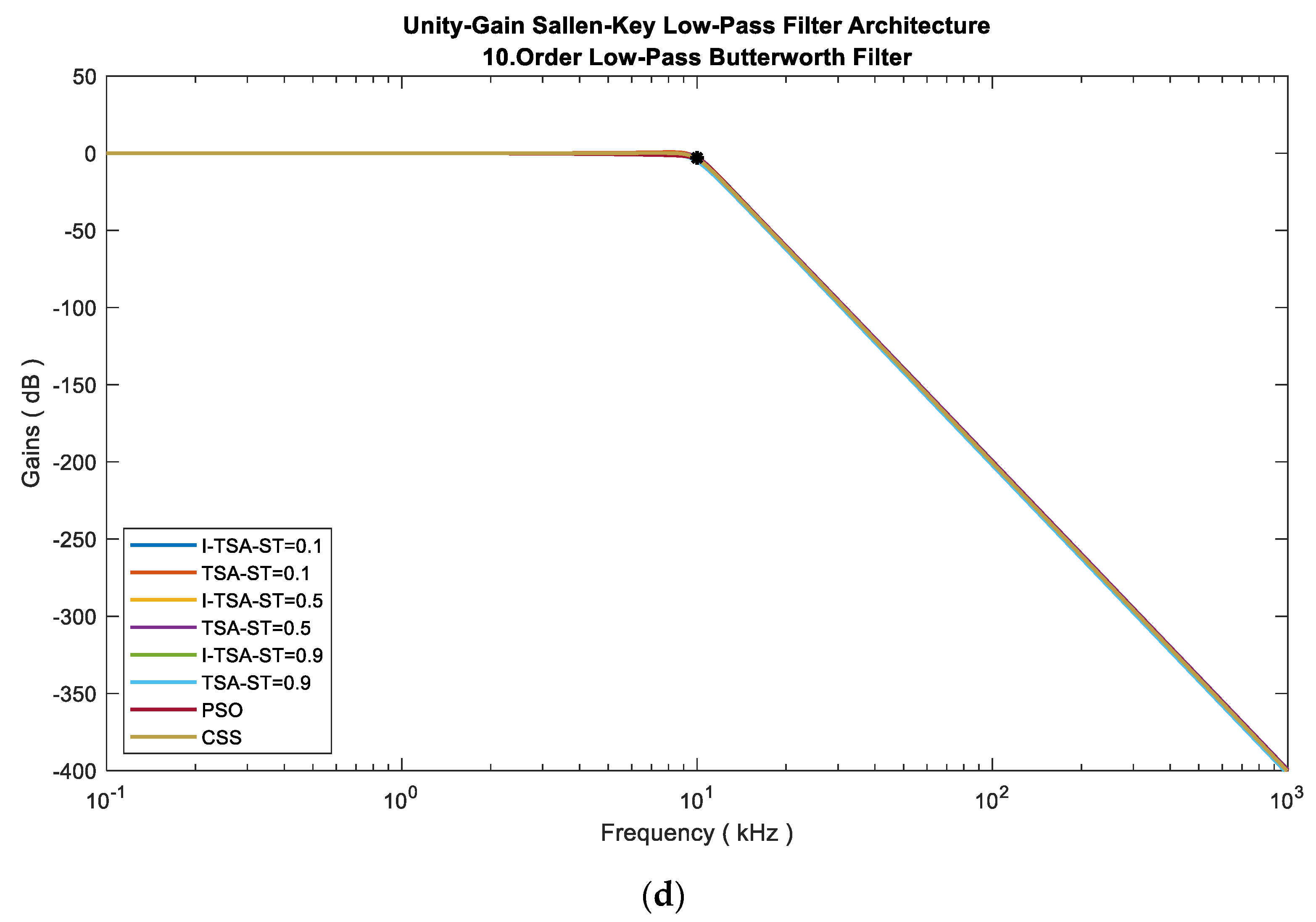
5.1.1. LPAF
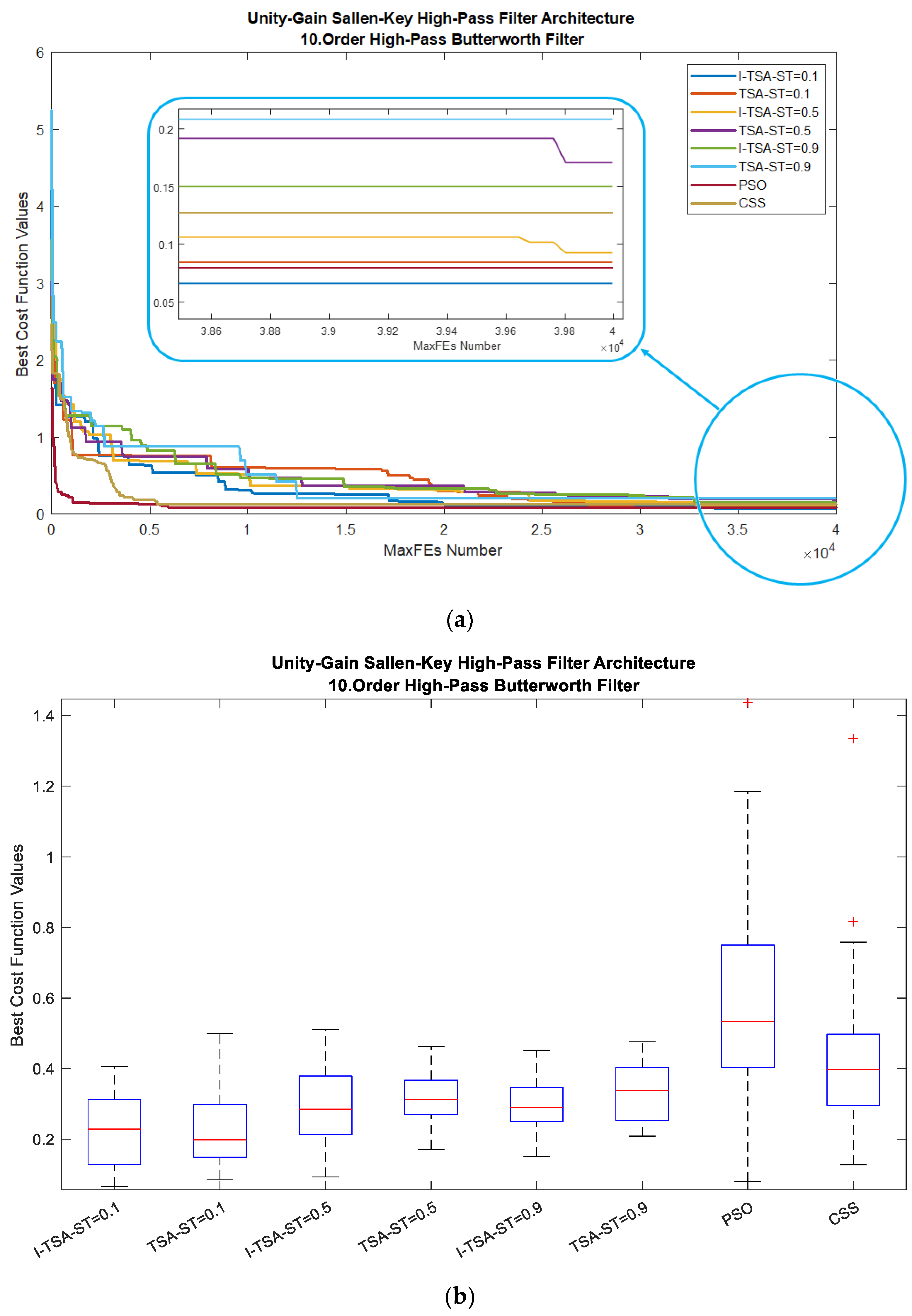
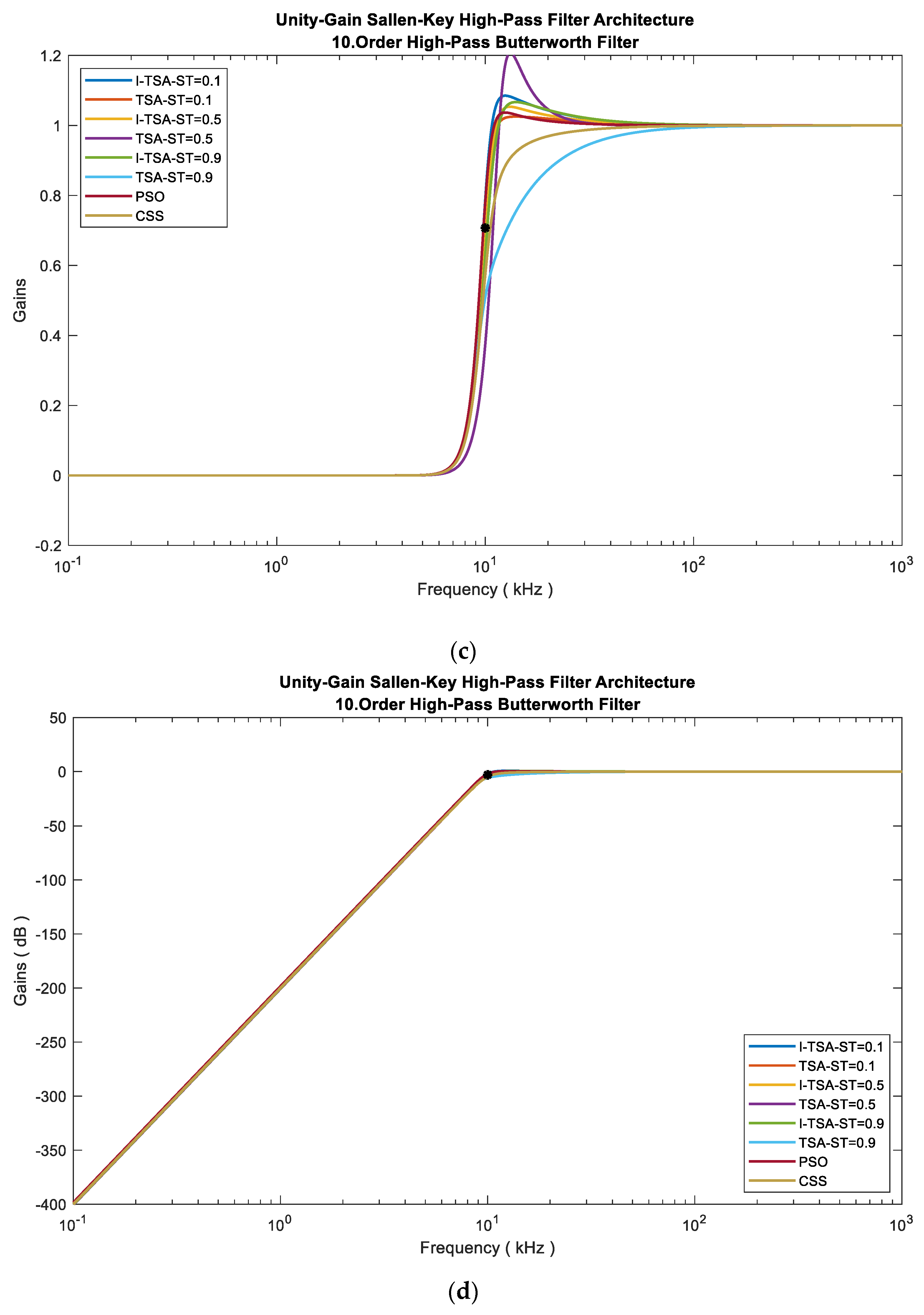
5.1.2. HPAF
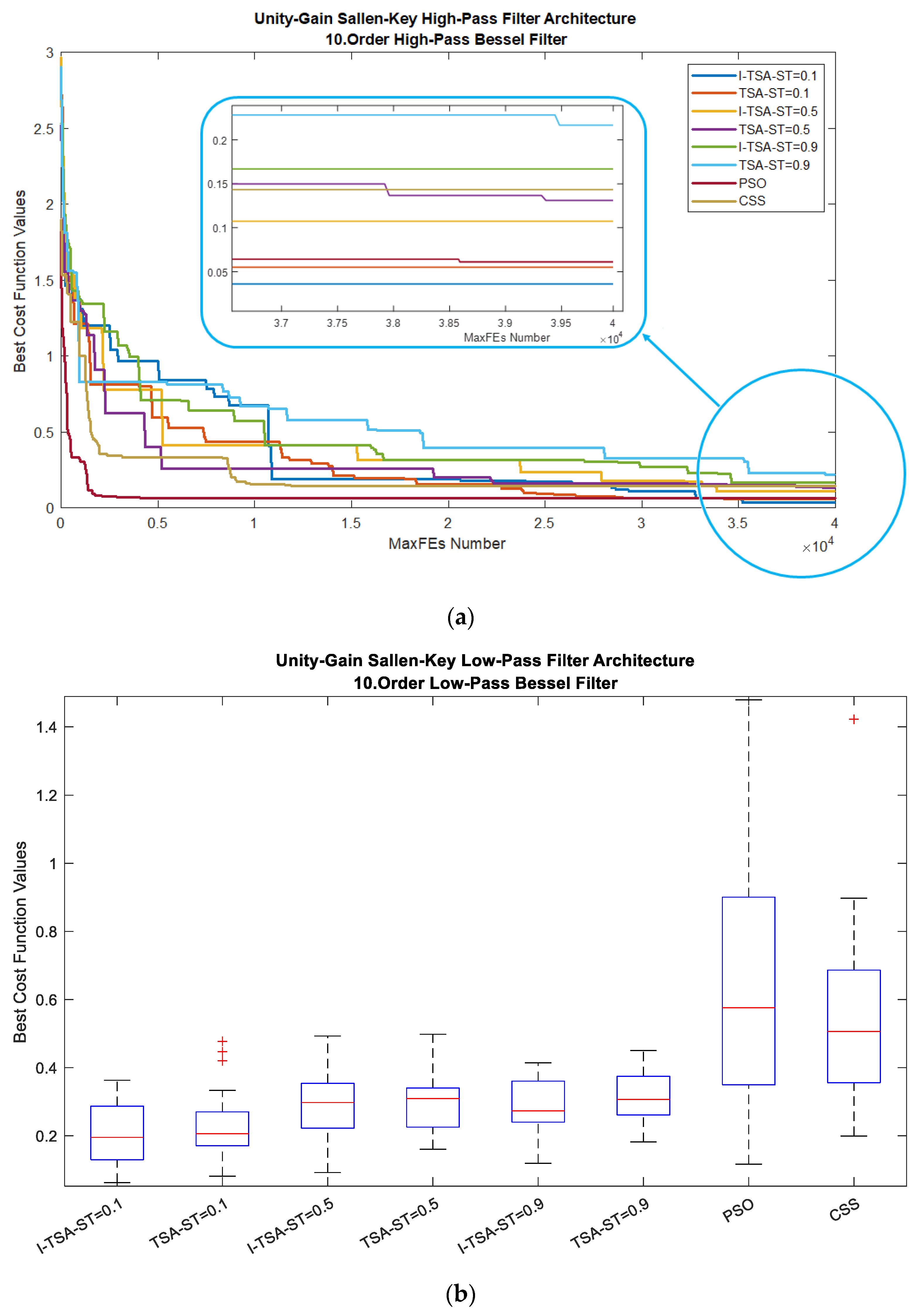
5.2. Bessel Filter (BF) Results
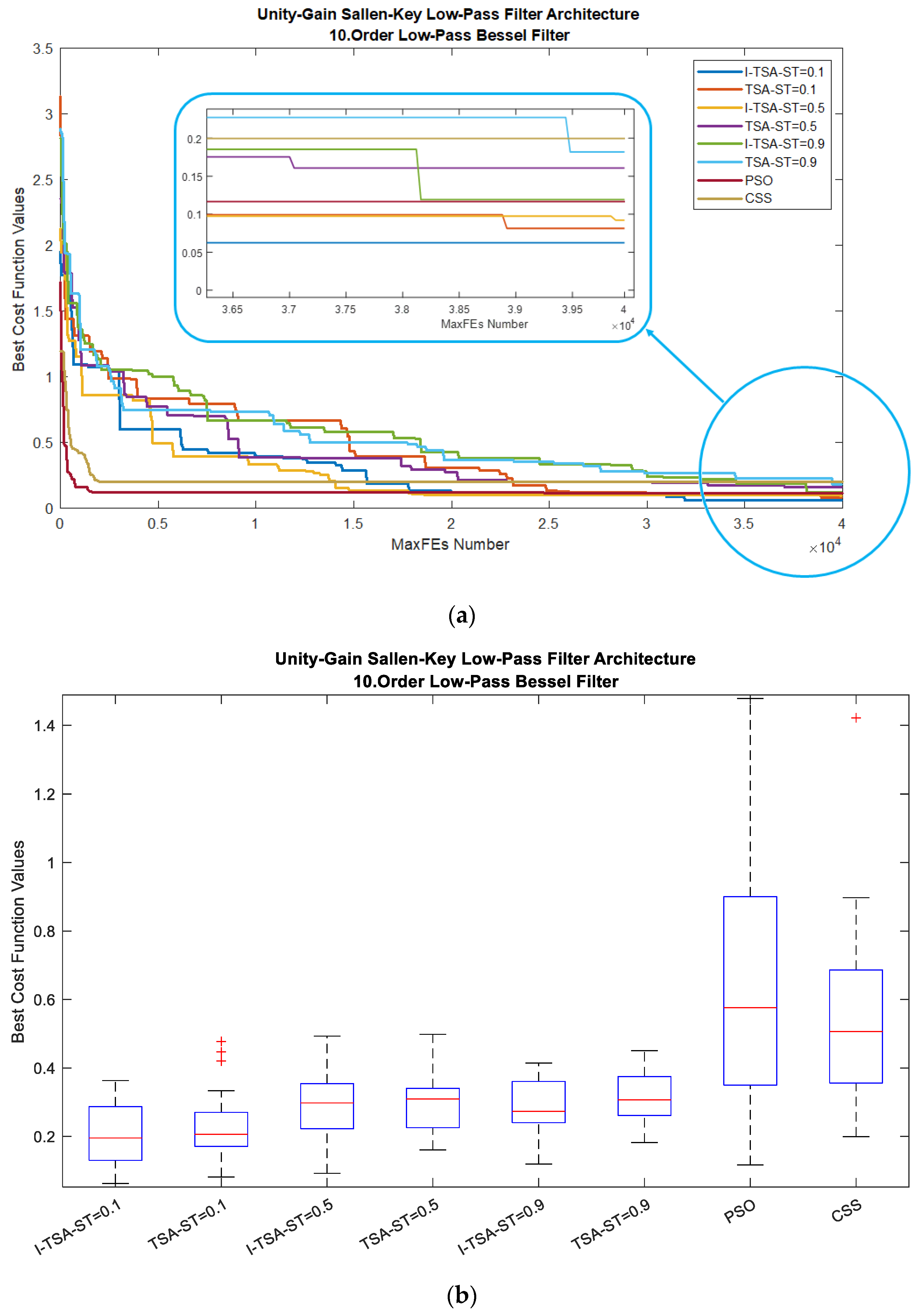
5.2.1. LPAF
5.2.2. HPAF
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Beşkirli, A.; Özdemir, D.; Temurtaş, H. A comparison of modified tree–seed algorithm for high-dimensional numerical functions. Neural Comput. Appl. 2020, 32, 6877–6911. [Google Scholar] [CrossRef]
- Beşkirli, A.; Temurtaş, H.; Özdemir, D. Determination with linear form of Turkey’s energy demand forecasting by the tree seed algorithm and the modified tree seed algorithm. Adv. Electr. Comput. Eng. 2020, 20, 27–34. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ. A new binary variant with transfer functions of Harris Hawks Optimization for binary wind turbine micrositing. Energy Rep. 2020, 6, 668–673. [Google Scholar] [CrossRef]
- Beşkirli, A.; Beşkirli, M.; Haklı, H.; Uğuz, H. Comparing energy demand estimation using artificial algae algorithm: The case of Turkey. J. Clean Energy Technol. 2018, 6, 349–352. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Tefek, M.F.; Uğuz, H.; Güçyetmez, M. A new hybrid gravitational search–teaching–learning-based optimization method for energy demand estimation of Turkey. Neural Comput. Appl. 2019, 31, 2939–2954. [Google Scholar] [CrossRef]
- Tefek, M.F. Artificial bee colony algorithm based on a new local search approach for parameter estimation of photovoltaic systems. J. Comput. Electron. 2021, 20, 2530–2562. [Google Scholar] [CrossRef]
- Tefek, M.F.; Arslan, M. Highway accident number estimation in Turkey with Jaya algorithm. Neural Comput. Appl. 2022, 34, 5367–5381. [Google Scholar] [CrossRef]
- Jiang, M.; Yang, Z.; Gan, Z. Optimal Components Selection for Analog Active Filters Using Clonal Selection Algorithms. In Advanced Intelligent Computing Theories and Applications. With Aspects of Theoretical and Methodological Issues; Springer: Berlin/Heidelberg, Germany, 2007; pp. 950–959. [Google Scholar]
- Shakoor, A.; Abbas, S.; Abbas, Z. Optimization of the Design Parameters of Low Pass Filter Using Genetic Algorithm. Univ. Wah J. Sci. Technol. 2019, 3, 55–60. [Google Scholar]
- De, B.P.; Kar, R.; Mandal, D.; Ghoshal, S.P. Optimal selection of components value for analog active filter design using simplex particle swarm optimization. Int. J. Mach. Learn. Cybern. 2015, 6, 621–636. [Google Scholar] [CrossRef]
- Temurtaş, H. The estimation of low and high-pass active filter parameters with opposite charged system search algorithm. Expert Syst. Appl. 2020, 155, 113474. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. Vortex search algorithm for the analog active filter component selection problem. AEU-Int. J. Electron. Commun. 2015, 69, 1243–1253. [Google Scholar] [CrossRef]
- Durmuş, B.; Temurtaş, H.; Özyön, S. The design of multiple feedback topology Chebyshev low-pass active filter with average differential evolution algorithm. Neural Comput. Appl. 2020, 32, 17097–17113. [Google Scholar] [CrossRef]
- Vural, R.A.; Bozkurt, U.; Yildirim, T. Analog active filter component selection with nature inspired metaheuristics. AEU-Int. J. Electron. Commun. 2013, 67, 197–205. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ. Parameter extraction for photovoltaic models with tree seed algorithm. Energy Rep. 2023, 9, 174–185. [Google Scholar] [CrossRef]
- Boumediene Ghaouti, G.; Meftah, B. An Optimized Clustering Approach using Tree Seed Algorithm for the Brain MRI Images Segmentation. Intel. Artif. 2023, 26, 44–59. [Google Scholar] [CrossRef]
- More, S. Image Constraint Technique Used by Bio-Inspired Tsa Optimized Algorithm for Large Memory Management. SSRN 2023, 8, 1–10. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ. An efficient tree seed inspired algorithm for parameter estimation of Photovoltaic models. Energy Rep. 2022, 8, 291–298. [Google Scholar] [CrossRef]
- Mandal, B.; Chatterjee, S.; Roy, P.; Mukherjee, I. A novel evolutionary algorithm named oppositional based chaotic tree seed algorithm (OCTSA) applied for energy cost minimization in hybrid microgrid system for different locations in India. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Venkatasubramanian, S. Optimal Cluster head selection-based Hybrid Moth Search Algorithm with Tree Seed algorithm for multipath routing in WSN. In Proceedings of the 2023 International Conference on Networking and Communications (ICNWC), Chennai, India, 5–6 April 2023; pp. 1–7. [Google Scholar]
- Liu, J.; Hou, Y.; Li, Y.; Zhou, H. A multi-strategy improved tree–seed algorithm for numerical optimization and engineering optimization problems. Sci. Rep. 2023, 13, 10768. [Google Scholar] [CrossRef]
- Sharshir, S.S.; Abd Elaziz, M.; Elsheikh, A. Augmentation and prediction of wick solar still productivity using artificial neural network integrated with tree–seed algorithm. Int. J. Environ. Sci. Technol. 2023, 20, 7237–7252. [Google Scholar] [CrossRef]
- Jiang, J.; Yang, X.; Li, M.; Chen, T. ATSA: An Adaptive Tree Seed Algorithm based on double-layer framework with tree migration and seed intelligent generation. Knowl.-Based Syst. 2023, 279, 110940. [Google Scholar] [CrossRef]
- Liu, J.; Hou, Y.; Li, Y.; Zhou, H. Advanced strategies on update mechanism of tree-seed algorithm for function optimization and engineering design problems. Expert Syst. Appl. 2024, 236, 121312. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Aslan, M.F.; Sabanci, K.; Ropelewska, E. A new approach to COVID-19 detection: An ANN proposal optimized through tree-seed algorithm. Symmetry 2022, 14, 1310. [Google Scholar] [CrossRef]
- Jiang, J.; Meng, X.; Qian, L.; Wang, H. Enhance tree-seed algorithm using hierarchy mechanism for constrained optimization problems. Expert Syst. Appl. 2022, 209, 118311. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S. Advances in Tree Seed Algorithm: A Comprehensive Survey. Arch. Comput. Methods Eng. 2022, 29, 3281–3304. [Google Scholar] [CrossRef]
- Kiran, M.S.; Hakli, H. A tree–seed algorithm based on intelligent search mechanisms for continuous optimization. Appl. Soft Comput. 2021, 98, 106938. [Google Scholar] [CrossRef]
- Chen, X.; Przystupa, K.; Ye, Z.; Chen, F.; Wang, C.; Liu, J.; Gao, R.; Wei, M.; Kochan, O. Forecasting short-term electric load using extreme learning machine with improved tree seed algorithm based on Lévy flight. Eksploat. I Niezawodn. 2022, 24, 153. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC′06), Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
- Wang, H.; Wu, Z.; Rahnamayan, S.; Liu, Y.; Ventresca, M. Enhancing particle swarm optimization using generalized opposition-based learning. Inf. Sci. 2011, 181, 4699–4714. [Google Scholar] [CrossRef]
- Gift, S.J.G.; Maundy, B. Active Filters. In Electronic Circuit Design and Application; Gift, S.J.G., Maundy, B., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 463–515. [Google Scholar]
- Beşkirli, M.; Egi, Y. An efficient hybrid-based charged system search algorithm for active filter design. Neural Comput. Appl. 2023, 35, 7611–7633. [Google Scholar] [CrossRef]
- Karki, J. Active low-pass filter design. Tex. Instrum. Appl. Rep. 2000. [Google Scholar]
- Sallen, R.P.; Key, E.L. A practical method of designing RC active filters. IRE Trans. Circuit Theory 1955, 2, 74–85. [Google Scholar] [CrossRef]
- Pactitis, S. Active Filters: Theory and Design; CRC Press: Boca Ranton, FL, USA, 2018. [Google Scholar]





| 1 | 1.1 | 1.2 | 1.3 | 1.5 | 1.6 | 1.8 | 2 | 2.2 | 2.4 | 2.7 | 3 |
| 3.3 | 3.6 | 3.9 | 4.3 | 4.7 | 5.1 | 5.6 | 6.2 | 6.8 | 7.5 | 8.2 | 9.1 |
| Algorithm | ST Value | Component | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|---|---|
| I-TSA | 0.1 | R1 | 1.6 | 1.5 | 6.8 | 1.5 | 3.0 |
| R2 | 1.6 | 2.2 | 3.3 | 1.8 | 2.0 | ||
| C1 | 10.0 | 7.5 | 2.2 | 4.3 | 1.0 | ||
| C2 | 10.0 | 10.0 | 5.1 | 22.0 | 43.0 | ||
| I-TSA | 0.5 | R1 | 1.8 | 3.9 | 3.3 | 3.0 | 1.3 |
| R2 | 1.5 | 1.2 | 1.8 | 4.3 | 1.0 | ||
| C1 | 10.0 | 5.6 | 4.3 | 2.0 | 2.2 | ||
| C2 | 10.0 | 10.0 | 10.0 | 10.0 | 91.0 | ||
| I-TSA | 0.9 | R1 | 1.0 | 3.3 | 4.3 | 5.1 | 2.0 |
| R2 | 1.2 | 7.5 | 6.8 | 3.9 | 4.7 | ||
| C1 | 15.0 | 2.7 | 2.0 | 1.6 | 0.8 | ||
| C2 | 15.0 | 3.6 | 4.3 | 8.2 | 36.0 |
| S1 | S2 | S3 | S4 | S5 | |||
|---|---|---|---|---|---|---|---|
| Target | FSF | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| Q | 0.5062 | 0.5612 | 0.7071 | 1.1013 | 3.1969 | ||
| Algorithm | ST Value | ||||||
| I-TSA | 0.1 | FSF | 0.994718 | 1.011655 | 1.003026 | 0.995847 | 0.990855 |
| Q | 0.500000 | 0.566924 | 0.714108 | 1.126277 | 3.212476 | ||
| 0.5 | FSF | 0.968586 | 0.983112 | 0.995847 | 0.990855 | 0.986544 | |
| Q | 0.497930 | 0.566838 | 0.728767 | 1.100163 | 3.188256 | ||
| 0.9 | FSF | 0.968586 | 1.026123 | 1.003650 | 0.985226 | 0.999020 | |
| Q | 0.497930 | 0.531904 | 0.714307 | 1.121816 | 3.170368 |
| Algorithm | ST Value | Best | Mean | Worst | Std. Dev. |
|---|---|---|---|---|---|
| I-TSA | 0.1 | 0.046585 | 0.212725 | 0.413537 | 0.094703 |
| 0.5 | 0.067909 | 0.291463 | 0.494240 | 0.100709 | |
| 0.9 | 0.091301 | 0.286216 | 0.448817 | 0.080759 | |
| TSA | 0.1 | 0.075820 | 0.224486 | 0.386590 | 0.089920 |
| 0.5 | 0.145739 | 0.313718 | 0.472144 | 0.085195 | |
| 0.9 | 0.150140 | 0.274506 | 0.423986 | 0.067385 | |
| PSO | - | 0.110755 | 0.527483 | 0.965142 | 0.269997 |
| CSS | - | 0.081702 | 0.378726 | 0.992566 | 0.236921 |
| Algorithm | ST Value | Component | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|---|---|
| I-TSA | 0.1 | R1 | 3.9 | 6.2 | 8.2 | 10.0 | 18.0 |
| R2 | 2.7 | 4.7 | 2.7 | 2.0 | 0.4 | ||
| C1 | 8.2 | 2.4 | 1.8 | 3.9 | 10.0 | ||
| C2 | 3.0 | 3.6 | 6.8 | 3.3 | 3.9 | ||
| I-TSA | 0.5 | R1 | 16.0 | 2.7 | 10.0 | 5.1 | 30.0 |
| R2 | 15.0 | 2.0 | 4.7 | 1.0 | 0.8 | ||
| C1 | 1.0 | 6.2 | 1.8 | 8.2 | 3.0 | ||
| C2 | 1.0 | 7.5 | 3.0 | 6.2 | 3.3 | ||
| I-TSA | 0.9 | R1 | 2.0 | 4.3 | 10.0 | 24.0 | 51.0 |
| R2 | 1.8 | 3.0 | 4.7 | 3.6 | 1.0 | ||
| C1 | 6.8 | 3.6 | 1.8 | 1.0 | 4.7 | ||
| C2 | 10.0 | 5.6 | 3.0 | 3.0 | 1.0 |
| S1 | S2 | S3 | S4 | S5 | |||
|---|---|---|---|---|---|---|---|
| Target | FSF | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| Q | 0.5062 | 0.5612 | 0.7071 | 1.1013 | 3.1969 | ||
| Algorithm | ST Value | ||||||
| I-TSA | 0.1 | FSF | 1.011257 | 0.996969 | 1.034331 | 1.008055 | 0.998849 |
| Q | 0.532231 | 0.562668 | 0.708953 | 1.114145 | 3.176892 | ||
| 0.5 | FSF | 0.973387 | 0.995642 | 1.000981 | 1.011737 | 0.980539 | |
| Q | 0.516398 | 0.578326 | 0.706166 | 1.118215 | 3.020861 | ||
| 0.9 | FSF | 0.983073 | 1.013258 | 1.000981 | 1.011573 | 0.972778 | |
| Q | 0.517397 | 0.584293 | 0.706166 | 1.118034 | 2.716184 |
| Algorithm | ST Value | Best | Mean | Worst | Std. Dev. |
|---|---|---|---|---|---|
| I-TSA | 0.1 | 0.066204 | 0.223354 | 0.405234 | 0.095903 |
| 0.5 | 0.092779 | 0.305070 | 0.510234 | 0.105158 | |
| 0.9 | 0.150058 | 0.298889 | 0.452366 | 0.070469 | |
| TSA | 0.1 | 0.084627 | 0.226826 | 0.499136 | 0.106131 |
| 0.5 | 0.171201 | 0.319772 | 0.463289 | 0.075065 | |
| 0.9 | 0.208470 | 0.331249 | 0.475878 | 0.079518 | |
| PSO | - | 0.079577 | 0.586805 | 1.436803 | 0.294510 |
| CSS | - | 0.127601 | 0.445885 | 1.334431 | 0.241027 |
| Algorithm | ST Value | Component | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|---|---|
| I-TSA | 0.1 | R1 | 3.9 | 2.2 | 1.5 | 1.2 | 10.0 |
| R2 | 3.3 | 1.0 | 3.0 | 1.2 | 3.9 | ||
| C1 | 2.2 | 4.7 | 2.7 | 3.6 | 0.3 | ||
| C2 | 2.4 | 6.2 | 4.7 | 10.0 | 3.3 | ||
| I-TSA | 0.5 | R1 | 9.1 | 4.7 | 3.9 | 7.5 | 3.3 |
| R2 | 7.5 | 10.0 | 6.8 | 3.0 | 5.1 | ||
| C1 | 1.0 | 1.0 | 1.1 | 0.8 | 0.6 | ||
| C2 | 1.0 | 1.3 | 2.0 | 2.7 | 4.7 | ||
| I-TSA | 0.9 | R1 | 6.2 | 2.2 | 10.0 | 1.0 | 1.3 |
| R2 | 10.0 | 1.0 | 3.6 | 1.0 | 1.0 | ||
| C1 | 1.0 | 5.1 | 0.9 | 4.7 | 2.0 | ||
| C2 | 1.0 | 6.2 | 1.8 | 11.0 | 16.0 |
| S1 | S2 | S3 | S4 | S5 | |||
|---|---|---|---|---|---|---|---|
| Target | FSF | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| Q | 0.5062 | 0.5612 | 0.7071 | 1.1013 | 3.1969 | ||
| Algorithm | ST Value | ||||||
| I-TSA | 0.1 | FSF | 1.930696 | 1.987760 | 2.106120 | 2.210485 | 2.442159 |
| Q | 0.520416 | 0.532364 | 0.621958 | 0.833333 | 1.420749 | ||
| 0.5 | FSF | 1.926499 | 2.036102 | 2.083637 | 2.254966 | 2.391306 | |
| Q | 0.497672 | 0.531745 | 0.648966 | 0.819741 | 1.414874 | ||
| 0.9 | FSF | 2.021270 | 1.908217 | 2.072583 | 2.213476 | 2.467593 | |
| Q | 0.486050 | 0.511060 | 0.620480 | 0.764922 | 1.402132 |
| Algorithm | ST Value | Best | Mean | Worst | Std. Dev. |
|---|---|---|---|---|---|
| I-TSA | 0.1 | 0.062378 | 0.208454 | 0.363140 | 0.092668 |
| 0.5 | 0.092212 | 0.301908 | 0.492980 | 0.100669 | |
| 0.9 | 0.119140 | 0.289782 | 0.414542 | 0.073533 | |
| TSA | 0.1 | 0.081274 | 0.227481 | 0.477295 | 0.097471 |
| 0.5 | 0.160654 | 0.296257 | 0.498181 | 0.086586 | |
| 0.9 | 0.181832 | 0.310810 | 0.450243 | 0.072830 | |
| PSO | - | 0.116503 | 0.645454 | 1.478782 | 0.330566 |
| CSS | - | 0.199537 | 0.541564 | 1.421876 | 0.264927 |
| Algorithm | ST Value | Component | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|---|---|
| I-TSA | 0.1 | R1 | 16.0 | 12.0 | 12.0 | 16.0 | 22.0 |
| R2 | 10.0 | 6.8 | 7.5 | 4.7 | 2.7 | ||
| C1 | 1.2 | 1.8 | 4.3 | 2.4 | 4.3 | ||
| C2 | 5.1 | 6.8 | 2.7 | 6.8 | 6.2 | ||
| I-TSA | 0.5 | R1 | 4.3 | 15.0 | 12.0 | 10.0 | 18.0 |
| R2 | 3.9 | 9.1 | 4.7 | 3.0 | 2.0 | ||
| C1 | 6.2 | 5.1 | 2.0 | 10.0 | 10.0 | ||
| C2 | 10.0 | 1.5 | 9.1 | 3.6 | 4.3 | ||
| I-TSA | 0.9 | R1 | 10.0 | 4.3 | 10.0 | 39.0 | 18.0 |
| R2 | 11.0 | 3.6 | 5.6 | 13.0 | 2.4 | ||
| C1 | 2.4 | 8.2 | 2.7 | 2.0 | 6.2 | ||
| C2 | 3.6 | 8.2 | 7.5 | 1.2 | 5.1 |
| S1 | S2 | S3 | S4 | S5 | |||
|---|---|---|---|---|---|---|---|
| Target | FSF | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| Q | 0.5062 | 0.5612 | 0.7071 | 1.1013 | 3.1969 | ||
| Algorithm | ST Value | ||||||
| I-TSA | 0.1 | FSF | 1.966145 | 1.985709 | 2.031034 | 2.201146 | 2.500364 |
| Q | 0.496701 | 0.540416 | 0.615713 | 0.810183 | 1.403687 | ||
| 0.5 | FSF | 2.026013 | 2.030378 | 2.013053 | 2.064865 | 2.472096 | |
| Q | 0.510367 | 0.538036 | 0.614122 | 0.805474 | 1.375686 | ||
| 0.9 | FSF | 1.937015 | 2.027119 | 2.115857 | 2.191742 | 2.322216 | |
| Q | 0.467099 | 0.546453 | 0.589547 | 0.838525 | 1.362803 |
| Algorithm | ST Value | Best | Mean | Worst | Std. Dev. |
|---|---|---|---|---|---|
| I-TSA | 0.1 | 0.036035 | 0.190635 | 0.353110 | 0.076729 |
| 0.5 | 0.107378 | 0.332173 | 0.620112 | 0.124932 | |
| 0.9 | 0.166924 | 0.337793 | 0.522845 | 0.084933 | |
| TSA | 0.1 | 0.054876 | 0.214660 | 0.513616 | 0.100502 |
| 0.5 | 0.130932 | 0.323992 | 0.527150 | 0.097837 | |
| 0.9 | 0.216784 | 0.366686 | 0.492966 | 0.082912 | |
| PSO | - | 0.061011 | 0.682382 | 1.360255 | 0.360903 |
| CSS | - | 0.143429 | 0.580740 | 1.075118 | 0.242949 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beşkirli, M.; Kiran, M.S. Optimization of Butterworth and Bessel Filter Parameters with Improved Tree-Seed Algorithm. Biomimetics 2023, 8, 540. https://doi.org/10.3390/biomimetics8070540
Beşkirli M, Kiran MS. Optimization of Butterworth and Bessel Filter Parameters with Improved Tree-Seed Algorithm. Biomimetics. 2023; 8(7):540. https://doi.org/10.3390/biomimetics8070540
Chicago/Turabian StyleBeşkirli, Mehmet, and Mustafa Servet Kiran. 2023. "Optimization of Butterworth and Bessel Filter Parameters with Improved Tree-Seed Algorithm" Biomimetics 8, no. 7: 540. https://doi.org/10.3390/biomimetics8070540
APA StyleBeşkirli, M., & Kiran, M. S. (2023). Optimization of Butterworth and Bessel Filter Parameters with Improved Tree-Seed Algorithm. Biomimetics, 8(7), 540. https://doi.org/10.3390/biomimetics8070540





