Development of a Wheel-Type In-Pipe Robot Using Continuously Variable Transmission Mechanisms for Pipeline Inspection
Abstract
:1. Introduction
| Actuator | Pneumatic Actuators | ||
|---|---|---|---|
| DC Motors | |||
| SMA | |||
| Power Supply | Cable | ||
| Battery | |||
| Locomotion | Active locomotion | Wheel type | Simple structure |
| Wall-press | |||
| screw-drive | |||
| Caterpillar type | Simple structure | ||
| Wall-press | |||
| Non-wheeled type | Inchworm | ||
| legged | |||
| Free swimming | |||
| Passive locomotion | PIG | ||
2. Robot Design
2.1. Design Objectives
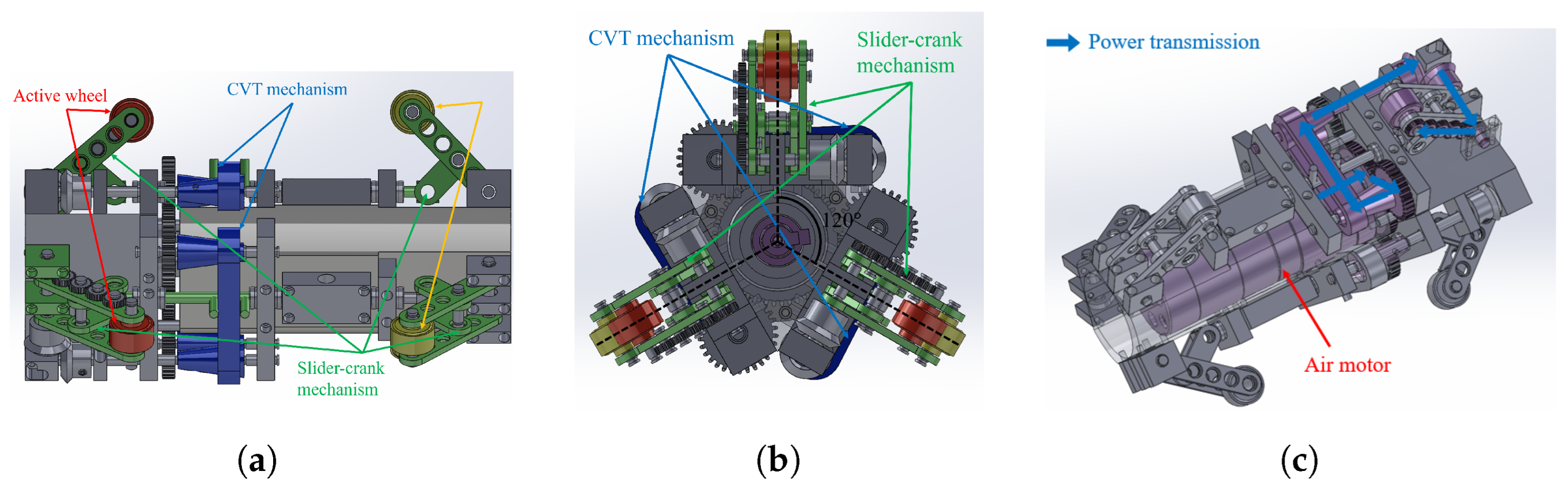
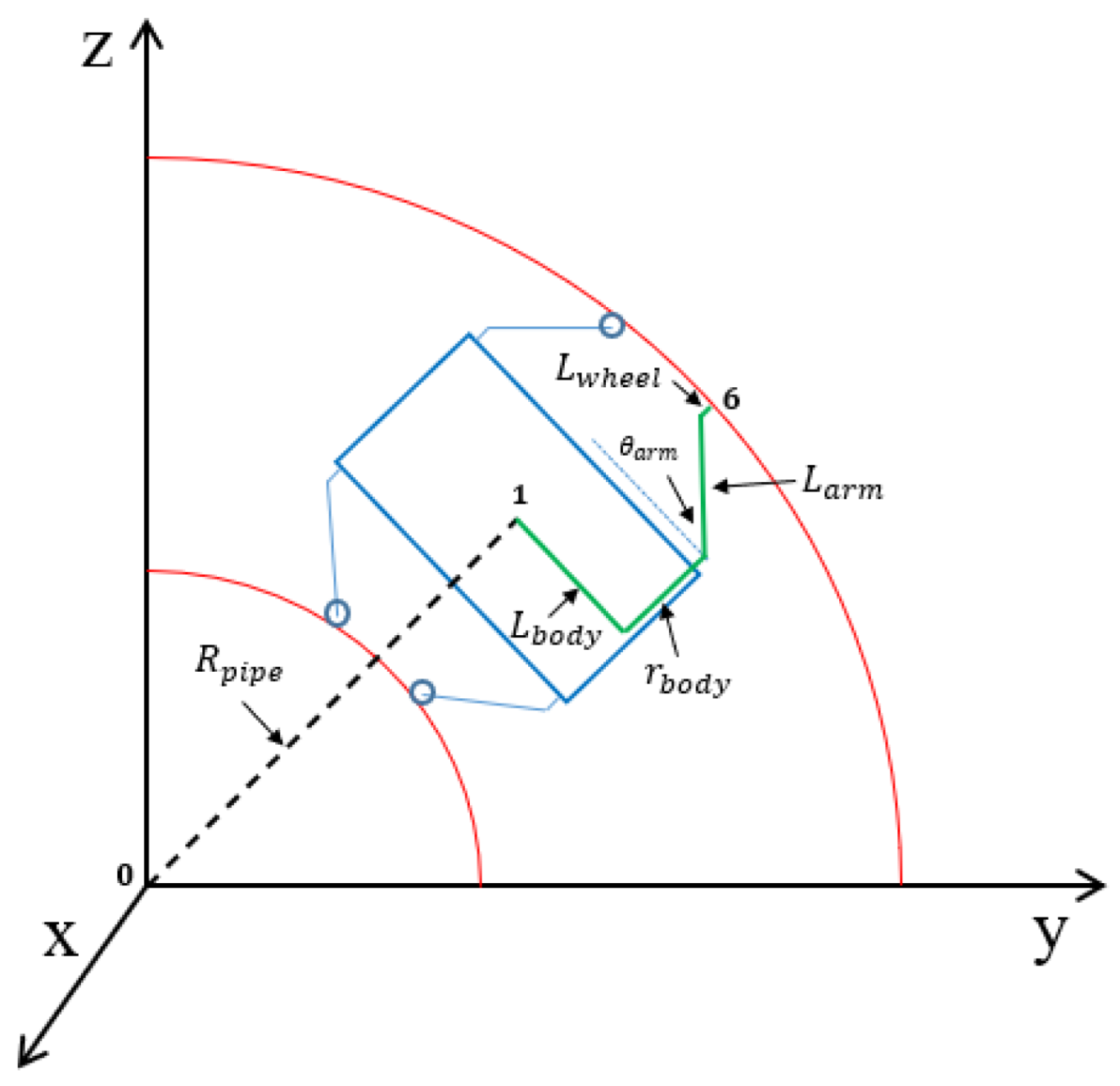
2.2. Overview of Robot
2.3. Slider-Crank Mechanism
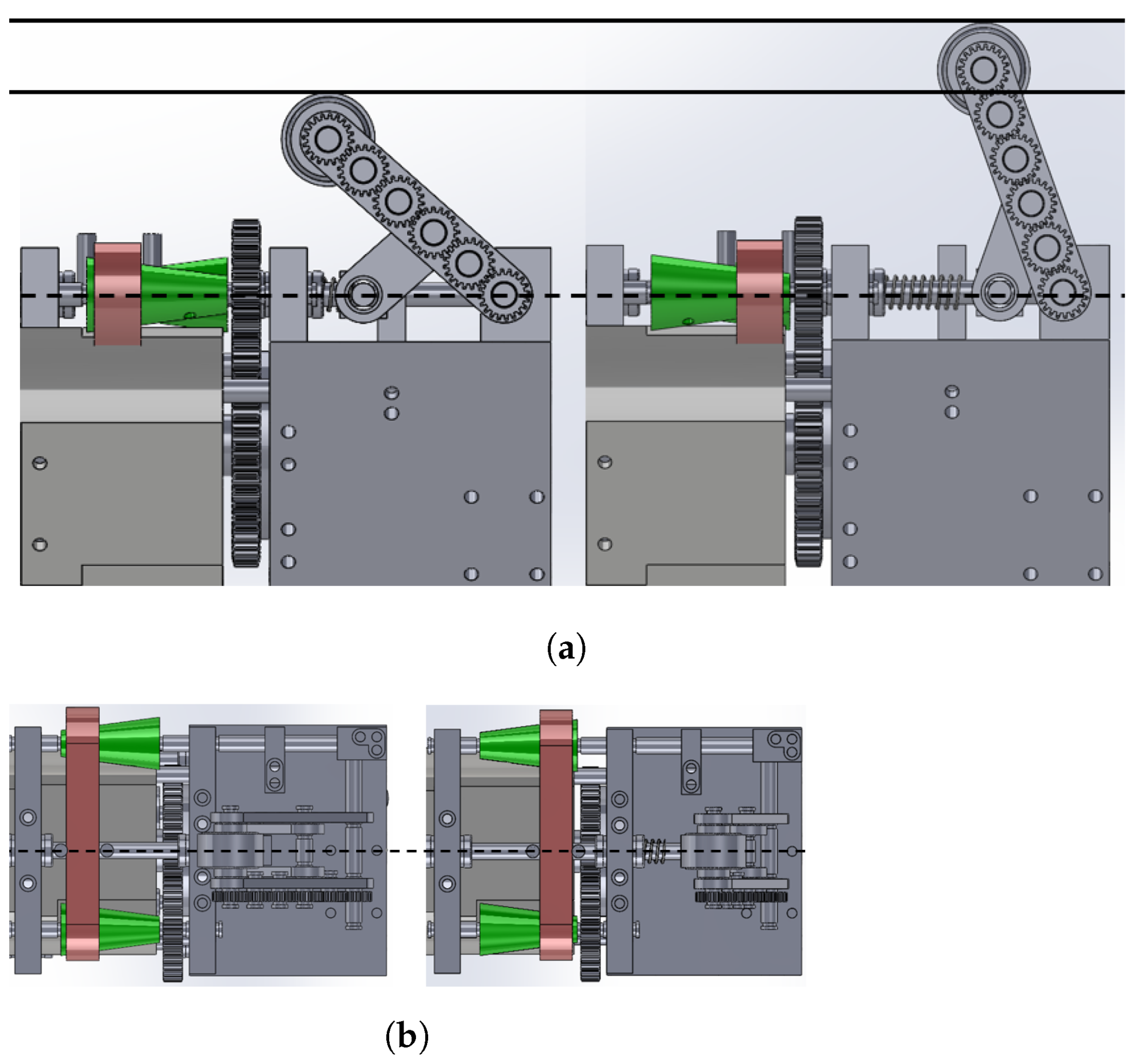
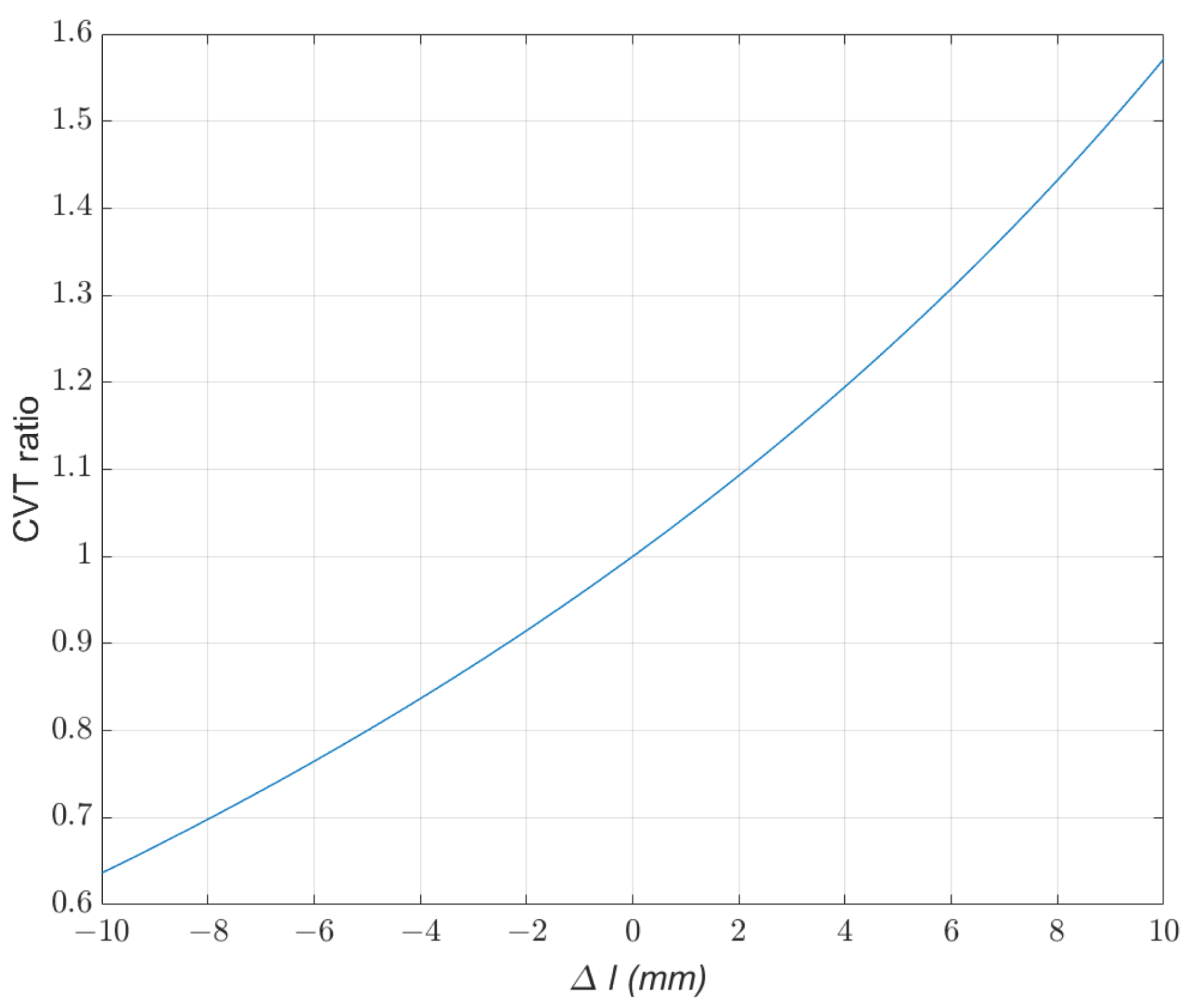
2.4. Cvt Mechanism
3. Simulation
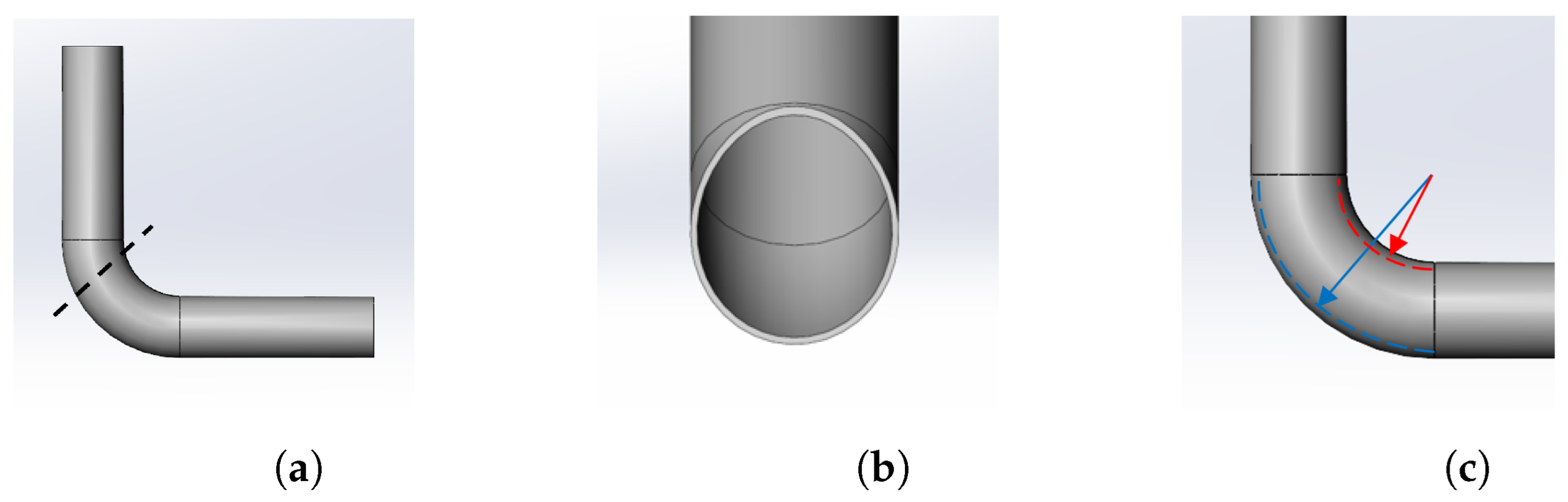
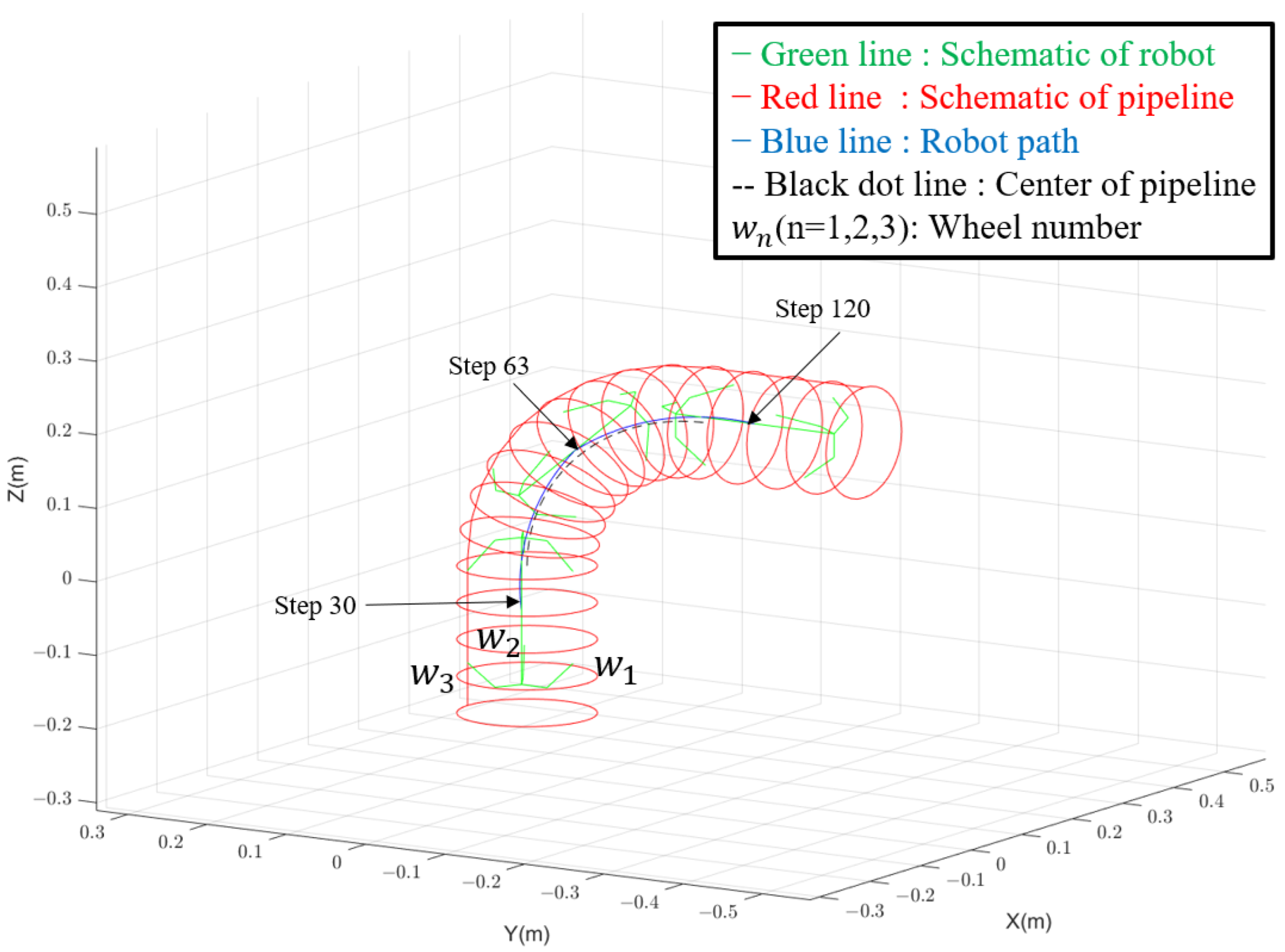
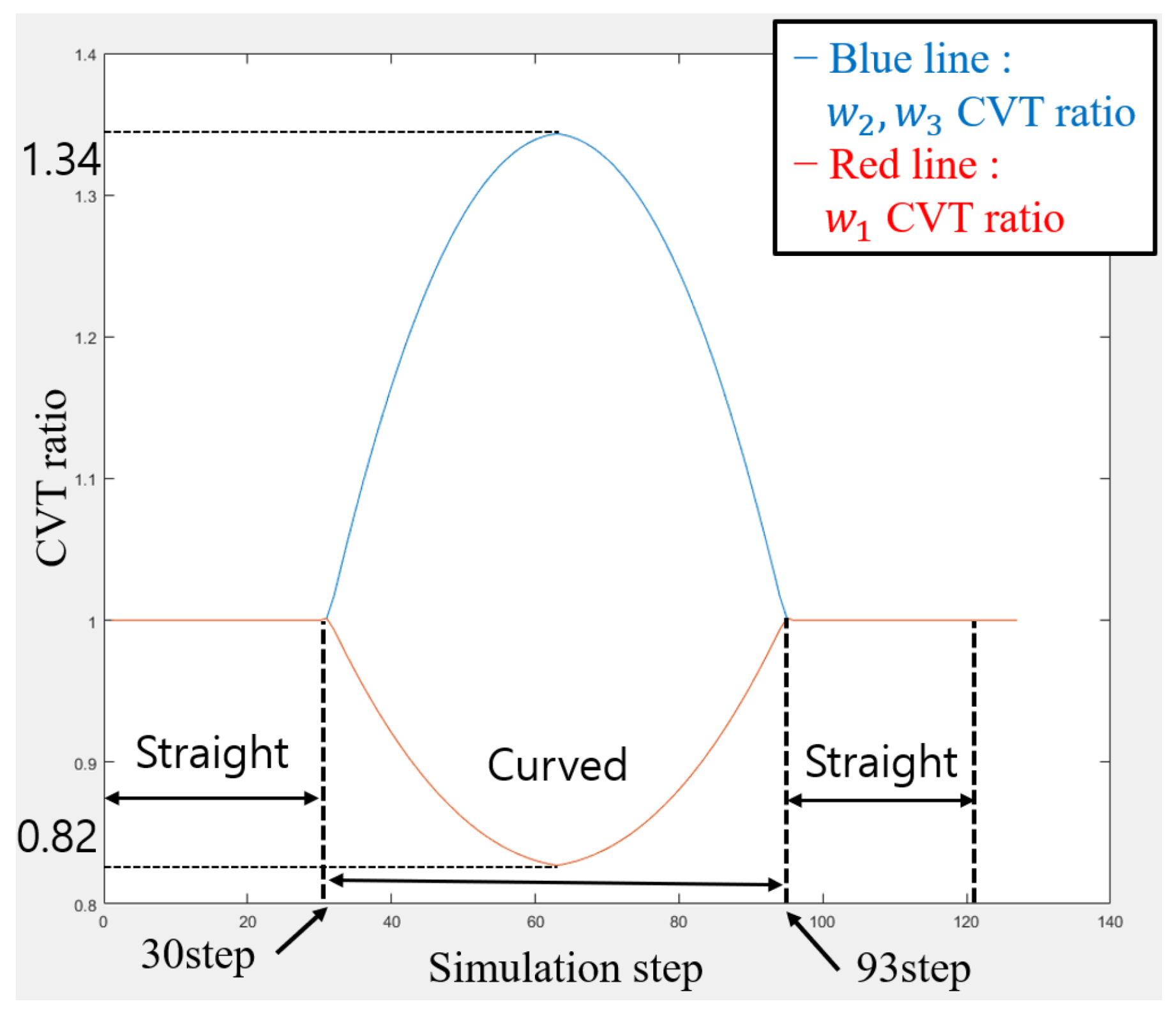
3.1. Simulation of the Robot Passing through A Curved Pipe
3.2. Minimum Radius of the Curved Pipe
4. Experiments
- Experiment 1: payload measurement. The focus of this experiment is on measuring the payload capability of the robot during vertical pipe climbing. The data collected in this experiment will also serve to validate the traction force target outlined in Section 2.3.
- Experiment 2: vertical pipe climbing. In Experiment 2, the objective is to validate the effectiveness of the slider-crank mechanism design and the spring parameters in generating sufficient force to counteract the weight of the robot during vertical pipe climbing.
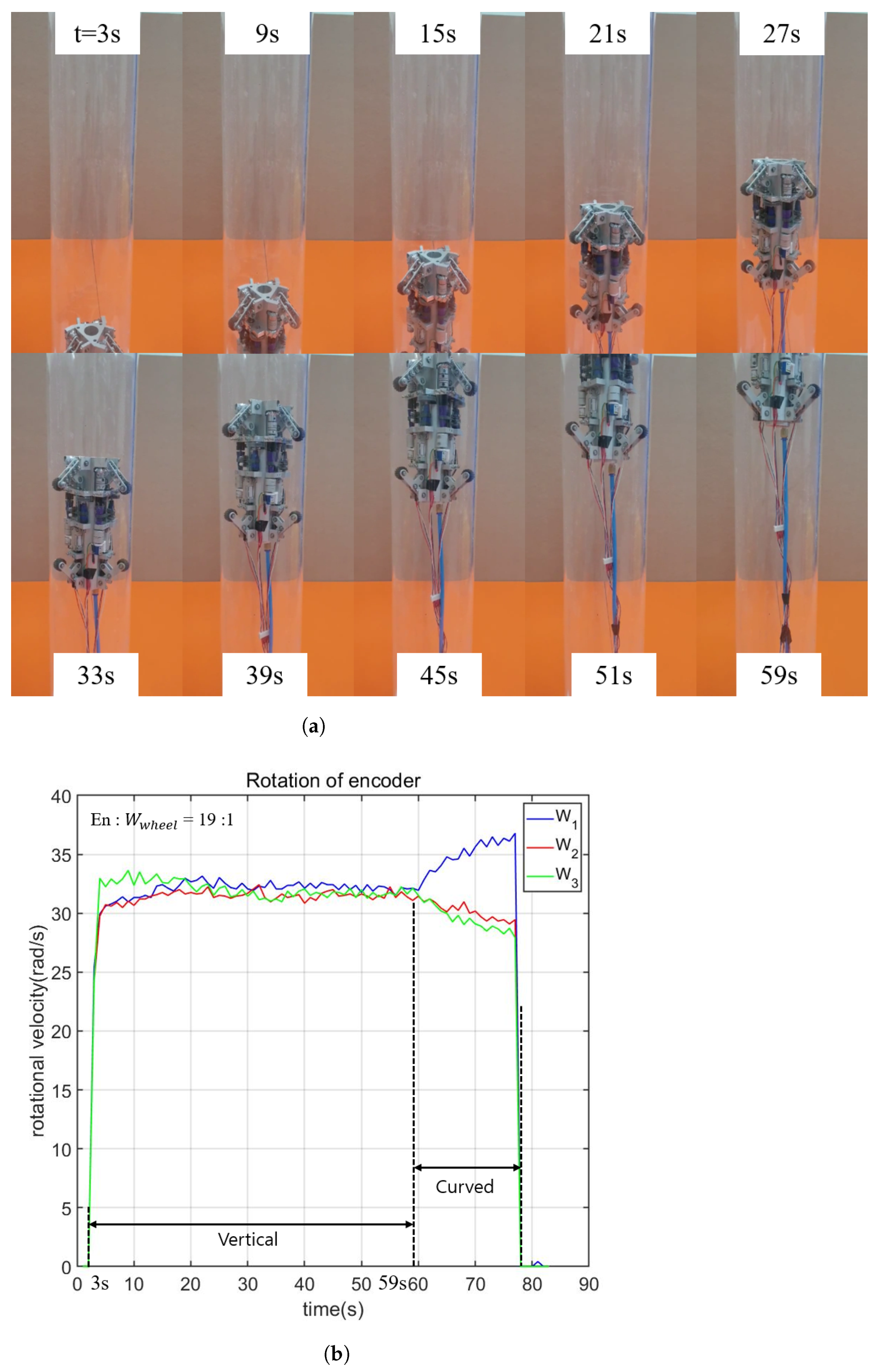
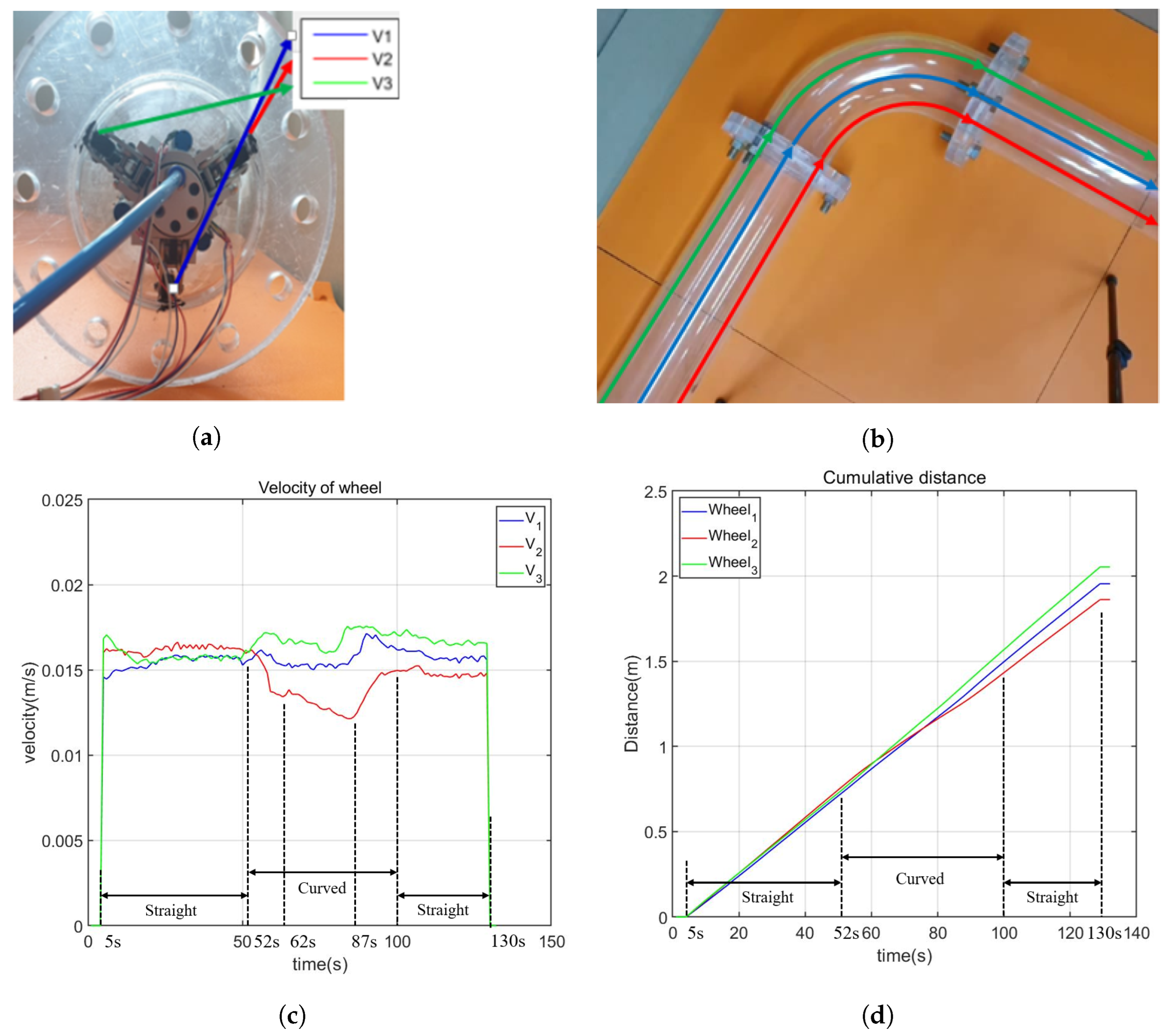
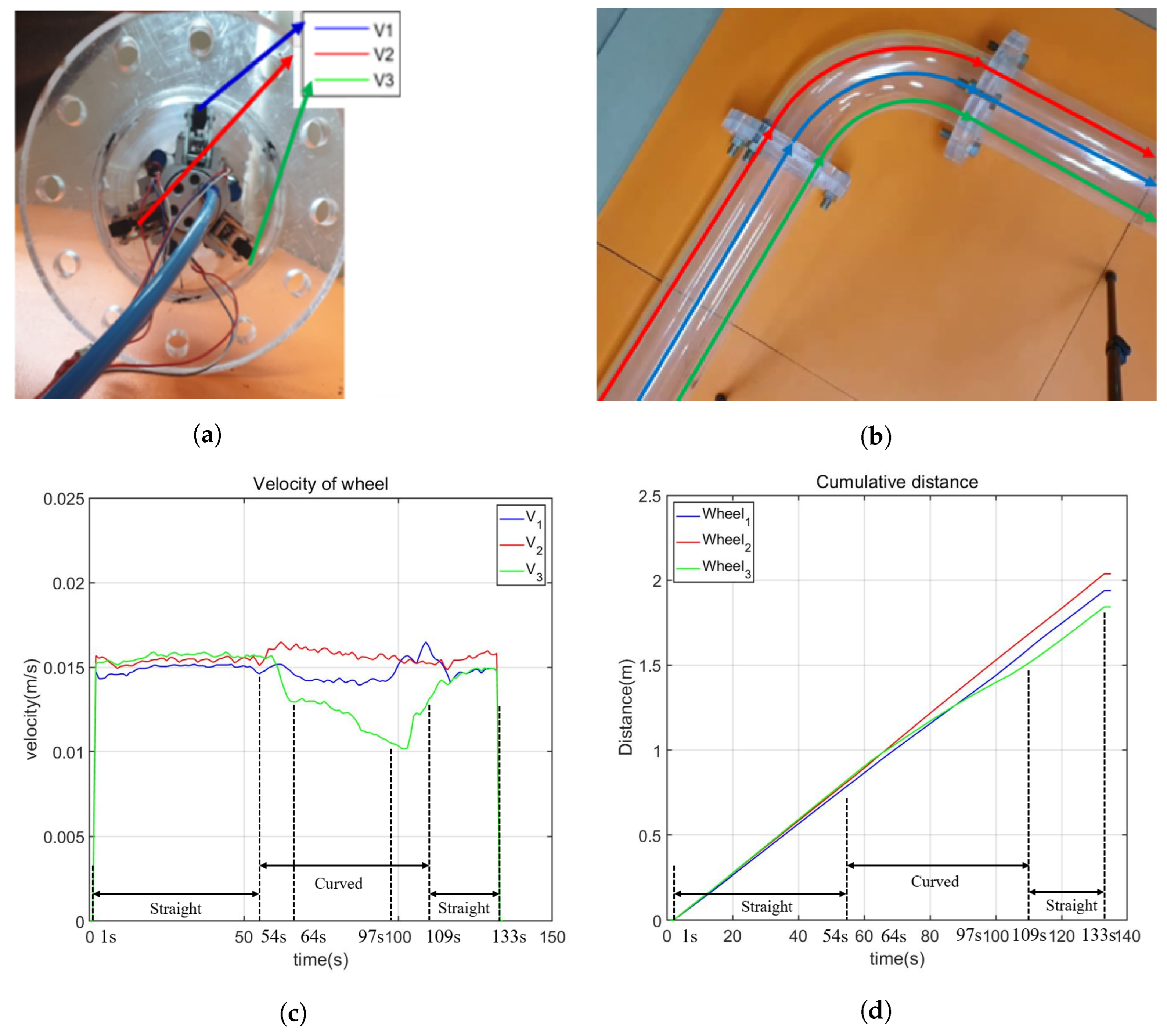
- Experiment 3: passing through the curved pipe. Experiment 3 is focused on validating the robot’s capability to navigate through a curved pipe. This experiment aims to confirm that each wheel can independently adjust its velocity, a crucial requirement for successful traversal through curved pipes.
4.1. Payload Measurement Experiment
4.2. Vertical Pipe Climbing
4.3. Curved Pipe Driving
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Han, S.; Ahn, J.; Moon, H. Remotely controlled prehensile locomotion of a two-module 3D pipe-climbing robot. J. Mech. Sci. Technol. 2016, 30, 1875–1882. [Google Scholar] [CrossRef]
- Rashid, M.; Yakub, F.; Zaki, S.; Ali, M.; Mamat, N.; Putra, S.; Roslan, S.; Shah, H.; Aras, M.; Arshad, M. Reconfigurable multi-legs robot for pipe inspection: Design and gait movement. Indian J. Geo-Mar. Sci. 2019, 48, 1132–1144. [Google Scholar]
- Miyasaka, K.; Kawano, G.; Tsukagoshi, H. Long-mover: Flexible tube in-pipe inspection robot for long distance and complex piping. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; pp. 1075–1080. [Google Scholar]
- Sato, H.; Mano, Y.; Ito, F.; Yasui, T.; Okui, M.; Nishihama, R.; Nakamura, T. Proposal for pipeline-shape measurement method based on highly accurate pipeline length measurement by IMU sensor using peristaltic motion characteristics. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 874–881. [Google Scholar]
- Kawaguchi, Y.; Yoshida, I.; Kurumatani, H.; Kikuta, T.; Yamada, Y. Internal pipe inspection robot. In Proceedings of the Proceedings of 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 1, pp. 857–862. [Google Scholar]
- Hadi, A.; Hassani, A.; Alipour, K.; Askari Moghadam, R.; Pourakbarian Niaz, P. Developing an adaptable pipe inspection robot using shape memory alloy actuators. J. Intell. Mater. Syst. Struct. 2020, 31, 632–647. [Google Scholar] [CrossRef]
- Wu, R.; Wan Salim, W.; Malhotra, S.; Brovont, A.; Park, J.; Pekarek, S.; Banks, M.K.; Porterfield, D. Self-powered mobile sensor for in-pipe potable water quality monitoring. In Proceedings of the 17th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Freiburg, Germany, 27–31 October 2013; Volume 1, pp. 14–16. [Google Scholar]
- Kakogawa, A.; Murata, K.; Ma, S. Automatic T-Branch Travel of an Articulated Wheeled In-Pipe Inspection Robot Using Joint Angle Response to Environmental Changes. IEEE Trans. Ind. Electron. 2022, 70, 7041–7050. [Google Scholar] [CrossRef]
- Bandala, A.A.; Maningo, J.M.Z.; Fernando, A.H.; Vicerra, R.R.P.; Antonio, M.A.B.; Diaz, J.A.I.; Ligeralde, M.; Mascardo, P.A.R. Control and mechanical design of a multi-diameter tri-legged in-pipe traversing robot. In Proceedings of the 2019 IEEE/SICE International Symposium on System Integration (SII), Paris, France, 14–16 January 2019; pp. 740–745. [Google Scholar]
- Li, P.; Tang, M.; Lyu, C.; Fang, M.; Duan, X.; Liu, Y. Design and analysis of a novel active screw-drive pipe robot. Adv. Mech. Eng. 2018, 10, 1687814018801384. [Google Scholar] [CrossRef]
- Kakogawa, A.; Nishimura, T.; Ma, S. Designing arm length of a screw drive in-pipe robot for climbing vertically positioned bent pipes. Robotica 2016, 34, 306–327. [Google Scholar] [CrossRef]
- Jang, H.; Kim, T.Y.; Lee, Y.C.; Song, Y.H.; Choi, H.R. Autonomous navigation of in-pipe inspection robot using contact sensor modules. IEEE/ASME Trans. Mechatron. 2022, 27, 4665–4674. [Google Scholar] [CrossRef]
- Abidin, A.S.Z.; Pauzi, M.F.A.M.; Sadini, M.M.; Zaini, M.H.; Chie, S.C.; Mohammadan, S.; Jamali, A.; Muslimen, R.; Ashari, M.F.; Jamaludin, M.S. Development of track wheel for in-pipe robot application. Procedia Comput. Sci. 2015, 76, 500–505. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, X.; Wang, Z.; Bi, Q.; Song, R.; Zhao, J.; Li, Y. A Tensegrity-Based Inchworm-Like Robot for Crawling in Pipes with Varying Diameters. IEEE Robot. Autom. Lett. 2022, 7, 11553–11560. [Google Scholar] [CrossRef]
- Hayashi, K.; Akagi, T.; Dohta, S.; Kobayashi, W.; Shinohara, T.; Kusunose, K.; Aliff, M. Improvement of pipe holding mechanism and inchworm type flexible pipe inspection robot. Int. J. Mech. Eng. Robot. Res. 2020, 9, 894–899. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, J. A review of wheeled mobile robots. Mach. Tool Hydraul. 2009, 37, 242–247. [Google Scholar]
- Roh, S.; Ryew, S.; Yang, J.; Choi, H. Actively steerable in-pipe inspection robots for underground urban gas pipelines. In Proceedings of the 2001 ICRA, IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, Republic of Korea, 21–26 May 2001; Volume 1, pp. 761–766. [Google Scholar]
- Zhao, W.; Zhang, L.; Kim, J. Design and analysis of independently adjustable large in-pipe robot for long-distance pipeline. Appl. Sci. 2020, 10, 3637. [Google Scholar] [CrossRef]
- Kwon, Y.S.; Yi, B.J. Design and motion planning of a two-module collaborative indoor pipeline inspection robot. IEEE Trans. Robot. 2012, 28, 681–696. [Google Scholar] [CrossRef]
- Liljebäck, P.; Pettersen, K.Y.; Stavdahl, Ø.; Gravdahl, J.T. A review on modelling, implementation, and control of snake robots. Robot. Auton. Syst. 2012, 60, 29–40. [Google Scholar] [CrossRef]
- Yu, X.; Chen, Y.; Chen, M.Z.; Lam, J. Development of a novel in-pipe walking robot. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 364–368. [Google Scholar]
- Jackson-Mills, G.H.; Shead, B.A.; Collett, J.R.; Mphake, M.; Fry, N.; Barber, A.R.; Boyle, J.H.; Richardson, R.C.; Jackson, A.E.; Whitehead, S. Non-assembly walking mechanism for robotic in-pipe inspection. In Proceedings of the Robotics for Sustainable Future: CLAWAR 2021 24, Virtual, 30 August–1 September 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 117–128. [Google Scholar]
- Savin, S.; Vorochaeva, L. Footstep planning for a six-legged in-pipe robot moving in spatially curved pipes. In Proceedings of the 2017 International Siberian Conference on Control and Communications (SIBCON), Astana, Kazakhstan, 29–30 June 2017; pp. 1–6. [Google Scholar]
- Wu, Y.; Chatzigeorgiou, D.; Youcef-Toumi, K.; Zribi, M. Modeling and parameter estimation for in-pipe swimming robots. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 2007–2013. [Google Scholar]
- Kazeminasab, S.; Sadeghi, N.; Janfaza, V.; Razavi, M.; Ziyadidegan, S.; Banks, M.K. Localization, mapping, navigation, and inspection methods in in-pipe robots: A review. IEEE Access 2021, 9, 162035–162058. [Google Scholar] [CrossRef]
- Tourajizadeh, H.; Sedigh, A.; Boomeri, V.; Rezaei, M. Design of a new steerable in-pipe inspection robot and its robust control in presence of pipeline flow. J. Mech. Eng. Sci. 2020, 14, 6993–7016. [Google Scholar] [CrossRef]
- Kazeminasab, S.; Banks, M.K. Towards long-distance inspection for in-pipe robots in water distribution systems with smart motion facilitated by particle filter and multi-phase motion controller. Intell. Serv. Robot. 2022, 15, 259–273. [Google Scholar] [CrossRef]
- Mangialardi, L.; Mantriota, G. The advantages of using continuously variable transmissions in wind power systems. Renew. Energy 1992, 2, 201–209. [Google Scholar] [CrossRef]
- Liu, H.; Han, L.; Cao, Y. Improving transmission efficiency and reducing energy consumption with automotive continuously variable transmission: A model prediction comprehensive optimization approach. Appl. Energy 2020, 274, 115303. [Google Scholar] [CrossRef]
- Tahboub, K.A.; Asada, H.H. Dynamics analysis and control of a holonomic vehicle with a continuously variable transmission. J. Dyn. Sys., Meas. Control 2002, 124, 118–126. [Google Scholar] [CrossRef]
- Kazeminasab, S.; Akbari, A.; Jafari, R.; Banks, M.K. Design, characterization, and control of a size adaptable in-pipe robot for water distribution systems. In Proceedings of the 2021 22nd IEEE International Conference on Industrial Technology (ICIT), Valencia, Spain, 10–12 March 2021; Volume 1, pp. 39–46. [Google Scholar]
- Roh, S.g.; Choi, H.R. Differential-drive in-pipe robot for moving inside urban gas pipelines. IEEE Trans. Robot. 2005, 21, 1–17. [Google Scholar]
- Pandian, S.R.; Takemura, F.; Hayakawa, Y.; Kawamura, S. Control performance of an air motor-can air motors replace electric motors? In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 1, pp. 518–524. [Google Scholar]
- Ali, S.N.; Hanif, A.; Ahmed, Q. Review in thermal effects on the performance of electric motors. In Proceedings of the 2016 International Conference on Intelligent Systems Engineering (ICISE), Islamabad, Pakistan, 15–17 January 2016; pp. 83–88. [Google Scholar]
- Kazeminasab, S.; Banks, M.K. SmartCrawler: A Size-Adaptable In-Pipe Wireless Robotic System with Two-Phase Motion Control Algorithm in Water Distribution Systems. Sensors 2022, 22, 9666. [Google Scholar] [CrossRef]
- An, J.; Lee, G.; Oh, I.; Moon, H.; Ryew, S. Navigation-oriented design for in-pipe robot in recursively divided sampling space with rapidly exploring random tree. J. Mech. Sci. Technol. 2017, 31, 5987–5995. [Google Scholar] [CrossRef]
- Jang, H.; Kim, H.M.; Lee, M.S.; Song, Y.H.; Lee, Y.; Ryew, W.R.; Choi, H.R. Development of modularized in-pipe inspection robotic system: MRINSPECT VII+. Robotica 2022, 40, 1361–1384. [Google Scholar]
- Wu, Y.; Mittmann, E.; Winston, C.; Youcef-Toumi, K. A practical Minimalism Approach to in-Pipe Robot Localization. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 3180–3187. [Google Scholar]
- Siqueira, E.; Azzolin, R.; Botelho, S.; Oliveira, V. Sensors data fusion to navigate inside pipe using Kalman Filter. In Proceedings of the 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Liu, Z.; Krys, D. The use of laser range finder on a robotic platform for pipe inspection. Mech. Syst. Signal Process. 2012, 31, 246–257. [Google Scholar] [CrossRef]
- Anjum, M.L.; Park, J.; Hwang, W.; Kwon, H.I.; Kim, J.H.; Lee, C.; Kim, K.S. Sensor data fusion using unscented kalman filter for accurate localization of mobile robots. In Proceedings of the ICCAS 2010, Gyeonggi-do, Republic of Korea, 27–30 October 2010; pp. 947–952. [Google Scholar]
- Maneewarn, T.; Thung-od, K. ICP-EKF localization with adaptive covariance for a boiler inspection robot. In Proceedings of the 2015 IEEE 7th International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Siem Reap, Cambodia, 15–17 July 2015; pp. 216–221. [Google Scholar]
- Wu, D.; Chatzigeorgiou, D.; Youcef-Toumi, K.; Ben-Mansour, R. Node localization in robotic sensor networks for pipeline inspection. IEEE Trans. Ind. Inform. 2015, 12, 809–819. [Google Scholar] [CrossRef]
- Worley, R.; Yu, Y.; Anderson, S. Acoustic echo-localization for pipe inspection robots. In Proceedings of the 2020 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Karlsruhe, Germany, 14–16 September 2020; pp. 160–165. [Google Scholar]
- Ma, K.; Schirru, M.; Zahraee, A.H.; Dwyer-Joyce, R.; Boxall, J.; Dodd, T.J.; Collins, R.; Anderson, S.R. PipeSLAM: Simultaneous localisation and mapping in feature sparse water pipes using the Rao-Blackwellised particle filter. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1459–1464. [Google Scholar]
- Yuan, X.; Martínez-Ortega, J.F.; Fernández, J.A.S.; Eckert, M. AEKF-SLAM: A new algorithm for robotic underwater navigation. Sensors 2017, 17, 1174. [Google Scholar] [CrossRef] [PubMed]
- Krys, D.; Najjaran, H. Development of visual simultaneous localization and mapping (VSLAM) for a pipe inspection robot. In Proceedings of the 2007 International Symposium on Computational Intelligence in Robotics and Automation, Jacksonville, FL, USA, 20–23 June 2007; pp. 344–349. [Google Scholar]
- Chuang, T.Y.; Sung, C.C. Learning and SLAM based decision support platform for sewer inspection. Remote Sens. 2020, 12, 968. [Google Scholar] [CrossRef]
- Aitken, J.M.; Evans, M.H.; Worley, R.; Edwards, S.; Zhang, R.; Dodd, T.; Mihaylova, L.; Anderson, S.R. Simultaneous localization and mapping for inspection robots in water and sewer pipe networks: A review. IEEE Access 2021, 9, 140173–140198. [Google Scholar] [CrossRef]








| Performance Indicator | Wheel Type | Caterpillar Type | Without Wheel Type | PIG | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simple Structure | Wall- Press | Screw- Drive | Simple Structure | Wall- Press | Snake | Inchworm | Legged | Free Swimming | ||
| Vertical Locomotion | × | ⋎ | ⋎ | × | ⋎⋎ | × | ⋎ | × | × | × |
| Maneuverability | ⋎⋎ | ⋎ | ⋎ | × | ⋎ | ⋎⋎ | × | ⋎ | ⋎⋎ | × |
| Variable Diameter Adaptability | × | ⋎⋎ | ⋎ | × | ⋎⋎ | ⋎ | ⋎ | × | × | ⋎ |
| Motion Efficiency | × | ⋎ | ⋎ | ⋎ | ⋎⋎ | × | ⋎ | × | ⋎ | × |
| Interference to Flow | ⋎ | ⋎⋎ | ⋎ | ⋎ | × | ×× | ×× | × | ⋎ | ⋎ |
| Output power (W) | 281 |
| Max. Torque (N.m) | 26.77 |
| Max. Speed (RPM) | 180 |
| Max. Air consumption (m3/min) | 0.22 |
| Weight (KG) | 1.1 |
| Size (D, L) | 55 mm, 108 mm |
| Horsepower (HP) | 6 |
| R.P.M | 1640 |
| Flow rate (l/min) | 230 |
| Pressure (BAR) | 6 |
| Capacity (l) | 50 |
| Noise (DB) | 72 |
| Weight (kg) | 63 |
| Size (l, w, h) | 67 mm, 39 mm, 80 mm |
| Minimum diameter (mm) | 135 |
| Maximum diameter (mm) | 185 |
| Length (mm) | 230 |
| Weight (kg) | 3.3 |
| Actuator | Air-motor 25.12 Nm |
| Maximum speed | 0.03 m/s |
| Maximum payload | 56.84 N |
| Ref (Type) | Capability (Pipe Types) | Dia.Range (mm) Length (mm) Weigh (kg) | Max.Speed (mm/s) Traction Force (N) | Velocity -Control -Method | Actuator Active Driven -Parts | On board -Electronics |
|---|---|---|---|---|---|---|
| Our robot (Wheel) | Horizontal, vertical, curved | 135–180 mm | 30 mm/s | passive | 1 air motor | no |
| 230 mm | 56.84 N | (CVT | 3 wheels | |||
| 3.3 kg | slider-crank) | |||||
| [8] (Wheel) | Horizontal, vertical, T-branch | 116–127 mm | 80 mm/s | active | 5 electric | E-motor |
| 51 mm | 202 N | (wheel control) | -motors | circuit board | ||
| 2.37 kg | 5 wheels | |||||
| [9] (Wheel) | Horizontal, vertical | 198–305 mm | N/A | active | 3 electric | E-motor |
| N/A | N/A | (wheel control) | -motor | E-magnet | ||
| 1.03 kg | 3 wheels | |||||
| [32] (Wheel) | Elbow, horizontal, vertical, T-branch | 85–109 mm | 150 mm/s | active | 3 electric | E-motor |
| 150 mm | 9.8 N | (differential | -motors | camera | ||
| 0.7 kg | -drive) | 2×3 wheels | ||||
| [11] (Screw) | Vertical, bent | 100–129 mm | 500 mm/s | active | 2 electric | E-motor |
| 175.8 mm | N/A | (angle | -motors | |||
| 0.7 kg | -control) | 3 wheels | ||||
| [6] (Caterpillar) | Vertical, inclined, bent | N/A | 260 mm/s | active | 1 electric | E-motor |
| 84 mm | N/A | (caterpillar | -motor, 3 SMAs | |||
| 0.3 kg | -control) | 2 caterpillars | ||||
| [12] (Caterpillar) | Bent pipes and T-branch | 480–650 mm | 24.17 mm/s | active | 4 electric | E-motor |
| 1995 mm | 324 N | (caterpillar | -motors | circuit board | ||
| 70.1 kg | -control) | 4 caterpillars | sensor | |||
| [18] (Caterpillar) | E-motor | |||||
| 950–1200 mm | 88.3 mm/s | active | 3 electric | E-putter | ||
| Horizontal | N/A | N/A | (caterpillar | -motors | camera | |
| 45.8kg | -control) | 3 caterpillars | ladar | |||
| pressure sensor | ||||||
| [19] (Caterpillar) | Elbows, T-branches, horizontal, vertical | 80–100 mm | 90 mm/s | active | 3 electric | E-motor |
| 78 mm | 1.18 N | (caterpillar | -motors | camera | ||
| 0.266 kg | -control) | 3 caterpillars | ||||
| [3] (Inchworm) | Vertical, Curved with U-turn | 50–150 mm | 24.6 mm/s | passive | pneumatic | no |
| 1000 mm | 16–37 N | (pressurized | -actuator | |||
| N/A | -unit) | 3 segment | ||||
| [21] (Leg) | Two horizontal plates | 30 mm | 50 mm/s | active | 1 electric | E-motor |
| 30 mm | N/A | (using leg) | -motor | |||
| 0.324 kg | 2 legs | |||||
| [22] (Leg) | No in-pipe test | 65–100 mm | 6 mm/s | active | 2 electric | E-motor |
| 33.06 mm | N/A | (using leg) | -motors | circuit board | ||
| 0.0945 kg | 6 × 1 set leg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Luong, T.; Moon, H. Development of a Wheel-Type In-Pipe Robot Using Continuously Variable Transmission Mechanisms for Pipeline Inspection. Biomimetics 2024, 9, 113. https://doi.org/10.3390/biomimetics9020113
Park J, Luong T, Moon H. Development of a Wheel-Type In-Pipe Robot Using Continuously Variable Transmission Mechanisms for Pipeline Inspection. Biomimetics. 2024; 9(2):113. https://doi.org/10.3390/biomimetics9020113
Chicago/Turabian StylePark, Jeongyeol, Tuan Luong, and Hyungpil Moon. 2024. "Development of a Wheel-Type In-Pipe Robot Using Continuously Variable Transmission Mechanisms for Pipeline Inspection" Biomimetics 9, no. 2: 113. https://doi.org/10.3390/biomimetics9020113
APA StylePark, J., Luong, T., & Moon, H. (2024). Development of a Wheel-Type In-Pipe Robot Using Continuously Variable Transmission Mechanisms for Pipeline Inspection. Biomimetics, 9(2), 113. https://doi.org/10.3390/biomimetics9020113






