Maneuvering Characteristics of Bilateral Amplitude–Asymmetric Flapping Motion Based on a Bat-Inspired Flexible Wing
Abstract
:1. Introduction
2. Materials and Methods
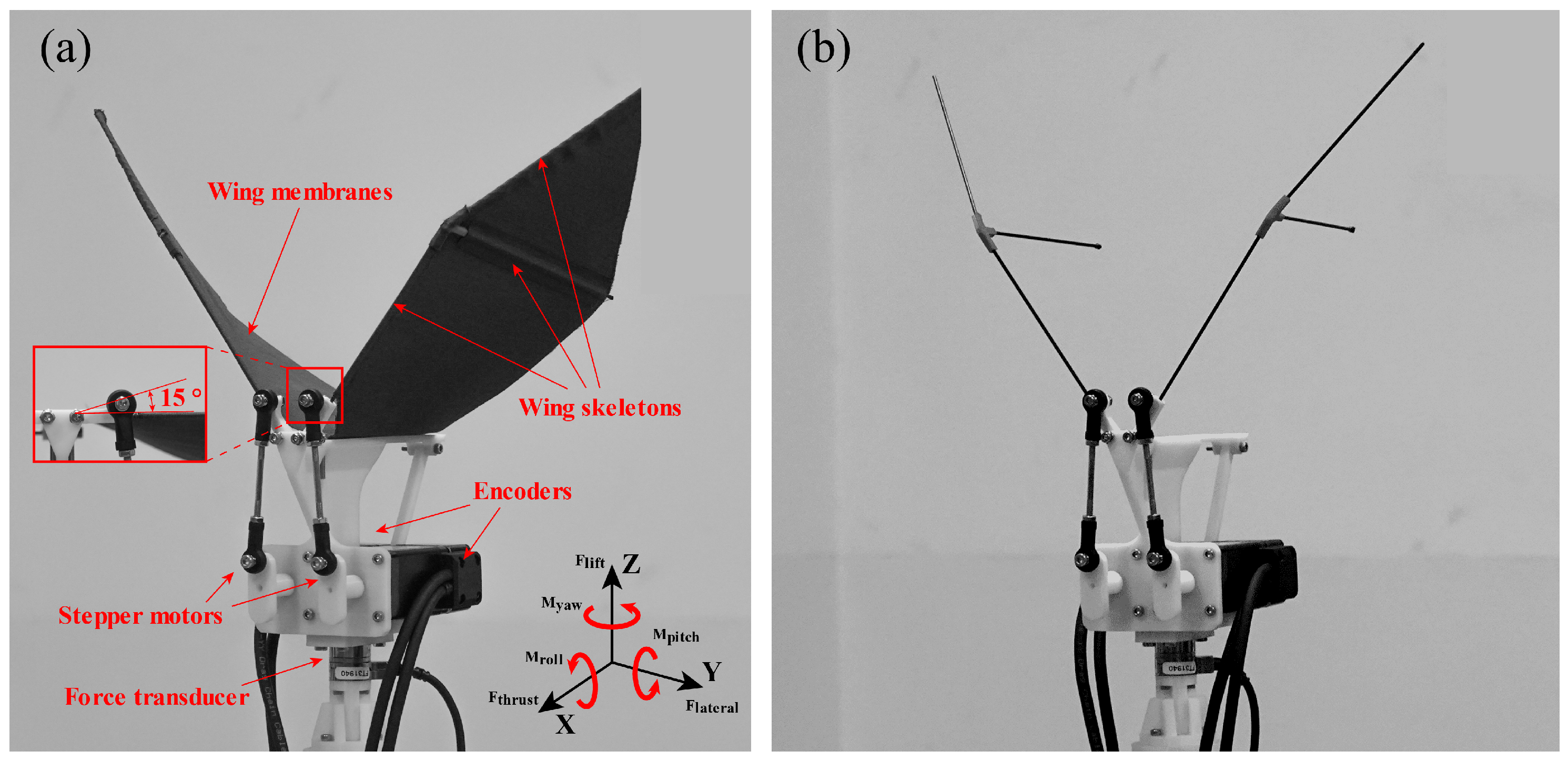
2.1. Model Description
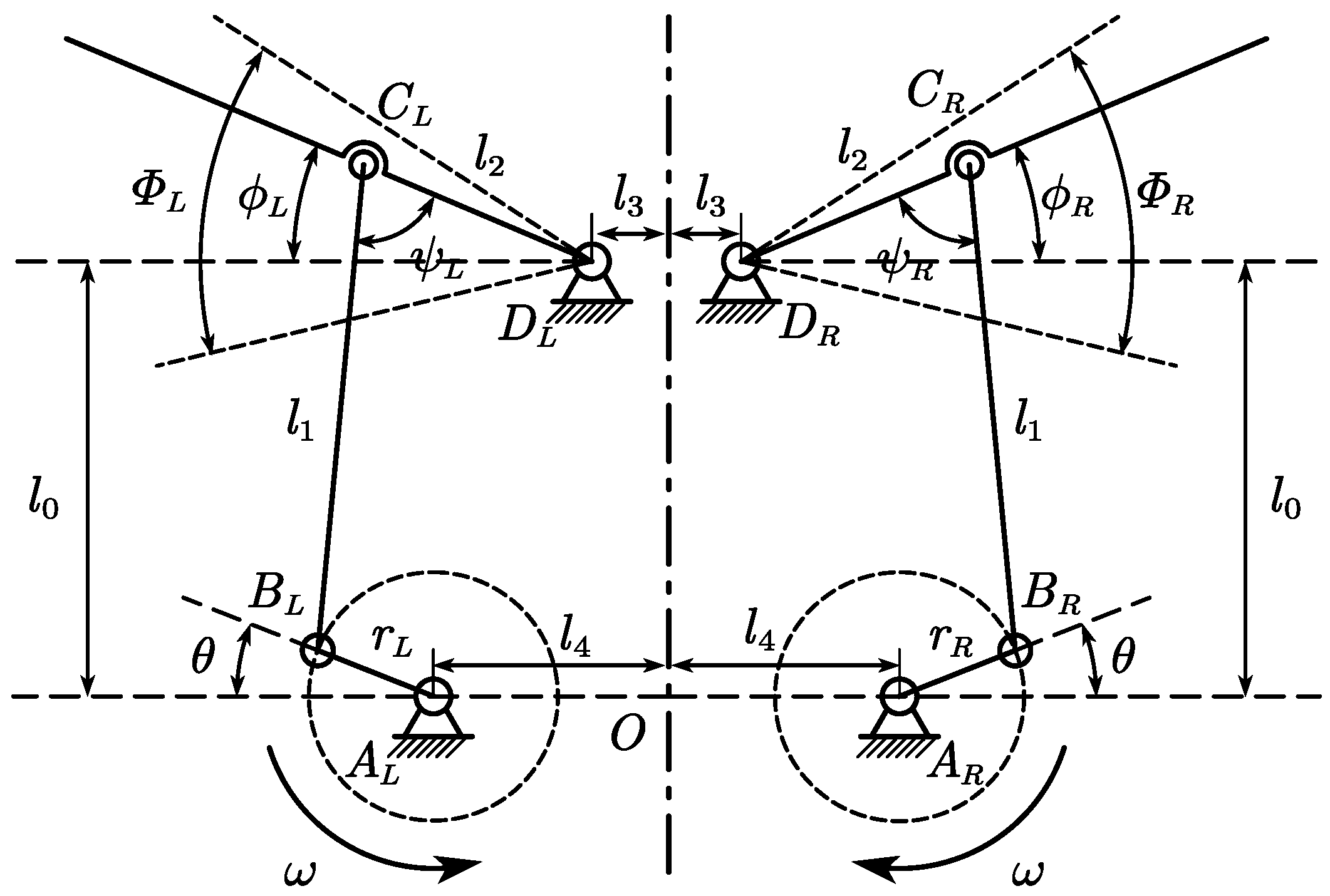
2.1.1. Flapping Mechanism
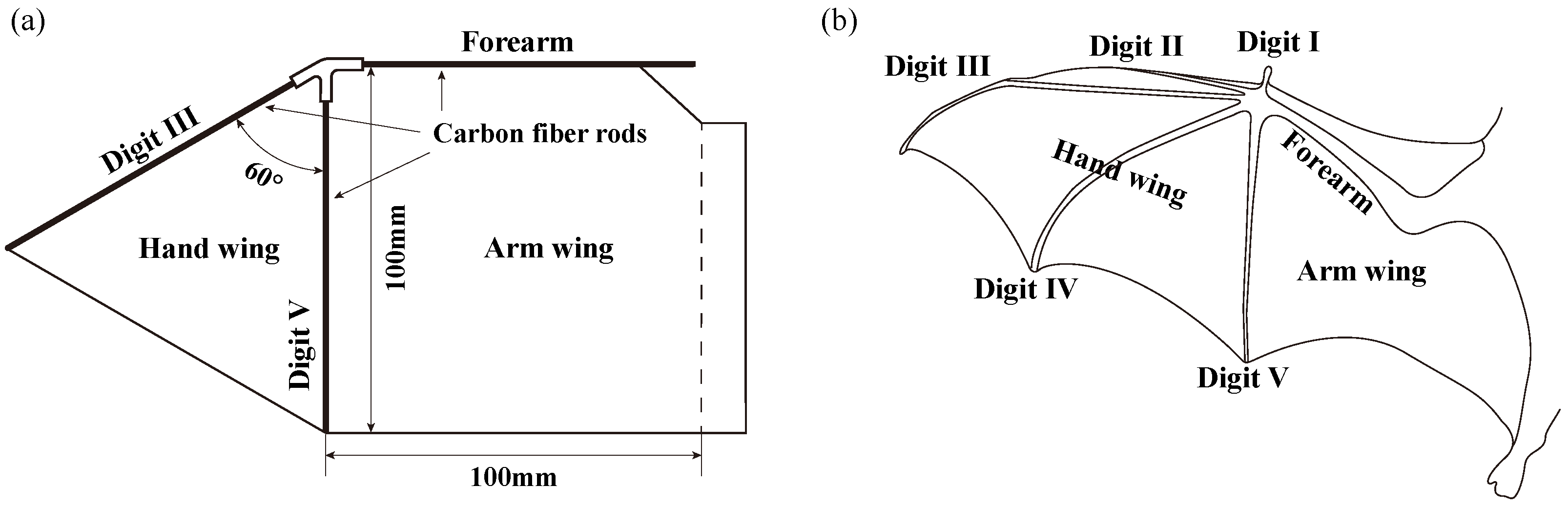
2.1.2. Wing Design
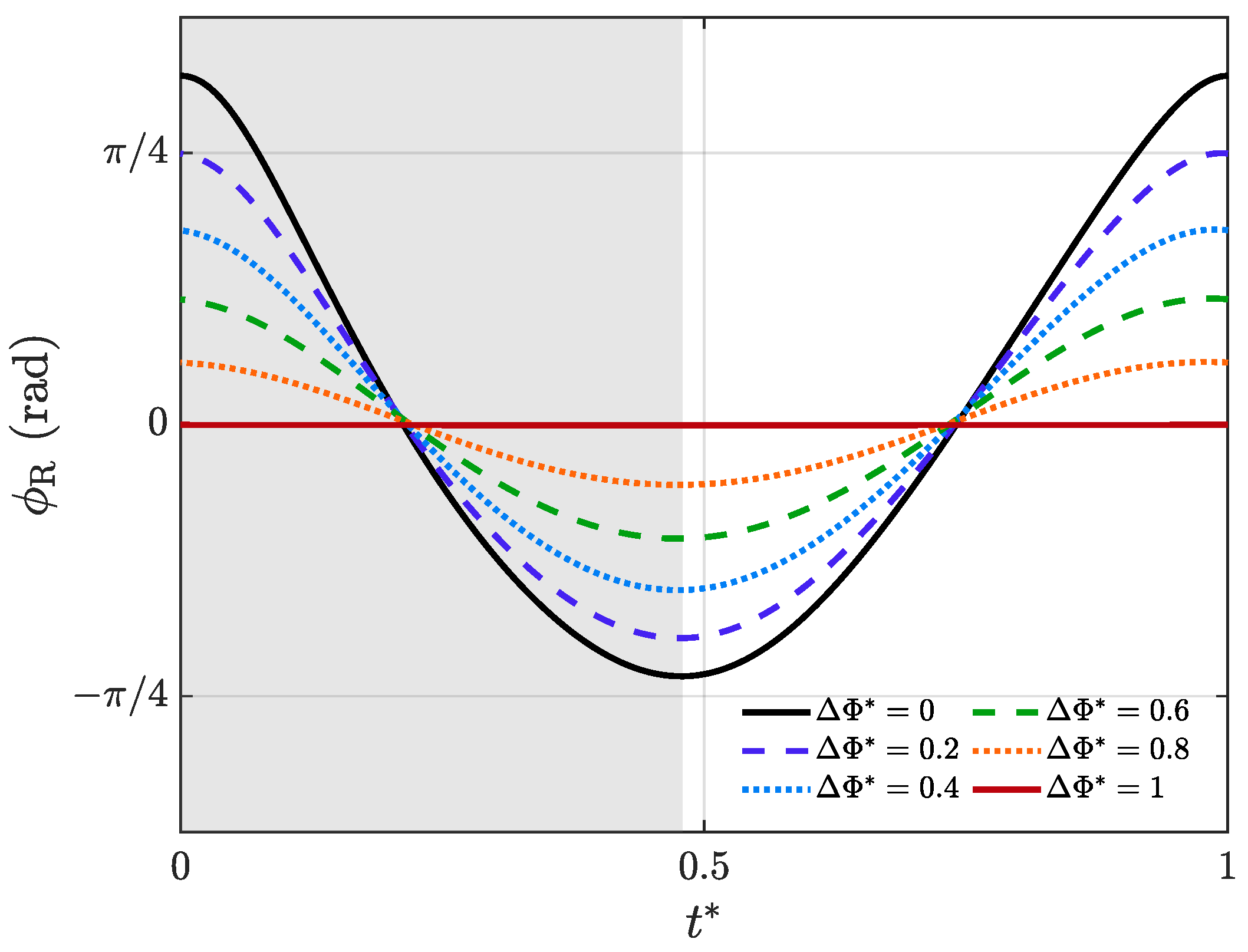
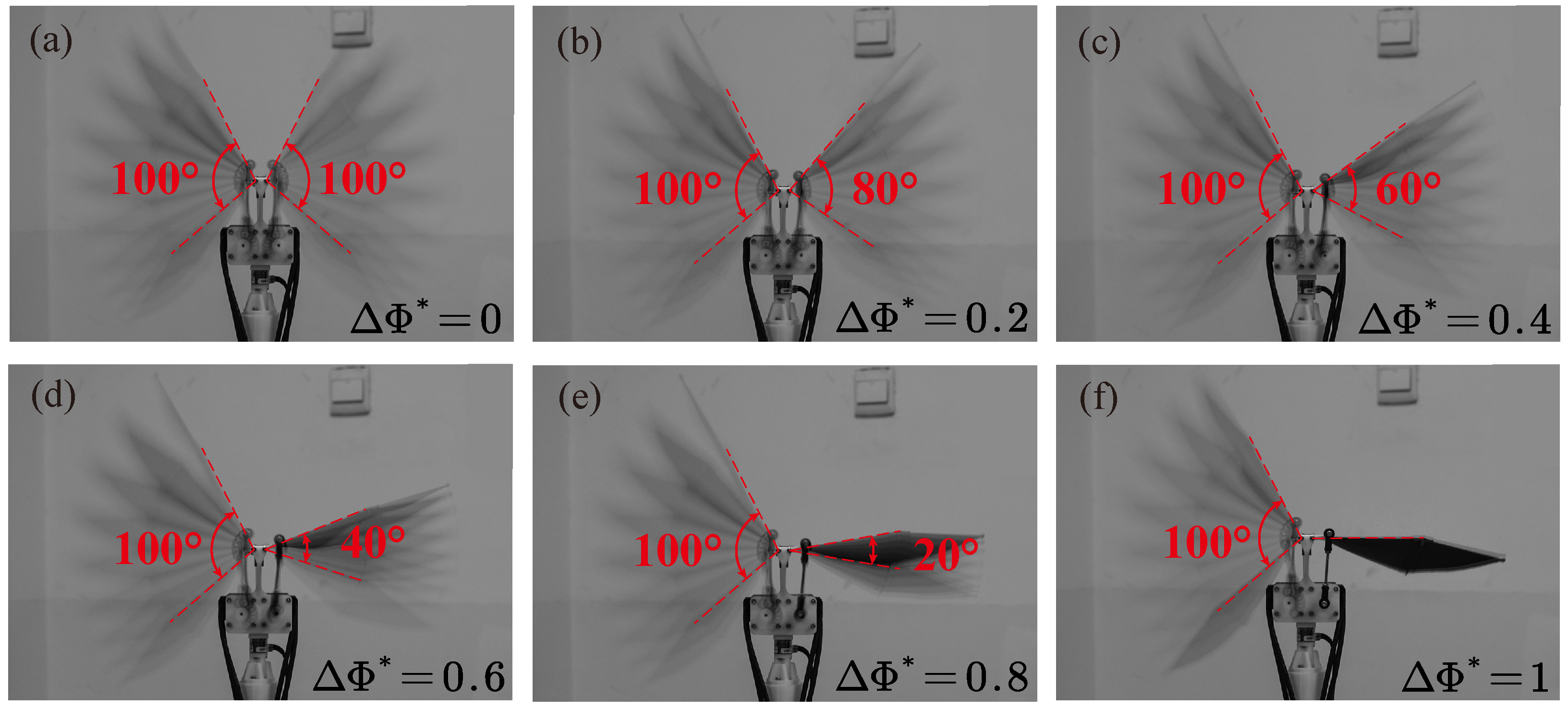
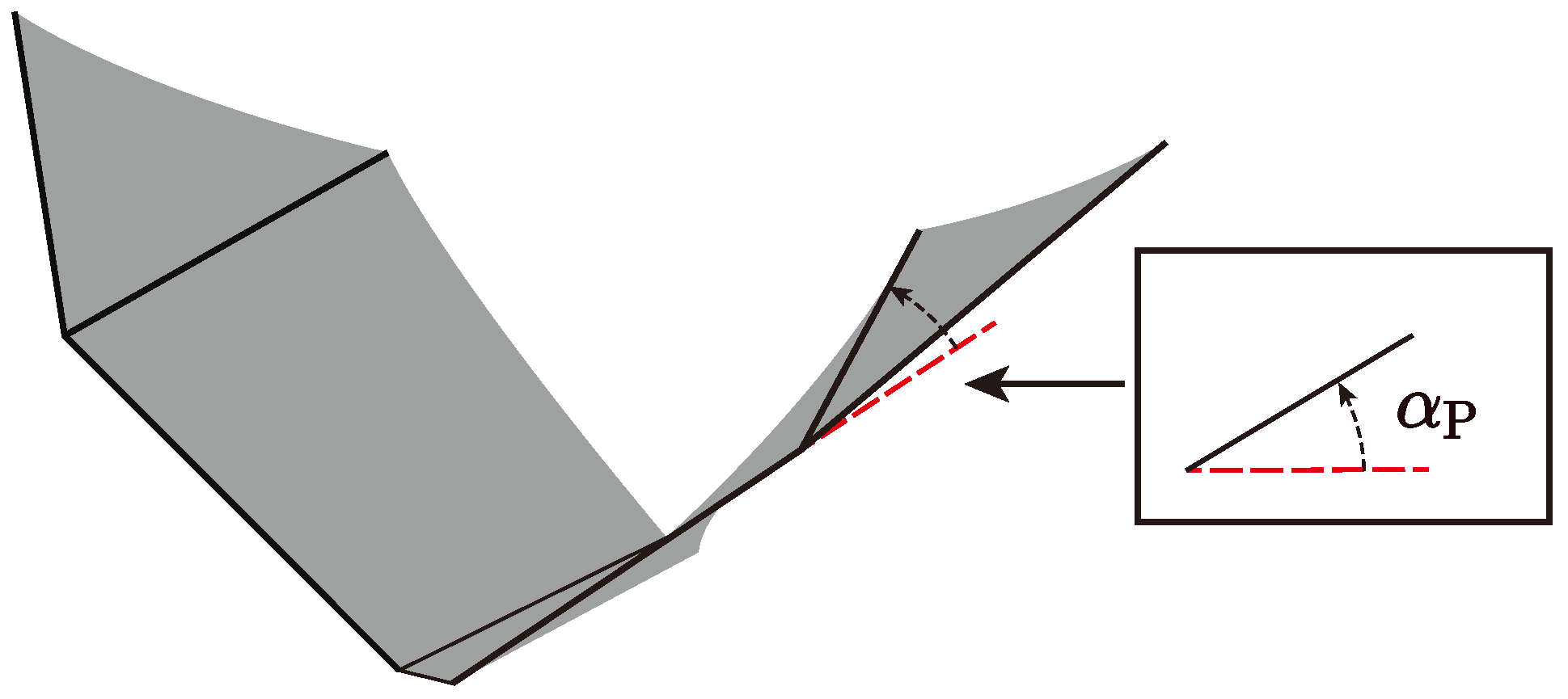
2.2. Kinematics Analysis
2.3. Experiment Setup
2.3.1. Force Measurement
2.3.2. Inertial Subtraction
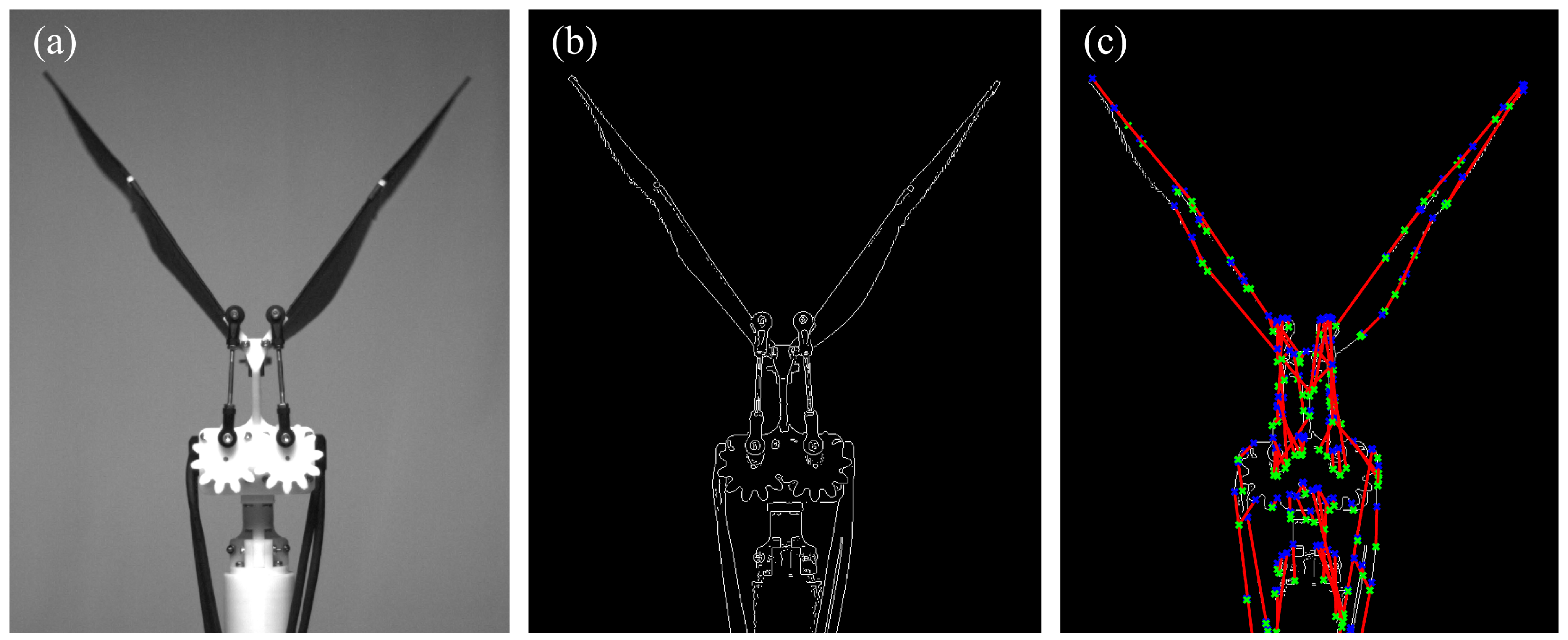
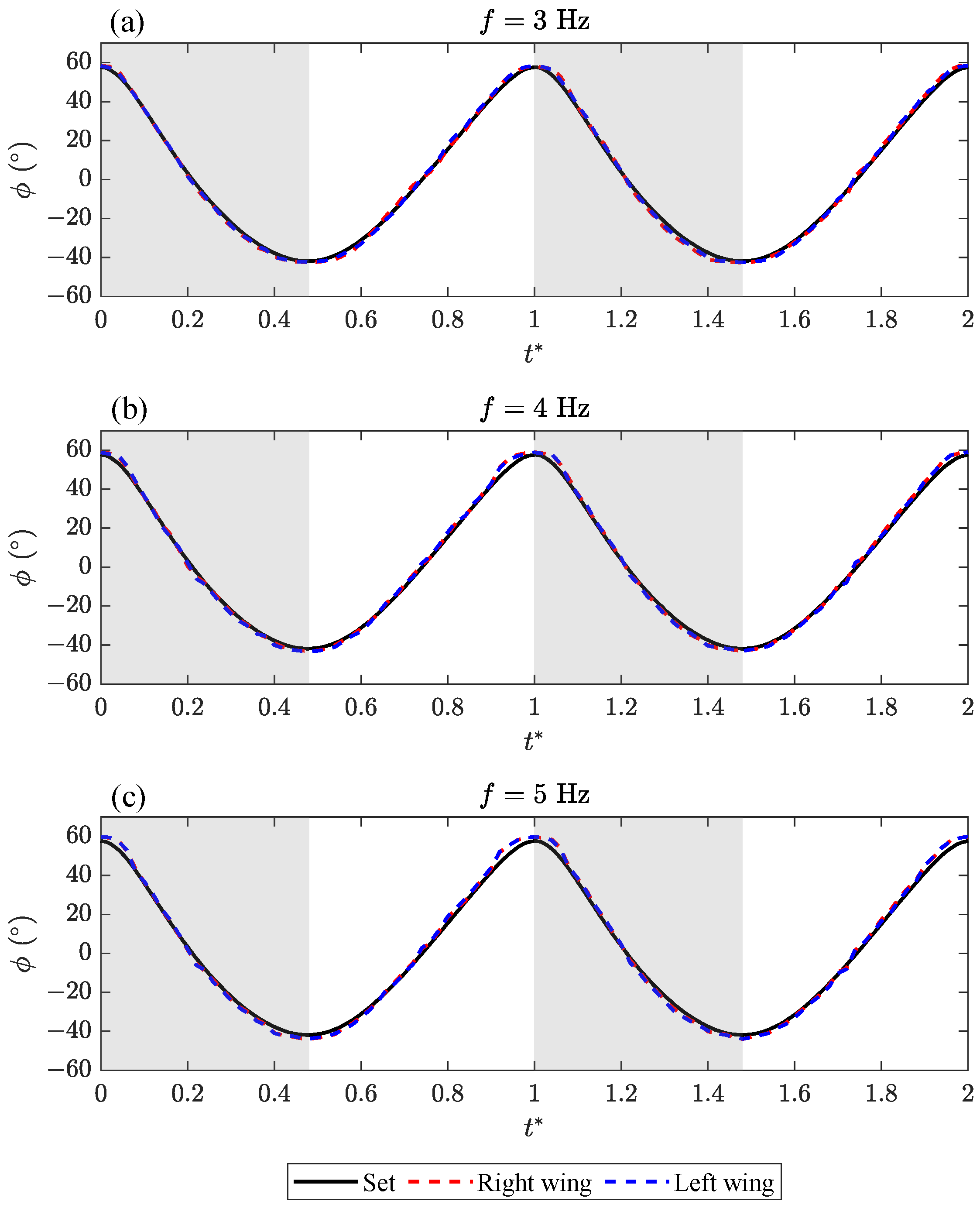
2.3.3. Kinematic Verification
3. Results and Discussion
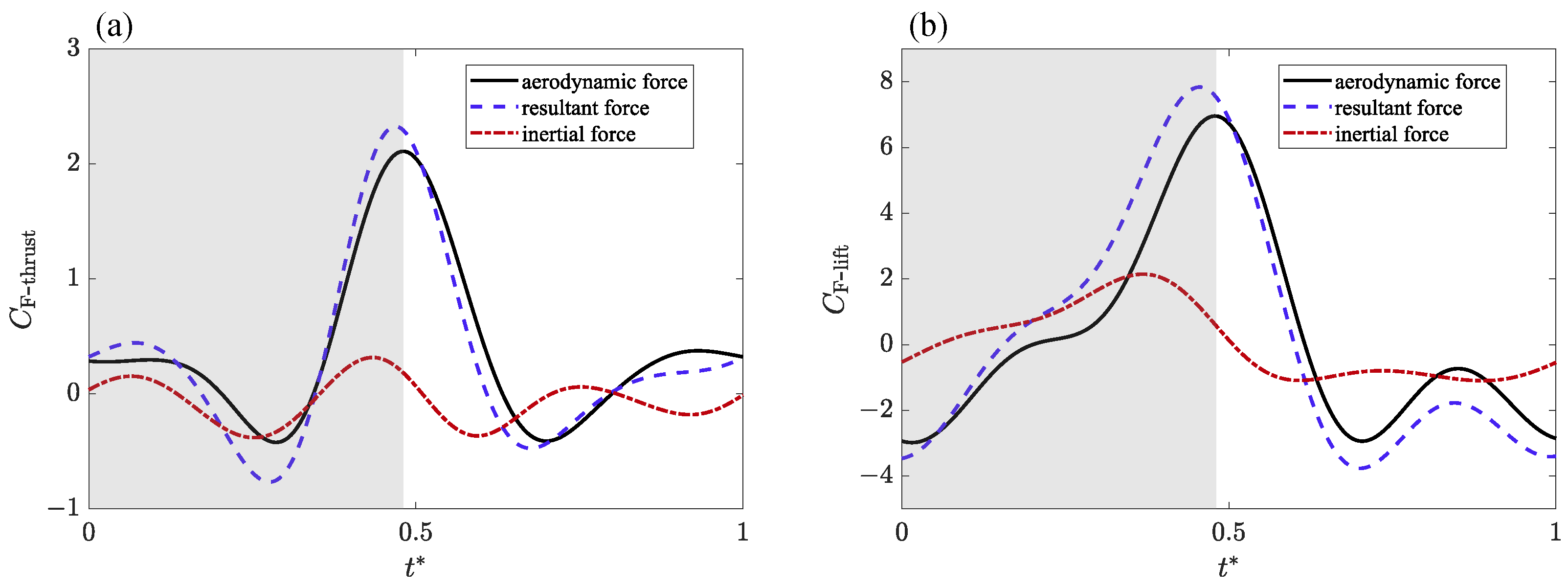
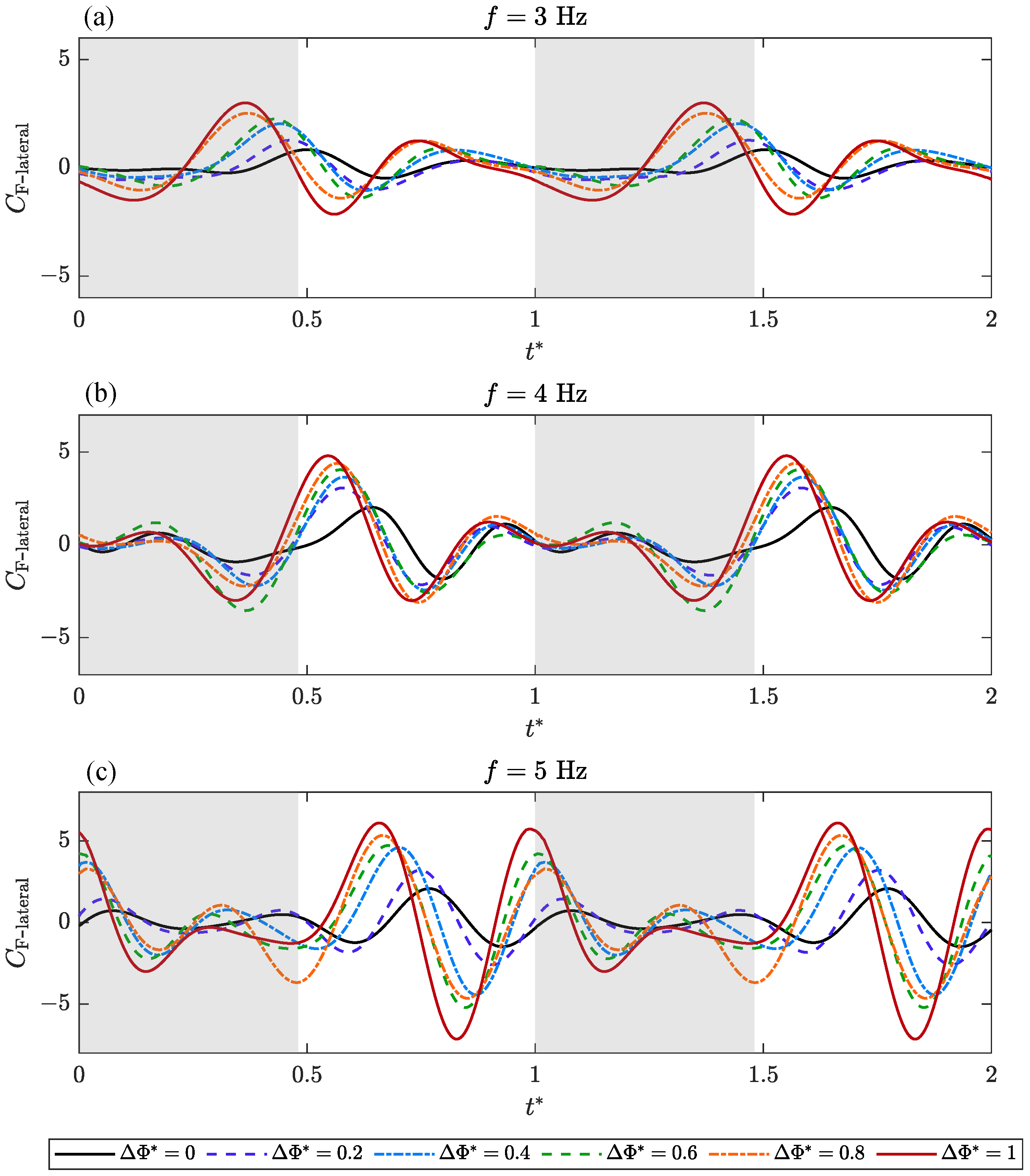
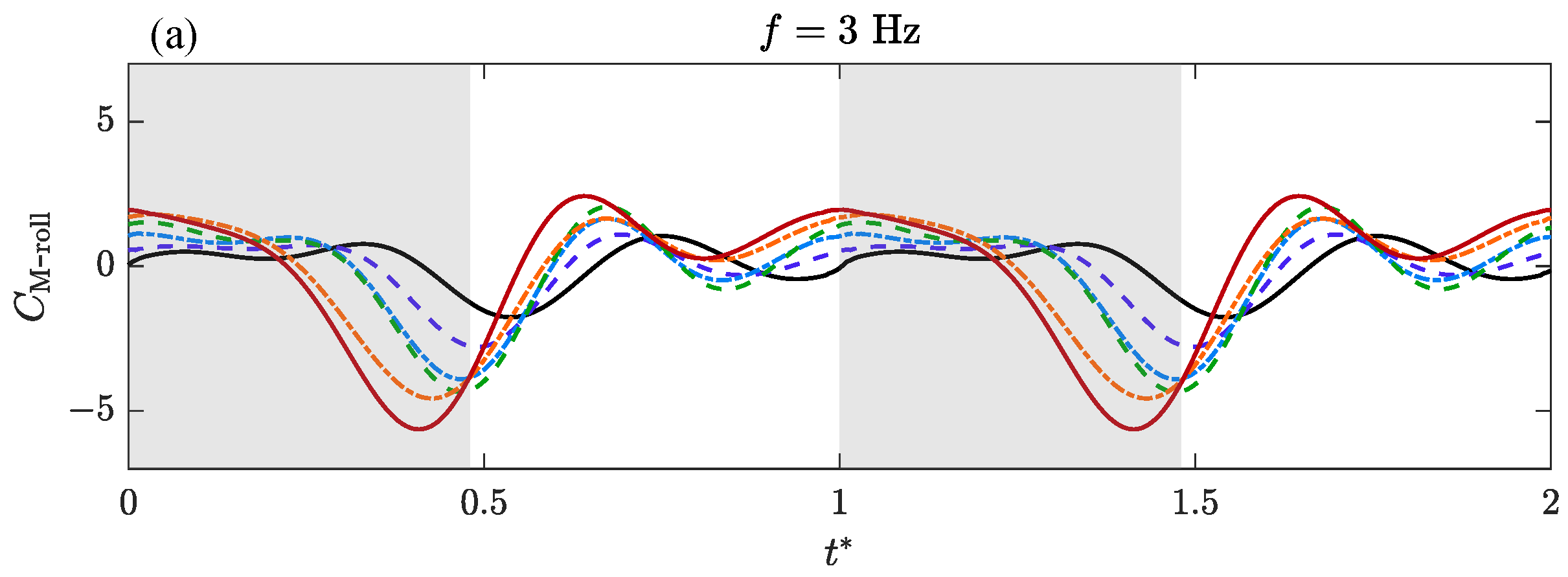
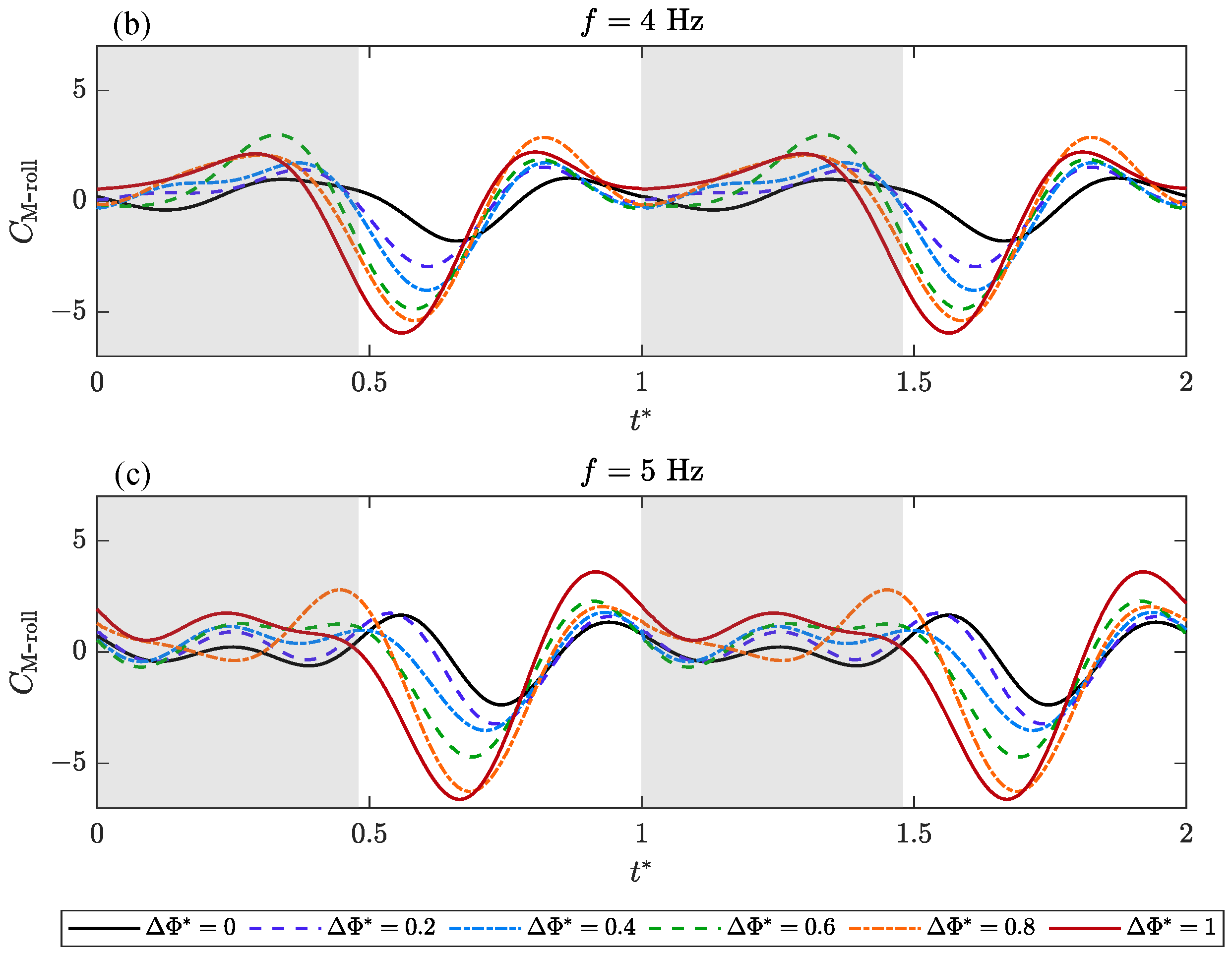
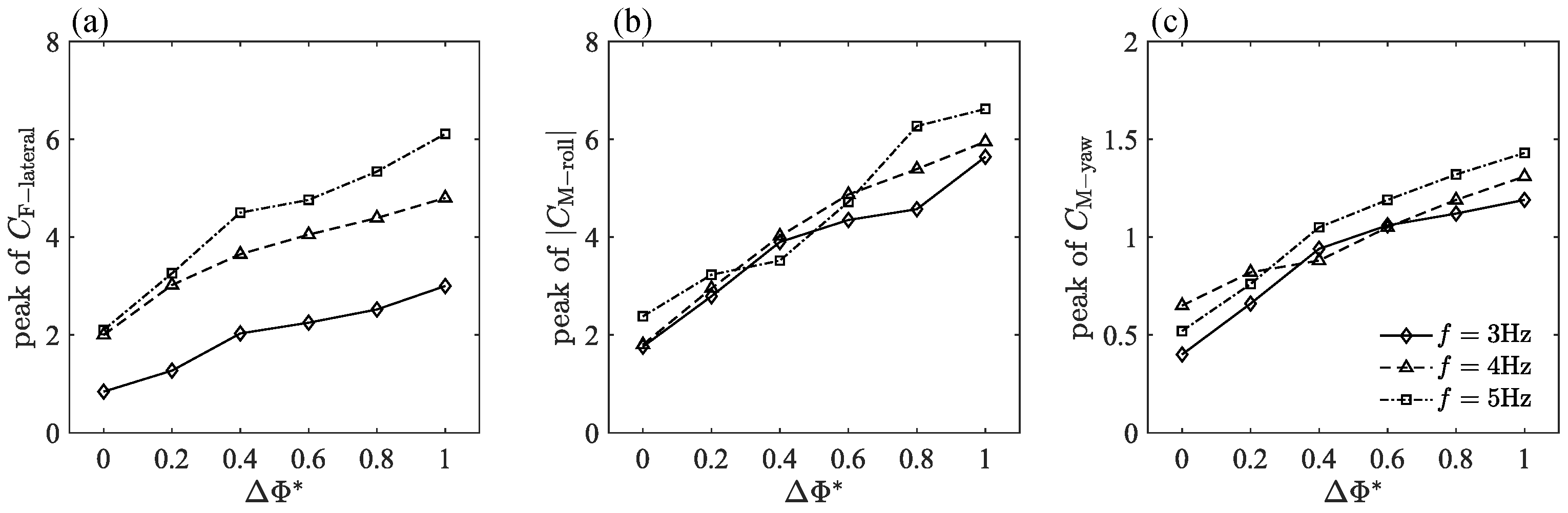
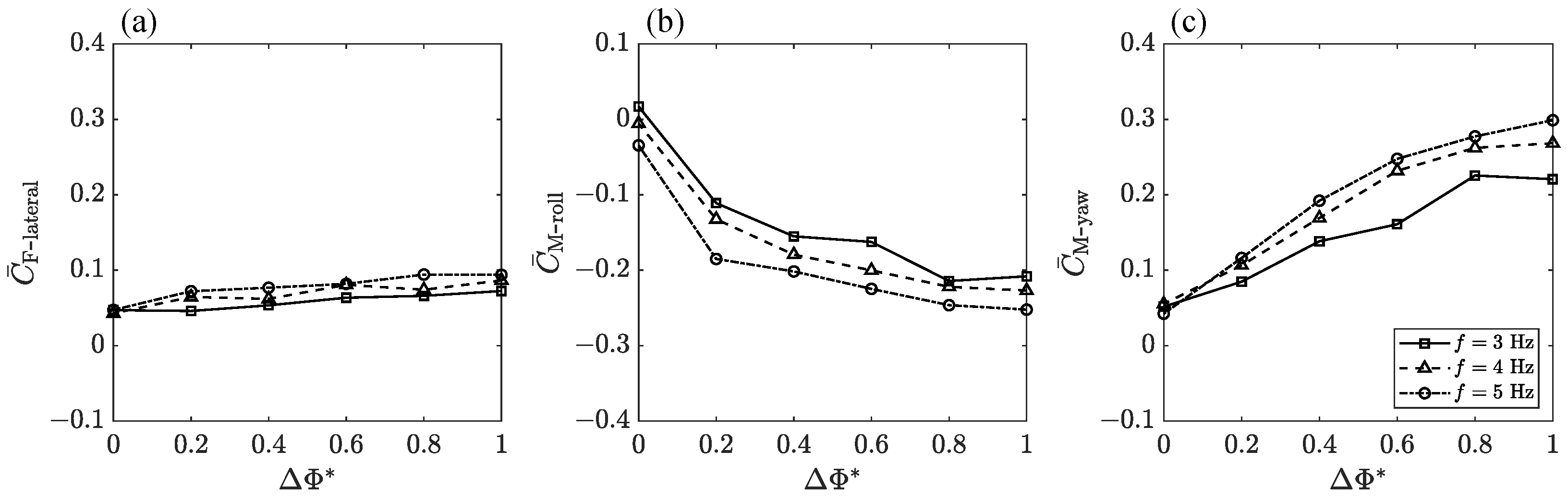
3.1. Transient Aerodynamic Performance
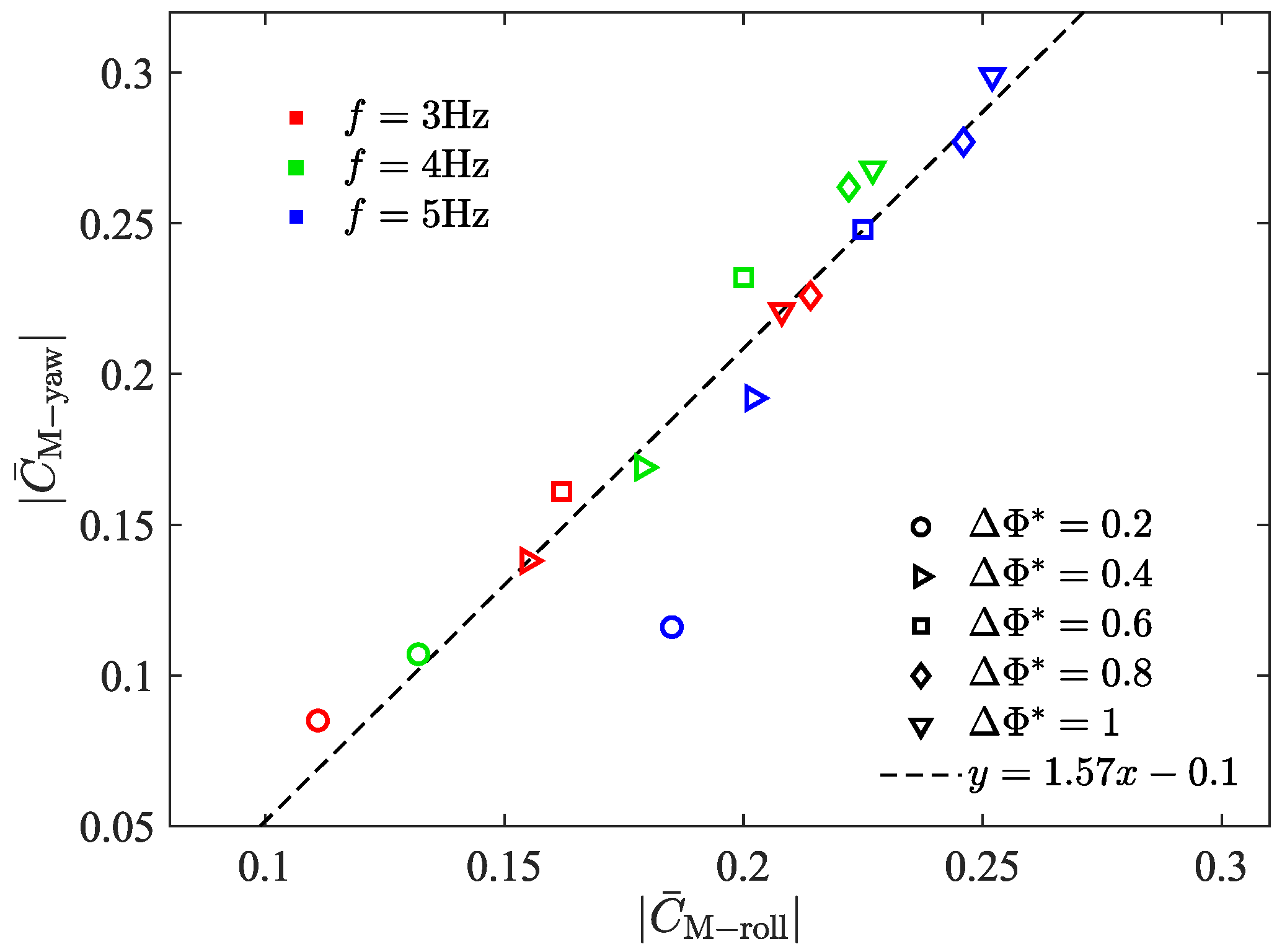
3.2. Cycle-Averaged Aerodynamic Performance
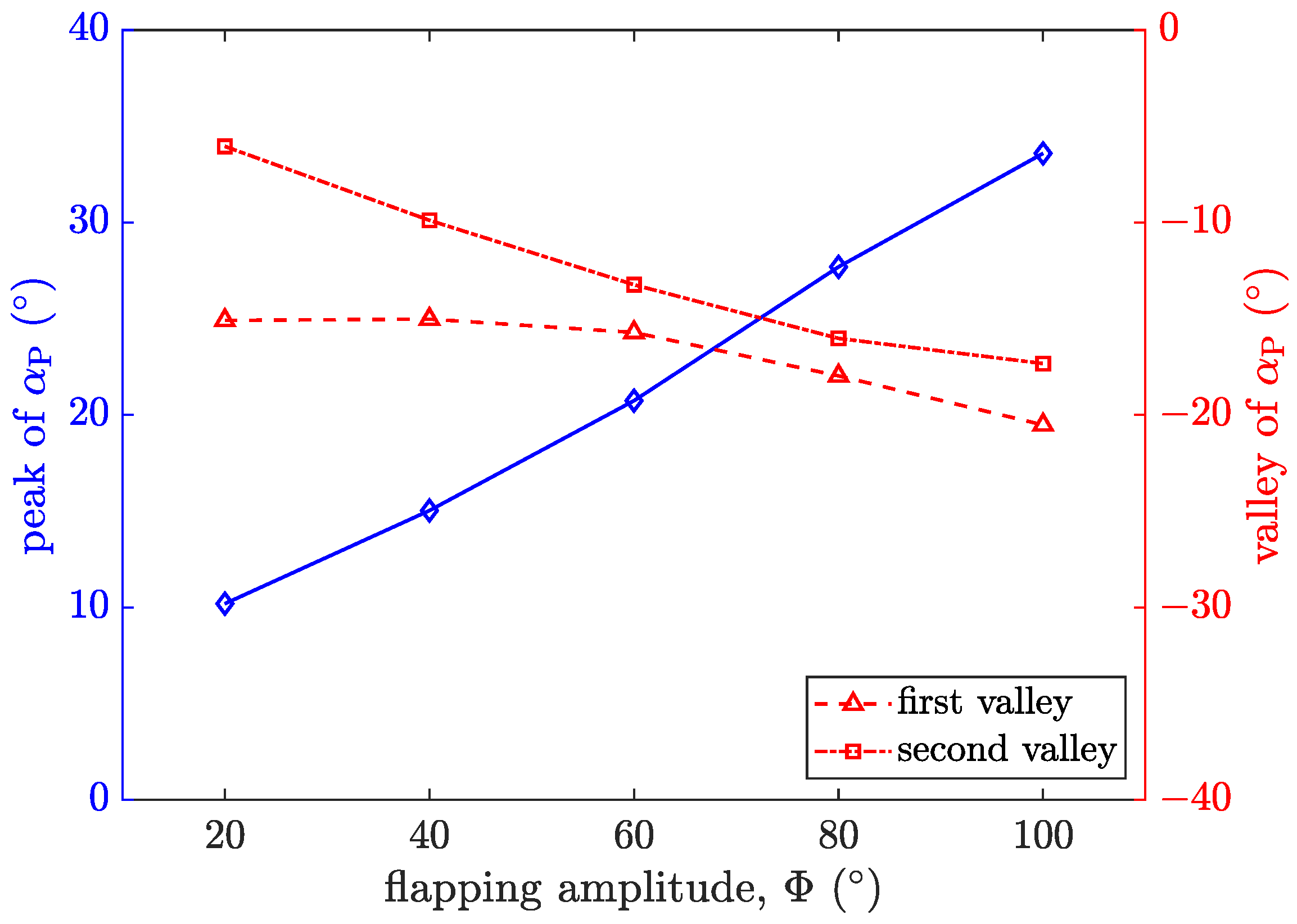
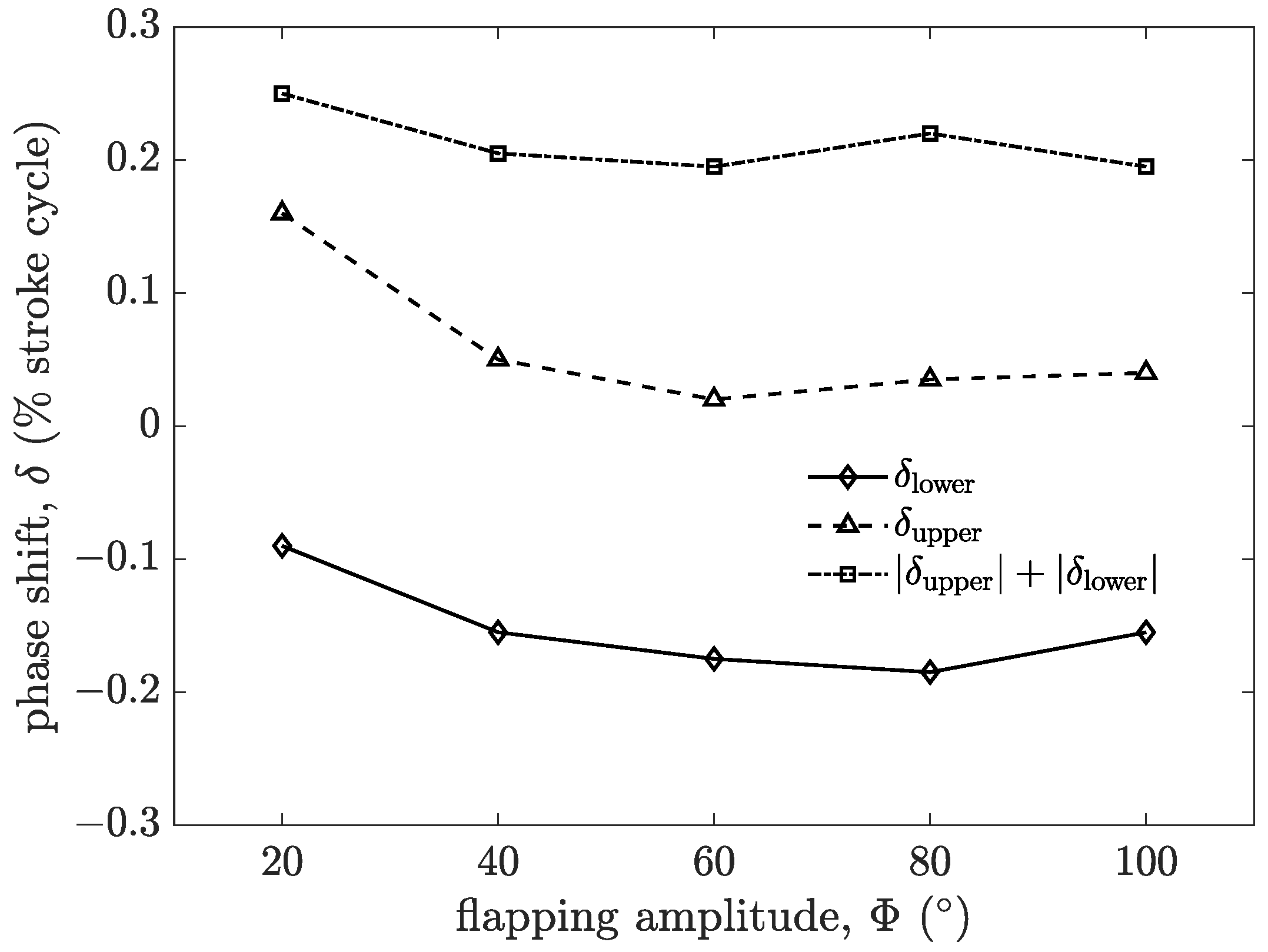
3.3. Passive Pitching Deformation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ward, T.A.; Fearday, C.J.; Salami, E.; Binti Soin, N. A bibliometric review of progress in micro air vehicle research. Int. J. Micro Air Veh. 2017, 9, 146–165. [Google Scholar] [CrossRef]
- Nakata, T.; Liu, H.; Tanaka, Y.; Nishihashi, N.; Wang, X.; Sato, A. Aerodynamics of a bio-inspired flexible flapping-wing micro air vehicle. Bioinspir. Biomim. 2011, 6, 045002. [Google Scholar] [CrossRef]
- Deng, S.; Percin, M.; van Oudheusden, B.; Remes, B.; Bijl, H. Experimental investigation on the aerodynamics of a bio-inspired flexible flapping wing micro air vehicle. Int. J. Micro Air Veh. 2014, 6, 105–115. [Google Scholar] [CrossRef]
- Finio, B.M.; Shang, J.K.; Wood, R.J. Body torque modulation for a microrobotic fly. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3449–3456. [Google Scholar] [CrossRef]
- Keennon, M.; Grasmeyer, J. Development of two MAVs and vision of the future of MAV design. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, OH, USA, 14–17 July 2003; p. 2901. [Google Scholar] [CrossRef]
- Baek, S.S.; Fearing, R.S. Flight forces and altitude regulation of 12 gram i-bird. In Proceedings of the 2010 3rd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010; pp. 454–460. [Google Scholar] [CrossRef]
- Keennon, M.; Klingebiel, K.; Won, H. Development of the nano hummingbird: A tailless flapping wing micro air vehicle. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 588. [Google Scholar] [CrossRef]
- Rose, C.J.; Mahmoudieh, P.; Fearing, R.S. Coordinated launching of an ornithopter with a hexapedal robot. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4029–4035. [Google Scholar] [CrossRef]
- Scheper, K.Y.; Tijmons, S.; de Visser, C.C.; de Croon, G.C. Behavior trees for evolutionary robotics. Artif. Life 2016, 22, 23–48. [Google Scholar] [CrossRef]
- Karásek, M.; Muijres, F.T.; De Wagter, C.; Remes, B.D.; De Croon, G.C. A tailless aerial robotic flapper reveals that flies use torque coupling in rapid banked turns. Science 2018, 361, 1089–1094. [Google Scholar] [CrossRef]
- Nguyen, Q.V.; Chan, W.L. Development and flight performance of a biologically-inspired tailless flapping-wing micro air vehicle with wing stroke plane modulation. Bioinspir. Biomim. 2018, 14, 016015. [Google Scholar] [CrossRef]
- Dudley, R. Mechanisms and implications of animal flight maneuverability. Integr. Comp. Biol. 2002, 42, 135–140. [Google Scholar] [CrossRef]
- Hedrick, T.; Usherwood, J.; Biewener, A. Low speed maneuvering flight of the rose-breasted cockatoo (Eolophus roseicapillus). II. Inertial and aerodynamic reorientation. J. Exp. Biol. 2007, 210, 1912–1924. [Google Scholar] [CrossRef] [PubMed]
- Hubel, T.Y.; Hristov, N.I.; Swartz, S.M.; Breuer, K.S. Changes in kinematics and aerodynamics over a range of speeds in Tadarida brasiliensis, the Brazilian free-tailed bat. J. R. Soc. Interface 2012, 9, 1120–1130. [Google Scholar] [CrossRef] [PubMed]
- Bode-Oke, A.T.; Zeyghami, S.; Dong, H. Flying in reverse: Kinematics and aerodynamics of a dragonfly in backward free flight. J. R. Soc. Interface 2018, 15, 20180102. [Google Scholar] [CrossRef]
- Menzer, A.; Ren, Y.; Guo, J.; Tobalske, B.W.; Dong, H. Wing Kinematics and Unsteady Aerodynamics of a Hummingbird Pure Yawing Maneuver. Biomimetics 2022, 7, 115. [Google Scholar] [CrossRef] [PubMed]
- Tobalske, B.W. Symmetry in Turns. Science 2009, 324, 190–191. [Google Scholar] [CrossRef] [PubMed]
- Henningsson, P.; Jakobsen, L.; Hedenström, A. Aerodynamics of manoeuvring flight in brown long-eared bats (Plecotus auritus). J. R. Soc. Interface 2018, 15, 20180441. [Google Scholar] [CrossRef] [PubMed]
- Windes, P.; Tafti, D.K.; Müller, R. Kinematic and aerodynamic analysis of a bat performing a turning-ascending maneuver. Bioinspir. Biomim. 2020, 16, 016019. [Google Scholar] [CrossRef]
- Finio, B.M.; Eum, B.; Oland, C.; Wood, R.J. Asymmetric flapping for a robotic fly using a hybrid power-control actuator. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 2755–2762. [Google Scholar] [CrossRef]
- Park, J.H.; Yang, E.P.; Zhang, C.; Agrawal, S.K. Kinematic design of an asymmetric in-phase flapping mechanism for MAVs. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 5099–5104. [Google Scholar] [CrossRef]
- Park, J.H.; Agrawal, S.K. Dynamic effects of asymmetric in-phase flapping (AIF) on forward flight. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3550–3555. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, H.; Xu, L.; Xie, P.; Wu, J.; Wang, C. Mechanism and Kinematics for Flapping Wing Micro Air Vehicles Maneuvering Based on Bilateral Wings. Int. J. Aerosp. Eng. 2022, 2022, 5759343. [Google Scholar] [CrossRef]
- Bahlman, J.W.; Swartz, S.M.; Breuer, K.S. Design and characterization of a multi-articulated robotic bat wing. Bioinspir. Biomim. 2013, 8, 016009. [Google Scholar] [CrossRef]
- Rahman, A.; Windes, P.; Tafti, D. Turning-ascending flight of a Hipposideros pratti bat. R. Soc. Open Sci. 2022, 9, 211788. [Google Scholar] [CrossRef] [PubMed]
- Hedenström, A.; Johansson, L.C. Bat flight: Aerodynamics, kinematics and flight morphology. J. Exp. Biol. 2015, 218, 653–663. [Google Scholar] [CrossRef]
- Bullen, R.; McKenzie, N. Scaling bat wingbeat frequency and amplitude. J. Exp. Biol. 2002, 205, 2615–2626. [Google Scholar] [CrossRef]
- Von Busse, R.; Hedenström, A.; Winter, Y.; Johansson, L.C. Kinematics and wing shape across flight speed in the bat, Leptonycteris yerbabuenae. Biol. Open 2012, 1, 1226–1238. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, Q.; Deng, X.; Sane, S.P. Aerodynamic effects of flexibility in flapping wings. J. R. Soc. Interface 2010, 7, 485–497. [Google Scholar] [CrossRef]
- Ma, K.Y.; Chirarattananon, P.; Fuller, S.B.; Wood, R.J. Controlled flight of a biologically inspired, insect-scale robot. Science 2013, 340, 603–607. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef]
- Kang, C.K.; Shyy, W. Scaling law and enhancement of lift generation of an insect-size hovering flexible wing. J. R. Soc. Interface 2013, 10, 20130361. [Google Scholar] [CrossRef]



| Variable | Value |
|---|---|
| Single wing length, R (mm) | 186.6 |
| Wingspan, b (mm) | 385.3 |
| Wing area, S () | 28,560 |
| Mean chord, (mm) | 74.1 |
| Aspect ratio | 5.2 |
| Structural Parameter | Length (mm) |
|---|---|
| 59.9 | |
| 64 | |
| 15.5 | |
| 5 | |
| 16.2 |
| 0 | 11.0 | 100 | 57.8 | −41.7 | 8.0 |
| 0.2 | 9.4 | 80 | 45.0 | −35.4 | 4.8 |
| 0.4 | 7.3 | 60 | 32.2 | −27.4 | 2.4 |
| 0.6 | 5.0 | 40 | 20.9 | −18.9 | 1.0 |
| 0.8 | 2.6 | 20 | 10.4 | −10.0 | 0.2 |
| 1 | 0 | 0 | −0.1 | −0.1 | −0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lilong, C.; Yu, Y. Maneuvering Characteristics of Bilateral Amplitude–Asymmetric Flapping Motion Based on a Bat-Inspired Flexible Wing. Biomimetics 2024, 9, 148. https://doi.org/10.3390/biomimetics9030148
Lilong C, Yu Y. Maneuvering Characteristics of Bilateral Amplitude–Asymmetric Flapping Motion Based on a Bat-Inspired Flexible Wing. Biomimetics. 2024; 9(3):148. https://doi.org/10.3390/biomimetics9030148
Chicago/Turabian StyleLilong, Chuyi, and Yongliang Yu. 2024. "Maneuvering Characteristics of Bilateral Amplitude–Asymmetric Flapping Motion Based on a Bat-Inspired Flexible Wing" Biomimetics 9, no. 3: 148. https://doi.org/10.3390/biomimetics9030148
APA StyleLilong, C., & Yu, Y. (2024). Maneuvering Characteristics of Bilateral Amplitude–Asymmetric Flapping Motion Based on a Bat-Inspired Flexible Wing. Biomimetics, 9(3), 148. https://doi.org/10.3390/biomimetics9030148





