Reinforcement Learning with Task Decomposition and Task-Specific Reward System for Automation of High-Level Tasks
Abstract
1. Introduction
2. Related Work
2.1. Hierarchical Reinforcement Learning
2.2. Soft Actor–Critic
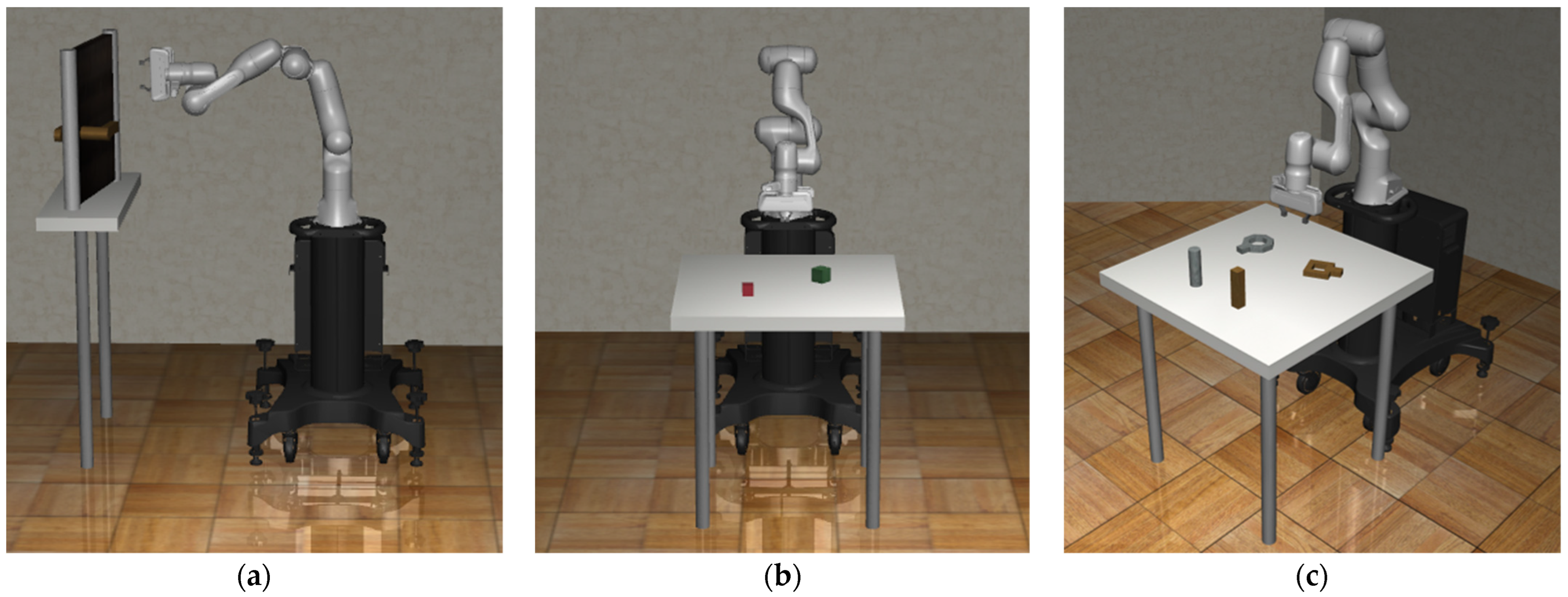
3. Proposed Method: Task Decomposition for High-Level Task
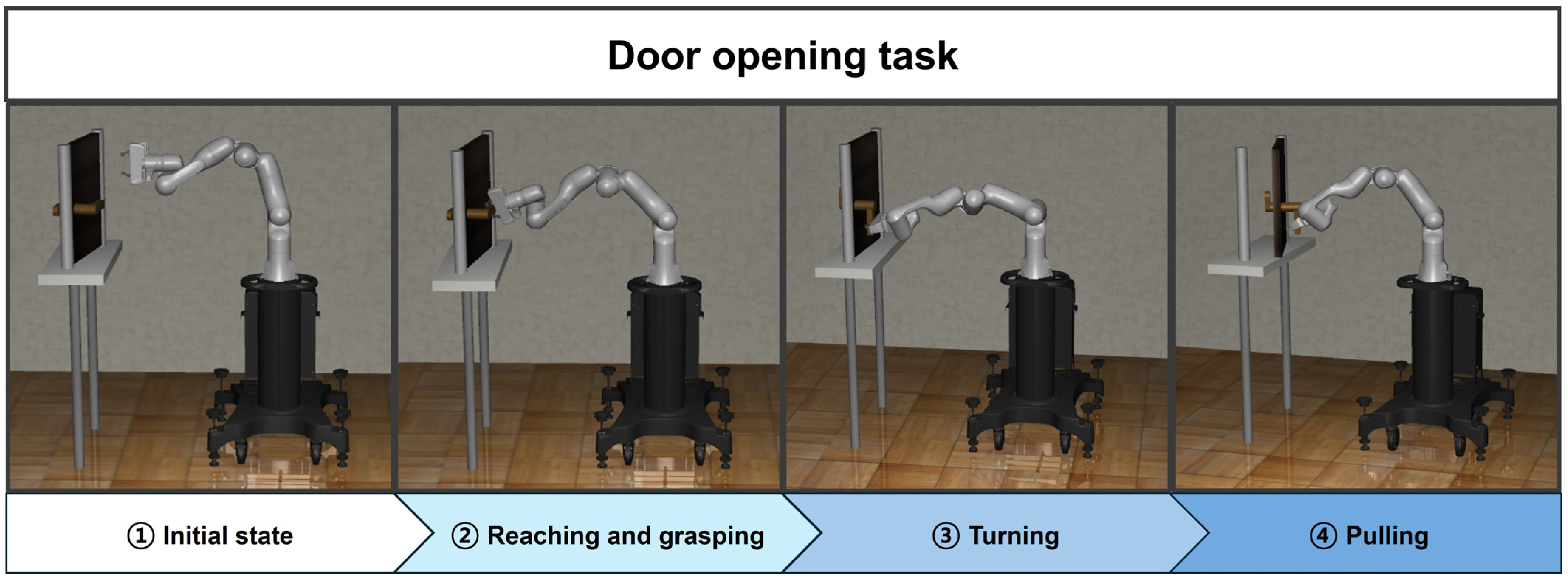
3.1. Door Opening
- Reaching task: reaching the door handle;
- Grasping task: grasping the door handle;
- Turning task: turning the door handle to unlock the door;
- Pulling task: pulling the door open while holding the handle.
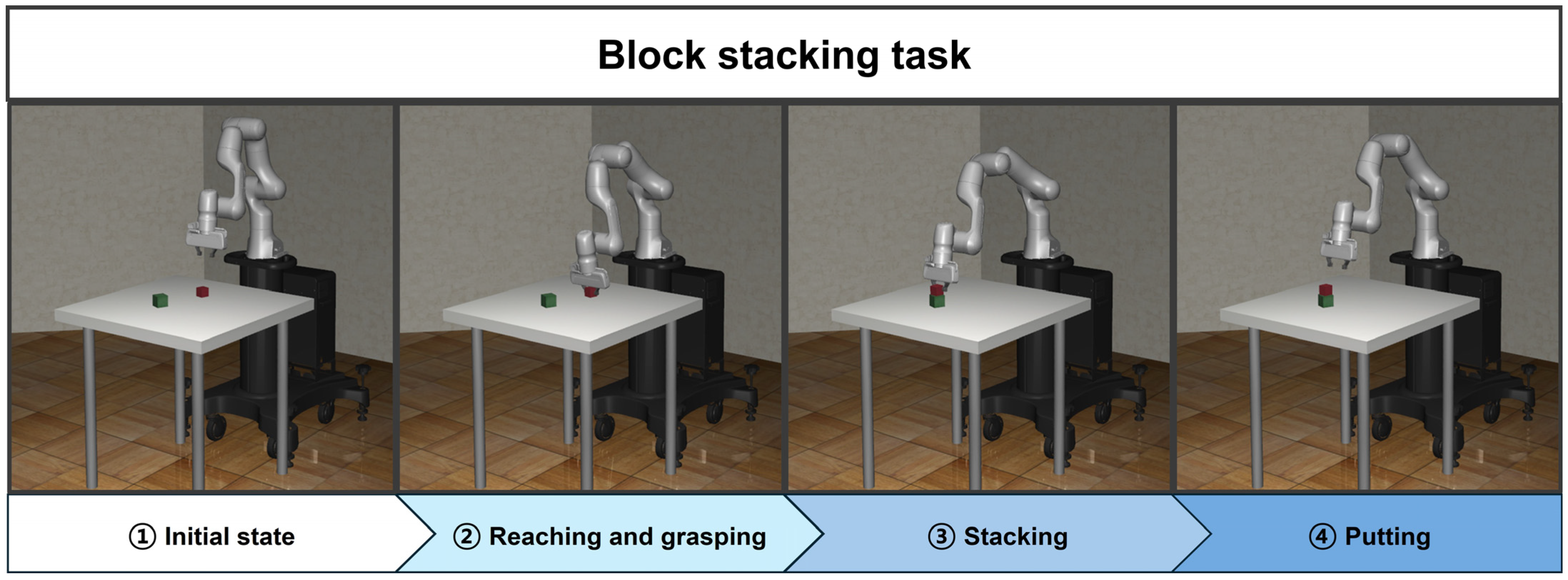
3.2. Block Stacking
- Reaching task: reaching the target block;
- Grasping task: grasping the target block;
- Reaching task: stacking the grasped target block on top of the base block;
- Putting task: putting the target block and checking the state of the stacked blocks.
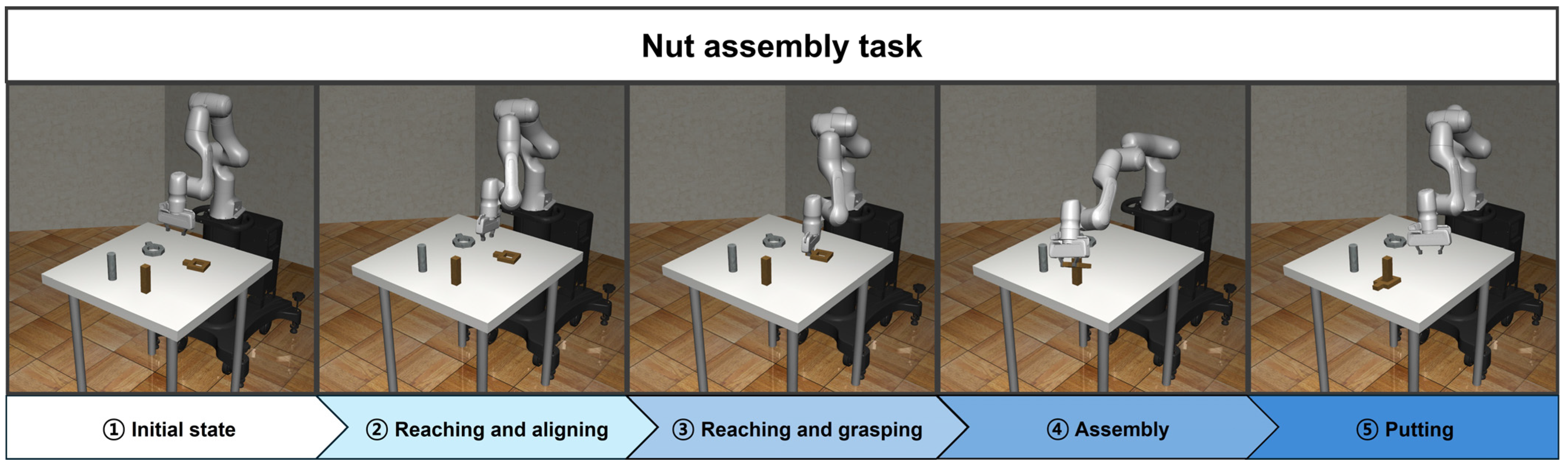
3.3. Nut Assembly
- Reaching task: reaching above the nut handle;
- Aligning task: aligning the orientation of the nut and the end effector;
- Reaching task: reaching the handle of the nut;
- Grasping task: grasping the handle of the nut;
- Assembly task: assembling the nut onto the peg;
- Putting task: checking the peg-in-hole state.
3.4. Designing States, Actions, and Task-Specific Reward System
3.4.1. States and Actions
3.4.2. Task-Specific Reward System for Reaching
3.4.3. Task-Specific Reward System for Turning and Pulling
3.4.4. Task-Specific Reward System for Aligning
3.4.5. Task-Specific Reward System for Assembly
4. Simulation Environment—Robosuite
5. Experimental Results
5.1. Door Opening
5.1.1. Reaching Agent for Approaching the Door Handle
5.1.2. Turning Agent for Unlocking
5.1.3. Pulling Agent for Opening Door
5.2. Block Stacking
5.2.1. Reaching Agent for Approaching the Target Block
5.2.2. Reaching Agent for Stacking the Block
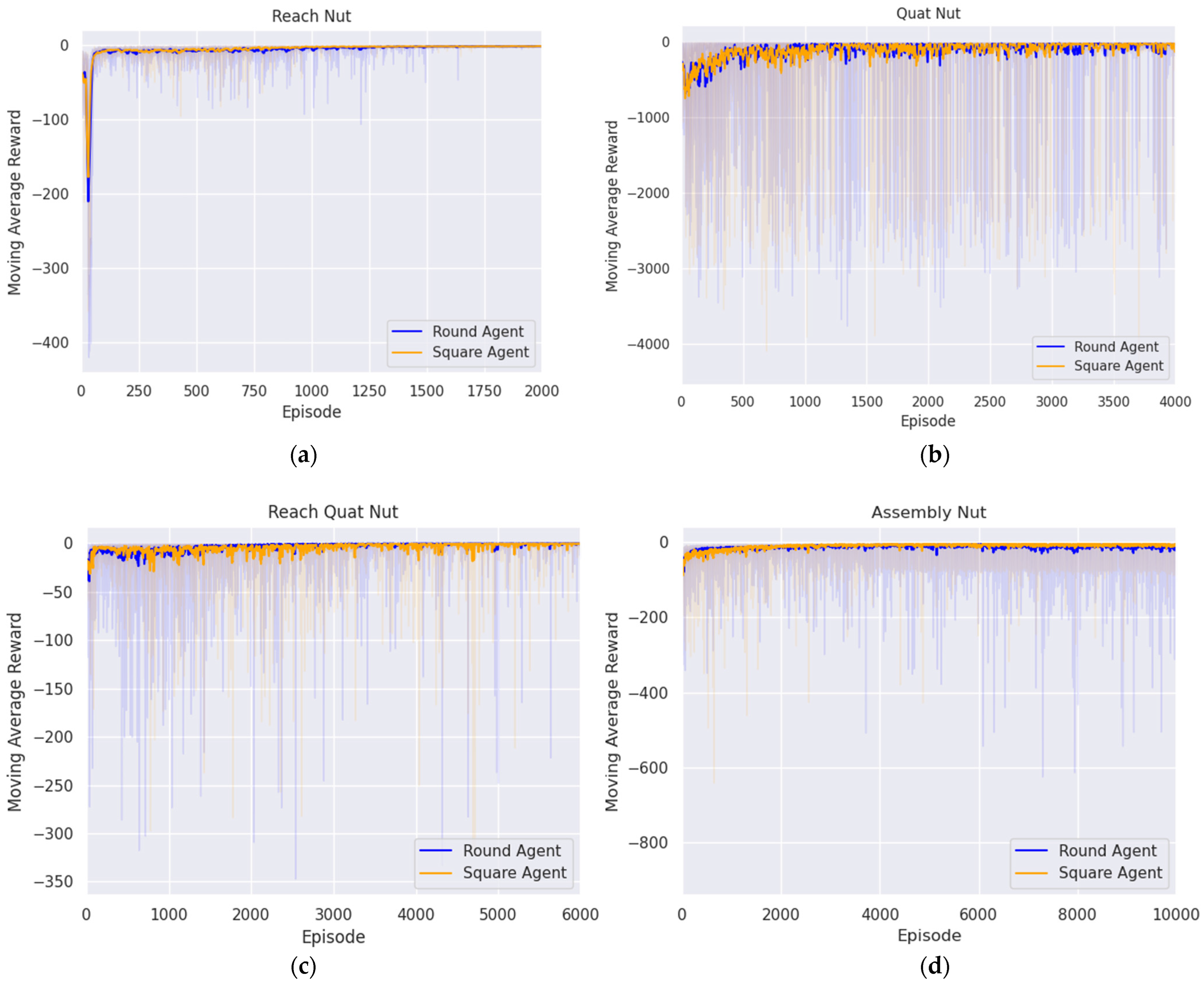
5.3. Nut Assembly
5.3.1. Reaching Agent for Approaching Nut Handle Above
5.3.2. Aligning Agent for Rotating Nut
5.3.3. Reaching Agent for Approaching Nut Handle
5.3.4. Assembly Agent for Peg in Hole
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nguyen, H.; La, H. Review of deep reinforcement learning for robot manipulation. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; pp. 590–595. [Google Scholar]
- Yudha, H.M.; Dewi, T.; Risma, P.; Oktarina, Y. Arm robot manipulator design and control for trajectory tracking; a review. In Proceedings of the 2018 5th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Malang, Indonesia, 16–18 October 2018; pp. 304–309. [Google Scholar]
- Sheridan, T.B. Human–robot interaction: Status and challenges. Hum. Factors 2016, 58, 525–532. [Google Scholar] [CrossRef] [PubMed]
- Ranz, F.; Hummel, V.; Sihn, W. Capability-based task allocation in human-robot collaboration. Procedia Manuf. 2017, 9, 182–189. [Google Scholar] [CrossRef]
- Kyrarini, M.; Leu, A.; Ristić-Durrant, D.; Gräser, A.; Jackowski, A.; Gebhard, M.; Nelles, J.; Bröhl, C.; Brandl, C.; Mertens, A. Human-Robot Synergy for cooperative robots. Facta Univ. Ser. Autom. Control. Robot. 2016, 15, 187–204. [Google Scholar]
- Ajoudani, A.; Zanchettin, A.M.; Ivaldi, S.; Albu-Schäffer, A.; Kosuge, K.; Khatib, O. Progress and prospects of the human–robot collaboration. Auton. Robot. 2018, 42, 957–975. [Google Scholar] [CrossRef]
- Berezina, K.; Ciftci, O.; Cobanoglu, C. Robots, artificial intelligence, and service automation in restaurants. In Robots, Artificial Intelligence, and Service Automation in Travel, Tourism and Hospitality; Emerald Publishing Limited: Bingley, UK, 2019; pp. 185–219. [Google Scholar]
- Wilson, G.; Pereyda, C.; Raghunath, N.; de la Cruz, G.; Goel, S.; Nesaei, S.; Minor, B.; Schmitter-Edgecombe, M.; Taylor, M.E.; Cook, D.J. Robot-enabled support of daily activities in smart home environments. Cogn. Syst. Res. 2019, 54, 258–272. [Google Scholar] [CrossRef] [PubMed]
- Bonci, A.; Cen Cheng, P.D.; Indri, M.; Nabissi, G.; Sibona, F. Human-robot perception in industrial environments: A survey. Sensors 2021, 21, 1571. [Google Scholar] [CrossRef] [PubMed]
- Kermorgant, O.; Chaumette, F. Dealing with constraints in sensor-based robot control. IEEE Trans. Robot. 2013, 30, 244–257. [Google Scholar] [CrossRef]
- Kasera, S.; Kumar, A.; Prasad, L.B. Trajectory tracking of 3-DOF industrial robot manipulator by sliding mode control. In Proceedings of the 2017 4th IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics (UPCON), Mathura, India, 26–28 October 2017; pp. 364–369. [Google Scholar]
- Santos, L.; Cortesão, R. Computed-torque control for robotic-assisted tele-echography based on perceived stiffness estimation. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1337–1354. [Google Scholar] [CrossRef]
- Xiao, H.; Li, Z.; Yang, C.; Zhang, L.; Yuan, P.; Ding, L.; Wang, T. Robust stabilization of a wheeled mobile robot using model predictive control based on neurodynamics optimization. IEEE Trans. Ind. Electron. 2016, 64, 505–516. [Google Scholar] [CrossRef]
- Demura, S.; Mo, Y.; Nagahama, K.; Yamazaki, K. A trajectory modification method for tool operation based on human demonstration using MITATE technique. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1915–1920. [Google Scholar]
- Katyal, K.D.; Brown, C.Y.; Hechtman, S.A.; Para, M.P.; McGee, T.G.; Wolfe, K.C.; Murphy, R.J.; Kutzer, M.D.; Tunstel, E.W.; McLoughlin, M.P. Approaches to robotic teleoperation in a disaster scenario: From supervised autonomy to direct control. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1874–1881. [Google Scholar]
- Fang, M.; You, F.; Yao, R. Application of virtual reality technology (VR) in practice teaching of sports rehabilitation major. J. Phys. Conf. Ser. 2021, 1852, 042007. [Google Scholar] [CrossRef]
- Shin, J.; Badgwell, T.A.; Liu, K.-H.; Lee, J.H. Reinforcement learning–overview of recent progress and implications for process control. Comput. Chem. Eng. 2019, 127, 282–294. [Google Scholar] [CrossRef]
- Liu, R.; Nageotte, F.; Zanne, P.; de Mathelin, M.; Dresp-Langley, B. Deep reinforcement learning for the control of robotic manipulation: A focussed mini-review. Robotics 2021, 10, 22. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Z.; Lu, B.; Cong, M.; Yu, H.; Zou, Q. A reinforcement learning-based framework for robot manipulation skill acquisition. IEEE Access 2020, 8, 108429–108437. [Google Scholar] [CrossRef]
- del Real Torres, A.; Andreiana, D.S.; Ojeda Roldán, Á.; Hernández Bustos, A.; Acevedo Galicia, L.E. A review of deep reinforcement learning approaches for smart manufacturing in industry 4.0 and 5.0 framework. Appl. Sci. 2022, 12, 12377. [Google Scholar] [CrossRef]
- Yang, X.; Ji, Z.; Wu, J.; Lai, Y.-K.; Wei, C.; Liu, G.; Setchi, R. Hierarchical reinforcement learning with universal policies for multistep robotic manipulation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4727–4741. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Strong, M.; Eldar, O. SHIRO: Soft Hierarchical Reinforcement Learning. arXiv 2022, arXiv:2212.12786. [Google Scholar]
- Marzari, L.; Pore, A.; Dall’Alba, D.; Aragon-Camarasa, G.; Farinelli, A.; Fiorini, P. Towards hierarchical task decomposition using deep reinforcement learning for pick and place subtasks. In Proceedings of the 2021 20th International Conference on Advanced Robotics (ICAR), Ljubljana, Slovenia, 6–10 December 2021; pp. 640–645. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Andrychowicz, M.; Wolski, F.; Ray, A.; Schneider, J.; Fong, R.; Welinder, P.; McGrew, B.; Tobin, J.; Pieter Abbeel, O.; Zaremba, W. Hindsight experience replay. Adv. Neural Inf. Process. Syst. 2017, 30. arXiv:1707.01495. [Google Scholar]
- Kim, B.; Kwon, G.; Park, C.; Kwon, N.K. The Task Decomposition and Dedicated Reward-System-Based Reinforcement Learning Algorithm for Pick-and-Place. Biomimetics 2023, 8, 240. [Google Scholar] [CrossRef] [PubMed]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Zhu, Y.; Wong, J.; Mandlekar, A.; Martín-Martín, R.; Joshi, A.; Nasiriany, S.; Zhu, Y. robosuite: A modular simulation framework and benchmark for robot learning. arXiv 2020, arXiv:2009.12293. [Google Scholar]


| Posture of the Robot Manipulator | ||
|---|---|---|
| : position and orientation of the end effector : cosine values of the joint angles : sine values of the joint angles : joint velocity : position and velocity of the gripper | ||
| Door opening | Block stacking | Nut assembly |
| : door handle position : positional difference between handle and end effector : door position : positional difference between door and end effector : hinge angle : handle angle | : position and orientation of the target block : positional difference between target block and end effector : position and orientation of the base block : positional difference between base block and end effector : positional difference between target block and base block | : position and orientation of the nut : positional difference between nut and end effector : nut handle position : positional difference between nut handle and end effector : peg position : positional difference between nut and peg |
| Subtask | Target Position | |||
|---|---|---|---|---|
| Reaching task in door opening | : door handle | 0.5 | 2 | 4 |
| First reaching task in block stacking | : block | 2 | 2 | 1 |
| Second reaching task in block stacking | : above target block | 2 | 2 | 1 |
| First reaching task in nut assembly | : above nut handle | 2 | 2 | 1 |
| Second reaching task in nut assembly | : nut handle | 2 | 2 | 1 |
| Subtask | |||
|---|---|---|---|
| Turning task in door opening | : door handle angle | 10 | |
| Pulling task in door opening | : hinge angle | 10 |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average |
|---|---|---|---|---|
| 100% | 100% | 100% | 99.8% | 99.95% |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average |
|---|---|---|---|---|
| 100% | 100% | 100% | 100% | 100% |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average |
|---|---|---|---|---|
| 99.6% | 100% | 100% | 100% | 99.9% |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average |
|---|---|---|---|---|
| 99.0% | 99.2% | 98.8% | 98.8% | 98.95% |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average |
|---|---|---|---|---|
| 96.0% | 95.2% | 94.6% | 95.2% | 95.25% |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average | |
|---|---|---|---|---|---|
| Square | 99.8% | 100% | 100% | 99.8% | 99.9% |
| Round | 99.9% | 99.6% | 100% | 100% | 99.875% |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average | |
|---|---|---|---|---|---|
| Square | 98.6% | 97.6% | 97.0% | 98.0% | 97.45% |
| Round | 97.2% | 97.8% | 96.6% | 98.0% | 97.4% |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average | |
|---|---|---|---|---|---|
| Square | 96.0% | 95.0% | 94.2% | 97.6% | 95.7% |
| Round | 98.8% | 97.6% | 99.0% | 98.4% | 98.45% |
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average | |
|---|---|---|---|---|---|
| Square | 80.4% | 81.8% | 80.2% | 80.8% | 80.8% |
| Round | 89.8% | 90.8% | 91.0% | 92.0% | 90.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, G.; Kim, B.; Kwon, N.K. Reinforcement Learning with Task Decomposition and Task-Specific Reward System for Automation of High-Level Tasks. Biomimetics 2024, 9, 196. https://doi.org/10.3390/biomimetics9040196
Kwon G, Kim B, Kwon NK. Reinforcement Learning with Task Decomposition and Task-Specific Reward System for Automation of High-Level Tasks. Biomimetics. 2024; 9(4):196. https://doi.org/10.3390/biomimetics9040196
Chicago/Turabian StyleKwon, Gunam, Byeongjun Kim, and Nam Kyu Kwon. 2024. "Reinforcement Learning with Task Decomposition and Task-Specific Reward System for Automation of High-Level Tasks" Biomimetics 9, no. 4: 196. https://doi.org/10.3390/biomimetics9040196
APA StyleKwon, G., Kim, B., & Kwon, N. K. (2024). Reinforcement Learning with Task Decomposition and Task-Specific Reward System for Automation of High-Level Tasks. Biomimetics, 9(4), 196. https://doi.org/10.3390/biomimetics9040196






