Design and Evaluation of a Bilateral Semi-Rigid Exoskeleton to Assist Hip Motion
Abstract
:1. Introduction
2. Materials and Methods
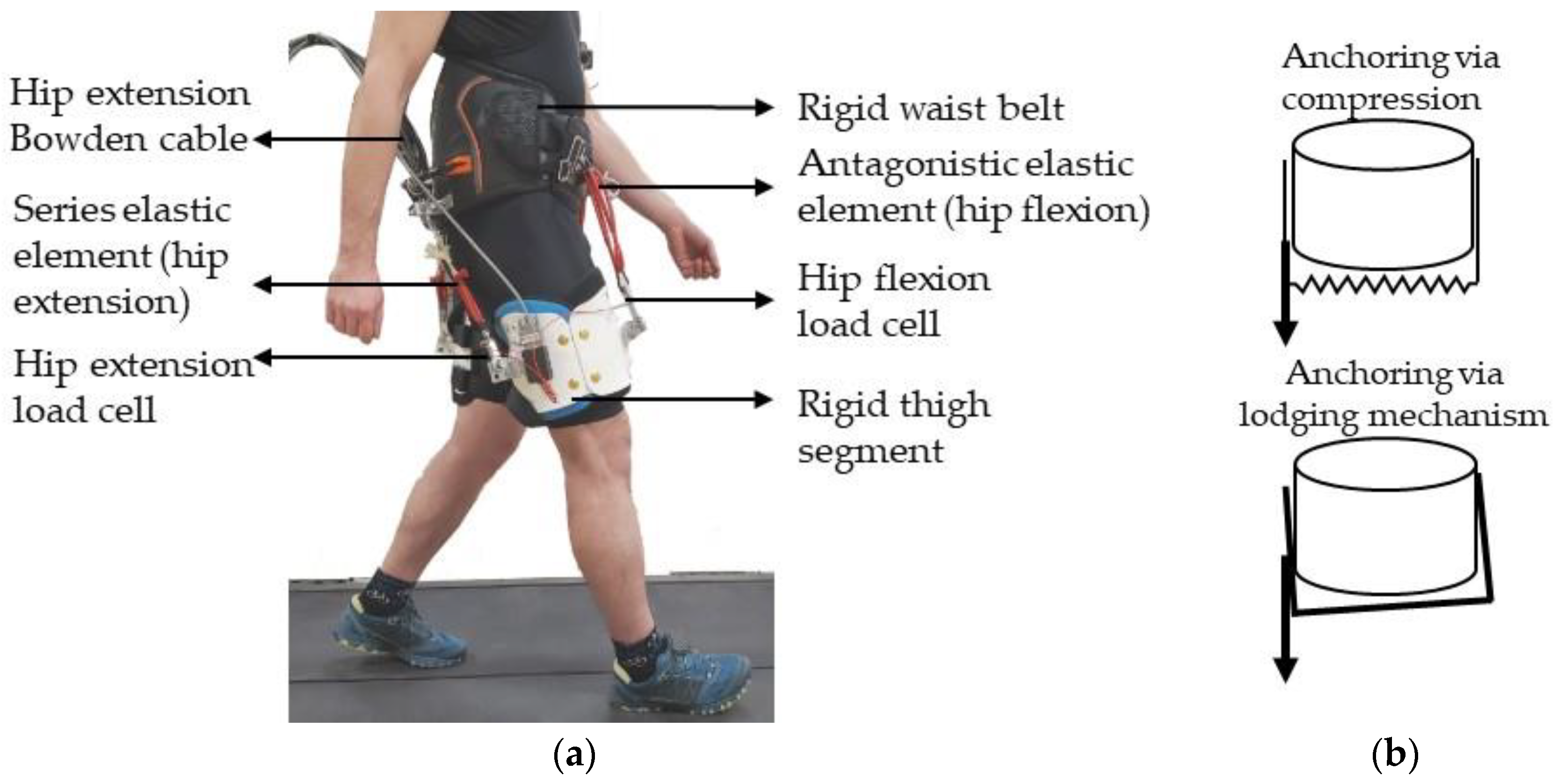
2.1. Hip Exoskeleton Design
2.2. Exoskeleton Controller
2.3. Exoskeleton Design and Control Optimization Protocol
2.4. Metabolic Cost and Biomechanics Evaluation Protocol
2.5. Statistical Analyses
3. Results
3.1. Device Optimization Results
3.2. Metabolic Cost and Biomechanics Evaluation Protocol Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mooney, L.M.; Rouse, E.J.; Herr, H.M. Autonomous Exoskeleton Reduces Metabolic Cost of Human Walking during Load Carriage. J. Neuroeng. Rehabil. 2014, 11, 80. [Google Scholar] [CrossRef]
- Collins, S.H.; Wiggin, M.B.; Sawicki, G.S. Reducing the Energy Cost of Human Walking Using an Unpowered Exoskeleton. Nature 2015, 522, 212–215. [Google Scholar] [CrossRef]
- Sawicki, G.S.; Ferris, D.P. A Pneumatically Powered Knee-Ankle-Foot Orthosis (KAFO) with Myoelectric Activation and Inhibition. J. Neuroeng Rehabil. 2009, 6, 23. [Google Scholar] [CrossRef]
- Lee, G.; Kim, J.; Panizzolo, F.A.; Zhou, Y.M.; Baker, L.M.; Galiana, I.; Malcolm, P.; Walsh, C.J. Reducing the Metabolic Cost of Running with a Tethered Soft Exosuit. Sci. Robot 2017, 2, 6708–6731. [Google Scholar] [CrossRef]
- Young, A.J.; Foss, J.; Gannon, H.; Ferris, D.P. Influence of Power Delivery Timing on the Energetics and Biomechanics of Humans Wearing a Hip Exoskeleton. Front. Bioeng. Biotechnol. 2017, 5, 4. [Google Scholar] [CrossRef]
- Ding, Y.; Kim, M.; Kuindersma, S.; Walsh, C.J. Human-in-the-Loop Optimization of Hip Assistance with a Soft Exosuit during Walking. Sci. Robot. 2018, 3, eaar5438. [Google Scholar] [CrossRef]
- Umberger, B.R. Stance and Swing Phase Costs in Human Walking. J. R. Soc. Interface 2010, 7, 1329–1340. [Google Scholar] [CrossRef]
- Kang, I.; Hsu, H.; Young, A. The Effect of Hip Assistance Levels on Human Energetic Cost Using Robotic Hip Exoskeletons. IEEE Robot. Autom. Lett. 2019, 4, 430–437. [Google Scholar] [CrossRef]
- Bryan, G.M.; Franks, P.W.; Song, S.; Voloshina, A.S.; Reyes, R.; O’Donovan, M.P.; Gregorczyk, K.N.; Collins, S.H. Optimized Hip–Knee–Ankle Exoskeleton Assistance at a Range of Walking Speeds. J. Neuroeng. Rehabil. 2021, 18, 152. [Google Scholar] [CrossRef]
- Lim, B.; Lee, J.; Jang, J.; Kim, K.; Park, Y.J.; Seo, K.; Shim, Y. Delayed Output Feedback Control for Gait Assistance With a Robotic Hip Exoskeleton. IEEE Trans. Robot. 2019, 35, 1055–1062. [Google Scholar] [CrossRef]
- Slade, P.; Kochenderfer, M.J.; Delp, S.L.; Collins, S.H. Personalizing Exoskeleton Assistance While Walking in the Real World. Nature 2022, 610, 277–282. [Google Scholar] [CrossRef]
- Yandell, M.B.; Tacca, J.R.; Zelik, K.E. Design of a Low Profile, Unpowered Ankle Exoskeleton That Fits Under Clothes: Overcoming Practical Barriers to Widespread Societal Adoption. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 712–723. [Google Scholar] [CrossRef]
- Sawicki, G.S.; Beck, O.N.; Kang, I.; Young, A.J. The Exoskeleton Expansion: Improving Walking and Running Economy. J. Neuroeng. Rehabil. 2020, 17, 25. [Google Scholar] [CrossRef]
- Kim, J.; Quinlivan, B.T.; Deprey, L.A.; Arumukhom Revi, D.; Eckert-Erdheim, A.; Murphy, P.; Orzel, D.; Walsh, C.J. Reducing the Energy Cost of Walking with Low Assistance Levels through Optimized Hip Flexion Assistance from a Soft Exosuit. Sci. Rep. 2022, 12, 11004. [Google Scholar] [CrossRef]
- Ding, Y.; Panizzolo, F.A.; Siviy, C.; Malcolm, P.; Galiana, I.; Holt, K.G.; Walsh, C.J. Effect of Timing of Hip Extension Assistance during Loaded Walking with a Soft Exosuit. J. Neuroeng. Rehabil. 2016, 13, 87. [Google Scholar] [CrossRef]
- Zhou, T.; Xiong, C.; Zhang, J.; Hu, D.; Chen, W.; Huang, X. Reducing the Metabolic Energy of Walking and Running Using an Unpowered Hip Exoskeleton. J. Neuroeng. Rehabil. 2021, 18, 95. [Google Scholar] [CrossRef]
- Browning, R.C.; Modica, J.R.; Kram, R.; Goswami, A. The Effects of Adding Mass to the Legs on the Energetics and Biomechanics of Walking. Med. Sci. Sport. Exerc. 2007, 39, 515–525. [Google Scholar] [CrossRef]
- Dembia, C.L.; Silder, A.; Uchida, T.K.; Hicks, J.L.; Delp, S.L. Simulating Ideal Assistive Devices to Reduce the Metabolic Cost of Walking with Heavy Loads. PLoS ONE 2017, 12, e0180320. [Google Scholar] [CrossRef]
- Mooney, L.M.; Herr, H.M. Biomechanical Walking Mechanisms Underlying the Metabolic Reduction Caused by an Autonomous Exoskeleton. J. Neuroeng. Rehabil. 2016, 13, 4. [Google Scholar] [CrossRef]
- Roberts, D.; Hillstrom, H.; Kim, J.H. Instantaneous Metabolic Cost of Walking: Joint-Space Dynamic Model with Subject-Specific Heat Rate. PLoS ONE 2016, 11, e0168070. [Google Scholar] [CrossRef]
- Mohammadzadeh Gonabadi, A.; Antonellis, P.; Malcolm, P. Differences between Joint-Space and Musculoskeletal Estimations of Metabolic Rate Time Profiles. PLoS Comput. Biol. 2020, 16, e1008280. [Google Scholar] [CrossRef] [PubMed]
- Nasiri, R.; Ahmadi, A.; Ahmadabadi, M.N. Reducing the Energy Cost of Human Running Using an Unpowered Exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 2026–2032. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, G.; Heimgartner, R.; Revi, D.A.; Karavas, N.; Nathanson, D.; Galiana, I.; Eckert-Erdheim, A.; Murphy, P.; Perry, D.; et al. Reducing the Metabolic Rate of Walking and Running with a Versatile, Portable Exosuit. Science 2019, 365, 668–672. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ajoudani, A.; Tsagarakis, N.G. Exo-Muscle: A Semi-Rigid Assistive Device for the Knee. IEEE Robot. Autom. Lett. 2021, 6, 8514–8521. [Google Scholar] [CrossRef]
- Schmidt, K.; Duarte, J.E.; Grimmer, M.; Sancho-Puchades, A.; Wei, H.; Easthope, C.S.; Riener, R. The Myosuit: Bi-Articular Anti-Gravity Exosuit That Reduces Hip Extensor Activity in Sitting Transfers. Front. Neurorobot. 2017, 11, 57. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Zhang, F.; Yang, L.; Fu, Y. Design and Modeling of a Hybrid Soft-Rigid Hand Exoskeleton for Poststroke Rehabilitation. Int. J. Mech. Sci. 2021, 212, 106831. [Google Scholar] [CrossRef]
- Gordon, C.C.; Blackwell, C.L.; Bradtmiller, B.; Parham, J.L.; Barrientos, P.; Paquette, S.P.; Corner, B.D.; Carson, J.M.; Venezia, J.C.; Rockwell, B.M.; et al. 2012 Anthropometric Survey of U.S. Army Personnel: Methods and Summary Statistics. 2014. Available online: https://dacowits.defense.gov/LinkClick.aspx?fileticket=EbsKcm6A10U%3D&portalid=48 (accessed on 31 January 2024).
- Caputo, J.M.; Collins, S.H. A Universal Ankle—Foot Prosthesis Emulator for Human Locomotion Experiments. J. Biomech. Eng. 2015, 136, 035002. [Google Scholar] [CrossRef] [PubMed]
- Gonabadi, A.M.; Antonellis, P.; Malcolm, P. A System for Simple Robotic Walking Assistavnce With Linear Impulses at the Center of Mass. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1353–1362. [Google Scholar] [CrossRef] [PubMed]
- Simha, S.N.; Wong, J.D.; Selinger, J.C.; Donelan, J.M. A Mechatronic System for Studying Energy Optimization during Walking. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1416–1425. [Google Scholar] [CrossRef]
- Zhang, J.; Collins, S.H. The Passive Series Stiffness That Optimizes Torque Tracking for a Lower-Limb Exoskeleton in Human Walking. Front. Neurorobot. 2017, 11, 68. [Google Scholar] [CrossRef]
- Brockway, J. Derivation of Formulae Used to Calculate Energy Expenditure in Man. Hum. Nutr. Clin. Nutr. 1987, 41, 463–471. [Google Scholar] [PubMed]
- Zhang, J.; Fiers, P.; Witte, K.A.; Jackson, R.W.; Poggensee, K.L.; Atkeson, C.G.; Collins, S.H. Human-in-the-Loop Optimization of Exoskeleton Assistance during Walking. Science 2017, 356, 1280–1284. [Google Scholar] [CrossRef]
- Selinger, J.C.; Donelan, J.M. Estimating Instantaneous Energetic Cost during Non-Steady-State Gait. J. Appl. Physiol. 2014, 117, 1406–1415. [Google Scholar] [CrossRef] [PubMed]
- Kadaba, M.P.; Ramakrishnan, H.K.; Wootten, M.E. Measurement of Lower Extremity Kinematics during Level Walking. J. Orthop. Res. 1990, 8, 383–392. [Google Scholar] [CrossRef]
- Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating Musculoskeletal Dynamics and Neuromuscular Control to Study Human and Animal Movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef] [PubMed]
- Hicks, J.L.; Uchida, T.K.; Seth, A.; Rajagopal, A.; Delp, S.L. Is My Model Good Enough? Best Practices for Verification and Validation of Musculoskeletal Models and Simulations of Movement. J. Biomech. Eng. 2015, 137, 020905. [Google Scholar] [CrossRef] [PubMed]
- Donelan, J.M.; Kram, R.; Kuo, A.D. Simultaneous Positive and Negative External Mechanical Work in Human Walking. J. Biomech. 2002, 35, 117–124. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis, 18th ed.; Addison-Wesley Publishing Company: Boston, MA, USA, 1977; ISBN 0201076160/9780201076165. [Google Scholar]
- Pratt, G.A.; Williamson, M.M. Series Elastic Actuators. In Proceedings of the Proceedings 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; 1995; Volume 1, pp. 399–406. [Google Scholar]
- Lewis, C.L.; Ferris, D.P. Walking with Increased Ankle Pushoff Decreases Hip Muscle Moments. J. Biomech. 2008, 41, 2082–2089. [Google Scholar] [CrossRef]
- Antonellis, P.; Mohammadzadeh Gonabadi, A.; Myers, S.A.; Pipinos, I.I.; Malcolm, P. Metabolically Efficient Walking Assistance Using Optimized Timed Forces at the Waist. Sci. Robot. 2022, 7, eabh1925. [Google Scholar] [CrossRef]
- Panizzolo, F.A.; Bolgiani, C.; Di Liddo, L.; Annese, E.; Marcolin, G. Reducing the Energy Cost of Walking in Older Adults Using a Passive Hip Flexion Device. J. Neuroeng. Rehabil. 2019, 16, 117. [Google Scholar] [CrossRef] [PubMed]
- Voloshina, A.S.; Kuo, A.D.; Daley, M.A.; Ferris, D.P. Biomechanics and Energetics of Walking on Uneven Terrain. J. Exp. Biol. 2013, 216, 3963–3970. [Google Scholar] [CrossRef] [PubMed]
- Bryan, G.M.; Franks, P.W.; Song, S.; Reyes, R.; O’Donovan, M.P.; Gregorczyk, K.N.; Collins, S.H. Optimized Hip-Knee-Ankle Exoskeleton Assistance Reduces the Metabolic Cost of Walking with Worn Loads. J. Neuroeng. Rehabil. 2021, 18, 161. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadzadeh Gonabadi, A.; Antonellis, P.; Dzewaltowski, A.C.; Myers, S.A.; Pipinos, I.I.; Malcolm, P. Design and Evaluation of a Bilateral Semi-Rigid Exoskeleton to Assist Hip Motion. Biomimetics 2024, 9, 211. https://doi.org/10.3390/biomimetics9040211
Mohammadzadeh Gonabadi A, Antonellis P, Dzewaltowski AC, Myers SA, Pipinos II, Malcolm P. Design and Evaluation of a Bilateral Semi-Rigid Exoskeleton to Assist Hip Motion. Biomimetics. 2024; 9(4):211. https://doi.org/10.3390/biomimetics9040211
Chicago/Turabian StyleMohammadzadeh Gonabadi, Arash, Prokopios Antonellis, Alex C. Dzewaltowski, Sara A. Myers, Iraklis I. Pipinos, and Philippe Malcolm. 2024. "Design and Evaluation of a Bilateral Semi-Rigid Exoskeleton to Assist Hip Motion" Biomimetics 9, no. 4: 211. https://doi.org/10.3390/biomimetics9040211
APA StyleMohammadzadeh Gonabadi, A., Antonellis, P., Dzewaltowski, A. C., Myers, S. A., Pipinos, I. I., & Malcolm, P. (2024). Design and Evaluation of a Bilateral Semi-Rigid Exoskeleton to Assist Hip Motion. Biomimetics, 9(4), 211. https://doi.org/10.3390/biomimetics9040211






