Numerical Analysis of Broadband Noise Generated by an Airfoil with Spanwise-Varying Leading Edges
Abstract
:1. Introduction
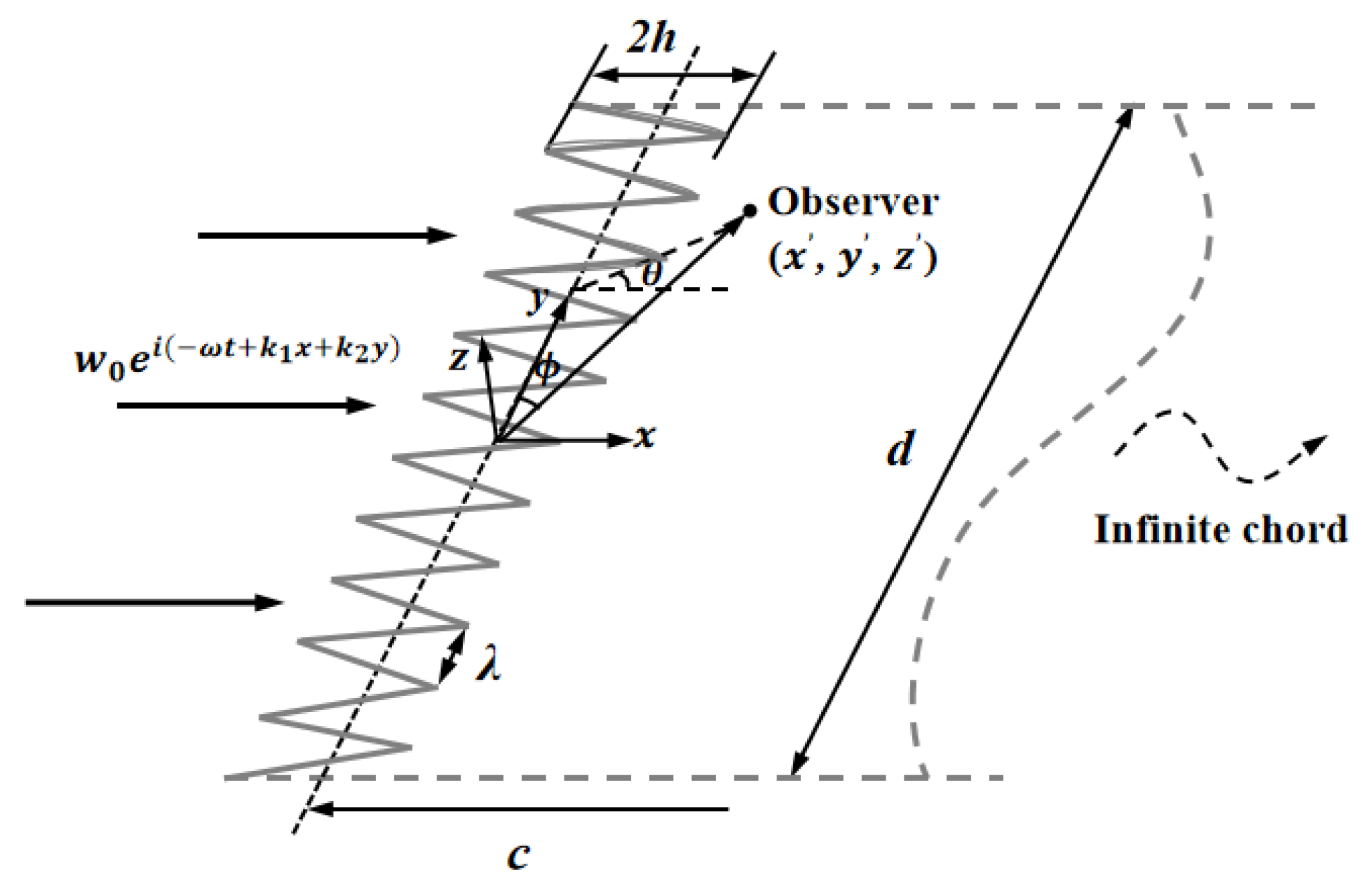
2. Analytical Formulation
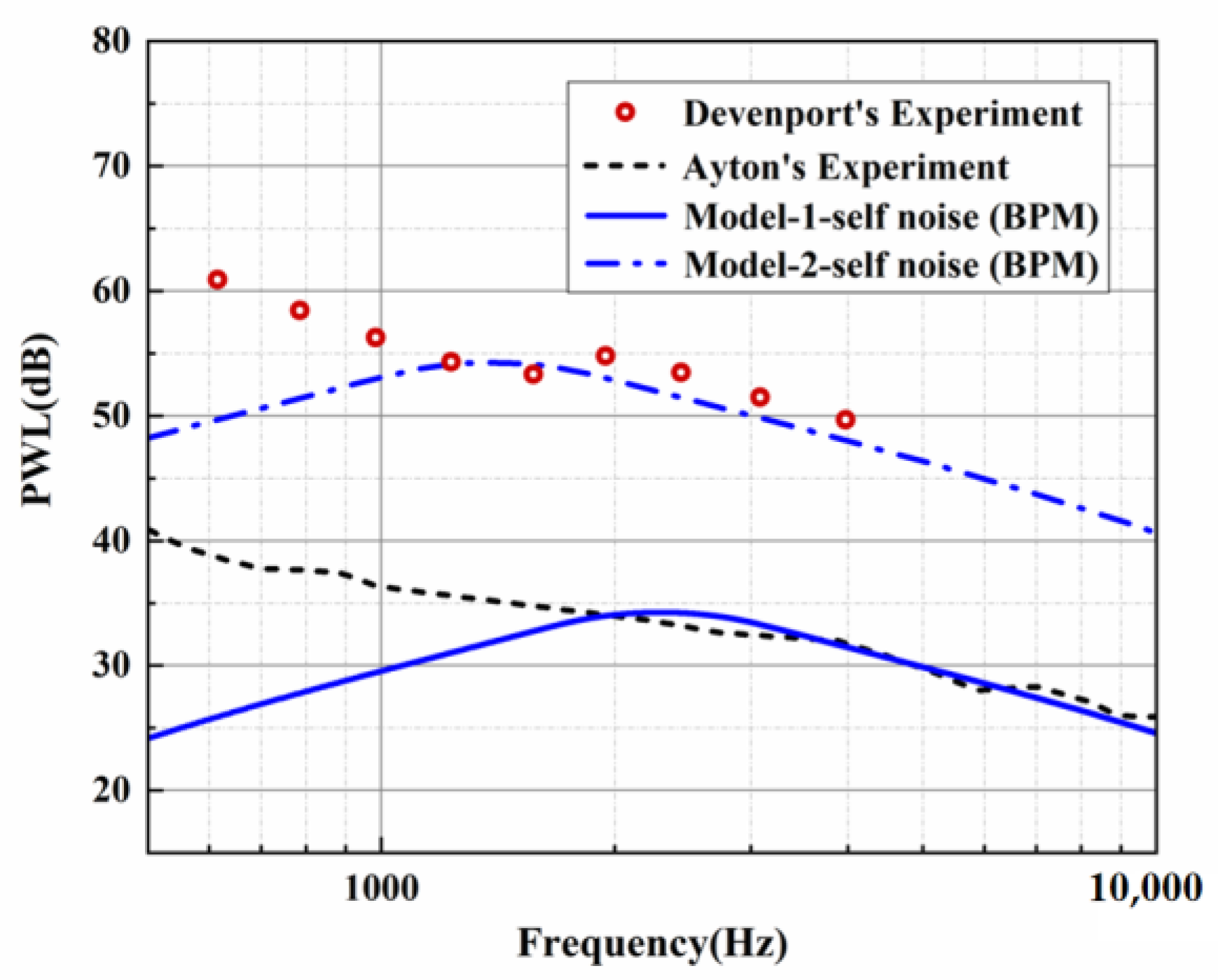
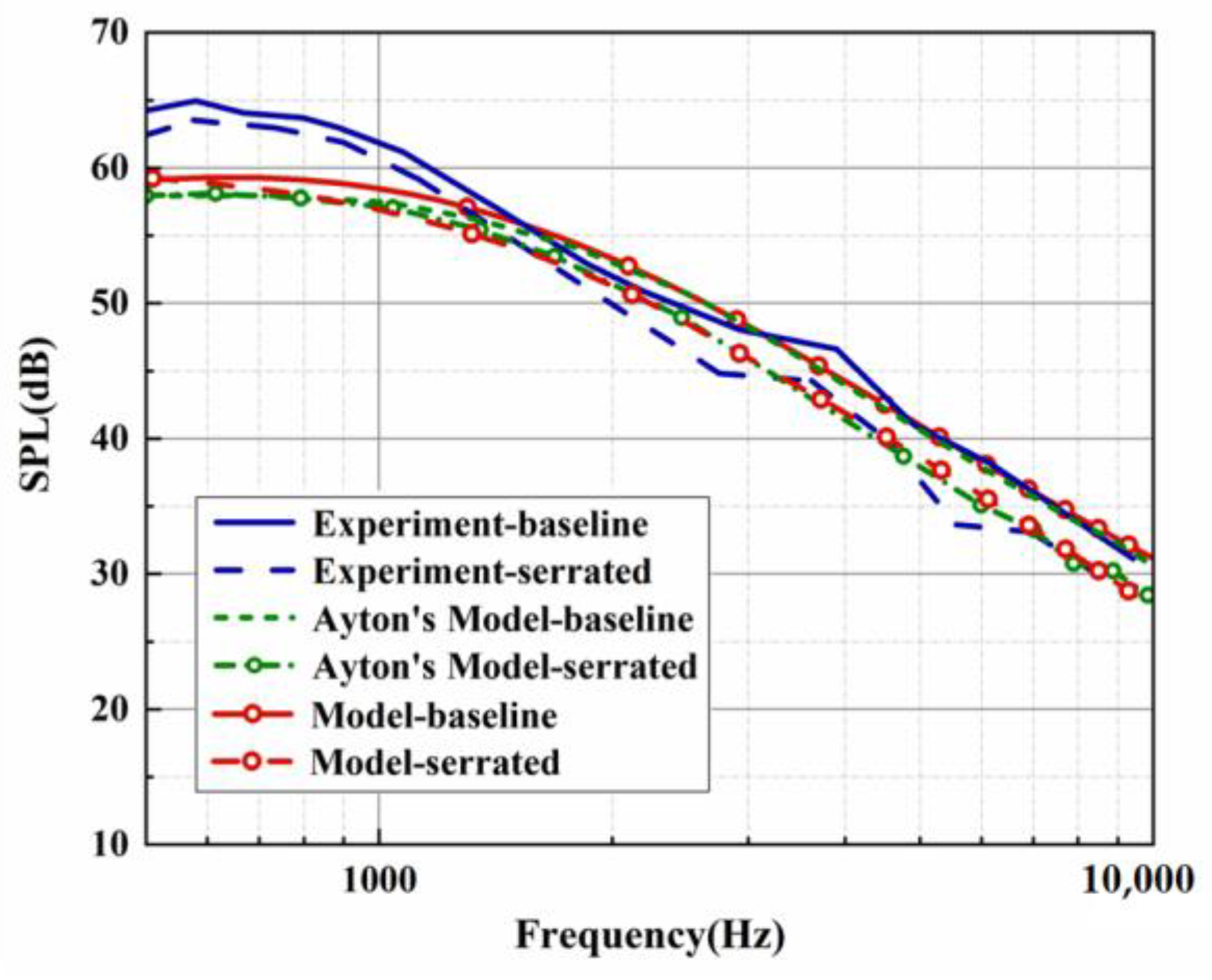
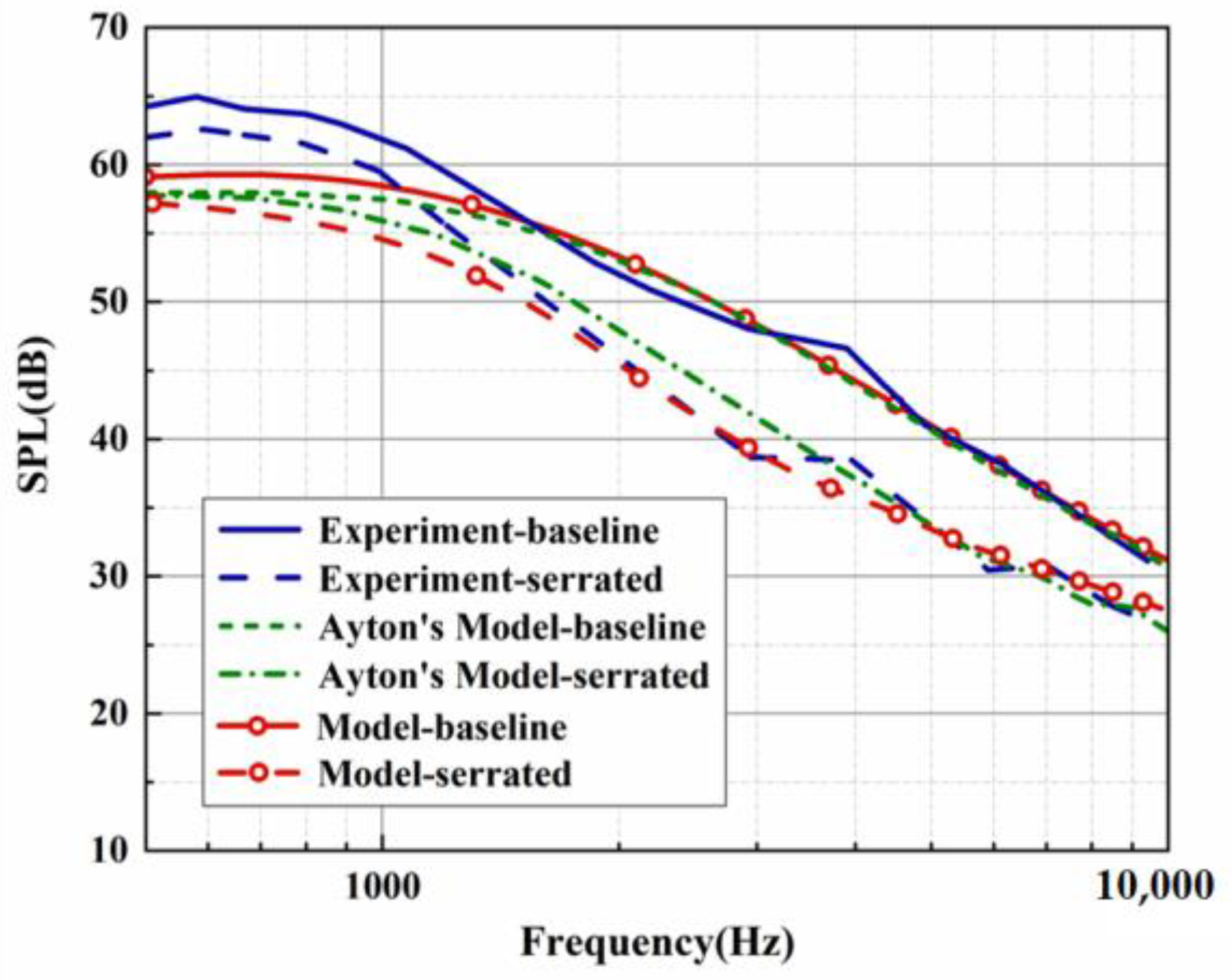
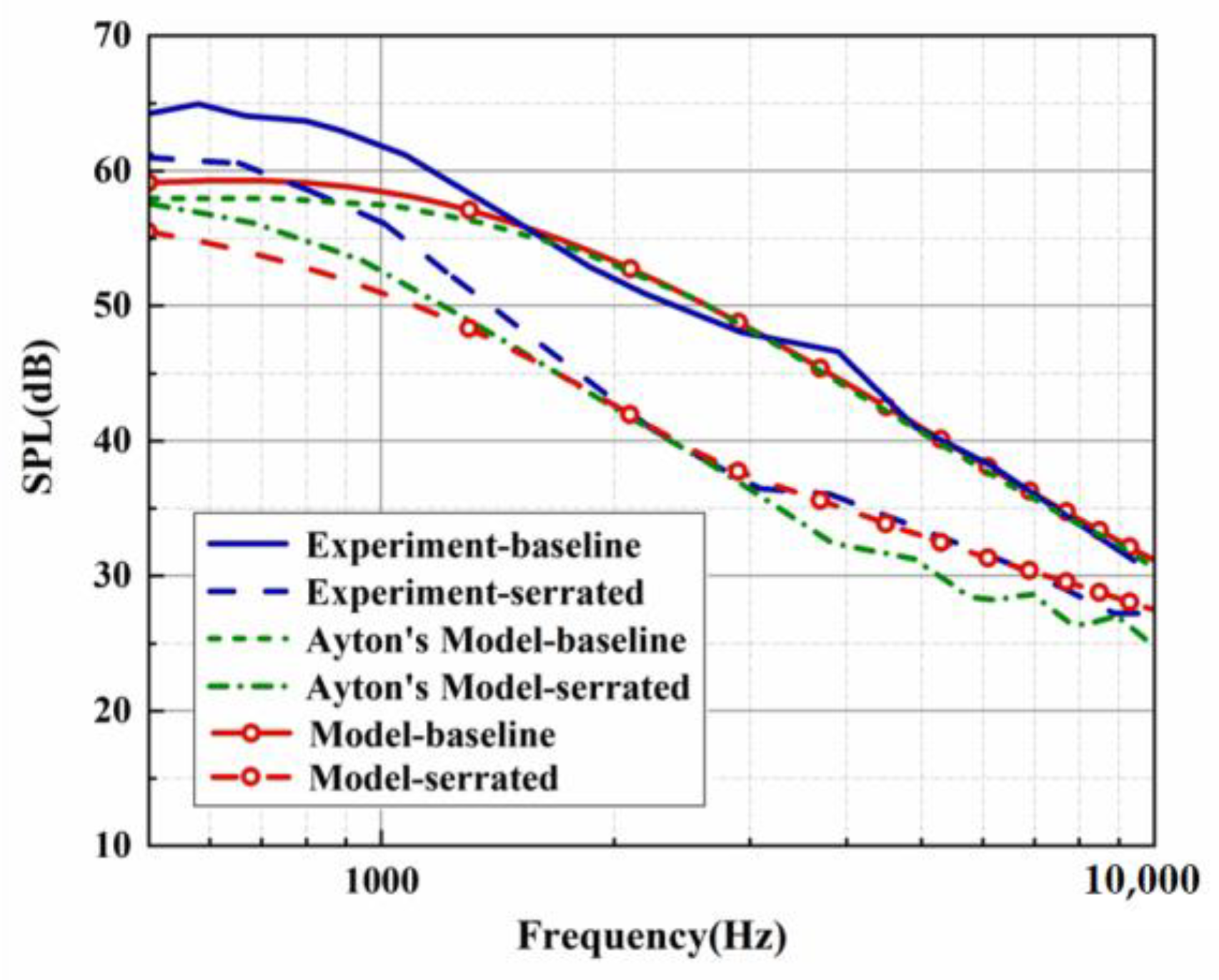
3. Comparison with Experiments
4. Acoustic Performance of Single-Wavelength Serrations
5. Acoustic Sensitivity of Double-Wavelength Serrations
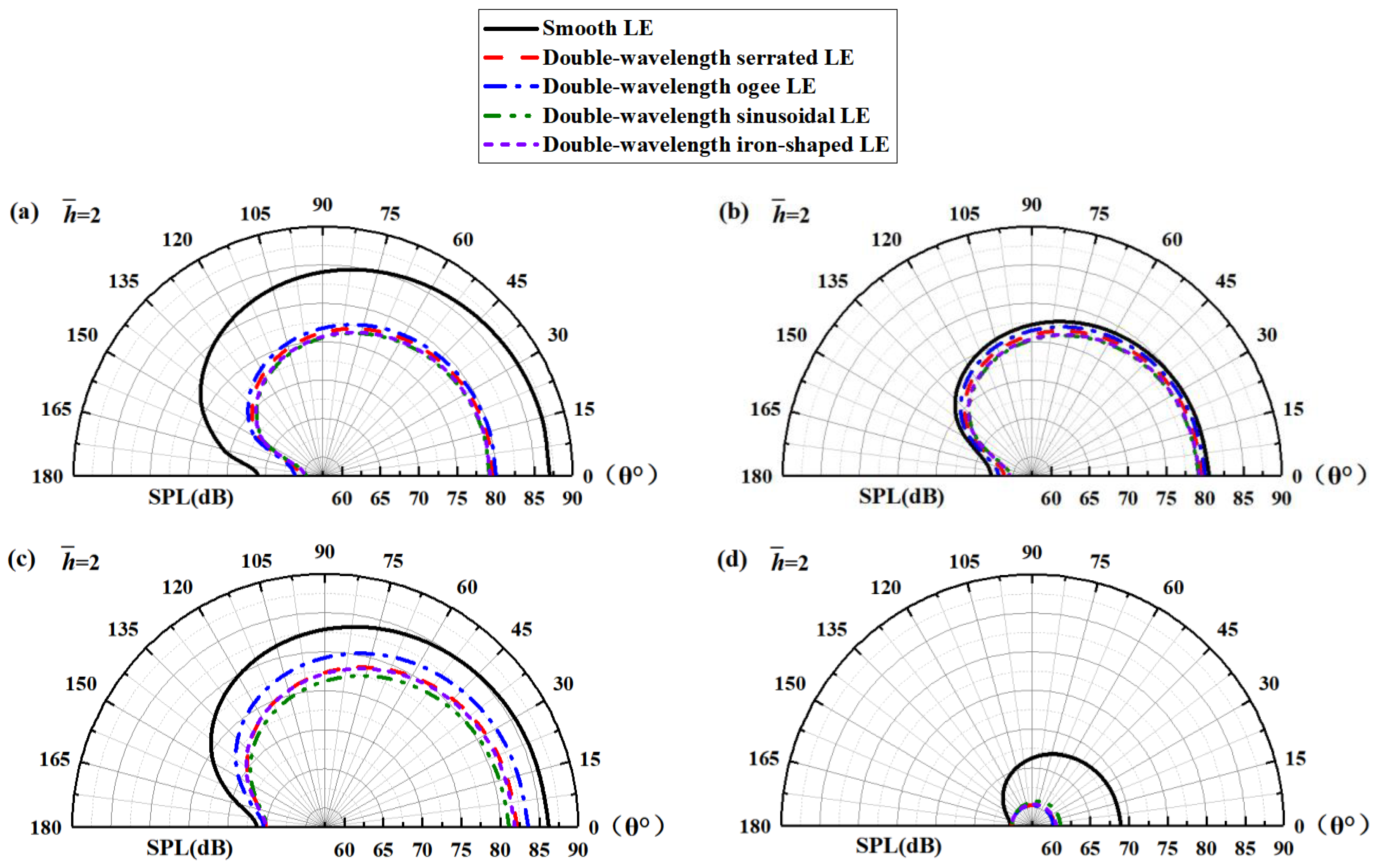
6. Results and Discussion
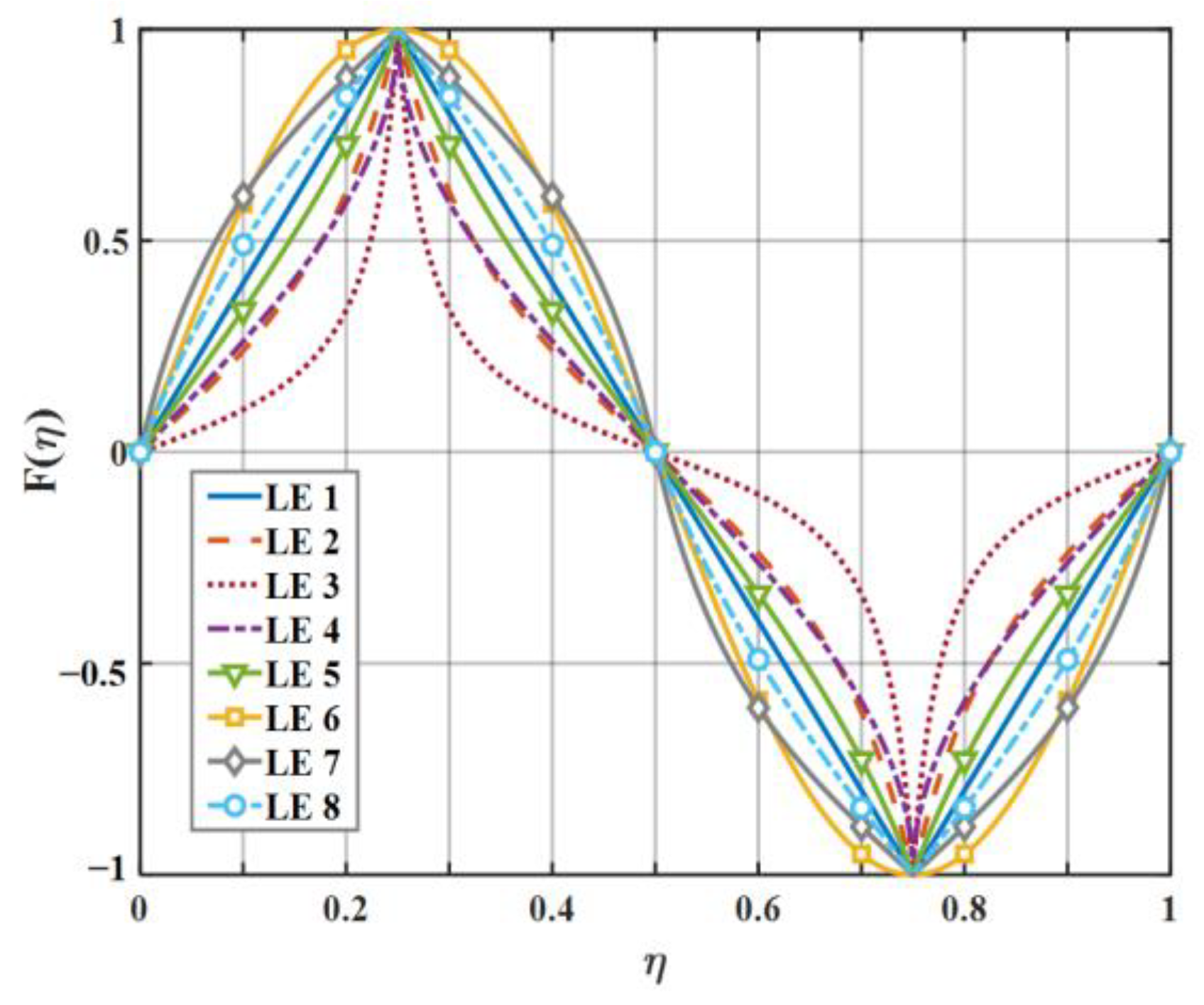
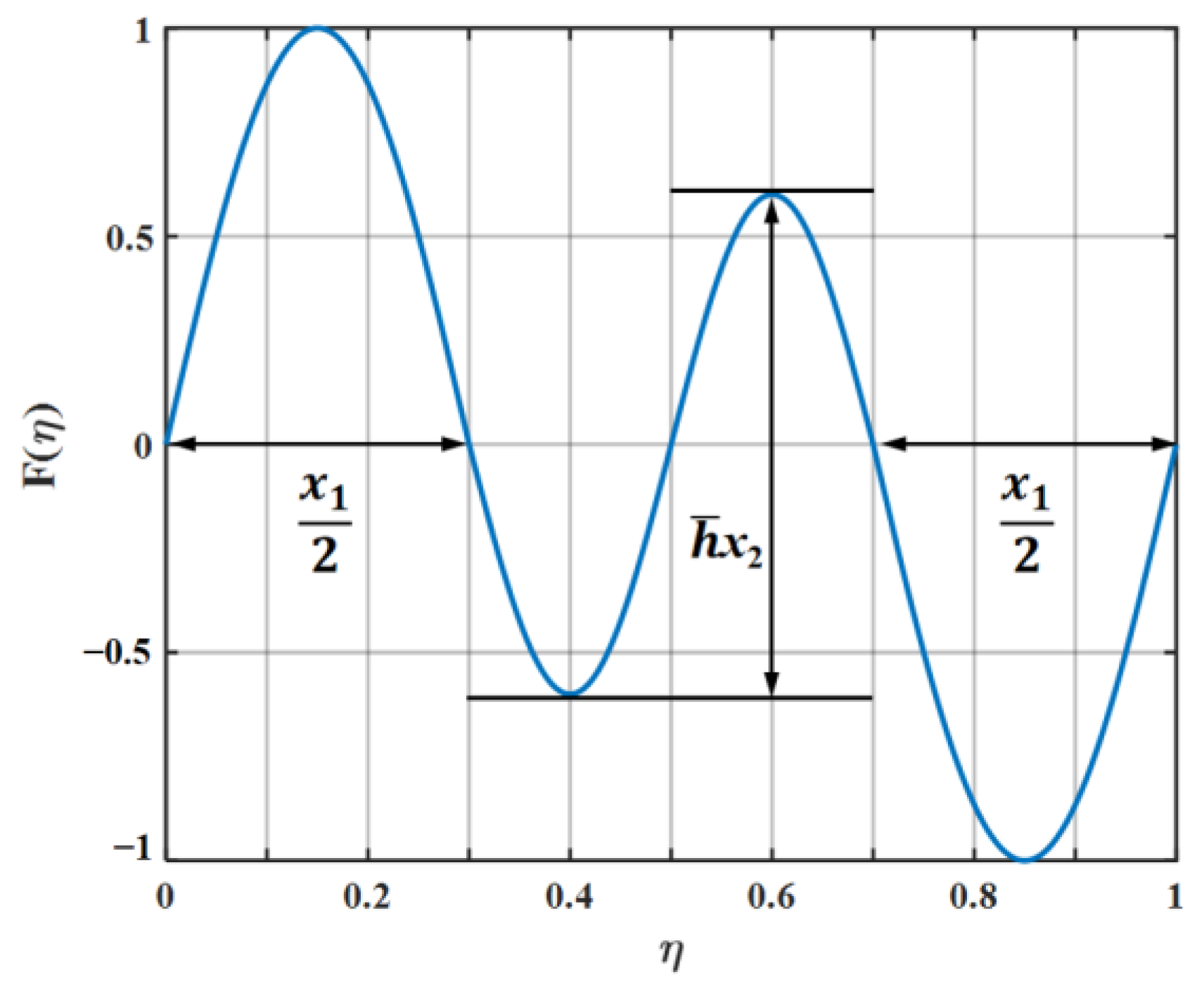
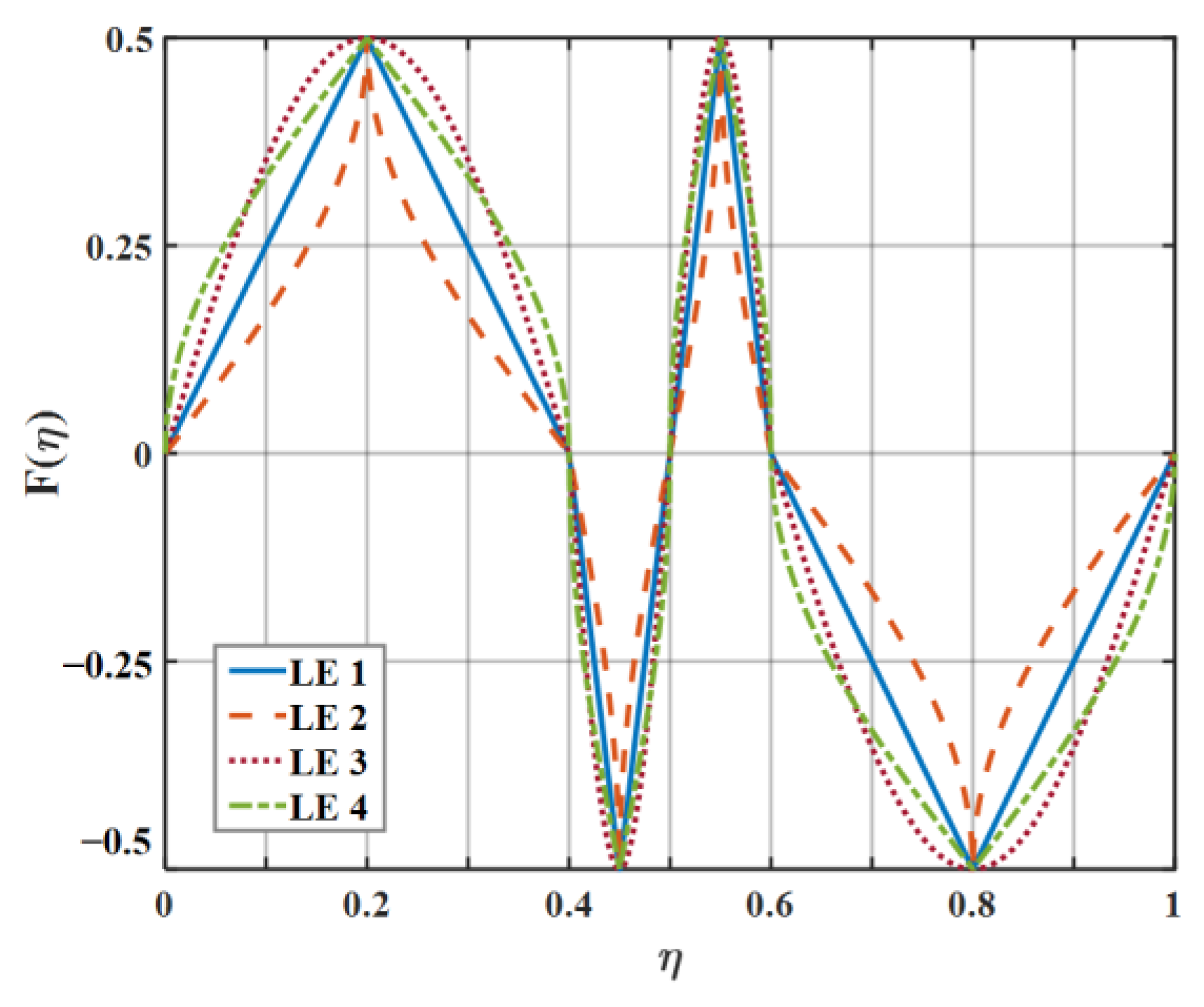
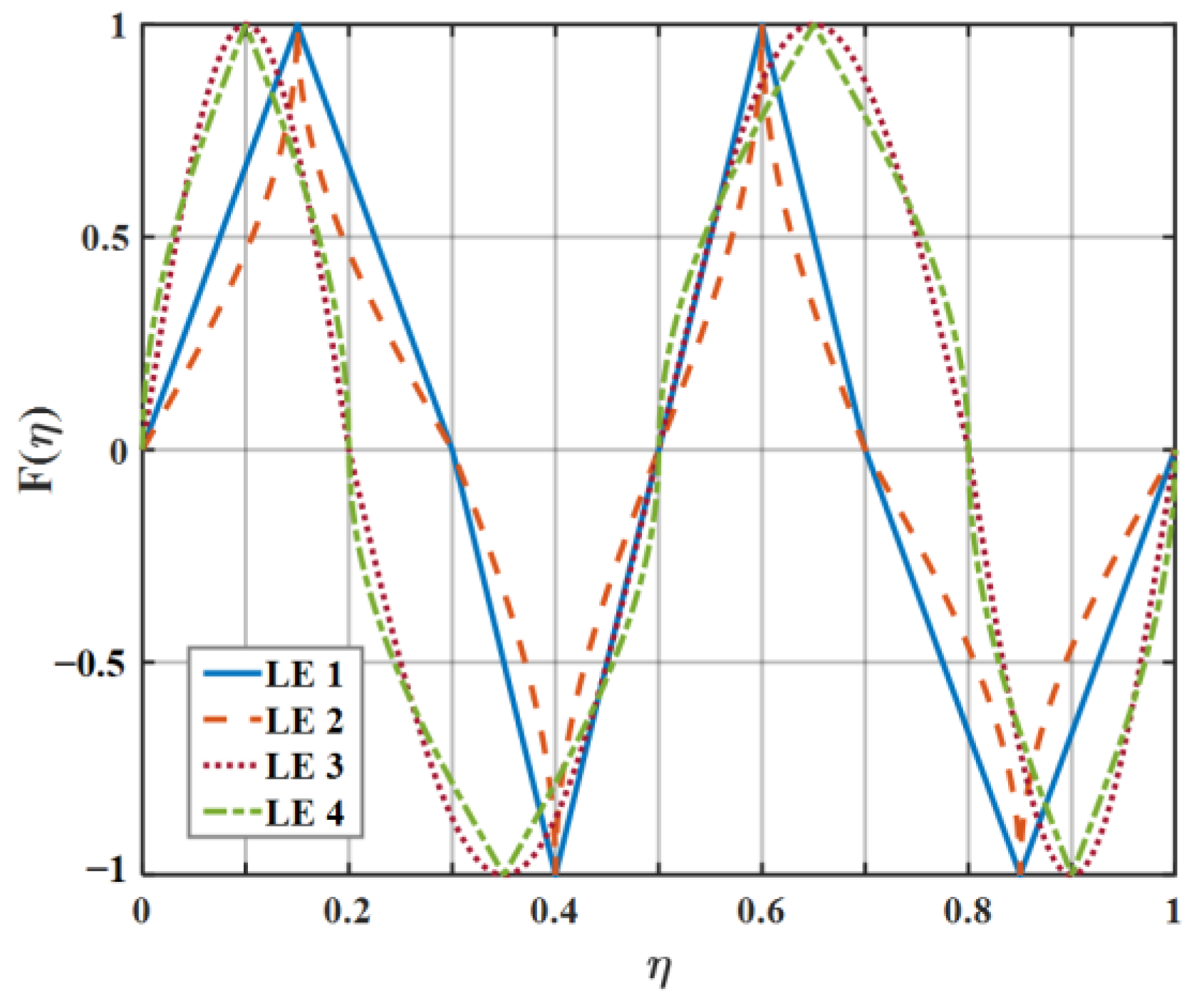
6.1. The Behavior of the Functions
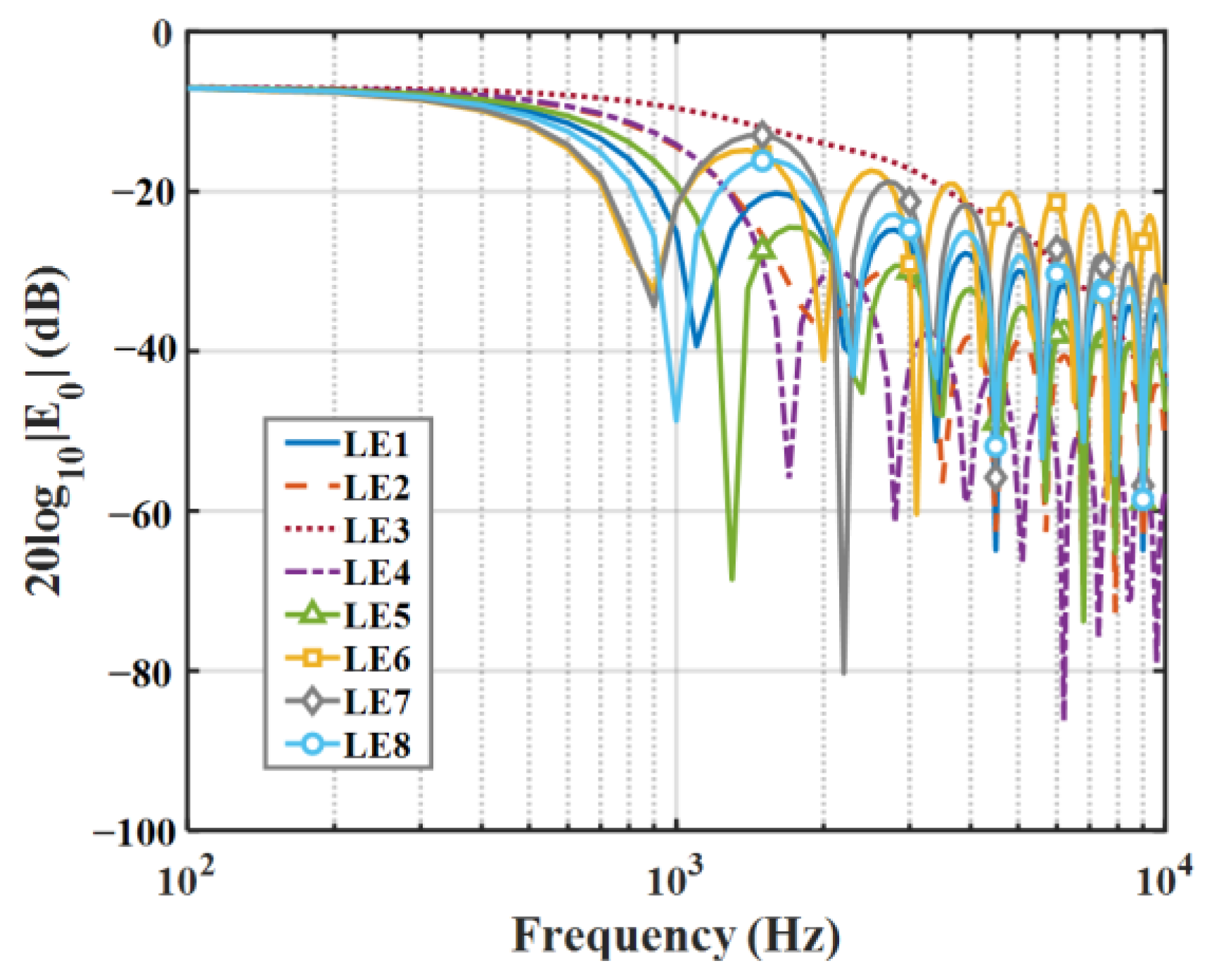
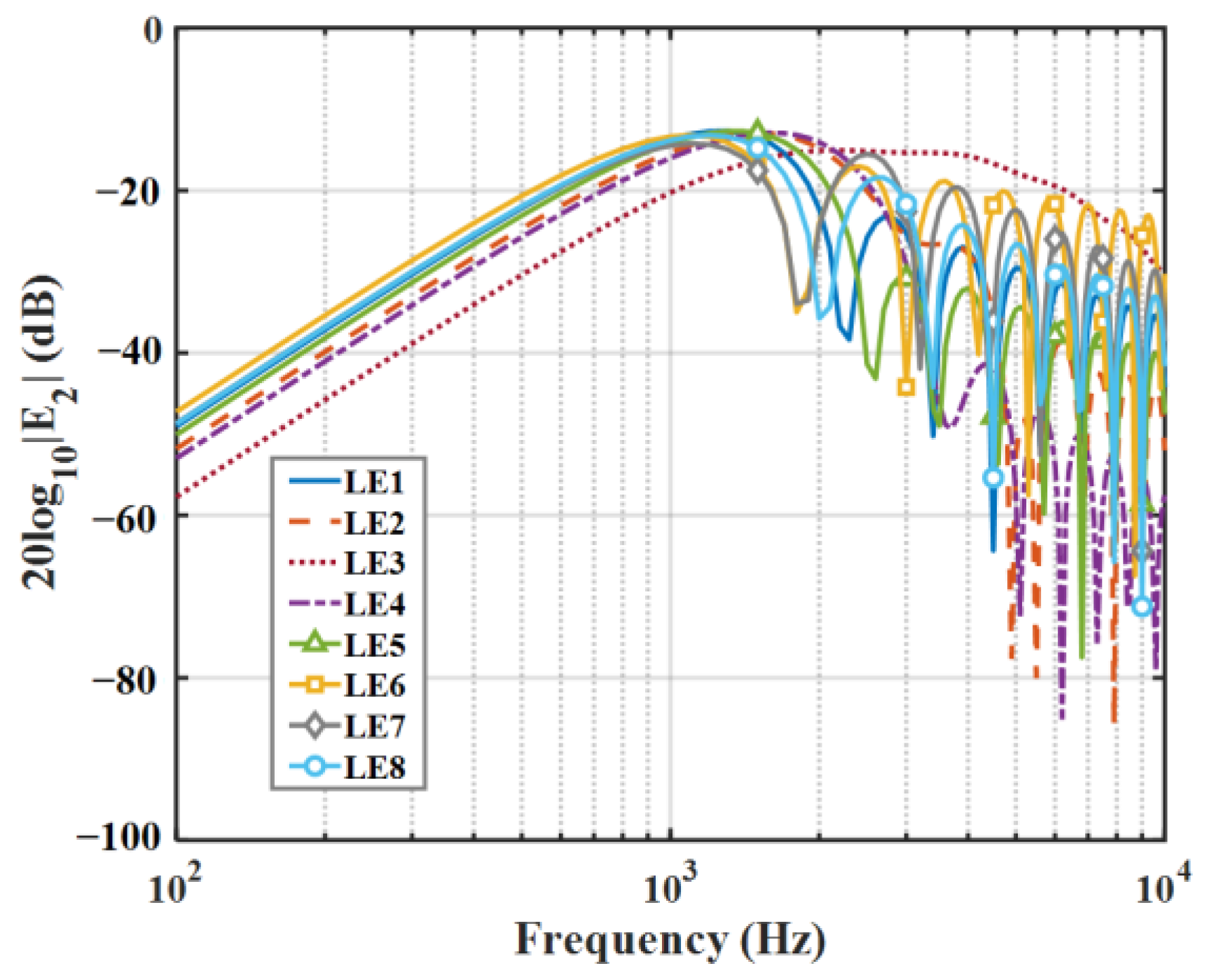
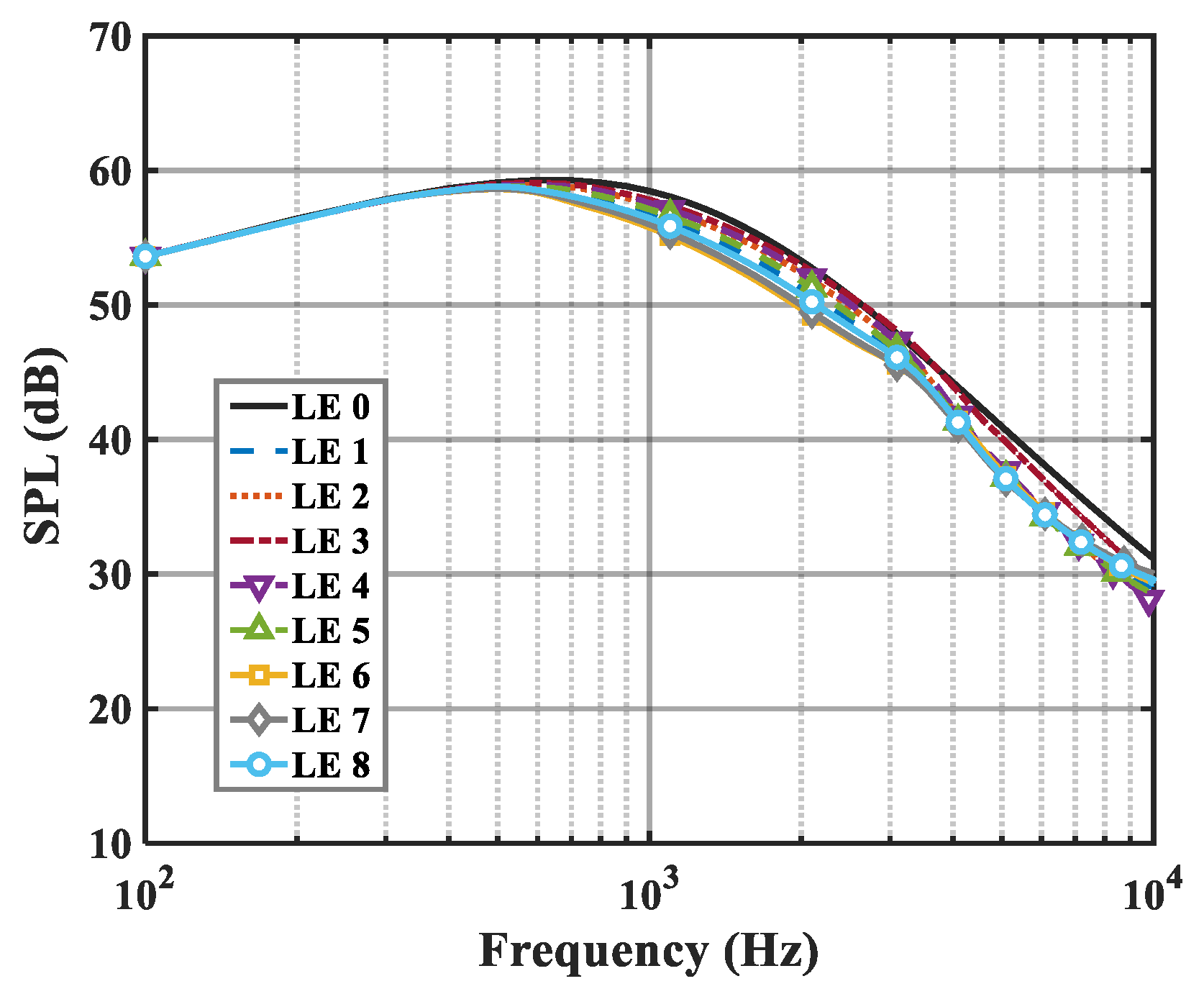
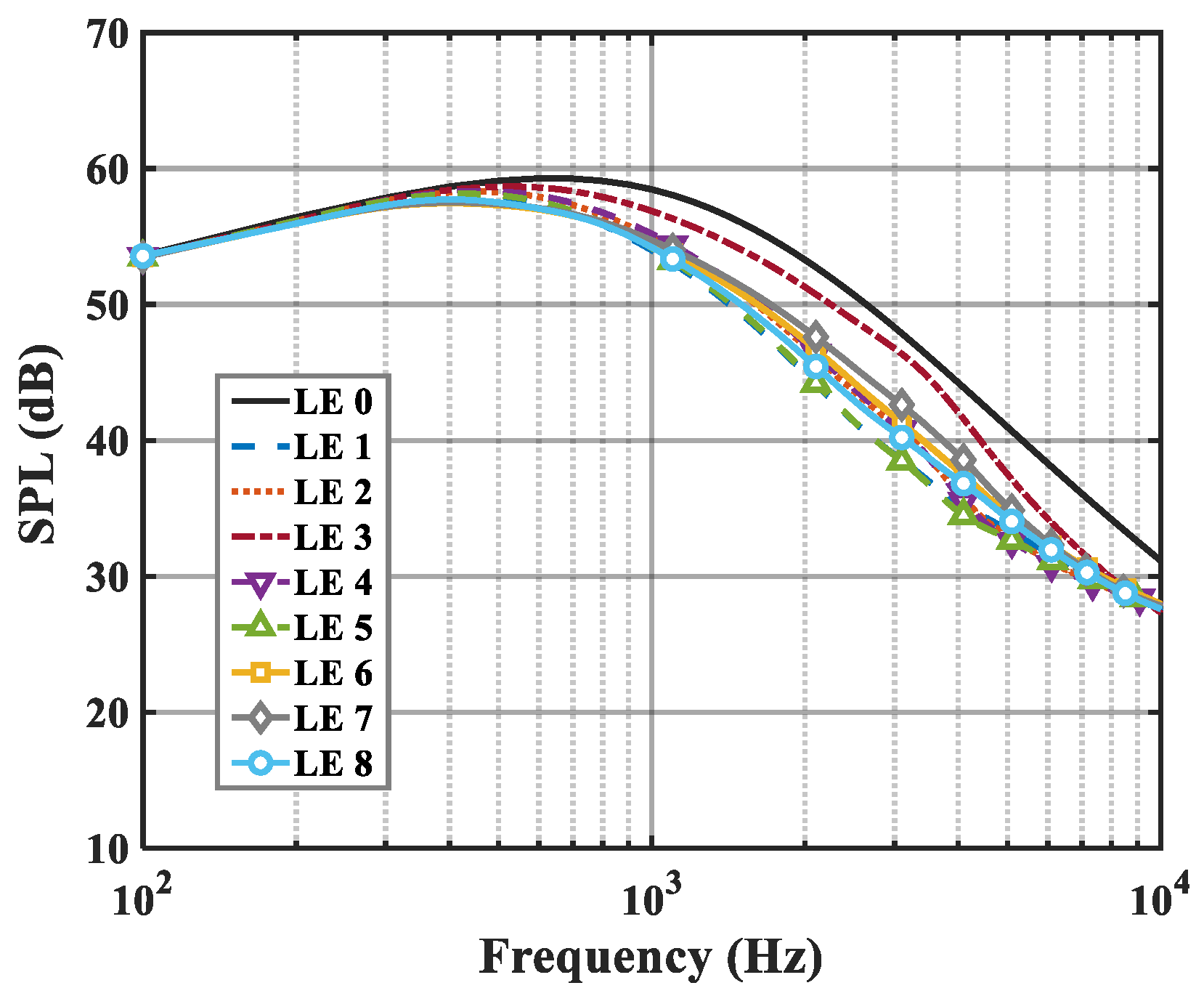
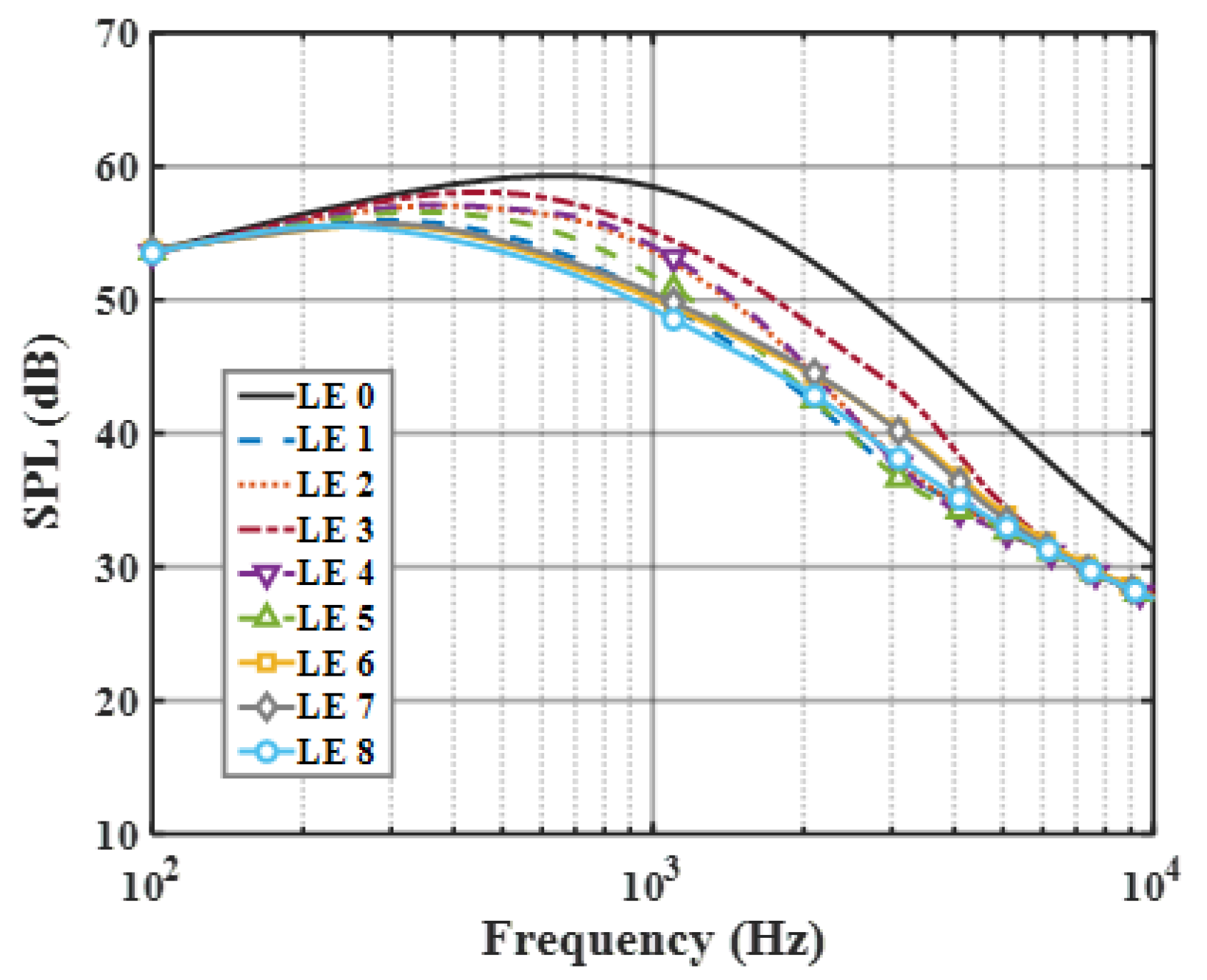
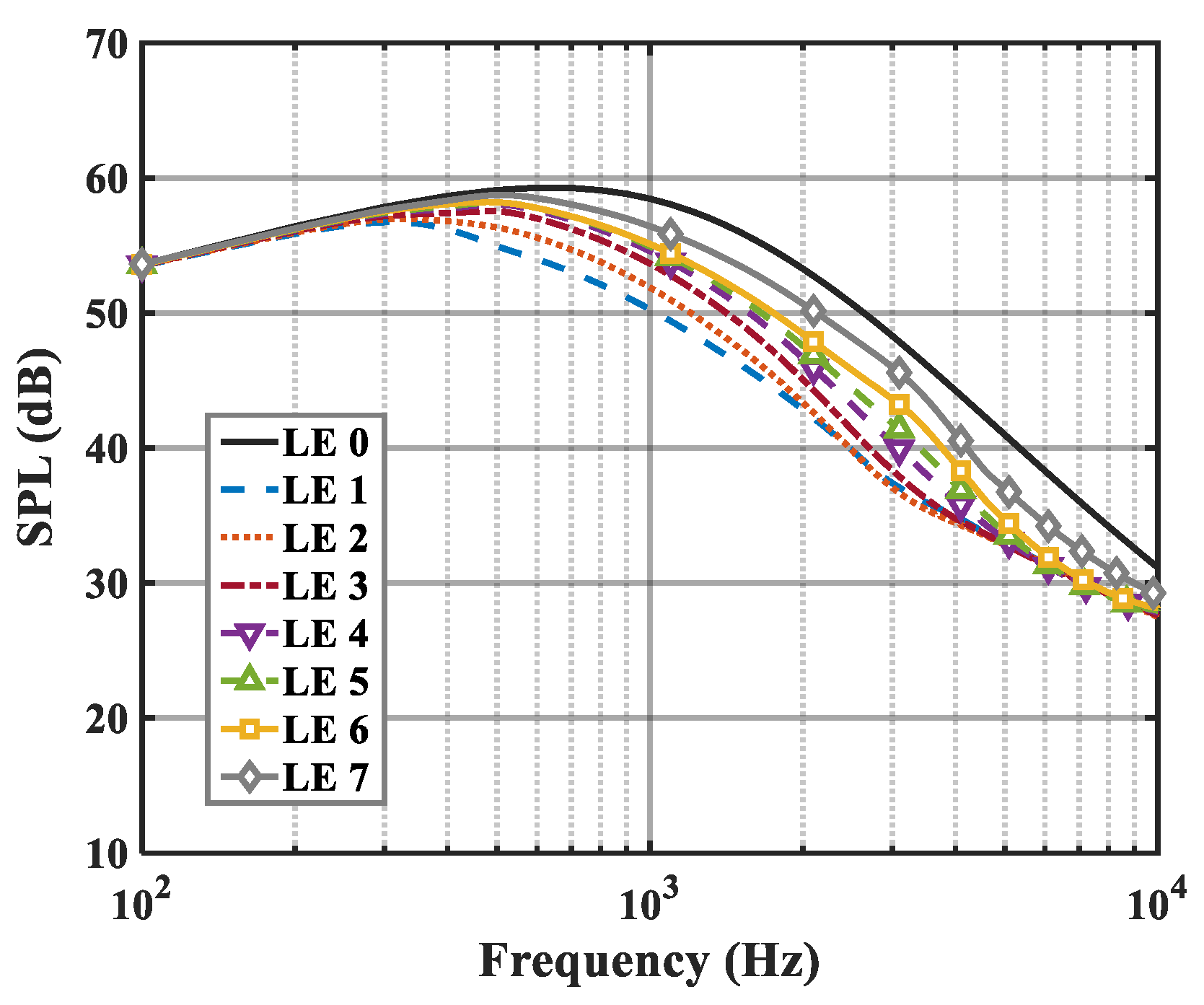
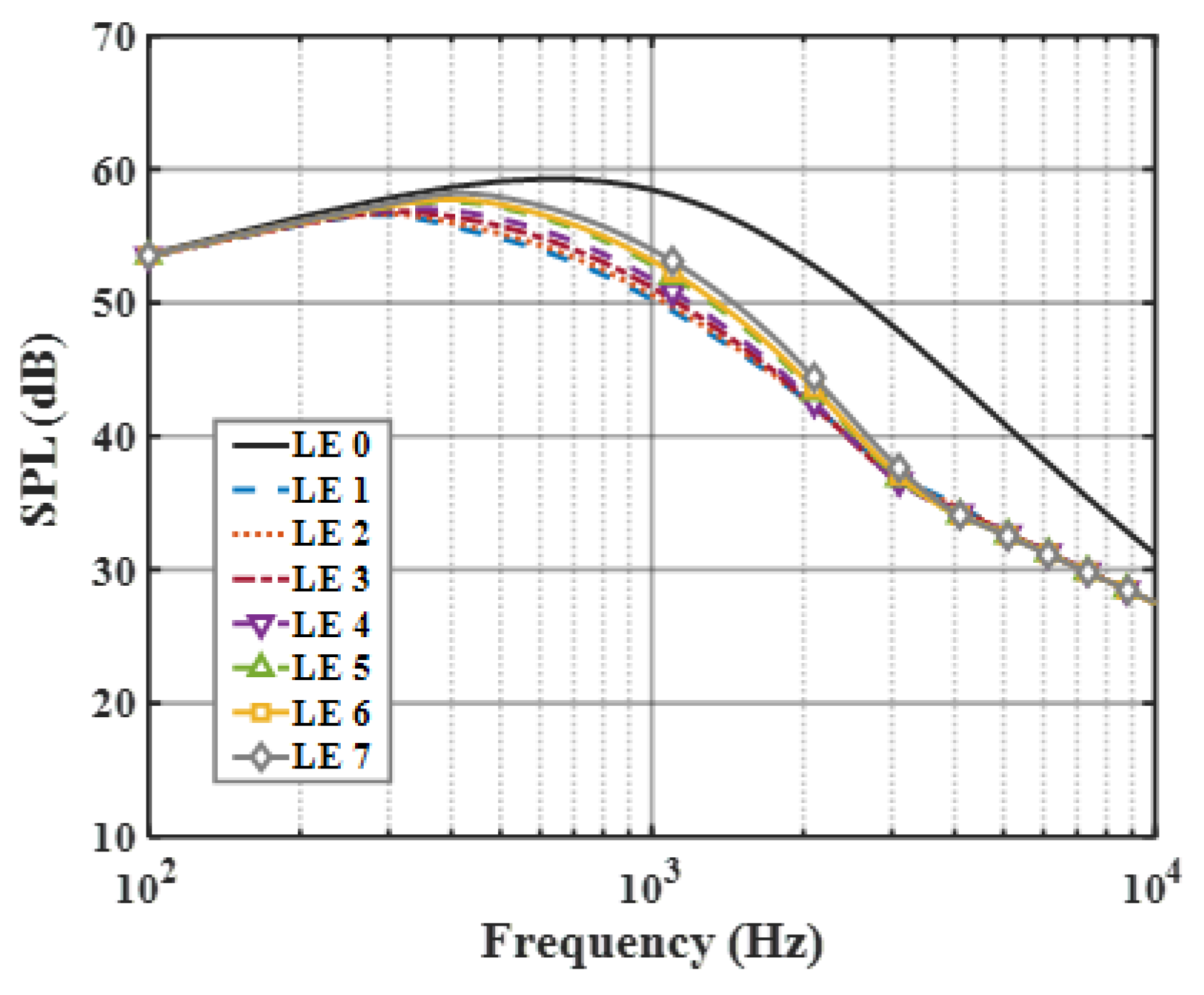
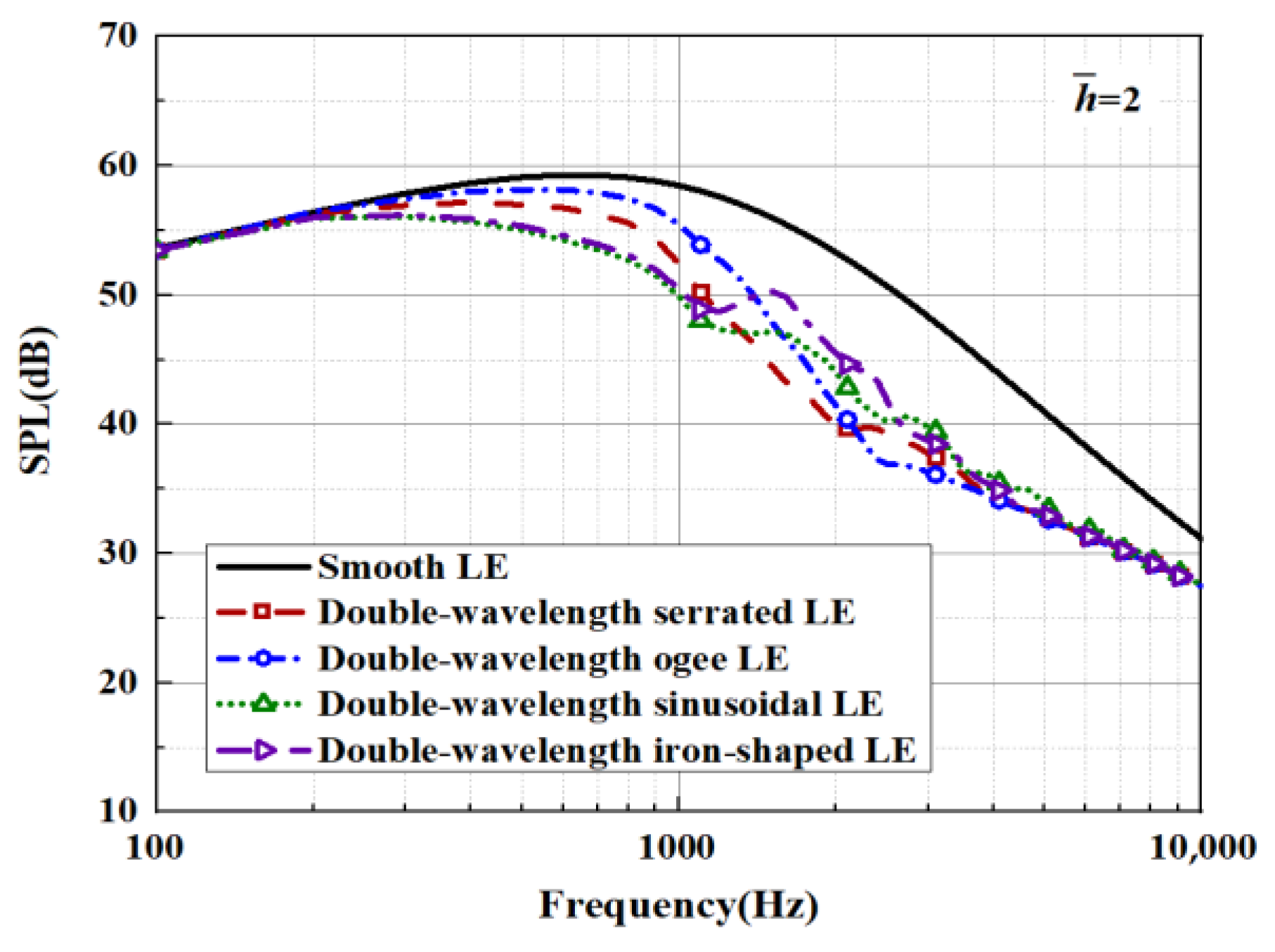
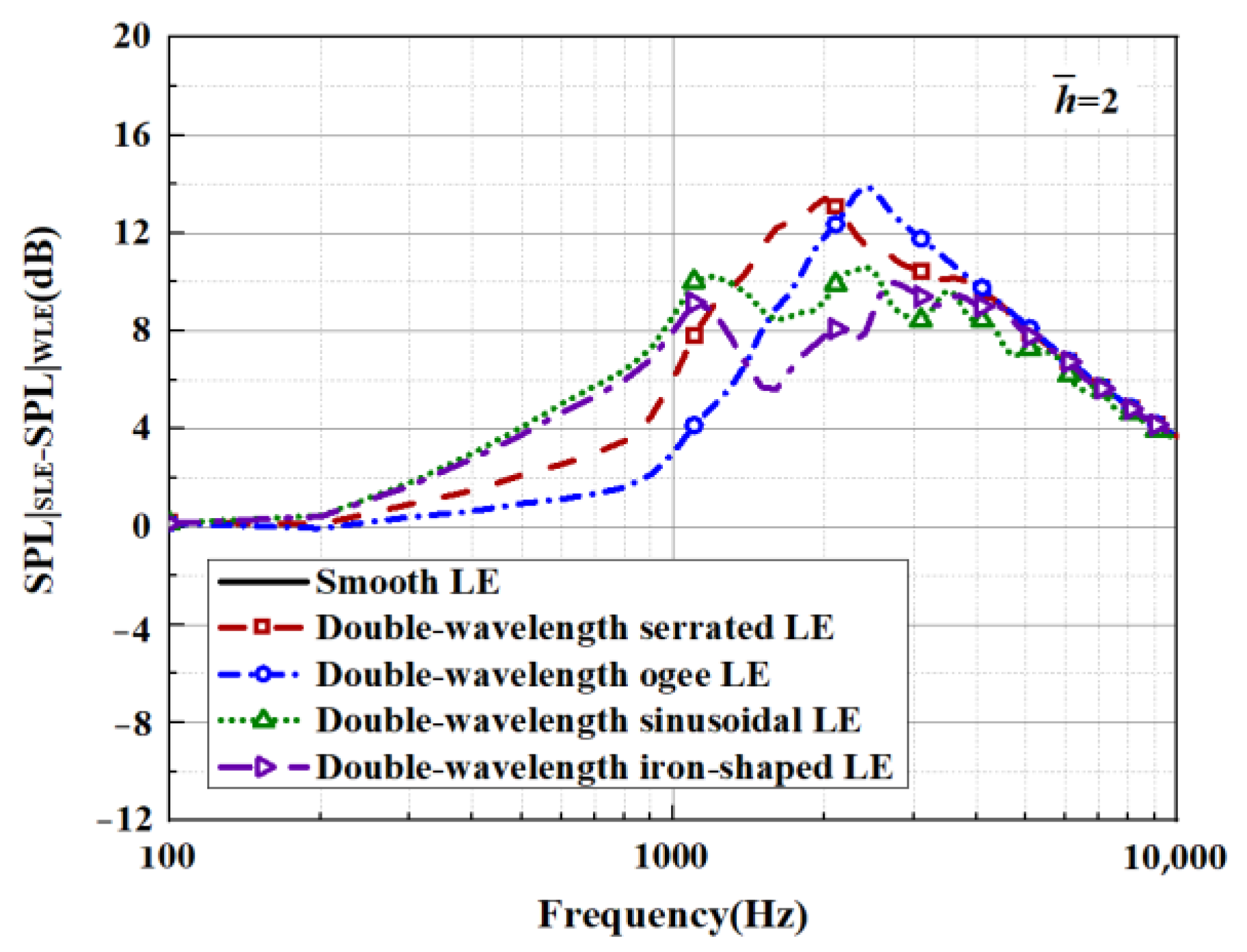
6.2. Sound Pressure Level (SPL)
6.3. Sound Pressure Level Integrated with Different Frequency Bands
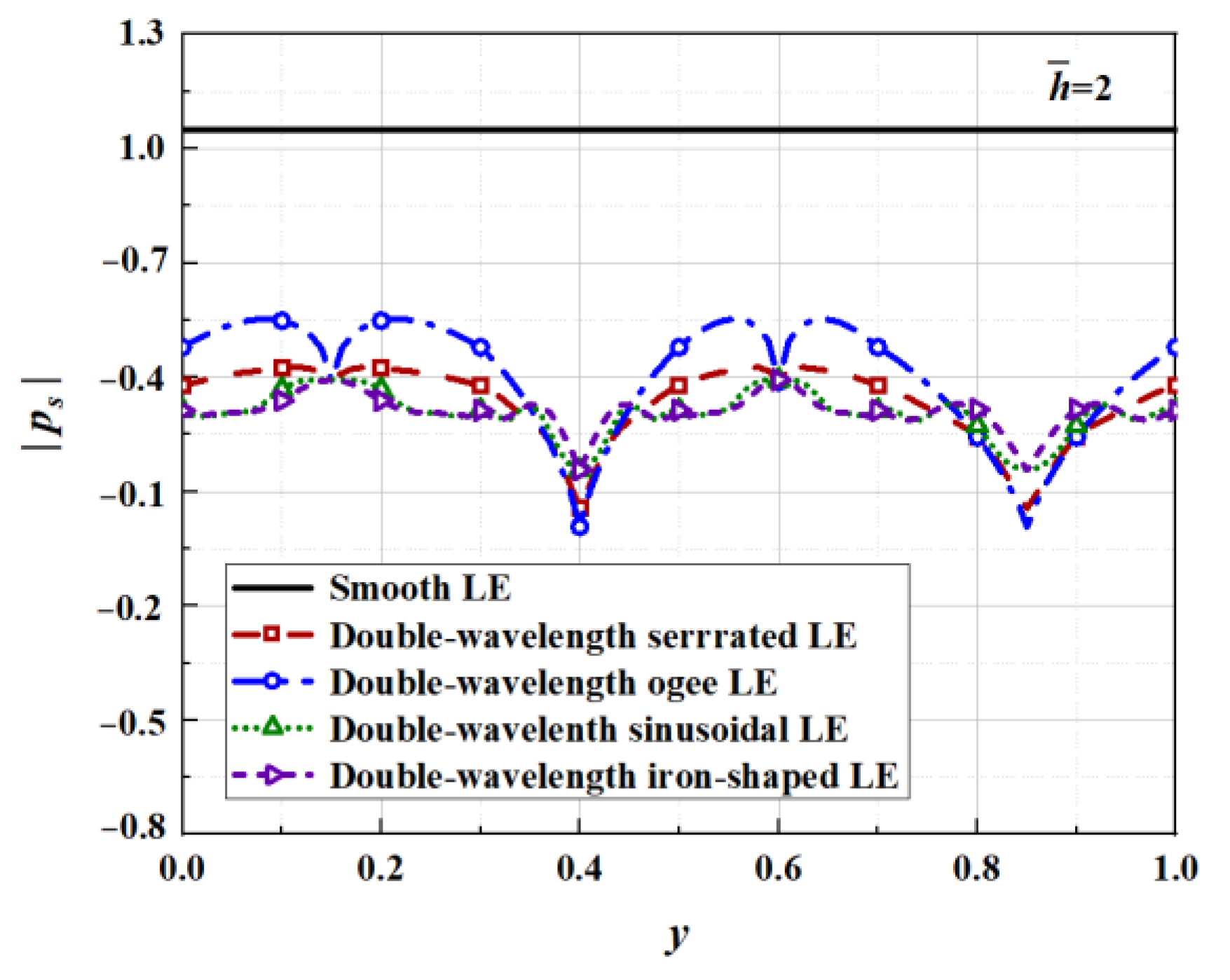
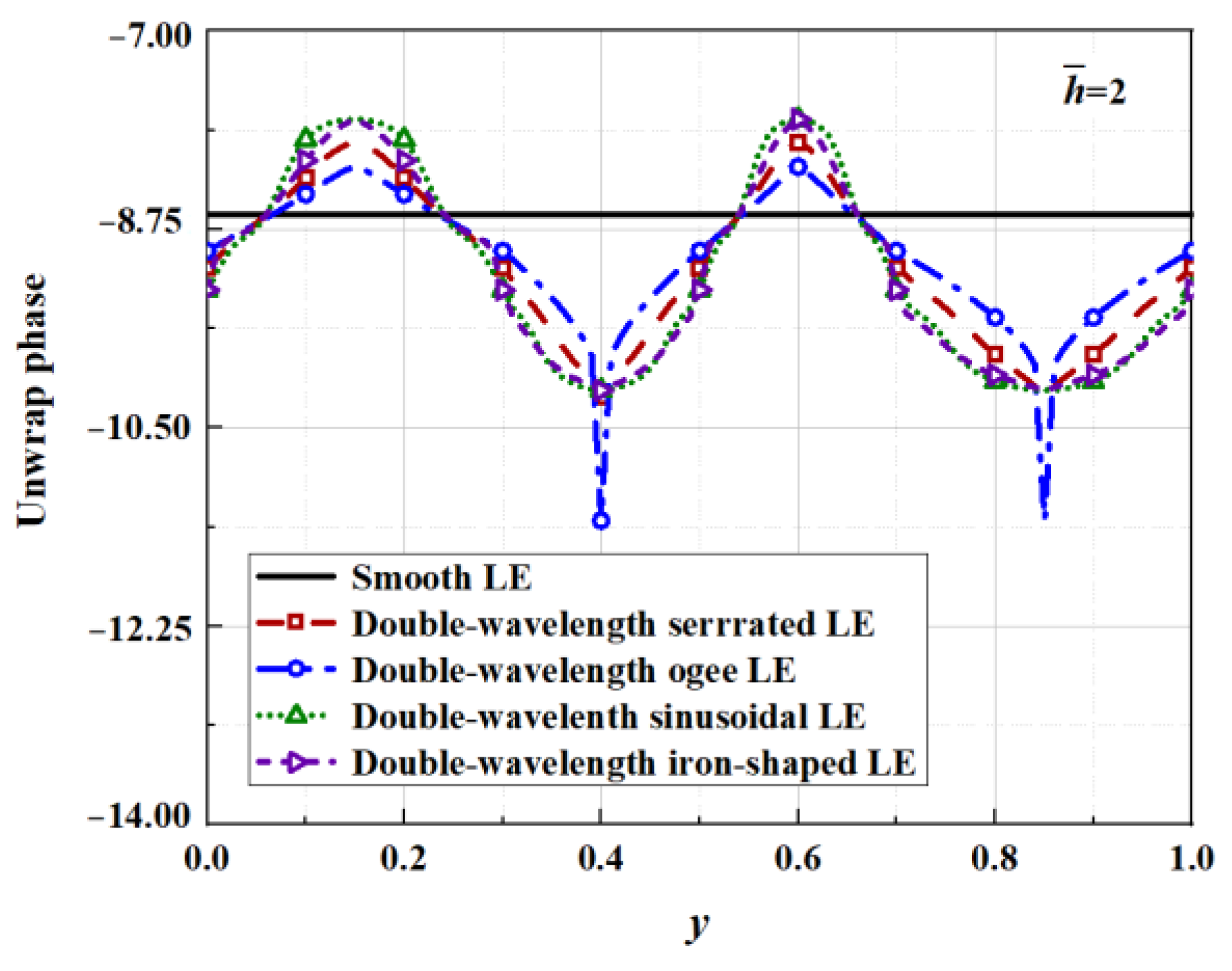
6.4. Surface Pressure and Phase Distributions
6.5. Directivity Characteristic of OASPL
7. Conclusions
- (1)
- Combined with the function associated with the shape factor, noise reduction at specific frequencies can be obtained in the low- and intermediate-frequency bands for serrations with a small curvature at non-smooth points. Moreover, it should be mentioned that spanwise-varying leading edges coping with a subsonic airflow interact with sharp serrations, resulting in an increase in additional broadband noise in the low-frequency regime compared with traditional serrations. And the performance in the high-frequency region is reversed. However, when the influence of trailing-edge self-noise is gradually enhanced with the increase in , the noise reduction advantage of large-curvature serrations at non-smooth points in the high-frequency region is weakened to a certain degree. For a single-value piecewise function in the unit wavelength range of 1 and 1/4 period, one must meet the condition in order to design a serration with excellent noise reduction performance at low and intermediate frequencies, while the opposite represents a good noise reduction level in the high-frequency region.
- (2)
- Aside from this, the acoustic optimality of double-wavelength serrations of different frequencies and phases is the key focused discussion. The noise reduction levels of shape factors, wavelengths, and amplitudes at different tip-to-root ratios are obtained through the design of trial numbers. It turns out that the shape factor was dominant at different tip-to-root ratios. The amplitude gradually replaces the wavelength with the increase in the tip-to-root ratio and transforms into the second most influential factor. Based on the premise of fixed wavelength and amplitude, the noise reduction level at performed best. This indicates that the larger the amplitude of the superimposed serrations, the more conducive it is to increasing the phase difference.
- (3)
- Both the sinusoidal function and the iron-shaped function performed well at different double-wavelength serrations, reducing the overall sound pressure level by up to 5.2 dB. Broadband noise in the 500–5000 Hz band was significantly reduced by 6.7 dB. The root-destructive interference was enhanced by the ogee-shaped serrations, increasing the local noise reduction effect and suppressing noise emissions in specific high-frequency regions. In the design of serrations, one can refer to the source cut-off mechanism of source radiation and introduce sharp structures such as narrow slits at the root to achieve local noise control, satisfying the design requirement of reducing high-frequency noise.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hersh, A.S.; Soderman, P.T.; Hayden, R.E. Investigation of Acoustic Effects of Leading-Edge Serrations on Airfoils. J. Aircr. 1974, 11, 197–202. [Google Scholar] [CrossRef]
- Graham, R.R. The Silent Flight of Owls. J. R. Aeronaut. Soc. 1934, 38, 837–843. [Google Scholar] [CrossRef]
- Rong, J.; Liu, H. Aeroacoustic Interaction between Owl-Inspired Trailing-Edge Fringes and Leading-Edge Serrations. Phys. Fluids 2022, 34, 011907. [Google Scholar] [CrossRef]
- Hu, H.; Yang, Y.; Liu, Y.; Liu, X.; Wang, Y. Aerodynamic and Aeroacoustic Investigations of Multi-Copter Rotors with Leading Edge Serrations during Forward Flight. Aerosp. Sci. Technol. 2021, 112, 106669. [Google Scholar] [CrossRef]
- Bampanis, G.; Roger, M.; Moreau, S. On a Three-Dimensional Investigation of Airfoil Turbulence-Impingement Noise and Its Reduction by Leading-Edge Tubercles. J. Sound Vib. 2022, 520, 116635. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, K.S.; Lacagnina, G.; Chaitanya, P.; Joseph, P.; Hasheminejad, S.M.; Pei Chong, T.; Shahab, M.F.; Omidyeganeh, M.; Pinelli, A. Aerodynamic and Aeroacoustic Optimization of Leading-Edge Undulation of a NACA 65(12)-10 Airfoil. AIAA J. 2022, 60, 2342–2353. [Google Scholar] [CrossRef]
- Krömer, F.; Czwielong, F.; Becker, S. Experimental Investigation of the Sound Emission of Skewed Axial Fans with Leading-Edge Serrations. AIAA J. 2019, 57, 5182–5196. [Google Scholar] [CrossRef]
- Chaitanya, P.; Joseph, P.; Narayanan, S.; Vanderwel, C.; Turner, J.; Kim, J.W.; Ganapathisubramani, B. Performance and Mechanism of Sinusoidal Leading-Edge Serrations for the Reduction of Turbulence–Aerofoil Interaction Noise. J. Fluid Mech. 2017, 818, 435–464. [Google Scholar] [CrossRef]
- Lyu, B.; Ayton, L.J.; Chaitanya, P. On the Acoustic Optimality of Leading-Edge Serration Profiles. J. Sound Vib. 2019, 462, 114923. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Li, D. Noise Reduction Mechanism of Airfoils with Leading-Edge Serrations and Surface Ridges Inspired by Owl Wings. Phys. Fluids 2021, 33, 015123. [Google Scholar] [CrossRef]
- Chaitanya, P.; Joseph, P.; Narayanan, S.; Kim, J.W. Aerofoil Broadband Noise Reductions through Double-Wavelength Leading-Edge Serrations: A New Control Concept. J. Fluid Mech. 2018, 855, 131–151. [Google Scholar] [CrossRef]
- Kim, J.W.; Haeri, S.; Joseph, P.F. On the Reduction of Aerofoil–Turbulence Interaction Noise Associated with Wavy Leading Edges. J. Fluid Mech. 2016, 792, 526–552. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Ghassabi, M.; Talebitooti, R. A Review Approach for Sound Propagation Prediction of Plate Constructions. Arch. Comput. Methods Eng. 2021, 28, 2817–2843. [Google Scholar] [CrossRef]
- Amiet, R.K. High Frequency Thin-Airfoil Theory for Subsonic Flow. AIAA J. 1976, 14, 1076–1082. [Google Scholar] [CrossRef]
- Lyu, B.; Azarpeyvand, M. On the Noise Prediction for Serrated Leading Edges. J. Fluid Mech. 2017, 826, 205–234. [Google Scholar] [CrossRef]
- Huang, X. Theoretical Model of Acoustic Scattering from a Flat Plate with Serrations. J. Fluid Mech. 2017, 819, 228–257. [Google Scholar] [CrossRef]
- Envia, E. Influence of Vane Sweep on Rotor-Stator Interaction Noise. Ph.D. Thesis, The University of Arizona, Tucson, AZ, USA, 1988. [Google Scholar]
- Ayton, L.J.; Kim, J.W. An Analytic Solution for the Noise Generated by Gust–Aerofoil Interaction for Plates with Serrated Leading Edges. J. Fluid Mech. 2018, 853, 515–536. [Google Scholar] [CrossRef]
- Chaitanya, P.; Narayanan, S.; Joseph, P.; Kim, J.W. Leading Edge Serration Geometries for Significantly Enhanced Leading Edge Noise Reductions. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar]
- Mathews, J.; Peake, N. Noise Generation by Turbulence Interacting with an Aerofoil with a Serrated Leading Edge. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015. [Google Scholar]
- Ayton, L.J.; Chaitanya, P. An Analytical and Experimental Investigation of Aerofoil–Turbulence Interaction Noise for Plates with Spanwise-Varying Leading Edges. J. Fluid Mech. 2019, 865, 137–168. [Google Scholar] [CrossRef]
- Lyu, B.; Ayton, L.J. Rapid Noise Prediction Models for Serrated Leading and Trailing Edges. J. Sound Vib. 2020, 469, 115136. [Google Scholar] [CrossRef]
- Kholodov, P.; Moreau, S. Optimization of Trailing-Edge Serrations with and without Slits for Broadband Noise Reduction. J. Sound Vib. 2021, 490, 115736. [Google Scholar] [CrossRef]
- Amiet, R.K. Acoustic Radiation from an Airfoil in a Turbulent Stream. J. Sound Vib. 1975, 41, 407–420. [Google Scholar] [CrossRef]
- Narayanan, S.; Chaitanya, P.; Haeri, S.; Joseph, P.; Kim, J.W.; Polacsek, C. Airfoil Noise Reductions through Leading Edge Serrations. Phys. Fluids 2015, 27, 025109. [Google Scholar] [CrossRef]
- Glegg, S.; Devenport, W. Aeroacoustics of Low Mach Number Flows; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil Self-Noise and Prediction; NASA Reference Publication (RP): Washington, DC, USA, 1989; ISBN 89N25673. [Google Scholar]
- Ffowcs Williams, J.; Hawkings, D. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Phil. Trans. R. Soc. Lond. A 1969, 264, 321–342. [Google Scholar] [CrossRef]
- Devenport, W.J.; Burdisso, R.A.; Borgoltz, A.; Ravetta, P.A.; Barone, M.F.; Brown, K.A.; Morton, M.A. The Kevlar-Walled Anechoic Wind Tunnel. J. Sound Vib. 2013, 332, 3971–3991. [Google Scholar] [CrossRef]
- Howe, M.S. Aerodynamic Noise of a Serrated Trailing Edge. J. Fluids Struct. 1991, 5, 33–45. [Google Scholar] [CrossRef]




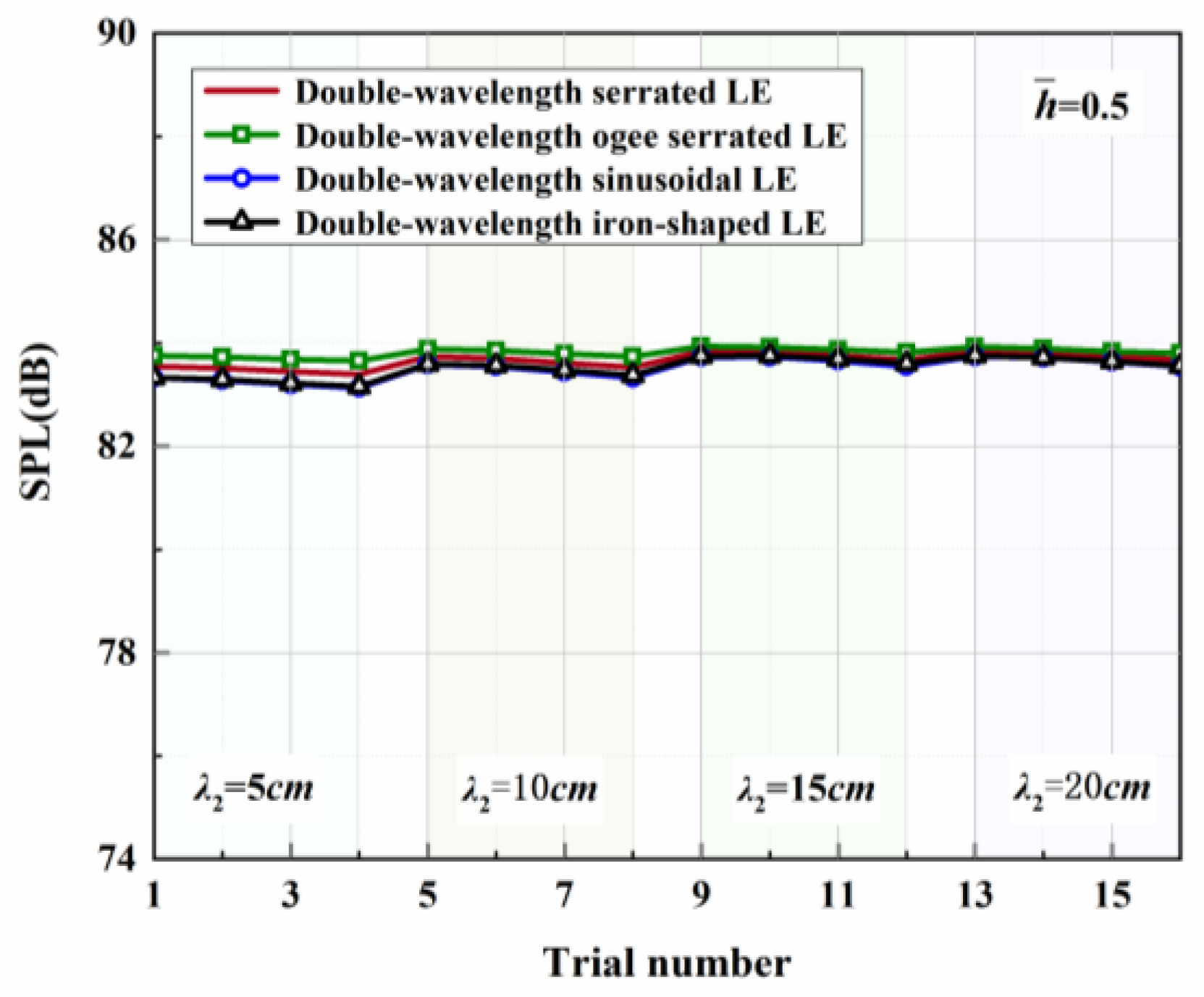
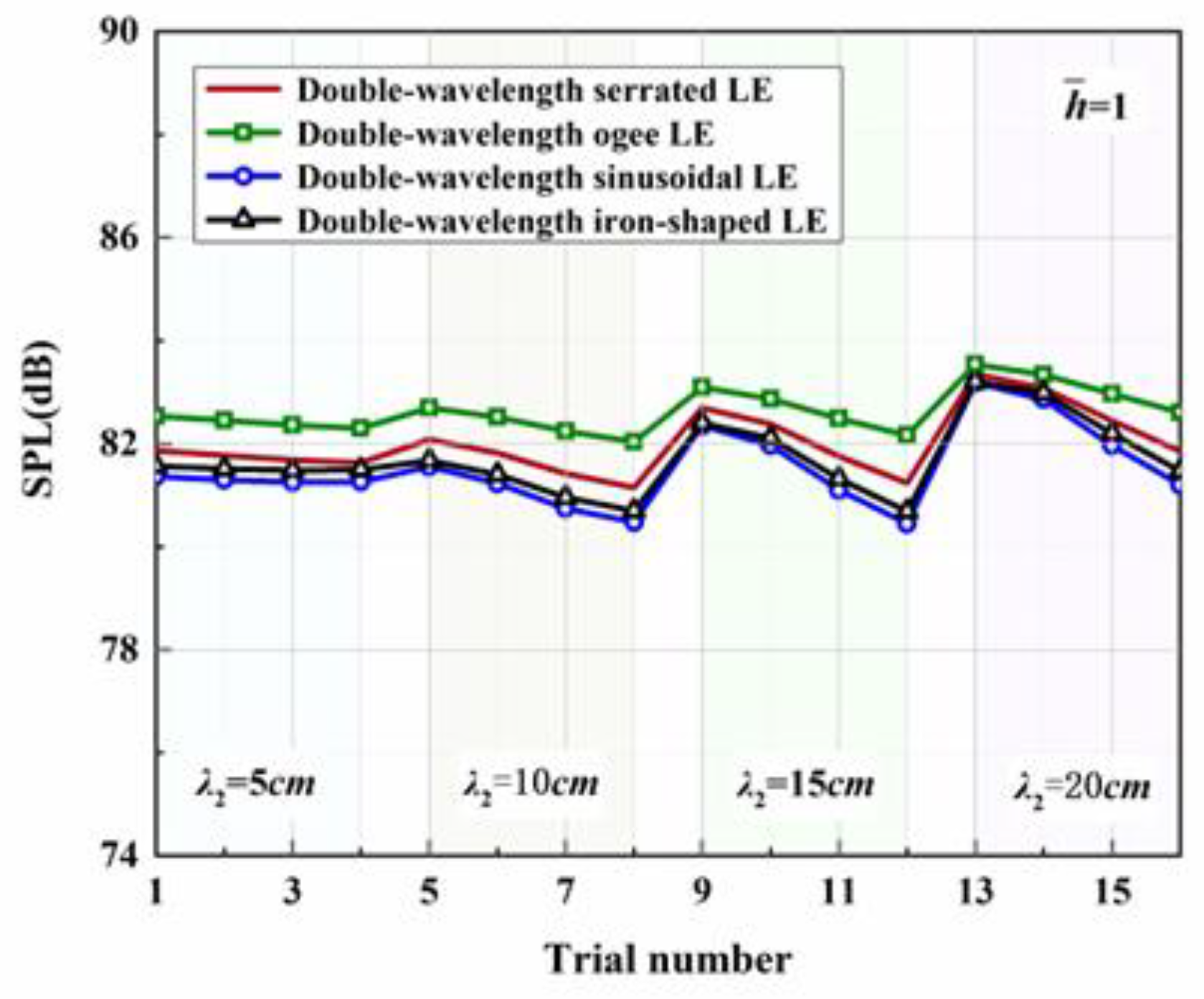

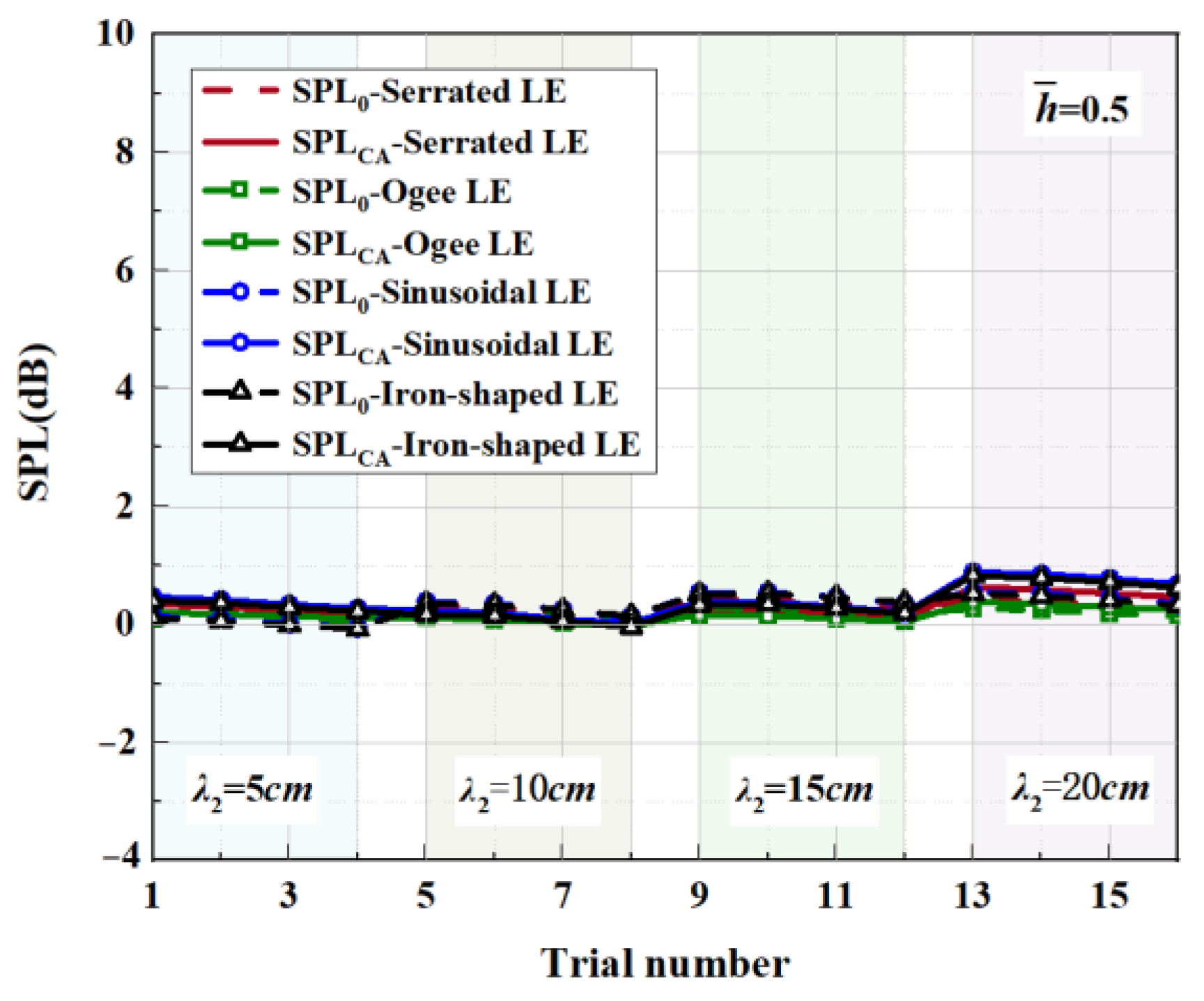

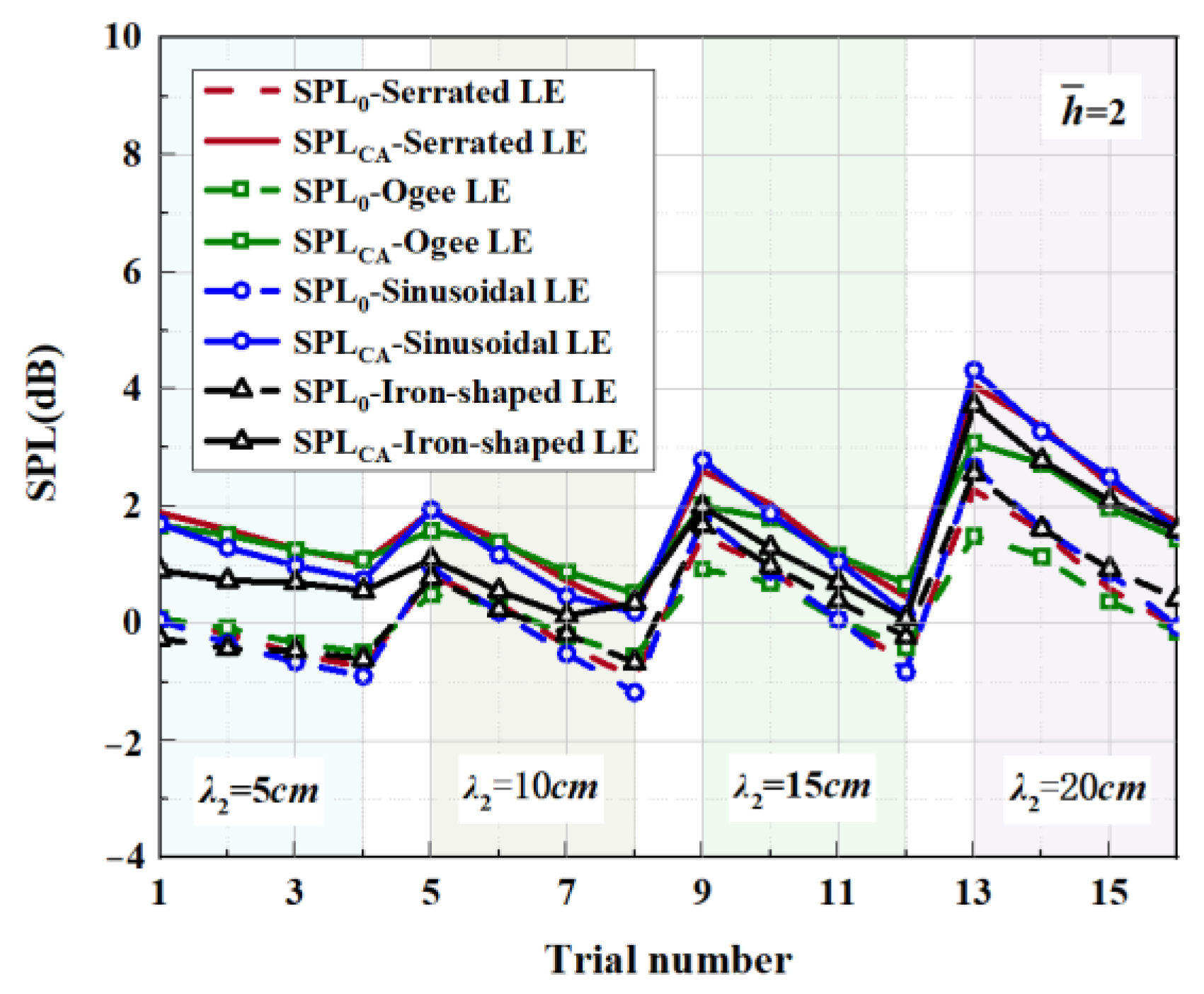



| Parameters | Shape | ||||
|---|---|---|---|---|---|
| Factors | A | B | C | D | E |
| Level 1 | Serrated | 0.2 | 0.2 | 0.8 | 1 |
| Level 2 | Ogee | 0.4 | 0.5 | 0.6 | 1 |
| Level 3 | Sinusoidal | 0.6 | 0.8 | 0.4 | 1 |
| Level 4 | Iron-shaped | 0.8 | 1 | 0.2 | 1 |
| Trial Number | Code Name | SPL (dB) | SPL1 | SPL2 | SPLCA | Results | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A1B1C1 | 0.2 | 0.2 | 81.3600 | −0.3541 | −2.3381 | −1.3461 | I1 |
| 2 | A1B1C2 | 0.2 | 0.5 | 81.2934 | −0.4207 | −1.2235 | 0.8221 | I2 |
| 3 | A1B1C3 | 0.2 | 0.8 | 81.2534 | −0.4607 | 0.0759 | 0.1924 | I3 |
| 4 | A1B1C4 | 0.2 | 1 | 81.2595 | −0.4546 | 0.9309 | 0.2382 | I4 |
| 5 | A1B2C1 | 0.4 | 0.2 | 81.5507 | 0.7586 | −2.2048 | 0.7231 | I5 |
| 6 | A1B2C2 | 0.4 | 0.5 | 81.2268 | 0.4347 | −1.4466 | 0.5060 | I6 |
| 7 | A1B2C3 | 0.4 | 0.8 | 80.7423 | −0.0498 | −0.5733 | −0.3116 | I7 |
| 8 | A1B2C4 | 0.4 | 1 | 80.4740 | −0.3181 | −0.0542 | −0.1862 | I8 |
| 9 | A1B3C1 | 0.6 | 0.2 | 82.3493 | 1 8211 | −1.4556 | 0.1828 | I9 |
| 10 | A1B3C2 | 0.6 | 0.5 | 81.9631 | 1.4349 | −0.9077 | 0.2636 | I10 |
| 11 | A1B3C3 | 0.6 | 0.8 | 81.0968 | 0.5686 | −0.4463 | 0.0612 | I11 |
| 12 | A1B3C4 | 0.6 | 1 | 80.4483 | −0.0799 | −0.3438 | −0.2119 | I12 |
| 13 | A1B4C1 | 0.8 | 0.2 | 83.1816 | 2.8530 | −0.7657 | 1.0437 | I13 |
| 14 | A1B4C2 | 0.8 | 0.5 | 82.8609 | 2 5323 | −0.2522 | 1.1401 | I14 |
| 15 | A1B4C3 | 0.8 | 0.8 | 81.9630 | 1.6344 | −0.1386 | 0.7479 | I15 |
| 16 | A1B4C4 | 0.8 | 1 | 81.1964 | 0.8678 | −0.5177 | 0.1751 | I16 |
| 17 | original | — | — | 84.0530 | — | — | — | — |
| Factors | A | B | C |
|---|---|---|---|
| 0.809 | 0.342 | 0.171 | |
| 3.092 | 1.096 | 1.027 | |
| 4.301 | 1.481 | 1.627 | |
| Order of the factors () | A > B > C | ||
| Order of the factors (1) | A > B > C | ||
| Order of the factors (2) | A > C > B | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, X.; Tian, C.; Li, D. Numerical Analysis of Broadband Noise Generated by an Airfoil with Spanwise-Varying Leading Edges. Biomimetics 2024, 9, 229. https://doi.org/10.3390/biomimetics9040229
Wang L, Liu X, Tian C, Li D. Numerical Analysis of Broadband Noise Generated by an Airfoil with Spanwise-Varying Leading Edges. Biomimetics. 2024; 9(4):229. https://doi.org/10.3390/biomimetics9040229
Chicago/Turabian StyleWang, Lei, Xiaomin Liu, Chenye Tian, and Dian Li. 2024. "Numerical Analysis of Broadband Noise Generated by an Airfoil with Spanwise-Varying Leading Edges" Biomimetics 9, no. 4: 229. https://doi.org/10.3390/biomimetics9040229
APA StyleWang, L., Liu, X., Tian, C., & Li, D. (2024). Numerical Analysis of Broadband Noise Generated by an Airfoil with Spanwise-Varying Leading Edges. Biomimetics, 9(4), 229. https://doi.org/10.3390/biomimetics9040229






