Effect of Frequency–Amplitude Parameter and Aspect Ratio on Propulsion Performance of Underwater Flapping-Foil
Abstract
:1. Introduction
2. Materials and Methods
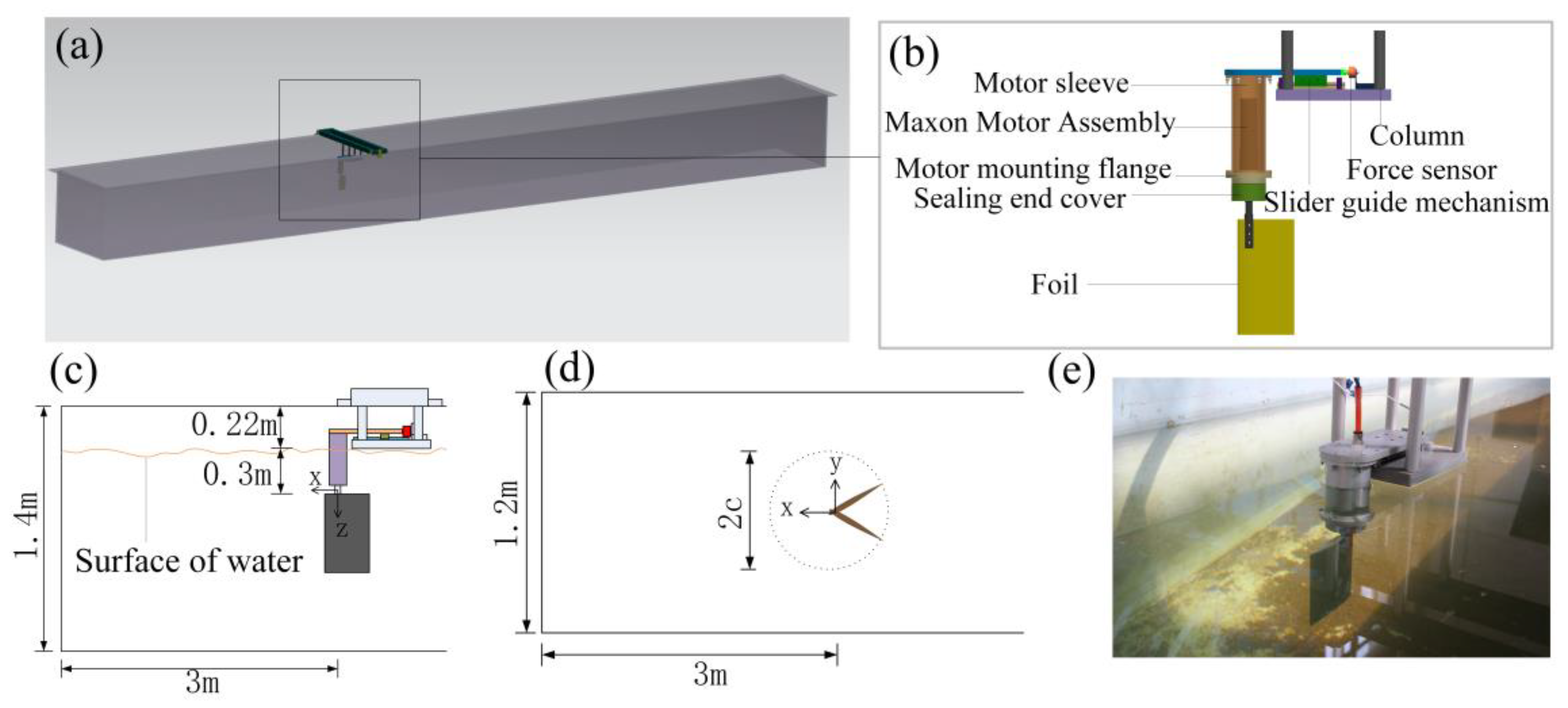
2.1. Experiment Setup
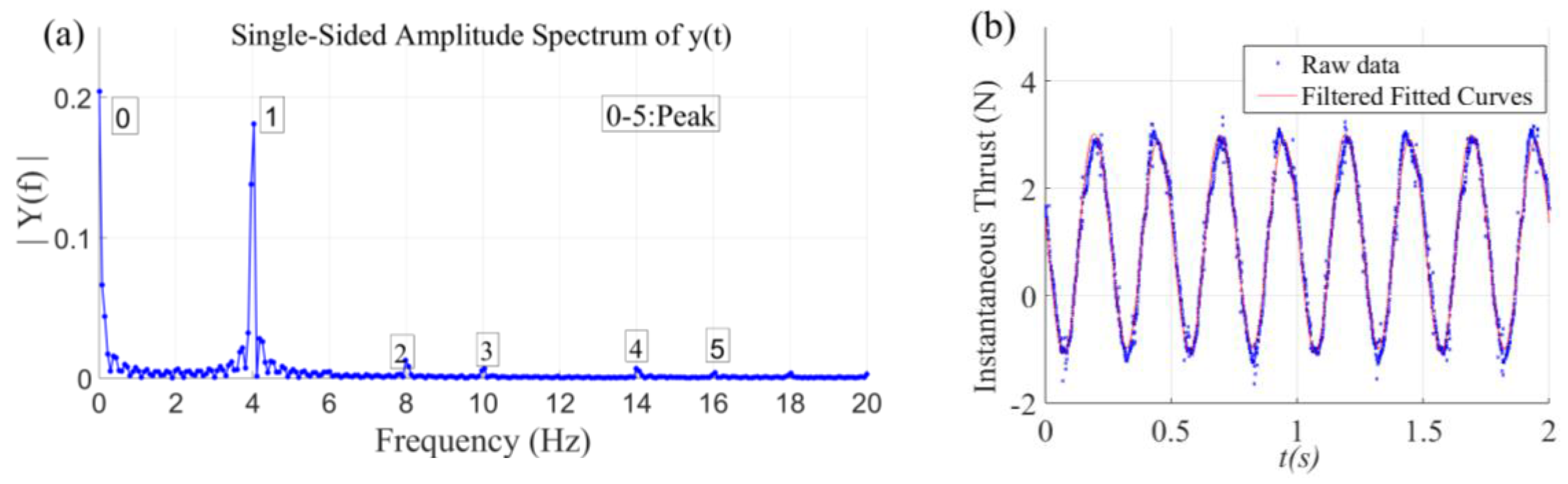
2.2. Data Processing Method
3. Results and Discussion
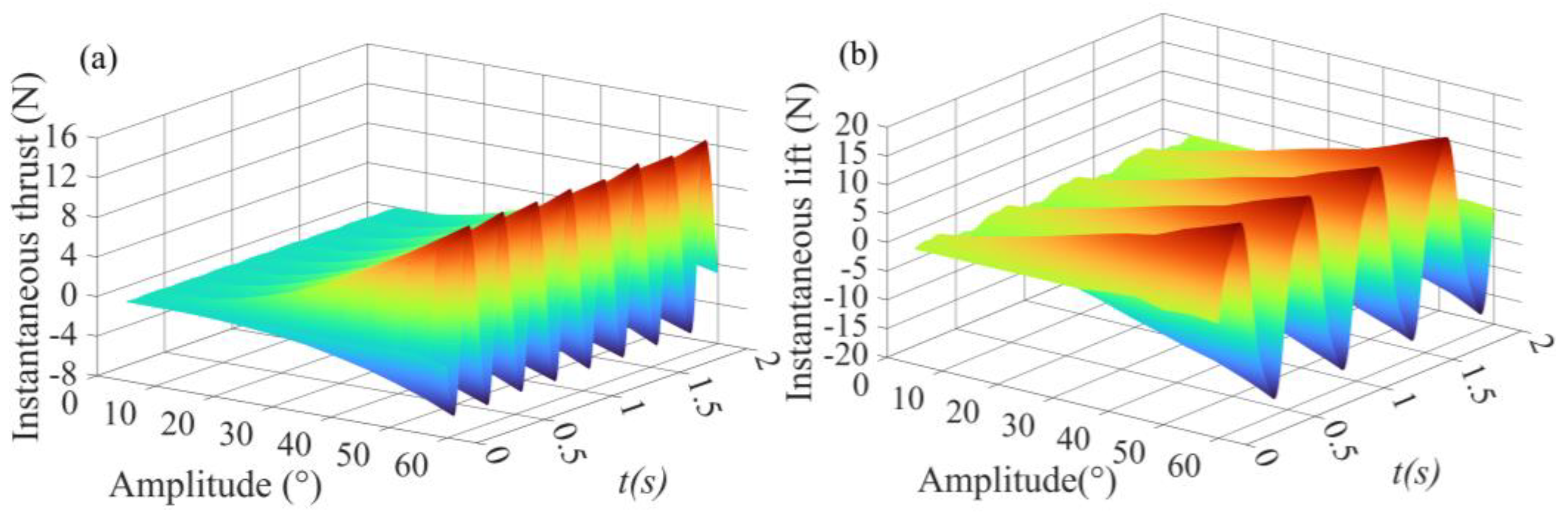
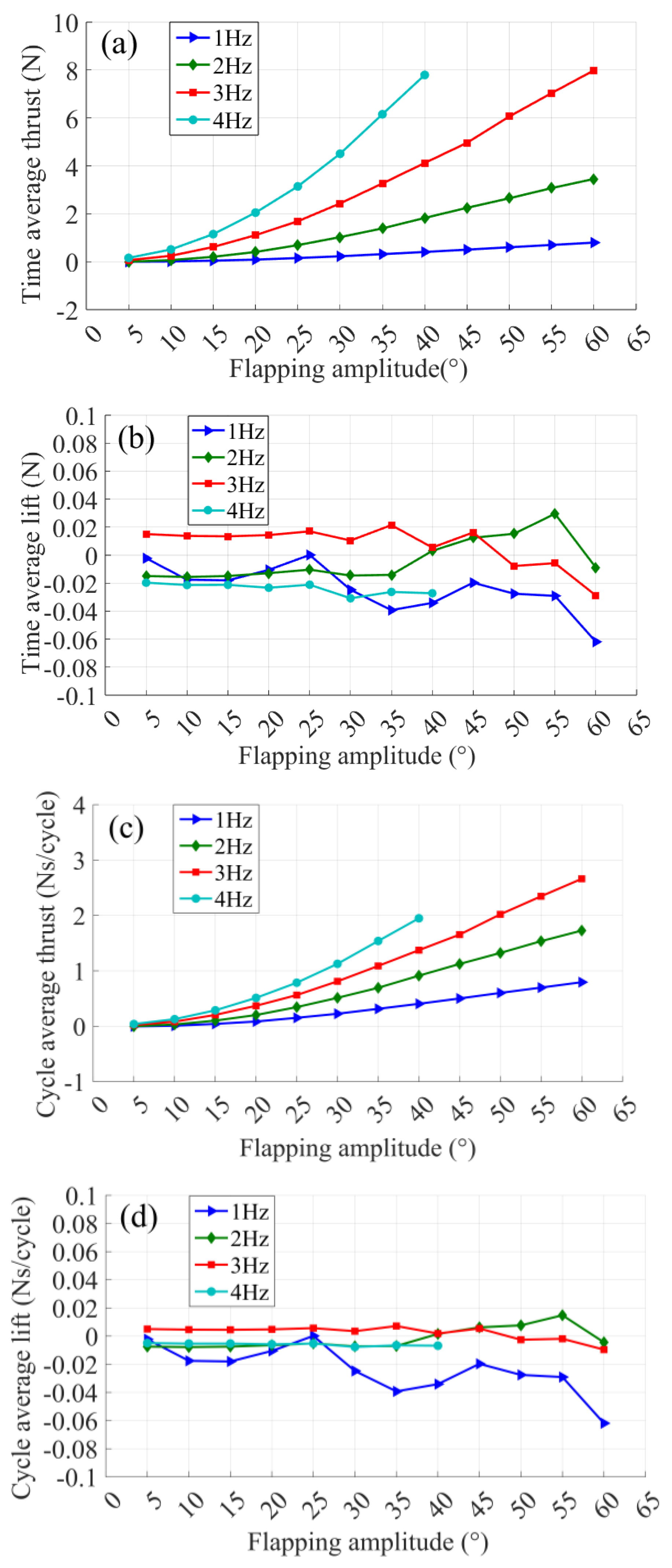
3.1. Effects of Frequency and Amplitude
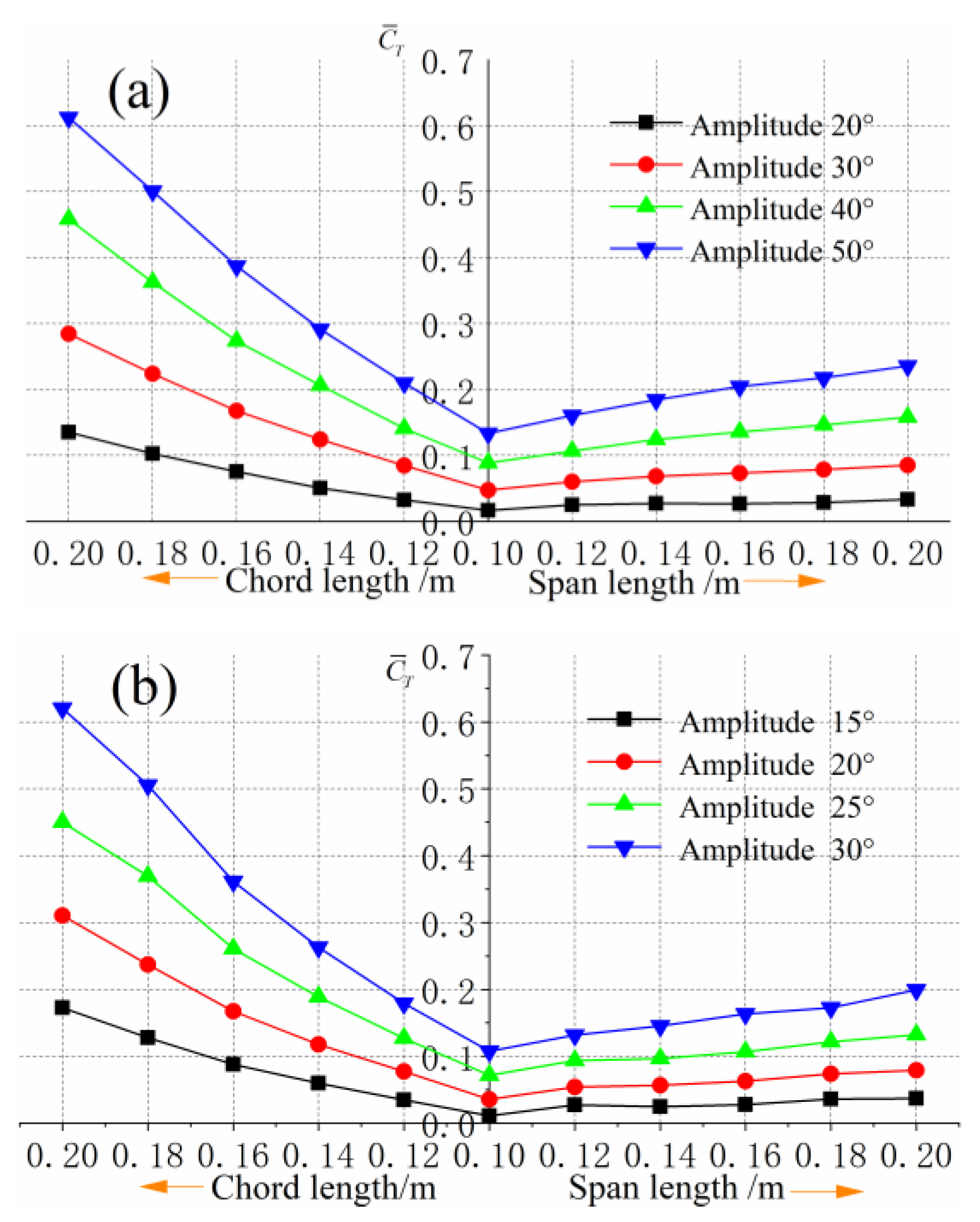
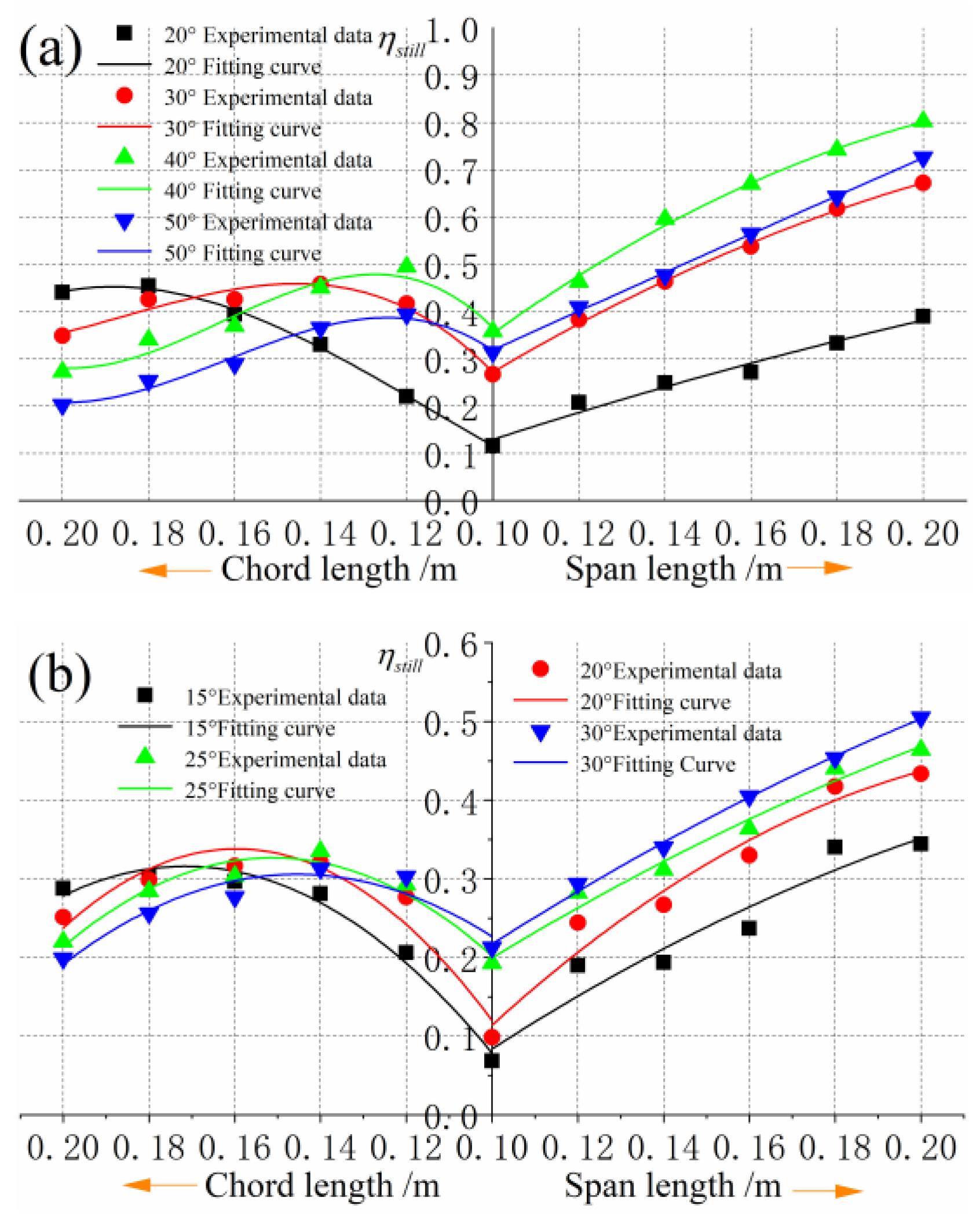
3.2. Effects of Aspect Ratio
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Neira, J.; Sequeiros, C.; Huamani, R.; Machaca, E.; Fonseca, P.; Nina, W. Review on Unmanned Underwater Robotics, Structure Designs, Materials, Sensors, Actuators, and Navigation Control. J. Robot. 2021, 2021, 5542920. [Google Scholar] [CrossRef]
- Li, Q.; Abdullah, S.; Rasani, M.R.M. A Review of Progress and Hydrodynamic Design of Integrated Motor Pump-Jet Propulsion. Appl. Sci. 2022, 12, 3824. [Google Scholar] [CrossRef]
- Salazar, R.; Campos, A.; Fuentes, V.; Abdelkefi, A. A review on the modeling, materials, and actuators of aquatic unmanned vehicles. Ocean Eng. 2018, 172, 257–285. [Google Scholar] [CrossRef]
- Chao, L.-M.; Cao, Y.-H.; Pan, G. A review of underwater bio-mimetic propulsion: Cruise and fast-start. Fluid Dyn. Res. 2017, 49, 044501. [Google Scholar] [CrossRef]
- Quinn, S.; Gaughran, W. Bionics—An inspiration for intelligent manufacturing and engineering. Robot. Comput. Manuf. 2010, 26, 616–621. [Google Scholar] [CrossRef]
- Fayemi, P.E.; Wanieck, K.; Zollfrank, C.; Maranzana, N.; Aoussat, A. Biomimetics: Process, tools and practice. Bioinspir. Biomim. 2017, 12, 011002. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Song, B.; Sun, Z.; Lang, X.; Yang, X. Dynamics Modeling and Experiment Validation for Piezoelec-tric-Transmission-Wing System. Int. J. Mech. Sci. 2023, 262, 108720. [Google Scholar] [CrossRef]
- Wu, T.Y. Fish Swimming and Bird/Insect Flight. Annu. Rev. Fluid Mech. 2011, 43, 25–58. [Google Scholar] [CrossRef]
- Costello, J.H.; Colin, S.P.; Dabiri, J.O.; Gemmell, B.J.; Lucas, K.N.; Sutherland, K.R. The Hydrodynamics of Jellyfish Swimming. Annu. Rev. Mar. Sci. 2021, 13, 375–396. [Google Scholar] [CrossRef]
- van der Geest, N.; Garcia, L.; Nates, R.; Godoy, D.A. New insight into the swimming kinematics of wild Green sea turtles (Chelonia mydas). Sci. Rep. 2022, 12, 18151. [Google Scholar] [CrossRef]
- Pan, Y.; Dong, H. Computational analysis of hydrodynamic interactions in a high-density fish school. Phys. Fluids 2020, 32, 121901. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, W.; Zheng, H.; Liu, B.; Liu, J.; Li, K. A novel anti-hydropressure piezoelectric jetting micro thruster for steering AUV. Int. J. Mech. Sci. 2024, 262, 108737. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Chen, Y.; Wainwright, D.K.; Kenaley, C.P.; Gong, Z.; Liu, Z.; Liu, H.; Guan, J.; Wang, T.; et al. A biorobotic adhesive disc for underwater hitchhiking inspired by the remora suckerfish. Sci. Robot. 2017, 2, eaan8072. [Google Scholar] [CrossRef]
- Liu, H.; Curet, O.M. Propulsive performance of an under-actuated robotic ribbon fin. Bioinspir. Biomim. 2017, 12, 036015. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Hu, D.; Guo, Y.; Ding, H.; Yang, G. Bio-inspired Filter Design Based on Vortex Control Mechanism of Parallel Groove Structure. J. Bionic. Eng. 2022, 20, 338–348. [Google Scholar] [CrossRef]
- Lee, J.; Park, Y.-J.; Cho, K.-J.; Kim, D.; Kim, H.-Y. Hydrodynamic advantages of a low aspect-ratio flapping foil. J. Fluids Struct. 2017, 71, 70–77. [Google Scholar] [CrossRef]
- Techet, A.H. Propulsive performance of biologically inspired flapping foils at high Reynolds numbers. J. Exp. Biol. 2008, 211, 274–279. [Google Scholar] [CrossRef] [PubMed]
- Floc’H, F.; Phoemsapthawee, S.; Laurens, J.M.; Leroux, J.B. Porpoising foil as a propulsion system. Ocean Eng. 2012, 39, 53–61. [Google Scholar] [CrossRef]
- Esfahani, J.; Barati, E.; Karbasian, H. Fluid structures of flapping airfoil with elliptical motion trajectory. Comput. Fluids 2015, 108, 142–155. [Google Scholar] [CrossRef]
- Wang, S.; He, G.; Zhang, X. Self-propulsion of flapping bodies in viscous fluids: Recent advances and perspectives. Acta Mech. Sin. 2016, 32, 980–990. [Google Scholar] [CrossRef]
- Jurado, R.; Arranz, G.; Flores, O.; García-Villalba, M. Numerical simulation of flow over flapping wings in tandem: Wingspan effects. Phys. Fluids 2022, 34, 017114. [Google Scholar] [CrossRef]
- Pedro, G.; Suleman, A.; Djilali, N. A numerical study of the propulsive efficiency of a flapping hydrofoil. Int. J. Numer. Methods Fluids 2003, 42, 493–526. [Google Scholar] [CrossRef]
- Ashraf, M.; Young, J.; Lai, J. Reynolds number, thickness and camber effects on flapping airfoil propulsion. J. Fluids Struct. 2011, 27, 145–160. [Google Scholar] [CrossRef]
- Tang, C.; Lu, X.-Y. Self-propulsion of a three-dimensional flapping flexible plate. J. Hydrodyn. 2016, 28, 033113. [Google Scholar] [CrossRef]
- Lagopoulos, N.S.; Weymouth, G.D.; Ganapathisubramani, B. Effect of aspect ratio on the propulsive performance of tandem flapping foils. Flow 2023, 3, E1. [Google Scholar] [CrossRef]
- Kumar, R.; Shin, H. Thrust Prediction of an Active Flapping Foil in Waves Using CFD. J. Mar. Sci. Eng. 2019, 7, 396. [Google Scholar] [CrossRef]
- Triantafyllou, M.; Techet, A.; Hover, F. Review of Experimental Work in Biomimetic Foils. IEEE J. Ocean. Eng. 2004, 29, 585–594. [Google Scholar] [CrossRef]
- Koochesfahani, M.M. Vortical patterns in the wake of an oscillating airfoil. AIAA J. 1989, 27, 1200–1205. [Google Scholar] [CrossRef]
- Parker, K.; von Ellenrieder, K.D.; Soria, J. Using stereo multigrid DPIV (SMDPIV) measurements to investigate the vortical skeleton behind a finite-span flapping wing. Exp. Fluids 2005, 39, 281–298. [Google Scholar] [CrossRef]
- Qadri, M.N.M.; Zhao, F.; Tang, H. Fluid-structure interaction of a fully passive flapping foil for flow energy extraction. Int. J. Mech. Sci. 2020, 177, 105587. [Google Scholar] [CrossRef]
- Thaweewat, N.; Phoemsapthawee, S.; Juntasaro, V. Semi-active flapping foil for marine propulsion. Ocean Eng. 2017, 147, 556–564. [Google Scholar] [CrossRef]
- Izraelevitz, J.S.; Triantafyllou, M.S. Adding in-line motion and model-based optimization offers exceptional force control au-thority in flapping foils. J. Fluid Mech. 2014, 742, 5–34. [Google Scholar] [CrossRef]
- Mackowski, A.W.; Williamson, C.H.K. Effect of pivot location and passive heave on propulsion from a pitching airfoil. Phys. Rev. Fluids 2017, 2, 013101. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, J.-K.; Chen, W.-S. Numerical and experimental studies of hydrodynamics of flapping foils. J. Hydrodyn. 2018, 30, 258–266. [Google Scholar] [CrossRef]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L.R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, H.; Chen, R.; Zhu, Y.; Shen, H.; Gao, Q. Effect of Frequency–Amplitude Parameter and Aspect Ratio on Propulsion Performance of Underwater Flapping-Foil. Biomimetics 2024, 9, 324. https://doi.org/10.3390/biomimetics9060324
Ding H, Chen R, Zhu Y, Shen H, Gao Q. Effect of Frequency–Amplitude Parameter and Aspect Ratio on Propulsion Performance of Underwater Flapping-Foil. Biomimetics. 2024; 9(6):324. https://doi.org/10.3390/biomimetics9060324
Chicago/Turabian StyleDing, Hao, Ruoqian Chen, Yawei Zhu, Huipeng Shen, and Qiang Gao. 2024. "Effect of Frequency–Amplitude Parameter and Aspect Ratio on Propulsion Performance of Underwater Flapping-Foil" Biomimetics 9, no. 6: 324. https://doi.org/10.3390/biomimetics9060324
APA StyleDing, H., Chen, R., Zhu, Y., Shen, H., & Gao, Q. (2024). Effect of Frequency–Amplitude Parameter and Aspect Ratio on Propulsion Performance of Underwater Flapping-Foil. Biomimetics, 9(6), 324. https://doi.org/10.3390/biomimetics9060324





