Optimal Design of Formulas for a Single Degree of Freedom Tuned Mass Damper Parameter Using a Genetic Algorithm and H2 Norm
Abstract
:1. Introduction
2. Review of Previous Studies
3. Numerical Modeling
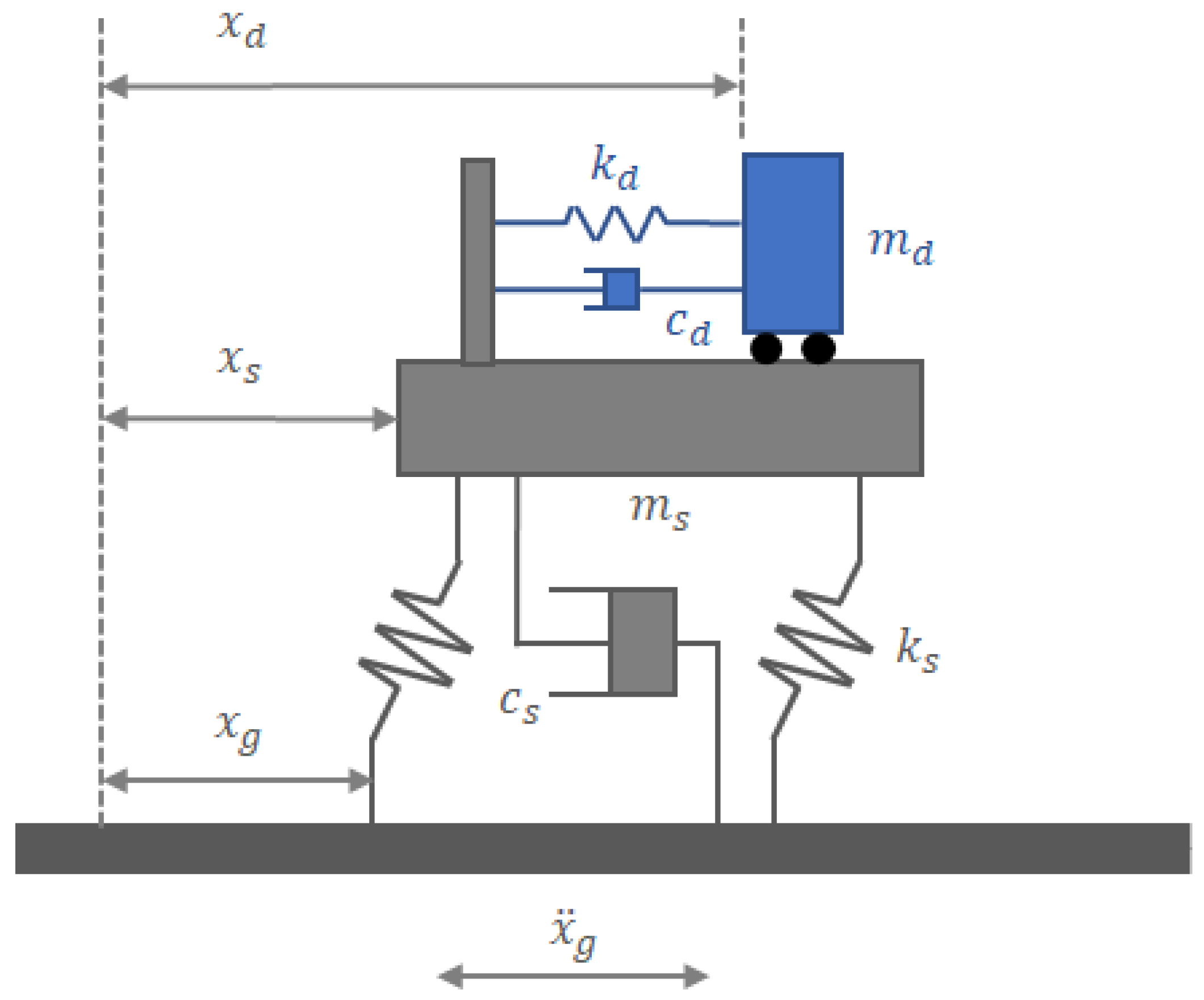
3.1. Equation of Motion
3.2. H2 Norm
3.3. Genetic Algorithm
| Algorithm 1. The Psuedo code of the GA |
| Begin t = 0 Initialize P(t) Evaluate P(t) Select P(t) from P(t) using elite and roulette wheel while (not termination condition) do crossover P(t + 1) to yield C(t) mutate C(t) evaluate C(t) select P(t + 1) from P(t) and C(t) t = t + 1 end end |
4. TMD Optimization for Damped SDOF Structure
4.1. Extraction of TMD Parameters
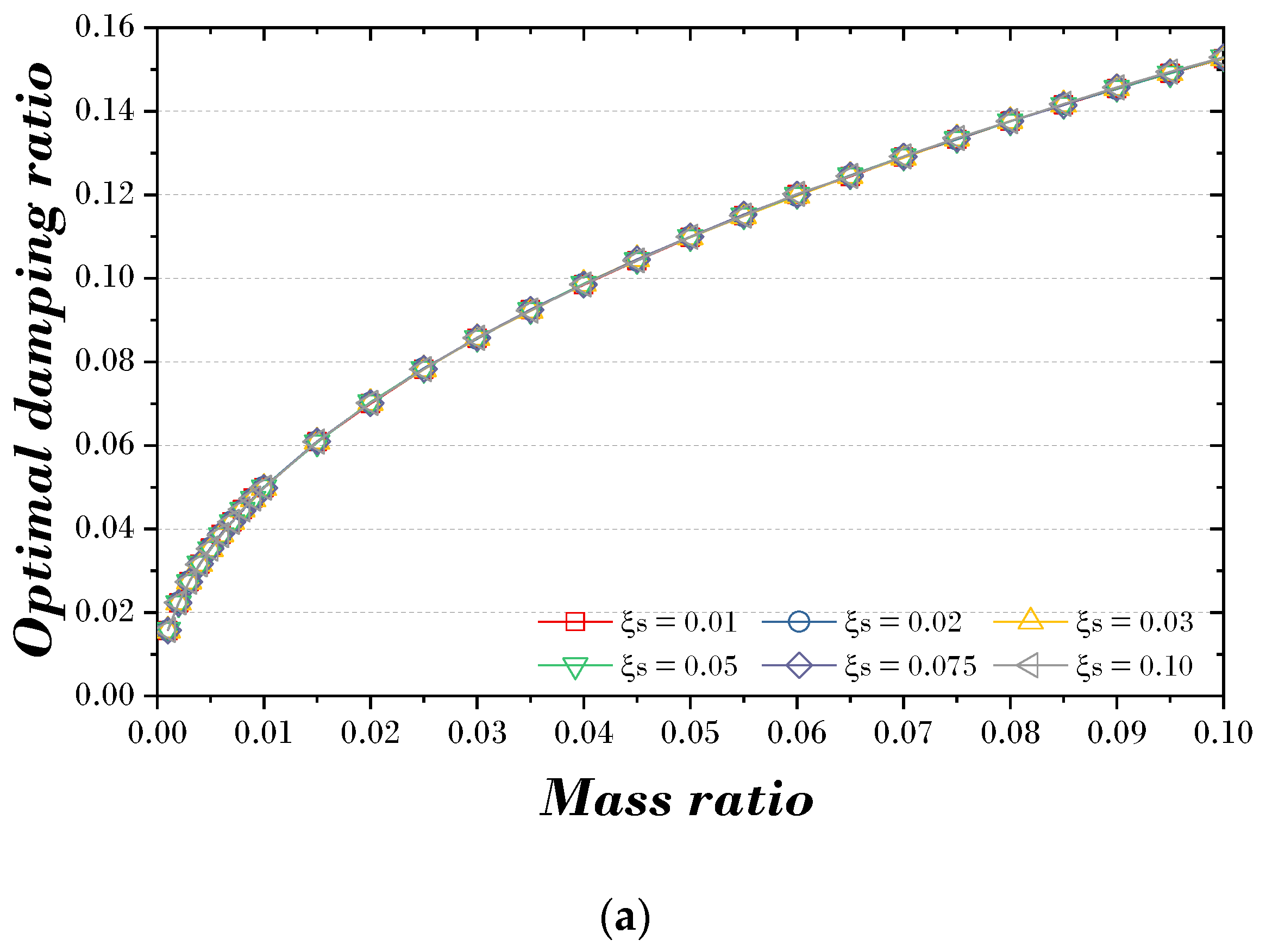
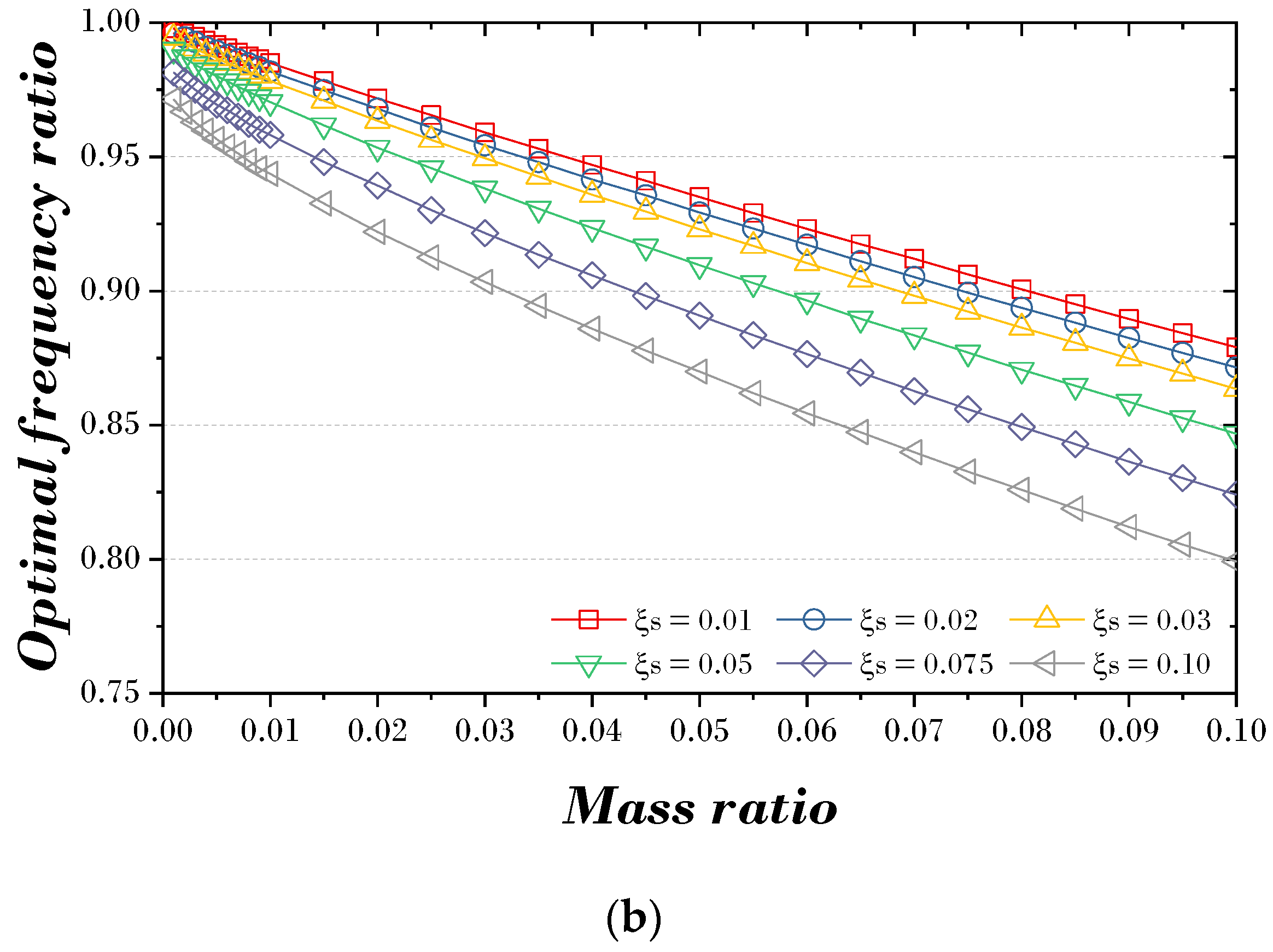
4.2. Deriving Explicit Formulas for TMD Parameters
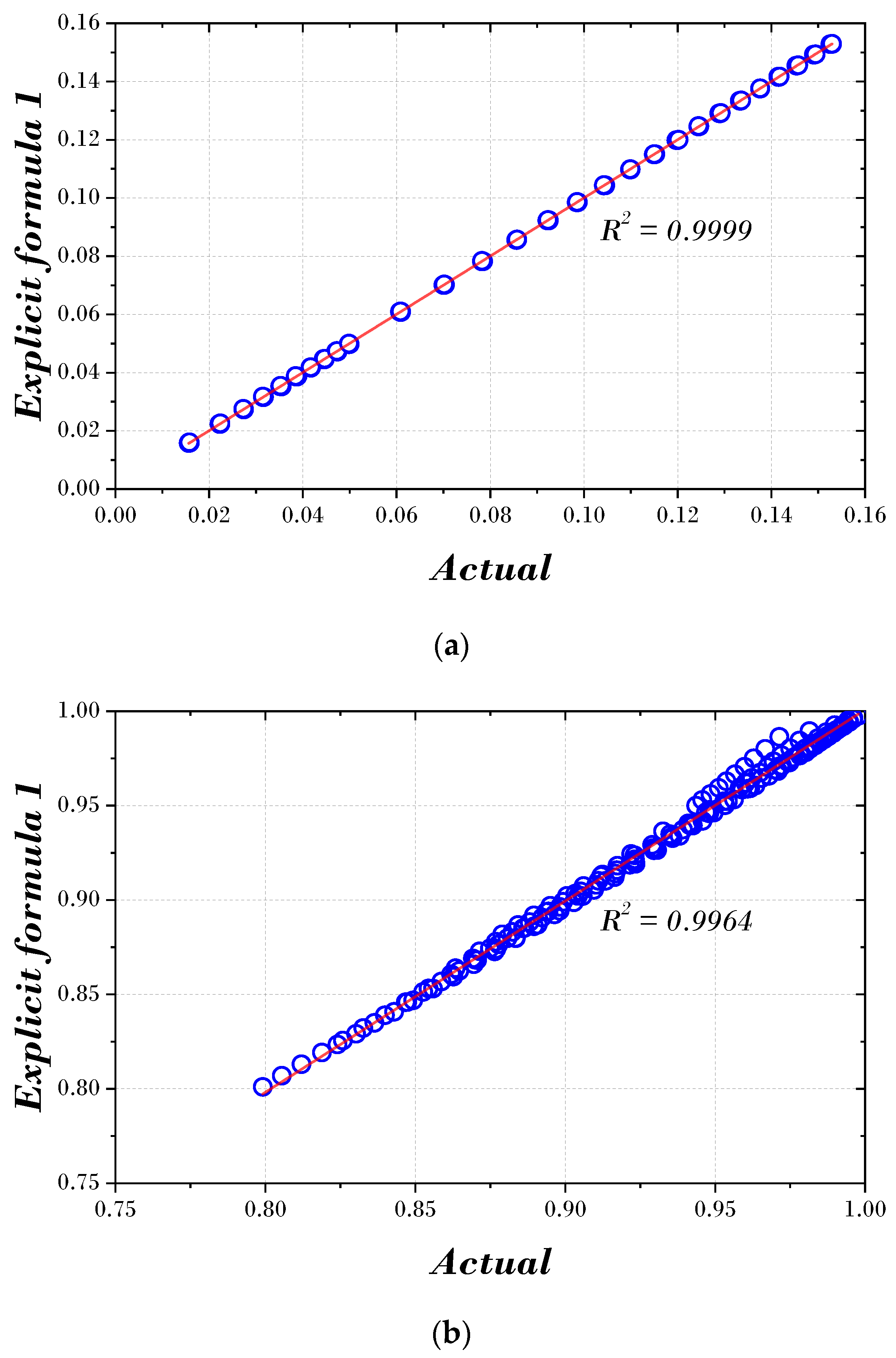
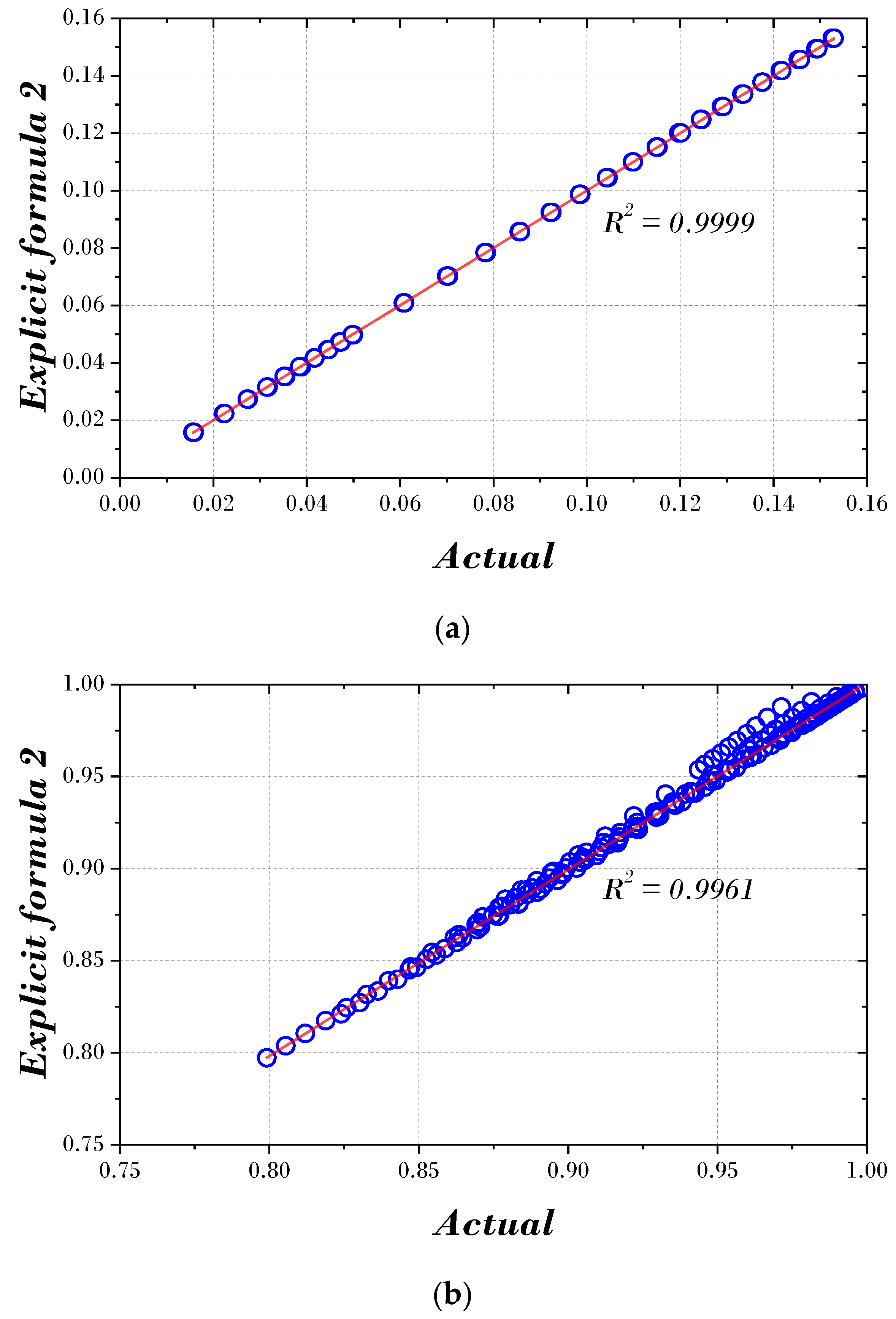
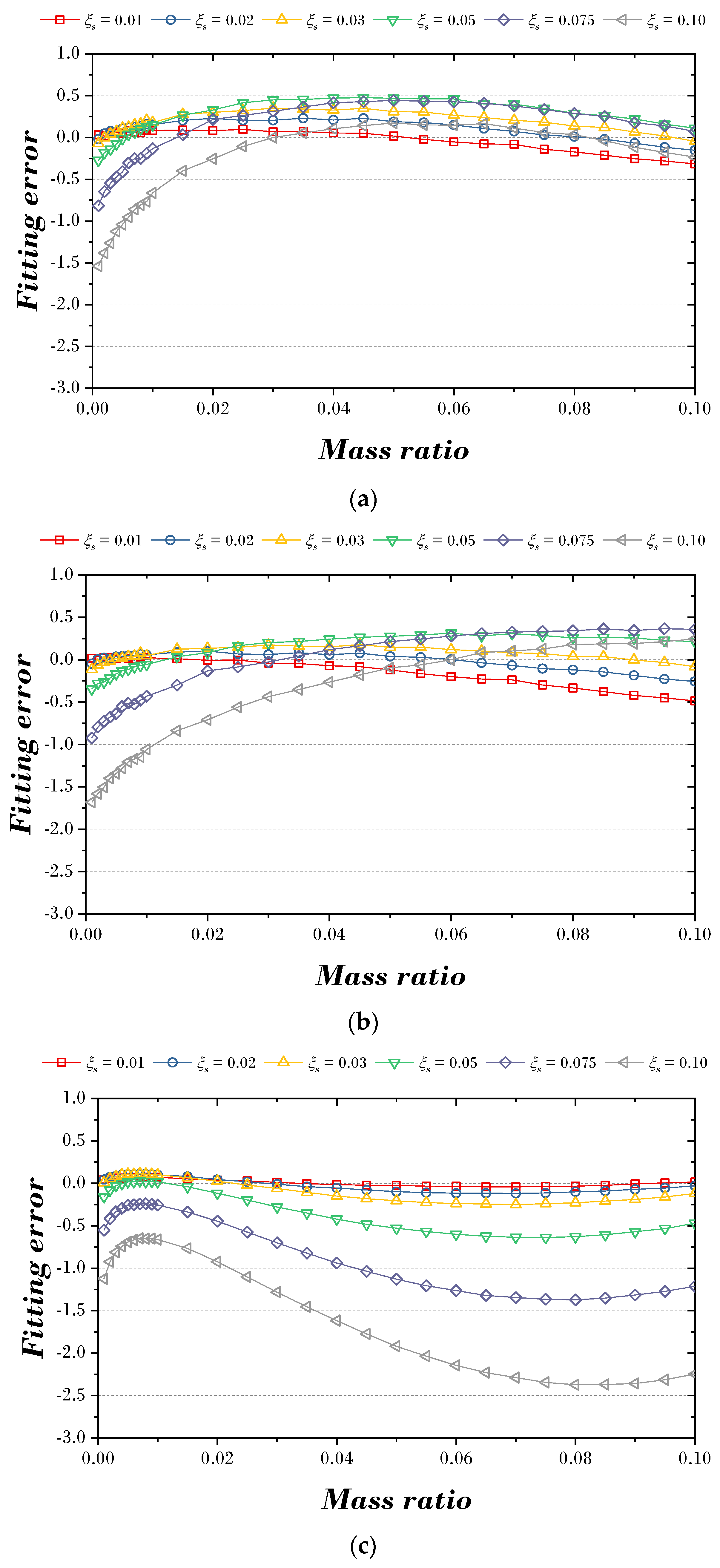
4.3. Verification of Explicit Formulas for Parameter of TMD
5. Optimal TMD Design for Damped MDOF Structure
5.1. Optimal TMD Parameters Using Explicit Formulas
5.2. Optimal TMD Parameters Using Explicit Formulas 1 and 2 and Previous Studies
6. Conclusions
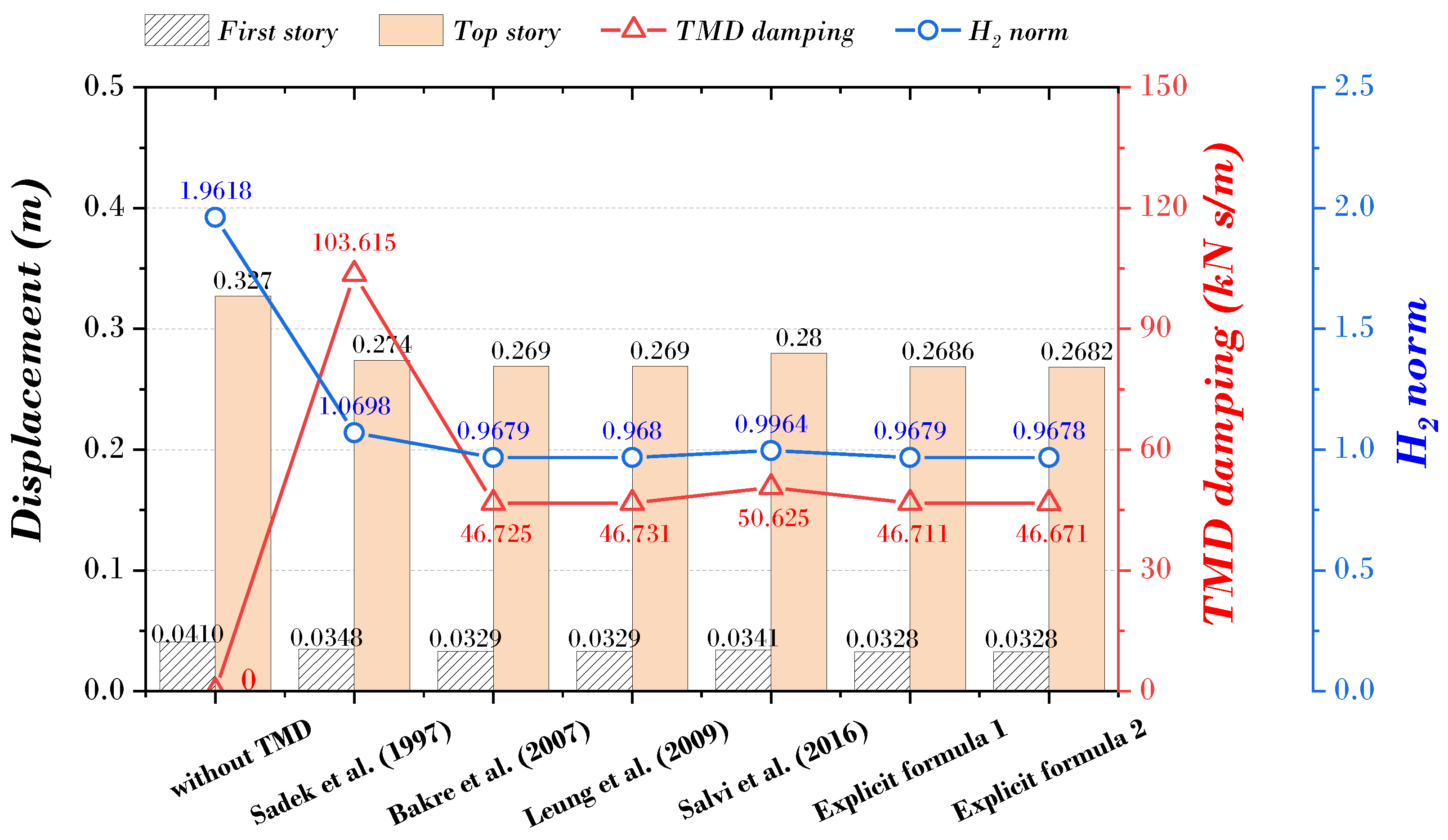
- Although the optimal parameters of the TMD were derived through various numerical techniques in previous studies, the setting of the TMD parameters may vary due to the influence of the main structure and various variables. In addition, it was confirmed that the parameters of the TMD proposed by previous studies were insufficient to be applied to all structures, and a similar trend was confirmed in the relationship between the H2 norm and displacement response (first, top story).
- Two explicit formulas were derived for optimizing TMD using GA and MATLAB curve fitting toolbox. The MAE and NRMSE for these two formulas’ optimal damping and frequency ratios were compared with previous studies. As a result, they decreased by 61.43% and 44.68%, respectively, in MAE and by 69.77% and 51.32%, respectively, in NRMSE.
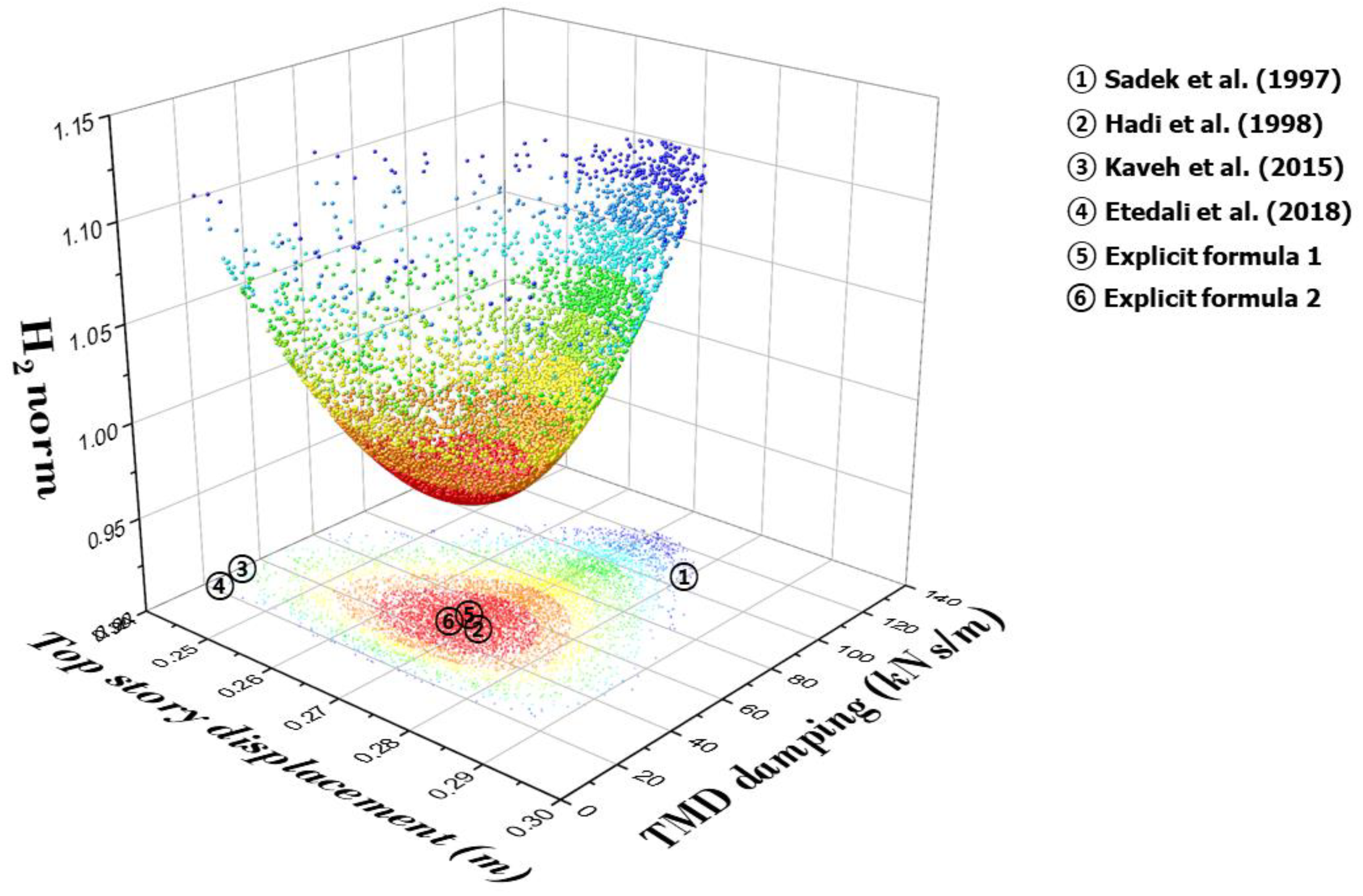
- As a result of performing the optimal TMD design installed on the MDOF structure, it was confirmed that the proposed two explicit formulas were most effective in reducing the structural responses, and the result of Explicit formula 2 was better than Explicit formula 1. In addition, the data distribution of the objective function H2 norm is a convex function with a minimum value. The results of Explicit formula 1 and Explicit formula 2 are concentrated in the region of the optimal solution. In this study, two explicit formulas were proposed that can quickly derive the optimal parameters of the TMD without complicated numerical analysis or simulation in the design process. In particular, the accuracy and reliability of the proposed model were secured through the multidimensional performance verification technique, and the basis for quantitatively evaluating the results of applying the optimal parameters of the TMD was laid. Compared to previous studies, the proposed two explicit formulas have superior response performance of the structure and are expected to be essential reference materials for TMD design.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| 0.001 | 0.016 | 0.998 | 0.016 | 0.996 | 0.016 | 0.994 | 0.016 | 0.990 | 0.016 | 0.981 | 0.016 | 0.971 |
| 0.002 | 0.022 | 0.996 | 0.022 | 0.995 | 0.022 | 0.992 | 0.022 | 0.987 | 0.022 | 0.978 | 0.022 | 0.967 |
| 0.003 | 0.027 | 0.995 | 0.027 | 0.993 | 0.027 | 0.990 | 0.027 | 0.984 | 0.027 | 0.975 | 0.027 | 0.963 |
| 0.004 | 0.032 | 0.993 | 0.031 | 0.991 | 0.032 | 0.988 | 0.032 | 0.982 | 0.032 | 0.972 | 0.031 | 0.960 |
| 0.005 | 0.035 | 0.992 | 0.035 | 0.989 | 0.035 | 0.987 | 0.035 | 0.980 | 0.035 | 0.969 | 0.035 | 0.957 |
| 0.006 | 0.039 | 0.990 | 0.039 | 0.988 | 0.039 | 0.985 | 0.039 | 0.978 | 0.039 | 0.967 | 0.038 | 0.954 |
| 0.007 | 0.042 | 0.989 | 0.042 | 0.986 | 0.042 | 0.983 | 0.042 | 0.976 | 0.042 | 0.965 | 0.042 | 0.951 |
| 0.008 | 0.045 | 0.987 | 0.044 | 0.985 | 0.045 | 0.982 | 0.045 | 0.974 | 0.044 | 0.962 | 0.045 | 0.948 |
| 0.009 | 0.047 | 0.986 | 0.047 | 0.983 | 0.047 | 0.980 | 0.047 | 0.972 | 0.047 | 0.960 | 0.047 | 0.946 |
| 0.01 | 0.050 | 0.985 | 0.050 | 0.982 | 0.050 | 0.978 | 0.050 | 0.970 | 0.050 | 0.958 | 0.050 | 0.944 |
| 0.015 | 0.061 | 0.978 | 0.061 | 0.975 | 0.061 | 0.971 | 0.061 | 0.962 | 0.061 | 0.948 | 0.061 | 0.933 |
| 0.02 | 0.070 | 0.972 | 0.070 | 0.968 | 0.070 | 0.963 | 0.070 | 0.953 | 0.070 | 0.939 | 0.070 | 0.922 |
| 0.025 | 0.078 | 0.966 | 0.078 | 0.961 | 0.078 | 0.956 | 0.078 | 0.946 | 0.078 | 0.930 | 0.078 | 0.912 |
| 0.03 | 0.086 | 0.959 | 0.086 | 0.954 | 0.086 | 0.950 | 0.086 | 0.938 | 0.086 | 0.922 | 0.086 | 0.903 |
| 0.035 | 0.093 | 0.953 | 0.093 | 0.948 | 0.092 | 0.943 | 0.092 | 0.931 | 0.092 | 0.913 | 0.092 | 0.894 |
| 0.04 | 0.098 | 0.947 | 0.099 | 0.942 | 0.099 | 0.936 | 0.099 | 0.923 | 0.099 | 0.906 | 0.099 | 0.886 |
| 0.045 | 0.104 | 0.941 | 0.104 | 0.936 | 0.105 | 0.930 | 0.104 | 0.916 | 0.105 | 0.898 | 0.104 | 0.878 |
| 0.05 | 0.110 | 0.935 | 0.110 | 0.929 | 0.110 | 0.923 | 0.110 | 0.910 | 0.110 | 0.891 | 0.110 | 0.870 |
| 0.055 | 0.115 | 0.929 | 0.115 | 0.923 | 0.115 | 0.917 | 0.115 | 0.903 | 0.115 | 0.884 | 0.115 | 0.862 |
| 0.06 | 0.120 | 0.923 | 0.120 | 0.917 | 0.120 | 0.910 | 0.120 | 0.896 | 0.120 | 0.876 | 0.120 | 0.854 |
| 0.065 | 0.124 | 0.917 | 0.125 | 0.911 | 0.125 | 0.904 | 0.125 | 0.890 | 0.125 | 0.870 | 0.124 | 0.847 |
| 0.07 | 0.129 | 0.912 | 0.129 | 0.905 | 0.129 | 0.898 | 0.129 | 0.883 | 0.129 | 0.863 | 0.129 | 0.840 |
| 0.075 | 0.133 | 0.906 | 0.133 | 0.899 | 0.133 | 0.892 | 0.133 | 0.877 | 0.133 | 0.856 | 0.134 | 0.833 |
| 0.08 | 0.138 | 0.901 | 0.138 | 0.894 | 0.138 | 0.886 | 0.138 | 0.871 | 0.138 | 0.849 | 0.138 | 0.826 |
| 0.085 | 0.142 | 0.895 | 0.142 | 0.888 | 0.142 | 0.881 | 0.142 | 0.865 | 0.141 | 0.843 | 0.142 | 0.819 |
| 0.09 | 0.145 | 0.890 | 0.145 | 0.882 | 0.145 | 0.875 | 0.146 | 0.859 | 0.146 | 0.836 | 0.146 | 0.812 |
| 0.095 | 0.149 | 0.884 | 0.149 | 0.877 | 0.149 | 0.869 | 0.149 | 0.853 | 0.149 | 0.830 | 0.149 | 0.805 |
| 0.1 | 0.153 | 0.879 | 0.153 | 0.871 | 0.153 | 0.863 | 0.153 | 0.847 | 0.153 | 0.824 | 0.153 | 0.799 |
References
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The current development of structural health monitoring for bridges: A review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, M.; Wan, N.; Deng, Z.; He, Z.; Luo, J. Missing measurement data recovery methods in structural health monitoring: The state, challenges and case study. Measurement 2024, 231, 114528. [Google Scholar] [CrossRef]
- Yucel, M.; Bekdaş, G.; Nigdeli, S.M.; Sevgen, S. Estimation of optimum tuned mass damper parameters via machine learning. J. Build. Eng. 2019, 26, 100847. [Google Scholar] [CrossRef]
- Frahm, H.H. Results of trials of the anti-rolling tanks at sea. J. Am. Soc. Nav. Eng. 1911, 23, 571–597. [Google Scholar] [CrossRef]
- Ormondroyd, J.; Den Hartog, J.P. The theory of the dynamic vibration absorber. J. Fluids Eng. 1928, 49, 021007. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations, 3rd ed.; McGRAW-HILL BOOK COMPANY: New York, NY, USA; London, UK, 1947. [Google Scholar]
- Warburton, G.B. Optimum absorber parameters for various combinations of response and excitation parameters. Earthq. Eng. Struct. Dyn. 1982, 10, 381–401. [Google Scholar] [CrossRef]
- Hadi, M.N.; Arfiadi, Y. Optimum design of absorber for MDOF structures. J. Struct. Eng. 1998, 124, 1272–1280. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Zhang, H. Particle swarm optimization of tuned mass dampers. Eng. Struct. 2009, 31, 715–728. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Soheili, S. Ant colony optimization of tuned mass dampers for earthquake oscillations of high-rise structures including soil–structure interaction. Soil Dyn. Earthq. Eng. 2013, 51, 14–22. [Google Scholar] [CrossRef]
- Özsarıyıldız, Ş.S.; Bozer, A. Finding optimal parameters of tuned mass dampers. Struct. Des. Tall Spec. Build. 2015, 24, 461–475. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Bekdaş, G. Design of tuned mass dampers via harmony search for different optimization objectives of structures. Engineering and Applied Sciences Optimization: Dedicated to the Memory of Professor MG Karlaftis; Springer: Berlin/Heidelberg, Germany, 2015; pp. 249–266. [Google Scholar]
- Bekdaş, G.; Nigdeli, S.M. Metaheuristic based optimization of tuned mass dampers under earthquake excitation by considering soil-structure interaction. Soil Dyn. Earthq. Eng. 2017, 92, 443–461. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Bekdaş, G. Optimum tuned mass damper design in frequency domain for structures. KSCE J. Civ. Eng. 2017, 21, 912–922. [Google Scholar] [CrossRef]
- Etedali, S.; Rakhshani, H. Optimum design of tuned mass dampers using multi-objective cuckoo search for buildings under seismic excitations. Alex. Eng. J. 2018, 57, 3205–3218. [Google Scholar] [CrossRef]
- Jin, L.; Li, B.; Lin, S.; Li, G. Optimal Design Formula for Tuned Mass Damper Based on an Analytical Solution of Interaction between Soil and Structure with Rigid Foundation Subjected to Plane SH-Waves. Buildings 2022, 13, 17. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations, 3rd ed.; Allyn and Bacon: Boston, MA, USA, 1947. [Google Scholar]
- Ioi, T.; Ikeda, K. On the dynamic vibration damped absorber of the vibration system. Bull. JSME 1978, 21, 64–71. [Google Scholar] [CrossRef]
- Warburton, G.B.; Ayorinde, E.O. Optimum absorber parameters for simple systems. Earthq. Eng. Struct. Dyn. 1980, 8, 197–217. [Google Scholar] [CrossRef]
- Bekdas, G.; Nigdeli, S.M. Optimization of tuned mass damper with harmony search. Metaheuristic Appl. Struct. Infrastruct. 2013, 14, 345–372. [Google Scholar]
- Bakre, S.V.; Jangid, R.S. Optimum parameters of tuned mass damper for damped main system. Struct. Control. Health Monit. Off. J. Int. Assoc. Struct. Control. Monit. Eur. Assoc. Control. Struct. 2007, 14, 448–470. [Google Scholar] [CrossRef]
- Sadek, F.; Mohraz, B.; Taylor, A.W.; Chung, R.M. A method of estimating the parameters of tuned mass dampers for seismic applications. Earthq. Eng. Struct. Dyn. 1997, 26, 617–635. [Google Scholar] [CrossRef]
- Villaverde, R. Reduction seismic response with heavily-damped vibration absorbers. Earthq. Eng. Struct. Dyn. 1985, 13, 33–42. [Google Scholar] [CrossRef]
- Salvi, J.; Rizzi, E. Closed-form optimum tuning formulas for passive tuned mass dampers under benchmark excitations. Smart Struct. Syst. Int. J. 2016, 17, 231–256. [Google Scholar] [CrossRef]
- Asami, T.; Wakasono, T.; Kameoka, K.; Hasegawa, M.; Sekiguchi, H. Optimum design of dynamic absorbers for a system subjected to random excitation. JSME Int. Journal. Ser. 3 Vib. Control. Eng. Eng. Ind. 1991, 34, 218–226. [Google Scholar] [CrossRef]
- Lee, C.L.; Chen, Y.T.; Chung, L.L.; Wang, Y.P. Optimal design theories and applications of tuned mass dampers. Eng. Struct. 2006, 28, 43–53. [Google Scholar] [CrossRef]
- Crandall, S.H.; Mark, W.D. Random Vibration in Mechanical Systems; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Kaveh, A.; Mohammadi, S.; Hosseini, O.K.; Keyhani, A.; Kalatjari, V.R. Optimum parameters of tuned mass dampers for seismic applications using charged system search. Iran. J. Sci. Technol. Trans. Civ. Eng. 2015, 39, 21. [Google Scholar]
- Singh, M.P.; Matheu, E.E.; Suarez, L.E. Active and semi-active control of structures under seismic excitation. Earthq. Eng. Struct. Dyn. 1997, 26, 193–213. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures; Pearson Education India: Delhi, India, 2007. [Google Scholar]
- Arfiadi, Y.; Frans, R. Shared vibration absorbers for connected SDOF structures. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2023; Volume 1195, No. 1; p. 012008. [Google Scholar]
- Liu, Y.; Lin, C.C.; Parker, J.; Zuo, L. Exact H2 optimal tuning and experimental verification of energy-harvesting series electromagnetic tuned-mass dampers. J. Vib. Acoust. 2016, 138, 061003. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J. Exploration-exploitation tradeoffs in metaheuristics: Survey and analysis. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 8633–8638. [Google Scholar]
- Holand, J.H. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, MI, USA, 1975; p. 32. [Google Scholar]
- Michalewicz, Z.; Janikow, C.Z.; Krawczyk, J.B. A modified genetic algorithm for optimal control problems. Comput. Math. Appl. 1992, 23, 83–94. [Google Scholar] [CrossRef]
- Grefenstette, J.J. Optimization of control parameters for genetic algorithms. IEEE Trans. Syst. Man Cybern. 1986, 16, 122–128. [Google Scholar] [CrossRef]
- Suryadi, D.; Prasetya, A.; Daratha, N.; Agustian, I. Optimum design of tuned mass damper parameters to reduce seismic response on structure using genetic algorithm. ASEAN Eng. J. 2023, 13, 41–49. [Google Scholar] [CrossRef]
- Marano, G.C.; Greco, R. Optimization criteria for tuned mass dampers for structural vibration control under stochastic excitation. J. Vib. Control. 2011, 17, 679–688. [Google Scholar] [CrossRef]
- Rana, R.; Soong, T.T. Parametric study and simplified design of tuned mass dampers. Eng. Struct. 1998, 20, 193–204. [Google Scholar] [CrossRef]
- Yucel, M.; Bekdaş, G.; Nigdeli, S.M. Machine learning-based model for prediction of optimum TMD parameters in time-domain history. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 192. [Google Scholar] [CrossRef]



| Index | Optimal Parameters of TMD | |
|---|---|---|
| ) | ) | |
| Den Hartog [17] | ||
| Ioi et al. [18] | ||
| Warburton [7] | ||
| Sadek et al. [22] | ||
| Bakre et al. [21] | ||
| Leung et al. [9] | ||
| Salvi et al. [24] | ||
| Index | Hadi et al. [8] | Lee et al. [26] | Özsarıyıldız et al. [11] | Kaveh et al. [28] | Etedali et al. [15] | |
|---|---|---|---|---|---|---|
| Domain | Frequency | Frequency | Frequency | Frequency + Time | Time | |
| Method | GA | GSS | DE | CSS | MOCS | |
| Parameters of main structure | Mass | 360 ton | ||||
| Damper | 6200 kN s/m | |||||
| Stiffness | 650,000 kN/m | |||||
| Parameters of TMD | Mass | 108 ton (3% of the total mass of the main structure) | ||||
| Damper | LB: 0 kN s/m, UB: 1000 kN s/m | |||||
| Stiffness | LB: 0 kN/m, UB: 4000 kN/m | LB: 0 kN/m, UB: 5000 kN/m | ||||
| Parameters | Value |
|---|---|
| population size | 30 |
| number of generations | 200 |
| crossover and mutation rates | 0.5:0.5 |
| elitist strategy | 3 |
| iteration termination criteria | 5000 |
| Parameter | Design Variables |
|---|---|
| ) | ) |
| ) | 1, 2, 3, 5, 7.5, 10% (A total of 6.) |
| ) | ≤ 0.3 |
| ) | ) |
| Parameter | () | () | () | () | |
|---|---|---|---|---|---|
| 0.0031 | 9.7353 | 0.2484 | 0.6354 | 0.9999 | |
| 1.2263 | 3.8063 | 1.0708 | 5.2784 | 0.9964 |
| Parameter | () | () | |
|---|---|---|---|
| 0.2494 | 0.6679 | 0.9999 | |
| 1.2263 | 7.0426 | 0.9961 |
| Story | Mass (ton) | Stiffness (kN/m) | Damping (kN s/m) | First Mode Shape |
|---|---|---|---|---|
| 10 | 98 | 34,310 | 442.599 | 1.3590 |
| 9 | 107 | 37,430 | 482.847 | 1.3211 |
| 8 | 116 | 40,550 | 523.095 | 1.2480 |
| 7 | 125 | 43,670 | 536.343 | 1.1460 |
| 6 | 134 | 46,790 | 603.591 | 1.0190 |
| 5 | 143 | 49,910 | 643.839 | 0.8710 |
| 4 | 152 | 53,020 | 683.958 | 0.7080 |
| 3 | 161 | 56,140 | 724.206 | 0.5340 |
| 2 | 170 | 52,260 | 674.154 | 0.3550 |
| 1 | 179 | 62,470 | 805.863 | 0.1750 |
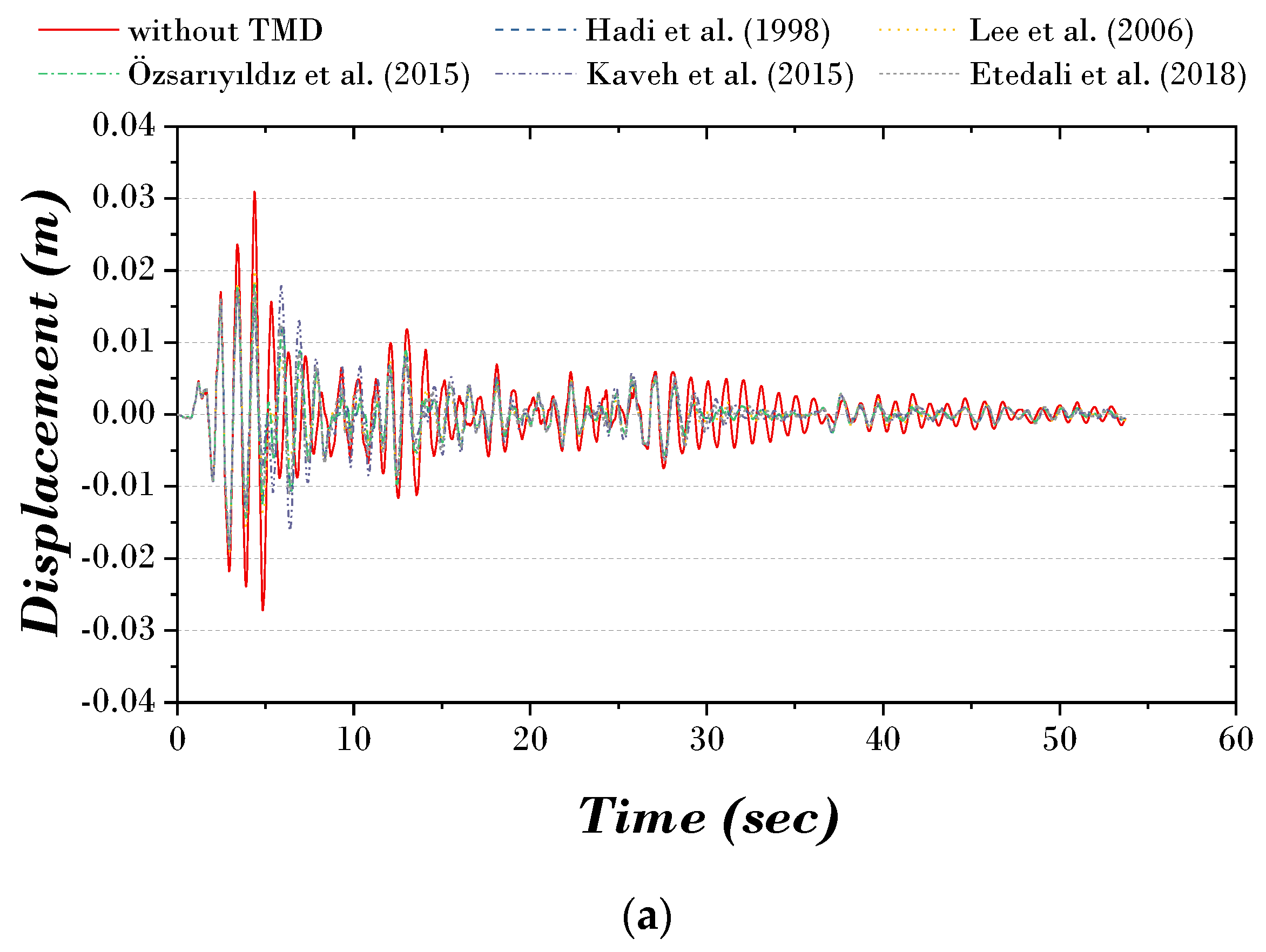
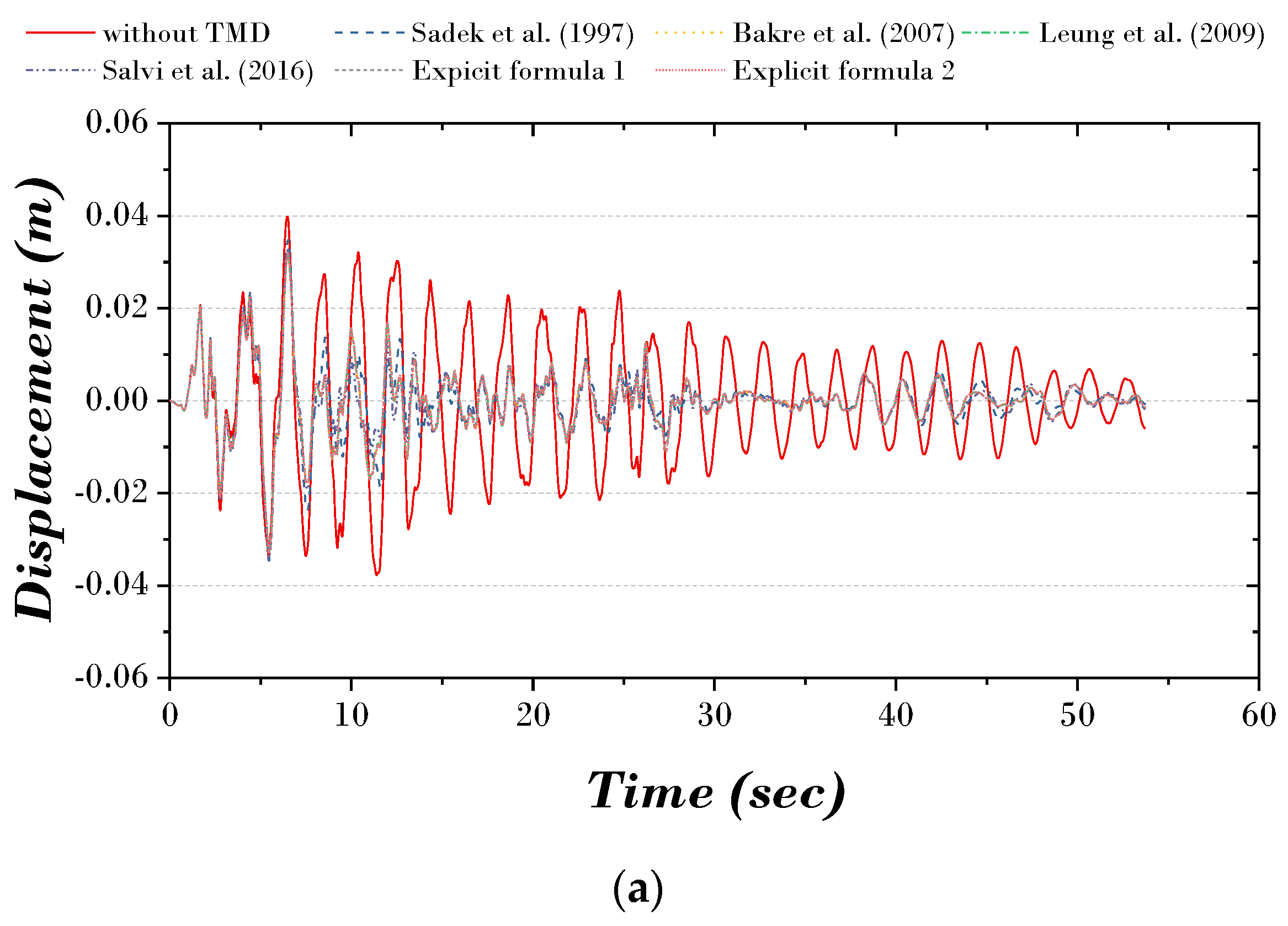
| Without TMD | With TMD | With TMD | With TMD | With TMD | With TMD | With TMD | |
|---|---|---|---|---|---|---|---|
| Sadek et al. [22] | Bakre et al. [21] | Leung et al. [9] | Salvi et al. [24] | Explicit Formula 1 | Explicit Formula 2 | ||
| 32.24 | 14.92 | 14.91 | 15.19 | 14.94 | 14.95 | ||
| 0.9316 | 0.9078 | 0.9088 | 0.9660 | 0.9068 | 0.9053 | ||
| 55.450 | 55.450 | 55.450 | 55.450 | 55.450 | 55.450 | ||
| 103.615 | 46.725 | 46.731 | 50.625 | 46.711 | 46.671 | ||
| 465.561 | 442.023 | 442.983 | 500.528 | 441.027 | 439.560 | ||
| 0.0410 | 0.0348 | 0.0329 | 0.0329 | 0.0341 | 0.0328 | 0.0328 | |
| 0.3270 | 0.2735 | 0.2688 | 0.2690 | 0.2800 | 0.2686 | 0.2682 | |
| 1.9618 | 1.0698 | 0.9679 | 0.9680 | 0.9964 | 0.9679 | 0.9678 |
| Without TMD | With TMD | With TMD | With TMD | With TMD | With TMD | With TMD | With TMD | |
|---|---|---|---|---|---|---|---|---|
| Warburton [7] | Sadek et al. [22] | Hadi et al. [8] | Kaveh et al. [28] | Etedali et al. [15] | Explicit Formula 1 | Explicit Formula 2 | ||
| 14.76 | 32.54 | 15.37 | 10.76 | 6.96 | 14.94 | 14.95 | ||
| 0.8940 | 0.9302 | 0.9035 | 0.8144 | 0.8393 | 0.9068 | 0.9053 | ||
| 55.450 | 55.450 | 55.450 | 55.450 | 55.450 | 55.450 | 55.450 | ||
| 45.500 | 104.400 | 47.900 | 30.234 | 20.144 | 46.711 | 46.671 | ||
| 428.700 | 464.100 | 437.900 | 355.758 | 377.800 | 441.027 | 439.560 | ||
| 0.0410 | 0.0360 | 0.0360 | 0.0340 | 0.0306 | 0.0300 | 0.0328 | 0.0328 | |
| 0.3270 | 0.3100 | 0.2810 | 0.2720 | 0.2427 | 0.2430 | 0.2686 | 0.2682 | |
| 1.9618 | 0.9688 | 1.0714 | 0.9677 | 1.0653 | 1.1184 | 0.9679 | 0.9678 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Lee, D.; Lee, S. Optimal Design of Formulas for a Single Degree of Freedom Tuned Mass Damper Parameter Using a Genetic Algorithm and H2 Norm. Biomimetics 2024, 9, 450. https://doi.org/10.3390/biomimetics9080450
Kim S, Lee D, Lee S. Optimal Design of Formulas for a Single Degree of Freedom Tuned Mass Damper Parameter Using a Genetic Algorithm and H2 Norm. Biomimetics. 2024; 9(8):450. https://doi.org/10.3390/biomimetics9080450
Chicago/Turabian StyleKim, Seunggoo, Donwoo Lee, and Seungjae Lee. 2024. "Optimal Design of Formulas for a Single Degree of Freedom Tuned Mass Damper Parameter Using a Genetic Algorithm and H2 Norm" Biomimetics 9, no. 8: 450. https://doi.org/10.3390/biomimetics9080450
APA StyleKim, S., Lee, D., & Lee, S. (2024). Optimal Design of Formulas for a Single Degree of Freedom Tuned Mass Damper Parameter Using a Genetic Algorithm and H2 Norm. Biomimetics, 9(8), 450. https://doi.org/10.3390/biomimetics9080450