Nature’s Load-Bearing Design Principles and Their Application in Engineering: A Review
Abstract
:1. Introduction
- Optimized through natural selection and tested diversity: Nature has been shaped by countless iterations of evolution, resulting in structures finely tuned to withstand the expected mechanical loads throughout an organism’s lifetime [1]. With several million organisms, nature offers a diverse array of optimized solutions under real conditions. Biological structures, though they might differ significantly from technical products, present coherent solutions pre-optimized for specific applications. By studying these evolutionary outcomes, engineers can leverage nature’s proven solutions to create structures that are equally well tailored to their intended operational mechanical load cases [2].
- Sustainable and resource-efficient: Nature excels in sustainable and resource-efficient solutions. Organisms evolve to minimize waste, maximize energy efficiency, and operate in harmony with their ecosystems. The combination of minimal material input and the use of materials that can be produced and degraded under physiological conditions, such as cellulose, chitin, lignin, silicate, calcium phosphate, and calcium carbonate, is particularly attractive for developing products within a circular economy framework [3]. These principles offer solutions for lightweight engineering designs that reduce ecological impact and promote sustainability—crucial in an era of resource scarcity and environmental degradation.
- Multi-functional, adaptable, and robust: Nature’s designs often display multi-functionality and adaptability, enabling efficient performance in diverse environments. For instance, diatom shells exhibit low weight, high mechanical resilience, and high permeability [4]. Such integrated functions have been challenging to optimize using conventional calculation tools. Technical lightweight products often assume very specific load cases, and methods such as topology optimization can provide excellent solutions for these scenarios. However, in reality, loads are versatile and include unexpected situations [5]. Natural lightweight structures are typically adapted to such variability by displaying complex, interconnected designs with minimal weaknesses, making them robust against deviations from anticipated load cases. This adaptability and robustness is especially relevant in load-bearing engineering components, which often need to respond to multiple loads and adapt to changing conditions.
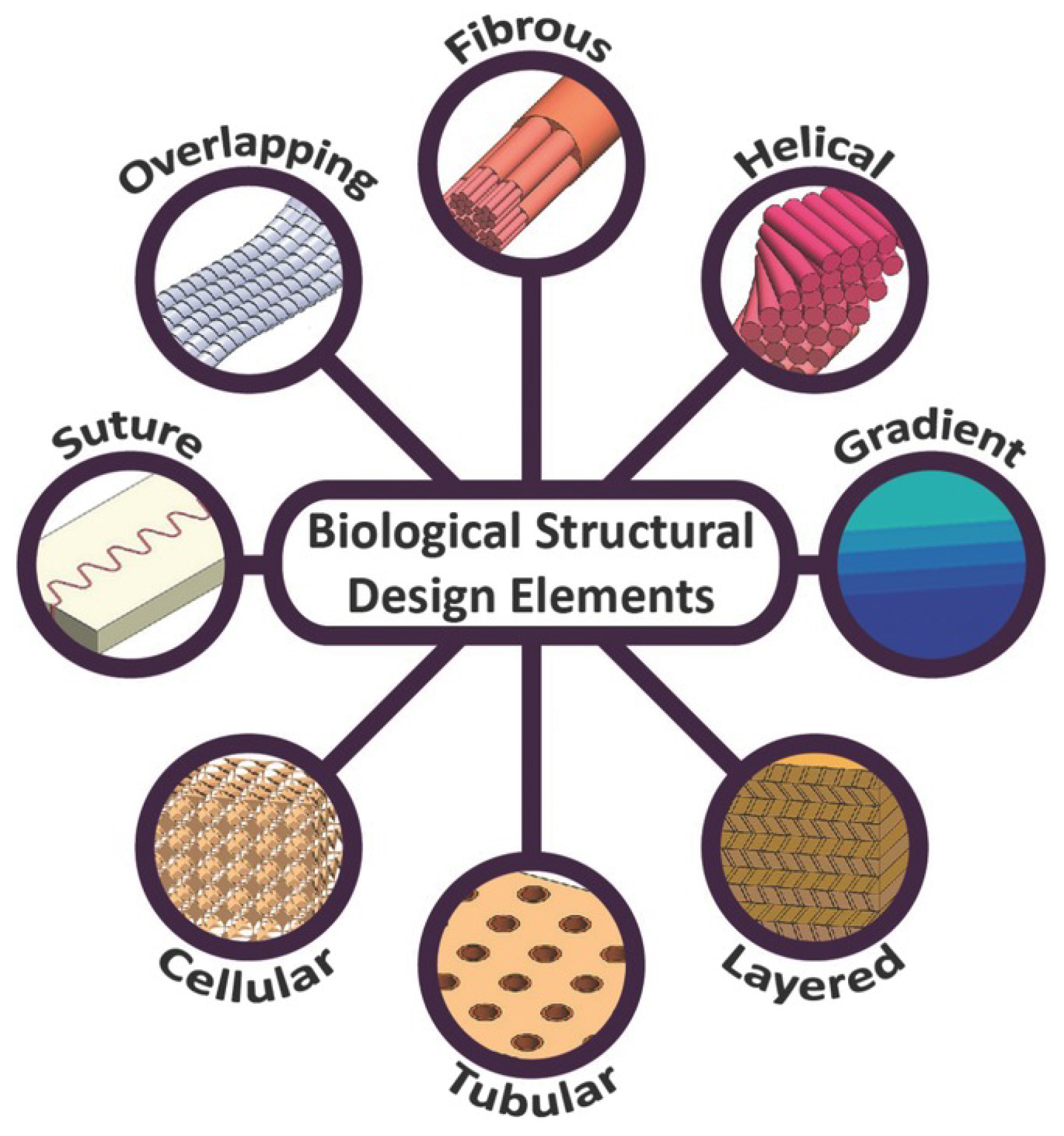
2. Hierarchically Structured Composites
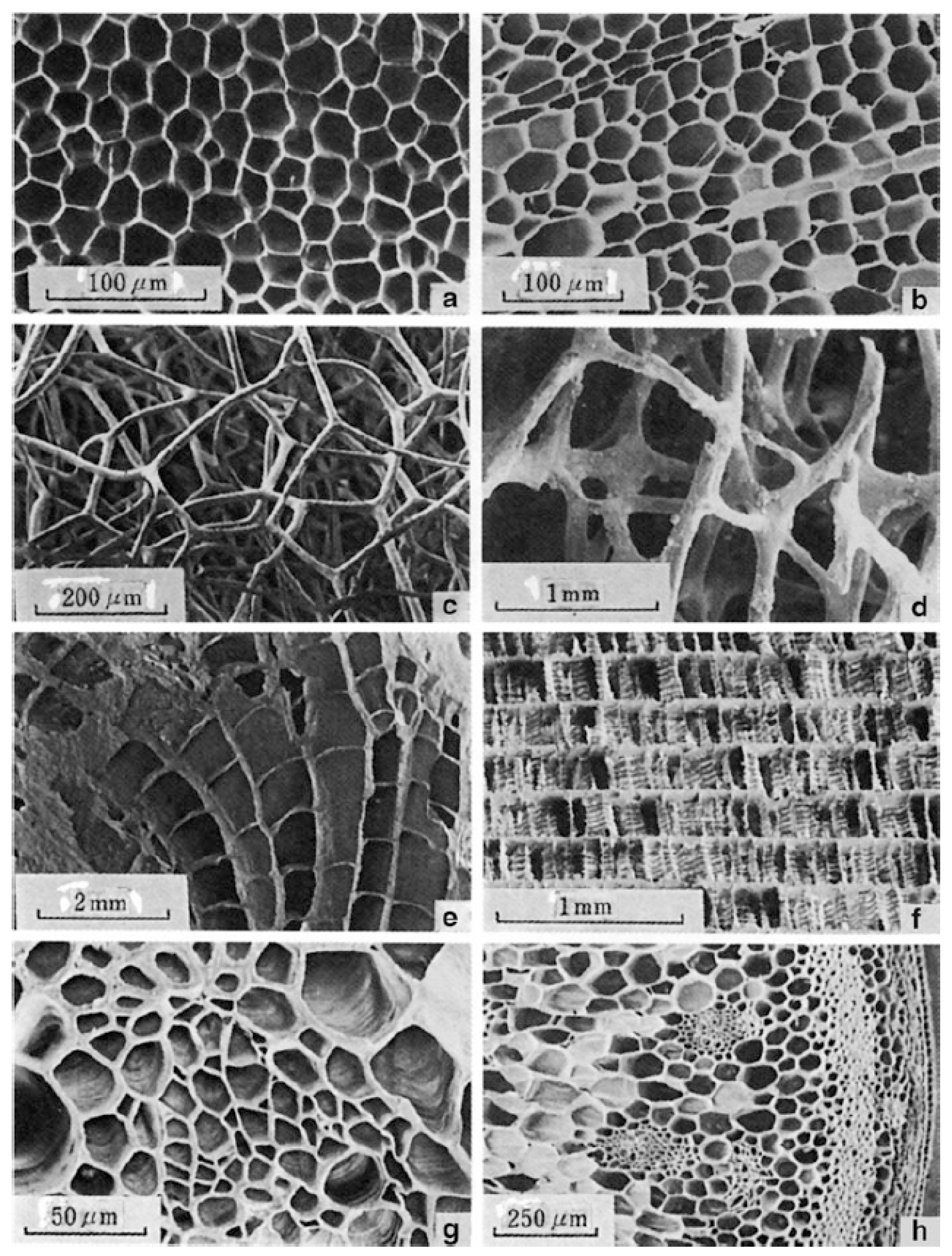
3. Cellular Structures
4. Functional Gradients
5. Hard Shell–Soft Core Architecture

6. Form Follows Function

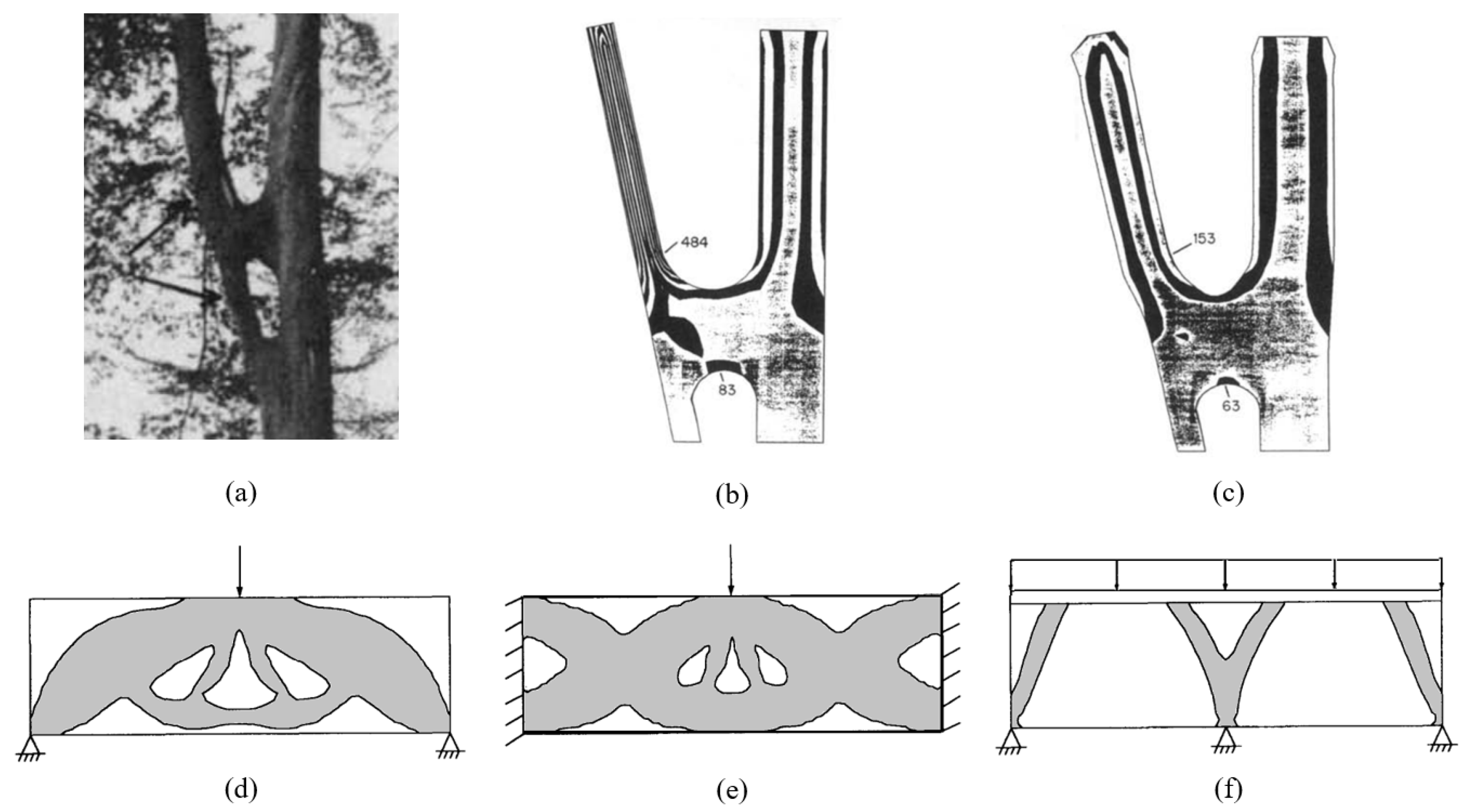
7. Robust Geometric Shapes
8. Challenges and Future Needs
9. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| CFD | Computational fluid dynamics |
| CT | Computed tomography |
| FEM | Finite element method |
| FGM | Functionally Graded Material |
| PSL | Principal stress line |
| SEM | Scanning electron microscopy |
| SKO | Soft kill option |
References
- Smetacek, V. A Watery Arms Race. Nature 2001, 411, 745. [Google Scholar] [CrossRef] [PubMed]
- Hamm, C. Evolution of Lightweight Structures: Analyses and Technical Applications; Springer: Dordrecht, Germany, 2015; Volume 6. [Google Scholar]
- Meyers, M.A.; Chen, P.Y.; Lin, A.Y.; Seki, Y. Biological Materials: Structure and Mechanical Properties. Prog. Mater. Sci. 2008, 53, 1–206. [Google Scholar] [CrossRef]
- Hamm, C.E.; Smetacek, V. Armor: Why, When and How? In Evolution of Primary Producers in the Sea; Falkowski, P., Knoll, A., Eds.; Elsevier: San Diego, CA, USA, 2007; pp. 311–332. [Google Scholar]
- Fang, J.; Sun, G.; Qiu, N.; Kim, N.H.; Li, Q. On Design Optimization for Structural Crashworthiness and its State of the Art. Struct. Multidiscip. Optim. 2017, 55, 1091–1119. [Google Scholar] [CrossRef]
- Purslow, P.P.; Vincent, J.F.V. Mechanical Properties of Primary Feathers from the Pigeon. J. Exp. Biol. 1978, 72, 251–260. [Google Scholar] [CrossRef]
- Smeathers, J.E.; Vincent, J.F.V. Mechanical Properties of Mussel Byssus Threads. J. Molluscan Stud. 1979, 45, 219–230. [Google Scholar] [CrossRef]
- Vincent, J.F. Insect Cuticle: A Paradigm for Natural Composites. Symp. Soc. Exp. Biol. 1980, 34, 183–210. [Google Scholar]
- Vincent, J.F.V. Fracture Properties of Plants. Adv. Bot. Res. 1990, 17, 235–287. [Google Scholar] [CrossRef]
- Lepora, N.F.; Verschure, P.; Prescott, T.J. The State of the Art in Biomimetics. Bioinspir. Biomimetics 2013, 8, 013001. [Google Scholar] [CrossRef]
- Ritchie, R. The Conflicts between Strength and Toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
- Gosline, J.M.; Guerette, P.A.; Ortlepp, C.S.; Savage, K.N. The Mechanical Design of Spider Silks: From Fibroin Sequence to Mechanical Function. J. Exp. Biol. 1999, 202, 3295–3303. [Google Scholar] [CrossRef]
- Vollrath, F. Strength and Structure of Spiders’ Silks. J. Biotechnol. 2000, 74, 67–83. [Google Scholar] [CrossRef] [PubMed]
- Olive, R.; Cohen, N. Deformation and Failure Mechanisms in Spider Silk Fibers. J. Mech. Phys. Solids 2024, 182, 105480. [Google Scholar] [CrossRef]
- Gosline, J.M.; DeMont, M.E.; Denny, M.W. The Structure and Properties of Spider Silk. Endeavour 1986, 10, 37–43. [Google Scholar] [CrossRef]
- Launey, M.E.; Buehler, M.J.; Ritchie, R.O. On the Mechanistic Origins of Toughness in Bone. Annu. Rev. Mater. Res. 2010, 40, 25–53. [Google Scholar] [CrossRef]
- Su, Y.; Shi, S.; Wang, C.; Wang, Z.; Li, P.; Zhang, S.; Fei, B.; Yang, Z.; Hu, J. Spider Silk-inspired Tough Materials: Multi-pathway Synthesis, Advanced Processing, and Functional Applications. Nano Today 2024, 55, 102188. [Google Scholar] [CrossRef]
- Lewis, R.V. Spider Silk: The Unraveling of a Mystery. Acc. Chem. Res. 1992, 25, 392–398. [Google Scholar] [CrossRef]
- Cranford, S.; Tarakanova, A.; Pugno, N.; Buehler, M. Nonlinear Material Behaviour of Spider Silk Yields Robust Webs. Nature 2012, 482, 72–76. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Sherman, V.; Gludovatz, B.; Schaible, E.; Stewart, P.J.; Ritchie, R. On the Tear Resistance of Skin. Nat. Commun. 2015, 6, 6649. [Google Scholar] [CrossRef]
- Masic, A.; Bertinetti, L.; Schuetz, R.; Galvis, L.; Timofeeva, N.; Dunlop, J.W.C.; Seto, J.; Hartmann, M.A.; Fratzl, P. Observations of Multiscale, Stress-Induced Changes of Collagen Orientation in Tendon by Polarized Raman Spectroscopy. Biomacromolecules 2011, 12, 3989–3996. [Google Scholar] [CrossRef] [PubMed]
- Gillies, A.R.; Lieber, R.L. Structure and Function of the Skeletal Muscle Extracellular Matrix. Muscle Nerve 2011, 44, 318–331. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Wu, Y.; Lu, S.; Yang, Z.; Huang, S. Spider-Silk-Inspired Heterogeneous Supramolecular Network with Strain-Stiffening, High Damping Capacity, and Supercontraction. Adv. Funct. Mater. 2023, 33, 2306071. [Google Scholar] [CrossRef]
- Vollrath, F.; Knight, D.P. Liquid Crystalline Spinning of Spider Silk. Nature 2001, 410, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Heim, M.; Keerl, D.; Scheibel, T. Spider Silk: From Soluble Protein to Extraordinary Fiber. Angew. Chem. Int. Ed. 2009, 48, 3584–3596. [Google Scholar] [CrossRef]
- Grunwald, I.; Rischka, K.; Kast, S.M.; Scheibel, T.; Bargel, H. Mimicking Biopolymers on a Molecular Scale: Nano(bio)technology Based on Engineered Proteins. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 1727–1747. [Google Scholar] [CrossRef]
- Branković, M.; Zivic, F.; Grujovic, N.; Stojadinovic, I.; Milenkovic, S.; Kotorcevic, N. Review of Spider Silk Applications in Biomedical and Tissue Engineering. Biomimetics 2024, 9, 169. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.; Li, F.; Zhu, Y.; Li, D.; Liu, X.; Wu, B.; Wu, H.A.; Fan, X.; Ji, X.; Chen, Y.; et al. Extremely Robust and Multifunctional Nanocomposite Fibers for Strain-Unperturbed Textile Electronics. Adv. Mater. 2023, 35, 2209527. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Wu, P. Hierarchically Structured Bioinspired Fibers Shaped by Liquid Droplets. Adv. Funct. Mater. 2024, 34, 2311704. [Google Scholar] [CrossRef]
- Liang, J.; Xu, J.; Zheng, J.; Zhou, L.; Yang, W.; Liu, E.; Zhu, Y.; Zhou, Q.; Liu, Y.; Wang, R.; et al. Bioinspired Mechanically Robust and Recyclable Hydrogel Microfibers Based on Hydrogen-Bond Nanoclusters. Adv. Sci. 2024, 11, 2401278. [Google Scholar] [CrossRef]
- Romaņuks, V.; Fridmanis, J.; Schmuck, B.; Bula, A.L.; Lends, A.; Senkane, K.; Leitis, G.; Gaidukovs, S.; Smits, K.; Rising, A.; et al. Biomimetic Spider Silk by Crosslinking and Functionalization with Multiarm Polyethylene Glycol. Adv. Funct. Mater. 2024, 2409487. [Google Scholar] [CrossRef]
- Chang, Z.; Shen, Y.; Xue, J.; Sun, Y.; Zhang, S. Fabrication of spider silk-inspired bio-based polymeric materials under dynamic nanoconfinement as high-strong, ultra-tough, and multifunctional plastic substitutes. Chem. Eng. J. 2023, 457, 140984. [Google Scholar] [CrossRef]
- Ollier, R.; Xiang, Y.; Yacovelli, A.; Webber, M. Biomimetic Strain-stiffening in Fully Synthetic Dynamic-covalent Hydrogel Networks. Chem. Sci. 2023, 14, 4796–4805. [Google Scholar] [CrossRef] [PubMed]
- Nath, D.; Ralhan, J.; Joseph, J.P.; Miglani, C.; Pal, A. Thermoresponsive Injectable Hydrogel to Mimic the Heat- and Strain-Stiffening Behavior of Biopolymers toward Muscle Cell Proliferation. Biomacromolecules 2024, 25, 853–863. [Google Scholar] [CrossRef] [PubMed]
- Kitchen, G.; Sun, B.; Kang, S. Bioinspired Nanocomposites with Self-adaptive Mechanical Properties. Nano Res. 2023, 17, 633–648. [Google Scholar] [CrossRef]
- Yu, L.; Huang, C.; Gong, Y.; Zheng, S.; Zhou, P.; Zhang, X.; Zou, Z.; Lyu, X. Ultrastretchable and Tough Poly(ionic liquid) Elastomer with Strain-Stiffening Ability Enabled by Strong/Weak Ionic Interactions. Macromolecules 2024, 57, 2339–2350. [Google Scholar] [CrossRef]
- Heuer, A.H.; Fink, D.J.; Laraia, V.J.; Arias, J.L.; Calvert, P.D.; Kendall, K.; Messing, G.L.; Blackwell, J.; Rieke, P.C.; Thompson, D.H.; et al. Innovative Materials Processing Strategies: A Biomimetic Approach. Science 1992, 255, 1098–1105. [Google Scholar] [CrossRef]
- McKittrick, J.; Chen, P.Y.; Tombolato, L.; Novitskaya, E.E.; Trim, M.W.; Hirata, G.A.; Olevsky, E.A.; Horstemeyer, M.F.; Meyers, M.A. Energy Absorbent Natural Materials and Bioinspired Design Strategies: A Review. Mater. Sci. Eng. C 2010, 30, 331–342. [Google Scholar] [CrossRef]
- Chen, P.Y.; McKittrick, J.; Meyers, M.A. Biological Materials: Functional Adaptations and Bioinspired Designs. Prog. Mater. Sci. 2012, 57, 1492–1704. [Google Scholar] [CrossRef]
- Mayer, G.; Sarikaya, M. Rigid Biological Composite Materials: Structural Examples for Biomimetic Design. Exp. Mech. 2002, 42, 395–403. [Google Scholar] [CrossRef]
- Vincent, J.; Wegst, U.G.K. Design and Mechanical Properties of Insect Cuticle. Arthropod Struct. Dev. 2004, 33, 187–199. [Google Scholar] [CrossRef]
- Chen, L.; Xu, W.; Lin, S.; Cheung, P.C.K. Cell Wall Structure of Mushroom Sclerotium (Pleurotus Tuber Regium): Part 1. Fractionation and Characterization of Soluble Cell Wall Polysaccharides. Food Hydrocoll. 2014, 36, 189–195. [Google Scholar] [CrossRef]
- Brunner, E.; Ehrlich, H.; Schupp, P.; Hedrich, R.; Hunoldt, S.; Kammer, M.; Machill, S.; Paasch, S.; Bazhenov, V.; Kurek, D.; et al. Chitin-Based Scaffolds are an Integral Part of the Skeleton of the Marine Demosponge Ianthella Basta. J. Struct. Biol. 2009, 168, 539–547. [Google Scholar] [CrossRef] [PubMed]
- Suneeta, K.; Rath, P.; Annamareddy, S. Chitosan from Shrimp Shell (Crangon crangon) and Fish Scales (Labeorohita): Extraction and Characterization. Afr. J. Biotechnol. 2016, 15, 1258–1268. [Google Scholar] [CrossRef]
- Rahman, A.; Halfar, J. First Evidence of Chitin in Calcified Coralline Algae: New Insights into the Calcification Process of Clathromorphum compactum. Sci. Rep. 2014, 4, 6162. [Google Scholar] [CrossRef] [PubMed]
- Ehrlich, H.; Worch, H. Sponges as Natural Composites: From Biomimetic Potential to Development of New Biomaterials. In Porifera Research: Biodiversity, Innovation and Sustainability; Custódio, M.R., Lobo-Hajdu, G., Hajdu, E., Muricy, G., Eds.; Museu Nacional (Brazil): Rio de Janeiro, Brazil, 2007; pp. 303–312. [Google Scholar]
- Park, H.; Schwartzman, A.F.; Tang, T.C.; Wang, L.; Lu, T.K. Ultra-lightweight Living Structural Material for Enhanced Stiffness and Environmental Sensing. Mater. Today Bio 2023, 18, 100504. [Google Scholar] [CrossRef] [PubMed]
- Naleway, S.E.; Porter, M.M.; McKittrick, J.; Meyers, M.A. Structural Design Elements in Biological Materials: Application to Bioinspiration. Adv. Mater. 2015, 27, 5455–5476. [Google Scholar] [CrossRef] [PubMed]
- Calvert, P. Biomimetic Ceramics and Composites. MRS Bull. 1992, 17, 37–40. [Google Scholar] [CrossRef]
- Raabe, D.; Sachs, C.; Romano, P. The Crustacean Exoskeleton as an Example of a Structurally and Mechanically Graded Biological Nanocomposite Material. Acta Mater. 2005, 53, 4281–4292. [Google Scholar] [CrossRef]
- Chen, B.; Peng, X.; Cai, C.; Niu, H.; Wu, X. Helicoidal Microstructure of Scarabaei Cuticle and Biomimetic Research. Mater. Sci. Eng. A 2006, 423, 237–242. [Google Scholar] [CrossRef]
- Weaver, J.C.; Milliron, G.W.; Miserez, A.; Evans-Lutterodt, K.; Herrera, S.; Gallana, I.; Mershon, W.J.; Swanson, B.; Zavattieri, P.; DiMasi, E.; et al. The Stomatopod Dactyl Club: A Formidable Damage-Tolerant Biological Hammer. Science 2012, 336, 1275–1280. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Y.; Zan, Q.; Guo, H.; Cai, S. Biomimetic Structure Design—A Possible Approach to Change the Brittleness of Ceramics in Nature. Mater. Sci. Eng. C 2000, 11, 9–12. [Google Scholar] [CrossRef]
- Mirzaeifar, R.; Dimas, L.; Qin, Z.; Buehler, M. Defect-Tolerant Bioinspired Hierarchical Composites: Simulation and Experiment. ACS Biomater. Sci. Eng. 2015, 1, 150414064726000. [Google Scholar] [CrossRef] [PubMed]
- Barthelat, F. The Fracture Mechanics of Biological Materials. In Mechanics and Physics of Fracture: Multiscale Modeling of the Failure Behavior of Solids; Ponson, L., Ed.; Springer International Publishing: Cham, Switzerland, 2023; pp. 255–282. [Google Scholar] [CrossRef]
- Wang, R.Z.; Suo, Z.; Evans, A.G.; Yao, N.; Aksay, I.A. Deformation Mechanisms in Nacre. J. Mater. Res. 2001, 16, 2485–2493. [Google Scholar] [CrossRef]
- Song, F.; Soh, A.K.; Bai, Y.L. Structural and Mechanical Properties of the Organic Matrix Layers of Nacre. Biomaterials 2003, 24, 3623–3631. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Bhushan, B. Hierarchical Structure and Mechanical Properties of Nacre: A Review. RSC Adv. 2012, 2, 7617–7632. [Google Scholar] [CrossRef]
- Gu, G.X.; Takaffoli, M.; Hsieh, A.J.; Buehler, M.J. Biomimetic Additive Manufactured Polymer Composites for Improved Impact Resistance. Extrem. Mech. Lett. 2016, 9, 317–323. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, L. 3D Printing of Biomimetic Composites with Improved Fracture Toughness. Acta Mater. 2019, 173, 61–73. [Google Scholar] [CrossRef]
- Feng, Q.; Cui, F.Z.; Pu, G.; Wang, R.Z.; Li, H.D. Crystal Orientation, Toughening Mechanisms and a Mimic of Nacre. Mater. Sci. Eng. C 2000, 11, 19–25. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Rim, J.E.; Barthelat, F.; Buehler, M.J. Merger of Structure and Material in Nacre and Bone—Perspectives on De Novo Biomimetic Materials. Prog. Mater. Sci. 2009, 54, 1059–1100. [Google Scholar] [CrossRef]
- Kakisawa, H.; Sumitomo, T. The Toughening Mechanism of Nacre and Structural Materials Inspired by Nacre. Sci. Technol. Adv. Mater. 2011, 12, 064710. [Google Scholar] [CrossRef]
- Huang, W.; Restrepo, D.; Jung, J.Y.; Su, F.Y.; Liu, Z.; Ritchie, R.O.; McKittrick, J.; Zavattieri, P.; Kisailus, D. Multiscale Toughening Mechanisms in Biological Materials and Bioinspired Designs. Adv. Mater. 2019, 31, e1901561. [Google Scholar] [CrossRef]
- Yang, F.; Xie, W.; Meng, S. Analysis and Simulation of Fracture Behavior in Naturally Occurring Bouligand Structures. Acta Biomater. 2021, 135, 473–482. [Google Scholar] [CrossRef]
- Chen, S.M.; Wen, S.M.; Zhang, S.C.; Wang, C.X.; Yu, S.H. Biological and Bioinspired Bouligand Structural Materials: Recent Advances and Perspectives. Matter 2024, 7, 378–407. [Google Scholar] [CrossRef]
- Ortiz, C.; Boyce, M.C. Bioinspired Structural Materials. Science 2008, 319, 1053–1054. [Google Scholar] [CrossRef]
- Studart, A.R. Towards High-Performance Bioinspired Composites. Adv. Mater. 2012, 24, 5024–5044. [Google Scholar] [CrossRef]
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.; Ritchie, R. Bioinspired Structural Materials. Nat. Mater. 2014, 14, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Wegst, U.G.K.; Ashby, M.F. The Mechanical Efficiency of Natural Materials. Philos. Mag. 2004, 84, 2167–2186. [Google Scholar] [CrossRef]
- Dörr, L.; Kohl, J.; Schweikert, M.; Lemloh, M.L. Unicellular Organisms with Versatile Solutions at the Micro-Scale: Functional Materials and Principles in Ciliates. Adv. Funct. Mater. 2023, 34, 2306113. [Google Scholar] [CrossRef]
- Fratzl, P.; Weinkamer, R. Nature’s Hierarchical Materials. Prog. Mater. Sci. 2007, 52, 1263–1334. [Google Scholar] [CrossRef]
- Fratzl, P. Biomimetic Materials Research: What Can We Really Learn from Nature’s Structural Materials? J. R. Soc. Interface R. Soc. 2007, 4, 637–642. [Google Scholar] [CrossRef]
- Munch, E.; Launey, M.E.; Alsem, D.H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Tough, Bio-Inspired Hybrid Materials. Science 2008, 322, 1516–1520. [Google Scholar] [CrossRef]
- Yao, H.B.; Fang, H.Y.; Wang, X.H.; Yu, S.H. Hierarchical Assembly of Micro-/Nano-Building Blocks: Bio-Inspired Rigid Structural Functional Materials. Chem. Soc. Rev. 2011, 40, 3764–3785. [Google Scholar] [CrossRef]
- Bonderer, L.J.; Studart, A.R.; Gauckler, L.J. Bioinspired Design and Assembly of Platelet Reinforced Polymer Films. Science 2008, 319, 1069–1073. [Google Scholar] [CrossRef]
- Bouville, F.; Maire, E.; Meille, S.; Van de Moortèle, B.; Stevenson, A.J.; Deville, S. Strong, Tough and Stiff Bioinspired Ceramics from Brittle Constituents. Nat. Mater. 2014, 13, 508–514. [Google Scholar] [CrossRef]
- Wei, J.; Pan, F.; Ping, H.; Yang, K.; Wang, Y.; Wang, Q.; Fu, Z. Bioinspired Additive Manufacturing of Hierarchical Materials: From Biostructures to Functions. Research 2023, 6, 0164. [Google Scholar] [CrossRef]
- Liang, X.; Chen, G.; Lei, I.M.; Zhang, P.; Wang, Z.; Chen, X.; Lu, M.; Zhang, J.; Wang, Z.; Sun, T.; et al. Impact-Resistant Hydrogels by Harnessing 2D Hierarchical Structures. Adv. Mater. 2023, 35, 2207587. [Google Scholar] [CrossRef]
- She, W.; Wu, Z.; Yang, J.; Pan, H.; Du, F.; Du, Z.; Miao, C. Cement-based Biomimetic Metamaterials. J. Build. Eng. 2024, 94, 110050. [Google Scholar] [CrossRef]
- Launey, M.; Munch, E.; Alsem, D.; Saiz, E.; Tomsia, A.; Ritchie, R. A Novel Biomimetic Approach to the Design of High-Performance Ceramic-Metal Composites. J. R. Soc. Interface 2009, 7, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Yaraghi, N.A.; Kisailus, D. Biomimetic Structural Materials: Inspiration from Design and Assembly. Annu. Rev. Phys. Chem. 2018, 69, 23–57. [Google Scholar] [CrossRef]
- Grunenfelder, L.K.; Suksangpanya, N.; Salinas, C.; Milliron, G.; Yaraghi, N.; Herrera, S.; Evans-Lutterodt, K.; Nutt, S.R.; Zavattieri, P.; Kisailus, D. Bio-Inspired Impact-Resistant Composites. Acta Biomater. 2014, 10, 3997–4008. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Venugopal, J.R.; El-Turki, A.; Ramakrishna, S.; Su, B.; Lim, C.T. Electrospun Biomimetic Nanocomposite Nanofibers of Hydroxyapatite/Chitosan for Bone Tissue Engineering. Biomaterials 2008, 29, 4314–4322. [Google Scholar] [CrossRef]
- Zhang, P.; Heyne, M.A.; To, A.C. Biomimetic Staggered Composites with Highly Enhanced Energy Dissipation: Modeling, 3D Printing, and Testing. J. Mech. Phys. Solids 2015, 83, 285–300. [Google Scholar] [CrossRef]
- Ghazlan, A.; Ngo, T.; Tan, P.; Xie, Y.M.; Tran, P.; Donough, M. Inspiration from Nature’s Body Armours—A Review of Biological and Bioinspired Composites. Compos. Part B Eng. 2021, 205, 108513. [Google Scholar] [CrossRef]
- Gu, G.X.; Takaffoli, M.; Buehler, M.J. Hierarchically Enhanced Impact Resistance of Bioinspired Composites. Adv. Mater. 2017, 29, 1700060. [Google Scholar] [CrossRef]
- Studart, A.R. Biological and Bioinspired Composites with Spatially Tunable Heterogeneous Architectures. Adv. Funct. Mater. 2013, 23, 4423–4436. [Google Scholar] [CrossRef]
- Martin, J.; Fiore, B.; Erb, R. Designing Bioinspired Composite Reinforcement Architectures via 3D Magnetic Printing. Nat. Commun. 2015, 6, 8641. [Google Scholar] [CrossRef]
- Chen, L.; Ballarini, R.; Kahn, H.; Heuer, A.H. Bioinspired Micro-Composite Structure. J. Mater. Res. 2007, 22, 124–131. [Google Scholar] [CrossRef]
- Dimas, L.; Buehler, M. Modeling and Additive Manufacturing of Bio-Inspired Composites with Tunable Fracture Mechanical Properties. Soft Matter 2014, 10, 4436–4442. [Google Scholar] [CrossRef] [PubMed]
- Zorzetto, L.; Ruffoni, D. Wood-Inspired 3D-Printed Helical Composites with Tunable and Enhanced Mechanical Performance. Adv. Funct. Mater. 2018, 29, 1805888. [Google Scholar] [CrossRef]
- Chen, Y.; Dang, B.; Wang, C.; Wang, Y.; Yang, Y.; Liu, M.; Bi, H.; Sun, D.; Li, Y.; Li, J.; et al. Intelligent Designs from Nature: Biomimetic Applications in Wood Technology. Prog. Mater. Sci. 2023, 139, 101164. [Google Scholar] [CrossRef]
- Cheng, Q.; Yin, J.; Wen, J.; Yu, D. Mechanical Properties of 3D-printed Hierarchical Structures Based on Sierpinski Triangles. Int. J. Mech. Sci. 2023, 247, 108172. [Google Scholar] [CrossRef]
- Han, S.; Xu, H.; Chen, F.; Wang, G. Construction Relationship between a Functionally Graded Structure of Bamboo and its Strength and Toughness: Underlying Mechanisms. Constr. Build. Mater. 2023, 379, 131241. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, X.X.; Wu, K.; Li, Z.; Lin, Y.; Liang, X.; Yang, Q.; Liu, T. Damping Chitin Hydrogels by Harnessing Insect-cuticle-inspired Hierarchical Structures. Cell Rep. Phys. Sci. 2023, 4, 101644. [Google Scholar] [CrossRef]
- Han, S.; He, Y.; Ye, H.; Ren, X.; Chen, F.; Liu, K.; Shi, S.; Wang, G. Mechanical Behavior of Bamboo, and its Biomimetic Composites and Structural Members: A Systematic Review. J. Bionic Eng. 2023, 21. [Google Scholar] [CrossRef]
- Shi, P.; Shen, Z.; Wang, H.; Li, Z.; Gu, Y.; Li, Y.; Yan, J.; Lin, Z.; Wang, M.; Yang, Y.; et al. Bioinspired, Heredity-derived Hierarchical Bulk Multifunctional Copper Alloys. Mater. Today 2023, 71, 22–37. [Google Scholar] [CrossRef]
- Vijayan, P.P.; Puglia, D. Biomimetic Multifunctional Materials: A Review. Emergent Mater. 2019, 2, 391–415. [Google Scholar] [CrossRef]
- Thein-Han, W.W.; Misra, R.D.K. Biomimetic Chitosan–Nanohydroxyapatite Composite Scaffolds for Bone Tissue Engineering. Acta Biomater. 2009, 5, 1182–1197. [Google Scholar] [CrossRef]
- Fernandez, J.G.; Ingber, D.E. Bioinspired Chitinous Material Solutions for Environmental Sustainability and Medicine. Adv. Funct. Mater. 2013, 23, 4454–4466. [Google Scholar] [CrossRef]
- Weiner, S.; Traub, W. Organization of Hydroxyapatite Crystals within Collagen Fibrils. FEBS Lett. 1986, 206, 262–266. [Google Scholar] [CrossRef]
- Weiner, S.; Traub, W. Bone Structure: From Ångstroms to Microns. FASEB J. 1992, 6, 879–885. [Google Scholar] [CrossRef]
- Yeni, Y.N.; Brown, C.U.; Wang, Z.; Norman, T.L. The Influence of Bone Morphology on Fracture Toughness of the Human Femur and Tibia. Bone 1997, 21, 453–459. [Google Scholar] [CrossRef]
- Ritchie, R.O.; Buehler, M.J.; Hansma, P. Plasticity and Toughness in Bone. Phys. Today 2009, 62, 41–47. [Google Scholar] [CrossRef]
- Guarino, V.; Gloria, A.; Raucci, M.G.; De Santis, R.; Ambrosio, L. Bio-Inspired Composite and Cell Instructive Platforms for Bone Regeneration. Int. Mater. Rev. 2012, 57, 256–275. [Google Scholar] [CrossRef]
- Wu, S.; Liu, X.; Yeung, K.W.K.; Liu, C.; Yang, X. Biomimetic Porous Scaffolds for Bone Tissue Engineering. Mater. Sci. Eng. R Rep. 2014, 80, 1–36. [Google Scholar] [CrossRef]
- Libonati, F.; Colombo, C.; Vergani, L. Design and Characterization of a Biomimetic Composite Inspired to Human Bone. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 772–781. [Google Scholar] [CrossRef]
- Libonati, F.; Vellwock, A.E.; Ielmini, F.; Abliz, D.; Ziegmann, G.; Vergani, L. Bone-Inspired Enhanced Fracture Toughness of De Novo Fiber Reinforced Composites. Sci. Rep. 2019, 9, 3142. [Google Scholar] [CrossRef]
- Tonsomboon, K.; Butcher, A.L.; Oyen, M.L. Strong and Tough Nanofibrous Hydrogel Composites Based on Biomimetic Principles. Mater. Sci. Eng. C 2017, 72, 220–227. [Google Scholar] [CrossRef]
- Kayacan, M.Y.; Üzün, A. Ballistic Performance of Novel Design of Bulletproof Plates Inspired by Biomimetic Approaches. Polym. Adv. Technol. 2023, 34, 299–316. [Google Scholar] [CrossRef]
- Stagni, A.; Trevisan, G.; Vergani, L.; Libonati, F. Bone Osteon-like Structures: A Biomimetic Approach Towards Multiscale Fiber-reinforced Composite Structures. Compos. Sci. Technol. 2024, 254, 110669. [Google Scholar] [CrossRef]
- Rho, J.Y.; Kuhn-Spearing, L.; Zioupos, P. Mechanical Properties and the Hierarchical Structure of Bone. Med. Eng. Phys. 1998, 20, 92–102. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Ashby, M.F.; Medalist, R.F.M. The Mechanical Properties of Cellular Solids. Metall. Mater. Trans. A 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Yang, T.; Jia, Z.; Wu, Z.; Chen, H.; Deng, Z.; Chen, L.; Zhu, Y.; Li, L. High Strength and Damage-tolerance in Echinoderm Stereom as a Natural Bicontinuous Ceramic Cellular Solid. Nat. Commun. 2022, 13, 6083. [Google Scholar] [CrossRef] [PubMed]
- Wallach, J.C.; Gibson, L.J. Mechanical Behavior of a Three-Dimensional Truss Material. Int. J. Solids Struct. 2001, 38, 7181–7196. [Google Scholar] [CrossRef]
- Kooistra, G.W.; Deshpande, V.S.; Wadley, H.N.G. Compressive Behavior of Age Hardenable Tetrahedral Lattice Truss Structures Made from Aluminium. Acta Mater. 2004, 52, 4229–4237. [Google Scholar] [CrossRef]
- Queheillalt, D.T.; Wadley, H.N.G. Pyramidal Lattice Truss Structures with Hollow Trusses. Mater. Sci. Eng. A 2005, 397, 132–137. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Young, P.; Raymont, D. Advanced Lightweight 316L Stainless Steel Cellular Lattice Structures Fabricated via Selective Laser Melting. Mater. Des. 2014, 55, 533–541. [Google Scholar] [CrossRef]
- Cao, X.; Duan, S.; Liang, J.; Wen, W.; Fang, D. Mechanical Properties of an Improved 3D-Printed Rhombic Dodecahedron Stainless Steel Lattice Structure of Variable Cross Section. Int. J. Mech. Sci. 2018, 145, 53–63. [Google Scholar] [CrossRef]
- Wang, P.; Yang, F.; Zheng, B.; Li, P.; Wang, R.; Li, Y.; Fan, H.; Li, X. Breaking the Tradeoffs between Different Mechanical Properties in Bioinspired Hierarchical Lattice Metamaterials. Adv. Funct. Mater. 2023, 33, 2305978. [Google Scholar] [CrossRef]
- Suresh, A.; Rowan, S.J.; Liu, C. Macroscale Fabrication of Lightweight and Strong Porous Carbon Foams through Template-Coating Pair Design. Adv. Mater. 2023, 35, 2206416. [Google Scholar] [CrossRef]
- Breish, F.; Hamm, C.; Kienzler, R. Diatom-inspired Stiffness Optimization for Plates and Cellular Solids. Bioinspiration Biomim. 2023, 18, 036004. [Google Scholar] [CrossRef]
- Bilhère-Dieuzeide, M.; Chaves-Jacob, J.; Buhon, E.; Biguet-Mermet, G.; Linares, J.M. Performance Domains of Bio-inspired and Triangular Lattice Patterns to Optimize the Structures’ Stiffness. Heliyon 2024, 10. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Campoli, G.; Yavari, S.A.; Sajadi, B.; Wauthle, R.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Mechanical Behavior of Regular Open-Cell Porous Biomaterials Made of Diamond Lattice Unit Cells. J. Mech. Behav. Biomed. Mater. 2014, 34, 106–115. [Google Scholar] [CrossRef]
- Shidid, D.; Leary, M.; Choong, P.; Brandt, M. Just-in-Time Design and Additive Manufacture of Patient-Specific Medical Implants. Phys. Procedia 2016, 83, 4–14. [Google Scholar] [CrossRef]
- Alabort, E.; Barba, D.; Reed, R.C. Design of Metallic Bone by Additive Manufacturing. Scr. Mater. 2019, 164, 110–114. [Google Scholar] [CrossRef]
- Olmo, E.; Grande, E.; Samartin, C.R.; Bezdenejnykh, M.; Torres, J.; Blanco, N.; Frovel, M.; Cañas, J. Lattice Structures for Aerospace Applications. In Proceedings of the 12th European Conference on Spacecraft Structures, Materials and Environmental Testing, Noordwijk, The Netherlands, 20–23 March 2012; Volume 691. [Google Scholar]
- Bici, M.; Brischetto, S.; Campana, F.; Ferro, C.G.; Seclì, C.; Varetti, S.; Maggiore, P.; Mazza, A. Development of a Multifunctional Panel for Aerospace Use through SLM Additive Manufacturing. Procedia CIRP 2018, 67, 215–220. [Google Scholar] [CrossRef]
- Voicu, A.D.; Hadăr, A.; Vlăsceanu, D. Benefits of 3D Printing Technologies for Aerospace Lattice Structures. Sci. Bull. “Mircea Cel Batran” Nav. Acad. 2021, 24, 8–16. [Google Scholar] [CrossRef]
- Thomas, J.; Alsaleh, N.A.; Ahmadein, M.; Elfar, A.A.; Farouk, H.A.; Essa, K. Graded Cellular Structures for Enhanced Performance of Additively Manufactured Orthopaedic Implants. Int. J. Adv. Manuf. Technol. 2024, 130, 1887–1900. [Google Scholar] [CrossRef]
- Tan, S.L.A.; Zhao, M.; Li, Z.; Wang, Z.; Li, X.; Zhai, W. Horsetail-inspired Lattice Structures for Bone Scaffold Applications. Int. J. Bioprinting 2024, 10, 2326. [Google Scholar] [CrossRef]
- Chang, C.M.; Wong, P.C.; Ou, S.L.; Ko, C.E.; Wang, Y.T. Optimizing Implant Lattice Design for Large Distal Femur Defects: Stimulating Interface Bone Growth to Enhance Osseointegration. Int. J. Bioprinting 2024, 10, 2590. [Google Scholar] [CrossRef]
- Khan, N.; Riccio, A. A Systematic Review of Design for Additive Manufacturing of Aerospace Lattice Structures: Current Trends and Future Directions. Prog. Aerosp. Sci. 2024, 149, 101021. [Google Scholar] [CrossRef]
- Rastegarzadeh, S.; Huang, J.; Wang, J. Architected Cellular Materials for Aerospace Components Design and Manufacturing. In Proceedings of the ASME Aerospace Structures, Structural Dynamics, and Materials Conference, 2023, San Diego, CA, USA, 19–21 June 2023; Volume 87141, p. V001T01A007. [Google Scholar]
- Wootton, R. The Geometry and Mechanics of Insect Wing Deformations in Flight: A Modelling Approach. Insects 2020, 11, 446. [Google Scholar] [CrossRef]
- Sack, L.; Scoffoni, C. Leaf Venation: Structure, Function, Development, Evolution, Ecology and Applications in the Past, Present and Future. New Phytol. 2013, 198, 983–1000. [Google Scholar] [CrossRef] [PubMed]
- Roth-Nebelsick, A.; Uhl, D.; Mosbrugger, V.; Kerp, H. Evolution and Function of Leaf Venation Architecture: A Review. Ann. Bot. 2001, 87, 553–566. [Google Scholar] [CrossRef]
- Sun, J.; Bhushan, B. The Structure and Mechanical Properties of Dragonfly Wings and Their Role on Flyability. Comptes Rendus Mécanique 2012, 340, 3–17. [Google Scholar] [CrossRef]
- Jongerius, S.; Lentink, D. Structural Analysis of a Dragonfly Wing. Exp. Mech. 2010, 50, 1323–1334. [Google Scholar] [CrossRef]
- Lin, S.; Chou, N.; Li, G.; Bao, D.; Cai, Y.; Xie, Y.M.; Wang, G. A Gradient-Evolutionary Coupled Topology Optimization for Sheet Reinforcement Based on the Mechanics of Voronoi Pattern on Dragonfly Wings. Adv. Eng. Softw. 2024, 190, 103600. [Google Scholar] [CrossRef]
- Kawabe, H.; Aoki, Y.; Nakamura, T. Novel Skin-Reinforcement Design by Cross–Longitudinal Layout Inspired by Dragonfly Wing. AIAA J. 2024, 62, 1311–1317. [Google Scholar] [CrossRef]
- Kawabe, H.; Aoki, Y.; Sugimoto, S.; Nakamura, T. Application of Macroscopic Structures on Dragonfly Wings to an Aircraft Design Approach. In Proceedings of the AIAA Aviation 2020 Forum, Virtual, 15–19 June 2020; p. 2664. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, J.; Hou, Y.; Breitkopf, P.; Zhu, J.; Zhang, W. Revisiting the Fibonacci Spiral Pattern for Stiffening Rib Design. Int. J. Mech. Sci. 2023, 246, 108131. [Google Scholar] [CrossRef]
- Linnemann, S.K.; Friedrichs, L.; Niebuhr, N.M. Stress-Adaptive Stiffening Structures Inspired by Diatoms: A Parametric Solution for Lightweight Surfaces. Biomimetics 2024, 9, 46. [Google Scholar] [CrossRef]
- Andresen, S.; Meyners, N.; Thoden, D.; Körfer, M.; Hamm, C. Biologically Inspired Girder Structure for the Synchrotron Radiation Facility PETRA IV. J. Bionic Eng. 2023, 20, 1996–2017. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Jacobsen, A.J.; Torrents, A.; Sorensen, A.E.; Lian, J.; Greer, J.R.; Valdevit, L.; Carter, W.B. Ultralight Metallic Microlattices. Science 2011, 334, 962–965. [Google Scholar] [CrossRef]
- Song, J.; Xu, S.; Xu, L.; Zhou, J.; Zou, M. Experimental Study on the Crashworthiness of Bio-Inspired Aluminum Foam-Filled Tubes under Axial Compression Loading. Thin-Walled Struct. 2020, 155, 106937. [Google Scholar] [CrossRef]
- Du, Y.; Gu, D.; Xi, L.; Dai, D.; Gao, T.; Zhu, J.; Ma, C. Laser Additive Manufacturing of Bio-Inspired Lattice Structure: Forming Quality, Microstructure and Energy Absorption Behavior. Mater. Sci. Eng. A 2020, 773, 138857. [Google Scholar] [CrossRef]
- Xiang, X.; Zou, S.; San Ha, N.; Lu, G.; Kong, I. Energy Absorption of Bio-Inspired Multi-Layered Graded Foam-Filled Structures Under Axial Crushing. Compos. Part B Eng. 2020, 198, 108216. [Google Scholar] [CrossRef]
- Thielen, M.; Schmitt, C.N.Z.; Eckert, S.; Speck, T.; Seidel, R. Structure–Function Relationship of the Foam-Like Pomelo Peel (Citrus maxima)—An Inspiration for the Development of Biomimetic Damping Materials with High Energy Dissipation. Bioinspir. Biomimetics 2013, 8, 025001. [Google Scholar] [CrossRef]
- Li, T.T.; Wang, H.; Huang, S.Y.; Lou, C.W.; Lin, J.H. Bioinspired Foam Composites Resembling Pomelo Peel: Structural Design and Compressive, Bursting and Cushioning Properties. Compos. Part B Eng. 2019, 172, 290–298. [Google Scholar] [CrossRef]
- San Ha, N.; Lu, G. A Review of Recent Research on Bio-Inspired Structures and Materials for Energy Absorption Applications. Compos. Part B Eng. 2020, 181, 107496. [Google Scholar] [CrossRef]
- Sharma, D.; Hiremath, S.S. Bio-Inspired Repeatable Lattice Structures for Energy Absorption: Experimental and Finite Element Study. Compos. Struct. 2022, 283, 115102. [Google Scholar] [CrossRef]
- Dara, A.; Bahubalendruni, M.A.R.; Mertens, A.J.; Balamurali, G. Numerical and Experimental Investigations of Novel Nature Inspired Open Lattice Cellular Structures for Enhanced Stiffness and Specific Energy Absorption. Mater. Today Commun. 2022, 31, 103286. [Google Scholar] [CrossRef]
- Kumar, A.; Collini, L.; Ursini, C.; Jeng, J.Y. Energy Absorption and Stiffness of Thin and Thick-Walled Closed-Cell 3D-Printed Structures Fabricated from a Hyperelastic Soft Polymer. Materials 2022, 15, 2441. [Google Scholar] [CrossRef]
- Hamzehei, R.; Zolfagharian, A.; Dariushi, S.; Bodaghi, M. 3D-printed Bio-inspired Zero Poisson’s Ratio Graded Metamaterials with High Energy Absorption Performance. Smart Mater. Struct. 2022, 31, 035001. [Google Scholar] [CrossRef]
- Ramakrishna, D.; Murali, G.B. Bio-inspired 3D-printed Lattice Structures for Energy Absorption Applications: A Review. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2023, 237, 503–542. [Google Scholar] [CrossRef]
- Yin, H.; Meng, F.; Zhu, L.; Wen, G. Optimization Design of a Novel Hybrid Hierarchical Cellular Structure for Crashworthiness. Compos. Struct. 2023, 303, 116335. [Google Scholar] [CrossRef]
- Pham, B.; Huang, S.C. A Novel Bio-inspired Hierarchical Tetrachiral Structure That Enhances Energy Absorption Capacity. J. Mech. Sci. Technol. 2023, 37. [Google Scholar] [CrossRef]
- Xiang, X.; Shao, D.; Pang, T.; Ngo, T.T.; Ha, N.S.; Zhang, S. Energy Absorption of Multilayer Aluminum Foam-filled Structures Under Lateral Compression Loading. Mech. Adv. Mater. Struct. 2024, 31, 659–675. [Google Scholar] [CrossRef]
- Huang, J.; Durden, H.; Chowdhury, M. Bio-Inspired Armor Protective Material Systems for Ballistic Shock Mitigation. Mater. Des. 2011, 32, 3702–3710. [Google Scholar] [CrossRef]
- Xu, T.; Liu, N.; Yu, Z.; Xu, T.; Zou, M. Crashworthiness Design for Bionic Bumper Structures Inspired by Cattail and Bamboo. Appl. Bionics Biomech. 2017, 2017, 5894938. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.Y.; Li, Y.; Zhao, W.Z.; Zou, S.C.; Zhou, G.; Wang, Y.L. Structure Design and Multi-Objective Optimization of a Novel Crash Box Based on Biomimetic Structure. Int. J. Mech. Sci. 2018, 138, 489–501. [Google Scholar] [CrossRef]
- Nian, Y.; Wan, S.; Wang, X.; Zhou, P.; Avcar, M.; Li, M. Study on Crashworthiness of Nature-Inspired Functionally Graded Lattice Metamaterials for Bridge Pier Protection Against Ship Collision. Eng. Struct. 2023, 277, 115404. [Google Scholar] [CrossRef]
- Essa, K.; Hassanin, H.; Attallah, M.M.; Adkins, N.J.; Musker, A.J.; Roberts, G.T.; Tenev, N.; Smith, M. Development and Testing of an Additively Manufactured Monolithic Catalyst Bed for HTP Thruster Applications. Appl. Catal. A Gen. 2017, 542, 125–135. [Google Scholar] [CrossRef]
- Busse, C.; Freund, H.; Schwieger, W. Intensification of Heat Transfer in Catalytic Reactors by Additively Manufactured Periodic Open Cellular Structures (POCS). Chem. Eng. Process.-Process. Intensif. 2018, 124, 199–214. [Google Scholar] [CrossRef]
- Haseltalab, V.; Dutta, A.; Yang, S. On the 3D Printed Catalyst for Biomass-bio-oil Conversion: Key Technologies and Challenges. J. Catal. 2023, 417, 286–300. [Google Scholar] [CrossRef]
- Zhao, X.; Karakaya, C.; Qian, M.; Zou, R.; Zhang, W.; Lu, Z.; Maiti, D.; Samanta, A.; Wan, W.; Liu, X.; et al. 3D Printing Synthesis of Catalysts. Mater. Today Sustain. 2024, 26, 100746. [Google Scholar] [CrossRef]
- Kim, T.; Zhao, C.Y.; Lu, T.J.; Hodson, H.P. Convective Heat Dissipation with Lattice-Frame Materials. Mech. Mater. 2004, 36, 767–780. [Google Scholar] [CrossRef]
- Maloney, K.J.; Fink, K.D.; Schaedler, T.A.; Kolodziejska, J.A.; Jacobsen, A.J.; Roper, C.S. Multifunctional Heat Exchangers Derived From Three-Dimensional Micro-Lattice Structures. Int. J. Heat Mass Transf. 2012, 55, 2486–2493. [Google Scholar] [CrossRef]
- Careri, F.; Khan, R.H.; Todd, C.; Attallah, M.M. Additive Manufacturing of Heat Exchangers in Aerospace Applications: A Review. Appl. Therm. Eng. 2023, 235, 121387. [Google Scholar] [CrossRef]
- Brambati, G.; Guilizzoni, M.; Foletti, S. Convective Heat Transfer Correlations for Triply Periodic Minimal Surfaces Based Heat Exchangers. Appl. Therm. Eng. 2024, 242, 122492. [Google Scholar] [CrossRef]
- Zhu, H.X.; Hobdell, J.R.; Windle, A.H. Effects of Cell Irregularity on the Elastic Properties of 2D Voronoi Honeycombs. J. Mech. Phys. Solids 2001, 49, 857–870. [Google Scholar] [CrossRef]
- Zhu, H.X.; Thorpe, S.M.; Windle, A.H. The Geometrical Properties of Irregular Two-Dimensional Voronoi Tessellations. Philos. Mag. A 2001, 81, 2765–2783. [Google Scholar] [CrossRef]
- van Egmond, D.A.; Yu, B.; Choukir, S.; Fu, S.; Singh, C.V.; Hibbard, G.; Hatton, B.D. The Benefits of Structural Disorder in Natural Cellular Solids. arXiv 2021, arXiv:2110.04607. [Google Scholar]
- Andresen, S.; Bäger, A.; Hamm, C. Eigenfrequency Maximisation by Using Irregular Lattice Structures. J. Sound Vib. 2020, 465, 115027. [Google Scholar] [CrossRef]
- Choukir, S.; Aranguren van Egmond, D.; Hatton, B.D.; Hibbard, G.D.; Singh, C.V. The Interplay between Constituent Material and Architectural Disorder in Bioinspired Honeycomb Structures. Int. J. Eng. Sci. 2023, 188, 103863. [Google Scholar] [CrossRef]
- Montemayor, L.C.; Wong, W.H.; Zhang, Y.W.; Greer, J.R. Insensitivity to Flaws Leads to Damage Tolerance in Brittle Architected Meta-Materials. Sci. Rep. 2016, 6, 20570. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Liao, W.; Dai, N.; Xie, Y.M. Anisotropic Design and Optimization of Conformal Gradient Lattice Structures. CAD Comput. Aided Des. 2020, 119, 102787. [Google Scholar] [CrossRef]
- Yang, H.; Cao, X.; Zhang, Y.; Li, Y. 3D-printed Bioinspired Cage Lattices with Defect-tolerant Mechanical Properties. Addit. Manuf. 2024, 82, 104036. [Google Scholar] [CrossRef]
- Kiakojouri, F.; De Biagi, V.; Abbracciavento, L. Design for Robustness: Bio-Inspired Perspectives in Structural Engineering. Biomimetics 2023, 8, 95. [Google Scholar] [CrossRef]
- De Biagi, V. Enhancing Structural Robustness by Complexity Maximisation. In Vestnik TSUAB. English Version Appendix; Politecnico di Torino: Turin, Italy, 2015; pp. 26–36. [Google Scholar]
- Huber, J.A.; Ekevad, M.; Girhammar, U.A.; Berg, S. Structural Robustness and Timber Buildings—A Review. Wood Mater. Sci. Eng. 2019, 14, 107–128. [Google Scholar] [CrossRef]
- Liu, Z.; Meyers, M.A.; Zhang, Z.; Ritchie, R.O. Functional Gradients and Heterogeneities in Biological Materials: Design Principles, Functions, and Bioinspired Applications. Prog. Mater. Sci. 2017, 88, 467–498. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing and Applications; Springer Science & Business Media: New York, NY, USA, 2013; Volume 5. [Google Scholar]
- Han, S.; Chen, F.; Yu, Y.; Chen, L.; Wang, G. Bamboo-inspired Strong, Tough and Stable Composites Derived from Renewable Bamboo. Ind. Crop. Prod. 2023, 194, 116292. [Google Scholar] [CrossRef]
- Mao, A.; Chen, J.; Bu, X.; Tian, L.; Gao, W.; Saiz, E.; Bai, H. Bamboo-Inspired Structurally Efficient Materials with a Large Continuous Gradient. Small 2023, 19, 2301144. [Google Scholar] [CrossRef]
- Keaveny, T.M.; Hayes, W.C. A 20-Year Perspective on the Mechanical Properties of Trabecular Bone. J. Biomech. Eng. 1993, 115, 534–542. [Google Scholar] [CrossRef]
- Keller, T.S.; Mao, Z.; Spengler, D.M. Young’s Modulus, Bending Strength, and Tissue Physical Properties of Human Compact Bone. J. Orthop. Res. 1990, 8, 592–603. [Google Scholar] [CrossRef] [PubMed]
- Aizenberg, J.; Weaver, J.; Thanawala, M.; Sundar, V.; Morse, D.; Fratzl, P. Skeleton of Euplectella sp: Structural Hierarchy from the Nanoscale to the Macroscale. Science 2005, 309, 275–278. [Google Scholar] [CrossRef] [PubMed]
- Miserez, A.; Weaver, J.C.; Thurner, P.J.; Aizenberg, J.; Dauphin, Y.; Fratzl, P.; Morse, D.E.; Zok, F.W. Effects of Laminate Architecture on Fracture Resistance of Sponge Biosilica: Lessons from Nature. Adv. Funct. Mater. 2008, 18, 1241–1248. [Google Scholar] [CrossRef]
- Mortensen, A.; Suresh, S. Functionally Graded Metals and Metal-Ceramic Composites: Part 1 Processing. Int. Mater. Rev. 1995, 40, 239–265. [Google Scholar] [CrossRef]
- Giannakopoulos, A.E.; Suresh, S. Indentation of Solids with Gradients in Elastic Properties: Part I. Point Force. Int. J. Solids Struct. 1997, 34, 2357–2392. [Google Scholar] [CrossRef]
- Suresh, S. Graded Materials for Resistance to Contact Deformation and Damage. Science 2001, 292, 2447–2451. [Google Scholar] [CrossRef]
- Tampieri, A.; Celotti, G.; Sprio, S.; Delcogliano, A.; Franzese, S. Porosity-graded Hydroxyapatite Ceramics to Replace Natural Bone. Biomaterials 2001, 22, 1365–1370. [Google Scholar] [CrossRef]
- Leong, K.F.; Chua, S.C.K.; Sudarmadji, N.; Yeong, W.Y. Engineering Functionally Graded Tissue Engineering Scaffolds. J. Mech. Behav. Biomed. Mater. 2008, 1, 140–152. [Google Scholar] [CrossRef]
- Pompe, W.; Worch, H.; Epple, M.; Friess, W.; Gelinsky, M.; Greil, P.; Hempel, U.; Scharnweber, D.; Schulte, K. Functionally Graded Materials for Biomedical Applications. Mater. Sci. Eng. A 2003, 362, 40–60. [Google Scholar] [CrossRef]
- Launey, M.E.; Ritchie, R.O. On the Fracture Toughness of Advanced Materials. Adv. Mater. 2009, 21, 2103–2110. [Google Scholar] [CrossRef]
- Barthelat, F.; Yin, Z.; Buehler, M.J. Structure and Mechanics of Interfaces in Biological Materials. Nat. Rev. Mater. 2016, 1, 16007. [Google Scholar] [CrossRef]
- Kokkinis, D.; Bouville, F.; Studart, A.R. 3D Printing of Materials with Tunable Failure via Bioinspired Mechanical Gradients. Adv. Mater. 2018, 30, 1705808. [Google Scholar] [CrossRef] [PubMed]
- Magrini, T.; Fox, C.; Wihardja, A.; Kolli, A.; Daraio, C. Control of Mechanical and Fracture Properties in Two-Phase Materials Reinforced by Continuous, Irregular Networks. Adv. Mater. 2024, 36, 2305198. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, B.; Liu, Z.; Zhang, Z.; Ritchie, R.O. Bioinspired Interpenetrating-phase Metal Composites. Prog. Mater. Sci. 2024, 144, 101281. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; Courier Corporation: Chelmsford, MA, USA, 2009. [Google Scholar]
- Vincent, J.F.V.; Owers, P. Mechanical Design of Hedgehog Spines and Porcupine Quills. J. Zool. 1986, 210, 55–75. [Google Scholar] [CrossRef]
- Lingham-Soliar, T.; Bonser, R.H.C.; Wesley-Smith, J. Selective Biodegradation of Keratin Matrix in Feather Rachis Reveals Classic Bioengineering. Proc. R. Soc. B 2009, 277, 1161–1168. [Google Scholar] [CrossRef]
- Karam, G.N.; Gibson, L.J. Elastic Buckling of Cylindrical Shells with Elastic Cores—I. Analysis. Int. J. Solids Struct. 1995, 32, 1259–1283. [Google Scholar] [CrossRef]
- Meyers, M.A.; McKittrick, J.; Chen, P.Y. Structural Biological Materials: Critical Mechanics-materials Connections. Science 2013, 339, 773–779. [Google Scholar] [CrossRef]
- Habibi, M.K.; Samaei, A.T.; Gheshlaghi, B.; Lu, J.; Lu, Y. Asymmetric Flexural Behavior from Bamboo’s Functionally Graded Hierarchical Structure: Underlying Mechanisms. Acta Biomater. 2015, 16, 178–186. [Google Scholar] [CrossRef]
- Silva, E.C.N.; Walters, M.C.; Paulino, G.H. Modeling Bamboo as a Functionally Graded Material: Lessons for the Analysis of Affordable Materials. J. Mater. Sci. 2006, 41, 6991–7004. [Google Scholar] [CrossRef]
- Dixon, P.G.; Gibson, L.J. The Structure and Mechanics of Moso Bamboo Material. J. R. Soc. Interface 2014, 11, 16007. [Google Scholar] [CrossRef] [PubMed]
- Vasiliev, V.V.; Razin, A.F. Anisogrid Composite Lattice Structures for Spacecraft and Aircraft Applications. Compos. Struct. 2006, 76, 182–189. [Google Scholar] [CrossRef]
- Totaro, G.; Gürdal, Z. Optimal Design of Composite Lattice Shell Structures for Aerospace Applications. Aerosp. Sci. Technol. 2009, 13, 157–164. [Google Scholar] [CrossRef]
- Chuang, W.; Zhu, J.; Wu, M.; Hou, J.; Zhou, H.; Meng, L.; Li, C.; Zhang, W. Multi-Scale Design and Optimization for Solid-Lattice Hybrid Structures and Their Application to Aerospace Vehicle Components. Chin. J. Aeronaut. 2021, 34, 386–398. [Google Scholar] [CrossRef]
- Dharmasena, K.P.; Wadley, H.N.; Williams, K.; Xue, Z.; Hutchinson, J.W. Response of Metallic Pyramidal Lattice Core Sandwich Panels to High Intensity Impulsive Loading in Air. Int. J. Impact Eng. 2011, 38, 275–289. [Google Scholar] [CrossRef]
- Xue, Z.; Hutchinson, J.W. A Comparative Study of Impulse-Resistant Metal Sandwich Plates. Int. J. Impact Eng. 2004, 30, 1283–1305. [Google Scholar] [CrossRef]
- Nuño, M.; Bühring, J.; Rao, M.N.; Schröder, K.U. Delamination Testing of AlSi10Mg Sandwich Structures with Pyramidal Lattice Truss Core Made by Laser Powder Bed Fusion. Chin. J. Mech. Eng. 2021, 34, 126. [Google Scholar] [CrossRef]
- Feng, Y.; Qiu, H.; Gao, Y.; Zheng, H.; Tan, J. Creative Design for Sandwich Structures: A Review. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420921327. [Google Scholar] [CrossRef]
- Guo, H.; Yuan, H.; Zhang, J.; Ruan, D. Review of Sandwich Structures Under Impact Loadings: Experimental, Numerical and Theoretical Analysis. Thin-Walled Struct. 2023, 196, 111541. [Google Scholar] [CrossRef]
- Birman, V.; Kardomateas, G.A. Review of Current Trends in Research and Applications of Sandwich Structures. Compos. Part B Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Ghanbari, J.; Panirani, P.N. A Hybrid Bio-Inspired Sandwich Structures for High Strain Rate Energy Absorption Applications. Sci. Rep. 2024, 14, 2865. [Google Scholar] [CrossRef] [PubMed]
- Karsandik, Y.; Sabuncuoglu, B.; Yildirim, B.; Silberschmidt, V.V. Impact Behavior of Sandwich Composites for Aviation Applications: A Review. Compos. Struct. 2023, 314, 116941. [Google Scholar] [CrossRef]
- Singh, P.; Sheikh, J.; Behera, B. Metal-Faced Sandwich Composite Panels: A Review. Thin-Walled Struct. 2023, 195, 111376. [Google Scholar] [CrossRef]
- Kausar, A.; Ahmad, I.; Rakha, S.A.; Eisa, M.; Diallo, A. State-of-the-Art of Sandwich Composite Structures: Manufacturing to High Performance Applications. J. Compos. Sci. 2023, 7, 102. [Google Scholar] [CrossRef]
- Thompson, D.W. On Growth and Form; Cambridge University Press: Cambridge, UK, 1917. [Google Scholar] [CrossRef]
- Rhee, H.; Horstemeyer, M.F.; Hwang, Y.; Lim, H.; Kadiri, H.E.; Trim, W. A Study on the Structure and Mechanical Behavior of the Terrapene Carolina Carapace: A Pathway to Design Bio-inspired Synthetic Composites. Mater. Sci. Eng. C 2009, 29, 2333–2339. [Google Scholar] [CrossRef]
- Gangwar, T.; Schillinger, D. Microimaging-informed Continuum Micromechanics Accurately Predicts Macroscopic Stiffness and Strength Properties of Hierarchical Plant Culm Materials. Mech. Mater. 2019, 130, 39–57. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant Biomechanics: An Engineering Approach to Plant Form and Function; University of Chicago Press: Chicago, IL, USA, 1992. [Google Scholar]
- Roland, J.; Reis, D.; Vian, B.; Roy, S. The Helicoidal Plant Cell wall as a Performing Cellulose-based Composite. Biol. Cell 1989, 67, 209–220. [Google Scholar] [CrossRef]
- Kerstens, S.; Decraemer, W.F.; Verbelen, J. Cell Walls at the Plant Surface Behave Mechanically like Fiber-reinforced Composite Materials. Plant Physiol. 2001, 127, 381–385. [Google Scholar] [CrossRef]
- Suslov, D.; Verbelen, J.; Vissenberg, K. Onion Epidermis as a New Model to Study the Control of Growth Anisotropy in Higher Plants. J. Exp. Bot. 2009, 60, 4175–4187. [Google Scholar] [CrossRef]
- Geitmann, A. Mechanical Modeling and Structural Analysis of the Primary Plant Cell Wall. Curr. Opin. Plant Biol. 2010, 13, 693–699. [Google Scholar] [CrossRef]
- Cordin, M.; Bechtold, T.; Pham, T. Effect of Fibre Orientation on the Mechanical Properties of Polypropylene-lyocell Composites. Cellulose 2018, 25, 7197–7210. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, D.; Sheng, Y. Performance-Driven 3D Printing of Continuous Curved Carbon Fibre Reinforced Polymer Composites: A Preliminary Numerical Study. Compos. Part B Eng. 2018, 151, 256–264. [Google Scholar] [CrossRef]
- Mu, R.; Diao, C.; Liu, H.; Wu, H.; Qing, L.; Zhao, S.; Li, L. Design, Preparation and Mechanical Properties of Full-field Aligned Steel Fiber Reinforced Cementitious Composite. Constr. Build. Mater. 2021, 272, 121631. [Google Scholar] [CrossRef]
- Li, N.; Link, G.; Wang, T.; Ramopoulos, V.; Neumaier, D.; Hofele, J.; Walter, M.; Jelonnek, J. Path-designed 3D Printing for Topological Optimized Continuous Carbon Fibre Reinforced Composite Structures. Compos. Part B Eng. 2020, 182, 107612. [Google Scholar] [CrossRef]
- Heitkamp, T.; Kuschmitz, S.; Girnth, S.; Marx, J.; Klawitter, G.; Waldt, N.; Vietor, T. Stress-adapted Fiber Orientation along the Principal Stress Directions for Continuous Fiber-reinforced Material Extrusion. Prog. Addit. Manuf. 2023, 8, 541–559. [Google Scholar] [CrossRef]
- Guo, Z.; Hou, Z.; Tian, X.; Zhu, W.; Malakhov, A.V.; Polilov, A.N.; Zhi, D.; Ding, H.; Lan, H. Optimization Design and 3D Printing of Curvilinear Fiber Reinforced Variable Stiffness Composites Based on Polar Coordinate Sweeping. Addit. Manuf. 2024, 88, 104272. [Google Scholar] [CrossRef]
- Ren, H.; Wang, D.; Liu, G.; Rosen, D.W.; Xiong, Y. Concurrent Optimization of Structural Topology and Toolpath for Additive Manufacturing of Continuous Fiber-Reinforced Polymer Composites. Comput. Methods Appl. Mech. Eng. 2024, 430, 117227. [Google Scholar] [CrossRef]
- He, S.; Ma, P.C.; Duan, M. Continuous Fiber Path Optimization in Additive Manufacturing: A Gradient-Based B-Spline Finite Element Approach. Addit. Manuf. 2024, 86, 104155. [Google Scholar] [CrossRef]
- Auer, D.; Bos, F.; Olabi, M.; Fischer, O. Fiber Reinforcement of 3D Printed Concrete by Material Extrusion Toolpaths Aligned to Principal Stress Trajectories. In Open Conference Proceedings; TIB Open Publishing: Hannover, Germany, 2023; Volume 3. [Google Scholar] [CrossRef]
- Wong, J.; Altassan, A.; Rosen, D.W. Additive Manufacturing of Fiber-Reinforced Polymer Composites: A Technical Review and Status of Design Methodologies. Compos. Part B Eng. 2023, 255, 110603. [Google Scholar] [CrossRef]
- Michell, A.G.M. LVIII. The Limits of Economy of Material in Frame-Structures. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1904, 8, 589–597. [Google Scholar] [CrossRef]
- Skelton, R.E.; de Oliveira, M.C. Optimal Tensegrity Structures in Bending: The Discrete Michell Truss. J. Frankl. Inst. 2010, 347, 257–283. [Google Scholar] [CrossRef]
- Arora, R.; Jacobson, A.; Langlois, T.R.; Huang, Y.; Mueller, C.; Matusik, W.; Shamir, A.; Singh, K.; Levin, D.I.W. Volumetric Michell Trusses for Parametric Design & Fabrication. In Proceedings of the 3rd Annual ACM Symposium on Computational Fabrication, Pittsburgh, PA, USA, 16–18 June 2019; pp. 1–13. [Google Scholar] [CrossRef]
- Kwok, T.H.; Li, Y.; Chen, Y. A Structural Topology Design Method Based on Principal Stress Line. CAD Comput. Aided Des. 2016, 80, 19–31. [Google Scholar] [CrossRef]
- Tam, K.M.; Mueller, C.T. Additive Manufacturing Along Principal Stress Lines. 3D Print. Addit. Manuf. 2017, 4, 63–81. [Google Scholar] [CrossRef]
- Xia, L.; Bi, M.; Wu, J.; Wang, F.; Wang, L.; Xie, Y.M.; Ma, G. Integrated Lightweight Design Method via Structural Optimization and Path Planning for Material Extrusion. Addit. Manuf. 2023, 62, 103387. [Google Scholar] [CrossRef]
- Ma, C.; Qiu, N.; Xu, X. A Fully Automatic Computational Framework for Beam Structure Design from Continuum Structural Topology Optimization. Struct. Multidiscip. Optim. 2023, 66, 250. [Google Scholar] [CrossRef]
- Liao, Y.; Zheng, Z.; Abdullahi, H.S.; Gao, S. Lattice Structure Design Based on Singularity-Separated Parameterization. Comput.-Aided Des. 2023, 155, 103437. [Google Scholar] [CrossRef]
- Niño-Álvarez, L.H.; Begambre-Carrillo, O.J. Multiobjective Topology Optimization of Planar Trusses Using Stress Trajectories and Metaheuristic Algorithms. Rev. Fac. Ing. Univ. Antioq. 2023, 107, 9–25. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, S.; Wang, Y.; Xiong, Y.; Zhu, J.; Lu, L.; Tang, Y. Stress-Driven Infill Mapping for 3D-Printed Continuous Fiber Composite with Tunable Infill Density and Morphology. Addit. Manuf. 2023, 62, 103374. [Google Scholar] [CrossRef]
- Huiskes, R. If Bone is the Answer, Then What is the Question? J. Anat. 2000, 197, 145–156. [Google Scholar] [CrossRef]
- Meyer, G.H.v. Die Architectur der Spongiosa, Archiv fur Anatomie. Physiol. Und Wiss. Med. 1867, 34, 615–625. [Google Scholar]
- Wolff, J. Das Gesetz der Transformation der Knochen. DMW-Dtsch. Med. Wochenschr. 1893, 19, 1222–1224. [Google Scholar] [CrossRef]
- Huang, C.; Ogawa, R. Mechanotransduction in Bone Repair and Regeneration. FASEB J. 2010, 24, 3625–3632. [Google Scholar] [CrossRef] [PubMed]
- Sampathkumar, A.; Yan, A.; Krupinski, P.; Meyerowitz, E.M. Physical Forces Eegulate Plant Development and Morphogenesis. Curr. Biol. 2014, 24, R475–R483. [Google Scholar] [CrossRef]
- Sahaf, M.; Sharon, E. The Rheology of a Growing Leaf: Stress-induced Changes in the Mechanical Properties of Leaves. J. Exp. Bot. 2016, 67, 5509–5515. [Google Scholar] [CrossRef] [PubMed]
- Guo, K.; Huang, C.; Miao, Y.; Cosgrove, D.J.; Hsia, K.J. Leaf Morphogenesis: The Multifaceted Roles of Mechanics. Mol. Plant 2022, 15, 1098–1119. [Google Scholar] [CrossRef] [PubMed]
- Alméras, T.; Clair, B. Critical Review on the Mechanisms of Maturation Stress Generation in Trees. J. R. Soc. Interface 2016, 13, 20160550. [Google Scholar] [CrossRef]
- Shigley, J.E.; Mitchell, L.D.; Saunders, H. Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Mattheck, C. Design and Growth Rules for Biological Structures and Their Application to Engineering. Fatigue Fract. Eng. Mater. Struct. 1990, 13, 535–550. [Google Scholar] [CrossRef]
- Mattheck, C.; Burkhardt, S. A New Method of Structural Shape Optimization Based on Biological Growth. Int. J. Fatigue 1990, 12, 185–190. [Google Scholar] [CrossRef]
- Mattheck, C. Design in Nature: Learning from Trees; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Baumgartner, A.; Harzheim, L.; Mattheck, C. SKO (Soft Kill Option): The Biological Way to Find an Optimum Structure Topology. Int. J. Fatigue 1992, 14, 387–393. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology Optimization Approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Deaton, J.D.; Grandhi, R.V. A Survey of Structural and Multidisciplinary Continuum Topology Optimization: Post 2000. Struct. Multidiscip. Optim. 2013, 49, 1–38. [Google Scholar] [CrossRef]
- Shin, S.; Shin, D.; Kang, N. Topology Optimization via Machine Learning and Deep Learning: A Review. J. Comput. Des. Eng. 2023, 10, 1736–1766. [Google Scholar] [CrossRef]
- Gutiérrez, A.; Guney, M.G.; Fedder, G.K.; Dávila, L.P. The Role of Hierarchical Design and Morphology in the Mechanical Response of Diatom-Inspired Structures via Simulation. Biomater. Sci. 2018, 6, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Salimon, A.I.; Cvjetinovic, J.; Kan, Y.; Statnik, E.S.; Aggrey, P.; Somov, P.A.; Salimon, I.A.; Everaerts, J.; Bedoshvili, Y.D.; Gorin, D.A. On the Mathematical Description of Diatom Algae: From Siliceous Exoskeleton Structure and Properties to Colony Growth Kinetics, and Prospective Nanoengineering Applications. In The Mathematical Biology of Diatoms; Wiley: Hoboken, NJ, USA, 2023; pp. 63–102. [Google Scholar] [CrossRef]
- Losic, D.; Pillar, R.J.; Dilger, T.; Mitchell, J.G.; Voelcker, N.H. Atomic Force Microscopy (AFM) Characterisation of the Porous Silica Nanostructure of Two Centric Diatoms. J. Porous Mater. 2007, 14, 61–69. [Google Scholar] [CrossRef]
- Hamm, C.E.; Merkel, R.; Springer, O.; Jurkojc, P.; Maier, C.; Prechtel, K.; Smetacek, V. Architecture and Material Properties of Diatom Shells Provide Effective Mechanical Protection. Nature 2003, 421, 841–843. [Google Scholar] [CrossRef] [PubMed]
- Maier, M.; Siegel, D.; Thoben, K.D.; Niebuhr, N.; Hamm, C. Transfer of Natural Micro Structures to Bionic Lightweight Design Proposals. J. Bionic Eng. 2013, 10, 469–478. [Google Scholar] [CrossRef]
- Laraudogoitia Blanc, I.; Hamm, C.; García de Cortázar, M.; Kaiser, N.; Savysko, O.; Girot Mata, F.A. Bioinspired Design for Lightweighting and Vibration Behavior Optimization in Large-Scale Aeronautical Tooling: A Comparative Study. Machines 2023, 11, 1067. [Google Scholar] [CrossRef]
- Kaiser, N.; Goossens, N.; Jimenez, A.; Laraudogoitia, I.; Psarras, S.; Tsantzalis, S. Advanced Manufacturing Concept of a Bio-inspired Reaction Wheel Rotor for Small-and Medium-sized Constellation Satellites. CEAS Space J. 2024, 16, 73–86. [Google Scholar] [CrossRef]
- Guo, X.L.; Kuang, M.; Li, F.; Liu, X.Y.; Zhang, Y.X.; Dong, F.; Losic, D. Engineering of Three Dimensional (3-D) Diatom@ TiO2@ MnO2 Composites with Enhanced Supercapacitor Performance. Electrochim. Acta 2016, 190, 159–167. [Google Scholar] [CrossRef]
- Ichihara, N.; Ueda, M. 3D-Printed High-Toughness Composite Structures by Anisotropic Topology Optimization. Compos. Part B Eng. 2023, 253, 110572. [Google Scholar] [CrossRef]
- Wu, J.; Sigmund, O.; Groen, J.P. Topology Optimization of Multi-Scale Structures: A Review. Struct. Multidiscip. Optim. 2021, 63, 1455–1480. [Google Scholar] [CrossRef]
- Lee, D.; Chen, W.; Wang, L.; Chan, Y.C.; Chen, W. Data-Driven Design for Metamaterials and Multiscale Systems: A Review. Adv. Mater. 2024, 36, 2305254. [Google Scholar] [CrossRef] [PubMed]
- Zhai, X.; Wang, W.; Chen, F.; Wu, J. Topology Optimization of Differentiable Microstructures. Comput. Methods Appl. Mech. Eng. 2024, 418, 116530. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, X.; Li, W.; He, S.; Zhao, P.; Hu, H.; Jia, Q.; Luo, M. 3D Printing of Topologically Optimized Wing Spar with Continuous Carbon Fiber Reinforced Composites. Compos. Part B Eng. 2024, 272, 111166. [Google Scholar] [CrossRef]
- Chandrasekhar, A.; Mirzendehdel, A.; Behandish, M.; Suresh, K. FRC-TOuNN: Topology Optimization of Continuous Fiber Reinforced Composites Using Neural Network. Comput.-Aided Des. 2023, 156, 103449. [Google Scholar] [CrossRef]
- Ruan, J.; Prasad, P. The Effects of Skull Thickness Variations on Human Head Dynamic Impact Responses. Stapp Car Crash J. 2001, 45, 395–414. [Google Scholar] [CrossRef]
- Auperrin, A.; Delille, R.; Lesueur, D.; Bruyère, K.; Masson, C.; Drazétic, P. Geometrical and Material Parameters to Assess the Macroscopic Mechanical Behaviour of Fresh Cranial Bone Samples. J. Biomech. 2014, 47, 1180–1185. [Google Scholar] [CrossRef]
- Micheletti, C.; Shah, F.A. Bone Hierarchical Organization through the Lens of Materials Science: Present Opportunities and Future Challenges. Bone Rep. 2024, 22, 101783. [Google Scholar] [CrossRef]
- Nygård, K.; McDonald, S.; González, J.; Haghighat, V.; Appel, C.; Larsson, E.; Ghanbari, R.; Viljanen, M.; Silva, J.; Malki, S. ForMAX–a Beamline for Multiscale and Multimodal Structural Characterization of Hierarchical Materials. J. Synchrotron Radiat. 2024, 31, 363–377. [Google Scholar] [CrossRef]
- Holm, E.A.; Cohn, R.; Gao, N.; Kitahara, A.R.; Matson, T.P.; Lei, B.; Yarasi, S.R. Overview: Computer Vision and Machine Learning for Microstructural Characterization and Analysis. Metall. Mater. Trans. A 2020, 51, 5985–5999. [Google Scholar] [CrossRef]
- Lu, W.; Lee, N.A.; Buehler, M.J. Modeling and Design of Heterogeneous Hierarchical Bioinspired Spider Web Structures Using Deep Learning and Additive Manufacturing. Proc. Natl. Acad. Sci. USA 2023, 120, e2305273120. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, H.; Qin, Q.; Qu, C.; Wang, J. Theoretical Modeling of the Mechanical Properties of Biological Fibers and Bundles with Hierarchical Chiral Structures. Acta Mech. Sin. 2023, 39, 622403. [Google Scholar] [CrossRef]
- Leuther, C.; Wilmers, J.; Bargmann, S. Generation of 3D Representative Volume Elements (RVEs) of Nacre. Softw. Impacts 2023, 17, 100534. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Moretti, P.; Zaiser, M. Enhanced Fault Tolerance in Biomimetic Hierarchical Materials: A Simulation Study. Phys. Rev. Mater. 2023, 7, 053612. [Google Scholar] [CrossRef]
- Buehler, M.J. A Computational Building Block Approach Towards Multiscale Architected Materials Analysis and Design with Application to Hierarchical Metal Metamaterials. Model. Simul. Mater. Sci. Eng. 2023, 31, 054001. [Google Scholar] [CrossRef]
- Feng, F.; Xiong, S.; Liu, Z.; Xian, Z.; Zhou, Y.; Kobayashi, H.; Kawamoto, A.; Nomura, T.; Zhu, B. Cellular Topology Optimization on Differentiable Voronoi Diagrams. Int. J. Numer. Methods Eng. 2023, 124, 282–304. [Google Scholar] [CrossRef]
- Lew, A.J.; Jin, K.; Buehler, M.J. Designing Architected Materials for Mechanical Compression via Simulation, Deep Learning, and Experimentation. npj Comput. Mater. 2023, 9, 80. [Google Scholar] [CrossRef]
- Chiu, Y.H.; Liao, Y.H.; Juang, J.Y. Designing Bioinspired Composite Structures via Genetic Algorithm and Conditional Variational Autoencoder. Polymers 2023, 15, 281. [Google Scholar] [CrossRef]
- Hooshmand, M.J.; Sakib-Uz-Zaman, C.; Khondoker, M.A.H. Machine Learning Algorithms for Predicting Mechanical Stiffness of Lattice Structure-Based Polymer Foam. Materials 2023, 16, 7173. [Google Scholar] [CrossRef]
- Park, D.; Lee, J.; Park, K.; Ryu, S. Hierarchical Generative Network: A Hierarchical Multitask Learning Approach for Accelerated Composite Material Design and Discovery. Adv. Eng. Mater. 2023, 25, 2300867. [Google Scholar] [CrossRef]
- Kil, T.; Bae, J.H.; Yang, B.; Lee, H.K. Multi-Level Micromechanics-Based Homogenization for the Prediction of Damage Behavior of Multiscale Fiber-Reinforced Composites. Compos. Struct. 2023, 303, 116332. [Google Scholar] [CrossRef]
- Vazeille, F.; Lebel, L.L. Envelope Enrichment Method for Homogenization of Non-Periodic Structures. Compos. Struct. 2024, 329, 117819. [Google Scholar] [CrossRef]
- Huang, L.; Yuan, H.; Zhao, H. An FEM-Based Homogenization Method for Orthogonal Lattice Metamaterials within Micropolar Elasticity. Int. J. Mech. Sci. 2023, 238, 107836. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, J.; Chen, Q.; Chatzigeorgiou, G.; Meraghni, F. Deep Homogenization Networks for Elastic Heterogeneous Materials with Two- and Three-Dimensional Periodicity. Int. J. Solids Struct. 2023, 284, 112521. [Google Scholar] [CrossRef]
- Ganghoffer, J.F.; Wazne, A.; Reda, H. Frontiers in Homogenization Methods towards Generalized Continua for Architected Materials. Mech. Res. Commun. 2023, 130, 104114. [Google Scholar] [CrossRef]
- Düster, A.; Sehlhorst, H.G.; Rank, E. Numerical Homogenization of Heterogeneous and Cellular Materials Utilizing the Finite Cell Method. Comput. Mech. 2012, 50, 413–431. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, P.F.; Xie, Y.M. Topology Optimization of Structures Composed of More than Two Materials with Different Tensile and Compressive Properties. Compos. Struct. 2023, 306, 116609. [Google Scholar] [CrossRef]
- Banh, T.T.; Lieu, Q.X.; Kang, J.; Ju, Y.; Shin, S.; Lee, D. A Novel Robust Stress-Based Multimaterial Topology Optimization Model for Structural Stability Framework Using Refined Adaptive Continuation Method. Eng. Comput. 2024, 40, 677–713. [Google Scholar] [CrossRef]
- Emmendoerfer, H., Jr.; Maute, K.; Fancello, E.A.; Silva, E.C.N. A Level Set-Based Optimized Design of Multi-Material Compliant Mechanisms Considering Stress Constraints. Comput. Methods Appl. Mech. Eng. 2022, 391, 114556. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, L.; Wang, J. Multi-Objective Optimization of Elliptical Tube Fin Heat Exchangers Based on Neural Networks and Genetic Algorithm. Energy 2023, 269, 126729. [Google Scholar] [CrossRef]
- Wang, H.; Ji, C.; Shi, C.; Yang, J.; Wang, S.; Ge, Y.; Chang, K.; Meng, H.; Wang, X. Multi-Objective Optimization of a Hydrogen-Fueled Wankel Rotary Engine Based on Machine Learning and Genetic Algorithm. Energy 2023, 263, 125961. [Google Scholar] [CrossRef]
- Luo, Y.; Li, M.; Yuan, H.; Liu, H.; Fang, Y. Predicting Lattice Thermal Conductivity via Machine Learning: A Mini Review. Npj Comput. Mater. 2023, 9, 4. [Google Scholar] [CrossRef]
- Teimourian, A.; Rohacs, D.; Dimililer, K.; Teimourian, H.; Yildiz, M.; Kale, U. Airfoil Aerodynamic Performance Prediction Using Machine Learning and Surrogate Modeling. Heliyon 2024, 10, e29377. [Google Scholar] [CrossRef] [PubMed]
- Freed, Y. Machine Learning-Based Predictions of Crack Growth Rates in an Aeronautical Aluminum Alloy. Theor. Appl. Fract. Mech. 2024, 130, 104278. [Google Scholar] [CrossRef]
- Li, Z.; Ma, W.; Zhu, H.; Deng, G.; Hou, L.; Xu, P.; Yao, S. Energy Absorption Prediction and Optimization of Corrugation-Reinforced Multicell Square Tubes Based on Machine Learning. Mech. Adv. Mater. Struct. 2022, 29, 5511–5529. [Google Scholar] [CrossRef]
- Okafor, C.E.; Iweriolor, S.; Ani, O.I.; Ahmad, S.; Mehfuz, S.; Ekwueme, G.O.; Chukwumuanya, O.E.; Abonyi, S.E.; Ekengwu, I.E.; Chikelu, O.P. Advances in Machine Learning-Aided Design of Reinforced Polymer Composite and Hybrid Material Systems. Hybrid Adv. 2023, 2, 100026. [Google Scholar] [CrossRef]
- Pantidis, P.; Mobasher, M.E. Integrated Finite Element Neural Network (I-FENN) for Non-Local Continuum Damage Mechanics. Comput. Methods Appl. Mech. Eng. 2023, 404, 115766. [Google Scholar] [CrossRef]
- Rade, J.; Jignasu, A.; Herron, E.; Corpuz, A.; Ganapathysubramanian, B.; Sarkar, S.; Balu, A.; Krishnamurthy, A. Deep Learning-Based 3D Multigrid Topology Optimization of Manufacturable Designs. Eng. Appl. Artif. Intell. 2023, 126, 107033. [Google Scholar] [CrossRef]
- Seo, J.; Kapania, R.K. Development of Deep Convolutional Neural Network for Structural Topology Optimization. AIAA J. 2023, 61, 1366–1379. [Google Scholar] [CrossRef]
- Faraz, M.R.; Hosseini, S.; Tarafdar, A.; Forghani, M.; Ahmadi, H.; Fellows, N.; Liaghat, G. Crashworthiness Behavior Assessment and Multi-Objective Optimization of Horsetail-Inspired Sandwich Tubes Based on Artificial Neural Network. Mech. Adv. Mater. Struct. 2023, 1–18. [Google Scholar] [CrossRef]
- Nepal, D.; Kang, S.; Adstedt, K.; Kanhaiya, K.; Bockstaller, M.; Brinson, L.; Buehler, M.; Coveney, P.; Dayal, K.; El-Awady, J.; et al. Hierarchically Structured Bioinspired Nanocomposites. Nat. Mater. 2023. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, M.; Lucherini, L.; Zhao, R.; Clarà Saracho, A.; Amstad, E. 3D Printing of Living Structural Biocomposites. Mater. Today 2023, 62, 21–32. [Google Scholar] [CrossRef]
- Ahn, S.J.; Lee, H.; Cho, K.J. 3D Printing with a 3D Printed Digital Material Filament for Programming Functional Gradients. Nat. Commun. 2024, 15, 3605. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lim, K.M.; Zhai, W. A Novel Class of Bioinspired Composite via Ultrasound-Assisted Directed Self-Assembly Digital Light 3D Printing. Appl. Mater. Today 2022, 26, 101388. [Google Scholar] [CrossRef]
- Bai, X.; Sun, Q.; Cui, H.; Guerzoni, L.P.B.; Wuttke, S.; Kiessling, F.; De Laporte, L.; Lammers, T.; Shi, Y. Controlled Covalent Self-Assembly of a Homopolymer for Multiscale Materials Engineering. Adv. Mater. 2022, 34, 2109701. [Google Scholar] [CrossRef]
- Hamoudi, H.; Berdiyorov, G.R.; Zekri, A.; Tong, Y.; Mansour, S.; Esaulov, V.A.; Youcef-Toumi, K. Building Block 3D Printing Based on Molecular Self-Assembly Monolayer with Self-Healing Properties. Sci. Rep. 2022, 12, 6806. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, D.; Wang, M.; Mao, R.; Zhao, H.; Huang, X.; GF Shen, S. Seamless Route of Self-Assembly and 3D Printing to Fabricate Hierarchical Mesoporous Bioactive Glass Scaffold for Customized Bone Regeneration with Enhanced Efficacy. Chem. Eng. J. 2022, 446, 137270. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, S.; Wei, Y.; Yue, Y.; Gao, M.; Li, Y.; Zeng, X.; Deng, X.; Kotov, N.A.; Guo, L.; et al. Multiscale Engineered Artificial Tooth Enamel. Science 2022, 375, 551–556. [Google Scholar] [CrossRef]
- Xin, A.; Su, Y.; Feng, S.; Yan, M.; Yu, K.; Feng, Z.; Lee, K.H.; Sun, L.; Wang, Q. Growing Living Composites with Ordered Microstructures and Exceptional Mechanical Properties. Adv. Mater. 2021, 33, 2006946. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Breish, F.; Hamm, C.; Andresen, S. Nature’s Load-Bearing Design Principles and Their Application in Engineering: A Review. Biomimetics 2024, 9, 545. https://doi.org/10.3390/biomimetics9090545
Breish F, Hamm C, Andresen S. Nature’s Load-Bearing Design Principles and Their Application in Engineering: A Review. Biomimetics. 2024; 9(9):545. https://doi.org/10.3390/biomimetics9090545
Chicago/Turabian StyleBreish, Firas, Christian Hamm, and Simone Andresen. 2024. "Nature’s Load-Bearing Design Principles and Their Application in Engineering: A Review" Biomimetics 9, no. 9: 545. https://doi.org/10.3390/biomimetics9090545
APA StyleBreish, F., Hamm, C., & Andresen, S. (2024). Nature’s Load-Bearing Design Principles and Their Application in Engineering: A Review. Biomimetics, 9(9), 545. https://doi.org/10.3390/biomimetics9090545





