Unsteady Aerodynamic Forces of Tandem Flapping Wings with Different Forewing Kinematics
Abstract
1. Introduction
2. Materials and Methods
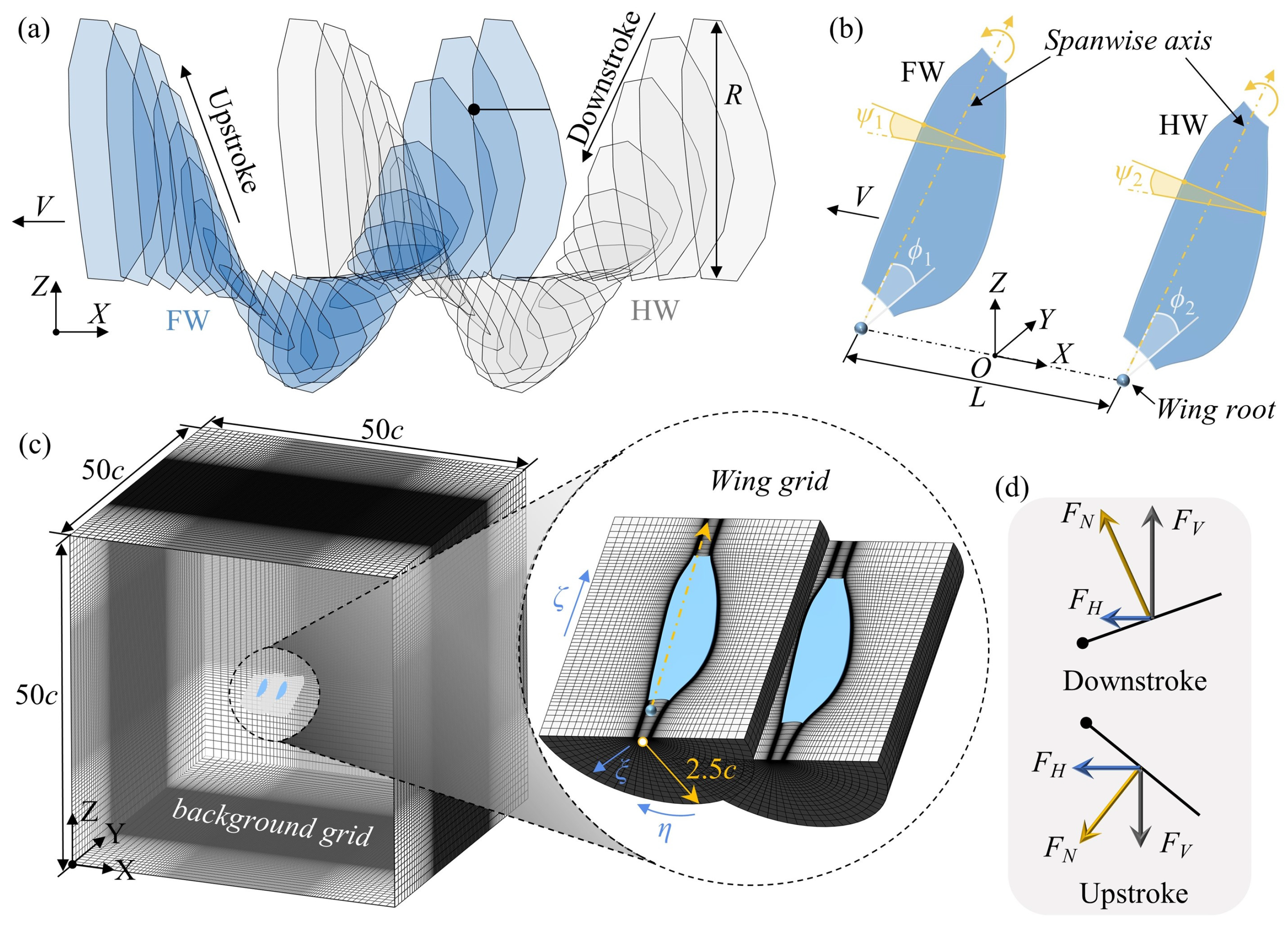
2.1. Geometry and Kinematics
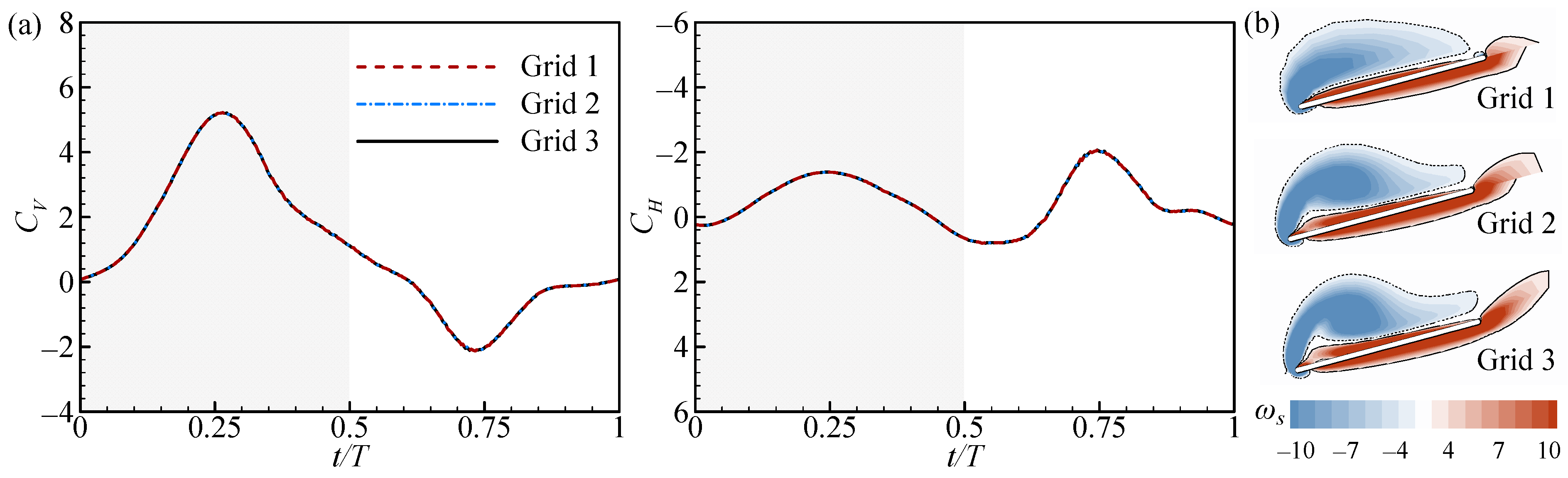
2.2. Computational Method and Validation
2.3. Data Analysis
3. Results
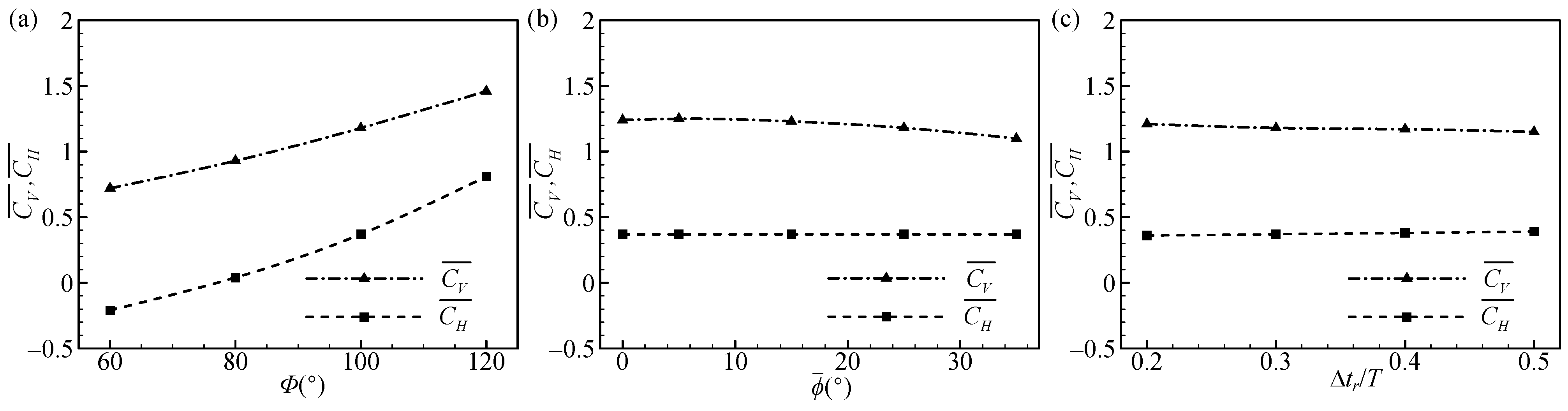
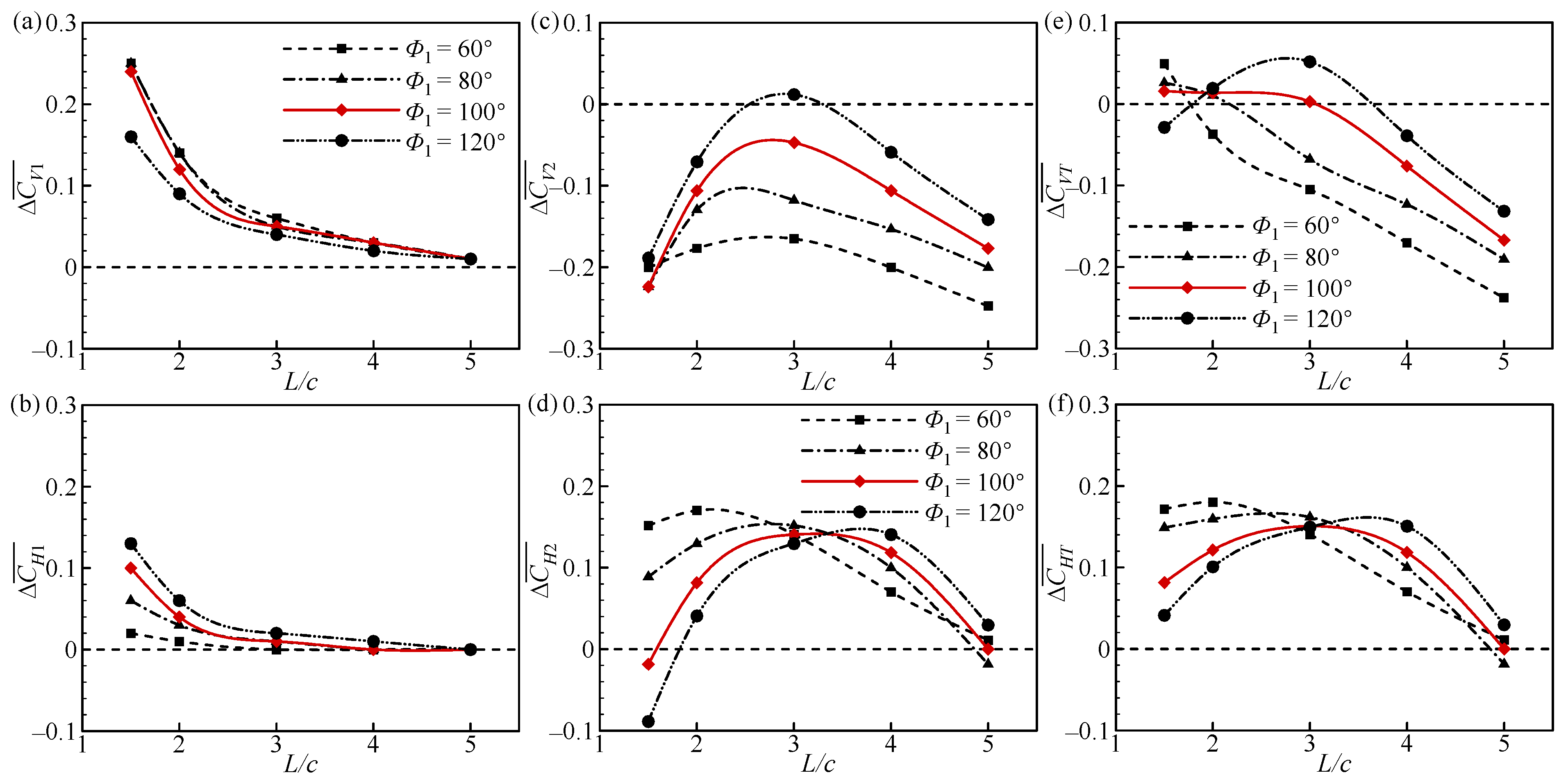
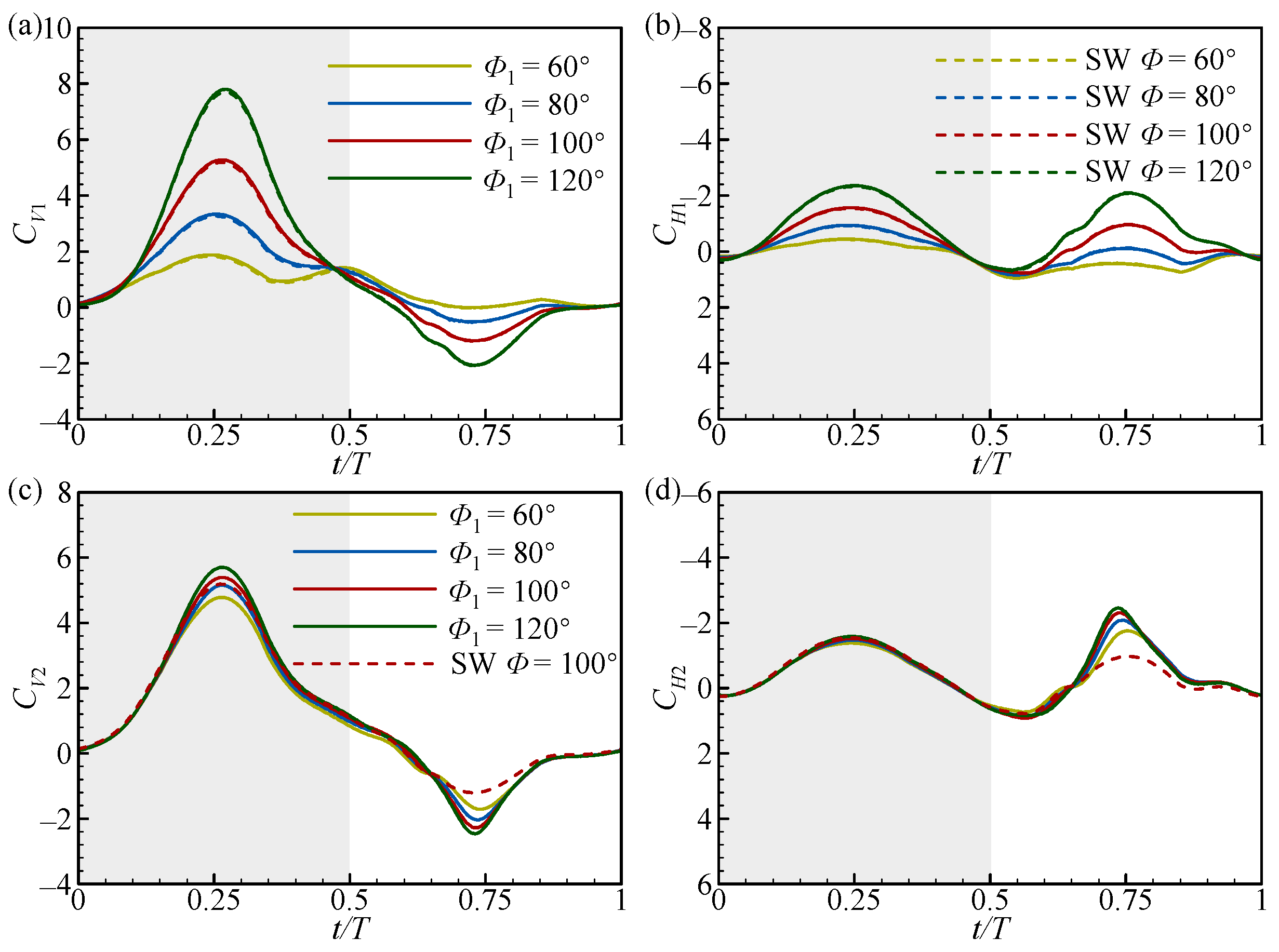
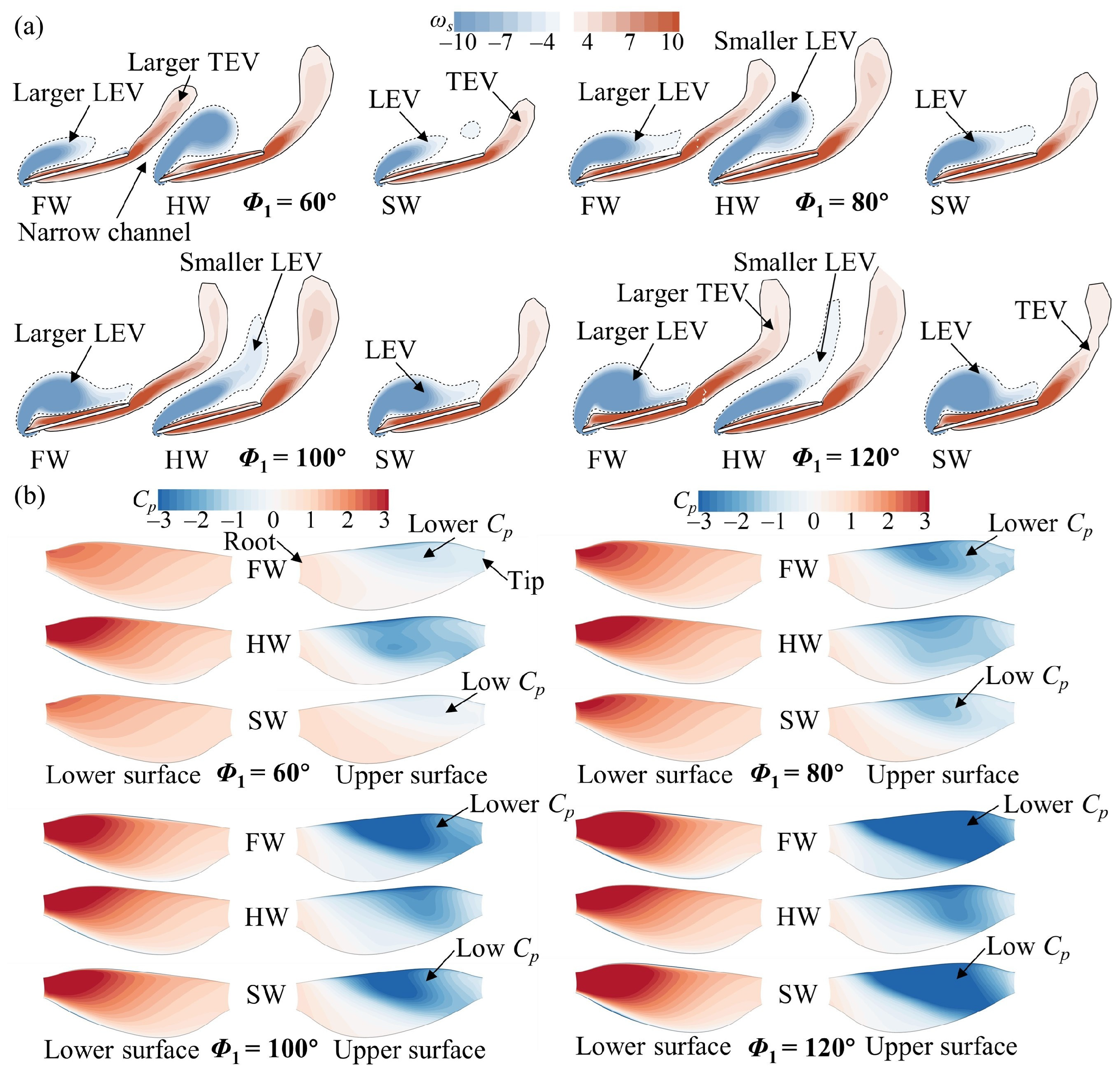
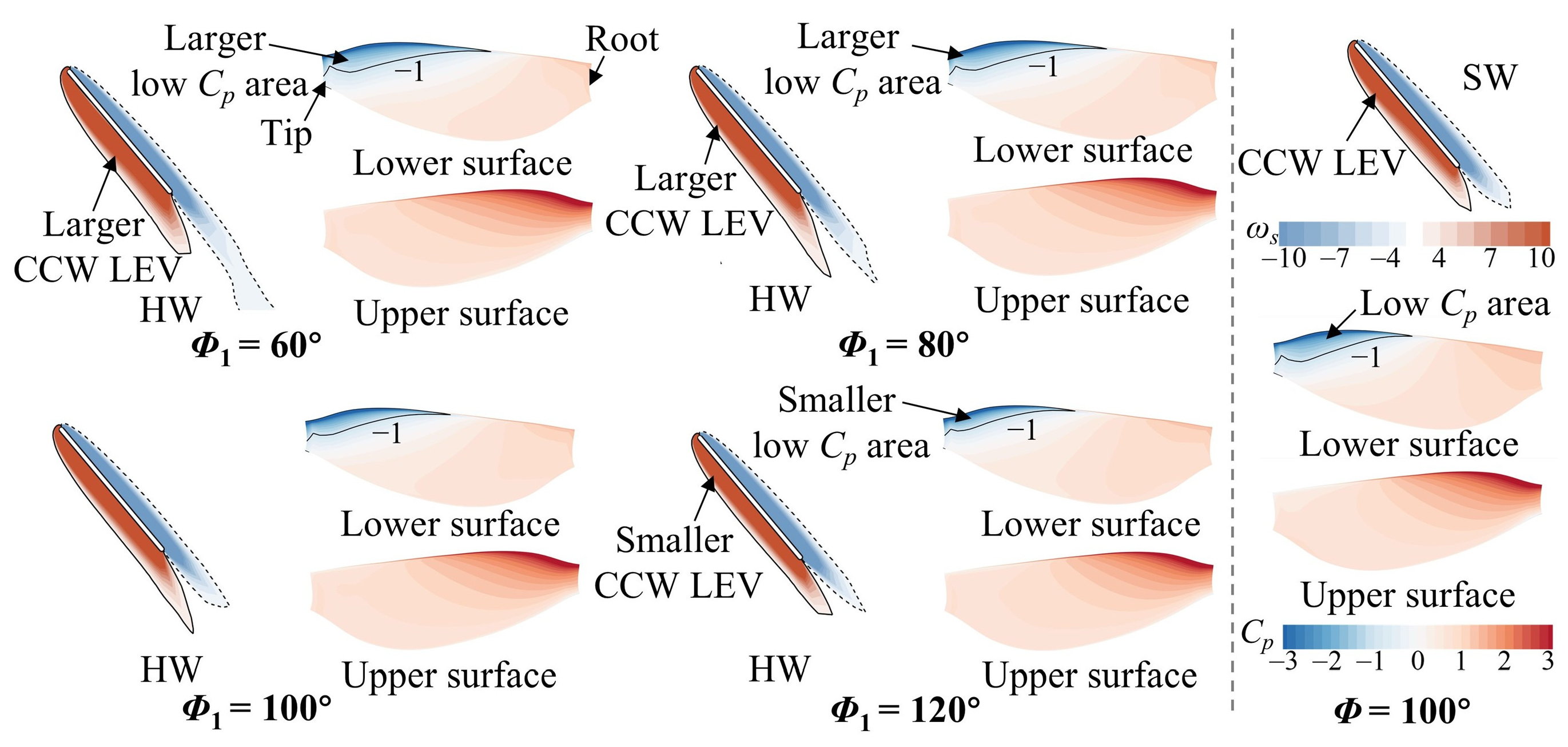
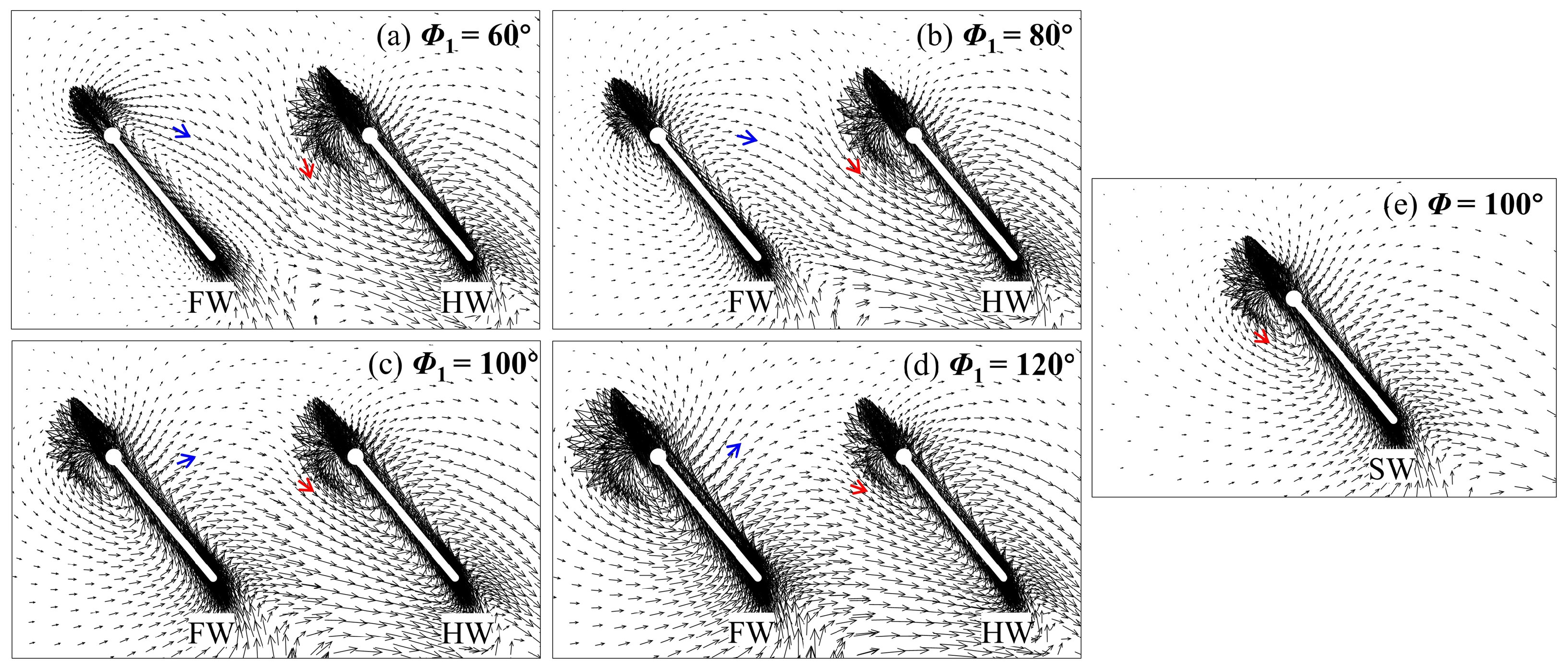
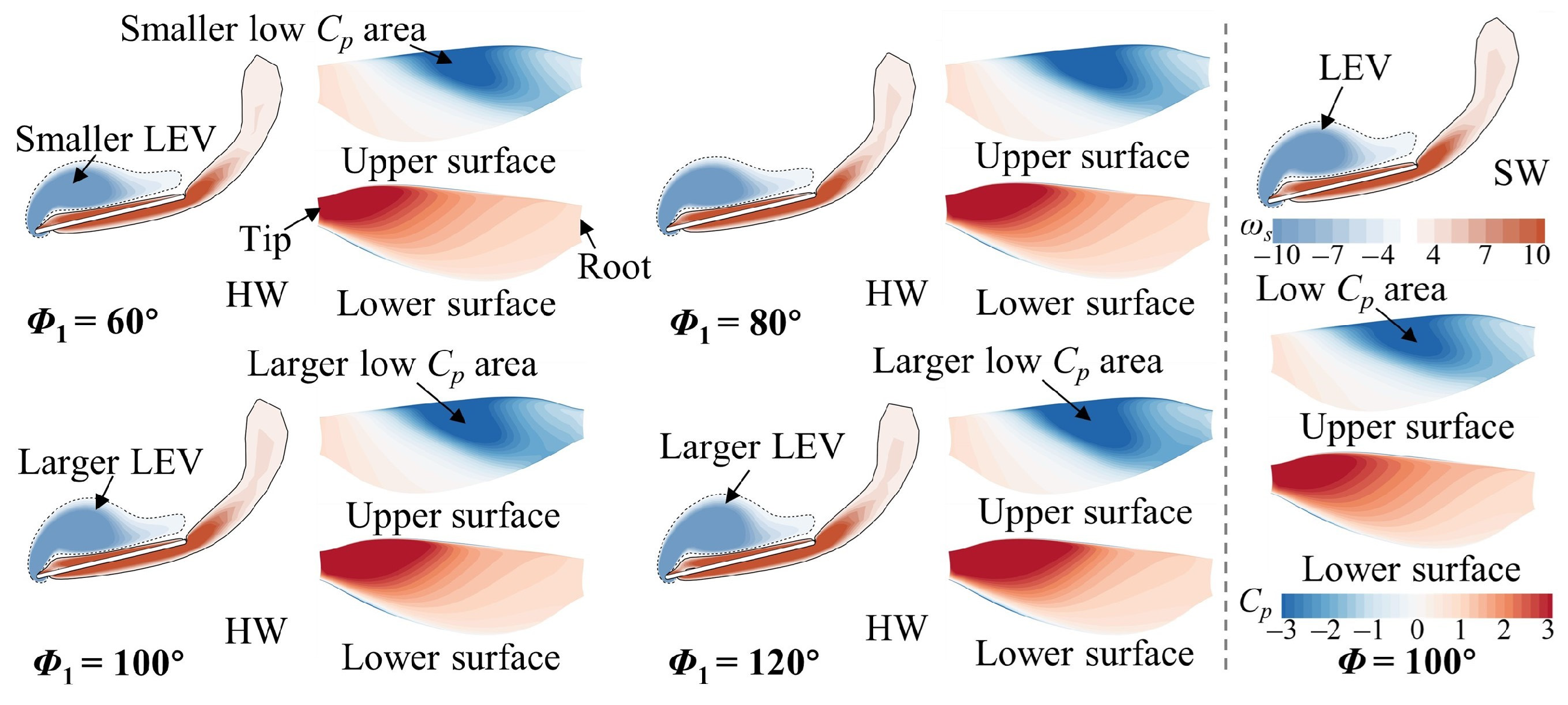
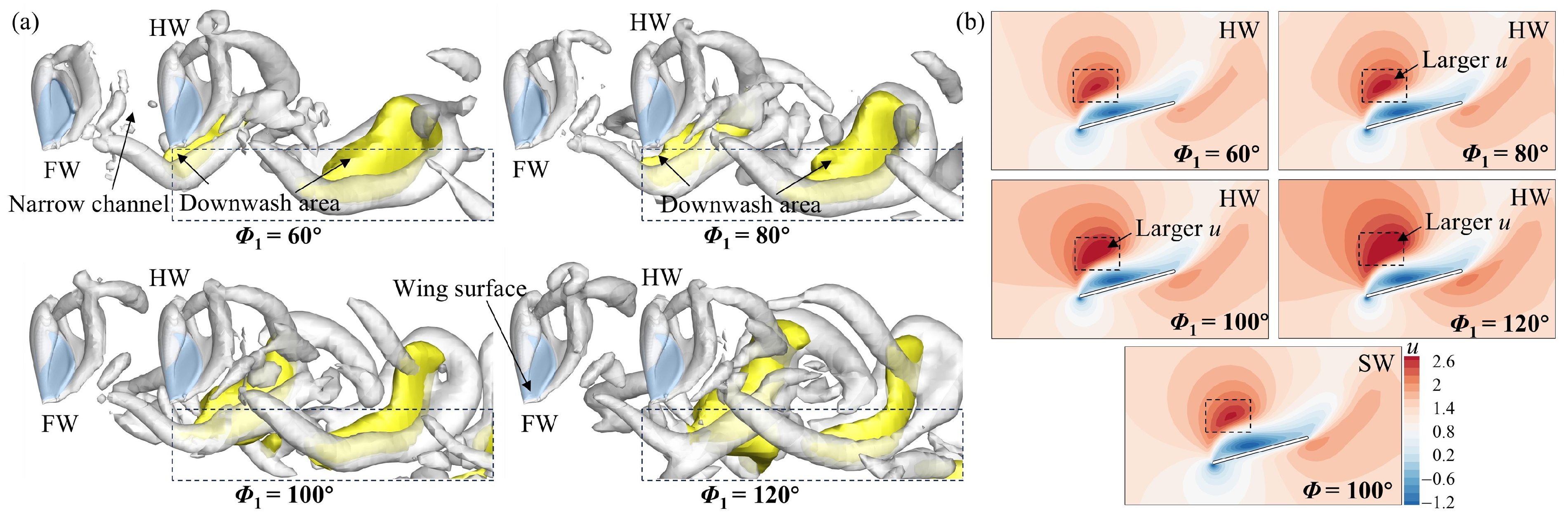
3.1. Effect of Φ1
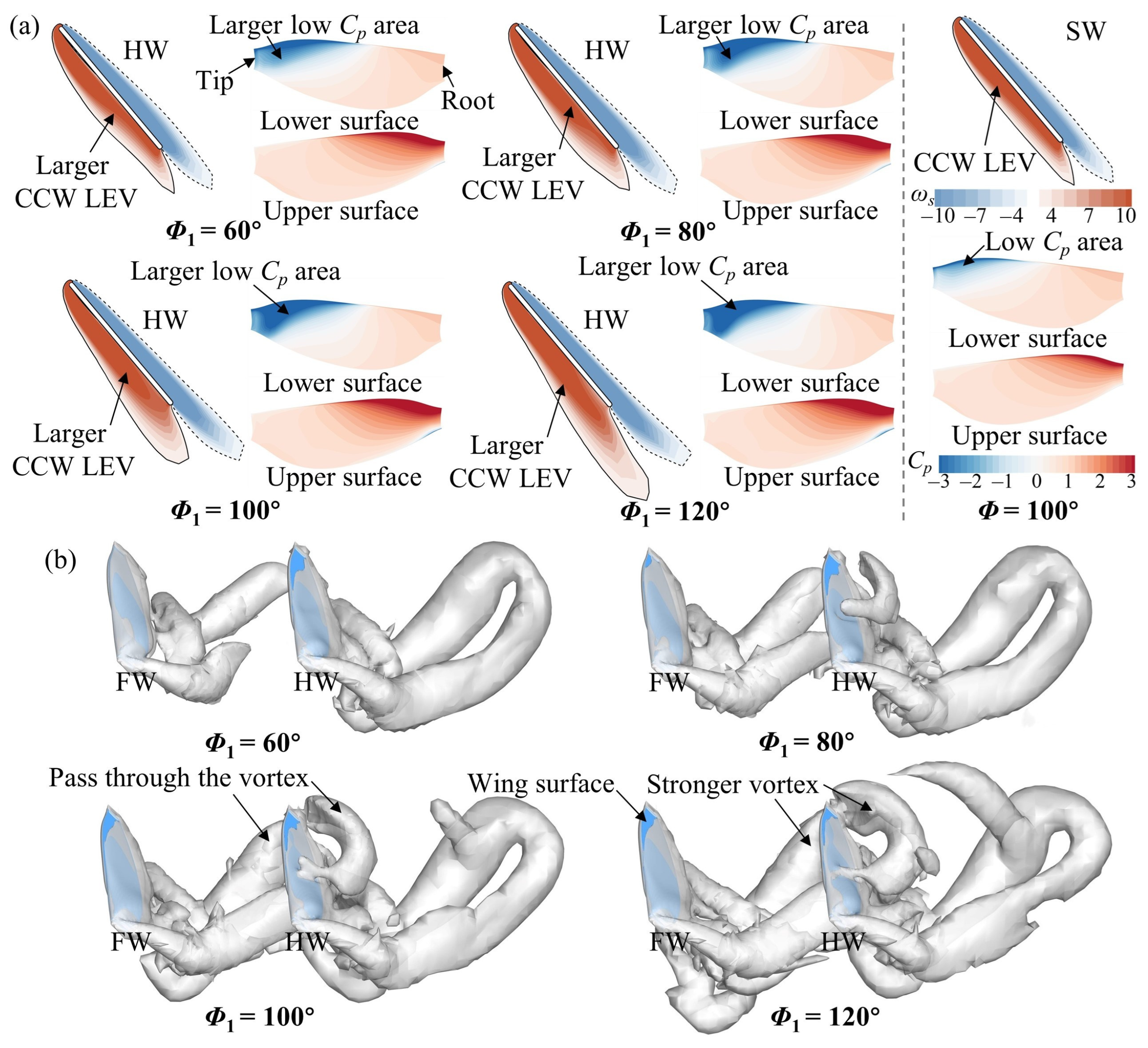
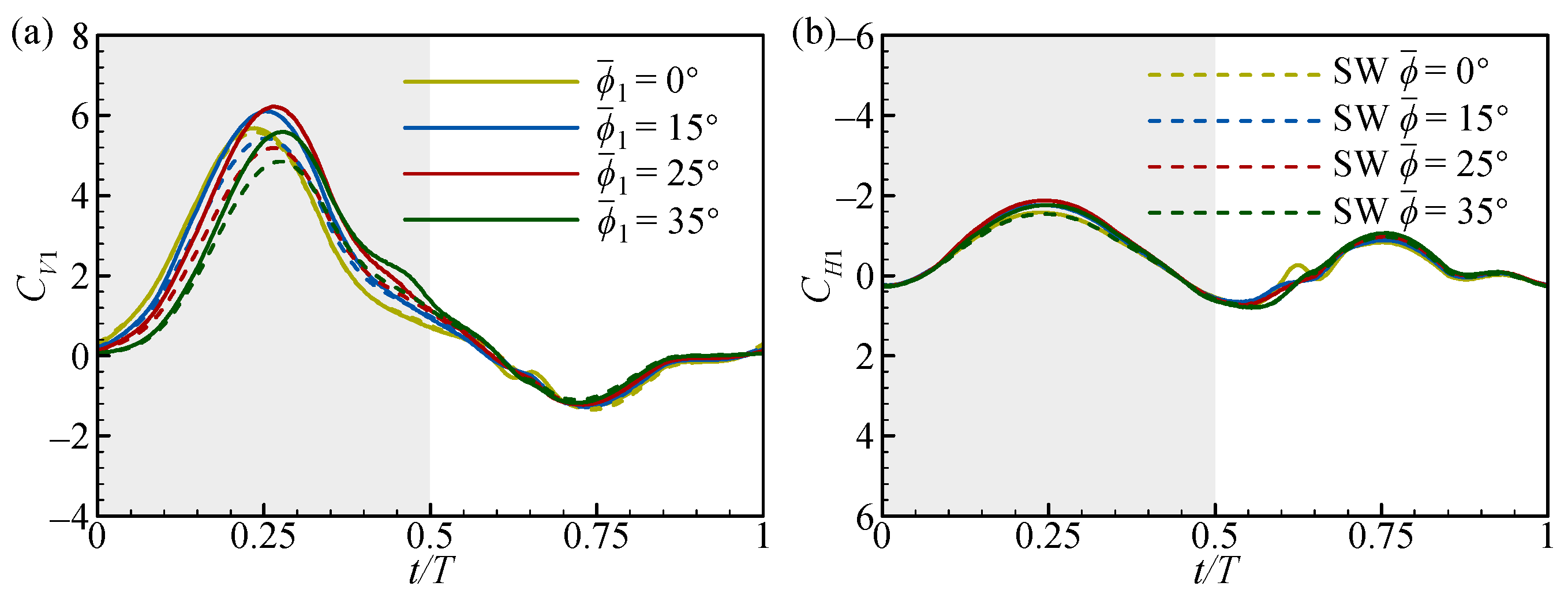
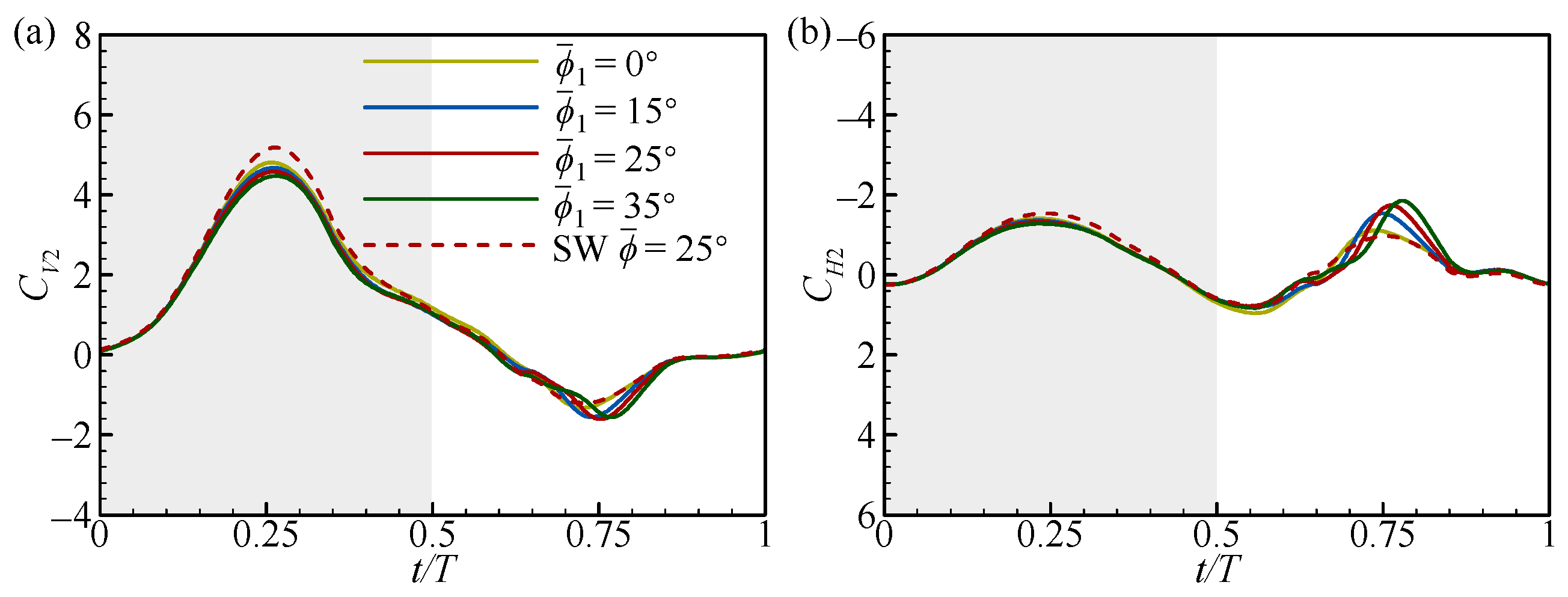
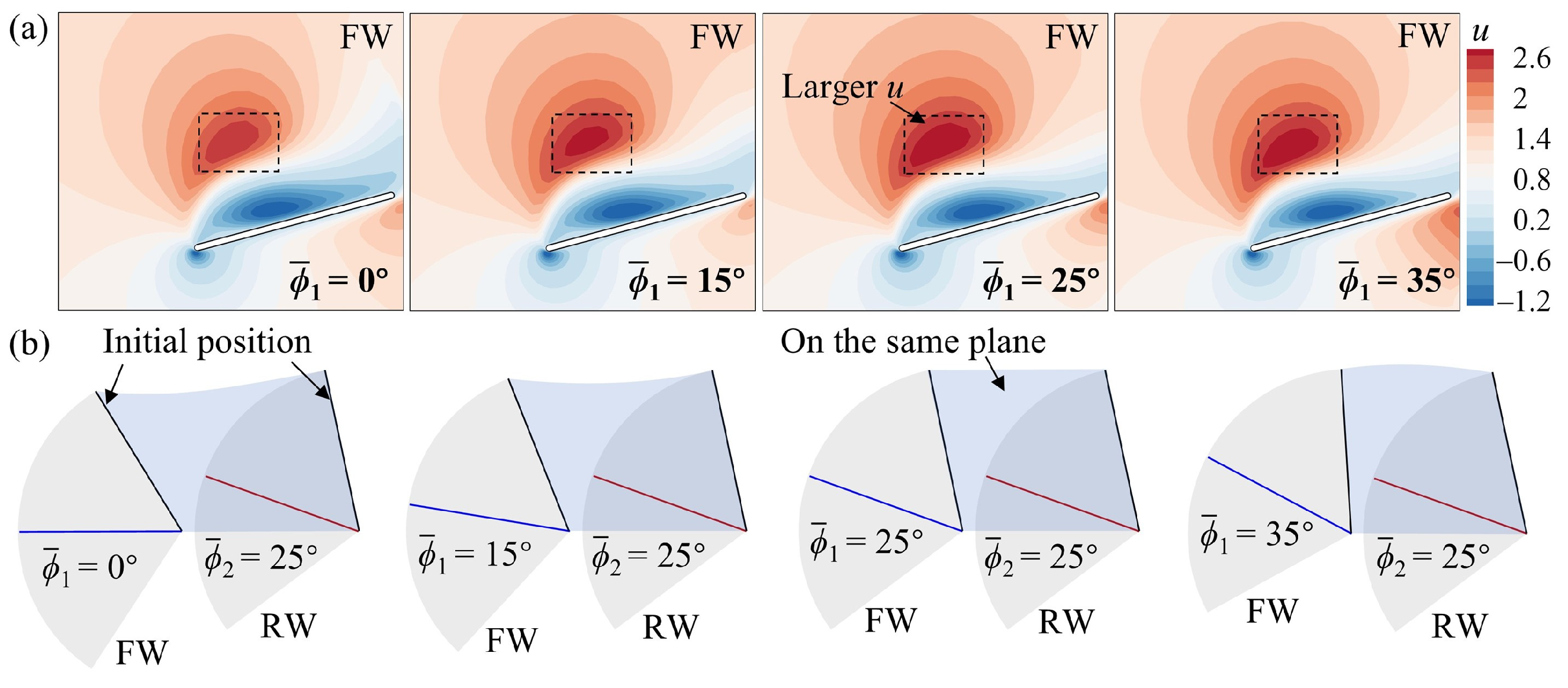
3.2. Effect of
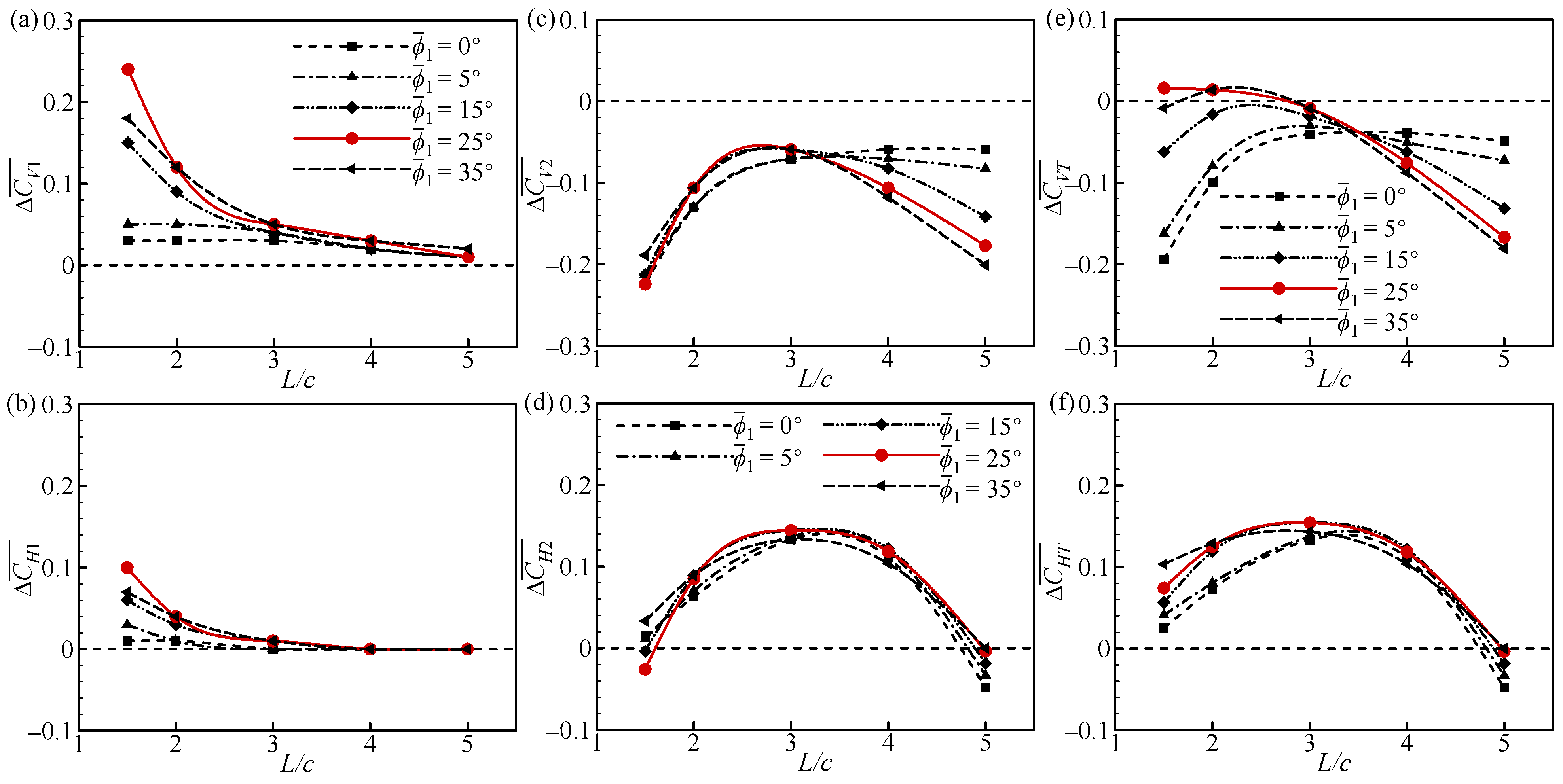
3.3. Effect of Δtr1
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wakeling, J.; Ellington, C. Dragonfly flight: II. Velocities, accelerations and kinematics of flapping flight. J. Exp. Biol. 1997, 200, 557–582. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, L.; Liu, H.; Yin, C. Measuring wing kinematics, flight trajectory and body attitude during forward flight and turning maneuvers in dragonflies. J. Exp. Biol. 2003, 206, 745–757. [Google Scholar] [CrossRef]
- Hefler, C.; Qiu, H.H.; Shyy, W. Aerodynamic characteristics along the wing span of a dragonfly Pantala flavescens. J. Exp. Biol. 2018, 221, jeb171199. [Google Scholar]
- Lai, Y.-H.; Lin, Y.-J.; Chang, S.-K.; Yang, J.-T. Effect of wing–wing interaction coupled with morphology and kinematic features of damselflies. Bioinspir. Biomim. 2020, 16, 016017. [Google Scholar] [CrossRef]
- Peng, L.; Pan, T.; Zheng, M.; Song, S.; Su, G.; Li, Q. Kinematics and aerodynamics of dragonflies (Pantala flavescens, Libellulidae) in climbing flight. Front. Bioeng. Biotech. 2022, 10, 795063. [Google Scholar] [CrossRef]
- Broering, T.M.; Lian, Y.-S. The effect of phase angle and wing spacing on tandem flapping wings. Acta Mech. Sin. 2012, 28, 1557–1571. [Google Scholar] [CrossRef]
- Lua, K.B.; Lu, H.; Zhang, X.; Lim, T.; Yeo, K. Aerodynamics of two-dimensional flapping wings in tandem configuration. Phys. Fluids 2016, 28, 121901. [Google Scholar] [CrossRef]
- Boschitsch, B.M.; Dewey, P.A.; Smits, A.J. Propulsive performance of unsteady tandem hydrofoils in an in-line configuration. Phys. Fluids 2014, 26, 051901. [Google Scholar] [CrossRef]
- Lagopoulos, N.; Weymouth, G.; Ganapathisubramani, B. Deflected wake interaction of tandem flapping foils. J. Fluid Mech. 2020, 903, A9. [Google Scholar] [CrossRef]
- Han, P.; Pan, Y.; Liu, G.; Dong, H.B. Propulsive performance and vortex wakes of multiple tandem foils pitching in-line. J. Fluid Struct. 2022, 108, 103422. [Google Scholar] [CrossRef]
- Muscutt, L.E.; Weymouth, G.D.; Ganapathisubramani, B. Performance augmentation mechanism of in-line tandem flapping foils. J. Fluid Mech. 2017, 827, 484–505. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, Y.; Tang, H. An experimental study on the forewing–hindwing interactions in hovering and forward flights. Int. J. Heat Fluid Flow 2016, 59, 62–73. [Google Scholar] [CrossRef]
- Rival, D.; Hass, G.; Tropea, C. Recovery of Energy from Leading- and Trailing-Edge Vortices in Tandem-Airfoil Configurations. J. Aircr. 2011, 48, 203–211. [Google Scholar] [CrossRef]
- Gungor, A.; Hemmati, A. Wake symmetry impacts the performance of tandem hydrofoils during in-phase and out-of-phase oscillations differently. Phys. Rev. E 2020, 102, 043104. [Google Scholar] [CrossRef]
- Joshi, V.; Mysa, R.C. Mechanism of wake-induced flow dynamics in tandem flapping foils: Effect of the chord and gap ratios on propulsion. Phys. Fluids 2021, 33, 087104. [Google Scholar] [CrossRef]
- Wang, G.; Ng, B.F.; Teo, Z.W.; Lua, K.B.; Bao, Y. Performance augmentation mechanism of tandem flapping foils with stroke time-asymmetry. Aerosp. Sci. Technol. 2021, 117, 106939. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Chen, L. Enhanced performance of tandem plunging airfoils with an asymmetric pitching motion. Phys. Fluids 2022, 34, 011910. [Google Scholar] [CrossRef]
- Sun, M.; Lan, S.L. A computational study of the aerodynamic forces and power requirements of dragonfly (Aeschna juncea) hovering. J. Exp. Biol. 2004, 207, 1887–1901. [Google Scholar] [CrossRef]
- Huang, H.; Sun, M. Dragonfly forewing-hindwing interaction at various flight speeds and wing phasing. AIAA J. 2007, 45, 508–511. [Google Scholar] [CrossRef]
- Kurt, M.; Moored, K.W. Flow interactions of two- and three-dimensional networked bio-inspired control elements in an in-line arrangement. Bioinspir. Biomim. 2018, 13, 045002. [Google Scholar] [CrossRef]
- Hu, Z.; Deng, X.Y. Aerodynamic interaction between forewing and hindwing of a hovering dragonfly. Act. Mech. Sin. 2014, 30, 787–799. [Google Scholar] [CrossRef]
- Usherwood, J.R.; Lehmann, F.-O. Phasing of dragonfly wings can improve aerodynamic efficiency by removing swirl. J. R. Soc. Interface 2008, 5, 1303–1307. [Google Scholar] [CrossRef]
- Lehmann, F.-O. Wing–wake interaction reduces power consumption in insect tandem wings. Exp. Fluids 2009, 46, 765–775. [Google Scholar] [CrossRef]
- Nagai, H.; Fujita, K.; Murozono, M. Experimental Study on Forewing-Hindwing Phasing in Hovering and Forward Flapping Flight. AIAA J. 2019, 57, 3779–3790. [Google Scholar] [CrossRef]
- Peng, L.; Zheng, M.; Pan, T.; Su, G.; Li, Q. Tandem-wing interactions on aerodynamic performance inspired by dragonfly hovering. R. Soc. Open Sci. 2021, 8, 202275. [Google Scholar] [CrossRef]
- Meng, X.G.; Chen, Z.S.; Zhang, Y.; Chen, G. Aerodynamic performance and flow mechanism of multi-flapping wings with different spatial arrangements. Phys. Fluids 2022, 34, 021907. [Google Scholar] [CrossRef]
- Meng, X.G.; Chen, Z.S.; Wang, D.S.; Jiang, S.J.; Chen, G. Aerodynamic interference of three flapping wings in tandem configuration. Phys. Fluids 2023, 35, 031911. [Google Scholar] [CrossRef]
- Broering, T.M.; Lian, Y.S. Numerical study of tandem flapping wing aerodynamics in both two and three dimensions. Comput. Fluids 2015, 115, 124–139. [Google Scholar] [CrossRef]
- Arranz, G.; Flores, O.; Garcia-Villalba, M. Three-dimensional effects on the aerodynamic performance of flapping wings in tandem configuration. J. Fluid Struct. 2020, 94, 102893. [Google Scholar] [CrossRef]
- Zou, P.-Y.; Lai, Y.-H.; Yang, J.-T. Effects of phase lag on the hovering flight of damselfly and dragonfly. Phys. Rev. E 2019, 100, 063102. [Google Scholar] [CrossRef]
- Wang, Z.J.; Russell, D. Effect of forewing and hindwing interactions on aerodynamic forces and power in hovering dragonfly flight. Phys. Rev. Lett. 2007, 99, 148101. [Google Scholar] [CrossRef]
- Liu, H.; Wang, S.; Liu, T. Vortices and Forces in Biological Flight: Insects, Birds, and Bats. Annu. Rev. Fluid Mech. 2024, 56, 147. [Google Scholar] [CrossRef]
- Pourfarzan, A.; Wong, J.G. Constraining optimum swimming strategies in plesiosaurs: The effect of amplitude ratio on tandem pitching foils. Phys. Fluids 2022, 34, 051908. [Google Scholar] [CrossRef]
- Chen, L.; Sun, W.; Wang, Y.Q. Effects of flapping deviation on the hovering performance of tandem pitching-plunging foils. Comput. Fluids 2023, 250, 105708. [Google Scholar] [CrossRef]
- Jurado, R.; Arranz, G.; Flores, O.; García-Villalba, M. Numerical simulation of flow over flapping wings in tandem: Wingspan effects. Phys. Fluids 2022, 34, 017114. [Google Scholar] [CrossRef]
- Lai, Y.-H.; Chang, S.-K.; Lan, B.; Hsu, K.-L.; Yang, J.-T. Optimal thrust efficiency for a tandem wing in forward flight using varied hindwing kinematics of a damselfly. Phys. Fluids 2022, 34, 061909. [Google Scholar] [CrossRef]
- Tiwari, S.; Chandel, S. Effect of stroke plane inclination on the hovering aerodynamic performance of tandem flapping foils. Bioinspir. Biomim. 2024, 19, 026002. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.H.; Sun, M. Unsteady aerodynamic forces of a flapping wing. J. Exp. Biol. 2004, 207, 1137–1150. [Google Scholar] [CrossRef]
- Chen, L.; Wu, J. Coexistence of dual wing–wake interaction mechanisms during the rapid rotation of flapping wings. J. Fluid Mech. 2024, 987, A16. [Google Scholar] [CrossRef]
- Meng, X.G.; Sun, M. Wing and body kinematics of forward flight in drone-flies. Bioinspir. Biomim. 2016, 11, 056002. [Google Scholar] [CrossRef]
- Zhu, H.J.; Sun, M. Kinematics Measurement and Power Requirements of Fruitflies at Various Flight Speeds. Energies 2020, 13, 4271. [Google Scholar] [CrossRef]
- Chen, Z.S.; Xie, Y.X.; Zhang, Y.; Li, L.; Meng, X.G. Aerodynamics of a flapping wing with stroke deviation in forward flight. Phys. Fluids 2024, 36, 051908. [Google Scholar] [CrossRef]
- Rogers, S.E.; Kwak, D.; Kiris, C. Steady and unsteady solutions of the incompressible Navier-Stokes equations. AIAA J. 1991, 29, 603–610. [Google Scholar] [CrossRef]
- Rogers, S.E.; Pulliam, T.H. Accuracy enhancements for overset grids using a defect correction approach. AIAA J. 1994, 94, 0523. [Google Scholar]
- Chang, M.; Xu, Z.Y.; Chen, Z.S.; Li, L.; Meng, X.G. Aerodynamic Performance of Three Flapping Wings with Unequal Spacing in Tandem Formation. J. Bionic Eng. 2024, 21, 1662–1676. [Google Scholar] [CrossRef]




| Flapping Amplitude (Φ1) | Flapping Mean Angle () | Pitch Rotation Duration (Δtr1) | Wing Spacing (L) |
|---|---|---|---|
| 60°, 80°, 100°, 120° | 25° | 0.3T | 1.5c, 2c, 3c, 4c, 5c |
| 100° | 0°, 5°, 15°, 25°, 35° | 0.3T | |
| 100° | 25° | 0.2T, 0.3T, 0.4T, 0.5T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xie, Y.; Meng, X. Unsteady Aerodynamic Forces of Tandem Flapping Wings with Different Forewing Kinematics. Biomimetics 2024, 9, 565. https://doi.org/10.3390/biomimetics9090565
Chen Z, Xie Y, Meng X. Unsteady Aerodynamic Forces of Tandem Flapping Wings with Different Forewing Kinematics. Biomimetics. 2024; 9(9):565. https://doi.org/10.3390/biomimetics9090565
Chicago/Turabian StyleChen, Zengshuang, Yuxin Xie, and Xueguang Meng. 2024. "Unsteady Aerodynamic Forces of Tandem Flapping Wings with Different Forewing Kinematics" Biomimetics 9, no. 9: 565. https://doi.org/10.3390/biomimetics9090565
APA StyleChen, Z., Xie, Y., & Meng, X. (2024). Unsteady Aerodynamic Forces of Tandem Flapping Wings with Different Forewing Kinematics. Biomimetics, 9(9), 565. https://doi.org/10.3390/biomimetics9090565







