Retrogradation of Truth and Omniscience

Abstract

Todd and Rabern have argued that assuming future contingents are untrue, together with accepting the principle of the retrogradation of truth ($p\to \mathbf{PF}\left(p\right)$), implies that it is metaphysically impossible that an omniscient entity exists. Since the possibility of an omniscient being is a metaphyisical and theological thesis that should not depend on assumed temporal semantics, Todd and Rabern conclude that, if one wishes to maintain the untruth of future contingents, one must reject the principle of the retrogradation of truth. This paper aims to show that Todd and Rabern’s argument fails. We present a temporal semantics in which future contingents are untrue, the principle of the retrogradation of truth is valid, and the potential existence of an omniscient and temporal being is preserved.

1. Introduction

Let us suppose that the future is metaphysically open. This means that the present state of the world and its laws do not determine every future state of the world. In this scenario, there are contingent futures—that is, future-tense sentences whose truth is not metaphysically determined by the present state and the laws of the world. There are various semantic theories concerning the truth value of contingent futures. According to many of these theories, contingent statements are not true. According to some, they are false; according to others, they are neither true nor false. For the purposes of this paper, we shall not distinguish among these theories and shall refer to the thesis that contingent futures are not true as Open Futurism ($\mathsf{OF}$).

Let us suppose that “it will rain tomorrow” is a future contingent when evaluated on December 9th. If we assume $\mathsf{OF}$, this sentence is untrue. Time passes, and now it is December 10th. Let us further assume that it rains on December 10th. How should we evaluate, from the perspective of December 10th, the proposition expressed by “it will rain tomorrow” as evaluated on December 9th? Many might intuitively consider this proposition to be true on December 9th. This shift in truth value is what we refer to as the Retrogradation of Truth ($\mathsf{RGT}$). Indeed, several semantic frameworks for future-tense sentences—though not all—accommodate this intuition.

Todd and Rabern in [1] have proposed a powerful argument against what they call Open-Closurism ($\mathsf{OC}$), which is the conjunction of two theses: (1) $\mathsf{OF}$ and (2) $\mathsf{RGT}$. They aim to show that $\mathsf{OC}$ has unacceptable consequences. Specifically, if one assumes $\mathsf{OC}$, it becomes necessary to deny the very possibility of an omniscient being. Although Todd and Rabern do not intend to endorse the existence of an omniscient entity, it seems peculiar for semantic principles to dictate conclusions about a complex metaphysical issue such as the possible existence of an omniscient being. Consequently, they argue that $\mathsf{OC}$ must be rejected. If one wishes to maintain $\mathsf{OF}$—that contingent futures are untrue—it becomes necessary to deny $\mathsf{RGT}$.

Although this argument appears very strong, we believe that it ultimately fails. To demonstrate that it does not achieve its goal, we will present a semantic framework that assumes $\mathsf{OC}$ while preserving the possibility of an omniscient entity. This will suffice to show that, pace Todd and Rabern, $\mathsf{OC}$ does not imply the impossibility of an omniscient being.

This paper is organized as follows. Section 2 provides a detailed exposition of Todd and Rabern’s argument. In Section 3, we introduce branching time semantics. Section 4 presents a specific $\mathsf{OC}$ semantic framework and demonstrates that it permits the possibility of a temporal omniscient entity, thereby refuting Todd and Rabern’s claim. Lastly, Section 5 concludes with final remarks.

2. Todd and Rabern’s Argument

Some temporal semantics validate $\mathsf{OC}$. For example, it is valid in Thomason’s supervaluationism (see [2]). This framework universally quantifies over all histories passing through the point of evaluation. A statement is supertrue if it is true in all these histories. Thus, contingent futures are not (super)true, but since, given a point of evaluation, $p\to \mathbf{PF}p$ is true across all histories passing through that point, $\mathsf{RGT}$ is a valid principle. Similarly, MacFarlane’s relativistic semantics (see [3,4]) validates $\mathsf{OC}$. When the context of assessment and the context of evaluation coincide, $\mathbf{F}p$ is not true. However, when the context of evaluation is in the past relative to the context of assessment, $\mathbf{F}p$ becomes true at the context of evaluation if p is true at the context of assessment.

On the other hand, $\mathsf{OC}$ is not valid in other temporal semantics. For example, Peircean semantics (see [5,6]) accepts $\mathsf{OF}$ but rejects $\mathsf{RGT}$. Conversely, classical Thin Red Line ($\mathsf{TRL}$) semantics rejects both $\mathsf{OF}$ and $\mathsf{RGT}$.1 However, it is possible to modify $\mathsf{TRL}$ semantics to validate $\mathsf{RGT}$. For example, $\mathsf{TRL}$ can be relativized to particular instants of time (see [8,9]), or $\mathsf{TRL}$ can be established at the post-semantic level rather than at the semantic level (see [10,11,12]). In any case, any form of $\mathsf{TRL}$ semantics rejects $\mathsf{OF}$. Todd and Rabern’s argument can thus be interpreted as an argument favoring Peirceanism or $\mathsf{TRL}$ semantics.

Let us now examine the details of this argument. For simplicity of exposition, we will sometimes refer to the omniscient entity as “God”. We also introduce a doxastic belief operator ($\mathsf{B}$), which is consistently intended to refer to the omniscient subject, where $\mathsf{B}p$ indicates that God believes p. The omniscience of God can be characterized by stating the principle of omni-accuracy:

Omni-accuracy 

$\phi \leftrightarrow \mathsf{B}\phi$

According to this principle, if God believes a certain proposition, that proposition is true. Moreover, if a proposition is true, then God believes it. Thus, God believes all and only true propositions. Introducing $\mathsf{RGT}$ yields the following result:2

$p\to {\mathbf{P}}_1\mathsf{B}\left({\mathbf{F}}_{1}p\right)$3

Let us now suppose that, on December 9th, it is indeterminate whether it will rain on December 10th. According to $\mathsf{OF}$, it is therefore not true on December 9th that it will rain on December 10th. Hence, God cannot believe on December 9th that it will rain on December 10th, as this would contradict omni-accuracy. However, if $\mathsf{RGT}$ is assumed, it is true on December 10th that on December 9th God believed it would rain on December 10th. We have, therefore, the following result: on December 9th, God does not believe p, but on December 10th it is true that God believed p on December 9th. This seems to contradict the fixity of the past: the past appears to change as time progresses. Therefore, the advocate of $\mathsf{OC}$ seems to be committed to situations as the following: at $t_1$ it is true that p is true at $t_0$, but at $t_2$ it is no more true that p is true at $t_0$ (where $t_0<t_1<t_2$). This seems highly counterintuitive.

The options available to a defender of $\mathsf{OC}$ appear limited:

(i)

Reject the principle of the fixity of the past. However, this is a very costly option. To be sure, it is entirely acceptable that the correctness of a belief or a statement might change over time. Suppose, for instance, that someone says on December 9th: “It will rain tomorrow”. If it is indeterminate whether it will rain the next day, it is also indeterminate whether this statement is correct. However, on December 10th, being a rainy day, one might say: “It is raining. You were right: your statement yesterday was correct”. Nevertheless, it seems unacceptable that on December 9th it is not true that God believes p, yet the next day it becomes true that on December 9th God believed p. The correctness of a belief is a relational fact between that belief and what makes it true. What makes it true may be a future fact that is not determined today. The fact that God believes something, however, is not a relational fact; it is entirely contained within a single moment in time. It thus seems that $\mathsf{OC}$ implies an intrinsic alteration of the past.4

(ii)

Reject Omni-accuracy. However, this implies that the existence of an omniscient being is not possible. As Todd and Rabern observe, “In general, one could argue that a semantic theory—a theory concerned with the logic and compositional structure of the language—ought not to settle certain substantive non-semantic questions” (p. 116).

Todd and Rabern conclude that $\mathsf{OC}$ must be rejected.

We consider this conclusion premature. In Section 4, we will present a double-indices semantics, inspired by MacFarlane’s relativism, in which $\mathsf{OC}$ does not imply that omni-accuracy cannot be predicated of an omniscient entity. However, before proceeding to the exposition of our framework, we introduce branching time semantics in the next section.

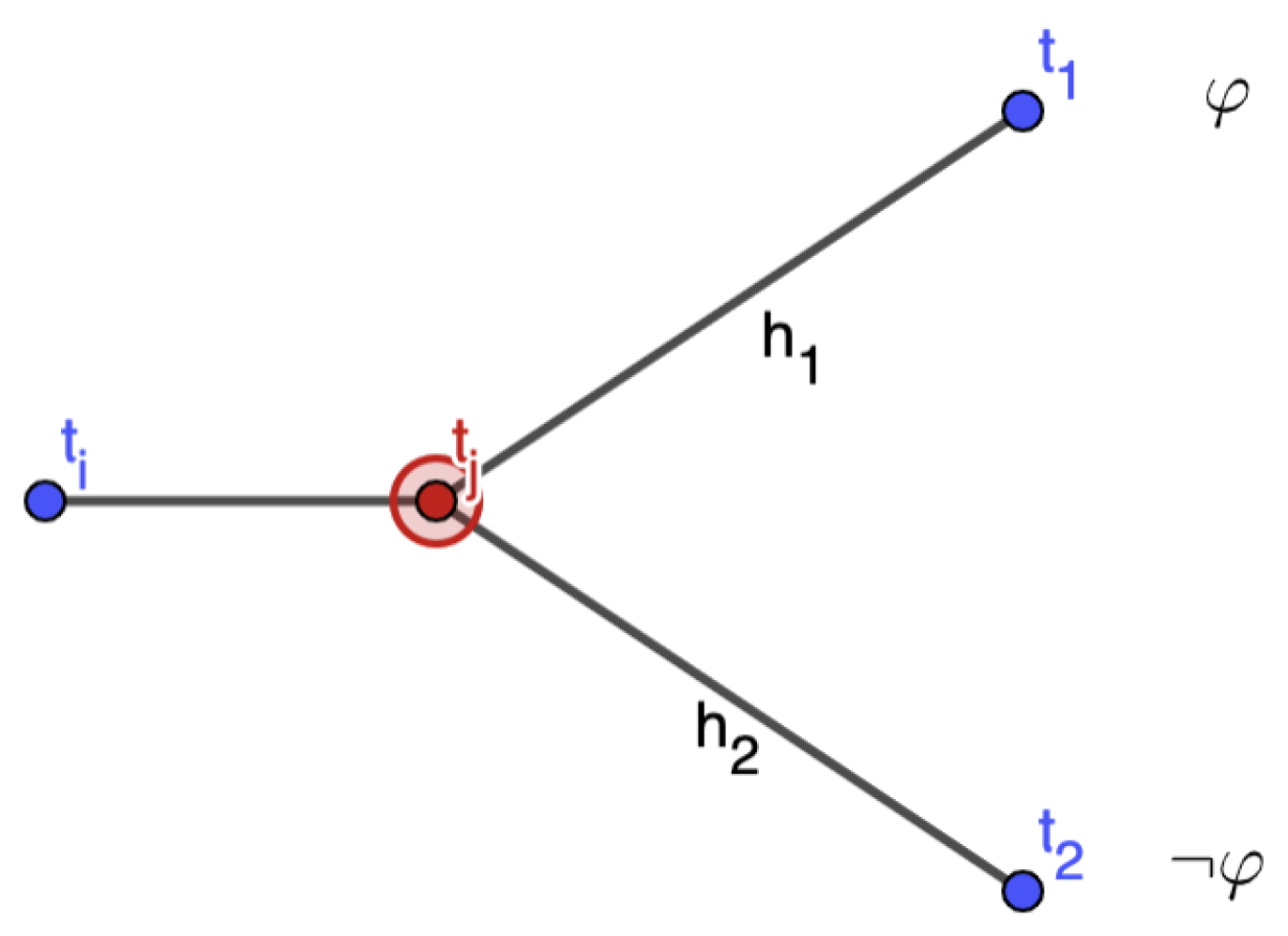
3. Branching Time and Evaluation of Future Tense Sentences

A branching time structure5 is defined as a pair consisting of a non-empty set of temporal instants and a precedence relation defined over them: $\mathcal{B}=\langle \mathbb{T},<\rangle$. Conceptually, the instants represent possible instantaneous states of the world, while < serves as the temporal precedence relation. This relation is thus asymmetric and transitive and satisfies (at minimum) the conditions of Backward Linearity ($\mathsf{BL}$) and Historical Connectedness ($\mathsf{HC}$).

($\mathsf{BL}$)

$\forall t\forall t_1\forall t_2((t_1<t\wedge t_2<t)\to (t_1=t_2\vee t_1<t_2\vee t_2<t_1))$

To put the above in words, two time instants that are in the past relative to t are either identical or related through <; this ensures that for each instant t, there is a unique preceding history.

($\mathsf{HC}$)

$\forall t_1\forall t_2\exists t(t\le t_1\wedge t\le t_2)$

$\mathsf{HC}$ posits that all instants share a common connection in the past.

Maximal subsets of time instants that are linearly ordered in t are defined as histories (h), representing the potential trajectories of events in the world. Propositional language includes a potentially infinite set of propositional variables ($\mathsf{Var}$) and two temporal operators, $\mathbf{P}$ and $\mathbf{F}$. ${\mathbf{P}}_n$ and ${\mathbf{F}}_n$, are the corresponding metrical operators: ${\mathbf{P}}_n$ means “n units of time before the moment of evaluation”, while ${\mathbf{F}}_n$ means “n units of time after the evaluation moment”.

$\mathsf{BL}$ ensures that each instant within the structure has a single past history, but potentially multiple future histories, depending on whether there is branching after that particular instant. Consider a scenario in which two distinct histories, namely $h_1$ and $h_2$, diverge from a given instant $t_0$. Suppose that in $h_1$, $\phi$ is true at some instant following $t_0$ whereas in $h_2$$\phi$ is true at no instant following $t_0$ How, then, should one interpret the formula $\mathbf{F}\phi$ evaluated at $t_0$?

A straightforward solution would be to relativize the truth conditions to particular histories, as in the Ockhamist framework. Hence, the formula $\mathbf{F}\phi$ is true at $t_0$ with respect to $h_1$ but false at $t_0$ with respect to $h_2$:

$$\begin{array}{ccc}\hfill \mathcal{M},t/h{\vDash }^{\mathsf{ock}}\mathbf{F}\phi & \iff & \exists t’>t,\mathcal{M},t’/h{\vDash }^{\mathsf{ock}}\phi \hfill \end{array}$$

$$\mathcal{M},t/h{⊭}^{\mathsf{ock}}\mathbf{F}\phi \iff \neg \exists t’>t,\mathcal{M},t’/h{\vDash }^{\mathsf{ock}}\phi$$

However, such an approach does not seem entirely satisfactory. Let us suppose we are planning a hike in the mountains for tomorrow. We would like to know what the weather conditions will be and, in particular, whether it will rain tomorrow. Imagine we receive the following response: in one future history, it will rain tomorrow, but in another, it will not. We would be disappointed by this answer. What we want to know is not whether it will rain in one history or another, but whether it will rain tout court.

There are several temporal semantics that have attempted to address this problem. These can be divided into two broad families depending on whether they allow for the possibility that contingent futures are true. As previously mentioned, we refer to those who deny this possibility as Open Futurists. Typically, Open Futurists universally quantify over the histories passing through a given instant in time and assert that a sentence is true if it is true in all the histories passing through that instant. In turn, Open Futurists can be distinguished into Peircean and Aristotelian camps.

Peirceans hold that all contingent futures are false. Accordingly, they impose the following truth conditions on a formula such as $\mathbf{F}\phi$ evaluated at time t:

$$\begin{array}{ccc}\hfill \begin{array}{c}\hfill \mathcal{M},t{\vDash }^{\mathsf{per}}\mathbf{F}\phi \end{array}& \iff & \forall h\in {\mathcal{H}}_t,\exists t’>t,t’/h{\vDash }^{\mathsf{ock}}\phi \hfill \end{array}$$

$$\mathcal{M},t{⫤}^{\mathsf{per}}\mathbf{F}\phi \iff \neg \forall h\in {\mathcal{H}}_t,\exists t’>t,t’/h{\vDash }^{\mathsf{ock}}\phi$$

where ${\mathcal{H}}_t$ denotes the set of histories that pass through t (${\mathcal{H}}_t=\left\{h\right|t\in h\}$).

Aristotelians, on the other hand, claim that contingent futures are neither true nor false. The truth conditions for future tense sentences can thus be expressed as follows:

$$\begin{array}{ccc}\hfill \begin{array}{c}\hfill \mathcal{M},t{\vDash }^{\mathsf{ar}}\mathbf{F}\phi \end{array}& \iff & \forall h\in {\mathcal{H}}_t,\exists t’>t,t’/h{\vDash }^{\mathsf{ock}}\phi \hfill \\ \hfill \mathcal{M},t{{\displaystyle ⫤}}^{\mathsf{ar}}\mathbf{F}\phi & \iff & \forall h\in {\mathcal{H}}_t,\neg \exists t’>t,t’/h{\vDash }^{\mathsf{ock}}\phi \hfill \end{array}$$

Otherwise, we have indeterminate truth conditions.

Those who assert that contingent futures can be true are typically Linearists. That is, they postulate the existence of a privileged history (often referred to as “the Thin Red Line”, or $\mathsf{TRL}$), which represents the actual history of the world. Although multiple histories may pass through the moment of evaluation, a formula such as $\mathbf{F}\phi$ is evaluated solely with respect to the $\mathsf{TRL}$:

$$\begin{array}{ccc}\hfill \begin{array}{c}\hfill \end{array}\mathcal{M},t{\vDash }^{\mathsf{trl}}\mathbf{F}\phi & \iff & \exists t’>t,t^{\prime }\in \mathsf{TRL},\mathcal{M},t’/h{\vDash }^{\mathsf{ock}}\phi \hfill \end{array}$$

As mentioned earlier, we do not distinguish here between Peirceans and Aristotelians. Open Futurists share the common view that a formula such as $\mathbf{F}\phi$ is true at an instant t when it is true in all the histories passing through t. What we aim to demonstrate is that such an Open Futurist truth clause for $\mathbf{F}\phi$ remains compatible with the possible existence of an omniscient entity, even when $\mathsf{RGT}$ is assumed. This is the topic of the following section.

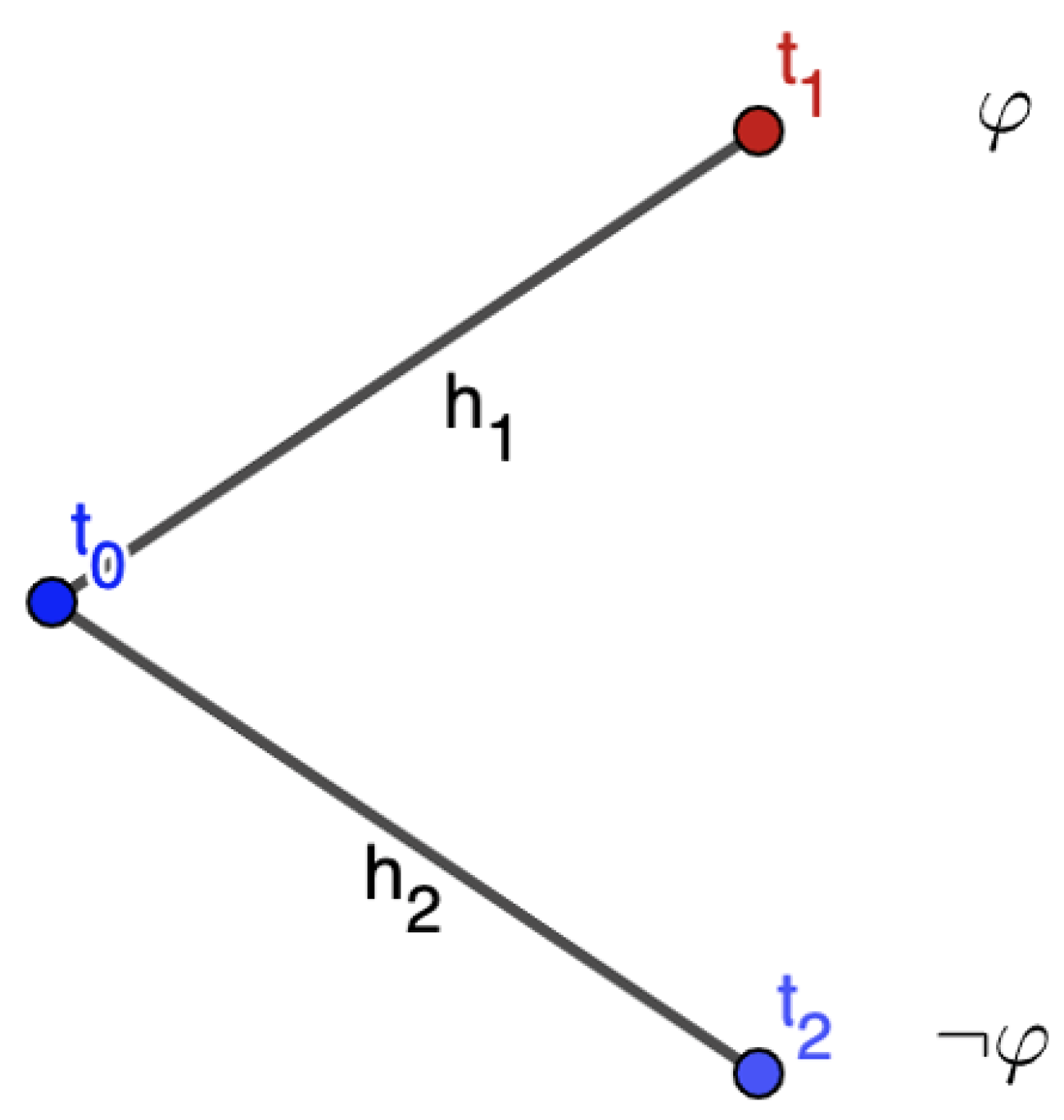
4. Retro-Believing and Retro-Truth

4.1. Double-Indices Semantics

It is time to develop our semantic system that allows us to overcome the Todd and Rabern problem.6 Naturally, our proposal will have to validate OC: in other words, it will be a theory in which future contingents are untrue. We can remain agnostic regarding the alternative between Aristotelianism and Peirceanism.

What is the intuition behind our proposal? It is rather simple, at least from an intuitive point of view, and to illustrate it, we will once again refer to an example similar to those discussed previously. When we ask whether a given sentence is true at a certain point in time, we usually wonder whether the world, at that moment, was arranged in such a way as to make that sentence true. This is particularly evident in the case of dated sentences such as, for example, “On 12 January 1803, Napoleon Bonaparte gave three kisses to Paolina”. The truth of this sentence depends on how things stood, particularly between Napoleon and Paolina, on 12 January 1803.

Let us complicate the picture a little and consider a tensed sentence expressed in the future, such as “it will rain tomorrow” (let us call it A for convenience). Assume that this sentence was uttered on 10 November 2024; now, the truth of this sentence depends on how things turn out on 11 November 2024. Since we have assumed that A is a contingent future event, we must say that on 10 November, A is untrue.

However, suppose that it did indeed rain on November 11 and that, a posteriori, it was true on November 10 that it would rain the next day. Now, what can we say about the truth of A, uttered on November 10? In the first case, that is, when it is still undetermined how things will turn out, it is indeterminate whether A is true, but in the second case, A is true.

Our semantics takes this situation into account precisely by introducing another index of evaluation in addition to the standard one; for this reason, it is a two-index semantics. The first index denotes the moment at which we evaluate the formula, while the second denotes the perspective from which we perform the evaluation. It is one thing to evaluate A on November 10 from the perspective of November 10. It is quite another to evaluate the truth value of A on November 10 from the perspective of November 11.

The second index has a natural interpretation as the “now” of the structure. Returning once again to the example, in the second case, we interpret the truth value of A, that is, “it will rain tomorrow” from today’s perspective—that is, knowing how things ultimately turned out. This is, in fact, a retrospective evaluation, and we will see that this has significant consequences. However, referring to “now” should not suggest any metaphysically committed stance toward tensed theories of time. Elsewhere, we have suggested that such a semantics is particularly well fitted to a realist conception of the present. Nevertheless, it is perfectly compatible with an indexical interpretation of “now” (cf. [18]).

Two-index systems are, of course, not new. Our framework is quite close to the one developed by MacFarlane. However, aside from differences in the logical behavior of certain operators, what distinguishes us from MacFarlane’s proposal is that, in his case, we find a semantics for tensed statements followed by a general post-semantics. In our framework, by contrast, everything is done at a single level—the semantic level.

Consider the following notation:

$$\begin{array}{cc}\hfill \begin{array}{c}\hfill \left(\mathrm{a}\right)\end{array}& \mathcal{M},t_i,t_j{\vDash }^{\mathsf{prs}}\phi \end{array}$$

This expression means that $\phi$ is true at $t_i$ when the present time is $t_j$. The first index ($t_i$) specifies the time at which the formula is assessed, while the second index ($t_j$) indicates the position of the present in the temporal structure.

The two temporal points may coincide, which would occur when $\phi$ is evaluated at t when t itself is the present time. In all cases, the evaluation instant (e.g., t) and the present instant (e.g., $t’$) must be related, such that one of the following conditions is satisfied: $t<t’$, $t\approx t’$, or $t’<t$.7 The truth clause for atomic formulas is as follows:

$$\begin{array}{cccc}\hfill \begin{array}{c}\hfill \left(\mathrm{b}\right)\end{array}& \mathcal{M},t_i,t_j{\vDash }^{\mathsf{prs}}\phi & \iff \hfill & \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),t_i/h{\vDash }^{\mathsf{ock}}\phi \end{array}$$

where ${\mathcal{H}}_{t_i}$ denotes the set of histories that pass through $t_i$ (${\mathcal{H}}_{t_i}=\left\{h\right|t_i\in h\}$), and $({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j})$ represents the intersection of the sets of histories. As said before, we can remain agnostic concerning future contingents that are not true. There are two possibilities. If we assume an Aristotelian semantics, we have the following clauses:

$$\begin{array}{cccc}\hfill \begin{array}{c}\hfill \left(\mathrm{c}\right)\end{array}& \mathcal{M},t_i,t_j{⊭}^{\mathsf{prs}}\phi & \iff \hfill & \neg \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),t_i/h{\vDash }^{\mathsf{ock}}\phi \end{array}$$

$$\begin{array}{cccc}\hfill \begin{array}{c}\hfill \left(\mathrm{d}\right)\end{array}& \mathcal{M},t_i,t_j{{\displaystyle ⫤}}^{\mathsf{prs}}\phi & \iff \hfill & \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),t_i/h{⊭}^{\mathsf{ock}}\phi \end{array}$$

In the first case, we say that $\phi$ is not true; in the second, we say that $\phi$ is false. Therefore, future contingents are neither true nor false.

If we assume a Peircean semantics, we have just one possibility:

$$\begin{array}{cccc}\hfill \begin{array}{c}\hfill \left(\mathrm{e}\right)\end{array}& \mathcal{M},t_i,t_j{⊭}^{\mathsf{prs}}\phi & \iff \hfill & \neg \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),t_i/h{\vDash }^{\mathsf{ock}}\phi \end{array}$$

Future contingents are therefore false. Since nothing essential in this paper depends on the choice between these two possibilities, we shall remain neutral with respect to them.

The following truth clauses can be straightforwardly derived:

$$\begin{array}{lll}\begin{array}{c}\mathcal{M},t_i,t_j{\vDash }^{\mathsf{prs}}\neg \phi \end{array}& \iff & \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),t_i/h{⊭}^{\mathsf{ock}}\phi \hfill \end{array}$$

$$\begin{array}{lll}\mathcal{M},t_i,t_j{\vDash }^{\mathsf{prs}}\phi \wedge \psi & \iff & \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),t_i/h{\vDash }^{\mathsf{ock}}\phi \\ & & \mathrm{and} \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),t_i/h{\vDash }^{\mathsf{ock}}\psi \end{array}$$

$$\begin{array}{lll}\mathcal{M},t_i,t_j{\vDash }^{\mathsf{prs}}\mathbf{P}\phi & \iff & \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),\exists t’<t_i,t’/h{\vDash }^{\mathsf{ock}}\phi \end{array}$$

The clauses lacking temporal operators naturally extend Ockhamist semantics. For the past, the second index is vacuous because there is only a single history, leading to a linear evaluation. However, for the future, the second index plays a more crucial role.

In Figure 1, the evaluation instant is $t_i$, while the present time is situated at $t_j$; the truth conditions for $\mathbf{F}\phi$ at $t_i$ are defined as follows:

$$\begin{array}{ccc}\hfill \begin{array}{c}\hfill \end{array}\mathcal{M},t_i,t_j{\vDash }^{\mathsf{prs}}\mathbf{F}\phi & \iff & \forall h\in ({\mathcal{H}}_{t_i}\cap {\mathcal{H}}_{t_j}),\exists t’>t_i,t’/h{\vDash }^{\mathsf{ock}}\phi \hfill \end{array}$$

There are two scenarios to consider (refer to Figure 2 and Figure 3): one where the present coincides with or precedes the evaluation instant, and another where the present time follows that instant:

(Case I). In this scenario, the present ($t_0$) coincides with the evaluation instant. Because ${\mathcal{H}}_{t_0}\cap {\mathcal{H}}_{t_0}={\mathcal{H}}_{t_0}$, both the $\phi$-branch and the $\neg \phi$-branch are still open. Thus, $\mathcal{M},t_0,t_0{⊭}^{\mathsf{prs}}\mathbf{F}\phi$.

(Case II). In this case, the present is positioned at $t_1$, which is subsequent to the evaluation instant ($t_0$). The history where $\neg \varphi$ holds is no longer accessible, since $h_2\notin {\mathcal{H}}_{t_0}\cap {\mathcal{H}}_{t_1}$. As a result, $\mathcal{M},t_0,t_1{\vDash }^{\mathsf{prs}}\mathbf{F}\phi$.

In the double-indices framework, the truth values of sentences vary dynamically as time progresses. Therefore, this framework vindicates $\mathsf{RGT}$ and our intuitions in favor of this principle.

4.2. The Possibility of Omniscience

The perspectival semantics we have just outlined allows for a natural treatment of certain issues related to the backward shifting of truth. Specifically, it allows us to distinguish two senses of the future: the future relative to the moment of evaluation—that is, the set of moments that follow the moment of evaluation—and the future relative to the perspective. When we evaluate, as is the relevant case, future-tense sentences from a future perspective, we are performing retro-evaluations; that is, we are considering the future as it appeared in the past, evaluating over a particular intersection of histories.

But how does all of this affect Todd and Rabern’s argument? To answer this question, we need to introduce one final element to our proposal: an element concerning the belief operator.

As you may recall, Todd and Rabern’s argument specifically concerned the belief states of an omniscient entity—belief states that, in light of the Open Future ($\mathsf{OF}$) thesis, became inconsistent. It is now a philosophical standard to model the concept of belief using a Kripkean semantics framework. Whether this formal apparatus is suitable for modeling the concept of divine belief is certainly debatable. In any case, it is quite plausible to consider belief as a representational concept: a subject believes that p when they represent the actual world in a certain way. This means that when we attribute a belief state to a subject—whether human or divine—we are referring to that subject’s own perspective. Note that this does not imply that there cannot be belief statements about the past, such as “Aristotle believed that there were four fundamental elements”, nor does it mean that there cannot be present beliefs referring to past events, as in “Emma believes that it rained yesterday”. What is important, however, is that when we evaluate a belief statement using our semantics, the perspective from which we perform the evaluation must be that of the doxastic subject. In belief contexts, in other words, interpretation is always centered on the moment the subject finds themselves in.

This has significant consequences. In particular, it implies that when we consider what we retrospectively believed in the past, we must shift the “now” backward, so that the perspective coincides with the past moment of evaluation.

This can be formally captured through the following belief semantic norm:

($\mathsf{bsn}$)

$\mathcal{M},t_i,t_j{\vDash }^{\mathsf{prs}}\mathsf{B}\left(\phi \right)\Rightarrow \mathcal{M},t_i,t_i{\vDash }^{\mathsf{prs}}\mathsf{B}\left(\phi \right)$

where $\phi$ can have any degree of logical complexity. A formula denoting a belief about a proposition of any complexity must be evaluated from a perspective that coincides with its evaluation instant. Therefore, ($\mathsf{bsn}$) changes the perspective index from $t_j$ to $t_i$.8

As a consequence, the Omni-accuracy principle $\phi \leftrightarrow \mathsf{B}\left(\phi \right)$ is reformulated as follows:

(Omn-$\mathsf{prs}$) 

For every t, $\mathcal{M},t,t{\vDash }^{\mathsf{prs}}\phi \leftrightarrow \mathsf{B}\left(\phi \right)$

The principle of Omni-accuracy must, therefore, be relativized to time. Consequently, we will say that every proposition that is true at any given moment is believed to be true by God at that moment and from that perspective. Thus, to anticipate what we will explain in more detail shortly, if a proposition $\phi$ is untrue at time t, from the perspective of t, God will not believe it to be true. Notice that if Aristotelism is assumed and $\phi$ lacks a truth value, then $\mathsf{B}\phi$ will also lack a truth value. However, this is not a problem given that the only important thing is that God does not believe that proposition.

Note that, since $\phi$ can have any logical complexity, it may include multiple temporal operators. Thus, at $t_0$, from the perspective of $t_0$, God believes what is true at other points of the structure from $t_0$’s perspective. For instance, if $\phi$ is true at $t_{-1}$ when $\mathsf{now}\left(t_0\right)$, then God believes at $t_0$ from $t_0$’s perspective that ${\mathbf{P}}_1\phi$. In symbolic notion,

$\mathcal{M},t_0,t_0{\vDash }^{\mathsf{prs}}{\mathbf{P}}_1\phi \leftrightarrow \mathsf{B}\left({\mathbf{P}}_1\phi \right)$

Thus, God believes at every instant what is true at any point in the structure from the perspective of that instant.

To sum up, our semantics involves two indices of evaluation: the first concerns the moment at which a formula is evaluated, while the second indicates the perspective from which we look at the world, so to speak. The perspective is important because, as we have seen from the truth clauses, it determines which histories are actually available for evaluation, and this, in turn, is crucial for determining the truth value of formulas that quantify over those available histories.

Divine beliefs always track the truth, as one would expect from an omniscient entity. However, they track the truth from the perspective in which we place God. If we refer to past divine beliefs, then we must shift the now backward or, to use a metaphor, rewind the tape of history until the present once again coincides with the moment of evaluation.

Let us now illustrate how our perspectival semantics, equipped with ($\mathsf{bsn}$), can respond to Todd and Rabern’s criticism. First, we will recapitulate Todd and Rabern’s argument in a semi-formal manner. For convenience, we will utilize metric temporal operators. Refer to Figure 4.9 Since $t_1\vDash \phi$ and, according to the hypothesis, $\mathsf{RGT}$ holds, we have that $t_1\vDash {\mathbf{P}}_1{\mathbf{F}}_1\phi$. However, ${\mathbf{F}}_1\phi$ is not true at $t_0$ as it is a future contingent at that time. Thus, it follows that $t_0\vDash \neg \mathsf{B}\left({\mathbf{F}}_1\phi \right)$ (see note 6), because God does not believe what is untrue. Yet, as it is true at $t_1$ that at $t_0$$\phi$ would be true the next day, God should have believed it. Instead, $t_1\vDash {\mathbf{P}}_1({\mathbf{F}}_1\phi \wedge \neg \mathsf{B}\left({\mathbf{F}}_1\phi \right))$. In other words, let us consider the scenario from the perspective of $t_1$ (where $\phi$ is true). In this context, two facts held true the previous day: on the one hand, $\phi$ would be true the next day, and on the other, God did not believe that $\phi$ would be true the next day. This would imply a form of ignorance on God’s part regarding the future truth of $\phi$.

We argue that, within our framework, Todd and Rabern’s argument becomes untenable. Let us analyze why.

Let us consider Figure 4. Starting from $\mathcal{M},t_1,t_1{\vDash }^{\mathsf{prs}}{\mathbf{P}}_1({\mathbf{F}}_1\phi \wedge \neg \mathsf{B}\left({\mathbf{F}}_1\phi \right))$, it follows that $\mathcal{M},t_1,t_1{\vDash }^{\mathsf{prs}}{\mathbf{P}}_1{\mathbf{F}}_1\phi \wedge {\mathbf{P}}_1\neg \mathsf{B}\left({\mathbf{F}}_1\phi \right)$, which in turn implies $\mathcal{M},t_1,t_1{\vDash }^{\mathsf{prs}}{\mathbf{P}}_1{\mathbf{F}}_1\phi$. Similarly, $\mathcal{M},t_1,t_1{\vDash }^{\mathsf{prs}}{\mathbf{P}}_1\neg \mathsf{B}\left({\mathbf{F}}_1\phi \right)$ holds, which means that, from today’s perspective, it was true that God did not believe yesterday that $\phi$ would be true. This leads to $\mathcal{M},t_0,t_1{\vDash }^{\mathsf{prs}}\neg \mathsf{B}\left({\mathbf{F}}_1\phi \right)$, indicating that, again from today’s standpoint, God did not believe yesterday that $\phi$ would be true. Does this imply that God was ignorant? No, God seems ignorant only if we consider the world from today’s metaphysically privileged perspective and interpret events in terms of what actually occurred.

If we want to correctly position ourselves at $t_0$, we must backdate the present; in other words, we must rewind the historical timeline. This is exactly what ($\mathsf{bsn}$) accomplishes: $\mathcal{M},t_0,t_1{\vDash }^{\mathsf{prs}}\neg \mathsf{B}\left({\mathbf{F}}_1\phi \right)$ entails $\mathcal{M},t_0,t_0{\vDash }^{\mathsf{prs}}\neg \mathsf{B}\left({\mathbf{F}}_1\phi \right)$. Thus, when $t_0$ was the present, God did not believe that $\phi$ would occur. Moreover, $\mathcal{M},t_0,t_0{⊭}^{\mathsf{prs}}{\mathbf{F}}_1\phi$ also holds because ${\mathbf{F}}_1\phi$ is a future contingent. Nonetheless, the fact that an omniscient entity does not believe what was not (yet) true is not problematic for its omniscience.

Todd and Rabern’s argument relies on a theoretical shift that retrogrades the truth and accuses an omniscient being of failing to know it. However, it is a retrograded truth, which is true only because the world has progressed, and what was once indeterminate is now determinate. By positioning ourselves at the temporal perspective of the omniscient entity at $t_0$ (i.e., moving the present to $t_0$), we obtain that the omniscient entity does not believe that $\phi$ will occur, since from $t_0$’s viewpoint, it is not true that $\phi$ will happen.

Conversely, from $t_1$’s perspective, it was true that $\phi$ would be true: $\mathsf{RGT}$ entails $\mathcal{M},t_0,t_1{\vDash }^{\mathsf{prs}}{\mathbf{F}}_1\phi$. Yet, this does not pose a problem for omniscience, because Todd and Rabern assume the omniscient entity’s belief pertains to the time when the present was $t_0$, not $t_1$. Additionally, $\mathcal{M},t_1,t_1{\vDash }^{\mathsf{prs}}{\mathbf{P}}_1{\mathbf{F}}_1\phi \wedge \mathsf{B}\left({\mathbf{P}}_1{\mathbf{F}}_1\phi \right)$ holds, which implies that $\mathcal{M},t_1,t_1{\vDash }^{\mathsf{prs}}\mathsf{B}\left({\mathbf{P}}_1{\mathbf{F}}_1\phi \right)$. In other words, it is true from today’s perspective that yesterday it was true that it would rain today and today God believes that yesterday, it was true that it would rain today.

In summary, when $\mathsf{now}\left(t_0\right)$, God does not believe ${\mathbf{F}}_1\phi$ since the world is seen from $t_0$’s perspective, according to which ${\mathbf{F}}_1\phi$ is not true. When $\mathsf{now}\left(t_1\right)$, God believes that ${\mathbf{F}}_1\phi$ was true the previous day, because from $t_1$’s perspective, it was true the previous day that $\phi$ would happen the next day. Consequently, God’s beliefs are always aligned with the truth. As time progresses, the truth values of propositions change; an omniscient God always believes at a time t what is true from that time’s perspective. In other words, God’s beliefs adapt as the truth values of propositions change over time, which is precisely what should be expected from an omniscient being.

Naturally, our argument can be challenged. The critical point is constituted by ($\mathsf{bsn}$). However, we believe that the reasons provided in support of it are solid. Clearly, this entire discussion assumes—as Todd and Rabern do—that God is a temporal entity and that tensed determinations can therefore be correctly applied to Him. In other words, within the context assumed here, it makes perfect sense to say that God believed yesterday that Emma would go to the party. This is a general theological view embraced, for instance, by Open Theists: for them, God’s temporality is not seen as a diminution of His perfection but rather as an essential element to ensure other divine attributes. However, our own view about the relationship between God and time (i.e., a timeless God) can be discussed. In the next section, we will deal with our view.

5. A Timeless God

The relationship between God and time has long been a subject of debate among philosophers of religion and theologians. Various solutions have been proposed in this regard. Todd and Rabern assume that God is a temporal entity. As we have seen, one of the premises of their argument is the following:

$p\to P_{1}B\left(F_{1}p\right)$

This means that God’s beliefs are temporally located. Therefore, God Himself is temporally located as well.10 However, this is not the only possible theory concerning the relationship between God and time: according to other conceptions, God is a timeless entity. If God exists outside of time, then Todd and Rabern’s argument does not hold, since it presupposes the temporality of His beliefs.

Advocates of a timeless God face other kinds of challenges. For instance, they must explain how a timeless entity can relate to a temporal world, particularly how such an entity can know this world and maintain causal relations with it. Here, we shall focus solely on the knowledge possessed by a timeless God. Can omniscience be attributed to a timeless God, and more specifically, can we account for divine omniscience using the two-index semantics presented in this article?

We believe the answer is affirmative, though certain modifications are required. Since it is no longer possible to locate God’s beliefs within time, it is also no longer possible to claim that God’s beliefs are indexed to a time and a perspective. Instead, God’s beliefs are indexed solely to His atemporal perspective.

We therefore introduce a special evaluation point, which we shall call e, relative to which we can express that God believes or does not believe something:

$M,e\vDash B\left(\phi \right)$

This means that, relative to model M and to God’s eternal standpoint e, God believes that $\phi$. If one accepts the theory of eternity proposed by [20]11, then e may be interpreted as the unique eternal reference frame postulated by these scholars, within which eternal entities exist.

An eternal God observes the entire temporal structure from His privileged perspective; He therefore sees what is true at each point within the temporal structure. For instance, He believes that a certain proposition is true at time t.

We can account for this by introducing dated propositions. In our new language, $\left[t\right]p$ means that p obtains at time t (e.g., “on December 28th, it rains”). However, it should be noted that in our framework, the truth value may still vary depending on the relevant perspective, particularly when the proposition includes a future operator. Let $Fp$ be the proposition that “Emma will attend the party”. Then $\left[t\right]Fp$ means that at time t, it is true that Emma will go to the party. In the two-index system presented here, such a proposition may have different truth values depending on the perspective from which it is evaluated, in particular if the perspective precedes or follows the date of the dated proposition. In the timeless conception of God proposed here, God not only perceives what happens at every point in the temporal structure, but He is also capable of considering all perspectives. His knowledge is therefore omni-perspectival. For instance, God believes that Emma will attend the party is not true relative to the index $\langle t,t\rangle$, but that it is true relative to the index $\langle t,t^{\prime }\rangle$. To account for this, we must introduce not only dated propositions, but also perspectival ones:

$\left[t\right]\left\{t^{\prime }\right\}\phi$

This means that $\phi$ obtains at t from the perspective $t^{\prime }$. We now have all the tools to combine God’s atemporal beliefs with the principle of retrograding truth. In particular, we have the following:

$M,e⊭B\left(\right[t\left]\right\{t\left\}Fp\right)$

$M,e\vDash B\left(\left[t\right]\left\{t^{\prime }\right\}Fp\right)$

From His privileged standpoint e, God does not believe that it is true at time t and from perspective t that Emma will attend the party. However, He does believe that it is true at time t and from perspective $t^{\prime }$ that Emma will attend the party.

It should be noted that, within this framework, propositions of the form $B\left(\phi \right)$ cannot be dated or relativized to a perspective, as they describe the beliefs of God, and God exists outside of time. Therefore, no index of the form $\left[t\right]$ or $\left\{t\right\}$ may be prefixed to $B\left(\phi \right)$.

This framework accounts for several key phenomena:

• Emma’s freedom: God knows that at time t and from the perspective of t, it is neither true nor false that Emma will attend the party. The future before her is thus indeterminate, and she is free to determine it as she wills.
• Divine omniscience: From the divine privileged standpoint, for every t and $t^{\prime }$, the following holds:

  $$\left[t\right]\left\{t^{\prime }\right\}\phi \leftrightarrow B\left(\left[t\right]\left\{t^{\prime }\right\}\phi \right)$$
  God knows the truth of every proposition and does not believe any proposition that is not true.
• The principle of retrogradation: While $\left[t\right]\left\{t\right\}Fp$ is not true, $\left[t\right]\left\{t^{\prime }\right\}Fp$ is. By changing the perspective—that is, the “present”—the truth value of future propositions also changes.

We conclude, therefore, that the knowledge of a timeless God is not incompatible with the principle of retrogradation of truth. It is thus possible to reconcile this principle with the beliefs of both a temporal and a timeless God.

6. Conclusions

In the semantic framework outlined in this paper, there is no point in time at which a formula is true without being believed as true by the omniscient being.12 This, we believe, encompasses all that can be required for an entity to be defined as omniscient. Our framework, therefore, demonstrates that $\mathsf{OC}$ and $\mathsf{RGT}$ are not incompatible with the possibility of an omniscient entity, thereby showing that Todd and Rabern’s argument fails to achieve its intended goal. The theoretical cost of our framework lies in the acceptance of ($\mathsf{bsn}$), which states that the attribution of belief to a subject at a specific time is constrained by the state of the universe at that time. We maintain that this is a minimal theoretical cost. Therefore, $\mathsf{OC}$ and $\mathsf{RGT}$ remain credible options within the domain of tense semantic theories.