On the Direction of Time: From Reichenbach to Prigogine and Penrose

Abstract

The question why natural processes tend to flow along a preferred direction has always been considered from within the perspective of the Second Law of Thermodynamics, especially its statistical formulation due to Maxwell and Boltzmann. In this article, we re-examine the subject from the perspective of a new historico-philosophical formulation based on the careful use of selected theoretical elements taken from three key modern thinkers: Hans Reichenbach, Ilya Prigogine, and Roger Penrose, who are seldom considered together in the literature. We emphasize in our analysis how the entropy concept was introduced in response to the desire to extend the applicability of the Second Law to the cosmos at large (Reichenbach and Penrose), and to examine whether intrinsic irreversibility is a fundamental universal characteristics of nature (Prigogine). While the three thinkers operate with vastly different technical proposals and belong to quite distinct intellectual backgrounds, some similarities are detected in their thinking. We philosophically examine these similarities but also bring into focus the uniqueness of each approach. Our purpose is not providing an exhaustive derivations of logical concepts identified in one thinker in terms of ideas found in the others. Instead, the main objective of this work is to stimulate historico-philosophical investigations and inquiries into the problem of the direction of time in nature by way of crossdisciplinary examinations of previous theories commonly treated in literature as disparate domains.

1. Introduction

There are three major problems in fundamental physics which have drawn the strongest attention of both scientists and philosophers: the problem of measurement in quantum physics [1,2,3,4,5], the problem of nonlocality and entanglement (also in quantum physics) [1,2,3,6], and the problem of the direction of time [7,8,9,10,11,12,13,14,15]. However, the last problem, that of time asymmetry in nature [8,16,17], is more universal in scope since it arises from within both classical and quantum physics and extends to biological [18,19,20] and social systems [19,20] through the deep connection it establishes between irreversibility and complexity [16,17,21,22]. The main focus of this article is on the third problem, that of the direction of temporal flow in nature’s fundamental processes.1

Interest in the subject of irreversible dynamics and the direction of time is currently strong, encompassing researches conducted by physicists, chemists, biologists, philosophers of nature, philosophers of science, historians, sociologist, neurologists, and others who might be interested in understanding the large-scale structure of energy-matter-information flow in various dynamical processes taking place in the microworld and/or the macroworld. The audience targeted by our article includes (though not limited to) a mixed group of scientists, philosophers, and historians who might be interested in learning more about the deeper implications of entropy and the Second Law, especially in terms of the large-scale problem of the Cosmos and the global orientation of dynamic processes in nature. However, out of the enormous literature already dedicated to this problem (see Section 2), we have selected only three figures on whom to ground our contribution: the philosopher Hans Reichenbach (1891–1953); the physicists, chemist, and philosopher Ilya Prigogine (1917–2003); and the mathematician and physicists Roger Penrose (born in 1931). Carefully selected fragments of their theories of time and dynamical change2 will be presented in Section 3, Section 5 and Section 6, respectively. Due to the central importance of Henri Poincaré in Prigogine’s theories in particular, and modern mathematics, philosophy, and physics in general, we review some of his impact in the short Section 4, serving as a transition from Reichenbach to Prigogine.

The three thinkers selected above share a common trait: their respective “solutions” of the problem of the direction of time are based on very complex and highly technical mathematical development that would require a book-length treatment if even a part of the mathematics involved is presented. Instead, our methodology here, in light of the mixed audience we originally have in mind, is to:

• Work with carefully selected consistent fragments of the original theory instead of the full formulations that might deal with additional problems other than the direction of time. That is, what is presented below is a partial view of some aspects of Reichenbach’s, Prigogine’s, and Penrose’s total novel and sophisticated formulations of the foundations of physics that originally included numerous proposals and solutions of problems in diverse areas of research, including gravitation, spacetime, probability, dissipative systems, quantum gravity, and others. On the other hand, our main focus here is on those specific aspects of this total body of their works that are related to irreversibility and the Second Law.
• Avoid working with the full mathematical details by extracting the conceptual essence of each theory and exhibiting it as the centre piece of each proposal. The objective here is to limit the length and focus of the investigation to a reasonable size allowing us to form some conceptual understanding of the problem of the direction of time developed using a historico-philosophical method.

In this manner, we manage to provide a new picture of entropy and dynamics since, to the best of our knowledge, the three thinkers we work with have never been treated in one place as is attempted here. It is our opinion that the best path toward understanding the very complex problems of entropy, change, and the direction of time in Nature is through a historical approach. In particular, we are inspired in this regard by the fine historico-philosophical studies of time, change, and dynamics found in the books by Sklar [11,23] and Barbour [25,26].

This article is structured as follows. In Section 2, we provide a very brief review of the main topics addressed here, which include irreversibility, time asymmetry, thermodynamic structures, and others, with additional references to some of the essential literature on the subject. This will set the stage for the more technical sections to follow. We start with Reichenbach in Section 3, whose views are analysed by working with a fragment of his thoughts on entropy, the Second Law, the Cosmos, taken from his last book, The Direction of Time [7]. We then examine, very briefly, the works of Henri Poincaré on dynamical system theory and its application to statistical mechanics due to the fundamental importance of Poincaré’s concepts in all areas of modern dynamics. Prigogine’s ideas are examined in Section 5, where again only a selected fragment is carefully developed and examined. Penrose’s latest cosmological theory, cyclic conformal cosmology (CCC) is treated in Section 6. A tentative comparative analysis and some critical assessments are given in Section 7. Finally, we end with conclusions.

2. Nature and Irreversibility

In the literature, the issue of the direction of time is most often discussed through the key term irreversibility, whose idea is that, in nature, most processes are always observed to unfold along a specific direction, conventionally named the “arrow of time” [17,27,28]. In fact, the smaller group of processes that are reversible constitute a minority within the totality of all processes. Roughly speaking, one may associate reversible processes with integrable systems, while nonintegrable configurations are linked to irreversibility [29].3 Examples of natural processes in which irreversibility is essential, i.e., the direction of time cannot be derived by appending to the known fundamental reversible microscopic equations of motion some general auxiliary boundary conditions, include the following:

• All transport and collision phenomena such as diffusion, viscous flow, chemical reactions, and heat flow [8,9,21,27,30,31,32]. The collision process is historically special because it presents the “standard model” of statistical thinking from Maxwell and Clausius to Boltzmann and early Prigogine.
• Spontaneous emission of radiation and the decay of unstable particles. This example is particularly important as decay processes are ubiquitous in nature, a topic that will be taken up again when we discuss Penrose’s cosmology.
• Biological processes such as growth, development, and phylogenetic change, all appear to be essentially irreversible [33,34]. The same applies to geological transformations and the unfolding of events in deep time [33,34,35].
• The dynamic flow associated with large-and-complex nonintegrable systems. More information on these systems, which include the important class of Large Poincaré Systems (LPS), will be given in Section 5. For now, it is sufficient to mention that such systems are in fact generic in nature. They are characterized by the dominance of regimes of instability and resonance, making long-time predictability impractical and essentially impossible [22]. In such systems, the direction of time is asymmetrical [8]. Examples include field-matter interactions, phase transitions, and strongly-coupled many-body systems.
• The dynamic flow associated with strongly-coupled interacting systems. This may include even systems with small number of degrees of freedom but with very strong mutual coupling between their constitutive components, leading to the collapse of the perturbation approach. It is this particular scenario that Dirac had in mind when he famously complained that the standard Hilbert space of quantum theory, introduced by John v. Neumann in [36], may not be able to accommodate strongly-interacting field theories [37].
• The reduction or “collapse” of quantum states, upon interaction with other systems, into one of the eigenvectors of the measurement operators. Indeed, the evolution of the quantum state (a vector in Hilbert space) follows a unitary and reversible evolution dictated by the solution of the fundamental dynamical equations of motion (Schrodinger equation, Heisenberg equation, and Liouville-von Neumann equation) [28]. On the other hand, to actualize a concrete physical result communicated to us through a measurement apparatus, the quantum state of the combined evolving system and the apparatus “reduces” or “collapses” into an element of the measurement operator’s spectrum [1,2,28,36].4 The unitary evolution process U, using Penrose’s terminology, and the reduction of the quantum state R, differ from each other in the essential aspect that, in contrast to U, the process R is irreversible [28,38,39,40].

Numerous irreversible processes, many not mentioned above, spanning a diverse group of examples in biology, psychology, cognitive science, neurology, sociology, economics, the earth sciences, and nanotechnology, can be exhibited and have been extensively investigated in the literature, e.g., see [19,20,41,42,43,44,45].

A deeper way to understand the classification of natural processes into reversible or irreversible is to look into the fundamental thermodynamic structure involved. This is captured by the Second Law of Thermodynamics, which states that for a closed system, entropy always increases or remains constant [46]. Ever since Clausius [47] and Boltzmann [48], and especially with Planck’s formulation of universal thermodynamics5 [49], the direction of the flow of a natural process is defined as the direction of entropy increase.6 A reversible process is characterized by zero entropy production (entropy does not change with time, as in thermal equilibrium). Roughly speaking, reversible processes are closely related to equilibrium thermodynamics (and statistical mechanics) [51]. This is the topic that has dominated the early phase of thermodynamics and statistical physics; it even remains (relatively speaking) the most popular formulation in theoretical physics up to today, though approached through a range of bewilderingly variable perspectives [28,49,51,52,53,54,55,56,57,58,59,60,61]. On the other hand, starting from the 1930s, but especially since the end of World War II, a new direction in thermodynamics and statistical mechanics research had emerged, that of nonequilibrium thermodynamic systems, covered and investigated by several texts [30,31,32,62,63,64,65,66,67]. Irreversible processes are the central subject of inquiry in the latter direction of research.

Another mode of inquiry by which the subjects of entropy and the direction of time are manifested in the literature is through the relation between the micro- and macroscopic worlds. Since the quantum and classical mechanical theories governing the microworld are reversible (the equations of motion are invariant to time reversal, see [15] for technical details), then an explanation of the observable direction of time is needed if various possible choices of the fundamental laws of the world, for example, Einstein fields equations and the Hamiltonian/Liouvillian equations of motion,7 which, while belonging to two distinct conceptual categories, are nevertheless both reversible [28] and are to be believed to constitute the ultimate dynamical laws of nature.8 However, all such attempts to derive macroscopic thermodynamics from the Hamiltonian formulations have either failed or only partially succeeded, usually with the heavy price of introducing additional (non-dynamical) assumptions such as Boltzmann’s molecular chaos hypothesis. A fairly comprehensive and deep analysis of this problem can be found in Sklar’s book [11]. See also Davies’ [12], which had influenced communities outside physics due to its generality and clarity. More recently, this subject was revived in a new treatment by Albert [14], while the relation between the macroscopic and microscopic structures was put into the perspective of Maxwell’s demon [55] in the book-length study [15]. Articles and books on the problem continue to be published almost every month, and we we cannot provide even a partially comprehensive survey of these results here.

In philosophy, the subject of irreversibility is essential for the set of the general philosophies of nature proposed by Aristotle, Spinoza, Leibniz, Schelling, Bergson, Russell, and Whitehead. However, the term itself is not used. Instead, each philosopher coins a distinct word or phrase in order to express the one and the same idea: the irreversible, forward-looking thrust or movement of nature, whether in Aristotle’s entelechy [69,70], Spinoza’s conatus [71], Leibniz’s lifeforce [72], Schelling’s dynamic aktions [73], Bergson’s elan vital [74], Russell’s asymmetric relations [75,76,77,78], or Whitehead’s nature’s perpetual creative advance [79,80]. Simondon’s ontology also models being in terms of the forward-looking process of the actualization of the virtual via individuation and ontogenesis [81,82], and so did Deleuze [83] in the late 1960s. The more comprehensive philosophy of nature developed by Deleuze and Guattari throughout the 1970s is based on the ontology of desire or desiring-production, which is somehow modeled after the Spinozist’s conatus seen as a nexus of cosmic perpetual processes of auto-striving and self-overcoming driving dynamical evolution and historical development [84,85].9

3. The Reichenbach Universe: Causal Nets, Branch Systems, Probability Lattices, and Cosmic Cross-Sections

3.1. The Fundamental Role of Topology in the Reichenbach Universe

Initially, Hans Reichenbach10 had reflected on nature and theorized about dynamics by traversing a quite unusual route: highlighting the topological structure of order relations [86]. This bold undertaking was realized by an original reorientation of thought toward the categories of time and temporality [86,87,88,89]. It is a natural emphasis on topology that is part of the overall legacy of Leibniz [72,90,91] and Russell [75,76,77,92,93], where the two had both been significantly influential on the young Reichenbach during a time when topology itself was still young though progressive field fighting numerous foes defending the reactionary old schools. In particular, Reichenbach was instrumental in explicitly formulating the concept of causal nets, where the entire cosmos is seen to follow a definite (deterministic or probabilistic) causal order with the characteristic structural form of a network of asymmetric (directed) relations connecting various nodes, a picture somehow prefiguring similar ideas proposed by Penrose and others by several years.11 Each node enjoys the principle of local time comparability, where spatiotemporal coincidence is taken to guarantee the ability to compare the local temporal flows of two processes that happen to share that point (or infinitesimal spacetime region). In fact, this principle is fundamental for the theoretical structure of general relativity [95,96]. However, Reichenbach went further by also postulating the principle of nonexistence of closed time-like loops in the spacetime manifolds that describe our cosmos. He called spacetime systems adhering to this property open systems [7] and considered the principle itself as an empirical one, ultimately to be decided by experiments and observations, and hence neither logical nor analytical. It is significant to note that in a certain sense, at least conceptually, Reichenbach somehow foreshadowed or partially “anticipated” Penrose’s brilliant use of differential topology to revitalize general relativity (GR) [94], where some of Reichenbach’s earlier key concepts, such as causality as topological order, nonexistence of closed loops, and causal nets, have all found their way to fruitful realizations by other researchers [94,95,97]. While the technical tools of differential topology itself were not used by Reichenbach himself in his book on spacetime [86], a conceptual essence pertaining to how information is propagated locally from one neighbourhood to another in order to reach a global setting can be found in the division dealing with general relativity in that same book (second half). This intrinsically topological mechanism, propagating information from the local to the global, was probably inspired by, or even executed through, Russell’s formal “logical” apparatus [77]; but, nevertheless, it encapsulates the defining feature of differential topology: understanding the relation between the global and local properties of topological manifolds using differential methods. Both Reichenbach and Penrose had approached this problem by focusing on the causal structure of relations between events inhabiting what is basically a Lorentzian spacetime manifold. However, it is mainly with Penrose, Wheeler, Hawking, and others that the causal topological program became fruitful in mainstream theoretical physics.

But we should not forget that very early on Reichenbach also discovered that the deep topological order-structure of time-relations in GR does not constitute the essence of dynamics; the latter, in fact, is dominated by a different type of topology, that related to the directionality of time-flows, and consequently the whole array of flow-flow comparability, a mathematical topic closer to Poincaré and his school than Boltzmann, should be called on and redeployed for a fully-fledged reformulation of the problem of dynamics.12 All that causality can do in physics is this: Once a causal net is established, then one may determine the directions of time flow in the global net by the local knowledge of how a single piece, causally connected with others, is directed in time. This conclusion is based on the principle of nonexistence of time-like loops, which further enhances its importance in classical physics. As explained by Reichenbach himself while discussing causal nets:

If several arrows depart from one point, we select one as we like. A combination of lines travelled through in this way may be called a causal chain. Travelling along causal chains we now make the discovery that we never travel to the starting point; or to put it another way, that there are no closed causal chains.13

However, as Reichenbach immediately emphasized, this principle of nonexistence of closed time-like loops is a topological order relation, i.e., not a geometrical structure:

The nonexistence of closed causal chains is a general property of the net; we shall say that the net is open. Obviously, if this property holds for one choice of the line direction, it holds likewise when all directions are reserved. This means that the openness of the net is an order property, not a direction property.14

Yet not only this principle is purely topological, but Reichenbach also observes that it is thoroughly an empirical question to decide whether a given causal net of events in a Lorentzian spacetime manifold is open or not:

It should be kept in mind that the openness of the causal chains represents an empirical fact and cannot be regarded as a logical necessity. There is nothing contradictory in imagining causal chains that are closed (…) Do we have conclusive evidence for the openness of the net? It cannot be said to follow from the equations of Newton’s mechanics; it is merely a generalization from experience in our space-time environment. Yet, for a long time, the openness was never questioned (…) The general theory of relativity has cast doubts upon this uncritical attitude.15

Now, as an example of how general relativity shattered the belief in the logical status of the nonexistence of closed time-like loops, later in his text Reichenbach will remind us about the fact that Einstein field equations themselves admit as viable mathematical solutions cosmological models with closed causal net structure. Consequently, if general relativity is to be considered “the ultimate theory of macroscopic physics”, then reversibility (lack of unique direction in nature), on one hand, and the topological order relation structure of how causal nets are configured globally (nonexistence of closed time-like loops), on the other other, become intimately related. Which, in our opinion, may explain why cosmology and irreversibility are organically connected to each other, a key theme in this article. Indeed, it is remarkable that the above passages were written in the early 1950s, just when when the “Topological Renaissance” of general relativity was about to take shape.

3.2. Reichenbach’s Ontology of Multiplicity and Branch Systems

While he himself had planted some of its principal seeds, Reichenbach chose not to nurture and grow the above mentioned line of investigation focused on topology. He seldom used Poincaré algebraic and geometrical topological ideas [98] in his research, opting instead for an alternative approach, an original one in our opinion, which is closer to the now classical—but by that time still radical—discourse of stochastic theory, especially the concepts of space and time ensembles (see more on this below). In fact, the global causal spacetime structure was taken by Reichenbach as a given starting datum or inceptual fact, while the issue of “time’s arrow”, the fundamental problem of dynamics, according to Reichenbach’s approach, is fully reduced to determining how a local time-flow section of the overall—i.e., global—flow’s underlying causal net is directed. Again, if no closed time-like loops exist, a state of affairs which by itself constitutes a global or cosmological constrain/condition, then one may exploit any given local fixation of the direction of time-flow to infer how larger domains (even the Cosmos itself?) are directed, a feat that may be achieved through the use of a procedure that—Reichenbach only hoped—would be easily carried out almost mechanically.

Let us remember again that Reichenbach, causality is an effective technique for propagating information from local to global sections of the world, an idea that, to the best of our knowledge, was first formulated and investigated extensively by Russell [92,93,99]. In this sense, Reichenbach can be considered a curious precursor to Penrose,16 the latter whose view will be taken up in Section 6. However, while Reichenbach used gravitation to merely acquire knowledge of the global causal net topological structure of the world [86], Penrose will dig deeper into the role played by gravitation (and fields in general) for the determination and prescription of entropy and dynamics at the cosmological scale [28,100].

The essential tenet of the Reichenbach Universe is that dynamics should be understood as engendered not merely by how a single and isolated dynamical system evolves in time, whether closed or open, but rather through collective stochastic interactions experienced by a multiplicity consisting of a large number of quasi-isolated systems all embedded somehow into a universal “cross-section of the world”.17 Therefore, this is an ontological worldview that highlights plurality, or what Deleuze and Guattari would later refer to by the term assemblage [85]. In essence, it is a rehabilitation of the great Leibnizian ontological scheme of monadology, a world seen to be composed of “smaller but universal” building blocks called monads [72].18

Nevertheless, Reichenbach’s main point is to propose a view on the arrow of time that is entirely based on the direction of entropy increase. Therefore, he accounts for the possibility that individual subsystems, if decoupled from their larger embedding “mother matrix”, need not lose their locally-defined time directions even if the entropy associated with the global matrix does not increase for a significant period of time. In other words, there is, at a certain level, a decoupling of the global matrix from its local constituents. The boundaries at which such separation take place are not rigid but fluid and are themselves dynamic. The precise technical term that Reichenbach adopted to describe those monadic self-contained “small worlds” or subsystems is branch systems. Each such system can be defined as a quasi-isolated, self-subsisting thermodynamic system embedded into a larger system such that the entropic flow of time in the smaller branch system need not follow that of the larger (embedding) system. In his own words, Reichenbach states:

A statistical definition of time direction presupposes a plurality of systems which in their initial phases are not isolated, but acquire their initial improbable states through interaction with other systems, and from then on remain isolated for some time.19

Therefore, it is not possible to define a unique direction of time by working with an isolated system. In our opinion, this is precisely how Reichenbach might had effectively moved beyond Boltzmann and the entire apparent “paradox” of time reversibility in classical dynamics. However, Reichenbach’s text does not contain a decisive break with Boltzmann approach from the mathematical point of view since a complete set of stochastic dynamical equations implementing his conceptual scheme were not found in the manuscript by the time of his sudden death. Nevertheless, Reichenbach deserves some credits for at least suggesting such possibility of deriving an effective direction of time from interacting stochastic quasi-differentiated branch-like ensembles rather than the plain statistical populations of Maxwell, Boltzmann, and Gibbs.

As the standard story now goes, the problem of the direction of time was initially inaugurated by Boltzmann’s colleagues in Vienna through their not-too-positive reaction to his work on the molecular structure of matter [104,105], then by the penetrating critique coming from Poincaré [11,106], Zermelo [107,108], the Ehrenfests [57], and Eddington; see Sklar [11] for an extended historical and conceptual examination. Indeed, there is no doubt that the reversibility argument leveled against Boltzmann is correct, which implies that for a closed or isolated system evolving under the dynamical laws of a conservative Hamiltonian, it is not possible to single out a preferred direction of time, which in turn means that entropy may increase or decrease. In particular, if all particle velocities belonging to a “typical” dynamical evolution were to be “manually” reversed in sign, then the entire system will undergo a perfectly legitimate Hamiltonian evolution with decreasing entropy [15] (This has already been verified in numerical experiments, e.g., see [8]).

Now, we should note that Reichenbach attempted to escape the reversibility argument by proposing what we may loosely consider a “non-Boltzmannian” reformulation of dynamics, though, strangely, he attributed it to Boltzmann, and, worse still, had not even carried it out in full through a complete and substantial mathematical formulation. This potential non-Boltzmannian formulation is the suggestion that the direction of time is not to be defined with respect to isolated dynamical Boltzmann-type systems, but instead relative to collections or clusters of such systems, those he decided to call “branch systems”. Not only that, these systems must be assumed to be undergoing either continuous mutual interactions, or that they did once interact in the past before becoming semi-closed or quasi-isolated (compare with many-body dynamical systems and issues such as correlation, relaxation, memory, coherence, decoherence, etc. [63]).

For conceptual clarity and concreteness, let us isolate the two basic ideas implicit in Reichenbach’s radical proposal:

RP₁ 

The direction of time involves neither single nor isolated systems, but ensembles (stochastic clusters) of quasi-isolated such systems called branch systems.

RP₂ 

There is or has been some mutual stochastic interactions (correlations) between these branch systems.

Throughout the main text of The Direction of Time [7], the Reichenbach Principles ${\mathbf{RP}}_1$ and ${\mathbf{RP}}_2$ are then together posed, analyzed, developed, and then deployed in various applications in order to derive a new form of entropy applied to the branch system ensemble, the latter which Reichenbach called space ensemble for the purpose of distinguishing it from the “time ensemble”. The terminology of ‘time-like ensemble’ is admittedly a lousy expression by which he means the time-flow associated with each branch system now viewed as a time series, i.e., not a genuinely ordered thermodynamic series since its “local entropy” is not the key to deducing the global direction of time.

3.3. Examples of Branch Systems and the Concept of Probability Lattice

A Reichenbachian branch system is supposed to be a “sub-world” behaving like a “pocket universe”, a quasi-isolated totality of natural processes evolving in relative independence from the outside world. A simple example given by Reichenbach himself is a trace or time capsule, a fossil, left by a prehistoric organism and preserved for millions or billions of years. While the overall climate-geophysical system has evolved under the rules dictated by the Second Law, where the entire Earth is approximately treated as a closed system exchanging only energy with outer space through the radiation emitted by the Sun then returned to space. However, inside this total system, a time capsule like a fossilized trace is a highly-ordered structure that did possess low entropy in the past but now operates with a different time scale. Hence, compared with the embedding (larger) system, the smaller subsystem, the time capsule, appears to violate the Second Law. Another example is a biological organism continuing to live (by reducing its entropy) while its habitat is burning (entropy is tending rapidly to maximum) [109]. In all such exemplary cases, Reichenbach clearly states that a branch system cannot continue to remain quasi-isolated indefinitely. In fact, he further postulated that most (if not all) branch systems tend to “reconnect” with the global advance of the general entropy curve, the latter being the curve quantifying the entropic progress of the global cross-section of the world out of which all branch systems had emerged at a previous common time (the moment or duration of former or current interactions and correlations posited by the Reichenbach Principle ${\mathbf{RP}}_2$ above).

At this point, Reichenbach reintroduced the important technical concept of probability lattice, which was developed in his earlier researches on the foundations of probability theory [88,89,110]. The idea is to consider probability series in two dimensions instead of one. The horizontal dimension is the direction of “time ensemble”, and here it corresponds to the dynamical evolution of branch systems (each taken individually). On the other hand, the vertical dimension is associated with the space ensemble, that is, the collection of all these individual branch systems. Therefore, apparent real dynamical evolution is applied only to branch systems (and it is reversible), while effective physical evolution, the dynamical flow generating actual change in the world, is the more complex direction emerging from the collective advance of the cross-section (the vertical line) from which branch systems (sub-worlds) keep branching out.

For this idea to work, each branch system must be considered (at least ontologically) independent from others, something like a Leibnizian monad [72] that is basically “windowless”. Why so? Because otherwise you will not obtain a true stochastic cluster, but only “parts” of a “larger system”. In other words, the very concept of space ensemble is a revolt against the ontology of part-whole, which appears to have been exhausted by classical dynamics as formulated in the works of Maxwell, Boltzmann, Gibbs, and Einstein. Reichenbach introduces here ontologically distinct branch systems, each with its own metaphysically independent time variable (reversible time with its own entropy, which may increase or decrease).

However, that does not imply that branch systems are fully indifferent to other branch systems, or to the global universe into whose cross-section they are embedded. In fact, Reichenbach postulated the mixing hypothesis to regulate the behaviour of the branch system assemblage, where strong probability relations hold between the “horizontal flows” (each branch system’s time evolution taken in itself) and “vertical directions” (the space ensemble probability limit, like in classical stochastic probability theory, see for example how a random process is typically defined in probability theory). Those rules of probabilistic discourse will not figure prominently in what follows and hence we avoid reviewing them in details, but see [7]. In fact, in our view, they represent the weakest link in Reichenbach’s argument. It is not clear whether these mixing rules are universal; they seem to have been designed by hand in order to produce some of the empirical results observable during Reichenbach’s time.

3.4. The Emergence of Time in the Reichenbach Universe

Putting it in Reichenbach’s spirit, the direction of time is an emergent time dimension generated by that relational structure latent in the nexus of thermodynamic space ensembles. Branch systems enter into direct communal relations among each other, which here would be regulated by rigorous probabilistic rules of intercourse, leading to the production of a definite entropy-increase-based direction of time. These include the framework of the probability lattice coupled with a set of carefully laid-out additional axioms formulated in Reichenbach’s main text [7], which will not be rehearsed here. None of these relations are logically necessary, and their acceptance is up to the researcher contemplating the problem. For us, the mixing property is more likely to prove inadequate. In fact, it is possible that even more comprehensive probability rules than those originally proposed by Reichenbach might be needed in the future.

The key issue is that the infamous reversibility argument levelled against Boltzmann [11] does not apply to space ensembles, but rather only to time ensembles. Therefore, Reichenbach sought a radical–and final–resolution to the paradox of entropy increase in classical dynamics by boldly altering the “rules of the game” originally set up by Boltzmann: instead of seeking an entropy state function associated with every single dynamical system, the entropy concept itself is now extended to apply to the “vertical direction” induced by space ensembles of multiple “parallel” branch systems coexisting with each other via ongoing or past interactions, but each evolving on its own with a local entropy function attached to it (this local entropy may increase or decrease, as predicted correctly by the reversibility argument). However, Reichenbach’s probability mixing rules induce a global structure of compatibility relations among the horizontal and vertical directions of time-flows, leading to a tight connective coordination between what happens locally in every quasi-isolated branch system and the world at large, i.e., the collective or global cross-section into which all branch systems are embedded and which they will eventually all rejoin in the future.

What about the cosmological scale? First, we need to distinguish between two technically distinct terms, "global" and "cosmological", which have been treated by us so far as roughly synonymous. In Reichenbach, the term global always refers to the topological sense of the word, not its common semantic shade as understood by the qualifier “at large”. The latter is in fact more adequately captured by the expression cosmological, which here means the global aspects of the entire spacetime manifold of the universe, including of course both space-like regions and causal (time-like) domains. Now, the Reichenbach Universe differs from the Boltzmann [111] or Poincaré Universes [112] by not being ultimately reducible to the what and how of a single dynamical system evolving in phase space according to Liouville’s rules [8,28,51].20 Instead, we must consider a collection of multiple, theoretically distinct, phase spaces all coexisting together inside what can be thought of as a “super-phase-space”. This latter concept itself is implicit in Reichenbach’s text, thought not actually formulated in explicit mathematical terms. In his own words:

That our universe, which is an isolated system, possesses a time direction, is due not merely to the rise of its general entropy curve, but to the fact that it includes a plurality of branch systems of the kind described.21

That is, it is the multiplicity of coexisting subsystems which provides a global tendency for entropy to increase, while the traditional Boltzmann–Gibbs formulation of the statistical thermodynamics of near-equilibrium closed systems is embedded as a semi-special case in the form of quasi-isolated thermodynamic branch systems that are in the main striving, pace Boltzmann, to increase their local entropy (with occasional failure as already observed by Maxwell [55]):

The direction of time is supplied by the direction of entropy, because the latter direction is made manifest in the statistical behaviour of large number of separate systems, generated individually in the general drive to more and more probable states.22

However, eventually, and interestingly enough, Reichenbach had to face the question of whether the general “vertical” entropy curve should be extended to apply to the total universe or only a part of it, which would then implicate us in the cosmological problem as we defined it above, and hence the subject of empirical cosmology becomes unavoidable. However, what we find so interesting is that Reichenbach had expressed extreme caution about whether the universe should be treated as finite or infinite, and that was written several years before the accidental experimental discovery in 1965 of the Cosmic Microwave Background Radiation (CMBR) of the universe [28]. Furthermore, he even stated that entropy is unlikely to be definable in the case of noncompact universe, a striking observation by Reichenbach in our opinion, and a shrewd decision that was ahead of its time, for we now know that Boltzmann entropy is fundamentally combinatorial, and hence is not generalizable to noncompact phase spaces in spite of repeated claims to the contrary often found in the literature.23

4. Interlude: Poincaré as the Crown Prince of Modern Dynamics

If Boltzmann (and Gibbs [114]) may be considered the undisputed founding king (or joint kings) of modern dynamical theories in statistical physics [104,105], then Poincaré certainly deserves the credits of being the second founder or the crown prince of the entire field [106]. However, it is also true that neither of the two would be personally pleased to hear such comparison being made. Indeed, it is hard to imagine two figures more intellectually opposed than Boltzmann and Poincaré. The former, a self-proclaimed Darwinian [115], believed in the essential role played by chance and indeterminism in nature, reintroducing and codifying stochastic (probability) concepts into physics. The second, however, while making brilliant contributions to the mathematical theory of probability, had firmly believed in a strictly deterministic and exactly ordered cosmos. Indeed, when it comes to interpreting the role played by accidents and randomness in nature, Poincaré was more of a Kantian than Darwinian, meaning that, as per mainstream interpretations of Kantianism, say neo-Kantianism, a fundamental importance is allotted to the human dimension of experience, for example through the innate schema of the transcendental subject’s interactions with nature and the concomitant process of interpreting causality [106,116,117]. An example illustrating this tendency in Poincaré is his theory of geometry, especially how the very geometrical concepts we form about nature can be shown to be based on the “interaction group” regulating our viewing of objects displaced and rotated around us.24 On the other hand, Darwinism downplays the human factor by expressing the latter as merely one animal phylogenetic evolutionary line among others, with more emphasis being laid on the statistical and aleatory nature of development than the characteristic Kantian preference for rules and exact a priori laws of discourse and interpretation of nature’s working methods [120]. This might explain why, throughout his intellectual career, Boltzmann had little passion for axiomatic formulations, preferring instead to work out general principles by first developing novel concrete population-based collective stochastic models [111], then generalizing or “abducting” laws of discourse in exactly the same manner as Darwin’s Malthusian approach to natural history [115].25 Incidentally (or not), Prigogine would later propose his own “resolution” of this conflict by suggesting that probability and chance are inherent in the very fabric of nonintegrable, complex nonlinear dynamical systems, therefore providing a way to joining Boltzmann and Poincaré in one system but without having to directly deal with the notorious subject of contrasting or unifying Kantianism and Darwinism.26

Poincaré’s contributions to the development of dynamics are numerous and multifaceted since he was able to turn out new ideas in almost every field, including physics, pure mathematics, mathematical physics, technology, and philosophy [98,106,116,125,126]. For instance, his introduction of the concept of recurrence is essential for fundamental theory in physics [127,128,129], mathematics [130], and their applications in many fields such as in astronomy and mechanics [112]. A lot has been said about how Poincaré delivered one of the most devastating attacks on Boltzmann’s program of deriving the arrow of time from purely mechanistic considerations, e.g., see the large literature on the relation between Poincaré’s recurrence theorem and dynamics in general [131], in particular Boltzmann’s H-theorem [11]. There is probably nothing that can better illustrate the fundamental impact of Poincaré on modern dynamics than the fact that the two previously quite separate disciplines of ordinary differential equations [132,133] and classical dynamics [134] have become essentially a unified subject largely dominated by Poincaréan concepts such as singularities, bifurcation, instability, integrablity, resonance, and recurrence [135,136].

However, it is also the same Poincaré who paved the way for the mathematical foundations of modern dynamical systems to serve as a basis for irreversible process in nature. The recurrence concept is closely related to the fundamental structure of instability of nonlinear differential equations, which was analysed by both Lyaponov [137] and Poincaré [112], roughly at the same time (end of the nineteenth century). Instabilities, together with associated bifurcation phenomena, imply that the evolution of some dynamical systems entering into states of “rich instability-singularity domains” will eventually be captured by the horizon of some chaotic attractors; hence, effectively, the dynamic system becomes both indeterministic and irreversible [8,9,138,139,140,141,142]. Such systems, whether Hamiltonian or non-Hamiltonian, are far from being rare or exceptional cases; in fact, they are generic; they can often be located within the category of nonintegrable dynamical systems [143,144,145]. Therefore, integrable systems should not be automatically considered the only possible models for time-reversible phenomena. Nonintegrable deterministic systems may be good models for irreversibility in nature as well [8].27

We should explain Poincaré’s role in this development. Strictly speaking, most of the detailed technical results characteristic of the modern theory of dynamical systems had emerged only after the first grand synthesis given by Birkhoff in his 1927 book [130]. This work built on Poincaré’s (and others) earlier findings as they relate to concepts of recurrence and ergodicity. In the late 1950s, the fundamental role played by instabilities was clarified in the works of Arnold, Kolmogroff, and Moser, e.g., see [135,138,146]. The importance of resonances, also discovered by Poincaré, was essential for elucidating the all-important structure of nonintegrability in dynamical systems, where the latter concept turned out to be the reason why the conventional perturbative approach collapses in such type of systems (nonintegrable dynamical theories), while it works nicely in integrable systems. Therefore, even though Poincaré himself died in 1912 just when the modern theory was beginning to take off, the entire field of investigation is justly credited to Poincaré’s fundamental research (and Lyabonov [137]) from the late nineteenth century.

5. Ilya Prigogine: The Ontological Inevitability of Dissipation

5.1. Irreversibility Is Not a Bug

With Prigogine, something original–almost revolutionary—begins to take place: irreversibility is no longer a “bug” that has to be removed from the system using probability arguments, the approach inaugurated by Boltzmann [48,111] following some earlier leads from Clausius [47,52] and Maxwell [53,54,55]. On the contrary, nature should be deemed ontologically irreversible in the sense that the existence of a directed arrow of time is neither an illusion nor a paradox to be “explained away” via some purportedly more fundamental underlying mechanistic model. Irreversibility is to be embraced as an unequivocal essential feature of the natural world [8,9]. For that to be the case, the almost ubiquitous belief in the fundamental status of the Hamiltonian function in classical physics (and the hermitian operator in the quantum world) as the sole generators of dynamics is cast into doubt, and the quasi-universal importance of nondissipative dynamics within the overall structure of modern theoretical physics is questioned.28

However, Prigogine’s reflections on irreversibility had not materialized in one full swoop; instead, it had taken the thinker several decades in order to mature and settle in, while slowly transitioning, in gradual fashion, from the less radical to the more heterodox and anti-mainstream ideas of his later years.29 In what follows, we concentrate only on some aspects of his total work, mainly selected fragments related to entropy, dynamics, and temporality. Some of Prigogine’s other books deal with more practical dimensions and applications of his theories, for example see [21,22,66]. The last book, The End of Certainty, is probably his most radical and comprehensive in scope, both philosophically and with respect to fundamental physics [10].

Let us summarize the state of his thinking shortly before 1980, the year by which Prigogine completed the publication of From Being to Becoming [8] and Order Out of Chaos [9]. The two main Prigoginean principles of natural philosophy we wish to single out and highlight from within that period are:

PP₁:

Irreversibility is fundamental at the microscopic level.

PP₂:

The origin of irreversibility is dynamical instability.

Here, ${\mathbf{PP}}_1$ serves as a reminder that, contra Boltzmann, Gibbs, Maxwell, and even Poincaré, the conservative Hamiltonian dynamical system does not enjoy a special status in mathematical physics. According to Prigogine, it is not the case that all processes of dissipation and losses should be interpreted as emergent macroscopic phenomena induced by a large number of particles colliding with each other in a pattern that appears to us more probabilistic than deterministic due to the intractability of the computational demands of the model. This view, that probability is due to ignorance, which more or less continues to dominate mainstream thinking in science in general, including theoretical physics, was openly challenged and eventually rejected by Prigogine, who, in our view, and maybe more than anyone else, should be credited with the demolition of the primacy of the conservative Hamiltonian dynamical law in fundamental physics.30

Regarding ${\mathbf{PP}}_2$, this refers to the revolutionary change of our understanding of dynamical systems around the turn of the twentieth century brought out by Lyaponov [137] and Poincaré [112,151], and further expanded and developed by many other mathematicians such as Kolmogrov, Arnold, Smale, and Moser.31 Here, we no longer can take points very close to each other in phase space as representative germs of what is essentially the same future of the system under consideration [22]. The reason is that when the system is strongly unstable, where such instability concepts can be defined very precisely in mathematical terms [132,143,145,152], then future trajectories emanating from extremely close points may diverge exponentially, leading to fundamentally stochastic or unpredictable future history of the system, and hence invalidating the Laplacian dogma of fully deterministic classical dynamics [8]. Even though these ideas have been known before Prigogine, his main contribution to this debate was the reintroduction of irreversibility into the essential fabric of nature via this very dynamical instability itself [9].

5.2. Prigoginean Dynamics

Prigogine’s take on irreversibility, at least in its initial formulation before 1980, was based on linking irreversibility with the emergence of some form of intrinsic stochasticity caused by dynamic instability. Initially, this may also point toward an implicit agreement between Prigogine’s position and the standard Maxwell–Boltzmann–Gibbs framework of statistical physics standardly treated in canonical texts such as Gibbs [114] and Tolman [51]. Indeed, in both the early Prigogine and the standard framework, the dynamical laws are taken to be fundamentally correct, while irreversibility is supposed to emerge out of some properties enjoyed by their solution, e.g., when the system under consideration is very strongly unstable like the case of Kolmogrov flows [143]. This means that nothing new should be added to the dynamical law itself, which, according to this view, is considered complete in itself.

It will be seen that Prigogine would shortly pivot toward a challenging rebuttal of this classical view. Note that even Penrose [28] and Barbour [26,61] appear to endorse the conservative Hamiltonian dynamical system framework (the N-body problem) as the de facto starting point of the whole investigation, while Prigogine will later, in fact beginning from the final chapters of his landmark 1980 book From Being to Becoming [8], propose that the very formulation of classical and quantum dynamical systems must be altered, where such unorthodox move involves the introduction of new “super-operators” that are posited as directly, and not implicitly, able to encapsulate the fundamental role played by irreversibility in nature. We may collect this claim by Prigogine in the following radical Prigoginean Principle:

PP₃:

The fundamental laws of dynamical evolution contain novel elements (super-fields and super-operators) that directly and explicitly generate the manifest irreversible future flow of the system.

Note that he book From Being to Becoming is not the first text where a statement like the above would appear in the literature. However, compared with other previous articles and parallel discussions, we believe Prigogine’s monograph represents a turning point in the history of the science of complexity and general dynamics in nature and life. The main advantage of this work is its emphasis on the conceptual structure of the problem and the new ideas advanced by nonequilibrium thermodynamics and statistical mechanics in order to deal with multiple dynamical issues, including the direction of time but also others (such as the meaning of probability, chance, determinism, order, chaos, singularities, bifurcation, and so on). Full acquaintance with this Prigogine’s book is, in our opinion, essential for any understanding of the latest evolution of philosophical reflection on the problem of irreversibility in nature.

Now, in order to substantiate the radical proposal ${\mathbf{PP}}_3$, a concrete reformulation of Hamiltonian mechanics is needed, which will be described below under the rubric of Prigoginean dynamics. This dynamical theory (or collection of such theories) includes a set of closely related proposals and implementations published over a span of two decades in collaboration with several other researchers. Most commonly, these are often called in Prigogine’s papers “the nonunitarty transformation theory” of dynamical systems. It is supposed to have supplied the “missing link” between reversible dynamics and irreversible thermodynamics [17]. It should be noted that the this topic is highly technical and its full understanding in the mathematical literature is still evolving (no comprehensive bibliographic survey on the nonunitary transformation will be given here). One reason is that the key idea of such nonstandard transformation relies on discovering an explicit construction of some sort of “coordinate change” in an infinite dimensional phase space (most often Liouville space) such that a monotonic Lyaponov or entropy-like function can be found, i.e., a function of the state space that is strictly decreasing with time.

While Poincaré’s resonances would inhibit the integrability of the important class of Large Poincaré Systems (LPS) [146], Prigoginean dynamical theory avoids this problem by committing itself to the performance of a double act:

(i)

First, moving from Hilbert space to Liouville space [63].32

(ii)

Second, transitioning from Liouville space to “rigged Liouville space” [29], where the latter is modelled after the well-known construction of “rigged Hilbert space”, originally due to Gelfand [153].33

In this way, the extended Liouville space serves as a superspace into which the traditional Hilbert/Liouville spaces are embedded.34 The key observation made by Prigogine was the following: The superspace formulation will lead to the introduction of complex spectral representations of the new “super-operators” (Hilbert/Liouville operators extended into the superspace of rigged Hilbert/Liouville space).35 This, in turn, introduces features strongly resembling irreversible dynamical flows, e.g., the emergence of semigroups instead of groups [29].36 The conclusion then would be that irreversibility is immanent to some classes of highly unstable nonlinear dynamical systems; i.e., a directed flow of time can be shown to be intrinsic to a large aggregate of highly-unstable and resonant (nonintegrable) dynamical systems. To borrow Prigogoine’s own way of putting it, the very possibility of exhibiting such reformulation suggests that both classical and quantum Prigoginean dynamical systems already break time symmetry and hence are compatible with the Second Law [29,157] (see Figure 1).

In a closely related formulation, Prigogine and collaborators worked out a purely stochastic “equivalence theory” between some classes of unstable dynamical systems (Bernoulli systems) and Markov stochastic systems [8,158]. The approach is based on an earlier work by B. Misra, who was able to find necessary and sufficient conditions for an abstract dynamical system to possess a state space global entropy function [159]. The necessary condition is that the flow is mixing, while a sufficient condition is operating with K-flows. Clearly, these ideas come from ergodic theory [143,160]. Using a brute-force method of calculations, Prigogine’s group demonstrated that instability and irreversibility are closely interrelated [158]. The conjecture they made is that these two concepts are in fact equivalent. Indeed, Misra, Prigogine, and Courbage write that the most important philosophical feature of their work is

(…)the close links it establishes between instability (expressed in terms of mixing and other ergodic properties), the inherent irreversibility (expressed in terms of the existence of Lyapounov variables M) and the intrinsic randomness (expressed in terms of the existence of an “equivalence” with a stochastic Markov process) of dynamical motion.37

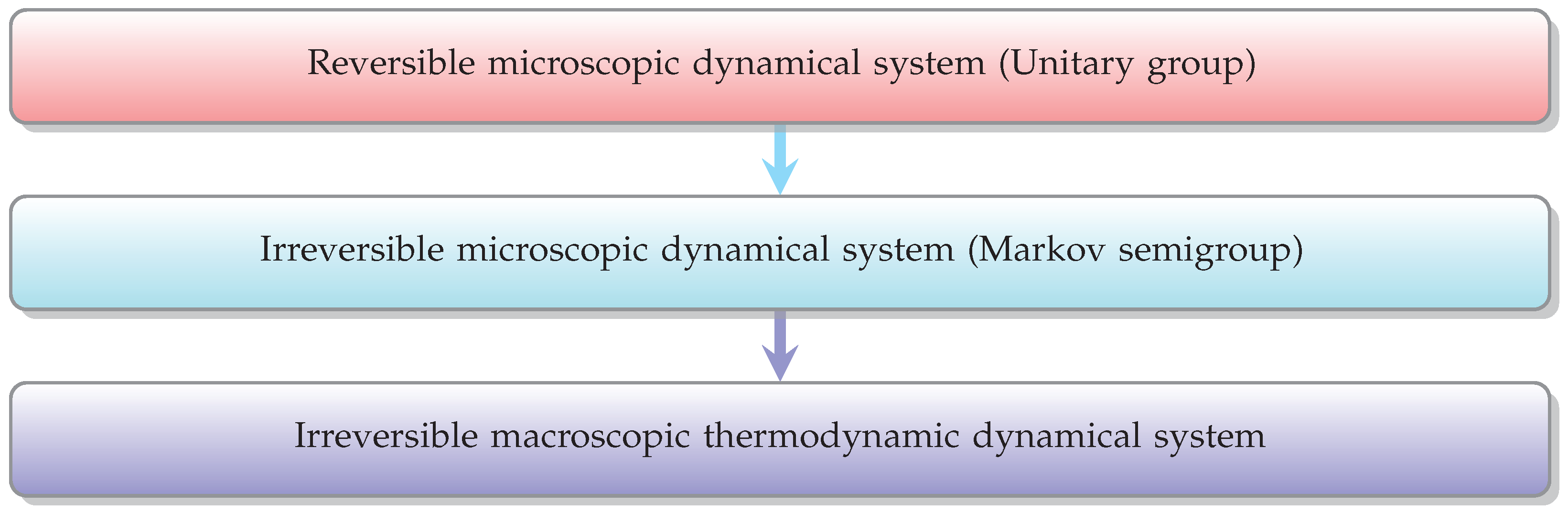
They key technical idea in this line of attack is to find a special nonunitary transformation that can convert a given dynamical system with rich instability structure into a Prigoginean dynamical system whose flow is governed by a semigroup of the Markov type. A precise mathematical procedure for deciding how stochastic processes in probability theory and deterministic dynamical systems can lead to each other was worked out earlier and will not be examined here [158]. In effect, Misra, Prigogine, and Courbage concluded that probability emerges in nonlinear nonintegrable dynamical systems even without recourse to any procedure of coarse-graining [158], a result repeated in numerous other publications [8,17,161].

As Prigogine’s reformulation of dynamics using nonunitary transformations is quite technical, it is not possible to fully interpret it or criticize it in a comprehensive fashion without going into considerable mathematical details, a task we leave to a future work. The full mathematical theory in its entirety can be found in some longer texts released by Prigogine’s groups [29,162,163]. We will not try to reconstruct the main ideas here, but readers interested in the mathematical machinery need to examine in depth the rough terrain of Gelfand space and its spectral theory. A graphical concept summary of this technical core of Prigoginean dynamics is given in Figure 1. Some additional information is given in Appendix A (Liouville space operator methods) and Appendix B (the extended space method).

6. Penrose on Entropy: The Cosmic-Scale Structure of Thermodynamics

6.1. Prigogine and Penrose: An Initial Assessment of Their Relationship

There are some striking similarities between Penrose and Prigogine [8,9,10] with regard to their overall respective approaches to the Second Law at the cosmological scale of the universe, though the actual technical details of their theories stem from radically different philosophical and mathematical backgrounds. Penrose operates principally from within the rigorous framework of general relativity approached through differential topology and geometry, while enriched with ideas from complex analysis. On the other hand, Prigogine’s experience is more with dynamical system theory, ergodic theory, and functional analysis. Penrose’s main area of interest in theoretical physics is general relativity (but he made many contributions in other domains as well), while Prigogine’s major playground is statistical physics.38 In spite of that, Prigogine, like Penrose, realized very early that gravitation plays a fundamental role in integrating the Second Law with dynamics. For example, at the beginning of a 1986 talk celebrating John. A. Wheeler, Prigogine stated:

The important point is that the part of the system which is slowly evolving to equilibrium has been itself brought out of equilibrium by a non-equilibrium process. May it be that matter is the nonequilibrium part of some cosmic nonequilibrium process which has also produced the black body radiation? We believe that we see a possibility that it may have been so by reconsidering the status of the second law in general relativity. We intend to give arguments that a new formulation of the second law is necessary which links the evolution of entropy to the cosmological state of the universe. We shall then show that we have to expect a cosmic nonequilibrium process leading to entropy production through the transfer of gravitational energy to matter. This process occurs at the time when the early closed or open universe leads to a “quasi-Minkowskian” description, as is the case in conformal coordinates.39

As we will see below when we consider some of Penrose’s ideas in more details, the above passage describes (at the high level, not the detailed content) almost the exact scope of Penrose’s program of the “exceptional status of the Second Law in physics”.

In regard to the notorious problem of measurement in quantum theory [1,2,3,4,5,165,166], Penrose and Prigogine take diametrically opposed approaches in the quest to identify the main culprit. Prigogine understands the core problem as the lack of a deep and fundamental integration of the Second Law into the very fabric of the structure of modern dynamical theories as such [17]. According to this view, if the laws of quantum physics are reformulated in such a way that the distinction between pure and mixed states disappears, then there will be no “measurement problem” in quantum mechanics since a pure state will naturally evolve irreversibly into a mixed state [167], and the right quantity to work with in this case would be density operators living inside an enlarged superspace, e.g., the rigged Hilbert/Liouville space (Gelfand space) [162].40 On the other hand, Penrose believes that the resolution of both the “problem of irreversiblity” and “the problem of measurment” lies in incorporating gravitational degrees of freedom into the essential formulation of all dynamical theories, ideally within the framework of a yet-to-be-discovered working theory of quantum gravity. This, according to Penrose, must be made in such a way that quantum theory itself shall be modified in order to make it compatible with the program of general covariance launched by Weyl and Einstein [168,169,170,171] of which general relativity is the best known example [40].

6.2. Entropy and Gravitation

Penrose advocates the view, no doubt inspired by Boltzmann, that one of the best explanations of why we live in an ordered universe right now comes from the fact that entropy in the past was just much lower than now. While this view is not original with Penrose, he has been instrumental in bringing the attention of the broader public to this simple but powerful Boltzmannian argument, especially at the cosmological level. Throughout his distinguished and still ongoing long career, Penrose has been relentlessly pursuing this task through a series of extremely well-articulated and original books, articles, and talks [28,38,39,40,100]. Most importantly, it is probably due to Penrose that the role of gravitation in entropy has been prominently brought into the picture, an idea that does not appear to have played a very essential role in the works of Boltzmann, Reichenbach, and even Prigogine.

In spite of that, Prigogine does refer to the role of gravity in producing far-from-equilibrium dynamical states of matter, for instance the large-scale spatiotemporal order of Benard convection [8]. There, he speculates that gravity constitutes a key factor ensuring that the system is effectively driven away from the state of thermal equilibrium. However, to the best of our knowledge, Prigogine had never formulated this profound observation in an all-encompassing account of how gravitation and entropy relate to each other in a universal manner. In fact, while no such account appears to exist even today, Penrose has gone further than others in bringing the subject into a mature form.41

For us, the importance of Penrose stems from his implicit advocacy of the crucial centrality of fields in the calculation of entropy and its production.42 Gravitation, the ultimate field-theoretic discourse, indeed changes the original philosophical program proposed by Boltzmann, which was highly tilted toward a mechanism of interaction dominated by inter-molecular collisions taking place within a passive flat spacetime [48,111,115]. Instead, with Penrose—then later Barbour [25,26]—we begin to directly and systematically take into account the role of continuous gravitational field in entropy production.

The initial singularity that produced our universe is deemed “very special” because it must correspond to an extraordinary low-entropy state [28]. Without this special initial state, Penrose believes, the present very high entropy level of the universe would not be explainable. However, why does the present universe possess very large entropy? Interestingly, Reichenbach repeatedly claimed in his last book, The Direction of Time [7], that the entropy of the present universe is very low, which might explains why, unlike Penrose, he never felt pressed to develop a Penrose-type argument about the special state of the Big Bang or initial singularity. Of course, two fundamental pillars of modern cosmology were not known in the 1950s when Reichenbach passed away: the Cosmological Microwave Background Radiation (CMBR), which experimentally confirmed the presence of Big Bang, and the discovery (or faith in the existence of) black hole radiation. Now, the entropy of the CMBR can be easily calculated since it follows the Planck thermal radiation law and is found to be extremely uniform (in angular directions), suggesting an isotropic initial state of the universe [28,40]. That, in turn, implies that the gravitational degrees of freedom were somehow “turned off” at the moment the of Big Bang and for some period of time after, at least until the onset of the decoupling era [100]. Otherwise, the presence of strong gravitational interactions will lead to very high entropy in the initial state instead of the very low entropy to be expected if Boltzmann Order Principle and dynamics [172] can be extrapolated to apply to the entire universe, a view Penrose continues to find unproblematic [28].43

6.3. The Penrose Cycles of Time Cosmogony

Penrose’s latest cosmological dynamical theory [100] revolves around a new and original proposal for the resolution of the paradox of how the Second Law and the global structure of the world are to be brought in together. The headline title of the new paradigm is Conformal Cyclic Cosmology (CCC), which is a body of thought comprising several principles. As we did with Reichenbach and Prigogine, what follows is not a review or critical assessment, but an interpretive analysis that aims at emphasizing some key ideas while exploring their connection with the other theories examined in the previous parts of this article. Here, we adhere to Penrose’s own presentation of CCC [100]. Because of the very high quality of this text, originally written for the general public, while the mathematical details of the cosmological model were relegated to carefully written appendices at the end of his book, our presentation of the original technical details will be brief. The main focus, instead, will be laid on extracting the essential conceptual and structural features of the CCC model as they relate to aspects of the problem of the direction of time treated in this article. Readers interested in learning more about how Penrose originally created the model are encouraged to directly consult Cycles of Time [100].

Let us first summarize the main themes of the CCC view. The largest scale structure of history, cosmological time, is here envisioned to encompass not only a single cosmos, but many; in fact, a potentially infinite succession of “sub-cosmoses”, each one being coextensive with a “typical universe” like ours. In contrast to the now popular multiverse and inflationary cosmologies often discussed in media and academia alike [173], the new Penrose Universe involves only a single “Super Cosmos”, where the latter is viewed as a linear succession of sub-cosmoses forming phases or stages of birth and death. A sub-cosmos is born in a Big Bang-like singularity, only to die out later by transforming all of its matter to purely bosonic radiation (mostly photons and gravitons). Afterward, a new cosmos is born out of the “ashes” (Cosmic Background Radiation, really the radiation produced in the previous sub-cosmos). After a short while, the newly born cosmos will begin to produce baryonic (and possibly non-baryonic) matter. Gravitation will kick in, then the expected evolutionary history described by the modern theory of gravitation will take control of the remaining stages of this cosmos. A process such as Penrose’s CCC constitutes a new kind of Eternal Return, a cosmic narrative reminding us of Proclus [174] and Nietzsche [175,176]. It is a clear sign of the continuing presence of Platonic (Idealistic) thinking right at the heart of modern science.44

We now give additional information on this cyclic cosmogony. The key idea in Penrose’s formulation is the need to explain the special status of the Big Bang: Why does it have such a ridiculously small entropy value? On the other hand, because of the fact that black holes are scattered around in the universe, for example, the gigantic cluster of black holes at the centres of galaxies like our Milky Way, the entropy of the present universe appears to be very high though not maximal. Pockets of low entropy still exist, most notably shining stars producing low-entropy electromagnetic radiation like our Sun.45 To solve this problem, Penrose has proposed two key ideas. First, he invoked the so-called Weyl Curvature Hypothesis (WCH) [28,38,39], which claims that the Weyl curvature46 is exactly zero at the moment of the Big Bang. This is motivated by the fact that such a global boundary condition constitutes a “quick and direct method” to encode into the structure of spacetime the observed fact that the gravitational degrees of freedom at the Big Band moment were somehow turned off. In order to correctly and rigorously implement this idea, Penrose was lead to another confrontation with conformal spacetime geometries, a group of special geometric models of spacetime that appear to work extremely well with a scenario in which the WCH is postulated. Conformal spacetime is essentially the geometry of spacetime when the only form of energy available is the electromagnetic energy of propagating light (photons) [28,40,100]. (This is why sometimes it is often referred to as “light cone geometry”). Here, it turns out that the Riemannian spacetime metric tensor $g_{\mu \nu }$ is not needed in full. Instead, we may operate merely with the angles between light cones in order to fully account for geometry and dynamics, hence the use of the technical term conformal in the title.47

The second key idea proposed by Penrose to resolve the low-entropy initial state paradox is related to the role played by black holes in modern cosmology. In fact, black holes are no longer taken as just some other class of curious objects that may exist in the universe such as stars, planets, or interstellar dust, but to constitute a fundamental and major dynamical player in the overall drama of the history of the cosmos. Here, every history of a sub-cosmos, i.e., every one of those phases repeated cyclically in the CCC framework, is to be inscribed between two types of singularities, the Big Bang and black holes. The Big Bang is unique and truly singular (though CCC’s use of conformal geometry would remove the mathematical technical singularity and replaces it with a smooth transition from a pre-Big Bang (old) cosmos to the subsequent post-Big Bang (new) cosmos). Black hole evaporation via Hawking radiation, the process of converting the enormous mass of the black hole to low-energy electromagnetic radiation [28,60], is the key process to be invoked here. According to Penrose, if we just wait “long enough”, the total mass of a black hole will transform into radiation, with the black hole itself, in all likelihood, eventually “finished off” in a final nonviolent pop. Now while this in itself is not new (it had been already hypothesized by Bekenstein, Wheeler, and Hawking, the original founders of black hole thermodynamics), Penrose has recently accentuated the position of black hole thermodynamic processes within the overall structure of modern cosmological thermodynamic theory. This is especially important for the various still raging battlefields of quantum cosmology [113], whose central tenet is the idea that the entirety of the universe can be described by a single physical state, most likely a quantum wavefunction or a vector in some Hilbert space.48 Here, Penrose would exploit black hole radiation to serve his agenda in two unique and distinct ways: First in conjunction with his key geometrical boundary-condition-like assumptions (the Weyl Curvature Hypothesis and the need for conformal spacetime geometry); and second with respect to the to paradox of very low-entropy state enjoyed by the Big Bang. Let us consider these two distinct ideas in turns. In between, a third fundamental idea will be introduced, the Penrose decay process.

6.3.1. First Use of Black Hole Thermodynamics

Although sparsely distributed within the total cosmos, black holes act like gigantic transformational machines, converting both baryonic (and possibly non-baryonic) energy–mass-momentum distributions and nearby bosonic particles captured by its event horizon to those peculiar, gravitationally-held, extremely concentrated matter states possessing an extraordinary high-entropy content.49 After cannibalizing the original low-entropy content of the initial mass distribution that kick-started the black hole formation process, a black hole would devour low-entropy states of matter and radiation, captured from the surrounding areas, in order to produce a very large value of entropy concentration localized in space but extending for aeions in (cosmic) time. Therefore, it appears that a black hole does behave like an entropy production machine, possibly the most powerful and efficient such machine in the universe (as per our present state of knowledge). Penrose did estimate the entropy of a black hole cluster, like that at the centre of our galaxy, and found it dwarfing the entropy of the observable CMBR radiation. On the other hand, Reichenbach, who died a decade before the discovery of CMBR, was led (in fact misled) by his (excusable in our opinion) ignorance of both CMBR and black hole entropy to assume that the entropy of the present universe is still low [7]. With Penrose, the acuteness of the spectacular numerical disproportionality between the present universe’s entropy, and what it should be at the initial Big Bang state, have become a major topic of intense investigation and research [179].

The black hole as an entropy production machine will first convert initial low-entropy mass and radiation distributions to high-entropy mass states.50 Next, through black hole radiation, these high-entropy massive states are converted to pure radiation, i.e., not fermionic mass. This is very important for Penrose’s CCC program to work. Indeed, since it is required that each sub-cosmos possesses a conformal spacetime geometry around the time of the Big Bang, there should be only bosons (photons and gravitons) around, but no fermions. Black hole radiation provides a path toward achieving this. If all matter and radiation eventually get captured by black holes, then after waiting for sufficiently long time, all captured mass-radiation will be returned back to spacetime but mostly in the form of electromagnetic radiation, leading to light-cone (conformal) geometry as our best mathematical description of spacetime in the asymptotic limit of the very distant future, i.e., the period immediately preceding the subsequent Big Bang which, in due time, will give rise to the next sub-cosmos succeeding ours, as per the CCC’s rules; then repeating the entire previous process, and so on, ad infinitum.51

6.3.2. The Penrose Baryonic Decay Process

However, a difficulty still exists in this proposal, which Penrose himself did recognize, and even had gone further to examine at length in his main work on CCC [100]. This is the fact that maybe some fermionic matter will not be captured by some black hole, and hence never get converted to photons by the black hole thermodynamic machine. This is possible because a sub-cosmos may contain positive—accelerating—clusters of matter distribution (for instance, due to some dark energy or positive cosmological constant mechanisms), leading to two fermionic worlds acquiring space-like separation. In such perfectly legitimate scenario, a fermionic matter distribution in one region will always be out of the event horizon of a black hole fully contained in the other space-like distant region. To solve this problem, Penrose has been toying with the bold speculative idea that all fermionic particles will eventually decay (to photons and gravitons). No direct experimental evidence of this exists today, though proton lifetimes have been investigated in the lab and were found to be extremely long. However, since for Penrose “time is plentiful”, he assumed that if we just wait “long enough”, then all protons and electrons (and other fermions) will decay into radiation (there are no perfectly stable particles in nature). If this is the case, then such decay mechanism, on the top of black hole radiation, will be sufficient to predict the complete transformation of all matter to photons (and possibly gravitons), hence forcing the geometry of the world, by that asymptotic future time, to effectively become exactly conformal.

6.3.3. Second Use of Black Hole Thermodynamics

There is now a small modification of the previous idea. In order to explain why the entropy of the new sub-cosmos, born after the previous universe had passed (smoothly) through the Big Bang,52 is indeed very low, Penrose noticed that the photons radiated by black hole radiation are in fact low-energy photons. Consequently, more photons exist to span the given energy stored in a black hole, and hence the number of degrees of freedom is larger. Using Boltzmann entropy formula, the previous scenario immediately leads to the fact that the radiation emitted by black holes, eventually accumulated throughout the aeons it will take for all black holes to fully evaporate, is low-entropy state of radiation. Since the new universe, which was just born out of the dying old sub-cosmos, will inherit this radiation as a legacy from its pre-Big Bang Universe, then together with the hypothesis of zero Weyl curvature, Penrose claimed that this explains or resolves the Second Law paradox when applied to the cosmos at large. Indeed, in this case, the presence of very low-entropy radiation-dominated initial state (Big Bang that is not truly a “bang singularity” any more, but a delicate smooth transition between two conformal spacetime worlds), together with gravitational degrees of freedom turned off by the WCH, explain the observable CMBR spectrum. In fact, Penrose believes that his CCC framework can replace the now dominant and popular inflationary and parallel universes models.

7. Comparative Analysis and Final Remarks

In this final section before the conclusion, our goal is to provide a concise high-level conceptual overview on the very difficult and still open problem of whether one can discover logical connections between Reichenbach’s, Prigogine’s, and Penrose’s various very distinct proposals related to the problem of the direction of time. Our approach in Section 7 is tentative, where no conclusive “hard fact” are derived or proved with regard to whether, for example, it can be shown that one key idea in Prigogine can be unequivocally traced to an earlier idea in Reichenbach (or Penrose), and so on. In fact, it is not only not clear whether such logical derivation of one thinker from another is possible, but we may question whether is is even philosophically interesting to do so. Nevertheless, we believe some provisional remarks on the relations between Reichenbach, Prigogine, and Penrose can be stated here. In what follows we present a series of brief reflections on this topic, but we leave a fully-fledged investigation of some of these observations to future research.

7.1. Penrose and Prigogine

Penrose’s cosmogony may be summarized as follows. Black holes are to be viewed as behaving like two thermodynamic machines connected in cascade:

(i)

The first machine converts mass-radiation distributions, initially given in whatsoever entropy state (but mostly in low-entropy state though), to the higher-entropy states of gravitationally concentrated mass.

(ii)

The second machine is a transformation of the high-entropy black hole mass-energy distribution into low-entropy pure radiation state.

These two machines are distinct though obviously not independent since, to the best of our expectations, the second machine will now follow on the heels of the first.53

In conjunction with these two cosmic thermodynamic machines, Penrose introduced a third fundamental process, the baryonic decay process, to ensure that only photons exist in the far-future of each sub-cosmos (cycle). It is interesting to add that if the hypothesized baryonic decay process (the gradual transformation of fermionic matter to radiation-only low-energy form54) does hold universally, which was precisely what Penrose proposed in order to guarantee the existence of strictly conformal spacetime geometry in the distant future of each phase universe (what we called sub-cosmos) [100], then black hole radiation is not in fact the only mechanism responsible for producing low-entropy radiation, i.e., contributing to creating the–overall—very low-entropy state of the initial Big Bang state, the reason being that, in addition to the previous mechanism, baryonic matter decay also should enter into this picture as a principal source of low entropy in nature. It remains true, though, that most of the mass distribution in the universe is eventually expected to be captured by black holes, so Hawking radiation would remain the main mechanism for enacting the second cosmic thermodynamic machine above.

Prigogine’s research on the reformulation of statistical mechanics and nonequilibrium thermodynamics may be invoked for a provisional attempt to suggest the possibility of establishing a link with Penrose’s thinking. Our starting point is the Prigogine’s superspace extension of Liouville space55 to Gelfand space (rigged Hilbert space) discussed in Section 5 and briefly reviewed in Appendix B. In the latter case, one works with generalized eigenvalue problems, where, in contrast to standard quantum mechanics, the eigenvalues of physical observables are generally complex. Indeed, by applying the generalized eigenvector construction (A10) or (A11) to specific models in quantum physics, most prominently the Friedrichs model, Prigogine and collaborators explicitly computed complex eigenvalues for interacting quantum large Poincaré systems with continuous spectrum [29].56 If this rigged Hilbert space construction can be applied to the Penrose conformal model of cosmology (CCC), then one may assume that in a yet-to-be-constructed extended superspace of this problem, a generalized eigenvector $|f\rangle$, similar to the one obtained for the Friedrichs model by the Prigogine group mentioned above, may be constructed for the CCC model, with the generic form of its unitary evolution specified by the formula:

$$e^{\mathrm{i}Ht}|f\rangle =e^{-\mathrm{i}\omega t}{e}^{-(\gamma /2)t}|f\rangle ,t>0.$$

(1)

Here, H is a proper global Hamiltonian under which the conformal cosmological model is assumed to evolve. The ket $|f\rangle$ is an eigenvector representing the particle (proton) state, while $\omega$ is its frequency. The complex nature of the eigenvalue of a self-adjoint operator like H within the generalized eigenvalue problem formalism described in Appendix B, which is possible only outside Hilbert space, e.g., in the Rigged Hilbert space formulation, is manifested by the decaying factor $exp(-\gamma /2t)$, where $\gamma$ is the decay rate of the particle process. Fundamental particles within this formulation of Prigoginean dynamics acquire then a “life-time” dimension absent in the original “pure” formulation of reversible quantum dynamics in regular Hilbert spaces. According to Prigogine and collaborators, this suggests that pure stable physical states are not the prototype in nature. Complex eigenvalues indicate that states have finite lifetimes [29]. In particular, baryonic matter, like protons, will eventually decay into electromagnetic radiation. This is of course the same as the Penrose process described in Section 6.3.2.57

However, Prigogine had arrived at the striking idea above through a completely different route compared to the one travelled by Penrose. The extension to Gelfand space was an idea that forced itself on Prigogine after decades worth of extensive collaborative research conducted by his sprawling Brussels-Austin group, involving numerous concrete models of various physical, chemical, and biological problems [148]. On the other hand, Penrose proposed his relatively recent decay process as one idea-assumption in order to ensure that his various other—essentially geometric—ideas, would consistently fit with each other. However, this baryonic decay assumption appears to have been introduced in Cycles of Time in a mode almost resembling an “after thought”, i.e., in an ad hoc fashion. The Penrosean geometric ideas (adapted to conformal geometry) [100] are traditional, in the sense that it is believed that the main structure of the world continues to be that of the Lorentz manifold of general relativity, evolving according to Einstein field equations, while other theories, such as quantum dynamics, need to conform to the strict background independence dicta of the generally covariant theory of gravitation [40], coupled to a set of carefully prescribed global “boundary conditions” such as the Weyl Curvature Hypothesis and entropy initial and final state conditions. Penrose then, and in contrast to Prigogine, does not believe that a new infinite-dimensional superspace such as the Gelfand space is needed. The consistency of the CCC model (Section 6) demonstrates that an alternative to Prigogine is indeed at least theoretically possible.

Now, from the conceptual perspective, introducing a decay process into what has been previously considered until very recently the exclusive realm of stable integrable dynamical systems (traditional classical and quantum Hamiltonian/Liouvillian dynamics [28]), amounts to “randomizing nature”. The reason, as we saw while discussing Prigogine, is that baryonic decay implies instability. For Prigogine, instability, together with Poincaré resonance (Section 4), are the major mechanisms leading to irreversibility. Penrose’s derivation of the irreversibility of cosmic evolution, while still presupposing reversible laws of evolution for the background universe (the Einstein field equations and the conservative Hamiltonian framework), is then somehow similar in spirit to Prigogine’s, though the technical details are poles apart. Indeed, both Prigogine and Penrose introduce dissipation (Penrose via the baryonic decay process, Prigogine’s through the Gelfand space extension) into the very fabric of nature.

Yet it is also very interesting to examine the essential methodological and philosophical differences between Prigogine and Penrose. The former is grounded in the enormously influential school of theoretical physics associated with L. Landau, with its acclaimed and powerful emphasis on statistical mechanics, condensed matter physics, and collective phenomena [181,182,183]. On the other hand, Penrose is rooted in the equally influential Weyl–Cartan’s school of German and French mathematical physics, with its deep entanglement with topology, group theory, geometry, variational analysis, and complex analysis [169,177,184]. The Weyl’s school is more philosophical and general, preferring to work with the global aspect of the problem at the broadest level possible, hence Penrose’s (and Hawking’s) celebrated approach to the differential topology of general relativity [94,97]. In his magisterial “comprehensive” treatise on physics and mathematical physics, The Road to Reality [28], one topic that is conspicuously missing in this massive tome is statistical physics, especially its applications to condensed-matter physics. Penrose probably does not consider statistical physics as fundamental as, for example, the Dirac equation or the Hamilton Principle, but in the Landau school, and with Prigogine in particular here, such approach is not acceptable. For throughout his life Prigogine had always been a man of examples and concrete models, preferring to reach general principles by inductions and generalizations of already fully-worked out specialized but representative examples. Penrose, on the other hand, works by abduction, meaning to intuit the general principle, such as the Weyl Curvature Hypotheses or the Penrose baryonic decay process, based on profound and careful analyses of extremely generic scenarios, best captured by the topological structure of the system. The best example of such enormously consequential approach to theoretical physics, of course, is the celebrated singularity theorems [97].

7.2. Reichenbach vs. Penrose/Prigogine

But the bare-minimum of the idea of introducing instability, decay, dissipation into nature, which, according to the above analysis, can be found in both Prigogine and Penrose, was already proposed by Hans Reichenbach in his posthumously published masterpiece The Direction of Time [7]. As we saw in Section 3, the emergence of a preferred direction of time is technically explained through the deployment of a novel branch-system-based ensemble ontology. Without the need to enter into the strictly mathematical details (they are not fully explicated by Reichenbach himself due to his sudden death before completing the manuscript), we identify the principle of intrinsic stochasticity as the key idea (Reichenbach Principle ${\mathbf{RP}}_1$) serving as an immanent “cause” of dynamic flow in nature. Prigogine’s approach to intrinsic randomness-via-instability examined above comes through the Poincaré detour, which Reichenbach had not traversed (the absence of interest in Poincaré in Reichenbach’s books and papers is hard to explain). Prigogine sees irreversibility emerging through instability and resonances, but Reichenbach was probably one of the first to philosophically elevate stochastic considerations to the main focus of the most fundamental level of description in nature, a step that Penrose, in our opinion, had not taken as explicitly and boldly as Reichenbach did.

Moreover, with respect to the comparison with Prigogine, Reichenbach attributed the generation of a preferred direction of dynamical evolution to strong interactions between branch systems and subsystems, especially the stochastic type of correlation phenomena typically found in complex systems. Prigogine would later take up this suggestion by Reichenbach by examining, albeit in more details, the fine microstructure of dynamic correlations in collective phenomena,58 but, again, while utilizing a style of mathematical physics closer to the Landau school [63].59

An interesting conceptual or philosophical parallelism between Reichenbach and Prigogine’s respective approaches to entropy can be seen in the manner by which each of them sometimes diverges from Boltzmann orthodox position. Prigogine’s nonunitarty transformation theory,60 for example, constructs an entropy variable for an irreversible dynamical system by solely relying on generic purely dynamical considerations, and without resort to Boltzmann’s classic definition of entropy as the logarithm of probability or sub-volume in phase space. In fact, Prigoginean dynamics can construct an entropy variable without even invoking probability concepts. With Reichenbach, a technically different route was used, yet with some conceptual similarity: in the effective advance of time in nature, the production of a preferred direction of time depends not only on the Boltzmannian criterion, which is here seen to rigorously apply to branch systems taken individually, but also to how those local Boltzmannian temporal flows mesh together in the vertical (ensemble or stochastic) time dimensions. Again, as in Prigogine, the concept of the production of a global time flow is seen to be an emergent one and it depends on collective interactions of subsystems. The methods utilized were distinct: With Prigogine, the theory of nonunitary transformations uses the Liouville formalism to derive a non-Boltzmannian entropy function that in turn will be exploited in order to explain the direction of time. With Reichenbach, on the other hand, special probability mixing rules are introduced as external laws regulating how local time flows (horizontal time) interact with ensemble time (vertical time) to produce the effective global advance of dynamical systems. Historically speaking, Reichenbach’s mixing rules were not destined to receive the wider attention that Prigogine’s Liouvillian dynamical formalism enjoyed. Overall, we believe that more research is needed in order to fully understand the relation between the Reichenbach-style approach to stochastic interaction/correlation mentioned above, on one hand, and, on the other hand, the corresponding classes of strong interactions in Large Poincaré Systems (LPS) and nonintegrable systems that Prigogine school has been indefatigably and continuously investigating for more than five decades. Before achieving that, a complete assessment of the Reichenbach/Prigogine relation will have to remain provisional.

Regarding potential personal and professional channels of interactions, to our best knowledge, Prigogine does cite Reichenbach’s book in some of his publications, especially in matters that have to do with causality and decay processes. However, from such sporadic references it is not possible to reconstruct a full and coherent story about how Reichenbach could have directly influenced the Brussels–Austin school. Nevertheless, Reichenbach was one of the most widely read philosophers of nature in the twentieth century. In addition, we already know that Prigogine was one of those relatively rare post-WWII philosophically-minded physicists, being widely read and in touch with the thought of some major contemporary postmodern philosophers such as Deleuze [83] and Simondon [81,82] as can be gleaned from his influential book, coauthored with I. Stengers, Order Out of Chaos [9]. Therefore, it is possible to assume that Reichenbach’s book was well-known in its entirety to Prigogine and his collaborators.

In terms of the Reichenbach/Penrose relation, we may safely assume that Penrose was either directly inspired or indirectly influenced by Reichenbach’s unique signature style of using topological order methods, e.g., causal net theories and ontologies, in order to construct the physical content of dynamical theories, such as gravitation and spacetime physics [86], or statistical, complex, and thermodynamic systems [7].61 The topological structure of spacetime, and its cosmological scope, are at the heart of the Reichenbachian stochastic dynamic take on the problem of the direction of time in Nature. Therefore, the germs of two of the main features of the Penrose world—global geometric formulations approached through topological methods and the emphasis on the boundary conditions of the Cosmos at large—are to be found in Reichenbach. The latter died in 1953, just when Penrose was starting his extraordinary career, and also roughly the same time when John A. Wheeler was beginning to turn into general relativity through a closer look into topology [185]. However, as far as we can tell, we are not aware of direct citations of Reichenbach by Penrose himself bringing to light a documentary evidence of a decisive influence of the former on the latter. Therefore, Reichenbach’s impact might have been filtered into Penrose’s mind through some other indirect pathways or convoluted circuits. It is also possible that Penrose invented his signature geometric-topological style by directly starting from Weyl’s [168,169,186] and Cartan’s [177] respective research programs. At least with respect to the latter possibility, that is how Penrose himself often likes to reflect on his intellectual development in his very sparse autobiographical remarks: He openly sees himself as a continuation of the geometric schools of Riemann, Cartan, and Weyl.

7.3. Concluding Remarks on Prigogine

Finally, let us now examine the overall status of the Prigoginean program. In contrast to the popular view of Maxwell that the Second Law’s validity is mainly statistical [55], within the general Prigoginean dynamical program, thermodynamics and traditional dynamics both merge into one and the same unified structure, that of dynamics as such. The microscopic world is irreversible [187]. This view is elegantly captured by Misra in the following text:

(…)it seems that the law of monotonic increase of entropy cannot be regarded as only of approximate validity. It is not the result of inaccuracies involved in macroscopic observations which in principle can be eliminated but is as rigorously valid a law of physical phenomena as the laws of microscopic dynamics. The relation between the thermodynamic and the (microscopic) dynamical descriptions of physical systems is not akin to the relation that exists between the sharply focused and blurred vision.62

Nevertheless, for Prigogine, a dynamical system is still defined exactly as in Boltzmann, that is, in a bottom-up approach where the molecular level grounds the upper (macroscopic) structure of reality:

By a dynamical theory we mean a theory where the properties of a macroscopic system are deduced from a mechanical model involving a “large” number of degrees of freedom. This is essentially the principal aim of statistical mechanics.63

In different words, Prigogine follows Boltzmann by proclaiming that entropy production is to be understood as immanent in the underlying mechanistic model of reality as such, which is here reduced to collisions and long-range interactions between molecular constituents. It is curious then to see how, in spite of all his scientific radicalism and bold innovations, Prigogine–philosophically speaking–had remained in essence a conservative thinker operating within the venerable modernist tradition of corpuscularism dating back to Descartes and Gassendi [188].

The other alternative, that entropy is a fundamental field on par with other existing fields, such as the electromagnetic and gravitational fields, or the increasing numbers of quantum fields introduced nowadays in cosmology [113] and high-energy physics [189], does not seem to have been taken up by many thinkers and writers within the large area of theoretical physics and the philosophy of nature. In fact, even in his various proposals for “alternative quantum theory” and “new frameworks for dynamical theories”, Prigogine is still a faithful follower of Boltzmann, though a much more sophisticated one. In a nutshell, our opinion is that Prigoginean dynamical theory is still, philosophically speaking, Boltzmannian, appearances to the contrary. A basic question remains open though: Out of the three thinkers, Reichenbach, Prigogine, and Penrose, who was able to break away the farthest from Boltzmann? We hope that further research in the future will help illuminate this issue based on the initial assessment outlined in this article.

8. Conclusions

We developed a new perspective on the general subjects of entropy flow and the direction of time, fundamental to irreversible processes in nature, built on a selected spectrum of ideas by Reichenbach, Prigogine, and Penrose, with emphasis on the cosmological formulation of the problem of time asymmetry in the world at large. Some of the main principles underlying the thinking of each one of these three figures were highlighted in a conceptual style emphasizing key assumptions and operating methodologies lurking in the back of their respective proposed resolutions of the problem of the direction of time. Afterwards, we attempted a provisional sweeping analysis of irreversible dynamics in nature, and also proposed some conceptual pathways and circuits of hidden interactions between several key technical ideas in the field. We believe that irreversibility is ontologically fundamental in nature (Prigogine), and that the tendency to focus on deriving the irreversible from the reversible under the slogan “derive the macroscopic from the microscopic” is misleading since even the microscopic level of reality is fundamentally irreversible in and through. Both Reichenbach and Prigogine believed that the breakdown of reversibility is organically connected to the emergence of a larger, extended space, a superspace, into which the revered conventional spaces of mathematical physics are embedded (Reichenbach’s stochastic superspace extending spacetime; Prigogine’s Gelfand space extending Hilbert space). But Penrose, a staunch advocate of the fundamental ontological status of spacetime, kept the latter at the center of his cyclic conformal cosmology. However, under the pressure to develop new cosmological theory taking into account the entropy production of the initial and final states, he was also forced to propose radical modifications to the standard model of cosmology, mostly in the form of boundary conditions and the Penrose baryonic decay process. We conjuncture that it would be interesting to investigate whether Penrose’s conformal cosmology can be reformulated dynamically within a quantum-cosmological model of gravitation where something like Gelfand space in Prigoginean dynamics can be recovered. To our best knowledge, a deeper connection between quantum geometrodynamics and Prigoginean dynamics (each independently leads to its own superspace structure) has not been sought nor considered, yet we suspect that some form of post-Hamiltonian/Lagrangian superspace formalism might eventually prove to be intimately connected with the problem of irreversibility in nature. Our presentation is far from being comprehensive. What we hope we have achieved here is providing a first attempt to synthesize and understand the thinking of three principal architects of modern physics and the philosophy of nature through selected fragments of their works. Since Reichenbach’s, Prigogine’s, and Penrose’s theories are very technically involved, such conceptual take, in our opinion, is necessary. Specific conclusions and overall opinions on each of these technical dimensions can be found in the various sections above. Further future research may expand our initial overall assessment into new directions.