Abstract
Modern computer microarchitectures build on well-established foundations that have encouraged a pattern of computational homogeneity that many cyberattacks depend on. We suggest that balanced ternary logic can be valuable to Internet of Things (IoT) security, authentication of connected vehicles, as well as hardware and software assurance, and have developed a ternary encryption scheme between a computer and smartcard based on public key exchange through non-secure communication channels to demonstrate the value of balanced ternary systems. The concurrent generation of private keys by the computer and the smartcard uses ternary schemes and cryptographic primitives such as ternary physical unclonable functions. While general purpose ternary computers have not succeeded in general use, heterogeneous computing systems with small ternary computing units dedicated to cryptographic functions have the potential to improve information assurance, and may also be designed to execute binary legacy codes.
1. Introduction
Hackers and cyber-criminals continuously probe and attack legacy infrastructure. The layers of assurance that are added to our systems after-the-fact can be themselves susceptible to the same attacks. It may be the time to ask the following question: should we consider radical architectural and infrastructural changes that may disrupt the status quo to support a healthier cyber-security ecosystem through computational diversity?
In this paper we specifically consider the re-introduction of ternary computing, a technology invented 150 years ago but that has seen little practical application because it has not demonstrated advantages over binary computing in terms of computability or performance. Ternary computing uses trits (three primitive values of 0, 1, and 2, or balanced values of −, 0, and +) to enable denser numerical encodings, support a fuzzy state, and give the cryptographer the opportunity to introduce new ciphering methods based on hardware primitives that can provide additional security.
If ternary computing has the potential to disrupt and change the landscape of cybersecurity, we must ask a second question: can the inherent complexity and implementation costs associated with ternary computing be mitigated such that this technology can be used as a compelling fortification against malicious entities? In this paper we summarize the limitations of current security protocols and we describe how the design of ternary computing units can take advantage of recent advances in semiconductor technology. As an example, we present the design of public key exchange protocols between a computer and a secure microcontroller using the Java Card OpenPlatform that takes advantage of ternary operations and representation. After presenting experiments related to ternary computing, we review the value of ternary computing to improve information assurance.
2. Limitations of Current Security Protocols
Currently, hackers, terrorists, and organized cyber-criminals are equipped with increasingly sophisticated tools and are too often able to compromise hardware and software assurance, the security of the internet of things (IoT) and cyber-physical systems (CPS), connected and autonomous vehicles, and data systems. The list of recent victims includes the power grid, IoT networks, hospitals, the National Security Agency (NSA), the Internal Revenue Service (IRS), local and national governments, banks, and major retailers. While hackers are constantly designing new malware attacks with the intent to find new vulnerabilities and exploit existing flaws, the “defense” has the difficult task to anticipate future attacks based on knowledge gained from previous attacks and known problems.
2.1. Threats in the Cyber-Space
CPS- and IoT-based systems are vulnerable to several threats, including [1]:
- Malware, worms, and viruses inserted by malicious entities. These threats can be dormant for years, but when activated, cause large scale damage;
- Breaches in access control due to password guessing, identity theft, insider and side channel attacks, and exposure of user account databases. Such breaches can result in illegitimate user access;
- Eavesdropping by listening over open network connections. This can compromise the integrity of the networks, confidential files, passwords, and other personal and corporate information;
- Man-in-the-middle attacks and war dialing, in which malicious agents pretend to be legitimate actors, and acquire information that can enable the exploitation of vulnerabilities;
- Protocol-based attacks, which can occur when the attacker has access to partial knowledge of security protocols. This can include host attacks, which exploit vulnerabilities of CPSs and their operating systems;
- Distributed denial-of-service (DDoS) attacks having with the objective to of overwhelming the communication between hosts and client devices. Often the constellation of IoTs does not have enough embedded security.
Interaction with people and social engineering represent an additional set of opportunities for malicious parties. For example, a malicious agent can pretend to be a legitimate system user that has lost a password and attempt to deceive administrators into “restoring” credentials. They can also pretend to be legitimate administrators, deceiving the users into divulging information.
2.2. Risk Mitigation
Known defenses and actions designed to mitigate these threats include firewalls, code signing, public key cryptography, data mining, machine learning, and artificial intelligence (AI).
Firewalls can be extremely effective in protecting systems against the attacks described above by strengthening access control and preventing malware from contaminating the network [1,2,3,4]. Firewalls can recognize upfront malicious users that do not comply with security protocols before they have a chance to create problems [4]. Commercially available firewalls, when deployed effectively, are valuable assets. Unfortunately, hackers often have access to large and diverse resources. Hackers can, for example when assisted by insiders, exploit mistakes in the firewall deployment, or use malware and phishing to open holes in a firewall [1]. And while encryption is a highly desirable component of a secure system, many of the aforementioned threats emerge due to breaches in access control, side channel attacks, and when IoT devices are “lost to the enemy” [1,2,3,4]. Fortunately, symmetric (Data Encryption Standard-DES, Advanced Encryption Standard-AES, Blowfish, one-time pad) and public key cryptography (Rivest-Shamir-Adleman-RSA, Elliptic Curve Cryptography-ECC, Diffie-Hellman-DH) can offer extremely effective information assurance.
The emergence of data mining, machine learning, and AI [5,6,7,8,9,10,11] has changed the overall landscape of cybersecurity. These methods have become increasingly effective at detecting sophisticated attacks by analyzing both the profile of the attacks and the damage as it unfolds [6]. Attacks of limited impact, when quickly contained, may be acceptable if used to learn more effective defenses [7]. When firewalls are deficient, methods based on machine learning and AI operate like drugs in the human body, and can quickly identify and mitigate the effect of viruses and worms [10,11]. Machine learning is also extremely effective for improving authentication schemes [9]. For example, Physically Unclonable Functions (PUF), as well as biometric functions, that generate cryptographic primitives in CPS such as “finger prints” of the hardware and the users, trend to drift when aging, or when subject to external factors such as temperature, humidity, or electro-magnetic noises. Machine learning and AI can learn how to better discriminate between these effects and hostile behavior [12]. As powerful and sophisticated as these methods are, one cannot underestimate the ability of hackers to improve the profile of their attacks and to develop new malware.
Firewalls, public key encryption, and artificial intelligence are also important pieces of a defensive strategy. In the next sections we will argue that computational heterogeneity and specifically ternary computation can provide additional levels of security that are complementary to these efforts, especially in protecting emerging applications such as the IoT, smart manufacturing, and autonomous systems.
3. Ternary Computing
3.1. Brief History of Ternary Computing
The first ternary calculating machine was built in 1840 and was constructed mainly of wood by the British mathematician Thomas Fowler. This machine was the subject of an analysis published in 2005 [13], which included the fabrication of a new machine based on Fowler’s design. Glusker et al. [13] produced a working device that was demonstrated in 2000. The architecture of this calculating machine was based on balanced ternary arithmetic handling trits of three possible values annotated (−, 0, +). One advantage of ternary logic is the ability to handle and store information more densely than with binary logic [14]. A data stream of N bits contains 2N possible combinations, while a stream of N trits contains 3N = 2N × 1.5N possible combinations.
Moscow State University engaged in a multi-year research program in ternary computing initiated in 1956 by S. L. Sobolev, and N.P. Brusenzov [15]. A working balanced ternary unit, “Setun”, was delivered in 1958 based on ferrite cores and semiconductor diodes. A second version, “Setun 70”, introduced in 1970, handled trytes consisting of 6 trits. Software that could run on ternary computers was developed concurrently [16]; however, the research effort in Russia was converted to binary computing after the successful manufacturing of 50 working prototypes. In the USA, ternary computing efforts also started in the 1950s and included the development of “Whirlpool”, a military computer designed by Massachusetts Institute of Technology (MIT) and Ternac (emulation of a ternary computer), a research project by the State University of NY at Buffalo [17].
The advantage of binary over ternary computing is simpler hardware representation and design. Moore’s law, which anticipates the possibility to increase the density of transistors in integrated circuits, has allowed the computing industry to focus successfully on the continuous improvement of binary architectures. The investment in binary software and tool design represents a considerable hardware-software legacy. At the same time, binary logic has not been completely dominant. L.A. Zadeh introduced “fuzzy logic” in the 1960s [18]. Zadeh’s observation was that many physical and biological phenomena are not modeled well by binary logic. Fuzzy logic and associated error correcting methods allow for ternary states which encode crisp and fuzzy values. The importance of fuzzy logic has grown over the years and is now an important and practical part of the AI field. As mainstream semiconductor technology approaches fundamental scaling limits, correcting intermediate or fuzzy states has become more important.
In quantum computing [19], the use of multiple-state algorithms allows practical implementation of algorithms such as the prime factorization of large natural numbers, representing a direct threat to modern cryptography. Quantum computing engines are not easy to fabricate, in part because of the difficulty of managing random errors. Some investigators have suggested that the use of ternary states and fuzzy logic can facilitate the design of quantum computers and quantum algorithms. Related work has explored the use of ternary quantum logic for representing quantum images and then developing ternary quantum circuits that perform basic image processing tasks [20].
In cryptography, the use of ternary states has been proposed to strengthen multi-factor authentication [21], physically unclonable functions (PUFs) [22,23], and random number generation [24].
3.2. Ternary Arithmetic
Balanced ternary arithmetic, based on the three states (−, 0, +) is used in this work rather than the usual radix-3 coding based on the states (0, 1, 2). One common mapping of balanced ternary to binary logic maps the “−” to the binary “0”, and the “+” to the binary “1”. The additional or unmapped ternary state “0” then represents a fuzzy state [13,14]. Decimal numbers can be converted to a balanced ternary representation by encoding positive and negative powers of three. An example of this process is demonstrated in Figure 1, where the first row enumerates decimal values that vary from −9 to +9, the second row enumerates the signed binary representations of those same values, and the third row enumerates their ternary representations. In the balanced ternary representation, the leading “−“, and “+” digits are not used as signs.

Figure 1.
Conversion decimal to binary to ternary. The first row is for decimal values, the second row for binary values, the third row for balanced ternary values.
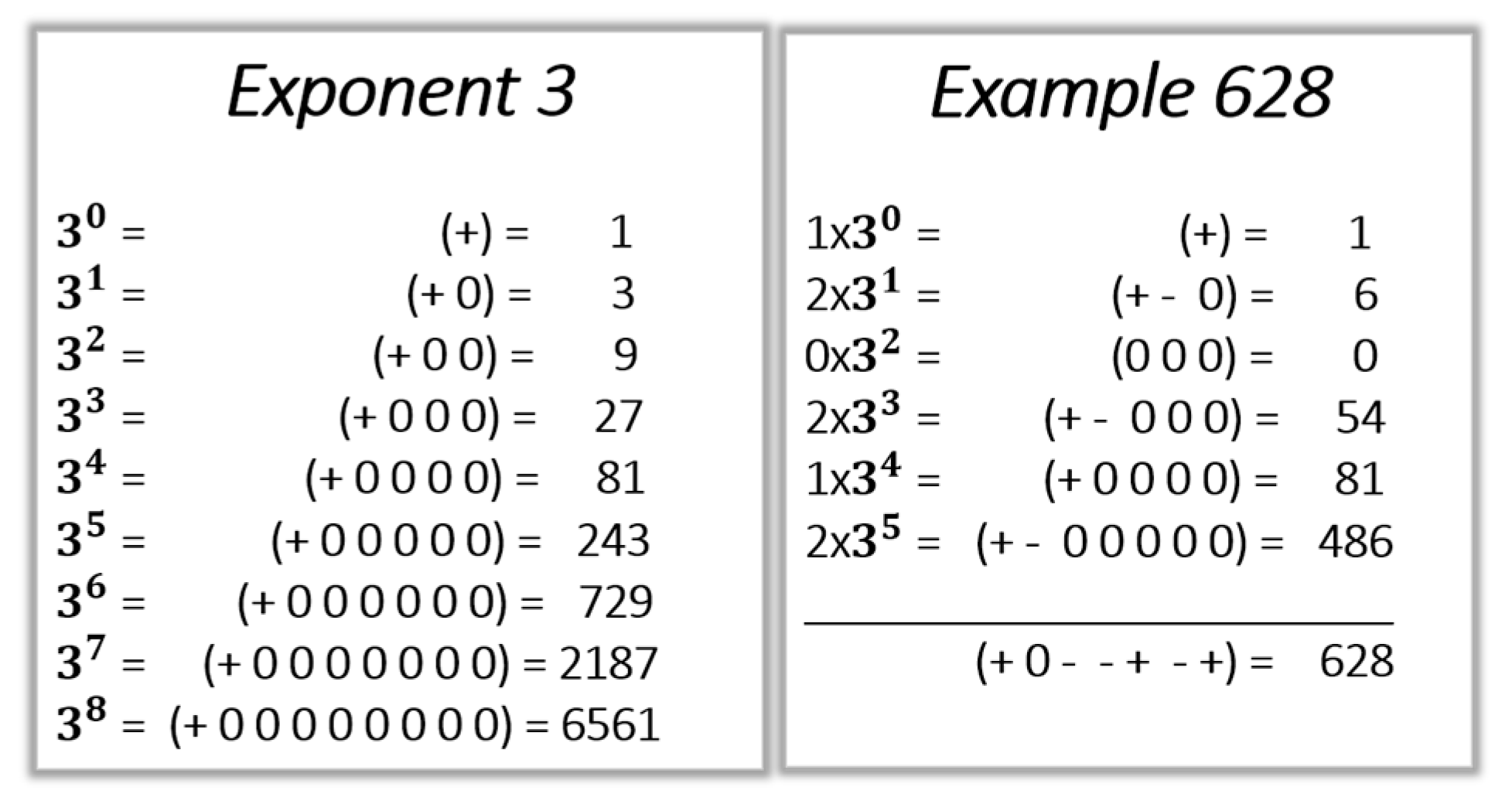
The additive inverse in ternary arithmetic is elegantly obtained by replacing the “−” digits by “+”, and vice versa. For example, +8 is (+0−), −8 is (−0+). The representation of 3N is a + followed by N “0” as shown in Figure 2. The right-hand panel of Figure 2 shows the conversion of 62810 to ternary.
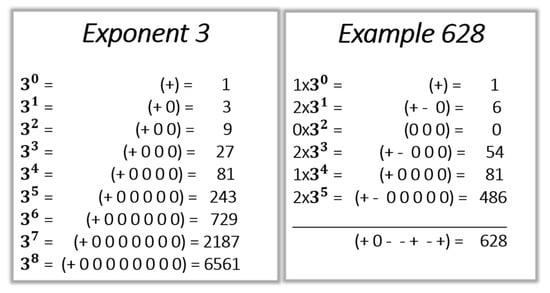
Figure 2.
On the left, values of 3N are expressed in ternary for N ϵ {0 to 8}; on the right, 628 in decimal is converted into ternary.
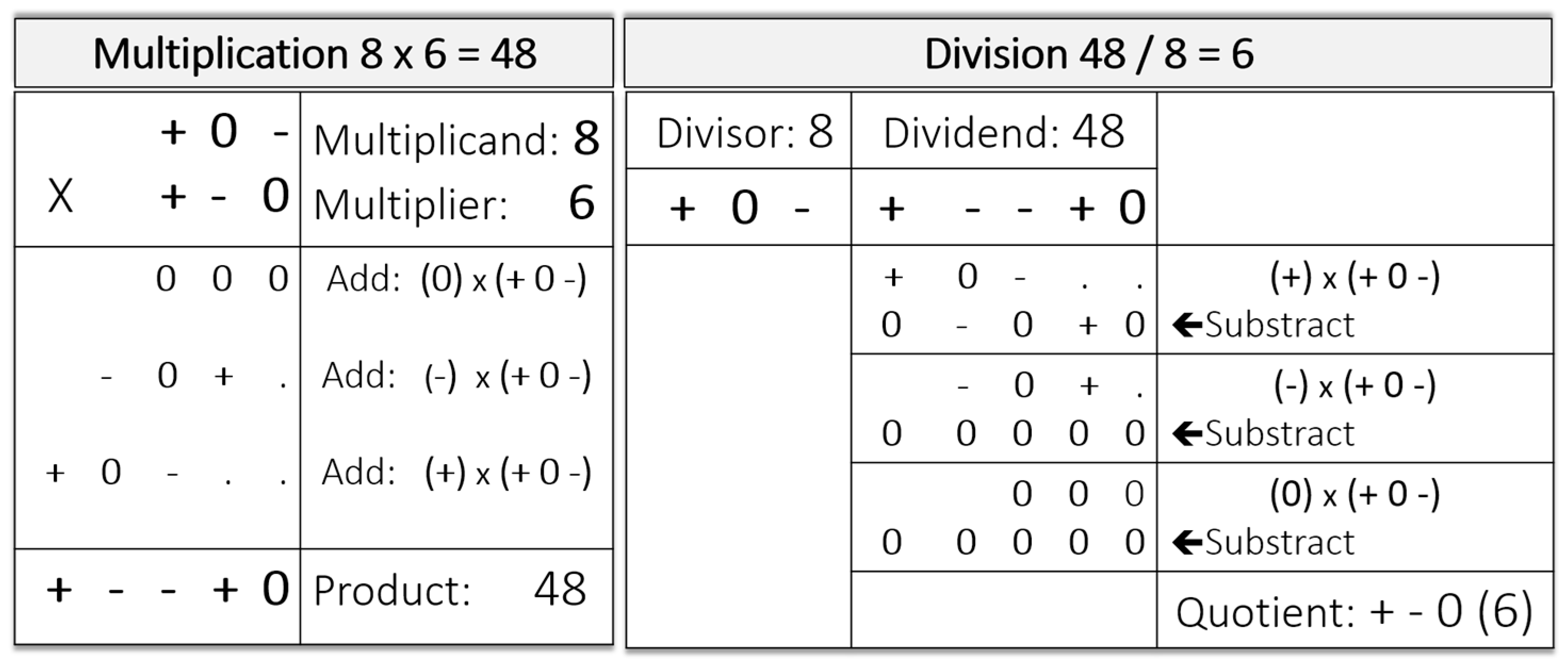
The basic arithmetic functions in balanced ternary logic include addition, subtraction, multiplication, and division and are described by Glusker et al. [13]. These arithmetic functions are not more complicated to implement than decimal or binary arithmetic. An example of addition is shown in Figure 2. Subtraction is accomplished by obtaining the inverse of the second number (i.e., replacing the “−” s by the “+” s, and vice versa) and then adding this inverse to the first number. Multiplication is accomplished by successive applications of addition, three in the case demonstrated in Figure 3. Division, in turn, is accomplished by successive applications of subtraction, again three in the example.
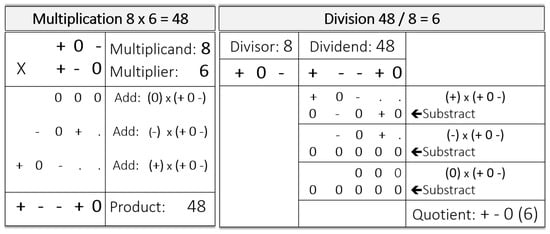
Figure 3.
Example of multiplication (8 × 6 = 48; left), and division (48/8 = 6; right).
3.3. Ternary Boolean Logic
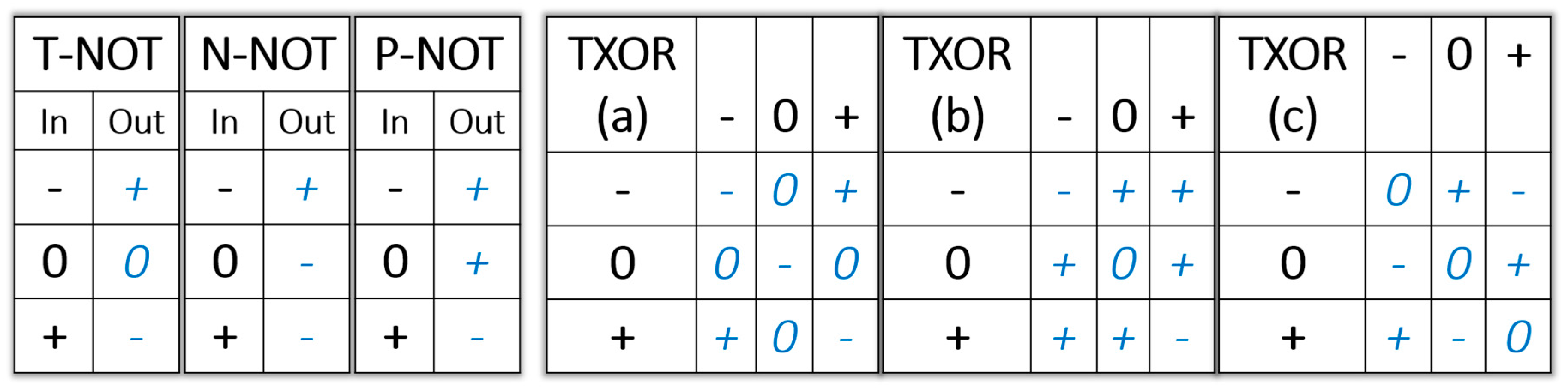
Ternary logic can be made compatible with binary logic by mapping the “−” to a binary “0” and mapping the “+” to a binary “1” [25,26]. Several additional logical operations can be defined to utilize the ternary “0”. For example, three Boolean NOT gates are used in ternary logic (Figure 4): T-NOT (−0+→+0−), P-NOT (−0+→++−), and N-NOT (−0+→+−−). The ternary gates XOR (a) and (b) shown in Figure 4 are both compatible with binary logic: {(−−) or (++)→−}; {(−+) or (+−)→+}. T-XOR (a) is often preferred, the Hamming distance between “0” and “0” is also “−”. The ternary XOR gate (c) is not compatible with the binary XOR gate. While the binary XOR gate is the Hamming distance modulo 2 of two bits, T-XOR (c) is the Hamming distance mod 3 between two trits.
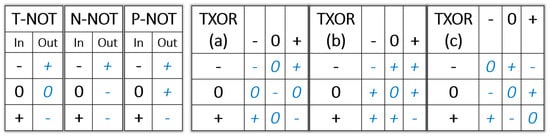
Figure 4.
(left) Three balanced ternary NOT gates; (right) three balanced ternary XOR gates.
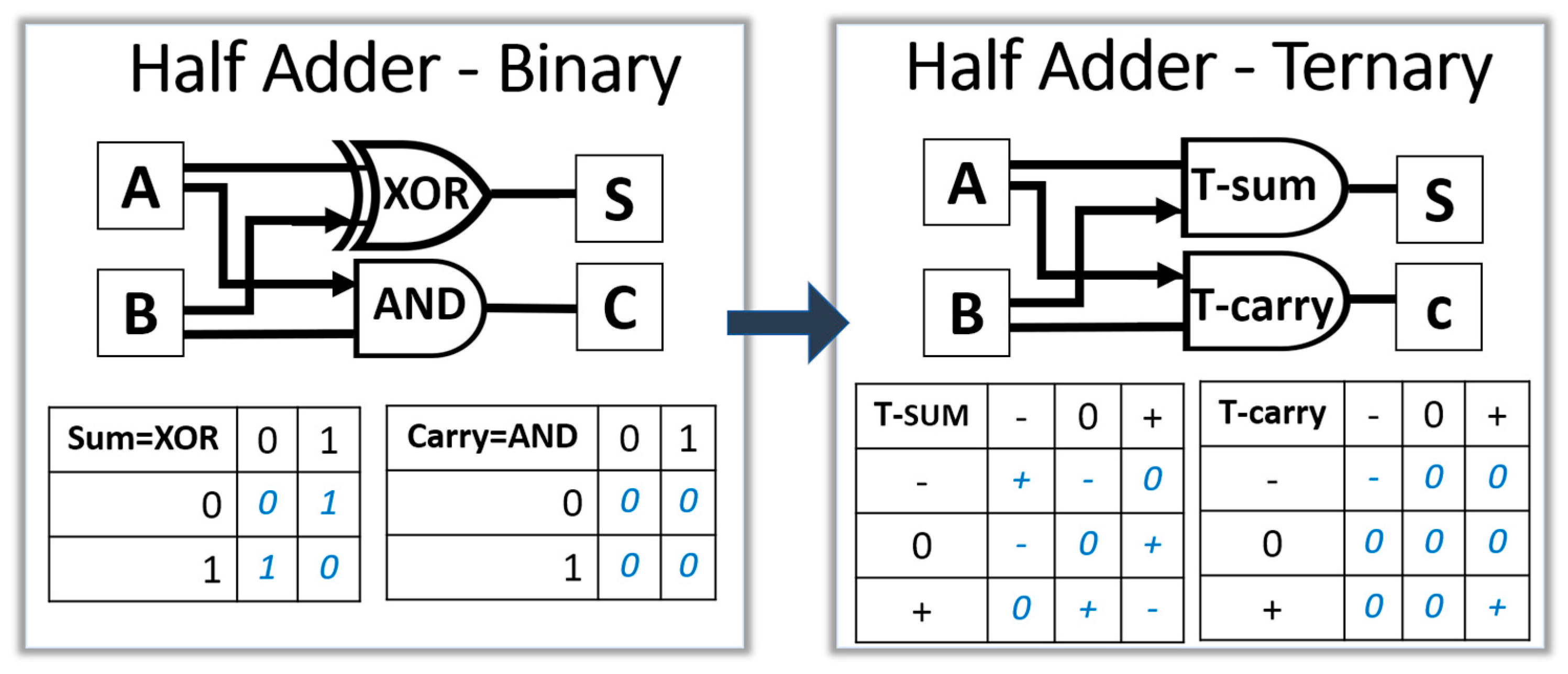
The relationship between arithmetic functions and binary logic cannot be directly applied to ternary logic. As shown in Figure 5, a half adder in binary logic can be designed with a XOR gate for the sum bit, and an AND gate for the carry bit. In ternary logic, the sum is an addition mod 3 and the carry is a T-AND: (−−→−), (++→+) [27].
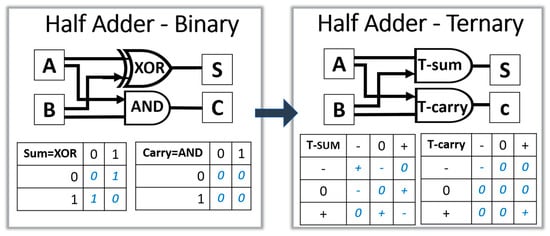
Figure 5.
(left) A block diagram of a half adder in binary logic; (right) the corresponding diagram in balanced ternary logic.
The use of ternary states gives an additional degree of freedom in developing algorithms for information assurance. Native ternary instruction sets can be selected to represent programs running on native ternary computers. Malware, viruses, worms, and other malicious codes designed for binary computers cannot run directly on native ternary computers without knowing the ternary instruction set used for a particular device at a particular time. Such protection is even more effective when the information needed to find a particular set of ternary instructions is encrypted.
3.4. Microelectronics for Ternary Computers
The implementation of ternary logic and ternary architectures has been described for contemporary microelectronic technologies such as Complementary Metal Oxide Semiconductor (CMOS), Flash, Dynamic Random Access Memory (DRAM), and even strategically important technologies such as Memristors and Resistive Random Access Memory (ReRAM).
Xu has shown that the design of ternary logic with traditional CMOS technologies can be accomplished by adding several threshold voltages to the MOS devices [28]. Srivastava et al. has shown that balanced ternary full adders can be designed with CMOS using a dual power supply [29]. Balla et al. also presented the design of a MOS ternary logic family [30]. Other investigators have presented similar work to implement multi-valued logic, a more general form of ternary logic [31]. Embedded ternary Static Random Access Memory (SRAM) cells can be designed with the same CMOS technology that is needed to design logic gates [32,33]. The leading-edge logic technologies for microprocessors and Field Programmable Gate Arrays (FPGA) usually offer only single threshold voltage CMOS, making the design of ternary computing engines challenging. It is encouraging to notice that advanced CMOS technology for embedded microcontrollers can offer multiple threshold voltages suitable for the design of native ternary microprocessors with SRAM caches without changes in the manufacturing technology.
Negative-and (NAND) and Negative-or (NOR) Flash Random Access Memory (RAM) can be designed as native ternary memory without any changes to the manufacturing process technology. As presented by Bennett et al. [34], the triple level cell Flash (TLC) is a mainstream technology that allows the packing of more bits per Flash memory array. For current commercial applications, the state machine of the Flash memory array converts the ternary information (or other multi-level representations) into binary information during data transfers to the memory bus [35]. Such Flash architectures can therefore be used to design non-volatile memories for native ternary computing units with design/software changes in the state machine.
The 1T Dynamic Random Access memory (DRAM) cells can contain one transistor and one capacitor each. After programming, the capacitors with the charge Q store 1s, and the ones with the charge “0” store 0s. Due to the constant leakage of these charges, they are compared during read cycles with the charge left on a reference cell that was initially charged with Q/2 [36,37]. Approximately every million cycles, the DRAM is refreshed. To design ternary DRAMs, the programming cycles need to store the three levels: 0, Q/2, and Q. During read cycles, the sense elements need to have the sensitivity to differentiate the three states, and the refresh rate would increase, reducing the speed of the memory. We think that most existing DRAM manufacturing process technologies are capable of supporting such operations with changes in the control circuitry.
The development of native ternary memories has been reported for carbon nanotubes [38], Magnetic Random Access Memories (MRAM) based on giant magneto resistance (GMR) [39], Memristors and ReRAMs [40]. One of the methods to create ternary states with memristors is to control the ramp up of the voltage between the electrodes of the cells, creating a conductive filament of variable cross-section, and obtain three different levels of resistivity, about 1–3 KΩ for the lowest state, 6–12 KΩ for the intermediary state, and higher than 15 KΩ for the highest state.
In summary, it is not currently possible to design native ternary computing engines with leading edge CMOS. However, current advanced manufacturing process technologies suitable for secure binary microcontrollers can be used to design ternary units with volatile and non-volatile embedded ternary memories.
4. Securing Client Devices
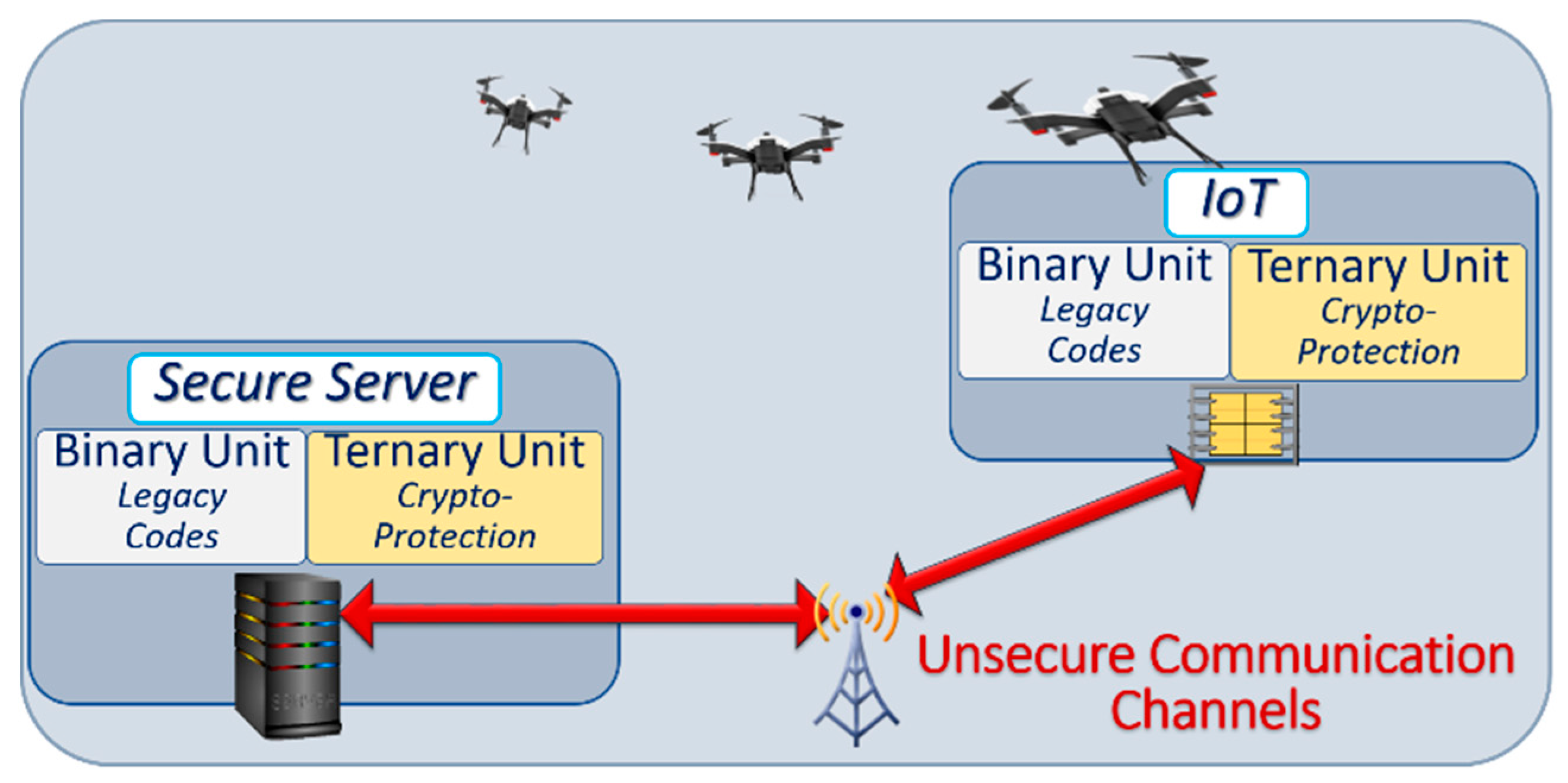
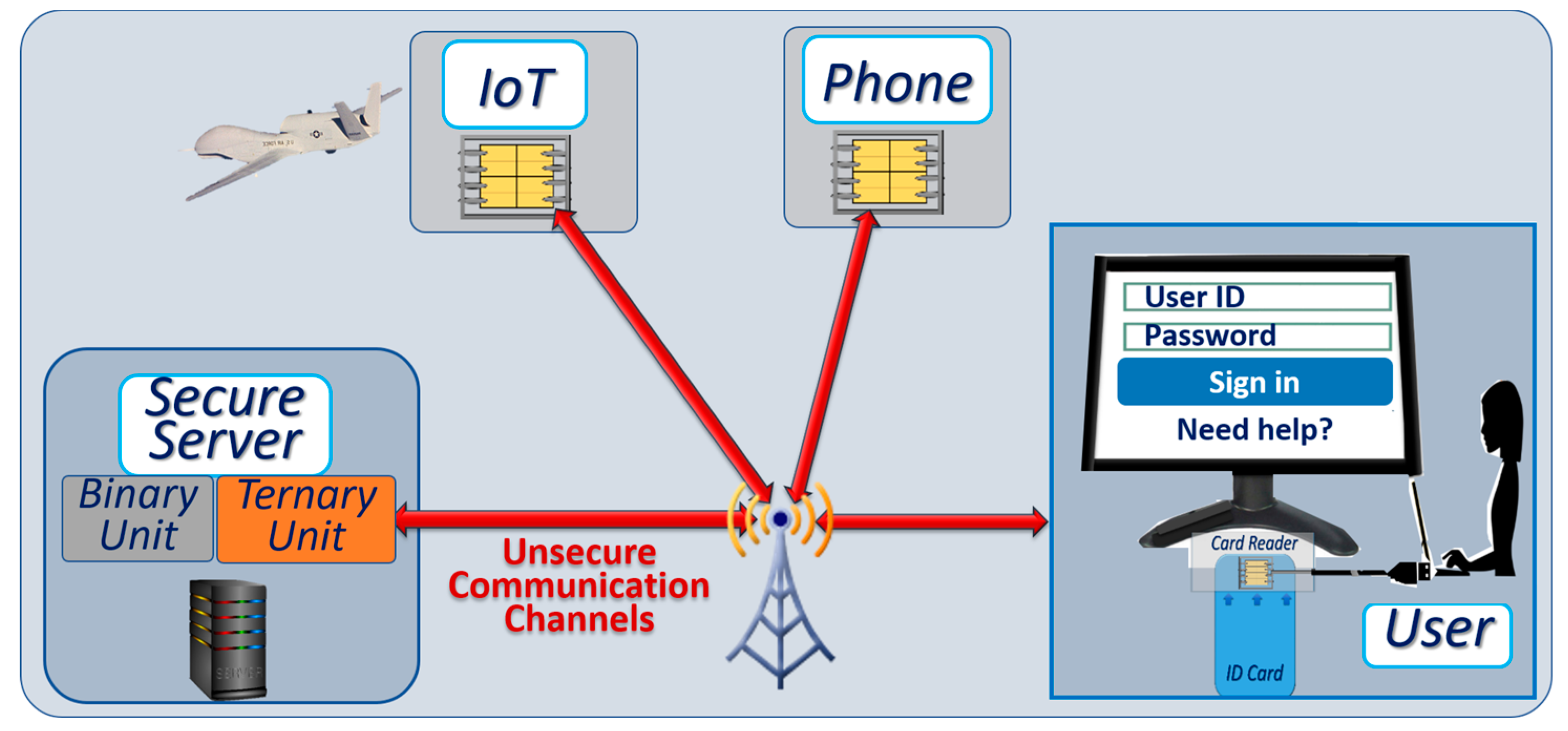
In Section 2 we outlined the objective of developing an architecture that takes advantage of ternary computation to mitigate attacks against networks of connected devices, without prohibitive impact on costs and power consumption. As illustrated in Figure 6, we assume that the communication channels between the secure server and the client devices are not secure.
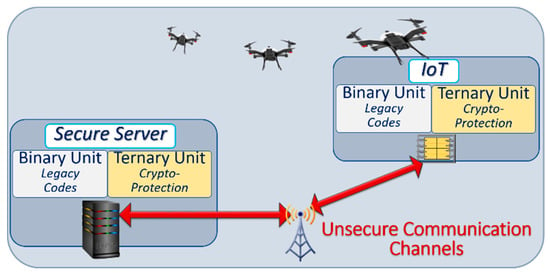
Figure 6.
Generic architecture showing a server and connected autonomous vehicles. Ternary computing units are inserted in each device for ternary cryptographic protection.
The architecture we propose has the following properties designed to integrate with legacy systems while incorporating a fundamentally different system architecture:
- ○
- Communication busses and peripherals are used such that ternary systems may integrate with binary systems.
- ○
- All communicating parties are equipped with low cost secure microcontrollers with at least one ternary computing unit, one binary computing unit, and secure embedded memories.
- ○
- Cryptographic protocols are based on native ternary logic for access control, including dynamically changing sets of passwords for access control with public–private key exchanges, and dynamically changing sets of ternary instructions that implement native ternary functions;
- ○
- Secure ternary memory to store cryptographic tables;
Binary legacy codes are executed on the binary computing units to maximize performance.
4.1. Heterogeneous Secure Microcontrollers
The international standard ISO7816 specifies the architecture of secure microcontrollers, also called secure elements [41], that are often used to protect smartcards, and IoT peripherals. These devices include a Reduced Instruction Set Computer (RISC) processor; secure, embedded, non-volatile RAM; SRAM; and a crypto-processor. The secure elements interact with the interface circuitry through serial ports, have internal clock generators, and secure operating systems such as Multos, Myfare, or Javacard. Certification by financial institutions requires that the microcontrollers have a full range of defensive technologies such as anti- Differental Power Analysis (DPA) measures, active filters above the chip to detect physical attacks, and a hardware implementation of some commonly used cryptographic algorithms such as AES, RSA, Standard Hash Algorithm SHA, and ECC [42,43,44,45,46].
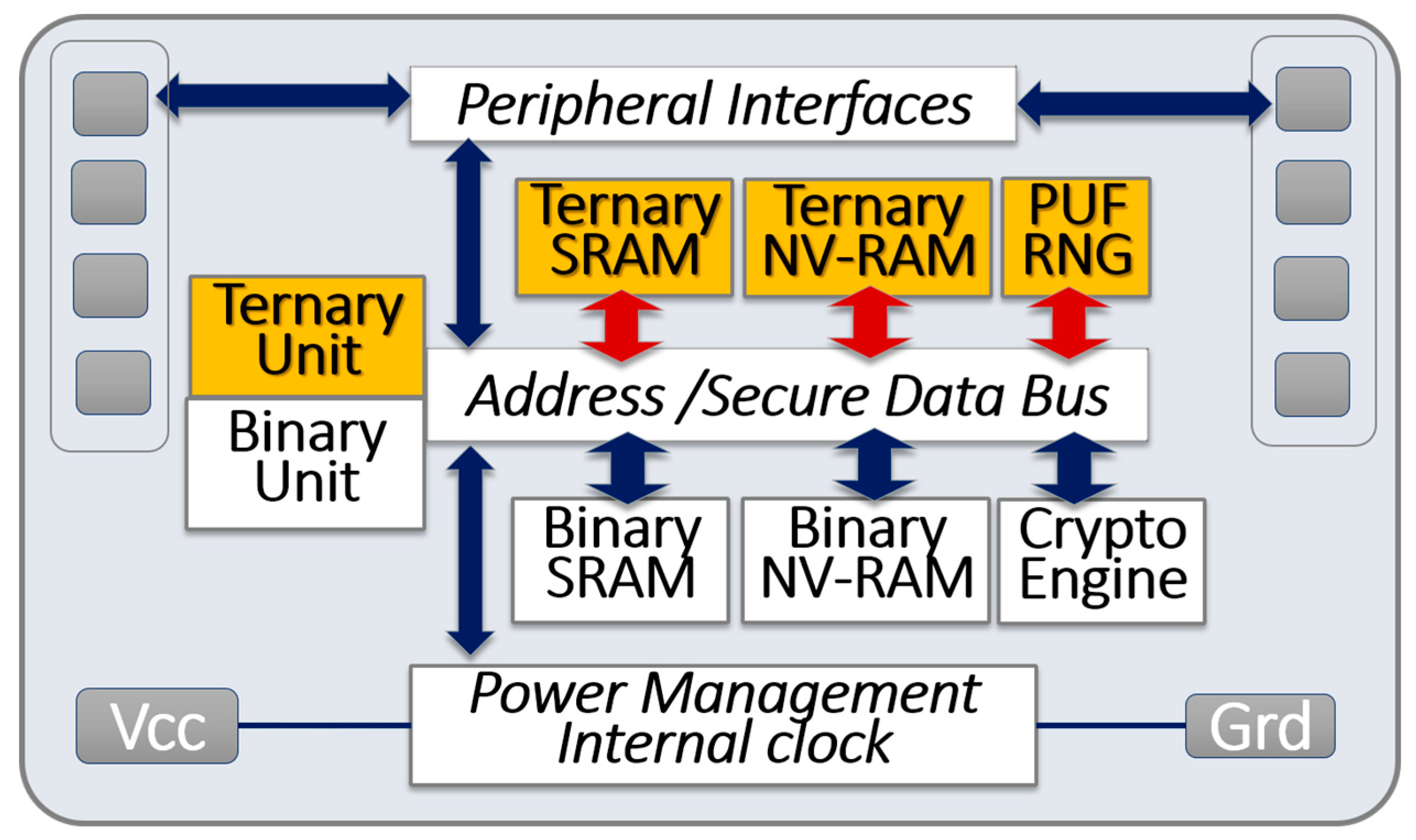
The suggested architecture is shown in Figure 7. The ternary unit, ternary RAM, PUF, and number generators (colored boxes in Figure 7) are added to the legacy architecture of mainstream microcontrollers (white boxes in Figure 7). Flikkema et al. recently introduced a similar multiple functional-unit concept that adapts processor architectures to IoT edge devices [47]. In such a heterogeneous architecture, an instruction/operand tuple router can direct operands to the appropriate functional unit (e.g., binary or ternary) for execution. Secure microcontrollers may be produced in high volume and available at low cost. As discussed in Section 3.4, the manufacturing processes of advanced microprocessors can offer multiple threshold voltages to design ternary logic gates. The size of the embedded memory has been a leading cost factor for microcontrollers, so the relative higher bit density of ternary memories could be advantageous.
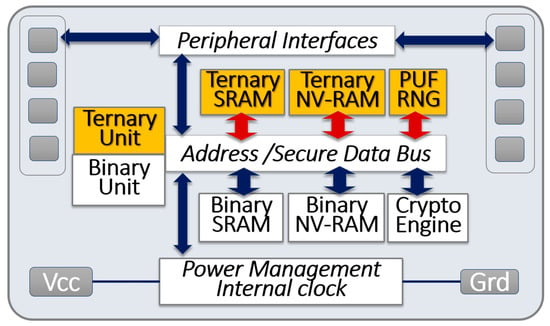
Figure 7.
Block diagram of a secure microcontroller with heterogeneous computing units, ternary memory blocks, and physically unclonable functions.
4.2. Cryptography with Ternary Tables
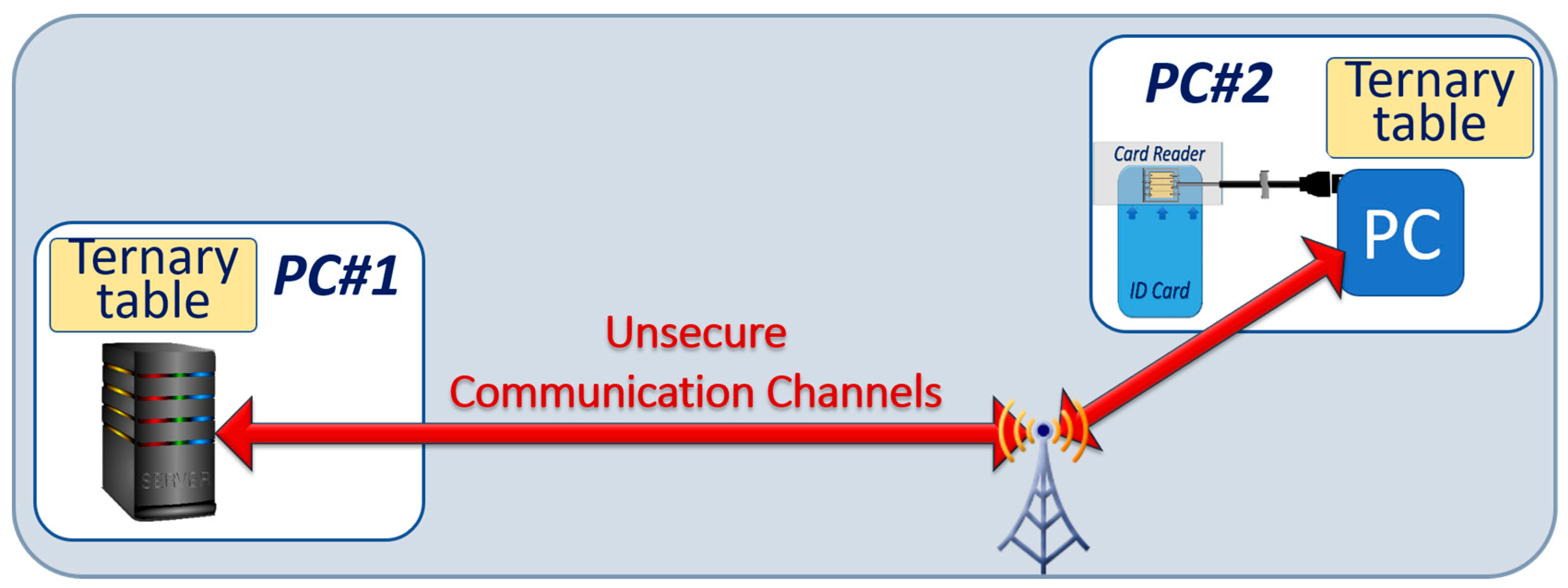
We have developed a public key distribution (PKD) protocol based on secure microprocessors integrated into an Identity ID card with ternary cryptographic tables. The architecture for this system is illustrated in Figure 8. To accelerate the development of this protocol, we used commercially available secure microcontrollers. Ternary logic was implemented by representing the ternary value “−” by the binary pair (01), the ternary value “0” by the binary pair (00), and the ternary value “+” by the binary pair (10). We selected smartcards fabricated by Infineon containing a 16-bit RISC processor (ARM), 80 KB non-volatile memory, and a crypto-processor having the capability to execute major cryptographic algorithms such as RSA, ECC, AES, and SHA [42,43,44,45,46]. We coded the protocol in the smartcard with Javacard operating system. Together with a Window 10 PC, two types of card readers were selected: contactless readers with Near Field Communication (NFC) protocol, and multifactor readers with an integrated PIN code reader.
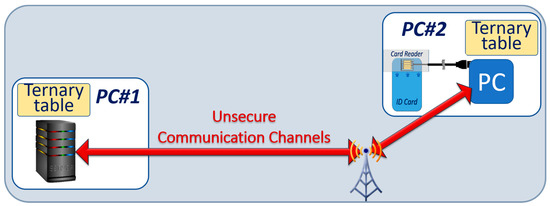
Figure 8.
Block diagram of the experimental set up to study the public key distribution with ternary tables. The tables are stored in the server, and in the smartcard.
Initial step: As part of this PKD protocol implementation, crypto-tables containing 256 × 256 randomly selected trits are downloaded to the smartcards, one table per client device, in a secure environment. For this purpose, we used commercially available random generators. The number of possible configurations for such tables is a staggering 365536, with an entropy of 103,868. This initial step is similar to the “personalization” step of commercial smartcards in which private keys are secretly downloaded on each card for RSA and ECC.
The public keys exchanged between the server, and the secure microcontroller contain 512 bits that are randomly generated each time an authentication cycle is needed. To initiate the process that generates private keys, the random numbers of the public keys are “exclusive or” (XORed) with a password to feed a Standard Hash Algorithm SHA-512 (or SHA-2) hash function. The resulting message digest of 512 bits is segmented into 32 blocks of 16 bits. The total number of possible message digests is 2256, an entropy of 256. To increase this entropy, the size of the random number can be increased to 512.
Generation of the private keys: Each of the 32 blocks points to their corresponding address in the table in order to read (in the table) 16 trits each, thereby generating a total of 16 × 32 = 512 trits. The number of possible ways to pick 32 addresses in 65,536 possible locations is (216)32 = 2512, an entropy of 512. From these 512 trits, public keys of 128 bits (or 256 bits) are generated with a masking process that eliminate the “0” states of the ternary streams. This process is based on the use of a secret mask of 512 bits, which encapsulate the knowledge of position of the “0s” in the table.
The server and the client devices, because they have access to identical tables, can independently generate the same private keys from the same public keys, and the same password. We encrypted authentication messages with AES-128 (AES 256 is not yet available on low-end smartcards) using these shared public keys.
Importance of the secret mask: The protocol that we developed is such that a third party cannot generate working private keys without knowing the secret mask, and the position of the cells with ternary “0” values; only the “−” and “+” states of the table are used to generate the binary private keys. Statistically, a stream of 512 trits contains about 171 “0”s. The probability that random masks of 512 bits leave 128 trits (or 256 trits) without any “0” states is close to 2−512 as the vast majority of the 2−512 possible configurations will miss at least one “0”. The secret masks are XORed with the message digests previously generated by the hash function. The resulting XORed messages are exchanged between communicating parties as part of the public keys.
Upon reception, the client devices use the first part of the public keys (the random numbers), and the passwords to retrieve the hash message digest, then XOR the second part of the public keys to retrieve the masks. Additional random “0s” are inserted as part of the mask to enhance the protection; the masks will be different in the event of a repeat.
While both public and private keys are binary data streams, the generation of the private keys from the public keys is based on the processing of the trits stored in the securely stored cryptographic tables. In this protocol at least two new random numbers are generated at each exchange, the public–private key pairs are used only once, and the precise knowledge of the position of the ternary state “0” in the table is needed. The typical size of the public keys is 1024 bit.
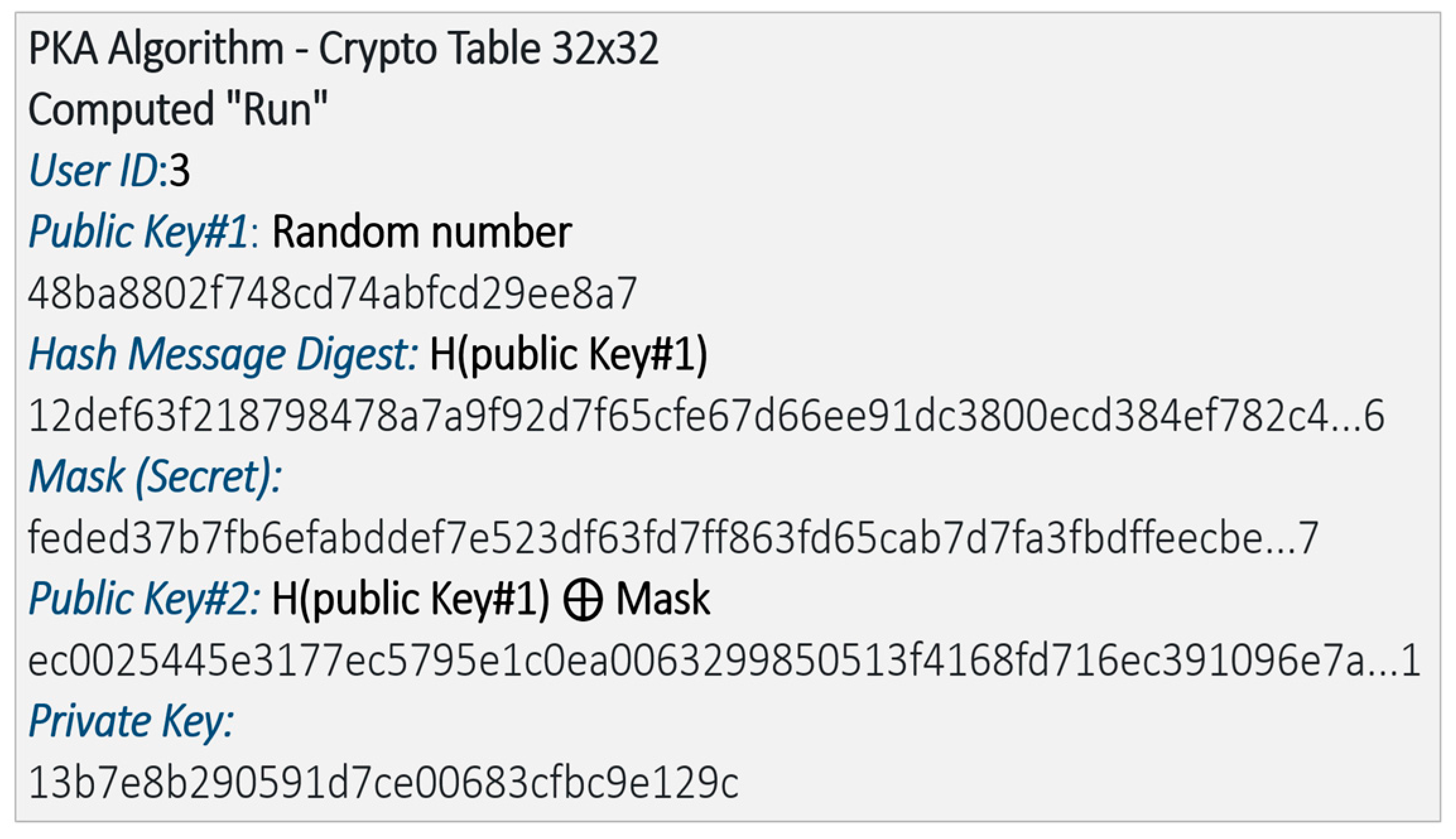
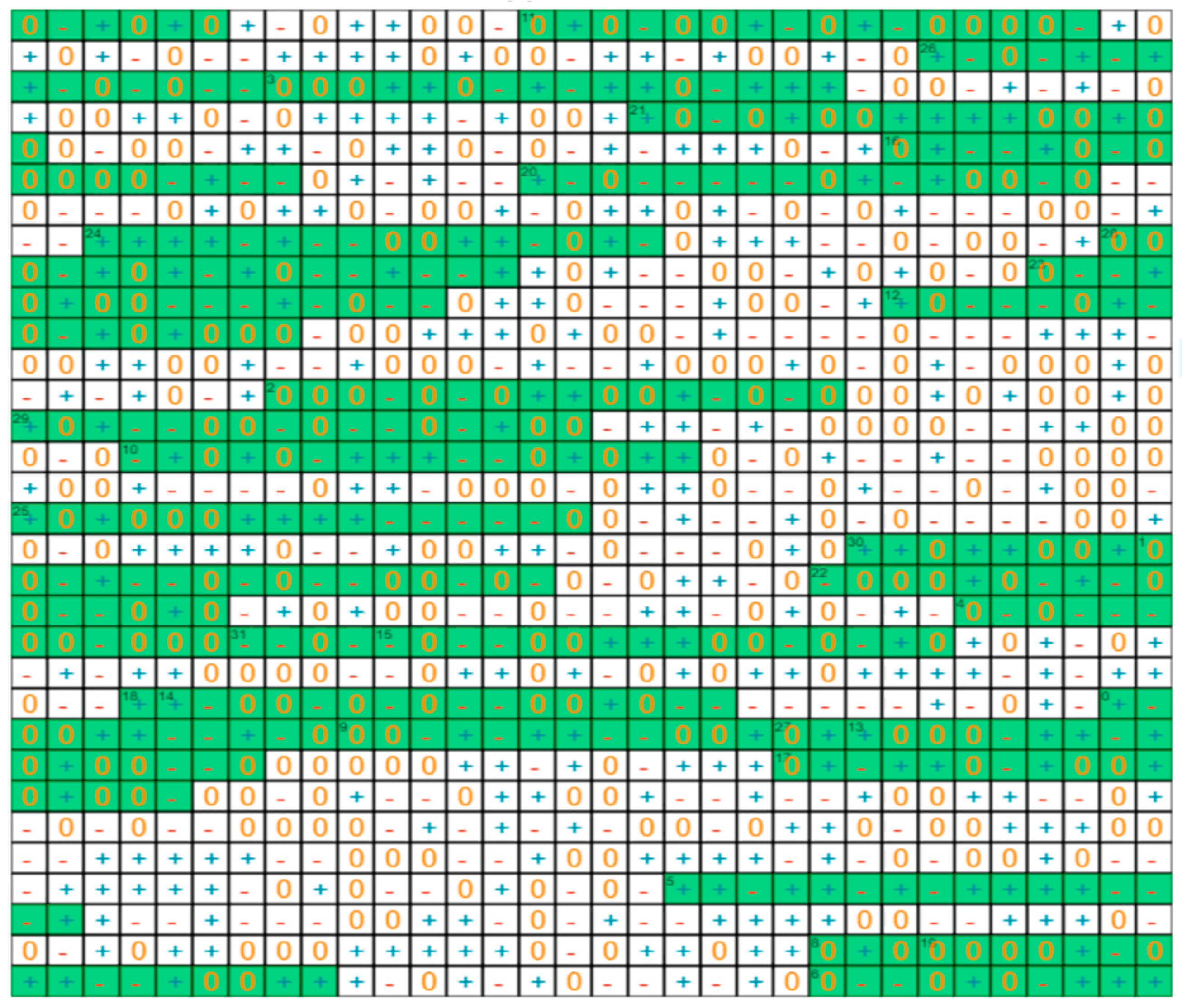
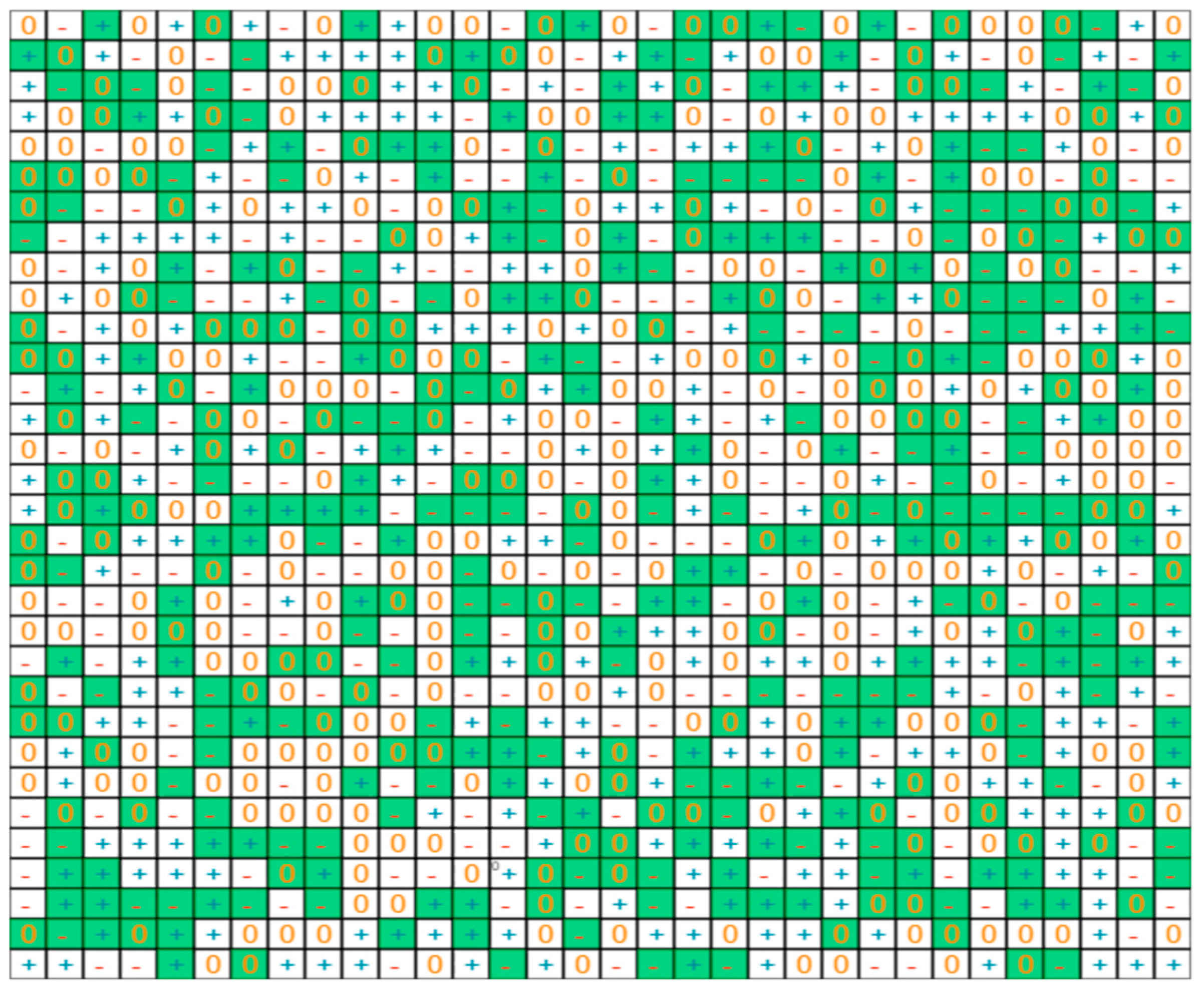
Implementation with smartcards: To demonstrate the protocol, we developed a small version with 32x32 tables of random trits. The algorithm of the public key exchange is summarized Figure 9. The cryptographic table is shown in Figure 10, and the table of the trits selected from it to generate the private key is shown in Figure 11.
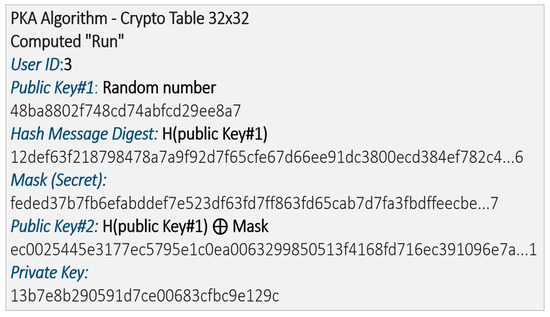
Figure 9.
Picture of the algorithm of the key distribution showing the public key, message digest, mask, and private key in hexadecimal.
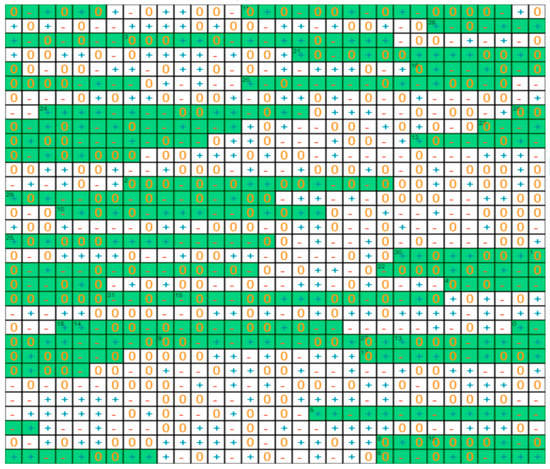
Figure 10.
Picture of the cryptographic table. Addresses 1 to 32 are selected from the hash digest message. The 16 trits extracted at each address (in green), are used to generate the private key.

Figure 11.
Picture of the addresses are ranked in order from left to right (1 to 32). The 16 trits extracted at each address are shown top to bottom. The trits in green generate the private key.
- ○
- The first portion of the public key is a stream of 512 bits, hexadecimal in the table.
- ○
- A hash message digest is generated from this key with SHA-2; 32 different addresses are generated from the message digest, and 16 trits are extracted at each address, in green in Figure 10.
- ○
- The mask is created with the knowledge of the location of the cells storing ternary state “0s” [48].
- ○
- The private key is generated by selecting only the “−” and “+”, as shown in green in Figure 11, and converting them to binary 0s and 1s.
- ○
- The public key is the combination of the initial random number and the mask XORed with the message digest.
- ○
- The client device with the same cryptographic table, and public key is in the same state and will generate the same private key.
The version of this algorithm with 256 × 256 tables and 256-bit private keys was also implemented.
Analysis and benchmark. We estimate that the time needed to exchange the key from the PC to the smartcard, to encrypt an authentication message with AES-128 on the smartcard, and to decrypt it on the PC is a fraction of a second. We do not have the capability in our lab to compare this protocol with other public key protocols when we use a smartcard. Thus, in order to benchmark the method, we implemented a scaled-up version of this protocol using two personal computers. The size of the private key was increased to 256 bits. We encrypted 3 MB files on one PC with AES-256, and decrypted them on the other PC. Back to back comparisons were made with both RSA (3072 bit), and ECC GF2n (256-bit keys).We measured and simulated that in our implementation less than 1000 clock cycles are needed for the public–private key generation and exchange. This can be contrasted with 500,000 clock cycles needed for RSA and 10,000 clock cycles for ECC GF2n. With large enough cryptographic tables, the number of independent combinations of public and private key is 21024. The protocol as described is based on AES 256 and SH-2, which are considered robust and quantum computer resistant. These two cryptographic methods can be upgraded with polymorphic protocols and SHA-3. The quality of the random number generator is pivotal to the quality of this scheme. In addition to using commercially available Random Number Generator (RNG), we are developing our own ternary Ternary Random Number Generator (TRNG) with ternary PUFs, see below Section 4.3. One limitation of this protocol, compared to RSA and ECC, is the inability to handle peer-to-peer communication without going through a server. This has not been a problem for the applications that we are targeting.
In summary, this key exchange protocol has the following attributes:
- ○
- Public keys can be changed at every communication to become one-time use only;
- ○
- Hash functions can be combined with multi-factor authentication to protect the public keys;
- ○
- Masking operations prevent third parties from randomly generating private keys;
- ○
- Power consumption and computing times are low and compatible with low cost IoT networks.
Increased randomness: In the protocol described above, as shown in Figure 10, 16 consecutive trits are extracted from the table at each address. To increase randomness and entropy, we enhanced the protocol by implementing a scheme where the 16 bits extracted from the cryptographic table at each of the 32 addresses are not necessarily consecutive. The results are illustrated in Figure 12. The 512 trits selected, in green, are now scattered randomly across the table. In this scheme, we also use parameters that vary at each address; therefore the method to extract 16 bits also varies at each address, and will vary again if an address is selected twice by the message digest. This new scheme offers additional protection, in particular during side channel analysis. The overall timing of the entire key exchange protocol was not noticeably degraded. We are currently developing and various types of enhanced schemes, evaluating the tradeoff between entropy and computational burden.
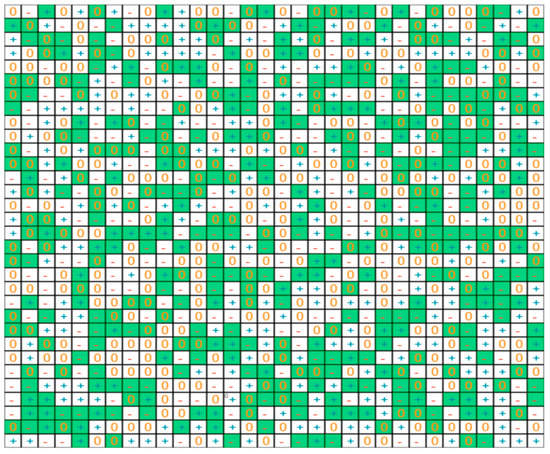
Figure 12.
Picture of additional randomness to extract 512 trits from the cryptographic tables. The cells selected to generate the private keys, in green in this table, are scattered randomly.
4.3. Ternary Physically Unclonable Functions
The scheme described in the previous section is based on the exchange between communicating parties holding cryptographic tables filled with random numbers. These tables can be replaced by memory arrays able to generate challenge–response pairs of physically unclonable functions (PUFs) [22,23,24]. PUFs can be considered the fingerprints of microelectronic components. In this scheme, the PUF-generating memory arrays are embedded in the secure element (Figure 3). The challenges are the initial measurements of the PUF [49,50,51,52], which are downloaded and stored in the cryptographic tables of the secure server. During the public key exchange, the memory-based PUFs of the IoT devices are queried to generate cryptographic tables filled with the responses, which are generated by re-measuring the physical elements of the memory arrays. In the case of perfect PUFs, the challenge–response pairs are identical, and the key exchange with PUF arrays is the same as described in Section 4.2. As PUF responses are not perfect, error correcting methods are needed for robust implementation [53,54]. These error correcting methods are based on the transmission of additional data streams between the communicating parties that can be called helpers. An example of such a helper is a sum-check that can be included as part of the public key.
The use of ternary states is extremely valuable in this scheme because ternary states can be used to classify the fuzzy cells of the PUF array. Only the cells that can be strongly classified as “−” or “+” are used for challenge-response generation [22], which drastically reduces the size of the helpers. From a security standpoint, PUFs are very powerful tools to prevent breaches in access control that are described in Section 2. Strong PUFs, when lost to a malicious agent, do not reveal the cryptographic tables.
4.4. Development of Ternary Computing Units
FPGAs could be constructed to support multiple threshold voltages and hardware description languages could represent this as a primitive feature of values. In practice, FPGAs and their supporting tools do not currently support ternary hardware primitives. While this makes the development of native ternary computing units challenging with current tools, we can implement ternary logic at a higher level of abstraction by using the mapping described in Section 4.2 to map ternary values to two-bit binary values. Using this functional abstraction, we have implemented a set of logical and arithmetic operations (see Section 3.2 and Section 3.3) that operate on trits and trytes using the balanced ternary representation. These algorithms have been implemented in SystemVerilog and provide the functional units for a de novo microarchitecture implementation of a ternary processor. The processor we have developed is modeled after the well-known MSP430, a 16-bit RISC processor developed by Texas Instruments. Our implementation has 31 instructions, 7 addressing modes, and uses a Harvard architecture. The implementation consists of roughly 1000 lines of System Verilog code and has been synthesized and tested on FPGAs. Supporting this hardware implementation, we also developed a ternary software tool chain. Our ternary assembler has a modular design that can target multiple architectures, has a novel macro system and provides a superset of the MSP430 assembly language (modelling some uncommonly used functionality). The assembler supports an extended instruction set that can use ternary instructions, addresses, and immediate values. Data may also be encoded using balanced ternary encoding. A series of test programs have been built to test the assembler and the FPGA implementation. These test functions include sorts such as bubble sort and simple hashing functions designed to test registers, stacks, and memory.
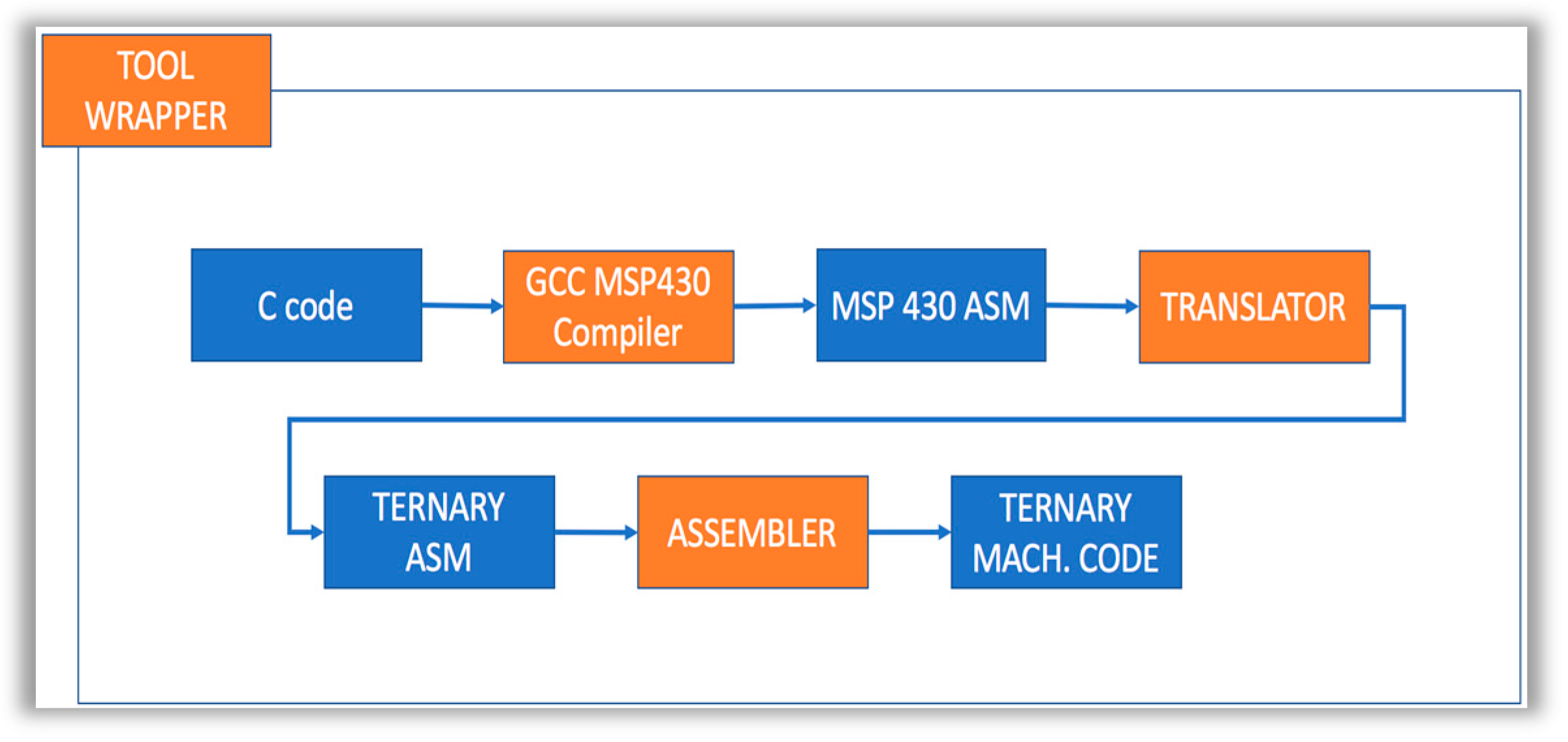
Because our ternary processor derives its instruction set from the MSP430, we also experimented with using the Generic non unix Compiler Collection (GCC) MSP430 (MSP 340 is a product of Texas Instrument Inc.) compiler to generate assembly code from the C code, then using our assembler to generate ternary machine code. A simplified non-secure development workflow is illustrated in Figure 13.
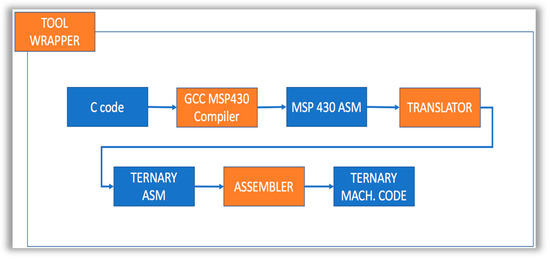
Figure 13.
Simplified pipeline for transforming C code to ternary machine code.
We tested our ternary C toolchain against a number of programs and verified that this approach works well for function calls, basic data structures, inline assembly and most of the C language. We successfully implemented quicksort and several other algorithms in C and ran those programs on our FPGA ternary processor implementation. Where this approach falls short is in cases where GCC (and in some cases the C language standard) makes assumptions about the machine representation of numbers (e.g., 2s complement) and optimization and implementation details that depend on those machine representation assumptions.
4.5. System Implementation of Ternary Computing
Specialized algorithms, such as those for image processing and deep learning, are increasingly reliant on the improvements in performance of specialized hardware (e.g., Generic Processor Unit (GPU) and FPGAs) over general-purpose processor architectures. This is driving a need for heterogeneous hardware platforms that utilize multiple, highly-specialized computer architectures. In this new paradigm, hardware advances should no longer be evaluated on their general-purpose advantages, but rather on their utility for addressing specific computing problems and their interoperability in a diverse computing ecosystem. The use of multiple functional units handling a dual binary/ternary instruction set is a promising approach to creating computing architectures that leverage the increased design freedom resulting from the addition of ternary hardware and software. These heterogeneous computing architectures are envisioned to be flexible enough to dynamically change instruction sets, decreasing a system’s susceptibility relative to conventional binary architectures. The future vision of a multi-platform ecosystem would include heterogeneous binary/ternary functional units in secure microcontrollers, crypto-systems, and full computing architectures, as illustrated in Figure 14. In each of these instantiations, the added ternary degree of freedom can be exploited for maximum security benefits while being balanced against resource constraints.
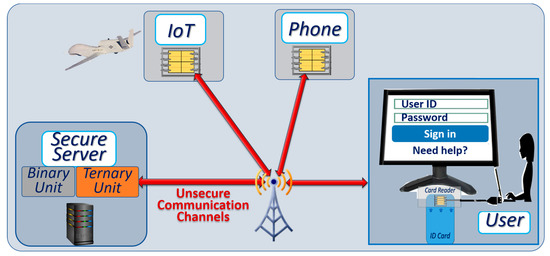
Figure 14.
Vision of computing eco system employing heterogeneous binary/ternary functional units.
5. Conclusions and Future Work
Based on this work, we can begin to answer the question posed earlier: “Can the inherent complexity and the implementation costs associated with ternary computing be mitigated such that this technology can be used as a compelling fortification against malicious entities?” The mainstream technologies used to manufacture embedded microcontrollers for IoT networks can offer, at little cost, CMOS devices with multiple thresholds to design heterogeneous binary/ternary units. We have also demonstrated important elements of the proposed architecture and expect the total cost associated with the addition of secure ternary computing primitives to secure elements will be low. The ternary cryptographic environment presented in this paper can offer the following protections:
- ○
- Malware, viruses and worms will not affect the ternary unit unless the malware is converted to native ternary logic. Continuously changing sets of ternary instructions on each machine, based on public key exchanges, are expected to make conversions between binary and ternary non-trivial;
- ○
- Breaches in access control will be reduced with the ternary PKD proposed here with the one-time public/private key pair minimizing the impact of a potential loss of the keys. The use of multi-factor authentication with subject–object pairing and passwords is suggested;
- ○
- Eavesdropping problems will be greatly reduced because all aspects of the ternary architecture can change constantly, such as the keys, the set of ternary instructions, and the authentication messages.
Man-in-the-middle attacks will be minimized by the proposed protocol’s requiring the knowledge of the position of the ternary states in the crypto-tables. The risk of DDoS is minimized due to lower contamination of IoT networks using the suggested ternary PKD. The effort needed to fully deploy an architecture based on ternary cryptography and heterogeneous computing units is not to be underestimated; however, our results strongly suggest the promise of such an approach. Next steps towards a full implementation of this vision include the development of an FPGA-based solution for a multiple functional-unit processor, followed by an Application Specific Integrated Circuit (ASIC) design derived from existing secure microcontroller designs. From a software perspective, the public key exchange described here needs to be coded in native ternary logic with access control and an encryption protocol. Our teams are currently engaged in exploring these directions as active continuing work.
Acknowledgments
The authors thank the students and faculty from Northern Arizona University, in particular Duane Booher, Bilal Habib, and Raul Chipana. We also thank the professionals of the Air Force Research Lab, Rome, NY, and Alion Science and Technology, who supported this effort.
Author Contributions
The five authors actively contributed to the research work that is presented in this paper. Bertrand Cambou developed the overall ternary cryptography schemes, and coordinated the writing of the paper. Christopher Philabaum was responsible to design the protocol presented in Section 4.3, and develop the prototype based on Javacards. Both Paul G. Flikkema, and James Palmer were jointly responsible to study and develop the Ternary Computing Units presented in Section 4.4. Donald Telesca is directing the overall project for AFRL, and was responsible to study the system implementation of Ternary Computing presented in Section 4.5.
Conflicts of Interest
The authors declare no conflict of interest.
Disclaimer
(a) The contractor acknowledges the government’s support in the publication of this paper. This material is based upon work funded by the Information Directorate, under AFRL Contract No. FA8075-16-D-0001. (b) Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of AFRL.
References
- Kamara, S.; Fahmy, S.; Schultz, E.; Kerschbaum, F.; Frantzen, M. Analysis of Vulnerabilities in the Internet Firewall. Comput. Secur. 2003, 22, 214–232. [Google Scholar] [CrossRef]
- Liu, A.X.; Gouda, M.G. Diverse Firewall Designs. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 1237–1251. [Google Scholar] [CrossRef]
- Yuan, L.; Chen, H.; Mai, J.; Chua, C.N.; Su, Z.; Mohapatra, P. Fireman: A Tool Kit for Firewall Modelling and Analysis. In Proceedings of the 2006 IEEE Symposium on Security and Privacy, Berkeley/Oakland, CA, USA, 21–24 May 2006. [Google Scholar]
- Kumar, R.; Talwar, I.M. Network Security using Firewall and Cryptographic Authentication. Int. J. Comput. Appl. 2012, 57, 13–19. [Google Scholar] [CrossRef]
- Dua, S.; Du, X. Data Mining and Machine Learning in Cybersecurity; CRC Press of Taylor & Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Buczak, A.; Guven, E. A Survey of Data Mining and Machine Learning Methods for Cybersecurity Intrusion Detection. IEEE Commun. Surv. Tutor. 2016, 18, 1153–1176. [Google Scholar] [CrossRef]
- Borgesltink, R.C.; Beaver, J.M.; Buckner, M.; Morris, T.; Adhikari, U.; Pan, S. Machine Learning for Power Systems Disturbance and Cyberattacks Discrimination. In Proceedings of the 7th International Symposium on Resilient Controls and Systems (ISRCS), Denver, CO, USA, 19–21 August 2014. [Google Scholar]
- Shiva, S.; Roy, S.; Dasgupta, D. Game Theory for Cybersecurity. In Proceedings of the 6th Annual Workshop on Cybersecurity and Information Intelligence Research, Oak Ridge, TN, USA, 21–23 April 2010. [Google Scholar]
- Linda, M.; Vollmer, T.; Wright, J. Fuzzy Logic Based Anomaly Detection for Embedded Network Security Cyber Sensor. In Proceedings of the IEEE Symposium on Computational Intelligence in Cyber Security (CICS), Paris, France, 11–15 April 2011. [Google Scholar]
- Elovici, Y.; Shabtai, A.; Moskovitch, R.; Tahan, G.; Glezer, C. Applying Machine Learning Technique for Detection of Malicious Code in Network Traffic. In Proceedings of the IEEE Symposium on Annual Conference on Artificial Intelligence, Alcala de Henares, Spain, 3–5 October 2007. [Google Scholar]
- Gandrotra, E.; Bansal, D.; Sofat, S. Malware Analysis and Classification—A survey. J. Inf. Secur. 2014, 5, 56–64. [Google Scholar]
- Cambou, B.; Afghah, F. PUF with Multi-states and Machine Learning. In Proceeding of the CryptArchi, La Grande Motte, France, 21–24 June 2016. [Google Scholar]
- Glusker, M.; Hogan, D.M.; Vass, P. The ternary calculating machine of Thomas Fowler. IEEE Ann. Hist. Comput. 2005, 27, 4–22. [Google Scholar] [CrossRef]
- Obiniyi, A.A.; Absalom, E.E.; Adako, K. Arithmetic Logic Design with Color Coded Ternary for Ternary Computing. Int. J. Comput. Appl. 2011, 26, 31–37. [Google Scholar]
- Brousentov, N.P.; Maslov, S.P.; Alvarez, J.R.; Zhogolev, E.A. Development of Ternary Computers at Moscow State University; Russian Virtual Computer Museum: Moscow, Russian, 2002. [Google Scholar]
- Dijkstra, E.W. Notes on Structured Programming; EWD 249 Technical University: Eindhoven, The Netherlands, 1969. [Google Scholar]
- Frieder, G. Ternary Computers, part 1: Motivation for ternary computers. In Proceedings of the Micro 5 Conference Record of the 5th Annual Workshop on Microprogramming, Urbana, IL, USA, 25–26 September 1972. [Google Scholar]
- Zadeh, L.A. Fuzzy algorithms. Inf. Control 1968, 12, 94–102. [Google Scholar] [CrossRef]
- Shor, P. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. J. Soc. Ind. Appl. Math. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Caraiman, S.; Manta, V. Image Representation and Processing Using Ternary Quantum Computing. In ICANNGA 2013; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7824. [Google Scholar]
- Cambou, B. Multi-Factor Authentication Using a Combined Secure Pattern. U.S. Patent 9,514,292, 16 July 2015. [Google Scholar]
- Cambou, B.; Orlowski, M. Design of PUFs with ReRAM and ternary states. In Proceedings of the 11th Annual Cyber and Information Security Research Conference, Oak Ridge, TN, USA, 5–7 April 2016. [Google Scholar]
- Cambou, B. PUF Generating Systems and Related Methods. U.S. Patent Disclosure No. 62/204912, 13 August 2015. [Google Scholar]
- Cambou, B. A XOR data compiler combined with PUF for TRNG. In Proceedings of the SAI/IEEE Computing Conference, London, UK, 18–20 July 2017. [Google Scholar]
- Gundersen, H. Aspect of Balanced Ternary Arithmetic Implemented Using CMOS Recharged Semi-Floating Gate Device. Ph.D. Thesis, Oslo University, Oslo, Norway, 2008. [Google Scholar]
- Profeanu, I. A ternary Arithmetic and Logic. In Proceedings of the World Congress on Engineering, London, UK, 30 June–2 July 2010. [Google Scholar]
- Ahmad, S.; Alam, M. Balanced Ternary Logic For improving Computing. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 5157. [Google Scholar]
- Wu, X.W. CMOS Ternary Logic Circuits. IEE Proc. 1990, 137, 21–27. [Google Scholar] [CrossRef]
- Srivastava, A.; Venkatapathy, K. Design and Implementation of a Low Power Ternary Full Adder. VLSI Des. 1996, 4, 75–81. [Google Scholar] [CrossRef][Green Version]
- Balla, P.C.; Antoniou, A. Low Power Dissipation MOS Ternary Logic Family. IEEE J. Solid State Circ. 1984, 19, 739–749. [Google Scholar] [CrossRef]
- Miller, D.M.; Thornton, M.A. Multiple Valued Logic: Concepts and Representations; Synthesis Lectures on Digital Circuits and Systems; Morgan & Claypool Publishers: London, UK, 2007. [Google Scholar]
- Wanjari, N.P.; Hajare, S.P. VLSI Design and Implementation of Ternary Logic Gates and Ternary SRAM Cell. Int. J. Electron. Comput. 2013, 2, 610–618. [Google Scholar]
- Nagaraju, P.; Vishnuvardhan, N. Ternary Logic Gates and Ternary SRAM Implementation in VLSI. Int. J. Sci. Res. 2014, 3, 1920–1924. [Google Scholar]
- Bennett, S.; Sullivan, J. The Characterization of TLC NAND Flash Memory, Leading to a Definable Endurance/Retention Trade-Off. WASET Int. J. Ind. Manuf. Eng. 2016, 10, 716–723. [Google Scholar]
- Zhirnov, V.; Mikolajick, T. Chapter 26: Flash Memories; Nanoelectronics and Information Technology; Waser, R., Ed.; Wiley: Berlin, Germany, 2012. [Google Scholar]
- Schroder, U.; Schroder, H.; Kingon, A.I.; Bottger, U. Capacitor-Based Random-Access Memories; Nanoelectronics and Information Technology; Waser, R., Ed.; Wiley-Vch: Berlin, Germany, 2012; pp. 635–654. [Google Scholar]
- Chang, K.K.; Yağlıkçı, A.G.; Ghose, S.; Agrawal, A.; Chatterjee, N.; Kashyap, A.; Lee, D.; O’Connor, M.; Hassan, H.; Mutlu, O. Understanding Reduced-Voltage Operation in Modern DRAM Chips: Characterization, Analysis, and Mechanisms; Cornell Technical Library: Ithaca, NY, USA, 2017. [Google Scholar]
- Lin, S.; Kim, Y.-B.; Lombardi, F. CNTFET-Based Design of Ternary Logic Gates and Arithmetic Circuits. IEEE Trans. Nanotechnol. 2011, 10, 217–225. [Google Scholar] [CrossRef]
- Cambou, B. Multilevel Magnetic Element. U.S. Patent 8,630,112, 14 January 2014. [Google Scholar]
- Khalid, M.; Singh, J. Memristor based unbalanced ternary logic gates. Anal. Integr. Circ. Signal Proc. 2016, 87, 399–406. [Google Scholar] [CrossRef]
- Cambou, B. Enhancing Secure Elements—Technology and Architecture. In Foundations of Hardware IP Protection; Springer Int. Publishing: New York, NY, USA, 2017. [Google Scholar]
- Paar, C.; Pezl, J. Understanding Cryptography—A Text Book for Students and Practitioners; Springer: New York, NY, USA, 2011. [Google Scholar]
- Mel, H.X.; Baker, D. Cryptography Decrypted; Addison-Wesley: New York, NY, USA, 2001. [Google Scholar]
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Rivest, R.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Pfleeger, C.P.; Pfleeger, S.L.; Margulies, J. Security in Computing, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2015. [Google Scholar]
- Flikkema, P.G.; Cambou, B. Adapting Processor Architectures for the Periphery of the IoT Nervous System. In Proceedings of the IEEE 3rd World Forum on Internet of Things (WF-IoT), Reston, VA, USA, 12–14 December 2016. [Google Scholar]
- Cambou, B.; Chipana, R.; Habib, B. Securing PUFs with Additional Random Ternary States; NAU Disclosure D2017-19; Northern Arizona University: Flagstaff, AZ, USA, 2016. [Google Scholar]
- Jin, Y. Introduction to hardware security. Electronics 2015, 4, 763–784. [Google Scholar] [CrossRef]
- Prabhu, P.; Akel, A.; Grupp, L.M.; Yu, W.-K.S.; Suh, G.E.; Kan, E.; Swanson, S. Extracting Device Fingerprints from Flash Memory by Exploiting Physical Variations. In Proceedings of the 4th International Conference on Trust and Trustworthy Computing, Pittsburgh, PA, USA, 22–24 June 2011. [Google Scholar]
- Holcomb, D.E.; Burleson, W.P.; Fu, K. Power up SRAM state as an identifying Fingerprint and Source of True Random Numbers. IEEE Trans. Comput. 2009, 58, 1198–1210. [Google Scholar] [CrossRef]
- Chen, A. Comprehensive Assessment of RRAM-based PUF for Hardware Security Applications. In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015. [Google Scholar]
- Beckmann, N.; Potkonjak, M. Hardware-Based Public-Key Cryptography with Public Physically Unclonable Functions. In Information Hiding; Springer: New York, NY, USA, 2009; pp. 206–220. [Google Scholar]
- Kang, H.; Hori, Y.; Katashita, T.; Hagiwara, M.; Iwamura, K. Cryptographic Key Generation from PUF Data Using Efficient Fuzzy Extractors. In Proceedings of the 2014 16th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, South Korea, 16–19 February 2014; pp. 23–26. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).