A Novel Ultra-Compact FPGA PUF: The DD-PUF
Abstract
:1. Introduction
2. Related Works
2.1. Butterfly PUF
2.2. Arbiter PUF
2.3. Pico-PUF
2.4. Ring-Oscillator PUF
2.5. Transient Effect Ring Oscillator PUF
3. Background
3.1. Randomness
- Mono-bit frequency test: aims to characterize the 1/0 bias of the response to a given challenge;
- Block frequency test: along with mono-bit frequency test, it checks the group bias of the PUF’s response;
- Cumulative sum test: it aims to study the number of 1s in the progressive partial sums of input sequence (the response in this context);
- Run test: it estimates the sequence of consecutive 1s and 0s in sub-string sets, evaluating if the number of oscillation between homogeneous strings is too fast or too slow;
- Longest run test: its purpose is to find the longest sequence of ones in n-bit strings subdivided in N sub-strings of M bits;
- Approximate entropy test: it scans M-bit sequences of a given response in order to find identical adjacent ones.
3.2. Uniqueness
3.3. Reliability
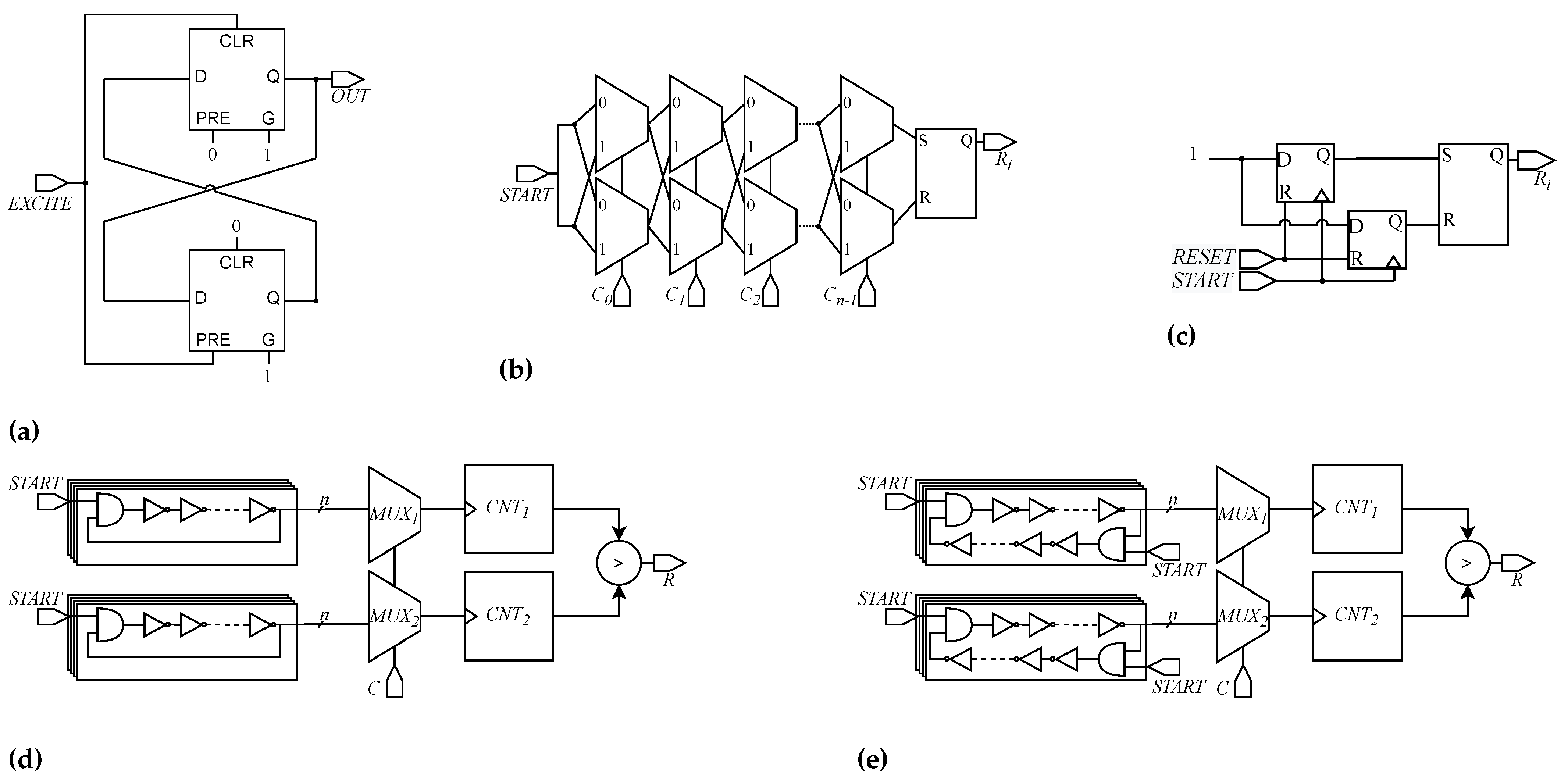
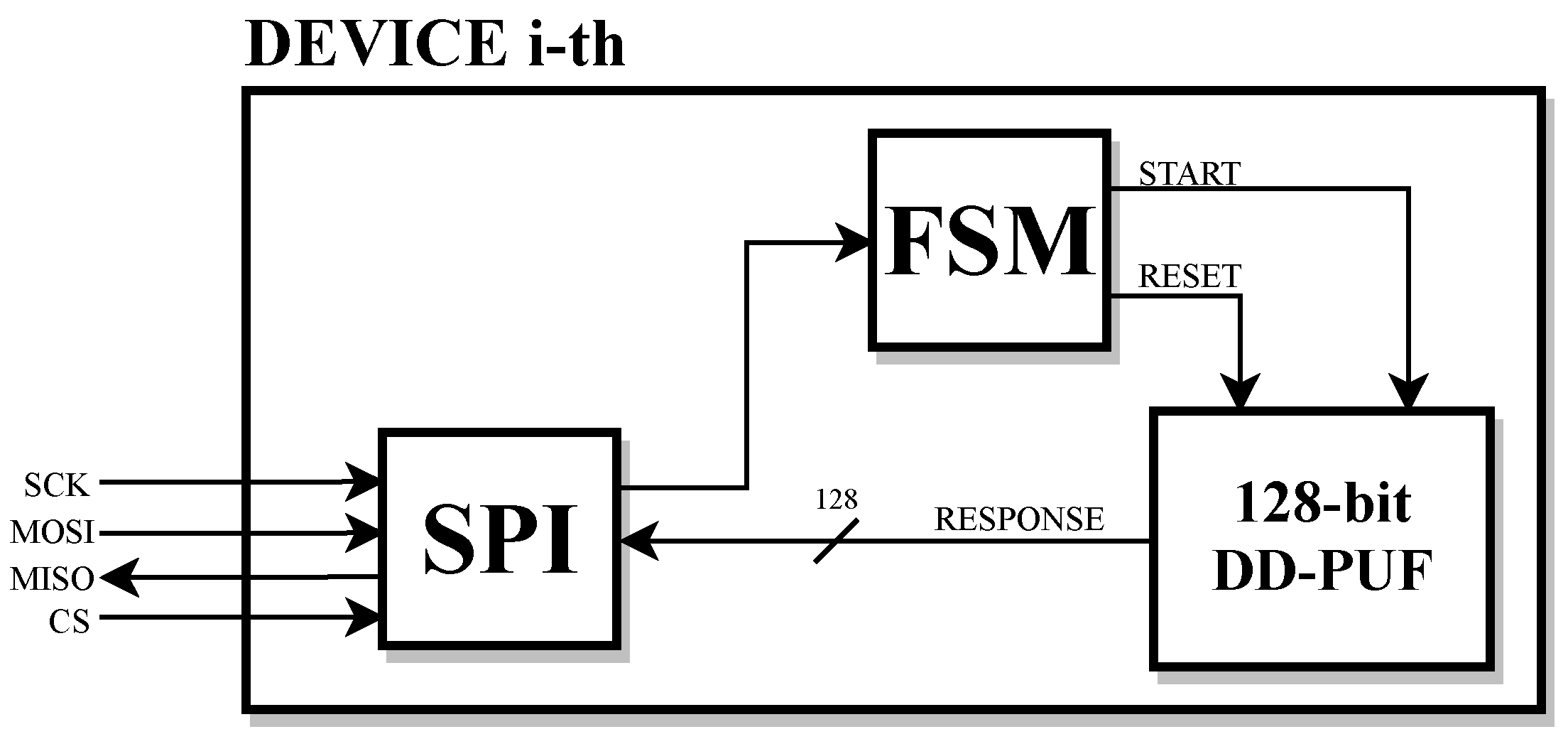
4. DD-PUF Architecture and Design
4.1. Architecture
- Initialization phase;
- Evaluation phase;
- Output phase.
4.2. FPGA Implementation
4.3. Discussion
5. Experimental Results
5.1. Setup
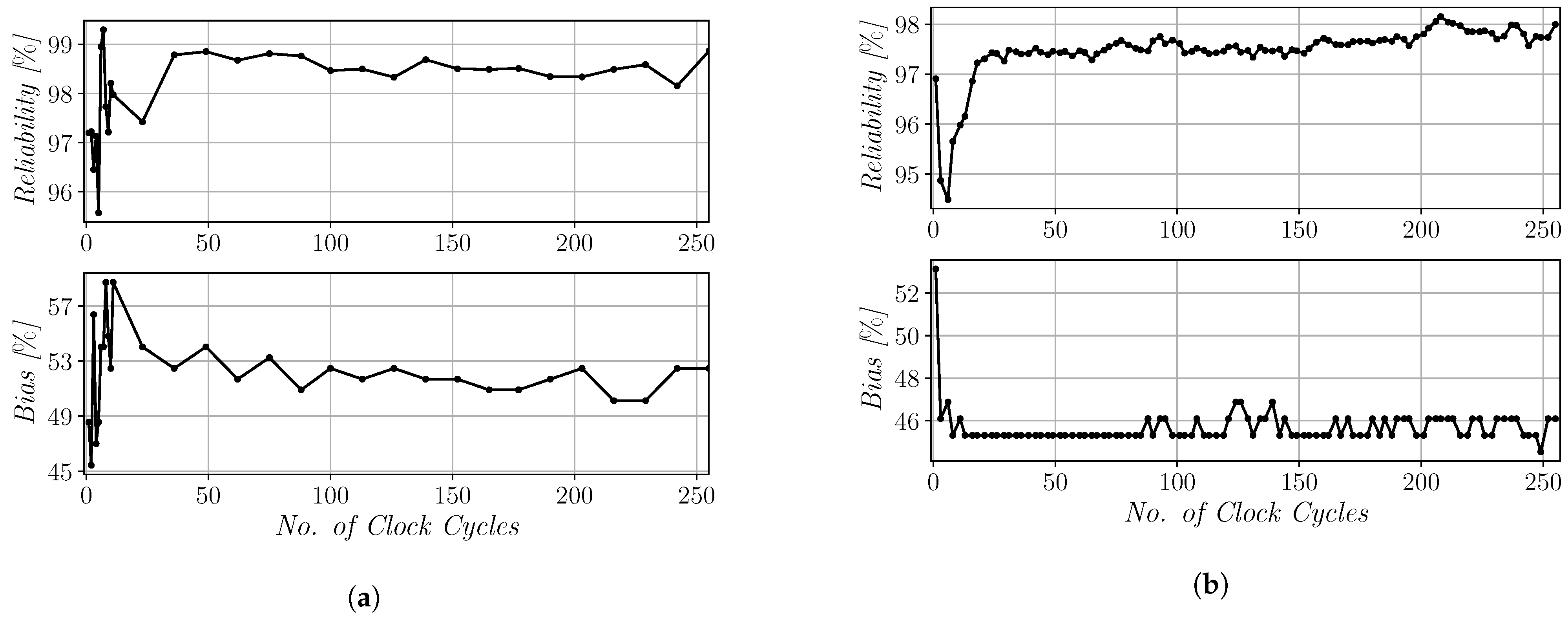
5.2. Reliability and Bias Results
5.3. Randomness and Uniformity Results
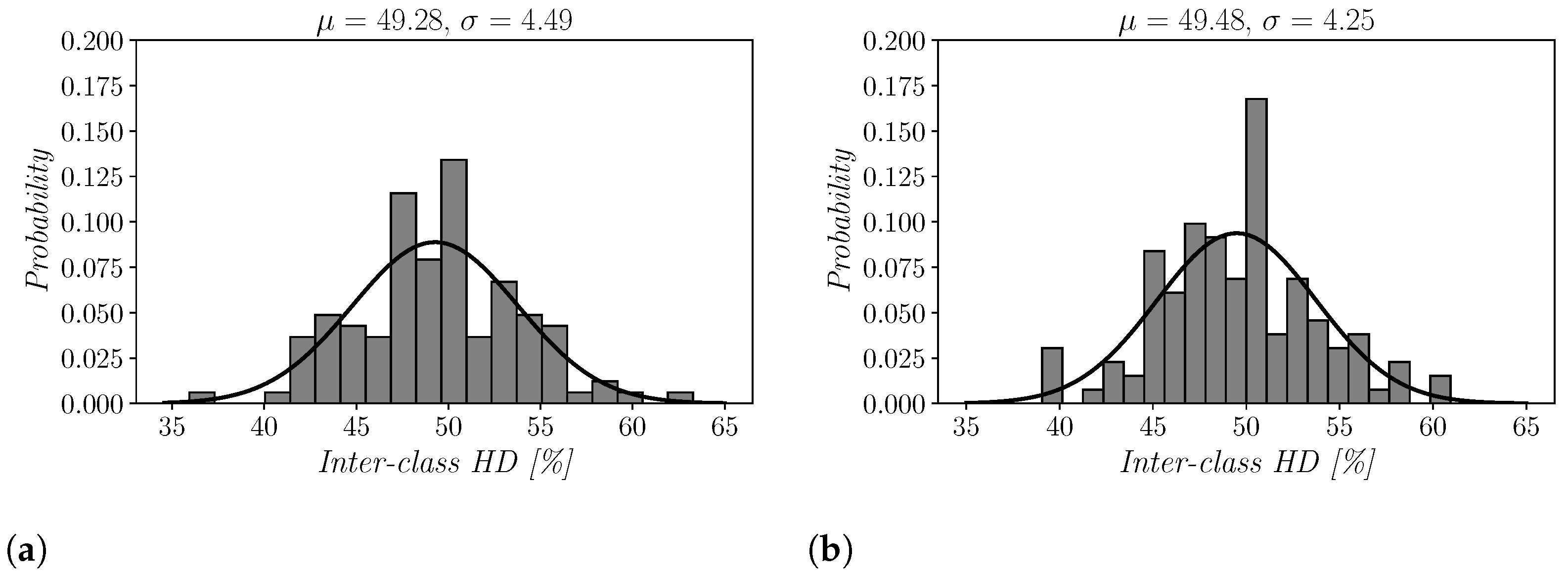
5.4. Uniqueness Results
6. Comparison with State of the Art
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rührmair, U.; Holcomb, D.E. PUFs at a glance. In Proceedings of the 2014 Design, Automation Test in Europe Conference Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Böhm, C.; Hofer, M. Physical Unclonable Functions in Theory and Practice; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Halak, B. Physically Unclonable Functions: From Basic Design Principles to Advanced Hardware Security Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Qureshi, M.A.; Munir, A. PUF-RAKE: A PUF-based Robust and Lightweight Authentication and Key Establishment Protocol. IEEE Trans. Dependable Secur. Comput. 2021. [Google Scholar] [CrossRef]
- Johnson, A.P.; Chakraborty, R.S.; Mukhopadhyay, D. A PUF-enabled secure architecture for FPGA-based IoT applications. IEEE Trans. Multi-Scale Comput. Syst. 2015, 1, 110–122. [Google Scholar] [CrossRef]
- Chatterjee, U.; Govindan, V.; Sadhukhan, R.; Mukhopadhyay, D.; Chakraborty, R.S.; Mahata, D.; Prabhu, M.M. Building PUF based authentication and key exchange protocol for IoT without explicit CRPs in verifier database. IEEE Trans. Dependable Secur. Comput. 2018, 16, 424–437. [Google Scholar] [CrossRef]
- Suh, G.E.; Devadas, S. Physical Unclonable Functions for Device Authentication and Secret Key Generation. In Proceedings of the 2007 44th ACM/IEEE Design Automation Conference, San Diego, CA, USA, 4–8 June 2007; pp. 9–14. [Google Scholar]
- Yilmaz, Y.; Gunn, S.R.; Halak, B. Lightweight PUF-based authentication protocol for IoT devices. In Proceedings of the 2018 IEEE 3rd International Verification and Security Workshop (IVSW), Costa Brava, Spain, 2–4 July 2018; pp. 38–43. [Google Scholar]
- Gu, C.; Hanley, N.; O’Neill, M. FPGA-based strong PUF with increased uniqueness and entropy properties. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Gu, C.; Chang, C.H.; Liu, W.; Hanley, N.; Miskelly, J.; O’Neill, M. A large-scale comprehensive evaluation of single-slice ring oscillator and PicoPUF bit cells on 28-nm Xilinx FPGAs. J. Cryptogr. Eng. 2020, 11, 1–12. [Google Scholar]
- Guajardo, J.; Kumar, S.S.; Schrijen, G.J.; Tuyls, P. FPGA Intrinsic PUFs and Their Use for IP Protection. In Proceedings of the Cryptographic Hardware and Embedded Systems-CHES 2007, 9th International Workshop, Vienna, Austria, 10–13 September 2007; pp. 63–80. [Google Scholar]
- Holcomb, D.E.; Burleson, W.P.; Fu, K. Power-Up SRAM State as an Identifying Fingerprint and Source of True Random Numbers. IEEE Trans. Comput. 2009, 58, 1198–1210. [Google Scholar] [CrossRef]
- Kumar, S.S.; Guajardo, J.; Maes, R.; Schrijen, G.J.; Tuyls, P. The Butterfly PUF: Protecting IP on every FPGA. In Proceedings of the IEEE International Workshop on Hardware-Oriented Security and Trust, HOST 2008, Anaheim, CA, USA, 9 June 2008; pp. 67–70. [Google Scholar]
- Merli, D.; Heyszl, J.; Heinz, B.; Schuster, D.; Stumpf, F.; Sigl, G. Localized electromagnetic analysis of RO PUFs. In Proceedings of the 2013 IEEE International Symposium on Hardware-Oriented Security and Trust, HOST 2013, Austin, TX, USA, 2–3 June 2013; pp. 19–24. [Google Scholar]
- Bossuet, L.; Ngo, X.T.; Cherif, Z.; Fischer, V. A PUF Based on a Transient Effect Ring Oscillator and Insensitive to Locking Phenomenon. IEEE Trans. Emerg. Top. Comput. 2014, 2, 30–36. [Google Scholar] [CrossRef]
- Lim, D.; Lee, J.W.; Gassend, B.; Suh, G.E.; van Dijk, M.; Devadas, S. Extracting secret keys from integrated circuits. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2005, 13, 1200–1205. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Sahoo, D.P.; Jin, C.; Mahmood, K.; Rührmair, U.; van Dijk, M. The Interpose PUF: Secure PUF Design against State-of-the-art Machine Learning Attacks. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 2019, 243–290. [Google Scholar] [CrossRef]
- Gu, C.; O’Neill, M. Ultra-compact and robust FPGA-based PUF identification generator. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 934–937. [Google Scholar] [CrossRef]
- Gu, C.; Murphy, J.; O’Neill, M. A unique and robust single slice FPGA identification generator. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, VIC, Australia, 1–5 June 2014; pp. 1223–1226. [Google Scholar]
- Gu, C.; Hanley, N.; O’Neill, M. Improved reliability of FPGA-based PUF identification generator design. ACM Trans. Reconfigurable Technol. Syst. (TRETS) 2017, 10, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Marchand, C.; Bossuet, L.; Mureddu, U.; Bochard, N.; Cherkaoui, A.; Fischer, V. Implementation and Characterization of a Physical Unclonable Function for IoT: A Case Study With the TERO-PUF. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 97–109. [Google Scholar] [CrossRef] [Green Version]
- Tebelmann, L.; Pehl, M.; Immler, V. Side-channel analysis of the TERO PUF. In International Workshop on Constructive Side-Channel Analysis and Secure Design; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–60. [Google Scholar]
- Yin, C.E.; Qu, G. Improving PUF security with regression-based distiller. In Proceedings of the 50th Annual Design Automation Conference 2013, DAC’13, Austin, TX, USA, 29 May–7 June 2013; pp. 1–6. [Google Scholar]
- Bassham, L.; Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Leigh, S.; Levenson, M.; Vangel, M.; Heckert, N.; Banks, D. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. In Proceedings of the Special Publication (NIST SP), National Institute of Standards and Technology, Gaithersburg, MD, USA, 16 September 2010. [Google Scholar]
- Gao, M.; Lai, K.; Qu, G. A highly flexible ring oscillator PUF. In Proceedings of the 51st Annual Design Automation Conference, San Francisco, CA, USA, 1–5 June 2014; pp. 1–6. [Google Scholar]
- Xu, T.; Potkonjak, M. Robust and flexible FPGA-based digital PUF. In Proceedings of the 2014 24th International Conference on Field Programmable Logic and Applications (FPL), Munich, Germany, 2–4 September 2014; pp. 1–6. [Google Scholar]
- Yin, C.E.; Qu, G.; Zhou, Q. Design and implementation of a group-based RO PUF. In Proceedings of the 2013 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 18–22 March 2013; pp. 416–421. [Google Scholar]
- Avaroğlu, E. The implementation of ring oscillator based PUF designs in Field Programmable Gate Arrays using of different challenge. Phys. A Stat. Mech. Its Appl. 2020, 546, 124291. [Google Scholar] [CrossRef]
- Reyneri, L.; Del Corso, D.; Sacco, B. Oscillatory metastability in homogeneous and inhomogeneous flip-flops. IEEE J. Solid-State Circuits 1990, 25, 254–264. [Google Scholar] [CrossRef]
- Xilinx. Spartan-6 FPGA Configurable Logic Block UG384 (v1.1), 23 February 2010. Available online: https://dokumen.tips/documents/xilinx-ug384-spartan-6-fpga-configurable-logic-block-user-guide.html (accessed on 1 September 2021).
- Bellizia, D.; Bongiovanni, S.; Olivieri, M.; Scotti, G. SC-DDPL: A Novel Standard-Cell Based Approach for Counteracting Power Analysis Attacks in the Presence of Unbalanced Routing. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2317–2330. [Google Scholar] [CrossRef]
- Eiroa, S.; Castro, J.; Martínez-Rodríguez, M.C.; Tena, E.; Brox, P.; Baturone, I. Reducing bit flipping problems in SRAM physical unclonable functions for chip identification. In Proceedings of the 2012 19th IEEE International Conference on Electronics, Circuits, and Systems (ICECS 2012), Seville, Spain, 9–12 December 2012; pp. 392–395. [Google Scholar]
- Selimis, G.; Konijnenburg, M.; Ashouei, M.; Huisken, J.; de Groot, H.; van der Leest, V.; Schrijen, G.J.; van Hulst, M.; Tuyls, P. Evaluation of 90nm 6T-SRAM as physical unclonable function for secure key generation in wireless sensor nodes. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 567–570. [Google Scholar]
- Chowdhury, S.; Xu, X.; Tehranipoor, M.; Forte, D. Aging resilient RO PUF with increased reliability in FPGA. In Proceedings of the 2017 International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 4–6 December 2017; pp. 1–7. [Google Scholar]
- Rahman, M.T.; Rahman, F.; Forte, D.; Tehranipoor, M. An Aging-Resistant RO-PUF for Reliable Key Generation. IEEE Trans. Emerg. Top. Comput. 2016, 4, 335–348. [Google Scholar] [CrossRef]
- Yamamoto, D.; Sakiyama, K.; Iwamoto, M.; Ohta, K.; Ochiai, T.; Takenaka, M.; Itoh, K. Uniqueness Enhancement of PUF Responses Based on the Locations of Random Outputting RS Latches. In Cryptographic Hardware and Embedded Systems—CHES 2011; Preneel, B., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 390–406. [Google Scholar]
- Maes, R.; Tuyls, P.; Verbauwhede, I. Intrinsic PUFs from flip-flops on reconfigurable devices. In Proceedings of the 3rd Benelux Workshop on Information and System Security (WISSec 2008), Eindhoven, The Netherlands, 13–14 November 2008; Volume 17, p. 2008. [Google Scholar]

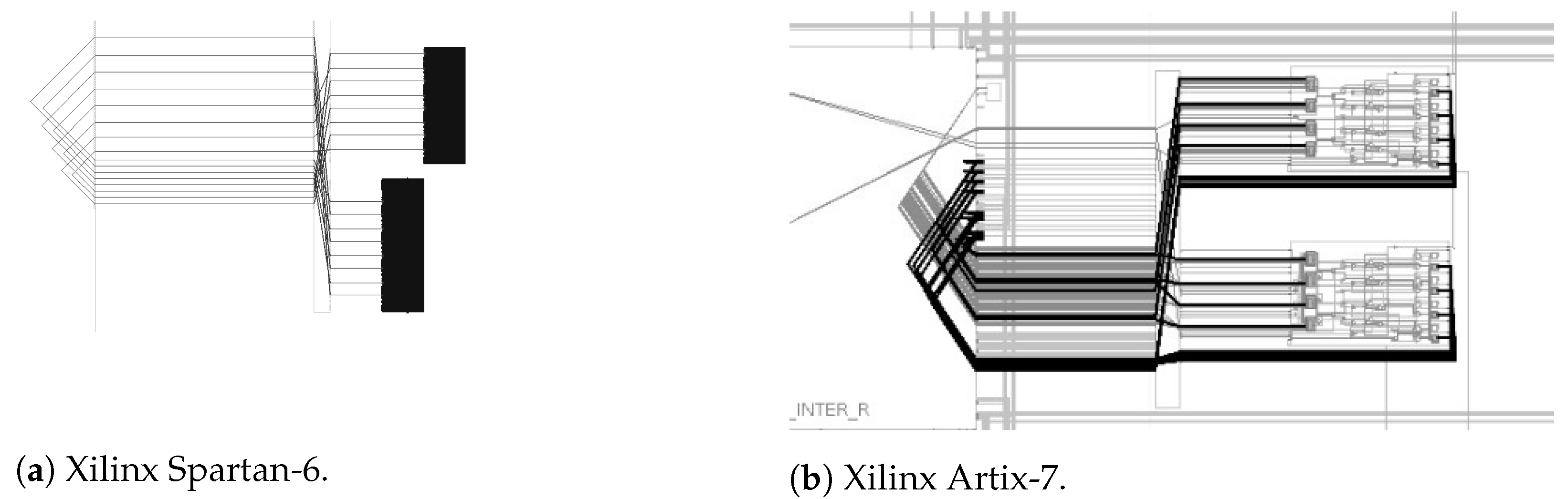




| Slice Position | Net-Differences | Spartan-6 Delay [ps] | Artix-7 Delay [ps] |
|---|---|---|---|
| UPPER | Q1,A-Q2,A | 43 | 1 |
| UPPER | Q1,B-Q2,B | 15 | 1 |
| LOWER | Q1,A-Q2,A | 37 | 4 |
| LOWER | Q1,B-Q2,B | 48 | 4 |
| Mono-Bit Test | Block Freq. Test | Cum. Test | Run Test | Longest Run Test | Approx. Entropy Test | |
|---|---|---|---|---|---|---|
| Spartan-6 | 0.860 | 0.687 | 0.819 | 0.077 | 0.249 | 0.334 |
| Artix-7 | 1.000 | 0.932 | 0.998 | 0.157 | 0.365 | 0.409 |
| Pass/Fail | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| This Work | This Work | [10] | [20] | [19] | [36] | [37] | [11] | [7] | [13] | |
|---|---|---|---|---|---|---|---|---|---|---|
| Year | 2021 | 2021 | 2020 | 2017 | 2014 | 2011 | 2008 | 2007 | 2007 | 2006 |
| PUF | DD | DD | Single Slice RO | Pico | Pico | Latch | Flip-Flop | SRAM | RO | Butterfly |
| Device | Artix-7 | Spartan-6 | Artix-7 | Artix-7 | Spartan-6 | Spartan-3E | Virtex-2 Pro | FPGA | Virtex-4 | Virtex-5 |
| Uniqueness [%] | 49.48 | 49.28 | 48.05 | 49.90 | 48.52 | 46.00 | ≈50.00 * | 49.97 | 46.15 | ≈50 |
| Reliability [%] | 98.33 | 98.37 | 99.30 | 94.53 | 93.00 | >87 | >95.00 * | >88 | 99.52 | 94.00 |
| Response-bit | 128 | 128 | 128 | 128 | 128 | 128 | 4096 | 128 | 128 | 64 |
| CLB/bit | 1/4 | 1/4 | 1 | 1 | 1 | - | - | - | - | 1 |
| Slice/bit | 1/2 | 1/2 | 1 | 1 | 1 | 2 | 1 | - | - | >2 |
| Res. | 64 slices | 64 slices | >256 slices | 128 slices | 128 slices | 256 slices | 4096 flip-flops | 4600 SRAM | 16x64 array | >128 slices |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Della Sala, R.; Bellizia, D.; Scotti, G. A Novel Ultra-Compact FPGA PUF: The DD-PUF. Cryptography 2021, 5, 23. https://doi.org/10.3390/cryptography5030023
Della Sala R, Bellizia D, Scotti G. A Novel Ultra-Compact FPGA PUF: The DD-PUF. Cryptography. 2021; 5(3):23. https://doi.org/10.3390/cryptography5030023
Chicago/Turabian StyleDella Sala, Riccardo, Davide Bellizia, and Giuseppe Scotti. 2021. "A Novel Ultra-Compact FPGA PUF: The DD-PUF" Cryptography 5, no. 3: 23. https://doi.org/10.3390/cryptography5030023
APA StyleDella Sala, R., Bellizia, D., & Scotti, G. (2021). A Novel Ultra-Compact FPGA PUF: The DD-PUF. Cryptography, 5(3), 23. https://doi.org/10.3390/cryptography5030023








