SCANN: Side Channel Analysis of Spiking Neural Networks
Abstract
:1. Introduction
2. Background
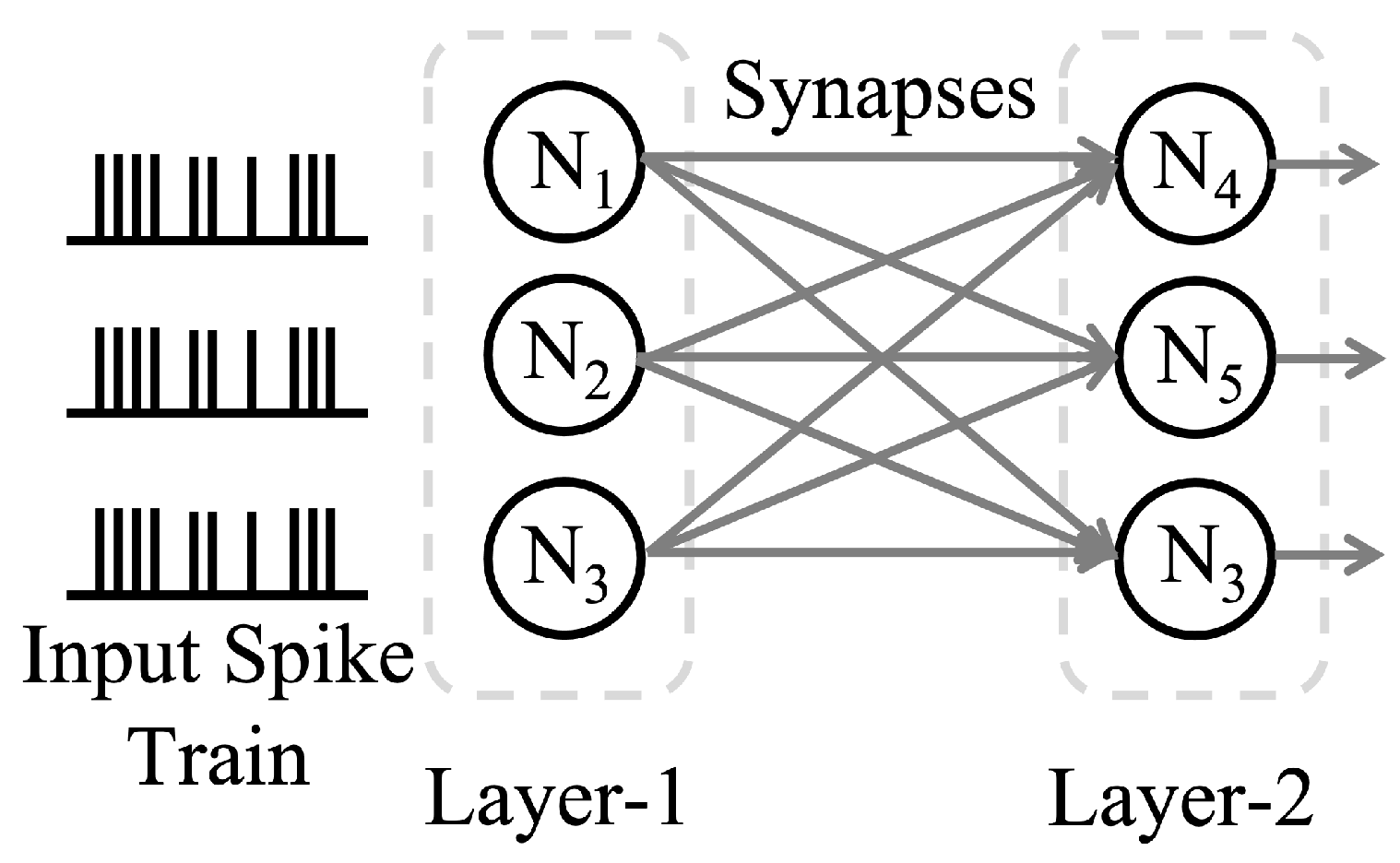
2.1. Overview of Spiking Neural Network
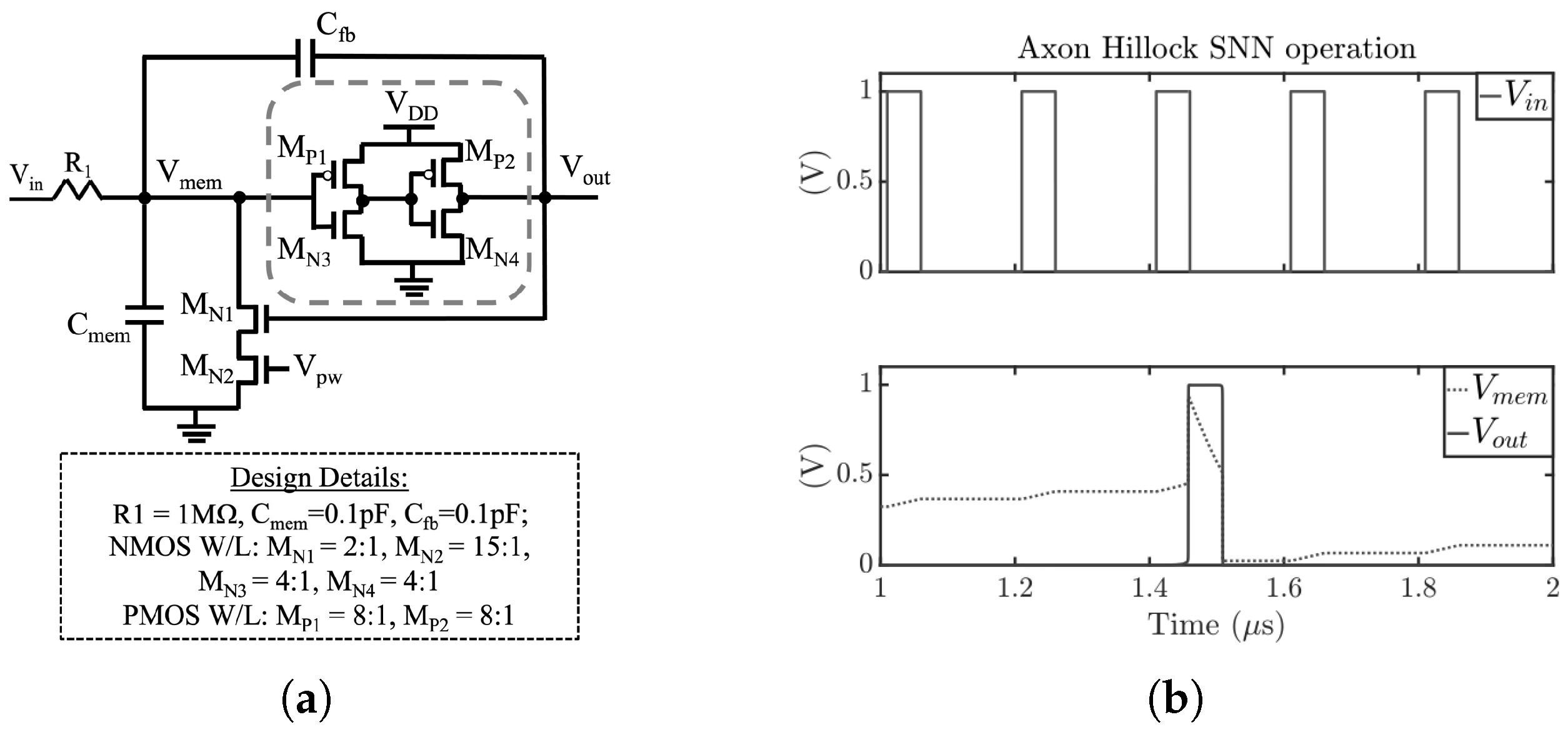
2.2. Axon Hillock Spiking Neuron Design and Implementation
2.3. Simulation Setup
2.4. SNN Side-Channel Analysis
3. SCANN Attacks Using Timing Side Channel
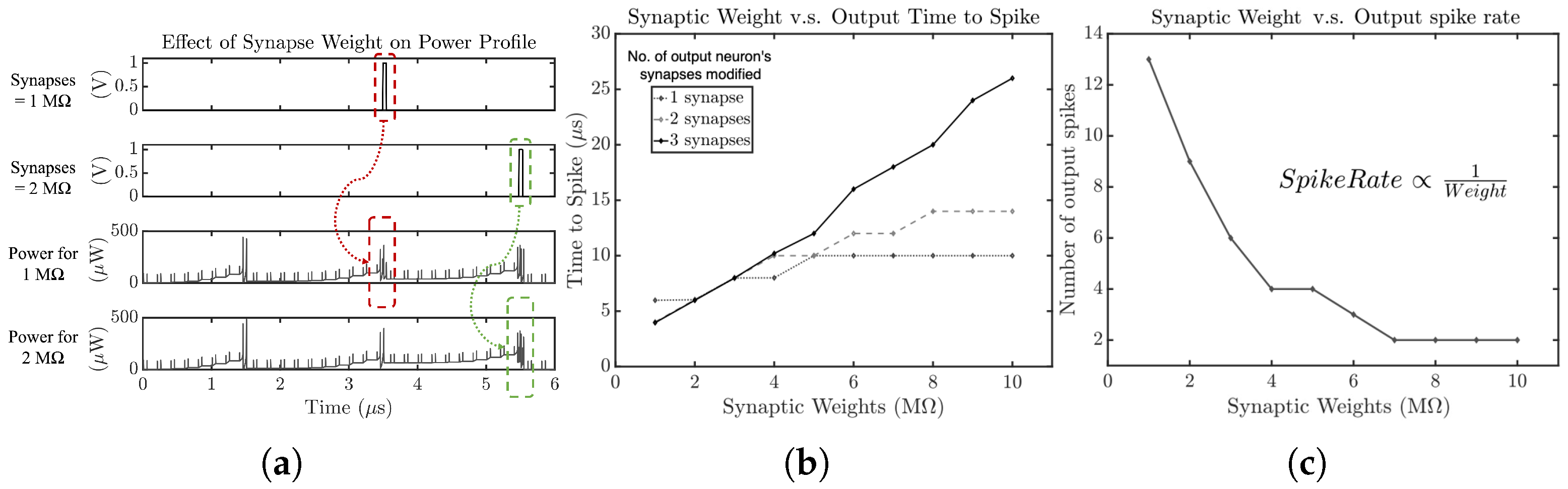
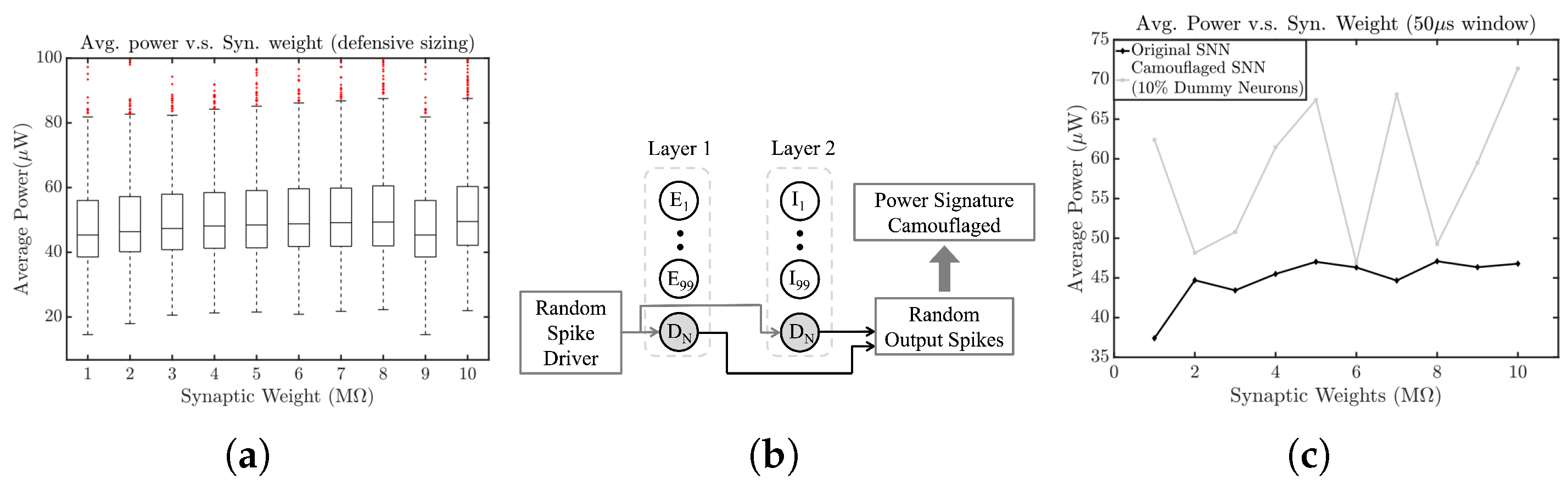
3.1. SCANN 1: Effect of Synaptic Weights
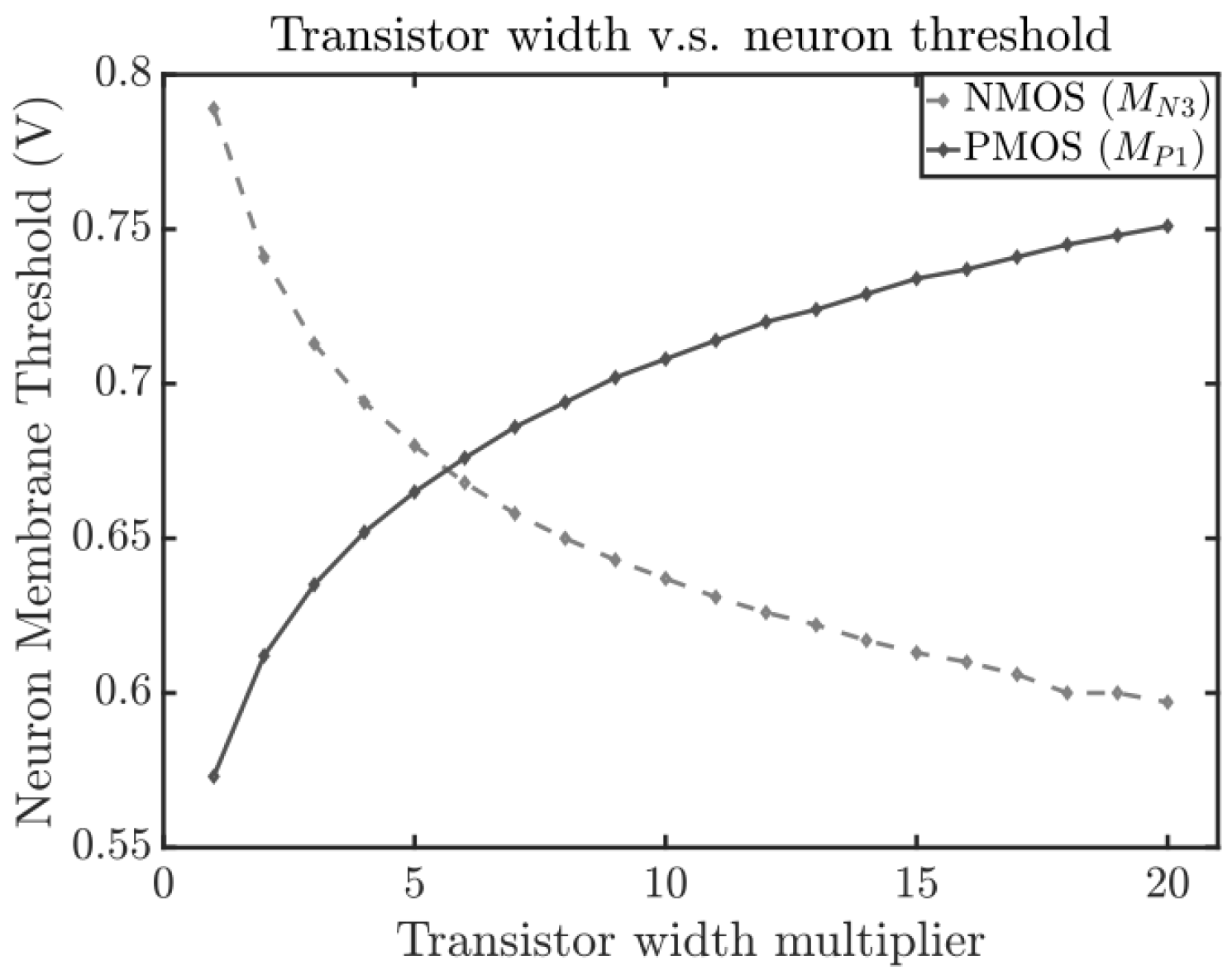
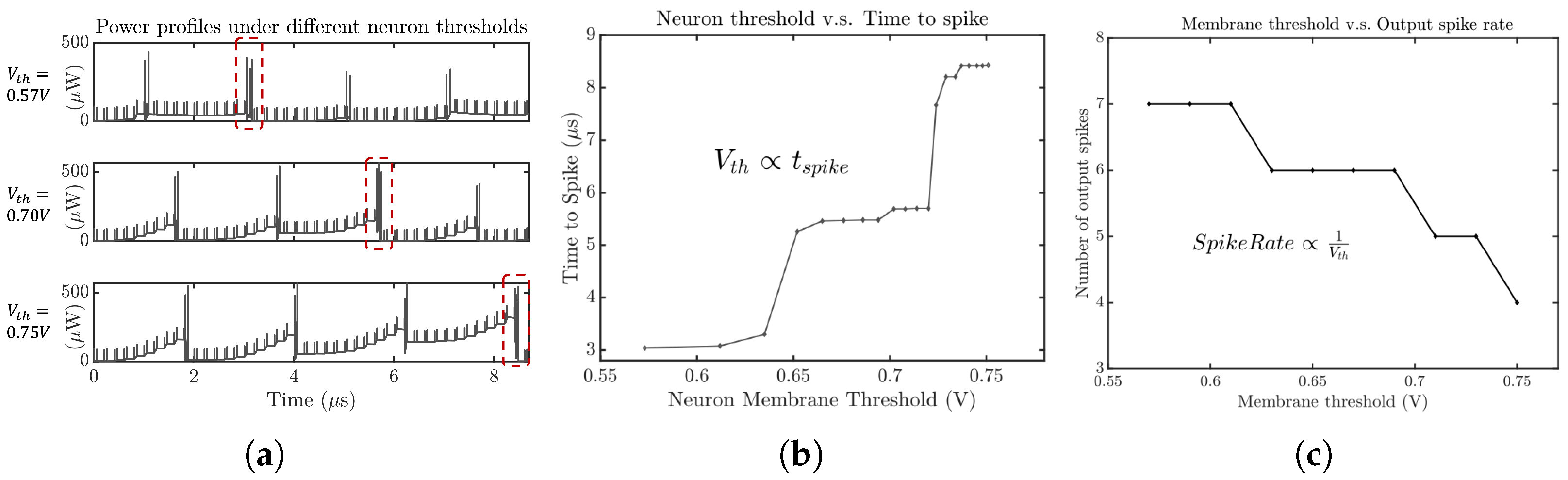
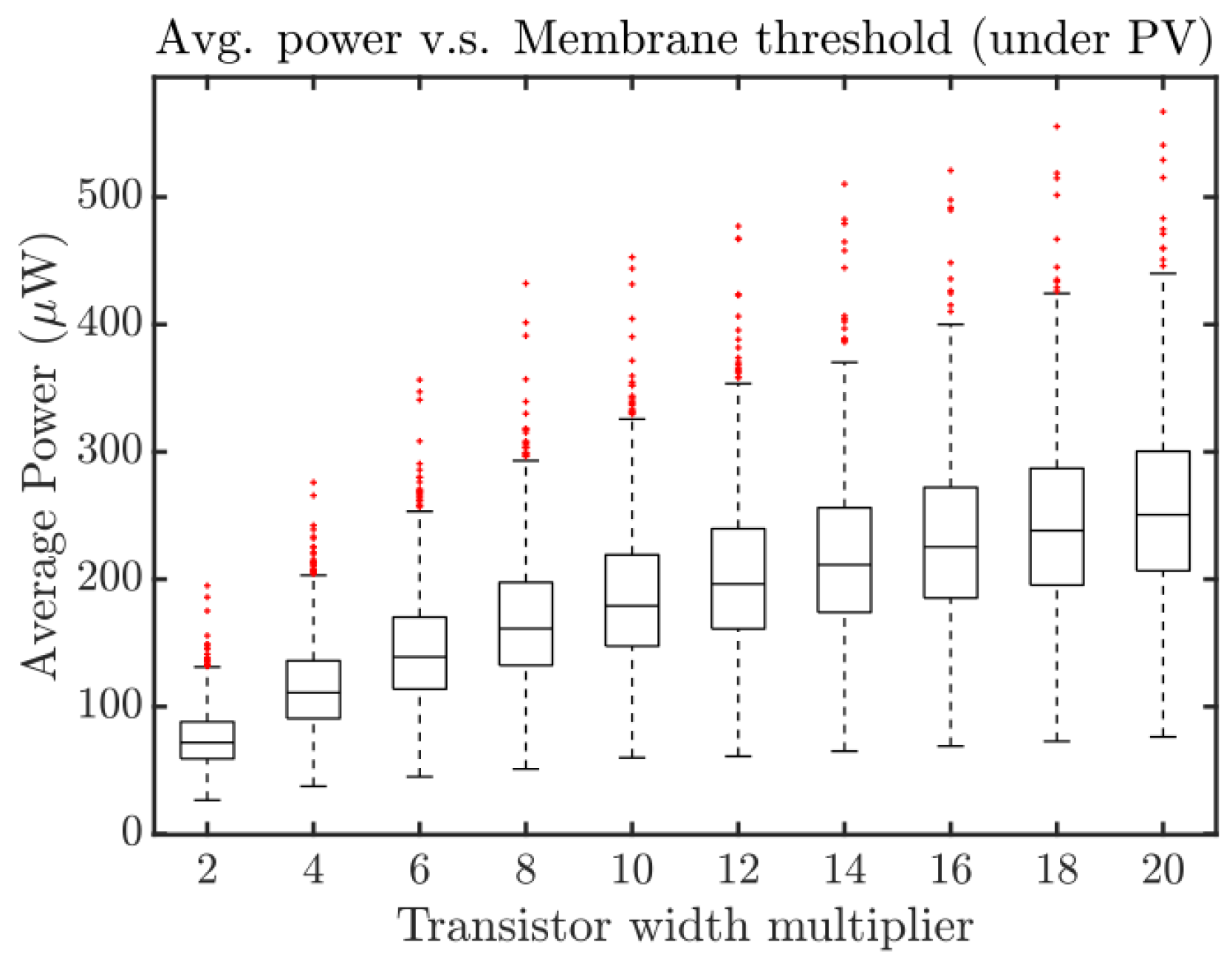
3.2. SCANN 2: Effect of Neuron Membrane Threshold
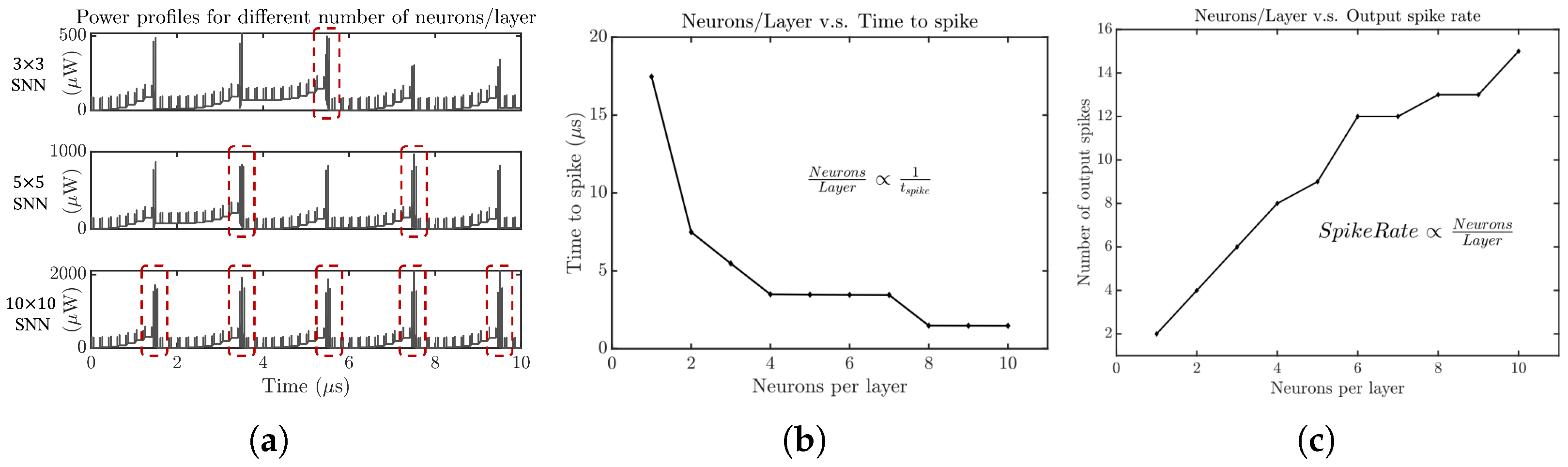
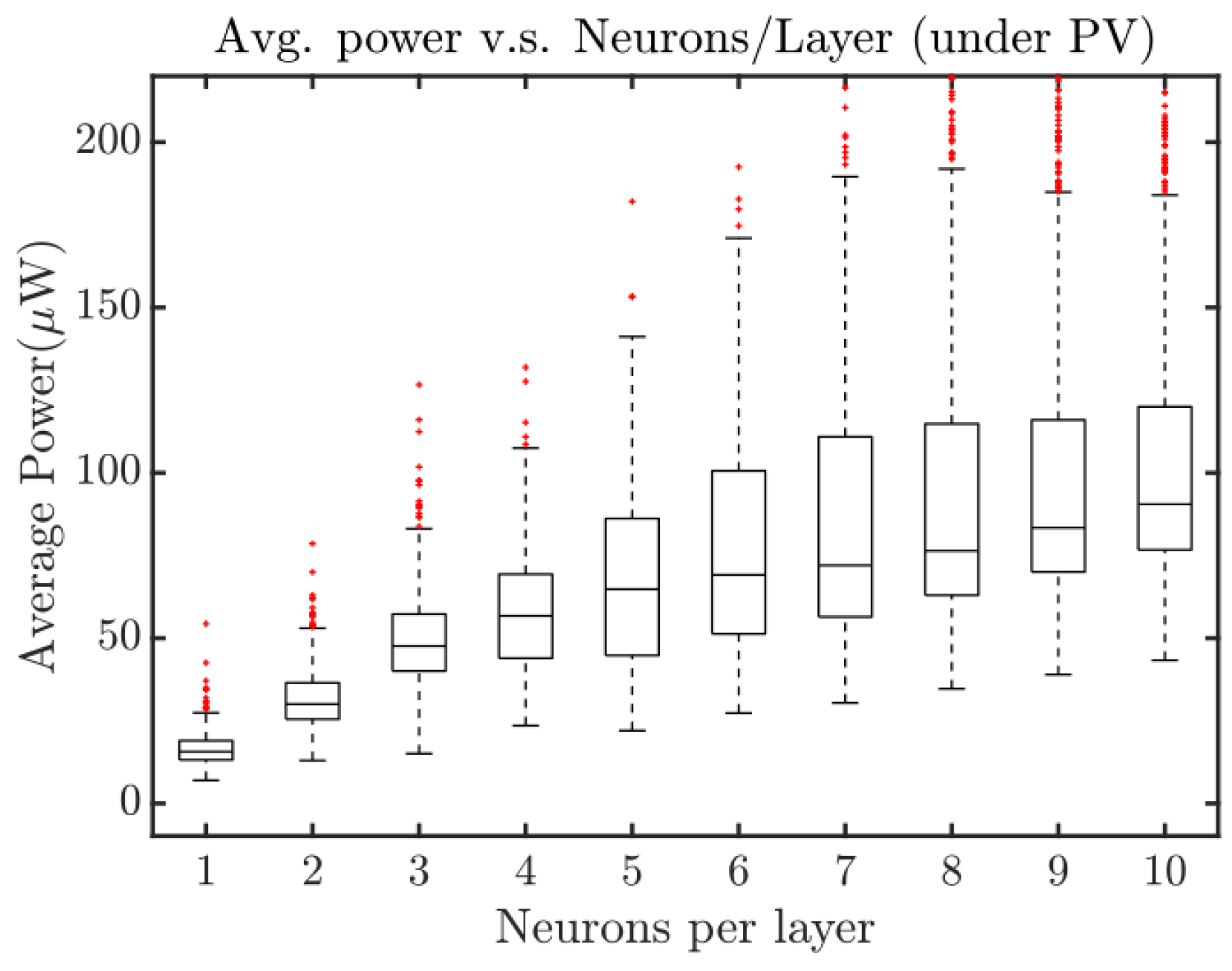
3.3. SCANN 3: Effect of Number of Neurons
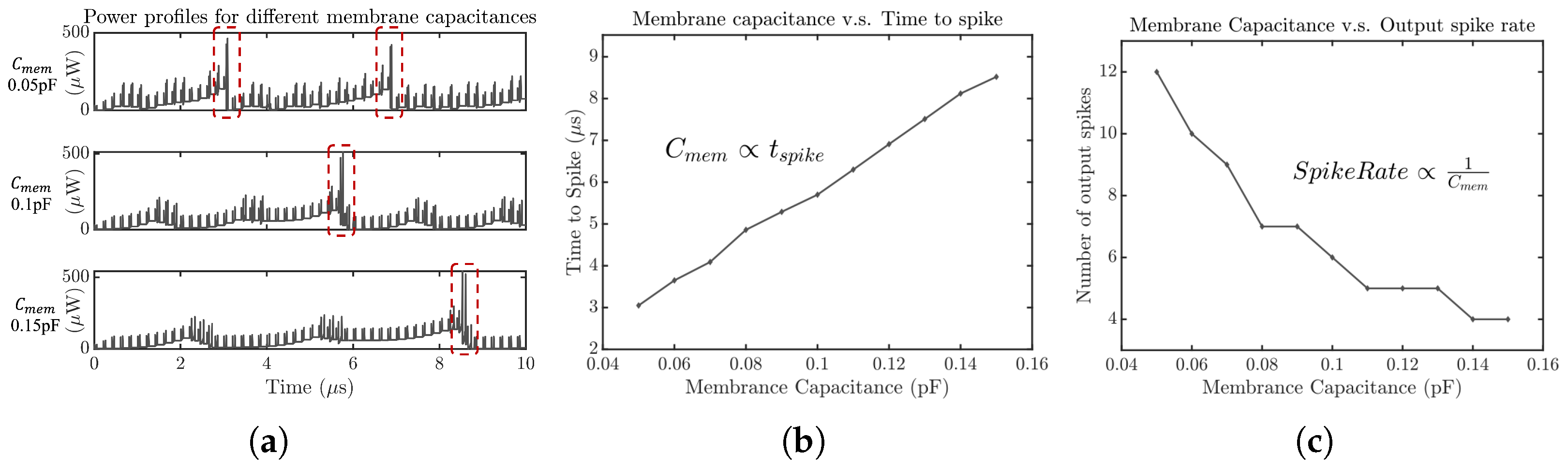
3.4. SCANN 4: Effect of Neuron Capacitance
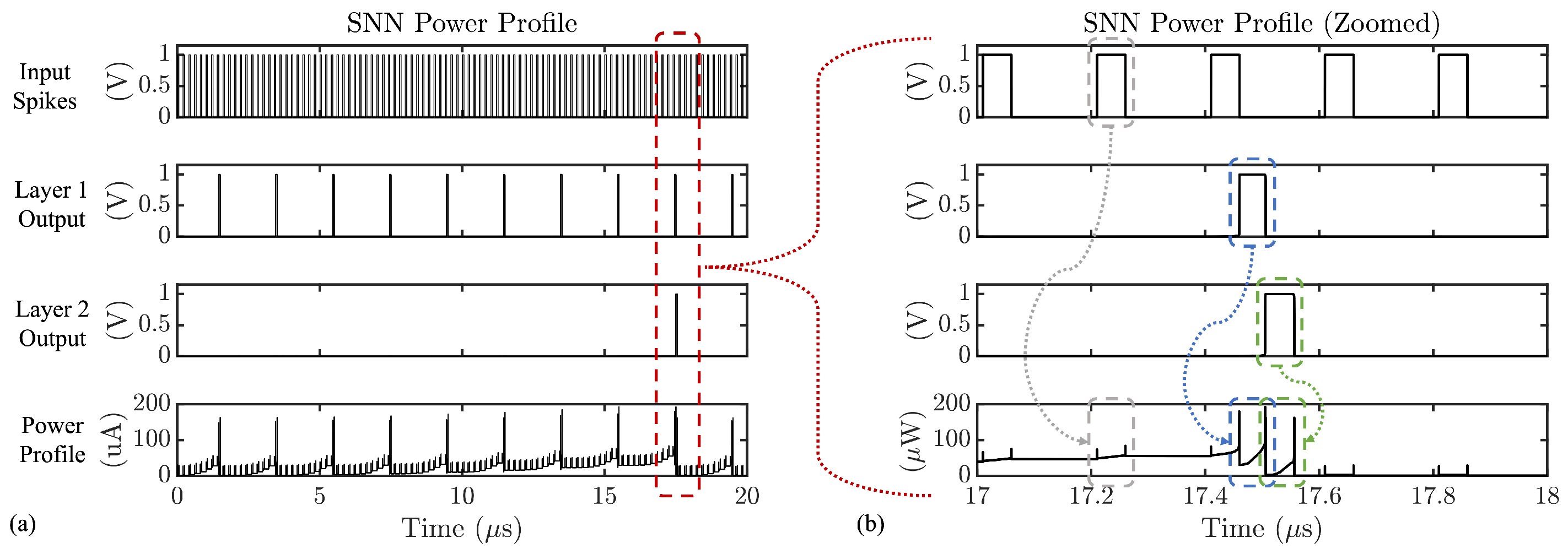
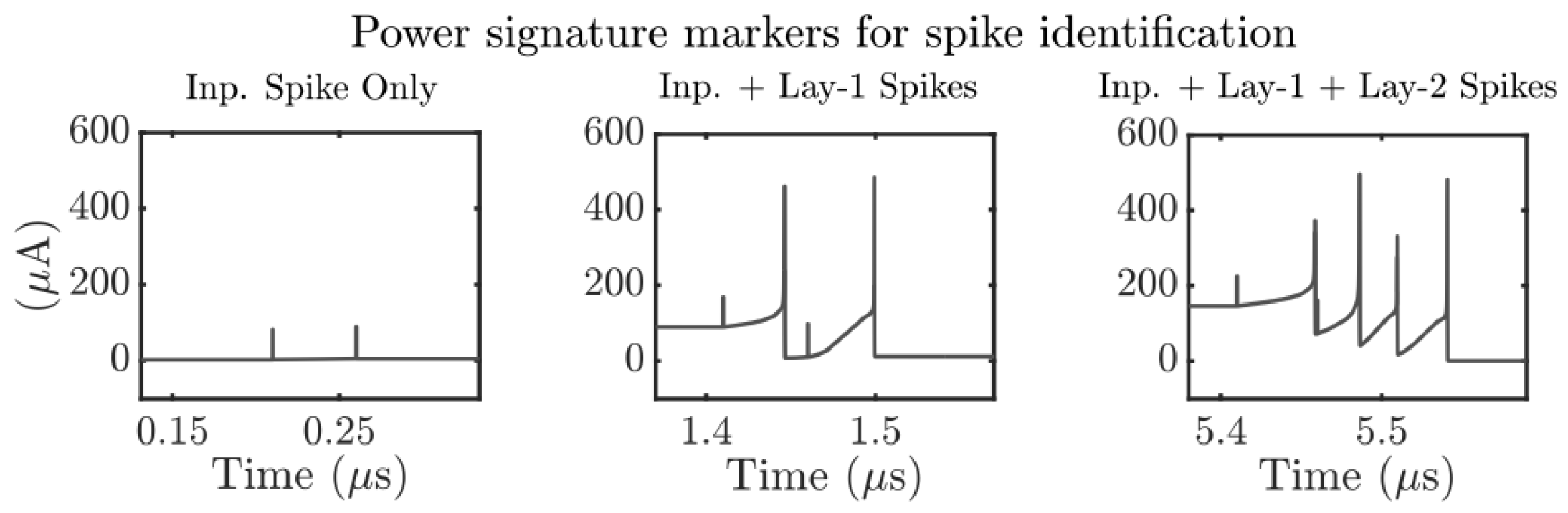
4. SCANN Attacks Using Power Side Channel
4.1. SCANN 5: Synaptic Weights
4.2. SCANN 6: Neuron Threshold
4.3. SCANN 7: Number of Neurons/Layer
4.4. SCANN 8: Neuron Membrane Capacitance
5. Discussion
5.1. Summary of Reverse Engineering Attacks
- SNN contains parameters: These include (a) synaptic weights, (b) neuron membrane threshold, (c) number of neurons per layer, and (d) membrane capacitance. Other assets (not studied in this paper) are the types of interconnections between layers and the SNN learning rate.
- SNN has vulnerabilities: Side channel power leakage reveals various design parameters due to (a) variation of power profile’s spike rate, and (b) SNN’s average power. Table 1 shows a summary of SCANN attacks to identify different SNN design parameters.
- SNN can face attack models: This includes adversarial side channel analysis (SCA) of the power supply to reverse engineer and derive SNN design parameters. These attacks are initiated during the application phase when the design parameters are fixed. Attacks not covered in this paper are (a) the generation of adversarial input samples to cause misclassification, (b) fault injection into synaptic weights, and (c) noise injection in input samples to attack specific neurons.
5.2. Process Variation Analysis
5.3. Feasibility of SCANN
5.4. Impact of Inputs and Connectivity
5.5. Defenses against SCANN
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaiser, J.; Tieck, J.C.V.; Hubschneider, C.; Wolf, P.; Weber, M.; Hoff, M.; Friedrich, A.; Wojtasik, K.; Roennau, A.; Kohlhaas, R.; et al. Towards a framework for end-to-end control of a simulated vehicle with spiking neural networks. In Proceedings of the 2016 IEEE International Conference on Simulation, Modeling, and Programming for Autonomous Robots (SIMPAR), San Francisco, CA, USA, 13–16 December 2016; pp. 127–134. [Google Scholar]
- Azghadi, M.R.; Lammie, C.; Eshraghian, J.K.; Payvand, M.; Donati, E.; Linares-Barranco, B.; Indiveri, G. Hardware implementation of deep network accelerators towards healthcare and biomedical applications. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1138–1159. [Google Scholar] [CrossRef] [PubMed]
- Whatmough, P.N.; Lee, S.K.; Brooks, D.; Wei, G.Y. DNN engine: A 28-nm timing-error tolerant sparse deep neural network processor for IoT applications. IEEE J. -Solid-State Circuits 2018, 53, 2722–2731. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Y.; Khosla, D. Spiking deep convolutional neural networks for energy-efficient object recognition. Int. J. Comput. Vis. 2015, 113, 54–66. [Google Scholar] [CrossRef]
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Heiberg, T.; Kriener, B.; Tetzlaff, T.; Einevoll, G.T.; Plesser, H.E. Firing-rate models for neurons with a broad repertoire of spiking behaviors. J. Comput. Neurosci. 2018, 45, 103–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A neuromorphic manycore processor with on-chip learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Tavanaei, A.; Ghodrati, M.; Kheradpisheh, S.R.; Masquelier, T.; Maida, A. Deep learning in spiking neural networks. Neural Netw. 2019, 111, 47–63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bagheri, A.; Simeone, O.; Rajendran, B. Adversarial training for probabilistic spiking neural networks. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]
- Venceslai, V.; Marchisio, A.; Alouani, I.; Martina, M.; Shafique, M. Neuroattack: Undermining spiking neural networks security through externally triggered bit-flips. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Marchisio, A.; Nanfa, G.; Khalid, F.; Hanif, M.A.; Martina, M.; Shafique, M. Is spiking secure? A comparative study on the security vulnerabilities of spiking and deep neural networks. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Nagarajan, K.; Li, J.; Ensan, S.S.; Kannan, S.; Ghosh, S. Fault injection attacks in spiking neural networks and countermeasures. Front. Nanotechnol. 2022, 3, 801999. [Google Scholar] [CrossRef]
- Nagarajan, K.; Li, J.; Ensan, S.S.; Khan, M.N.I.; Kannan, S.; Ghosh, S. Analysis of power-oriented fault injection attacks on spiking neural networks. In Proceedings of the 2022 Design, Automation & Test in Europe Conference & Exhibition (DATE), Antwerp, Belgium, 14–23 March 2022; pp. 861–866. [Google Scholar]
- Kocher, P.; Jaffe, J.; Jun, B. Differential power analysis. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–18 August 1999; pp. 388–397. [Google Scholar]
- Brier, E.; Clavier, C.; Olivier, F. Optimal statistical power analysis. In Cryptology ePrint Archive; International Association for Cryptologic Research: Bellevue, WA, USA, 2003. [Google Scholar]
- Kocher, P.C. Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. In Proceedings of the Advances in Cryptology—CRYPTO ’96, Santa Barbara, CA, USA, 18–22 August 1996; Koblitz, N., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 104–113. [Google Scholar]
- Brumley, D.; Boneh, D. Remote timing attacks are practical. Comput. Netw. 2005, 48, 701–716. [Google Scholar] [CrossRef]
- Quisquater, J.J.; Samyde, D. Electromagnetic analysis (ema): Measures and counter-measures for smart cards. In Proceedings of the International Conference on Research in Smart Cards, Cannes, France, 19–21 September 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 200–210. [Google Scholar]
- Gandolfi, K.; Mourtel, C.; Olivier, F. Electromagnetic analysis: Concrete results. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Taipei, Taiwan, 25–28 September 2017; Springer: Berlin/Heidelberg, Germany, 2001; pp. 251–261. [Google Scholar]
- Batina, L.; Bhasin, S.; Jap, D.; Picek, S. CSI neural network: Using side-channels to recover your artificial neural network information. arXiv 2018, arXiv:1810.09076. [Google Scholar]
- Garaffa, L.C.; Aljuffri, A.; Reinbrecht, C.; Hamdioui, S.; Taouil, M.; Sepulveda, J. Revealing the Secrets of Spiking Neural Networks: The Case of Izhikevich Neuron. In Proceedings of the 2021 24th Euromicro Conference on Digital System Design (DSD), Palermo, Spain, 1–3 September 2021; pp. 514–518. [Google Scholar]
- Indiveri, G.; Linares-Barranco, B.; Hamilton, T.J.; Schaik, A.v.; Etienne-Cummings, R.; Delbruck, T.; Liu, S.C.; Dudek, P.; Häfliger, P.; Renaud, S.; et al. Neuromorphic silicon neuron circuits. Front. Neurosci. 2011, 5, 73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alibart, F.; Pleutin, S.; Guérin, D.; Novembre, C.; Lenfant, S.; Lmimouni, K.; Gamrat, C.; Vuillaume, D. An organic nanoparticle transistor behaving as a biological spiking synapse. Adv. Funct. Mater. 2010, 20, 330–337. [Google Scholar] [CrossRef] [Green Version]
- Abu-Hassan, K.; Taylor, J.D.; Morris, P.G.; Donati, E.; Bortolotto, Z.A.; Indiveri, G.; Paton, J.F.; Nogaret, A. Optimal solid state neurons. Nat. Commun. 2019, 10, 5309. [Google Scholar] [CrossRef] [Green Version]
- Gkoupidenis, P.; Schaefer, N.; Garlan, B.; Malliaras, G.G. Neuromorphic functions in PEDOT: PSS organic electrochemical transistors. Adv. Mater. 2015, 27, 7176–7180. [Google Scholar] [CrossRef]
- Nawrocki, R.A.; Voyles, R.M.; Shaheen, S.E. Neurons in polymer: Hardware neural units based on polymer memristive devices and polymer transistors. IEEE Trans. Electron Devices 2014, 61, 3513–3519. [Google Scholar] [CrossRef]
- Mead, C.; Ismail, M. Analog VLSI Implementation of Neural Systems; Springer: Berlin/Heidelberg, Germany, 1989; Volume 80. [Google Scholar]
- Mehonic, A.; Kenyon, A.J. Emulating the electrical activity of the neuron using a silicon oxide RRAM cell. Front. Neurosci. 2016, 10, 57. [Google Scholar] [CrossRef] [PubMed]
- Lashkare, S.; Chouhan, S.; Chavan, T.; Bhat, A.; Kumbhare, P.; Ganguly, U. PCMO RRAM for integrate-and-fire neuron in spiking neural networks. IEEE Electron Device Lett. 2018, 39, 484–487. [Google Scholar] [CrossRef]



| SNN Design Parameter | Spike Rate (SCANN 1–4) | Average Power (SCANN 5–8) |
|---|---|---|
| Synapse Weight | ✓ | ✓ |
| Neuron Threshold | ✓ | ✓ |
| Neurons/Layer | ✓ | ✓ |
| Neuron Capacitance | ✓ | ✗ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagarajan, K.; Roy, R.; Topaloglu, R.O.; Kannan, S.; Ghosh, S. SCANN: Side Channel Analysis of Spiking Neural Networks. Cryptography 2023, 7, 17. https://doi.org/10.3390/cryptography7020017
Nagarajan K, Roy R, Topaloglu RO, Kannan S, Ghosh S. SCANN: Side Channel Analysis of Spiking Neural Networks. Cryptography. 2023; 7(2):17. https://doi.org/10.3390/cryptography7020017
Chicago/Turabian StyleNagarajan, Karthikeyan, Rupshali Roy, Rasit Onur Topaloglu, Sachhidh Kannan, and Swaroop Ghosh. 2023. "SCANN: Side Channel Analysis of Spiking Neural Networks" Cryptography 7, no. 2: 17. https://doi.org/10.3390/cryptography7020017
APA StyleNagarajan, K., Roy, R., Topaloglu, R. O., Kannan, S., & Ghosh, S. (2023). SCANN: Side Channel Analysis of Spiking Neural Networks. Cryptography, 7(2), 17. https://doi.org/10.3390/cryptography7020017






