Improve Parallel Resistance of Hashcash Tree

Abstract

Denial of Service (DoS) attacks remain a persistent threat to online systems, necessitating continual innovation in defense mechanisms. In this work, we present an improved algorithm for mitigating DoS attacks through the augmentation of client puzzle protocols. Building upon the foundation of hashcash trees, a recently proposed data structure combining hashcash and Merkle trees, we introduce a new version of the data structure that enhances resistance against parallel computation (a common tactic employed by attackers). By incorporating the labels of children and the next node in a breadth-first traversal into the hash function, we establish a sequential processing order that inhibits parallel node evaluation. The added dependency on the next node significantly elevates the complexity of constructing hashcash trees, introducing a linear number of synchronization points and fortifying resilience against potential attacks. Empirical evaluation demonstrates the efficacy of our approach, showcasing its ability to accurately control puzzle difficulty while bolstering system security against DoS threats.

1. Introduction

Denial of service (DoS) attacks target resources such as websites, applications, and servers, rendering them unavailable for their intended purpose and posing a significant threat to the integrity of the Internet community [1]. These attacks result in substantial losses [2,3] and have spurred the development of sophisticated detection methods [4,5,6,7,8]. Dwork and Noar [9] proposed the use of proof-of-work (PoW) mechanisms to contrast the proliferation of spam emails, requiring a computational stamp to access a service, for example, forwarding a message in the case of emails. PoW, a cryptographic proof method, entails one party (the prover) demonstrating to others (the verifiers) that a specified computational effort has been expended, which verifiers can subsequently validate with minimal effort on their part [10]. While PoW schemes are asymmetrical in favor of verifiers, posing moderate computational challenges for provers but facilitating easy solution verification, when applied to DoS mitigation, clients act as provers seeking access to a service while servers serve as verifiers providing the required service.

Client puzzle protocols constitute a cornerstone in the realm of DoS mitigation, leveraging PoW mechanisms to thwart malicious attacks. These protocols, categorized into challenge–response and solution–verification paradigms, mandate clients to engage in computational tasks to access services facilitated by servers. In challenge–response scenarios, servers proffer puzzles for clients to decipher, while in solution–verification contexts, clients autonomously formulate puzzles based on service specifications. Hashcash [11], a prominent cryptographic PoW algorithm, finds ubiquitous application across both protocol types. In challenge–response configurations employing hashcash, servers challenge clients to identify string extensions with predetermined hash properties, while in solution–verification scenarios, hashcash operates on service descriptors. These protocols epitomize an asymmetrical allocation of computational effort, requiring iterative attempts from the prover while imposing minimal verification overhead on the verifier. However, a notable limitation of hashcash lies in its dependency on the length of the required all-zeros prefix to dictate puzzle difficulty. Coelho [12] introduced a solution–verification protocol based on hash trees, offering superior control over puzzle difficulty. Hash tree structures assign labels to leaves by concatenating hashed leaf indices with service descriptions, while internal nodes receive labels by hashing concatenated child labels. While effective in regulating prover effort, practical implementation of this protocol necessitates handling large hash trees, posing storage and computational challenges.

In a recent study [13], researchers posed three research questions aimed at advancing client puzzle protocols within the domain of cybersecurity. The first question sought to ascertain the feasibility of crafting a client puzzle protocol founded on hashcash, albeit with enhanced control over puzzle difficulty. Concurrently, another question delved into the prospect of formulating a client puzzle protocol rooted in hash trees, yet requiring more compact tree structures compared to those previously proposed by Coelho [12]. These research questions were comprehensively addressed, unveiling promising avenues for protocol refinement and optimization. However, the investigation encountered partial resolution concerning the final question about the resistance of the protocol to parallel computation. While substantial progress was made in elucidating the efficacy of the protocol in mitigating parallel computational threats, further exploration remains imperative to achieve comprehensive insights into its resilience under varied operational conditions. In fact, the protocol features a logarithmic number of synchronization points relative to the total number of nodes.

In a nutshell, the primary contribution of this recent study involves the development of a modified challenge–response protocol, structured into two distinct phases (Figure 1). In the first phase, the prover tackles a puzzle generated by the verifier and submits a commitment upon puzzle resolution. The subsequent phase requires the prover to furnish proof of solution validity. This protocol introduces a novel puzzle mechanism centered on constructing a tree with specific labeling criteria, enabling precise control over puzzle difficulty by adjusting parameters such as the length of the all-zeros prefix and the number of nodes. This new data structure, named hashcash tree merges elements from hashcash and hash trees to enhance puzzle complexity management and solution verification efficiency. Partial parallelization is possible in the construction of hashcash trees due to the interdependence of node label computation on the labels of child nodes, from which the logarithmically many synchronization points arise. Further improvements on the parallel resistance of the protocol were left as a future research line.

In this article, we actively engage with this critical research line. Parallel computation represents a sophisticated technique wherein multiple computational tasks are executed concurrently, posing a formidable challenge to the efficacy and integrity of the protocol. To directly address this significant challenge, our research endeavors to introduce synchronization points into the computational framework. These synchronization points serve as pivotal checkpoints strategically positioned within the computational process, facilitating the alignment and coordination of diverse computations. By incorporating synchronization points, we aim to foster a seamless and harmonized progression of computational tasks, thereby enhancing the ability of the protocol to effectively manage and control concurrent operations. Our approach entails substantial modifications to the underlying data structure, constituting a fundamental transformation aimed at augmenting the resilience of the protocol to parallel computation threats. Whereas previous iterations of the protocol relied on synchronization points scaled logarithmically in accordance with the total number of nodes, our new strategy entails a significant escalation in the number of synchronization points. This amplification, now directly aligned with the linear expansion of nodes, provides an exponential increase in the number of synchronization points. Importantly, this change is transparent to the end-user; just as the end-user did not directly interact with or perceive the hashcash computations before, they remain unaware of these processes now.

2. Background

This section summarizes the main notions involved in the definition of the two-phase challenge–response protocol based on hashcash trees [13].

2.1. Hash Functions and Hashcash

The term string is commonly used to refer to binary strings, which are sequences of elements from the set ${\{0,1\}}^{*}$, representing binary digits or bits. The empty string is denoted by $ϵ$. The term prefix describes the initial segment of a string s, specifically the first n bits where $n\in \mathbb{N}$; this segment is represented as $\mathit{prefix}(s,n)$. The concatenation of two strings $s,s^{\prime }$ is denoted by $s\left|\right|s^{\prime }$. The expression $s\left|\right|x$ is sometimes used informally to represent the concatenation of a string s with the binary string representation of a non-negative integer x. We define the concatenation of a string s with itself $n\in \mathbb{N}$ times, denoted as $s^n$, through the following definition: $s^0=ϵ$; $s^{n+1}=s^n\left|\right|s$ for $n\ge 1$. The i-th element of a string s, and in general of a sequence or tuple, is denoted by ${s|}_i$.

Example 1.

Considering the concatenation $11110000\left|\right|328$, assuming an 8-bit representation of the integer 328, we obtain 11110000101001000. The string ${\left(010\right)}^4$ becomes 010010010010. ■

A hash function is a type of function that transforms strings of any length into strings of a consistent length. If $m\in {\mathbb{N}}^{+}$ is a positive integer representing this fixed length, the signature of the hash function is defined as follows:

$$\begin{array}{c}\hfill h:{\{0,1\}}^{*}\to {\{0,1\}}^m.\end{array}$$

(1)

For a string s being an element of the set ${\{0,1\}}^{*}$, the result $h\left(s\right)$ generated by the hash function h is called the hash value of s; s is called the message. Additionally, cryptographic hash functions ensure the following properties:

(i)

the probability of a particular hash value for a message is $2^{-m}$;

(ii)

finding a message that matches a given hash value is unfeasible (preimage resistance);

(iii)

finding a second message that matches the hash value of a given message is unfeasible (second-preimage resistance);

(iv)

finding two different messages that yield the same hash value is unfeasible (collision resistance).

Hashcash is a (nondeterministic) function that depends on a hash function h and a positive integer k. It associates every input string s from the set of binary strings with any pair $〈h\left(s\right|\left|x\right),x〉$ such that x is a natural number and $\mathit{prefix}\left(h\right(s\left|\right|x),k)=0^k$. Let $h_k\left(s\right)$ represent any acceptable output $〈h\left(s\right|\left|x\right),x〉$ of the hashcash function configured with parameters h and k. Hashcash essentially requires identifying partial hash collisions within the prefix of zeros of length k, and the most efficient method for achieving this is through brute force [14]; see Algorithm 1. If we assume that the brute force algorithm starts with $x=0$, obtaining a valid output value $〈h\left(s\right||x^{\prime }),x^{\prime }〉$ necessitates computing $x^{\prime }+1$ hash values. Overall, hashcash incurs an unbounded probabilistic cost, implying that theoretically, the brute force algorithm could iterate indefinitely. However, the probability of not finding a solution diminishes rapidly toward zero. Conversely, confirming that $〈h\left(s\right|\left|x\right),x〉$ constitutes a valid output entails computing just one hash value, as shown in Algorithm 2.

Algorithm 1: Hashcash(s, h, k)

Algorithm 2: HashcashVerify($〈\mathit{hash}\_\mathit{value},x〉$, s, h, k)

1 return $\mathit{prefix}(\mathit{hash}\_\mathit{value},k)=0^k$ and $\mathit{hash}\_\mathit{value}=h\left(s\right|\left|x\right)$;

2.2. Hashcash Trees

A labeled binary tree T can be described as either an empty set ∅ or a quadruple $〈r,\ell ,L,R〉$, where r represents the root node (of T), ℓ denotes the label associated with r, and L and R are labeled binary trees referred to as the left child and the right child, respectively, of both T and r; r, L, and R are represented as $\mathit{root}\left(T\right)$, $\mathit{left}\left(T\right)$, and $\mathit{right}\left(T\right)$, respectively. (In the subsequent context, the term tree denotes labeled binary trees). Nodes of a tree are defined inductively: $\mathit{nodes}(\varnothing ):=\varnothing$; $\mathit{nodes}\left(〈r,\ell ,L,R〉\right):=\left\{r\right\}\cup \mathit{nodes}\left(L\right)\cup \mathit{nodes}\left(R\right)$. When both L and R are empty, the node r is also referred to as a leaf. Leaves of a tree are defined inductively: $\mathit{leaves}(\varnothing ):=\varnothing$; $\mathit{leaves}\left(〈r,\ell ,\varnothing ,\varnothing 〉\right):=\left\{r\right\}$; $\mathit{leaves}\left(〈r,\ell ,L,R〉\right):=\mathit{leaves}\left(L\right)\cup \mathit{leaves}\left(R\right)$, if $L\ne \varnothing$ or $R\ne \varnothing$. An internal node of T is any node within T that is not a leaf, thus defined as $\mathit{internal}\left(T\right):=\mathit{nodes}\left(T\right)\setminus \mathit{leaves}\left(T\right)$. Let $v\in \mathit{nodes}\left(T\right)$ be a node of $T=〈r,\ell ,L,R〉$. The label of v in T is defined inductively: $\mathit{label}(v,\varnothing ):=ϵ$; $\mathit{label}(v,T):=\ell$ if $v=r$; $\mathit{label}(v,T):=\mathit{label}(v,L)$ if $v\in \mathit{nodes}\left(L\right)$; $\mathit{label}(v,T):=\mathit{label}(v,R)$ if $v\in \mathit{nodes}\left(R\right)$. The level of v in T is defined inductively: $\mathit{level}(v,T):=1$ if $v=r$; $\mathit{level}(v,T):=1+\mathit{level}(v,L)$ if $v\in \mathit{nodes}\left(L\right)$; $\mathit{level}(v,T):=1+\mathit{level}(v,R)$ if $v\in \mathit{nodes}\left(R\right)$. A tree is considered perfect if every internal node has nonempty children, and all leaves are situated at the same level. (For the subsequent discussions, only perfect trees are under consideration). The height of a tree corresponds to the depth at which its leaves are situated. The order of v within T is determined using breadth-first search (BFS) or level-order search as follows: $\mathit{order}(r,T):=1$; for each occurrence of $〈v,{\ell }^{\prime },L^{\prime },R^{\prime }〉$ in T, $\mathit{order}(\mathit{root}\left(L^{\prime }\right),T):=2·\mathit{order}(v,T)$ and $\mathit{order}(\mathit{root}\left(R^{\prime }\right),T):=2·\mathit{order}(v,T)+1$. Note that T can be efficiently represented using a one-based $\mathit{arr}$ of size $\left|\mathit{nodes}\right(T\left)\right|$, where $\mathit{arr}\left[i\right]=\mathit{label}(v,T)$ whenever $\mathit{order}(v,T)=i$.

A hash tree, also known as a Merkle tree, is a tree structure where each leaf node contains the hash value of a data block, and each internal node contains the hash value computed from the concatenation of the hash values of its child nodes. In this context, a data block refers to any piece of information within a commitment scheme, representing concealed data that remain unalterable. Moreover, sharing the hash value linked to the root ensures the integrity of the entire hash tree, preventing any modification to its labels. To ascertain that a particular data block $s_i$ (where $i\in [1..2^n]$) within a sequence $s_1,\dots ,s_{2^n}$ associated with the hash tree T (for $n\in \mathbb{N}$) has not been altered, it is adequate to examine the nodes along the path from the leaf labeled with $h\left(s_i\right)$ to the root. The verification process entails examining the labels of these nodes and the hash values of their child nodes; in formulas, if $v_o$ denotes the node of T such that $\mathit{oder}(v_o,T)=o$, the labels involved in the verification of $s_i$ are $\mathit{label}(v_{\lfloor i·2^{-j}\rfloor },T)$ and $\mathit{label}(v_{\lfloor i·2^{-j}\rfloor +1},T)$ for $j\in [0..n-1]$.

The definition of the hashcash tree is based on fixed parameters: a hash function h and a positive integer k. Remember that $h_k\left(s\right)$ denotes any pair $〈h\left(s\right|\left|x\right),x〉$ where $x\in \mathbb{N}$ and $\mathit{prefix}\left(h\right(s\left|\right|x),k)=0^k$. Consider a string s and a positive integer $n\in {\mathbb{N}}^{+}$. Define the (nondeterministic) sequence of labels ${\left({\ell }_i\right)}_{i\in {\mathbb{N}}^{+}}$ as follows:

$$\begin{array}{c}\hfill {\ell }_i:=\left\{\begin{array}{cc}{h}_k\left(s\left|\right|i\left|\right|\left({\ell }_{2i}{|}_1\right)\left|\right|\left({\ell }_{2i+1}{|}_1\right)\right)\hfill & \mathrm{if}i\in [1..n];\hfill \\ 〈ϵ,0〉\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(2)

The hashcash tree of size n for the string s is a perfect tree T with a height of $\lceil {\mathit{log}}_2\left(n\right)\rceil$. In this tree, for each node v, if its order in the tree T is i, then the label of the node v is set to ${\ell }_i$. To construct a hashcash tree of size n, the process begins by calculating the labels of the nodes at the highest level (i.e., the leaves), which corresponds to $\lceil {\mathit{log}}_2\left(n\right)\rceil$. Subsequently, the algorithm iteratively computes the labels of nodes at preceding levels until reaching the root node. Overall, the algorithm executes n hashcash computations.

Similar to a hash tree, verifying a leaf i within a hashcash tree T entails examining the nodes along the path from i to the root of T, as well as their children; see Algorithm 4. More precisely, the algorithm validates the prefixes of all hash values associated with these nodes (lines 8–9), recalculating hash values only for nodes along the path from i to the root of T (lines 2–6).

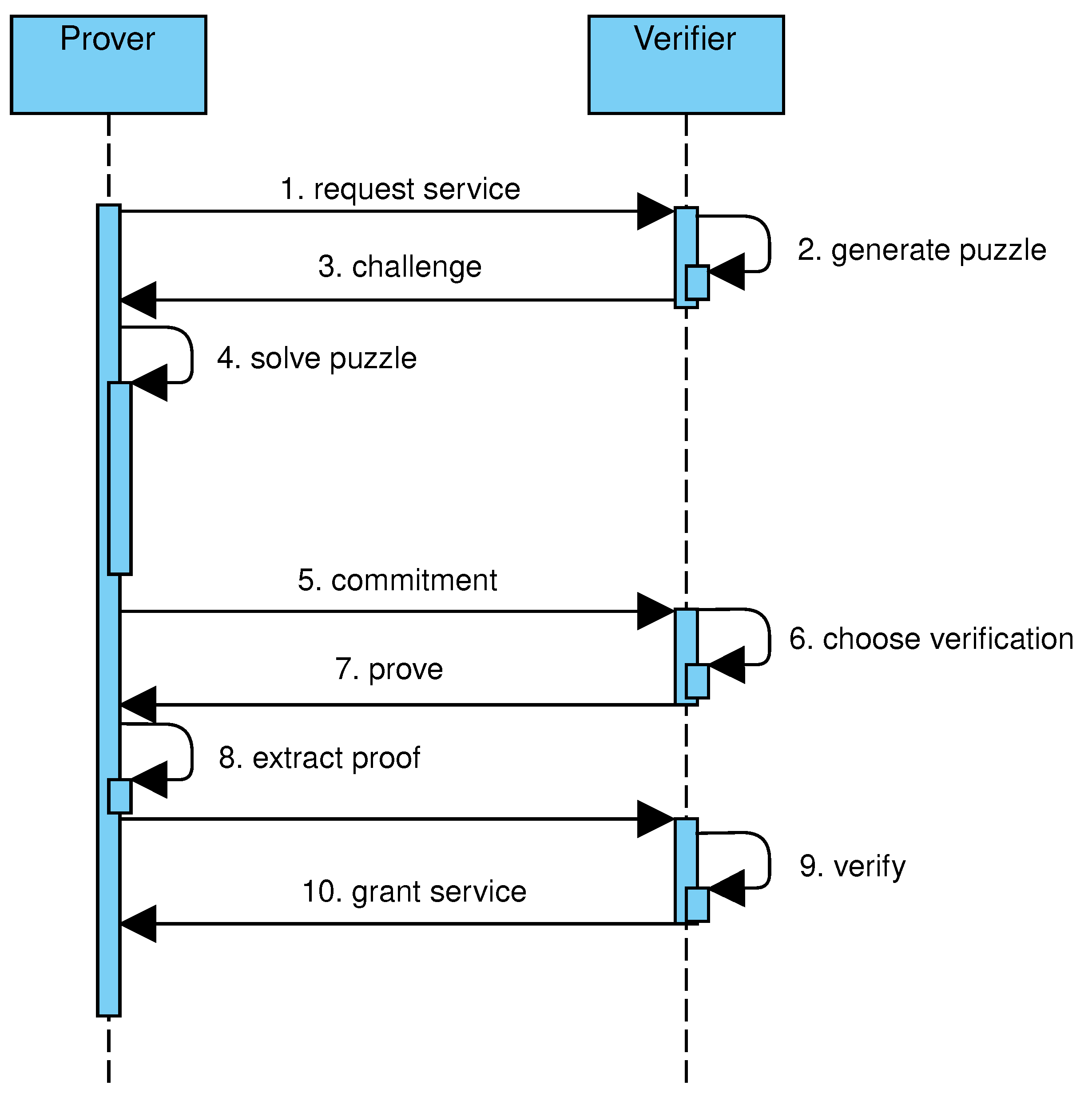
2.3. Client Puzzle Protocols

A client puzzle protocol (CPP) consists of two participants: a verifier V and a prover P. P must utilize a resource of V that is computationally expensive. Before handling the request from P, V challenges P to solve a puzzle. The two-phase challenge–response CPP (see Figure 1) based on Algorithms 3 and 4 involves the following procedures:

• At the beginning, the verifier V generates and retains a master key denoted as $\mathit{mk}$.
• To initiate the process, the prover P must transmit a request $\mathit{req}$ to V. To accomplish this, P sends $\mathit{Req}:=h\left(\mathit{req}\right)$ to V.
• Based on its current workload, V determines the difficulty parameter $n\in {\mathbb{N}}^{+}$, generates a timestamp t indicating the deadline for completing the protocol, calculates $s:=h\left(\mathit{mk}\right|\left|\mathit{Req}\right|\left|n\right|\left|t\right)$, and transmits $〈s,n,t〉$ to P.
• P computes and generates the hashcash tree T of size n for s using Algorithm 3 and subsequently transmits $〈\mathit{sol},s,n,t,\mathit{Req}〉$ to V. Here, $\mathit{sol}$ is ${\mathit{label}\left(\mathit{root}\left(T\right)\right)|}_1$.
• V verifies that $s=h\left(\mathit{mk}\right|\left|\mathit{Req}\right|\left|n\right|\left|t\right)$; ensures that t represents a future timestamp; randomly chooses a number i within the range $[2^{H-1}..2^H-1]$ (referring to a leaf node); and sends $〈I,i〉$ to P, where $I:=h\left(\mathit{mk}\right|\left|\mathit{Req}\right|\left|\mathit{sol}\right|\left|i\right)$.
• P sends $〈\mathit{req},S,I,i,s,n,t,\mathit{Req}〉$ to V, where S comprises the labels associated with nodes along the path from i to the root as well as their child nodes; in formulas, S represents the sequence containing ${\ell }_1$ for $j\in [1..\lceil {\mathit{log}}_2\left(n\right)\rceil ]$, ${\ell }_{2·\lfloor i·2^{-j}\rfloor }$, and ${\ell }_{2·\lfloor i·2^{-j}\rfloor +1}$. (As an optimization, integer witnesses for labels that are not on the path from i to the root can be excluded).
• V checks all the following conditions: $s=h\left(\mathit{mk}\right|\left|\mathit{Req}\right|\left|n\right|\left|t\right)$; t is in the future; $I=h\left(\mathit{mk}\right|\left|\mathit{Req}\right|\left|\mathit{sol}\right|\left|i\right)$, where $\mathit{sol}$ is ${\ell }_1{|}_1$ in S (i.e., the hash value linked to the root of the partial hashcash tree transmitted by P); S is valid; $\mathit{Req}=h\left(\mathit{req}\right)$. If all criteria are satisfied, the request $\mathit{req}$ is handled.

At step 7, the validation of S involves verifying that each label ${\ell }_j$ along the path from i to the root is computed according to (2); Algorithm 4 is used for this purpose.

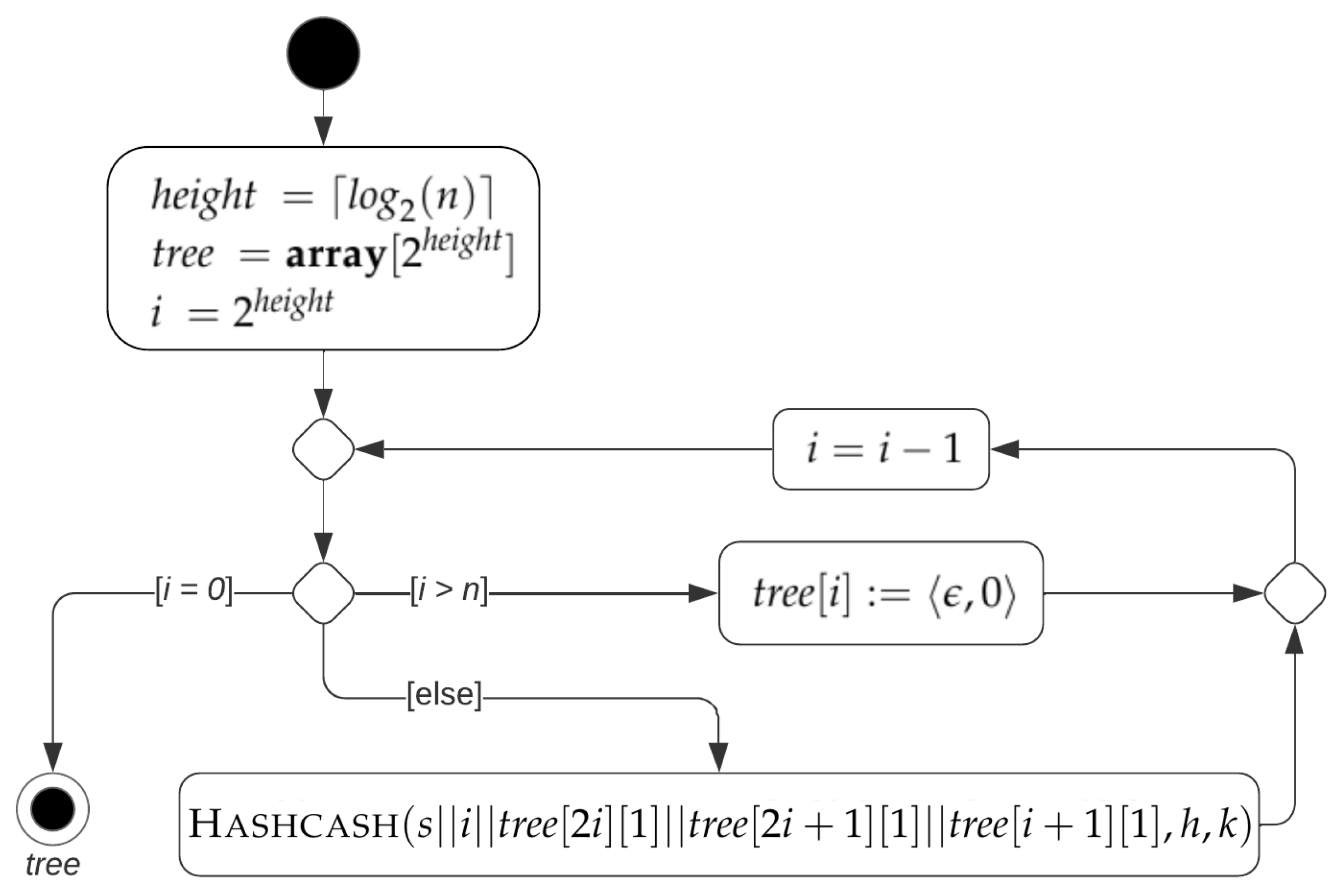
Algorithm 3: HashcashTree(s, n, h, k)

Algorithm 4: HashcashTreeVerify(T, i, s, n, h, k)

3. Hashcash Tree with Improved Parallel Resistance

In order to improve the parallel resistance of hashcash trees, we modify the way labels of nodes are computed. In the refined hashcash tree, the label of each node is generated by computing the hashcash of a string that encompasses not only the labels of the children nodes but also incorporates the label of the subsequent node in a BFS. This slight alteration in the label generation process introduces a significant enhancement by incorporating additional synchronization points into the computational framework. By including the label of the subsequent node in the sequence along with the labels of the children nodes, each node label becomes intricately intertwined with its subsequent nodes. This creates more frequent points within the computation where different tasks must align or synchronize, effectively introducing more synchronization points into the process. As a result, the protocol gains heightened resistance to parallel computation, as tasks are forced to be computed sequentially.

Formally, the new label of the i-th node is defined as follows:

$$\begin{array}{c}\hfill {\ell }_i:=\left\{\begin{array}{cc}{h}_k\left(s\left|\right|i\left|\right|\left({\ell }_{2i}{|}_1\right)\left|\right|\left({\ell }_{2i+1}{|}_1\right)\left|\right|\left({\ell }_{i+1}{|}_1\right)\right)\hfill & \mathrm{if}i\in [1..n];\hfill \\ 〈ϵ,0〉\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(3)

Accordingly, line 7 of Algorithm 3 is modified as follows:

  7’

$\mathit{tree}\left[i\right]:=$ Hashcash$\left(s\right|\left|i\right|\left|\mathit{tree}\right[2i\left]\right[1\left]\right|\left|\mathit{tree}\right[2i+1\left]\right[1\left]\right|\left|\mathit{tree}\right[i+1\left]\right[1],h,k)$;

Regarding the verification procedure reported in Algorithm 4, two changes are needed.

First of all, line 5 is modified by including the label of the following node in BFS:

  5’

$\mathit{next}:=\mathit{label}(v_{i+1},T)$ $\mathbf{if}$ $i<n$ $\mathbf{else}$ $ϵ$;

  5”

if not HashcashVerify$(\mathit{label}(v_i,T),s|\left|i\right|\left|\mathit{left}\right|\left|\mathit{right}\right||\mathit{next},h,k)\mathbf{then}$

Finally, it is required to verify the prefix of the following node; therefore, line 8 is modified as follows:

  8” if

$\mathit{prefix}\left(\mathit{label}(v_{2i},T){|}_1\right)\ne 0^k \mathbf{or} \mathit{prefix}\left(\mathit{label}(v_{2i+1},T){|}_1\right)\ne 0^k\mathbf{or}$

$\mathit{prefix}\left(\mathit{label}(v_{i+1},T){|}_1\right)\ne 0^k\mathbf{then}$

Activity diagrams of the modified versions of Algorithms 3 and 4 are shown in Figure 2 and Figure 3. It can be observed that the label of each node depends on those of the children and next node in BFS. In the construction of a hashcash tree (Figure 2), the number of hashcash computations stays the same as in the previous version, as the only difference is the message that is passed to the hashcash function. In the verification of a hashcash tree (Figure 3), the dependency on the next node in BFS ensures that the labels have been computed sequentially, from the last node in BFS to the root, while the dependency on the children allows for restricting the nodes to verify to those in the path from a leaf to the root.

The CPP presented in Section 2 is adapted to the modified algorithms as follows (we report only the modified steps):

4’

P computes and generates the hashcash tree T of size n for s using the modified version of Algorithm 3 shown in Figure 2; subsequently, it transmits $〈\mathit{sol},s,n,t,\mathit{Req}〉$ to V. Here, $\mathit{sol}$ is ${\mathit{label}\left(\mathit{root}\left(T\right)\right)|}_1$.

6’

P sends $〈\mathit{req},S,I,i,s,n,t,\mathit{Req}〉$ to V, where S comprises the labels associated with nodes along the path from i to the root as well as their child nodes and subsequent nodes in BFS; in formulas, S represents the sequence containing ${\ell }_1$ and, for $j\in [1..\lceil {\mathit{log}}_2\left(n\right)\rceil ]$, ${\ell }_{2·\lfloor i·2^{-j}\rfloor }$, ${\ell }_{2·\lfloor i·2^{-j}\rfloor +1}$, and ${\ell }_{\lfloor i·2^{-j}\rfloor +1}$. (As an optimization, integer witnesses for labels that are not on the path from i to the root can be excluded).

7’

V checks all the following conditions: $s=h\left(\mathit{mk}\right|\left|\mathit{Req}\right|\left|n\right|\left|t\right)$; t is in the future; $I=h\left(\mathit{mk}\right|\left|\mathit{Req}\right|\left|\mathit{sol}\right|\left|i\right)$, where $\mathit{sol}$ is ${\ell }_1{|}_1$ in S (i.e., the hash value linked to the root of the partial hashcash tree transmitted by P); S is valid; $\mathit{Req}=h\left(\mathit{req}\right)$. Here, the validation of S involves verifying that each label ${\ell }_j$ along the path from i to the root is computed according to (3); the modified version of Algorithm 4 shown in Figure 3 is used for this purpose. If all criteria are satisfied, the request $\mathit{req}$ is handled.

The original version of the CPP based on hashcash trees provides partial resistance to parallel computation: Indeed, it was shown that any parallel implementation of the original HashcashTree$(s,n,h,k)$ includes at least $\lceil {\mathit{log}}_2\left(n\right)\rceil$ sequential hashcash computations (i.e., calls to Algorithm 1; Theorem 3 in [13]). The result is derived from the observation that the hashcash tree exhibits resistance to parallel computation along its paths. Specifically, the labels of internal nodes are determined by computing hashcash output values for strings that encompass the hash values linked to their respective child nodes. This methodology unveils that the height of the hashcash tree serves as an indicator of its resistance to parallel computation. The addition of the label of next node in BFS to the message passed to hashcash exponentially improves this indicator.

Theorem 1.

Any parallel implementation of the modified HashcashTree $(s,n,h,k)$ (Figure 2) includes at least n sequential calls to Algorithm 1.

Proof. 

The computation of the label of each node in the hashcash tree, including all leaves but the last in BFS (i.e., node $v_n$), is a synchronization point: the computation of the label of every node but $v_n$ cannot start before the label of the next node in BFS is completed. It turns out that n sequential calls to hashcash are required, and the proof is complete. □

Thanks to the presence of the labels of the child nodes, other computational properties of the CPP are preserved. In particular, Theorems 1 and 2 in [13] are unaffected:

• The probability that HashcashTree$(s,n,h,k)$ terminates after computing $N+n$ hash values is

  $$\begin{array}{c}\hfill \left(\genfrac{}{}{0pt}{}{N+n-1}{N}\right){(1-2^{-k})}^N·2^{-k·n}\end{array}$$

  for all $N\in \mathbb{N}$. On average, the number of unused hash values computed by Algorithm 3 (via Algorithm 1) is $n·(1-2^{-k})·2^k$, with variance $n·(1-2^{-k})·2^{2k}$.
• HashcashTreeVerify$(T,i,s,n,h,k)$ terminates after computing at most $\lceil {\mathit{log}}_2\left(n\right)\rceil$ hash values.

4. Implementation and Experiment

In this section, we present the implementation and evaluation of a new version of the hashcash tree data structure. We leveraged the proof-of-concept code for the hashcash tree presented in [13] as a foundation. This code is available on GitHub (https://github.com/alviano/hashcash-tree; accessed on 1 July 2024). To facilitate a performance comparison, we also implemented a parallel algorithm to construct the original version of the hashcash tree. This implementation utilizes the ProcessPoolExecutor class from Python’s concurrent. futures library (https://docs.python.org/dev/library/concurrent.futures.html; accessed on 1 July 2024) to execute tasks asynchronously using a pool of worker processes.

To assess the performance and properties of the newly developed data structure, we integrated benchmark code within the implemented codebase. These benchmarks aim to answer the following specific research questions:

Q1

Overhead of the New Data Structure: This question investigates the additional processing time or resource consumption introduced by the new data structure compared to the original version. We will measure the overhead by comparing the execution times of equivalent operations on both data structures for various input sizes and configurations.

Q2

Parallel Resistance Weakness: This question explores the vulnerability of the original hashcash tree to parallelized construction attempts. We will identify parameter settings (e.g., tree size and hash function choice) under which the effectiveness of the original data structure deteriorates when utilizing parallel processing for construction. This will involve running the parallel construction algorithm for the original data structure with various parameter combinations and analyzing the impact on execution time and security properties.

By answering these questions, we aim to gain insights into the trade-offs between performance and security offered by the new data structure and identify potential weaknesses in the possibility to parallelize the construction of the original hashcash tree.

Our experiments were conducted on a high-performance computing system equipped with a dual CPU AMD EPYC 7313 processor. Each CPU offers 16 cores, resulting in a total of 32 processing cores available for parallel execution. The system boasts a generous 2TB of RAM, providing ample memory for data processing. To ensure consistent results and prevent resource exhaustion on the host machine, we imposed a time limit of 600 s (10 min) per experiment run and limited memory usage to a maximum of 16GB per run.

Our benchmarks focused on evaluating the performance of both the original and new hashcash tree data structures under varying conditions. We manipulated three key parameters:

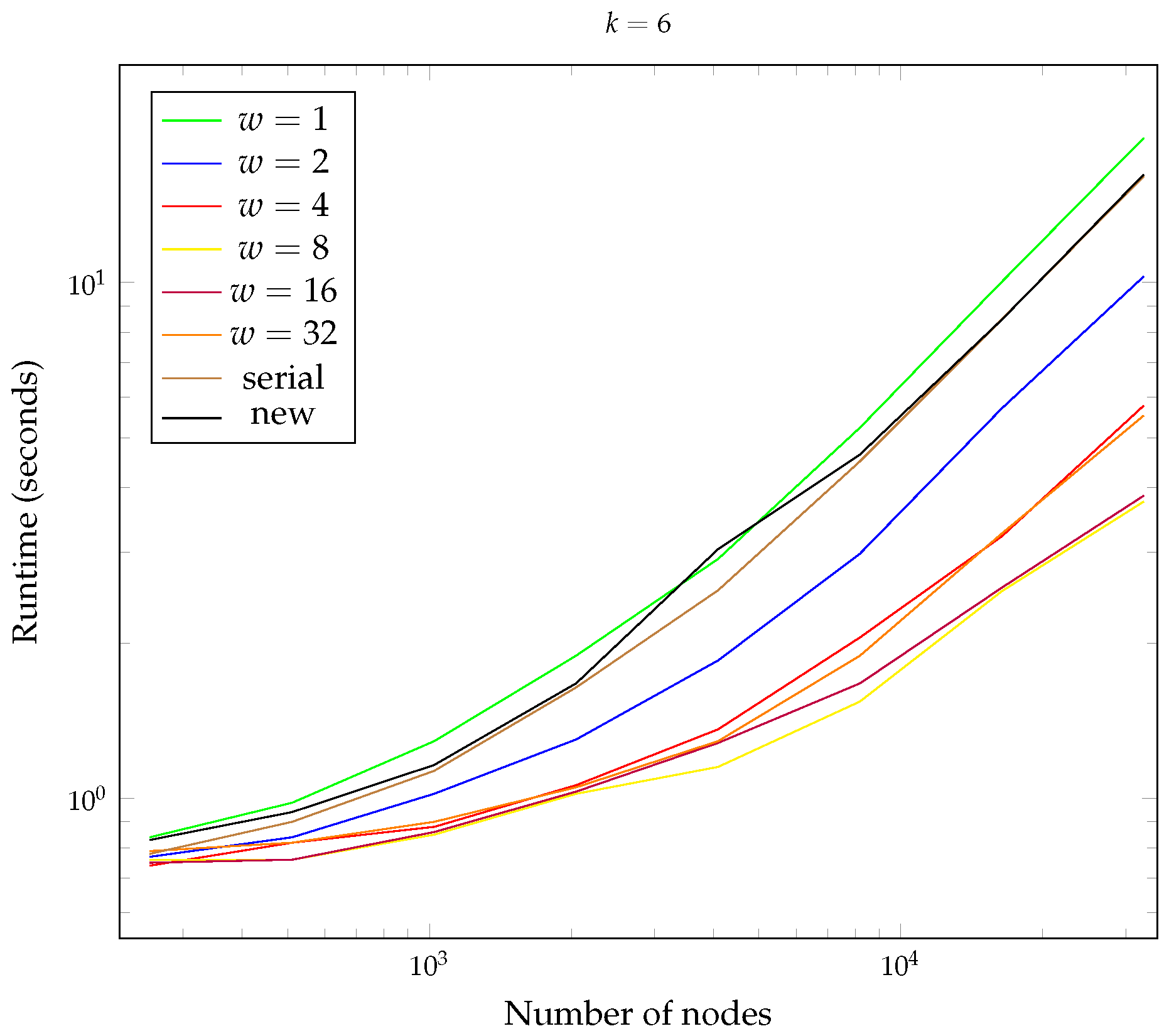
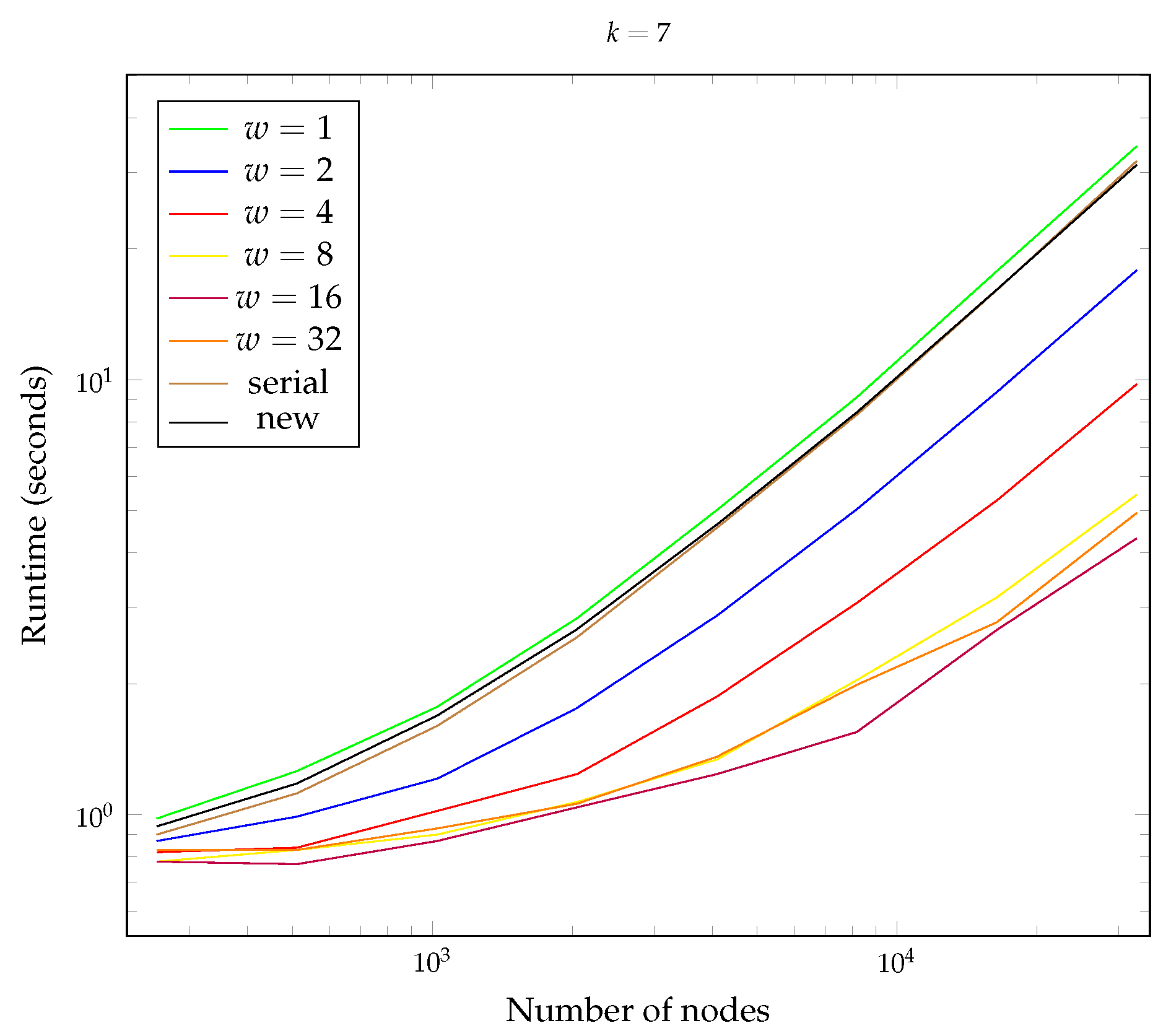
• Prefix Length (k): This parameter controls the difficulty of the proof-of-work mechanism within the hashcash tree. We varied the prefix length (denoted by k) to assess its impact on construction time.
• Number of Nodes: This parameter determines the size of the hashcash tree, directly influencing the number of hashing operations required during construction, and therefore providing a fine-grained control on the difficulty of the proof-of-work mechanism within the hashcash tree. We experimented with different tree sizes to understand the scalability of both data structures.
• Number of Parallel Workers (w): This parameter is specific to the parallel construction algorithm for the original hashcash tree. It controls the number of worker processes utilized for concurrent execution. By varying the number of workers (denoted by w), we aimed to identify potential weaknesses in the possibility to parallelize the construction of the original hashcash tree.

We measured the runtime required to build both the original and new hashcash tree data structures. This involved running multiple experiments for various combinations of the three parameters mentioned above. For the original data structure, we recorded the runtime of the serial construction algorithm as well as the parallel construction algorithm with different numbers of worker processes.

The detailed results of our experiments are presented in Figure 4, Figure 5 and Figure 6. As an initial observation, consistent across all plots, the construction time of the new data structure closely matches the runtime of the original hashcash tree built using the serial algorithm. This finding directly addresses research question Q1: the new data structure does not introduce any significant overhead in terms of processing time compared to the previous version. This is a promising result, suggesting that the new data structure offers enhanced functionality without compromising performance on the core construction operation. Figure 4 sheds light on research question Q2, which explores the vulnerability of the original hashcash tree to parallelization. Here, we observe a critical interplay between the prefix length (k) and the effectiveness of parallel construction (parameter w). For short prefix lengths ($k=4$), the computation associated with each node in the hashcash tree is relatively fast. This swift computation time renders parallelization inefficient due to the overhead introduced by communication and synchronization between worker processes. This inefficiency is particularly evident when comparing the serial and parallel construction times for $k=4$. The serial construction finishes significantly faster than the parallel version with just one worker. As the prefix length increases ($k=5$), the workload for each node becomes more intensive. This allows the parallel approach to demonstrate some performance gains, but these gains are limited. With $k=5$, some speedup is observed up to $w=4$ workers. However, the trend changes for even longer prefixes ($k=6$, 7, and 8, as shown in Figure 5 and Figure 6). Here, the increased workload per node due to the longer prefix makes parallelization more advantageous. We observe a clear reduction in construction time when utilizing a larger number of parallel workers ($w=8$ for $k=6$ or 7 and $w=16$ for $k=8$).

Based on these observations, we can conclude that the original hashcash tree exhibits a weakness in its partial parallel resistance when the prefix length surpasses $k=4$ zeros. This finding is particularly relevant considering the recommendation of $k=4$ or 5 zeros for prefix length in the previous work [13]. Our analysis provides evidence that $k=4$ remains the preferred choice for the original hashcash tree to maintain its parallel resistance. For scenarios requiring a longer prefix (e.g., $k=5$), the new data structure emerges as a more suitable option, likely due to its inherent design inhibiting parallelization of node construction. This highlights the advantage of the new data structure in situations where stronger proof-of-work guarantees are necessary.

In order to test the puzzle protocol under varying conditions, we used the stress-ng utility (https://github.com/ColinIanKing/stress-ng; accessed on 1 July 2024) to simulate increasing workloads. In particular, we used the command stress-ng --cpu n, where n was assigned values between 1 and 32, to spawn n workers, each of which uses a CPU at 100%. Prefix length was fixed to 4 and the size of the hashcash tree was increased from 15 to 255 nodes. We measured the CPU usage (user time + system time) of both server and client to address 1000 (one thousand) requests, as well as the elapsed real (wall clock) time used by the process. Results are shown in

Table 1. Stress test of the puzzle protocol. Times expressed in seconds.

	Size
Stress	15	31	63	127	255
1	38% (8.54 s)	38% (10.63 s)	31% (14.47 s)	25% (23.11 s)	18% (39.38 s)
2	39% (8.66 s)	35% (10.68 s)	30% (14.68 s)	23% (22.77 s)	17% (39.22 s)
4	43% (8.48 s)	38% (10.54 s)	30% (14.58 s)	23% (22.87 s)	17% (38.61 s)
8	38% (8.75 s)	35% (10.61 s)	29% (14.77 s)	23% (22.44 s)	16% (38.75 s)
16	38% (8.58 s)	34% (10.86 s)	28% (14.88 s)	21% (22.73 s)	16% (39.09 s)
32	35% (8.94 s)	32% (11.55 s)	27% (15.15 s)	30% (24.10 s)	11% (52.86 s)

, where we report the wall clock time and the percentage of CPU time used by the server (with respect to the total CPU time used by both the server and the client; we recall here that the time of the server includes the CPU usage for running FastAPI). It can be observed that even for hashcash trees of small size (15 or 31 nodes), the server has to address an easier computational task than the one addressed by the client. Finally, we observe that the effort of the server is not significantly affected by the workload of the server, which anyhow is expected to be monitored to determine the size of hashcash trees: in case the server is overloaded, access to resources is granted only after the client computes a hashcash tree of relatively large size so as to delay the rate of incoming requests.

5. Related Work

Detecting DoS attacks remains a significant challenge, often requiring sophisticated techniques like machine learning approaches [4,5,6] (see also the survey by de Neira et al. [7]). As a proactive measure, prevention techniques offer valuable protection for critical services and organizational assets [15,16]. This work focuses on client puzzle protocols as a preventative technique specifically designed to mitigate DoS attacks.

The concept of client puzzles originated with Juels and Brainard [17], who proposed their use to prevent DoS attacks. The core principle behind client puzzles is that they are solvable by a legitimate user within a reasonable time frame (polynomial time) while requiring a minimal amount of computational resources. This allows the server to grant access to its resources only upon receiving a valid solution to a newly presented client puzzle. Similar concepts were explored by Dwork and Naor [9] with the introduction of pricing functions to combat junk emails, and by Rivest, Shamir, and Wagner [18] with timed-lock puzzles for timed-release cryptography. Effective client puzzles are expected to possess several key properties:

• Unforgeability: it should be computationally infeasible for an attacker to forge a valid solution without actually solving the puzzle [19].
• Difficulty: solving a client puzzle should require a sufficient amount of computational effort to deter attackers from launching resource-intensive DoS attacks.
• Determinable Difficulty: ideally, the server should be able to determine the difficulty level of the puzzle beforehand [20].
• Parallel Computation Resistance: the puzzle’s difficulty should not significantly decrease when attackers attempt to solve it using parallel processing techniques [20].

Client puzzles can be broadly categorized into two main classes based on the computational resource they primarily rely on during the solving process: CPU-bound and memory-bound puzzles.

• CPU-bound Client Puzzles: In this category, the effort required by the prover (typically a client) to solve the puzzle is measured by the number of CPU cycles needed. Several client puzzle schemes fall under this category, as presented in the works by Back et al. (2002) [11], Chen et al. (2009) [19], Dwork and Naor (1992) [9], Jakobsson and Juels (1999) [21], Juels and Brainard (1999) [17], Rivest et al. (1996) [18], Tritilanunt et al. (2007) [22], and Waters et al. (2004) [23].
• Memory-bound Client Puzzles: For memory-bound client puzzles, the solving effort is measured by the number of memory lookups required. The primary motivation behind memory-bound puzzles stems from the observation that CPU power can vary significantly across different computers, whereas memory access speeds tend to be more uniform. This is supported by works from Abadi et al. (2005) [24], Dean (2001) [25], and Doshi and Moore (2006) [26].

This work elaborates on the Client Puzzle Protocol (CPP) introduced in [13]. It is a CPU-bound CCP and leverages a combination of hashcash [11] and hash trees [27]. The primary challenge associated with using hashcash alone stems from its unbounded probability cost. The only parameter that controls the difficulty of a hashcash puzzle is the prefix length (k). However, both the difficulty and variance of the puzzle increase exponentially with increasing k values. To address this limitation and gain finer control over puzzle difficulty, Juels and Brainard (1999) proposed a CPP that essentially involves solving multiple sub-puzzles [17]. However, the solutions to all such sub-puzzles have to be transmitted and verified, which is practically unfeasible. In contrast, verifying a hashcash tree only necessitates a logarithmic number of solution verifications. Coelho (2008) introduced a CPP based on hash trees [12]. This CPP can be viewed as a variant of the solution–verification version of the CPP given in Section 2.3, but with a key difference. In Coelho’s CPP, the prefix length is fixed at $k=0$ (effectively disabling hashcash) [11]. The tree is then constructed based on the service description, and a selection of leaves are chosen for verification based on the root hash value. While this approach offers high precision in determining puzzle difficulty, it suffers from the potential for rapid growth in hash tree size. This poses a significant challenge, as the prover needs to store (or recompute) the entire hash tree to provide verification labels, which are only discovered after calculating the root hash. In contrast, the CPP we opted for leverages smaller trees. This is achieved by enabling hashcash, which allows for controlling the difficulty by adjusting the length of the required prefix for each individual node within the tree.

This work addresses a potential weakness identified in the original hashcash tree data structure: its susceptibility to a parallel processing attack. Traditionally, the construction of hashcash trees involved minimal synchronization between processing units, allowing an attacker to distribute the workload across multiple processors and potentially solve the puzzles significantly faster. This could render the DoS prevention mechanism less effective. To address this issue, we introduced strategic synchronization points within the construction process of the hashcash tree. These synchronization points act as dependencies, essentially forcing different processing units (e.g., CPU cores) to wait for each other at specific stages. This deliberate introduction of dependencies effectively disrupts the attacker’s ability to fully parallelize the workload, hindering their attempt to exploit the system’s resources. We further validated this approach through empirical studies. Our experiments confirm that the original version of the hashcash tree exhibited a significant weakness in its parallel resistance. In contrast, the modified version incorporating synchronization points demonstrated a substantial improvement in this aspect. This improvement translates to a more robust defense against DoS attacks, as parallelization becomes less advantageous for attackers.

In addition to the improvements introduced by the hashcash tree method, it is important to compare it with other DoS mitigation techniques to provide a comprehensive understanding of its relative advantages and limitations. In particular, we consider here memory-bound puzzles and machine-learning-based anomaly detection. Memory-bound puzzles are designed to be computationally intensive in terms of memory access rather than CPU usage. They are particularly effective against attackers using specialized hardware optimized for CPU-bound tasks. Among their strengths, memory-bound puzzles are difficult to solve with specialized hardware, ensuring a more level playing field between attackers and legitimate users. On the other hand, these puzzles can be inefficient on devices with limited memory, potentially leading to denial of service to legitimate users as well. While memory-bound puzzles are effective in certain scenarios, they cannot be employed to protect services that are accessed by general audience, who may use devices with limited memory. Machine learning techniques for DoS mitigation involve training models to detect anomalies in network traffic that may indicate an ongoing attack. Among their strengths, machine learning models can adapt to new attack patterns and have the potential for high accuracy in detecting sophisticated attacks. On the other hand, these techniques require extensive datasets for training, are complex to implement, and can suffer from false positives and negatives. While machine learning offers adaptability and accuracy, hashcash trees provide a simpler and more deterministic approach. They are easier to implement and do not require large datasets for training. Additionally, hashcash trees can be deployed in real-time scenarios with predictable performance, unlike machine learning models which might require periodic retraining and tuning. Nonetheless, it is also important to note that a more advanced mitigation method can be obtained by combining machine-learning-based anomaly detection systems and hashcash trees, essentially by determining the parameters controlling the difficulty in constructing the hashcash tree based on the anomaly level detected by the machine learning algorithms.

As a final remark, our work builds upon the concept of PoW for securing decentralized systems. Recent research by Baniata and Kertesz (2024) [28] analyzed the security of PoW-based blockchains, identifying a critical difficulty level where attackers can exploit the system with minimal resources. This emphasizes the need for robust security measures alongside increasing difficulty. Additionally, Agarwal (2024) [29] proposed a PoW algorithm using Corona Graphs as an alternative to SHA-based hashing in blockchains. This approach allows for scalable difficulty based on graph size. While our work does not directly address PoW for blockchains, it contributes to the broader field of securing systems through cryptographic techniques. Our focus lies on leveraging PoW for client-side puzzles to prevent DoS attacks, offering a complementary approach to securing centralized systems.

6. Conclusions

In this work, we presented an improved version of the hashcash tree data structure designed to mitigate Denial-of-Service (DoS) attacks. We addressed a key limitation of the original design—its weakness against parallel processing attacks. Our approach involved strategically introducing synchronization points within the construction process, effectively disrupting an attacker’s ability to fully exploit parallelization for faster puzzle solving. We conducted benchmark experiments to evaluate the effectiveness of our modifications. The results confirmed that the original hashcash tree exhibited a significant vulnerability to parallelization, depending on the adopted length of the prefix. In contrast, the improved version incorporating synchronization points demonstrated a substantial improvement in parallel resistance. This translates to a more robust defense against DoS attacks. Our work highlights the importance of considering potential weaknesses in cryptographic constructions, particularly when parallelization is a possibility. The proposed modifications offer a valuable enhancement to the hashcash tree, making it a more reliable and secure solution for DoS prevention. Finally, it is important to observe that our puzzle protects the application layer, while lower layers need different protection mechanisms to prevent, among other attacks, volumetric attacks (e.g., UDP floods) or protocol attacks (e.g., SYN floods).