Analysis of a Dynamic Calibration Target for Through-Wall and Through-Rubble Motion Sensing Doppler Radar

Abstract

Through-wall and through-barrier motion-sensing systems are becoming increasingly important tools to locate humans concealed behind barriers and under rubble. The sensing performance of these systems is best determined with appropriately designed calibration targets, which are ones that can emulate human motion. The effectiveness of various dynamic calibration targets that emulate human respiration, heart rate, and other body motions were analyzed. Moreover, these targets should be amenable to field deployment and not manifest angular or orientation dependences. The three targets examined in this thesis possess spherical polyhedral geometries. Spherical geometries were selected due to their isotropic radar cross-sectional characteristics, which provide for consistent radar returns independent of the orientation of the radar transceiver relative to the test target. The aspect-independence of a sphere allows for more accurate and repeatable calibration of a radar than using a nonspherical calibration artifact. In addition, the radar cross section (RCS) for scattering spheres is well known and can be calculated using far-field approximations. For Doppler radar testing, it is desired to apply these calibration advantages to a dynamically expanding-and-contracting sphere-like device that can emulate motions of the human body. Monostatic RCS simulations at 3.6 GHz were documented for each geometry. The results provide a visual way of representing the effectiveness of each design as a dynamic calibration target for human detection purposes.

1. Introduction

Through-wall and through-rubble Doppler radar has proven to be an effective tool for human detection. Through-wall Doppler radar has become popular with the military and law enforcement, where through-wall sensing can locate people and help to diffuse a hostile situation. Through-rubble Doppler radar has found its niche in natural disaster events as well, where survivors buried under mounds of rubble can be detected, located, and brought to safety [1]. As the technology behind these radar systems evolves, research is underway to develop accurate, human-like calibration targets that can be used for the testing and optimization of these systems [2]. Radar calibration targets emulating human breathing and heartbeat are useful for the testing and optimization of these systems in realistic scenarios.

The ideal through-wall and through-rubble Doppler radar calibration target should provide (1) a radar cross section (RCS) that is nominally equivalent to that of a human and (2) an RCS that remains relatively constant at all viewing angles. In Doppler radar testing, the target’s RCS will largely impact the radar’s ability to distinguish between that target and the ambient noise around it. If the calibration target’s RCS is too small, the target may be undetectable. On the other hand, if its RCS is too large, the radar receiver front-end may be driven into saturation. Both these circumstances could result in a radar system being improperly tuned for human detection. For this reason, it is of great importance that the RCS of the calibration target resembles the radar cross section of a human [3]. Furthermore, it is likely that a through-barrier calibration target would be placed in rugged conditions (e.g., immersed in a rubble pit) during testing. In such a setting, the target is likely to move or rotate, which could be detrimental to the calibration process if its RCS is dependent on the viewing angle.

The ideal geometry for the calibration target that would satisfy both the above requirements is the perfect-electrical-conductor (PEC) sphere. PEC spheres have long been used for calibration due to the following properties: Firstly, the nondependence of its RCS on the viewing angle greatly simplifies the calibration procedure—a slight tilt or misalignment will not change the RCS of the sphere. Secondly, a sphere’s RCS is described by well-known formulas and can be easily calculated given its radius and the probing wavelength [4]. When operating in the optical region (i.e., when the radius is much larger than the radar wavelength), the RCS is simply a function of its size. This property allows the calibration target to be properly scaled so that its RCS nominally matches that of a human.

Since the calibration target is tailored for human sensing Doppler radar, it is paramount that the sphere is dynamic and capable of mimicking human physiological motion associated with heartbeat and respiration. This can be accomplished by dividing the sphere into multiple sections, thereby forming a spherical polyhedron. Each section of the polyhedron can then be controlled separately via linear actuators. As the actuators push and pull in unison, the polyhedron resembles a sphere repeatedly expanding and contracting. After proper dimensioning of the target, these oscillatory movements will bear resemblance to a human torso’s movements, such as respiration and heartbeat. The sections must move in unison to maintain the aspect independent RCS. However, the gaps that form when each section of the sphere moves radially to the expanded state may cause the desired aspect independence to be compromised because of the electrical discontinuities of the gaps. For this reason, various polyhedra were analyzed to determine the optimal number of sections, where optimal is based on a tradeoff between the number of sections and the uniformity of the RCS. The electromagnetic simulations were performed using a transmit frequency of 3.6 GHz, which is representative of frequencies used in through-barrier radar systems. In the following sections, we discuss our findings and select a polyhedron geometry that demonstrates potential as a through-wall and through-rubble human sensing Doppler radar calibration target.

2. Characteristics of Humans

2.1. Physical Characteristics

The physical characteristics of humans were first studied and analyzed to determine the attributes of the “average” male and female subjects. The basis for “average” was based on an analysis of data published by the Centers for Disease Control and Prevention (CDC) through the US Department of Health and Human Services [5]. The three statistics considered were height, weight, and body mass index (BMI). These data were gathered on adults 20+ years in age. Over 10,000 humans were polled in the CDC study. The average adult male had a height of 175.9 cm. For females, the average height was 162.1 cm. The average male and female adult weighed 88.7 kg and 75.4 kg. The average BMI indices for male and female adults were 28.6 kg/m² and 28.7 kg/m², respectively.

Based on the above information, RCS data were collected on 20 test subjects in [6]. This list was sorted through to identify males and females who best fit the “average” description.

Table 1. Availability of radar data from test subjects who best represented the average male and female adult.

Subject No.	Age (y)	Gender	Height (cm)	Weight (kg)	BMI (kg/m2)
10	22	Male	171.0	80.8	27.6
12	24	Male	180.3	86.1	26.5
15	75	Female	162.0	67.0	25.5
17	33	Female	178.0	84.8	26.8

shows the physical characteristics of two average subjects in each gender.

2.2. Radar Characteristics

The radar cross section (RCS) of a target is a measure of how “bright” it is to radar illumination. It is denoted by $\sigma$, has units of square meters (m²), and is defined as [7]

$$\sigma =4\pi \frac{\mathrm{power} \mathrm{per} \mathrm{unit} \mathrm{solid} \mathrm{angle} \mathrm{scattered} \mathrm{back} \mathrm{towards} \mathrm{the} \mathrm{transmitter}}{\mathrm{power} \mathrm{per} \mathrm{unit} \mathrm{area} \mathrm{in} \mathrm{wave} \mathrm{incident} \mathrm{on} \mathrm{target}}$$

(1)

under the assumption that plane wave conditions exist, i.e., that the target is in the far field of the radar antennas. The RCS of a target is a function of its material properties, structure, and surface characteristics; the frequency or wavelength and polarization of the illuminating source; and the viewing aspect or angle. Theoretical formulas for a target’s RCS have been developed only for simple shapes, while numerical methods are employed for more complicated geometries. The RCS is also expressed in decibels relative to one square meter (dBm², also denoted as dBsm in some publications). The relationship is $\sigma ({\mathrm{dBm}}^2)=10{\log }_{10}\sigma ({\mathrm{m}}^2)$. Thus, an RCS of 1 m² translates to 0 dBm².

2.2.1. Radar Cross Section of Humans

Gross Characteristics

The human body’s RCS is highly variable and full of complexities. A full 360° scan of any person will show jaggedness and numerous protrusions that will, in turn, produce a complicated scattering pattern. In addition to the irregular shape, human skin is made up of several layers that attenuate, absorb, and reflect incident energy. These elements combine to form an RCS value that is dependent on body position, stance, and transmitting and receiving angles.

Measurements and simulation studies have been made on characterizing the RCS of a human. The RCS of a man of height 182 cm weighing 90 kg has been measured at different orientations at five discrete frequencies between 410 MHz and 9.375 GHz [8]. At a frequency of 2.89 GHz, the RCS values were measured as 0.409 m², 0.198 m², and 0.613 m² from the front, side, and rear, respectively, at HH polarization (which means that the incident wave is horizontally polarized and that the receiver was oriented to receive horizontal polarization). Corresponding values at VV polarization were measured as 0.496 m², 0.260 m², and 0.719 m², respectively. For the human body, the highest radar return tends to come from the back due to its large surface area. The monostatic RCS response at this orientation angle behaves similar to that of a flat plate. Therefore, the RCS is higher when viewed from the back compared with the front, while the RCS from the side is significantly smaller.

More recent measurements were made from the front over the entire frequency range from 1 GHz to 5 GHz of three humans whose heights varied between 180 cm and 182 cm, and weights varied between 80 kg and 88 kg [9]. At a frequency of 3.5 GHz, the RCS for VV polarization ranged from 0.4 m² to 0.52 m², while the RCS for HH polarization ranged from 0.4 m² to 0.7 m². A typical value used in computations for the RCS of a human at microwave frequencies when viewed from the front is taken as 1 m² [10].

Effects of Breathing and Heartbeat

The effects respiration has on RCS measurements has been studied in many ways recently using a variety of radar systems [11,12,13]. Breathing will cause the amount of energy that is backscattered toward the radar to vary. Oscillatory motion due to breathing causes the RCS of humans to be continuously Doppler modulated with each breath. The RCS of a human’s breathing movements was measured by specifically isolating the RCS of the Doppler modulations from that of the nonbreathing human [14,15]. The results showed a relatively linear correlation between frequency and RCS over a frequency band ranging from 500 MHz to 2 GHz. The averaged data show the RCS increasing from roughly −42 dBm² (6.3 × 10⁻⁵ m²) to −22 dBm² (6.3 × 10⁻³ m²) as a function of frequency from 500 MHz to 2 GHz.

Further research focused on determining the effective radar cross section (ERCS) due to breathing and heartbeat [6]. ERCS differs from the traditional RCS in that it involves only certain regions of a body and not the body as a whole. The ERCS studied in [11] applied to the parts of the human body that are in motion due to respiration and heartbeat, and nothing else. Thus, the ERCS can be considered equivalent to the differential RCS caused by breathing action. Obviously, the traditional RCS of a human will be much larger than the ERCS being analyzed. This is because the RCS accounts for all the other parts of the body (i.e., arms, legs, head, etc.) that the ERCS method does not. These other body parts were irrelevant to our research because we considered them to be motionless; thus, these will appear on a Doppler radar as static clutter at the zero Doppler frequency. As a result, Doppler signatures from cardiopulmonary movements will show up outside of the static clutter region. Therefore, it is important that our calibration target specifically resembled the human’s ERCS. To this end, we concentrated only on ERCS data gathered from several human subjects.

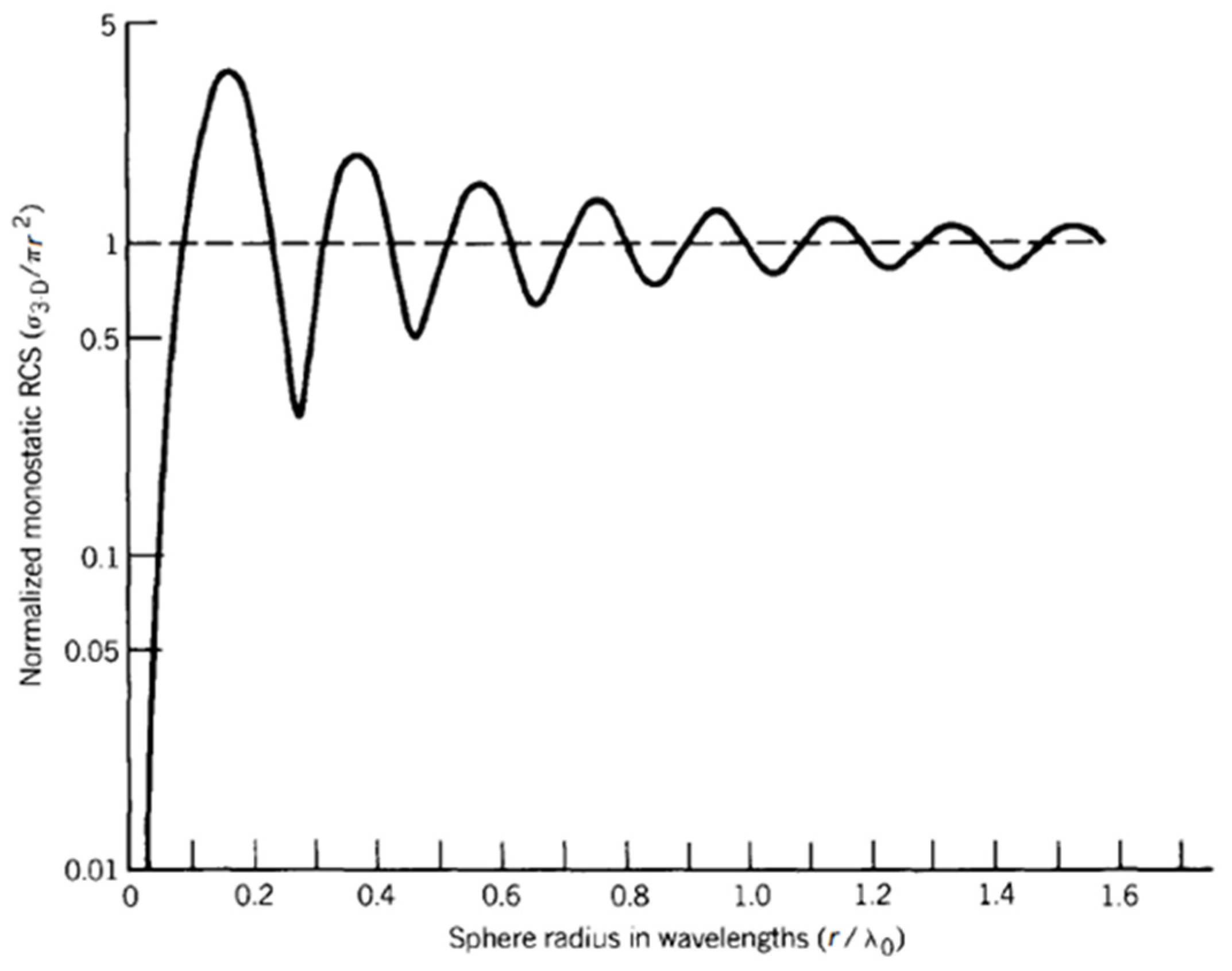
Calibration Sphere for Mimicking Human Radar Cross Section

The PEC sphere is an essential tool in radar-related testing due to the constancy of its RCS with respect to its viewing and illumination angles. Due to the sphere’s angular independence, accurate calibration can be achieved by simply knowing only the distance between the source and target. The RCS of a sphere of radius $r$ (normalized to its projected disk area $\pi r^2$) when illuminated at a wavelength of ${\lambda }_0$ is shown as a function of its radius-to-wavelength ratio ($r/{\lambda }_0$) in Figure 1. The oscillations in the normalized RCS for $r/{\lambda }_0$ values approximately within the range 0.1–1 are caused by the interference between the backscattered and the creeping waves.

As deduced from Figure 1, the RCS of a PEC sphere approaches its projected area $\pi r^2$ when the sphere is large, compared with the wavelength, i.e., when it operates in the so-called optical region. The onset of the optical region is generally considered when $r/{\lambda }_0>2$. This region is very favorable for calibration since the RCS is dependent on just one factor, i.e., the sphere’s radius. All other parameters (i.e., frequency, aspect angle) become irrelevant. It is because of these properties that we design our target with spherical-like architecture. Ideally, our target would appear to the radar exactly as a smooth sphere. To add a dynamic element to our design, however, there will be some tradeoffs between the angle independence of the RCS and the number of sections in our target.

In order to mimic a typical human’s RCS of 1 m² in the optical region, the radius of the corresponding sphere is $\sqrt{1/\pi }$ m = 0.564 m = 56.4 cm. The optical region for a sphere of this size corresponds to a wavelength of less than one-half this value, i.e., 28.2 cm, or a frequency greater than 1.063 GHz. Thus, at frequencies higher than about 1 GHz, the RCS of the sphere will equal 1 m². Although uncertainties in the measured RCS of a sphere have been found to be between −2.1 dB and +1.4 dB [16], which translates to an RCS value in the range 0.62 m² to 1.38 m², this variation is unimportant in our application, as the sphere is used merely to emulate a human whose RCS itself can vary beyond this range of values.

Considering the radar characteristics of the average male and female discussed in Section 2.1 and listed in Table 1, the ERCS values and the corresponding sphere radii, assuming operation in the optical region, are given in

Table 2. Mean ERCS values from measurements at 2.4 GHz and 5.8 GHz of test subjects who best represented the average male and female adult under different viewing conditions.

Subject No.	Gender	Supine Condition		Prone Condition		Fetal-Like Side Condition
		ERCS (m2)	Sphere Radius (cm)	ERCS (m2)	Sphere Radius (cm)	ERCS (m2)	Sphere Radius (cm)
10	Male	0.003	3.1	0.045	12.0	0.002	2.5
12	Male	n/a	n/a	0.249	28.2	0.003	3.1
15	Female	0.03	9.8	0.008	5.0	0.0003	1.0
17	Female	0.112	18.9	0.018	7.6	0.013	6.4

for a human lying down and illuminated and viewed from nominally 0° (normal to the surface on which the subject is lying) [6]. The measured ERCS values shown in Table 2 are caused by motion due to respiration and heartbeat alone while lying down and represent mean values from measurements at 2.4 GHz and 5.8 GHz. There appears to be wide variability between subjects, which cannot be well explained.

One particular observation is that the ERCS, when taken from the side of a human (“Fetal-Like Side Condition” of Table 2), will be very small when compared with the ERCS in the prone condition. This is logical because the region of the body moving, when viewed from the side, has a small surface area. These data show that more than one expanding/contracting spherical target may be necessary to represent the human population. However, for the purpose of the initial design and development of the target, a larger ERCS value with its corresponding larger sphere radius is used. Thus, an ERCS value of about 0.2 m² was selected for design, which is close to the highest ERCS value of an adult person in the prone condition, i.e., being viewed from above while lying face down.

Human Radar Cross Section Emulation Considerations

Assuming operation in the optical region, a human torso ERCS value of 0.2 m² can be obtained using a sphere with a radius of approximately 25 cm. In order to remain in the desirable optical region, the wavelength must be less than one-half this value, i.e., 12.5 cm; therefore, the frequency must be greater than 2.4 GHz.

We were faced with a unique challenge in that our spherical design had to possess the ability to expand and contract radially for simulating a Doppler shift in frequency induced by breathing and to be mechanically robust so that it could be deployed and used in an outdoor rubble pile or similar harsh environment. A mechanically operated hollow spherical polyhedron was chosen for the design of the target. The spherical polyhedron is essentially a perfect sphere divided into a number, n, of spherical sections. Figure 2 shows three different types of spherical polyhedra. Sectioning the sphere in such a manner supports the expansion and contraction of the target as a whole by simultaneous displacement of all the sections. It is envisioned that the center of each face will be connected to an internal mechanism that would cause the sections to oscillate radially back and forth.

The major issue with this approach is the gaps that would be formed between the sections when the target expands. Although the expansion is likely to be on the scale of millimeters, these gaps will introduce electrical discontinuities that can affect the design goal of an aspect-independent RCS. To analyze this effect, we performed RCS simulations on various spherical polyhedral structures. The end goal was to determine a geometry that best maintained sphere-like calibration qualities while in the expanded state.

3. Simulation of RCS of Sphere-Like Polyhedra

3.1. Simulation Parameters

The five geometries simulated were the tetrahedron (4 faces), hexahedron (6 faces), octahedron (8 faces), dodecahedron (12 faces), and icosahedron (20 faces) shapes. Each polyhedron was assumed to be a hollowed PEC and 25 cm in radius, with a shell thickness of 2 mm. Thus, the simulated target was a hollow spherical shell. For the target in its expanded state, each section was assumed to be radially displaced outward by 10 mm away from the center of the target. This can be thought of as the maximum displacement a human’s torso would move during respiration. In the target’s contracted state, the radial displacement of each face was assumed to be 0.2 mm away from the center of the sphere-like target structure. This small expansion was used to implement the electrical discontinuities that still exist in the contracted state due to the fact that each section is a separate piece.

RCS simulations were performed at 3.6 GHz for each geometry in both contracted and expanded states, resulting in a total of 10 simulations. The frequency of 3.6 GHz represents the average frequency of the ERCS data provided in [6] and is in the range of frequencies (3 GHz to 4 GHz) that are optimal for radar probing through walls and rubble, as they provide the best tradeoff between antenna size, spatial resolution, availability of high Doppler frequencies (which suggests transmit frequencies greater than 2.5 GHz), and signal attenuation through materials such as concrete, brick, and cinder block (which suggest frequencies less than 5 GHz) [17].

Simulations were performed for VV polarization (the other polarization arrangements would yield the same results as the VV because of the sphericity of the target). In both the contracted and the expanded state, the target was confirmed to be operating in the optical region based on the wavelength value of 8.33 cm. The theoretical RCS of a perfect sphere is computed to be 0.196 m² (−7.07 dBm²) for the same radius as that of our target in its contracted state and 0.212 m² (−6.73 dBm²) for the same radius as that of our target in its expanded state. These calculations assume a perfect sphere with no discontinuities or gaps; the electrical discontinuities in our target caused by the sections may cause different RCS results.

3.2. Model Creation

Constructive solid geometry (CSG) is a popular method for generating complex solids in computing. The simulation models were generated using CSG techniques. This method functions by finding polygonal boundaries among two solids and performing Boolean operations at the boundary points [18]. Spherical polyhedra were generated by circumscribing a polyhedron inside a sphere. The intersection points between the polyhedron and the sphere define the vertices for each face of the calibration model (thus defining a spherical polyhedron). Once the vertices for the sections of the calibration model were established, the polyhedron inside the sphere was deleted. After this step, all that remained was the spherical polyhedron that would be used as the simulation model.

If the sphere was a bit larger and did not exactly circumscribe the polyhedron, the processing was carried out to project the intersection points from the vertices of the polyhedron to the surface of the sphere. Once these vertices were defined on the sphere, the same process as mentioned above was performed to form the model. This technique allowed for spherical polyhedra to be generated that have small gaps between their sections.

3.3. Simulation Results

The simulations were performed using a physical optics (PO) solver in the FEKO computational electromagnetic software. The frequency was selected to be 3.6 GHz, consistent with the average of the 2.4 GHz and 5.8 GHz frequencies used for ERCS measurements in [6]. The results are shown graphically in a three-dimensional format. The most important characteristics we are looking for in these results are the aspect independence of the RCS and an RCS value close to 0.2 m². Ideally, a geometry will possess a constant RCS over its entire surface even while expanded. The five geometries considered are shown in Figure 3.

Simulation results on all the five geometries investigated have been published recently [19]. The best results for RCS consistency were obtained for the six-faced hexahedron and the eight-faced octahedron, which are discussed here.

3.3.1. Simulation Results on Hexahedron

Monostatic RCS simulation results for the hexahedron are shown in Figure 4, for both the contracted and the expanded states. We observed that the RCS was consistent (RCS values varied between nominally 0.175 m² and 0.210 m²) in the contracted state, with values close to that of the theoretical value of 0.2 m². The expanded state showed much less consistency in RCS than the contracted state, with the variation primarily between 0.140 m² and 0.245 m². Slight differences in the RCS characteristics in the expanded state in Figure 4b under different viewing aspects were due to the differences in the orientations of the segments. Small differences in the values and locations of the bright spots (red, orange, and yellow colors) could be observed. Although this variation was not ideal, it was within 1.5 dB of the desired value. Unfortunately, higher RCS values, approaching 0.35 m², occurred in small areas on the target, concentrated mostly toward the center of the sections.

3.3.2. Simulation Results on Octahedron

Simulation results for the octahedron are shown in Figure 5, for both the contracted and the expanded states. Once again, the RCS remained very consistent when the target was in its contracted state. As before, small differences in the values and locations of the bright spots (red, orange, and yellow colors) in the expanded state observed in Figure 5b could be attributed to the differences in the orientations of the segments under different viewing aspects. The octahedron also showed better RCS consistency in its expanded state, compared with the hexahedron. The variability in RCS was small, similar in range to that of the hexahedron. Although there were a few high RCS values that exist toward the center of the faces, they appeared to be confined to smaller areas, compared with the hexahedron.

3.3.3. Simulation Results on Other Shapes

For the tetrahedron in the contracted state, the target’s RCS appears constant over the entirety of the surface at the computed value of 0.2 m² [19]. However, the RCS in the expanded state was less consistent and varied more than either the hexahedron or octahedron. Values as high as 0.35 m² were observed at several locations. These bright spots on the target indicated that using the tetrahedron geometry for a calibration target is not optimal.

The dodecahedron showed great RCS consistency while contracted but large amounts of inconsistencies when expanded [19]. In the expanded state, there were several localized spots with RCS values of 0.35 m². A clear pattern could be seen where bright spots existed at the center of each pentagonal section and at intersections where three sections intersect.

Similar to all other geometries, the icosahedron showed excellent RCS consistency over the entirety of its surface in the contracted state [19]. In the expanded state, there appeared high levels of inconsistency, most likely due to the high number of discontinuities.

3.3.4. Choice of Shape for Calibration Target

Some observations were made when analyzing the simulation results. First, our target performed exceptionally well in the contracted state for all geometries. Although we had small electrical discontinuities between faces, these were not large enough to prevent RCS consistency across the surfaces of the targets and to be near the ideal value of 0.2 m². Secondly, the RCS tended to be greater around the gaps while in the expanded state. A possible reason could be the occurrence of constructive interference when the RF energy passes through the gaps, reflects from the inside surface of a far section toward the radar, and then combines with energy reflected from the front outside surface of the target. Fortunately, the change in RCS was approximately 17%, which is not significant for this application.

Of the five geometries studied (data of only two are shown here), the octahedron was chosen for the design of the calibration target. This decision was based on the following factors: consistency of the scattering (RCS) profile, build complexity, and spherical projection.

The scattering profile was based on data gathered from the monostatic RCS simulations. From our simulation results, it appeared that both the hexahedron and octahedron would be acceptable because they showed the best RCS consistency in the expanded state.

From a build complexity viewpoint, both the hexahedron and octahedron were suitable because of the number of moving sections. The internal mechanism of the dynamic calibration target design would consist of linear actuators for each section and a control system to move each section simultaneously. It was important that the number of sections would be kept reasonably low due to the build complexity and motion synchronization. Of the five geometries, the dodecahedron and icosahedron would be clearly the hardest to build and to synchronize motion. Moreover, their scattering profiles did not appear to be better than the hexahedron or octahedron.

The spherical projection requirement referred to how well the target maintains its sphericity in the expanded state. For example, the tetrahedron was very poor at this because it possessed just four sections. When the four sections moved radially outward, large areas in the gaps of the target were formed in which the reflected waves did not have a velocity vector toward the radar. This was in contrast to the icosahedron target, where there were 20 moving radially and, thus, very few areas existed without a reflected-wave velocity vector moving toward the radar. These reflected-wave velocity vectors were very critical for performing Doppler measurements.

Based on these criteria, the octahedron was selected as the optimal polyhedron for the design and fabrication of a polyhedral target. The next section discusses a fabricated but not mechanically functional target to validate the RCS simulations.

4. Prototype Design and Initial Measurement Results

A prototype was constructed to validate the simulation results presented in Section 3.3. The prototype formed an octahedron geometry capable of two states: full contraction and full radial expansion by 10 mm. RCS data were gathered, and the scattering profile of the object was analyzed. The prototype was designed initially to be manually expanded and contracted but with the intention of adding internal actuator mechanisms at a later date.

4.1. Prototype Design Considerations

A fully constructed CAD model of the prototype with its cutaway view is shown in Figure 6. The model was generated using the SolidWorks computer-aided design software and maintained all the dimensions used in the simulation model. The face sections of the octahedron were all separate parts (eight total). The drawing of an individual section is shown in Figure 7. The sections had a thickness of 2 mm. A holed connector piece was mounted directly on the center of the inside face. This was designed so that one end of a 1.905 cm dowel rod could be tightly inserted, thus forming an arm on the piece. The other end of this dowel rod was then connected to a central sphere, shown in Figure 8. This object served as the base of the device. The sphere had eight holes specifically placed so that an octahedron could be formed when the dowel rods, connected to the eight sections, were inserted. For the octahedron to form properly, the dowel rods must all be cut to a length of 21.27 cm. This would form a fully contracted octahedron. To mimic the radial expansion, new dowel rods were cut with an additional 10 mm in length. These dowel rods had a length of nominally 22.26 cm. The shorter rods were taken out and replaced with the longer rods. This technique was useful in that the radial expansion distance could continuously be changed and tested by simply replacing the dowel rods. A complete assembly of the face sections was also created using computer-aided design software to validate the prototype’s structure. Each Individual part was able to connect together and form a fully contracted octahedron.

4.2. Prototype Construction Using 3D Printing and Coating

The device was constructed using 3D printing. In order to be printable, the parts had to be slightly modified because a 3D printer prints an object from the bottom up, layer by layer. For this reason, each layer must be completely filled with material so that it can serve as a base for the next layer. Each section was formed by splitting it into two smaller equally sized pieces. One of these split pieces is shown in Figure 9a. The central sphere is shown in Figure 9b.

The manufactured parts are shown in Figure 10. The parts were printed using polylactic acid (PLA) plastic, which is a lightweight dielectric material. Once printed, the original designs were restored by gluing the two halves together. The front surface of each section was covered with taut copper tape with wrinkles of less than 1 mm in height, which satisfied the Rayleigh roughness criterion ($<{\lambda }_0/8$) and thus could be considered to approximate a smooth PEC.

4.3. Radar Cross-Sectional Measurements

Radar cross-sectional measurements of the fabricated expanded target were performed in an anechoic chamber at a frequency of about 3.6 GHz. At this frequency, the wavelength ${\lambda }_0$ was approximately 8.333 cm. Calibration was performed using a metal sphere of radius $r$ equal to about 30.48 cm. For this size, it was confirmed that the sphere was in the optical region at a frequency of 3.6 GHz, that is, $r/{\lambda }_0>2$. Thus, the RCS of the calibration sphere, given by $\pi r^2$, was calculated to be approximately 0.292 m² or −5.348 dBm².

Measurements were performed using the network analyzer connected to wideband horn antennas at each port. The range to the target from the antennas was about 7.19 m, as measured by a laser rangefinder. This distance ensured that the target was in the far-field region of the antenna. Figure 11 shows the geometry of the measurement setup. The targets were mounted on a low-reflectivity stand, as shown in Figure 12.

The target reflection function, given by the value of $s_{21}$ that was measured by the network analyzer in the arrangement shown in Figure 11, was converted to dB using $s_{21}(\mathrm{dB})=10{\log }_{10}{\left|s_{21}\right|}^2=20{\log }_{10}\left|s_{21}\right|$. The target reflection function represents the propagation from the transmit antenna to the target, the reflection from the target, and the propagation from the target to the receive antenna. Thus, embedded within the $s_{21}$ was the RCS of the target.

By performing a wideband frequency-domain measurement over a bandwidth of 1 GHz (from 3 to 4 GHz) and taking its inverse Fourier transform, the time-domain response of the spherical target was obtained, as shown in Figure 13. The response from the sphere was well above the noise floor, by more than 20 dB. Furthermore, the target reflection occurred at a round trip time of about 48 ns from the antenna, which translated to a target range of approximately 7.2 m. This value compared well with the measured range of nominally 7.19 m.

The substitution method was employed to compute the target’s RCS, ${\sigma }_{\mathrm{Target}}$. In this method, the reflection function, $s_{21,\mathrm{CAL}}$, of the calibration target and the reflection function, $s_{21,\mathrm{Target}}$, of the spherical target in the expanded state were measured. This method permits the cancellation of common parameters, such as the transmit power, antenna gains, target range, etc., from the radar range equation. Using this method, the unknown target’s RCS, ${\sigma }_{\mathrm{Target}}$, is obtained using [20],

$${\sigma }_{\mathrm{Target}}({\mathrm{m}}^2)={\sigma }_{\mathrm{CAL}}({\mathrm{m}}^2)\left(\frac{{\left|s_{21,\mathrm{Target}}\right|}^2}{{\left|s_{21,\mathrm{CAL}}\right|}^2}\right)$$

(2)

which can be recast as [21].

$${\sigma }_{\mathrm{Target}}({\mathrm{dBm}}^2)={\sigma }_{\mathrm{CAL}}({\mathrm{dBm}}^2)+s_{21,}{}_{\mathrm{Target}}(\mathrm{dB})-s_{21,}{}_{\mathrm{CAL}}(\mathrm{dB})$$

(3)

In our case, the RCS of the calibration target, ${\sigma }_{\mathrm{CAL}}$, was approximately −5.348 dBm².

As mentioned in Section 3.1, for reference purposes, we note that the sphere’s RCS in the expanded state was about −6.73 dBm². RCS measurements were made for two cuts: (1) ϕ = 0°, θ = 0° to 360°; (2) ϕ = 45°, θ = 0° to 360°. These geometries are shown in Figure 14. The changes in θ occurred in about 20° increments. for a total of 18 points per orbit. The rotations were performed manually by aligning the foam column with predrawn angle markings on the ground. The changes in ϕ were performed by manually adjusting the target’s orientation with respect to the antennas.

Measured RCS data for both ϕ cuts, using Equation (3), are shown in Figure 15. Additionally, shown for comparison purposes is the theoretical value of −6.73 dBm². We observed that the fabricated sphere generally followed azimuthally independent RCS characteristics with values close to the theoretical value. Differences were typically less than 1 dB, with a few higher deviations of up to 4 dB. The azimuth-averaged measured values were 1.2 dB and 0.1 dB lower than the theoretical value for the ϕ = 0° and ϕ = 45° cases in Figure 15a,b, respectively. Corresponding standard deviations were computed as 2 dB and 1.6 dB, respectively. Averages and standard deviations were computed in the log scale, i.e., in dB. Overall, the fabricated expanded sphere maintained the expected RCS value as obtained via theory.

5. Conclusions

The overall goal of this study was to design and develop a target that could be used as an aspect-independent spherical calibration device for testing through-wall and through-rubble Doppler radar systems. Of the geometries investigated, the octahedron appeared to be optimum based on its RCS characteristics in both its contracted and expanded states and the number of sections used in its manufacture. There was very little variation in the simulated RCS on the surface of the target, thus showing a reflection behavior almost identical to that of a PEC sphere. Upon testing, our manufactured prototype exhibited results similar to that seen in the simulations. Overall, the simulated design provides a consistent scattering profile over the entirety of its surface with the exception of a few small (on average, less than 5% of the nominal value or within 0.22 dB) fluctuations in RCS. As noted previously, these minor fluctuations are to be expected due to the presence of gaps, and these fluctuations will not impact our application for the calibration target.

It is possible that the calibration target may become damaged due to impact with hard surfaces, causing valleys and hills on its surface. The RCS of a typical damaged target was characterized via simulations to assess its RCS variability from the designed value. Valleys of 2 cm depth and hills of 2 cm height were simulated on the target surface of size extending up to 10 cm × 10 cm, and the corresponding RCS values were computed. Our results showed that the RCS changes were less than 1.2 dB at all displacements and viewing angles for the dented target representations [22].