Opportunities for Bright Beam Generation at the Argonne Wakefield Accelerator (AWA)
Abstract
:1. Introduction
2. The AWA Upgraded Photoinjector
3. Beam Brightness Optimization
3.1. Methods
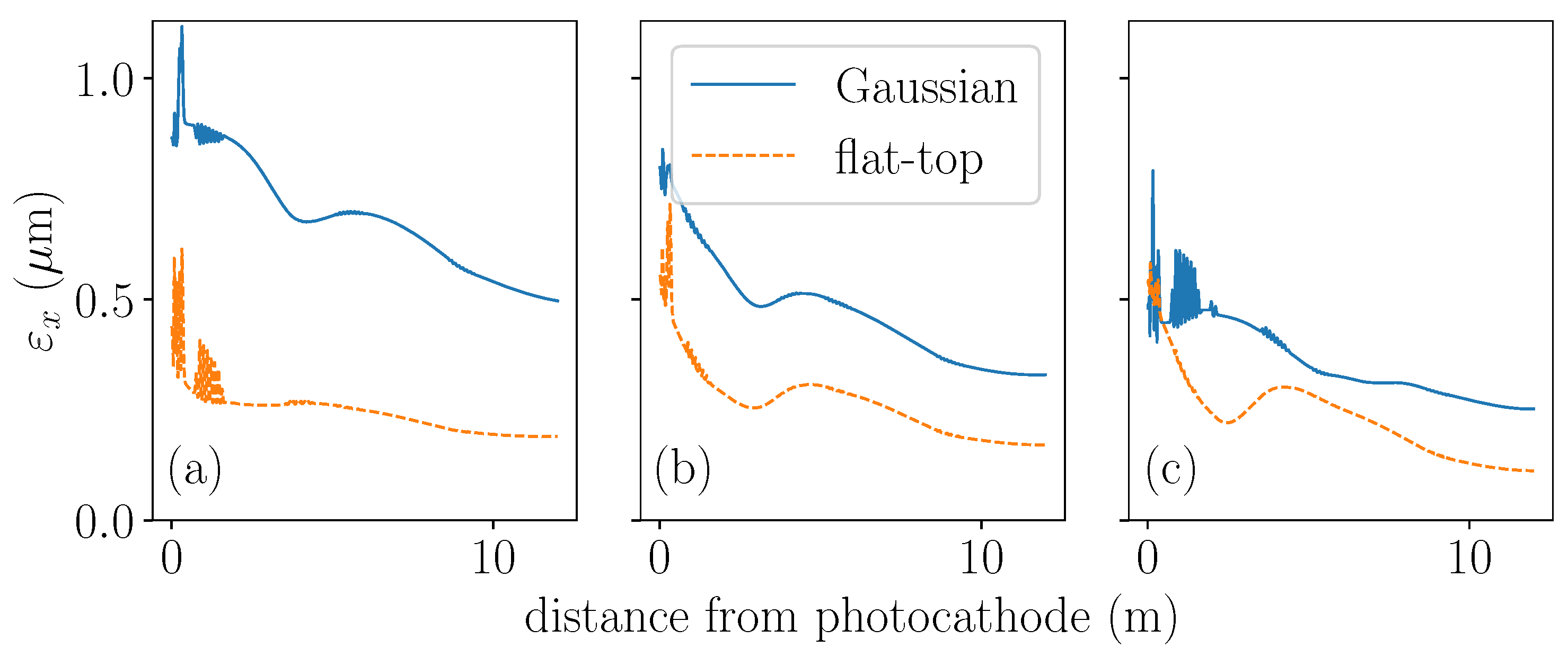
3.2. Results
3.3. Impact of 3D Fields
3.4. Opportunity for Peak Current Enhancement via Magnetic Bunch Compression
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Power, J.; Conde, M.; Gai, W.; Li, Z.; Mihalcea, D. Upgrade of the Drive LINAC for the AWA Facility Dielectric Two-Beam Accelerator. Conf. Proc. C 2010, 100523, THPD016. [Google Scholar]
- Qian, H.; Kwiatkowski, S.; Papadopoulos, C.; Paret, Z.; Sannibale, F.; Staples, J.; Wells, R. Analysis and optimization of coupler kick in APEX. In Proceedings of the 2013 Particle Accelerator Conference (PAC’13), Pasadena, CA, USA, 29 September–4 October 2013; pp. 607–609. [Google Scholar]
- Parzyck, C.T.; Galdi, A.; Nangoi, J.K.; DeBenedetti, W.J.I.; Balajka, J.; Faeth, B.D.; Paik, H.; Hu, C.; Arias, T.A.; Hines, M.A.; et al. Single-Crystal Alkali Antimonide Photocathodes: High Efficiency in the Ultrathin Limit. Phys. Rev. Lett. 2022, 128, 114801. [Google Scholar] [CrossRef] [PubMed]
- Frame, E.; Kim, S.; Lu, X.; Piot, P.; Power, J.; Scott, D.; Wisniewski, E. Simulations of the Upgraded Drive-Beam Photoinjector at the Argonne Wakefield Accelerator. In Proceedings of the International Particle Accelerator Conference (IPAC’22), Bangkok, Thailand, 12–17 June 2022; JACoW Publishing: Geneva, Switzerland, 2022; pp. 2015–2018. [Google Scholar] [CrossRef]
- Fortin, F.A.; Rainville, F.M.D.; Gardner, M.A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary Algorithms Made Easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Floettmann, K. ASTRA—A Space Charge Tracking Algorithm. 2017. Available online: http://www.desy.de/~mpyflo/ (accessed on 1 June 2023).
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Karkare, S.; Adhikari, G.; Schroeder, W.A.; Nangoi, J.K.; Arias, T.; Maxson, J.; Padmore, H. Ultracold Electrons via Near-Threshold Photoemission from Single-Crystal Cu(100). Phys. Rev. Lett. 2020, 125, 054801. [Google Scholar] [CrossRef] [PubMed]
- Luiten, O.J.; van der Geer, S.B.; de Loos, M.J.; Kiewiet, F.B.; van der Wiel, M.J. How to Realize Uniform Three-Dimensional Ellipsoidal Electron Bunches. Phys. Rev. Lett. 2004, 93, 094802. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.J. Rf and space-charge effects in laser-driven rf electron guns. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1989, 275, 201–218. [Google Scholar] [CrossRef]
- Xiao, L.; Ge, L.; Li, Z.; Ng, C.K. Advances in Multiphysics Modeling for Parallel Finite-Element Code Suite ACE3P. IEEE J. Multiscale Multiphysics Comput. Tech. 2019, 4, 298–306. [Google Scholar] [CrossRef]
- Ha, G.; Cho, M.H.; Namkung, W.; Power, J.G.; Doran, D.S.; Wisniewski, E.E.; Conde, M.; Gai, W.; Liu, W.; Whiteford, C.; et al. Precision Control of the Electron Longitudinal Bunch Shape Using an Emittance-Exchange Beam Line. Phys. Rev. Lett. 2017, 118, 104801. [Google Scholar] [CrossRef]
- Marzouk, A.A.; Piot, P.; Ryne, R. First-Principle Simulations of Electron-Bunch Compression Using a Large-Scale Liénard-Wiechert Solver. In Proceedings of the 2022 Advanced Accelerator Conference, Hauppauge, NY, USA, 6–11 November 2022. [Google Scholar]
- Ryne, R.D.; Mitchell, C.E.; Qiang, J.; Carlsten, B.E.; Yampolsky, N.A. Large-Scale Simulation of Synchrotron Radiation using a Lienard-Wiechert Approach. In Proceedings of the IPAC’12, NewOrleans, LA, USA, 2–25 May 2012; JACoW Publishing: Geneva, Switzerland, 2012; pp. 1689–1691. [Google Scholar]






| Parameter | Range |
|---|---|
| Laser rms spot size | 0.02–5 mm |
| Laser launch phase | −40–40 |
| Peak field on photocathode | 40–80 MV/m |
| Linac C1 and C2 phase | −50–50 |
| Linac C1 and C2 amplitude | 10–20 MV/m |
| Solenoid LB peak magnetic field | 0–0.4 T |
| Solenoid LF peak magnetic field | −0.4–0 T |
| Solenoid LM peak magnetic field | −0.4–0 T |
| Solenoid LS1 peak magnetic field | 0–0.5 T |
| Photocathode MTE (meV) | 250 | 60 | 5 |
|---|---|---|---|
| Beamline Settings | |||
| Laser rms spot size (mm) | 0.146 | 0.239 | 0.255 |
| Laser launch phase () | −2.88 | 5.30 | −3.08 |
| Peak field on photocathode (MV/m) | 75.12 | 64.62 | 72.37 |
| Cavity C1 phase () | −49.82 | −43.17 | −49.52 |
| Cavity C1 amplitude (MV/m) | 19.96 | 17.73 | 19.97 |
| Cavity C2 phase () | −49.96 | −48.25 | 11.21 |
| Cavity C2 amplitude (MV/m) | 10.18 | 11.01 | 13.53 |
| LB peak magnetic field (T) | 0.34 | 0.25 | 0.32 |
| LF peak magnetic field (T) | −0.34 | −0.26 | −0.32 |
| LM peak magnetic field (T) | −0.25 | −0.25 | −0.24 |
| LS1 peak magnetic field (T) | 0.02 | 0.04 | 0.08 |
| Beam parameters | |||
| Kinetic energy K (MeV) | 37.53 | 36.71 | 39.96 |
| Transverse emittance (µm) | 0.190 | 0.170 | 0.112 |
| Bunch length (mm) | 0.674 | 0.596 | 0.570 |
| Peak current (A) | 16.85 | 17.43 | 16.95 |
| Brightness (TA·m) | 466.63 | 603.16 | 1350.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frame, E.; Al Marzouk, A.; Chubenko, O.; Doran, S.; Piot, P.; Power, J.; Wisniewski, E. Opportunities for Bright Beam Generation at the Argonne Wakefield Accelerator (AWA). Instruments 2023, 7, 48. https://doi.org/10.3390/instruments7040048
Frame E, Al Marzouk A, Chubenko O, Doran S, Piot P, Power J, Wisniewski E. Opportunities for Bright Beam Generation at the Argonne Wakefield Accelerator (AWA). Instruments. 2023; 7(4):48. https://doi.org/10.3390/instruments7040048
Chicago/Turabian StyleFrame, Emily, Afnan Al Marzouk, Oksana Chubenko, Scott Doran, Philippe Piot, John Power, and Eric Wisniewski. 2023. "Opportunities for Bright Beam Generation at the Argonne Wakefield Accelerator (AWA)" Instruments 7, no. 4: 48. https://doi.org/10.3390/instruments7040048
APA StyleFrame, E., Al Marzouk, A., Chubenko, O., Doran, S., Piot, P., Power, J., & Wisniewski, E. (2023). Opportunities for Bright Beam Generation at the Argonne Wakefield Accelerator (AWA). Instruments, 7(4), 48. https://doi.org/10.3390/instruments7040048







