1. Introduction
The presence of low-energy antideuterons
in cosmic rays is considered to be a golden channel for the identification of Dark-Matter annihilations in the galaxy. The expected astrophysical background due to secondary antinuclei produced by high-energy protons colliding with the interstellar medium is kinematically suppressed for kinetic energies below a few GeV/n. Thus, the search for a rare component of low-energy antinuclei in cosmic rays allows testing for the presence of primordial antimatter and the nature of Dark Matter [
1,
2].
The AMS02 magnetic spectrometer is currently the most sensitive experiment for antinuclei search in cosmic rays. However, AMS02 cannot efficiently explore the sub-GeV region with the mass reconstruction based on the particle time of flight. The current
search of AMS02 in the [2–3.8] GeV/n region with the powerful identification technique based on the ring imaging Cherenkov detector provides ≈7 candidates in the
mass region, where a few events are expected due to
background [
3]. Regarding antihelium, conversely, the AMS02 spectrometer provided a tantalizing hint for an unexpected presence of antihelium in cosmic rays; ≈10 events are reported in the rigidity region from −40 GV to −15 GV with a mass compatible with antihelium. A careful study of all the hypothetical systematics on the evaluation of the expected, negligible background for these events is still ongoing [
4].
The GAPS balloon experiment develops a different signature with respect to existing and past magnetic spectrometers, where stopping antinuclei will form an exotic atom whose characteristic X-rays should be detected to identify the antiparticle mass [
5,
6]. The first flight of the GAPS balloon is scheduled for the austral summer of 2024–2025. The GAPS experiment will explore
in the kinetic energy region 100–250 MeV/n. To pursue the peculiar X-ray signature, the GAPS collaboration developed 2.5 mm thick Si(Li) detectors with 1 keV resolution but also with a very large dynamic range (10 keV–100 MeV). The 1440 Si(Li) sensors of the GAPS tracker will be cooled to ≈−40 °C thanks to a large oscillating heat pipe cooling system. A challenging task of the GAPS experiment is to reduce the very large (≈MHz) particle rate down to a (still quite large) >50 kHz trigger rate [
5]. A ToF-based trigger system should be able to identify and reject “on the fly” most of the incoming p and He nuclei. This is one of the main difficulties also for the trigger strategy of future large space-based spectrometers like ALADInO [
7] or AMS100 [
8].
The innovative detection approach for , developed for the PHeSCAMI (Pressurized Helium Scintillating Calorimeter for AntiMatter Identification) project, will allow a relatively simple trigger strategy and provide an additional identification signature for in helium gas in a room temperature detector.
2. Metastable States in Helium
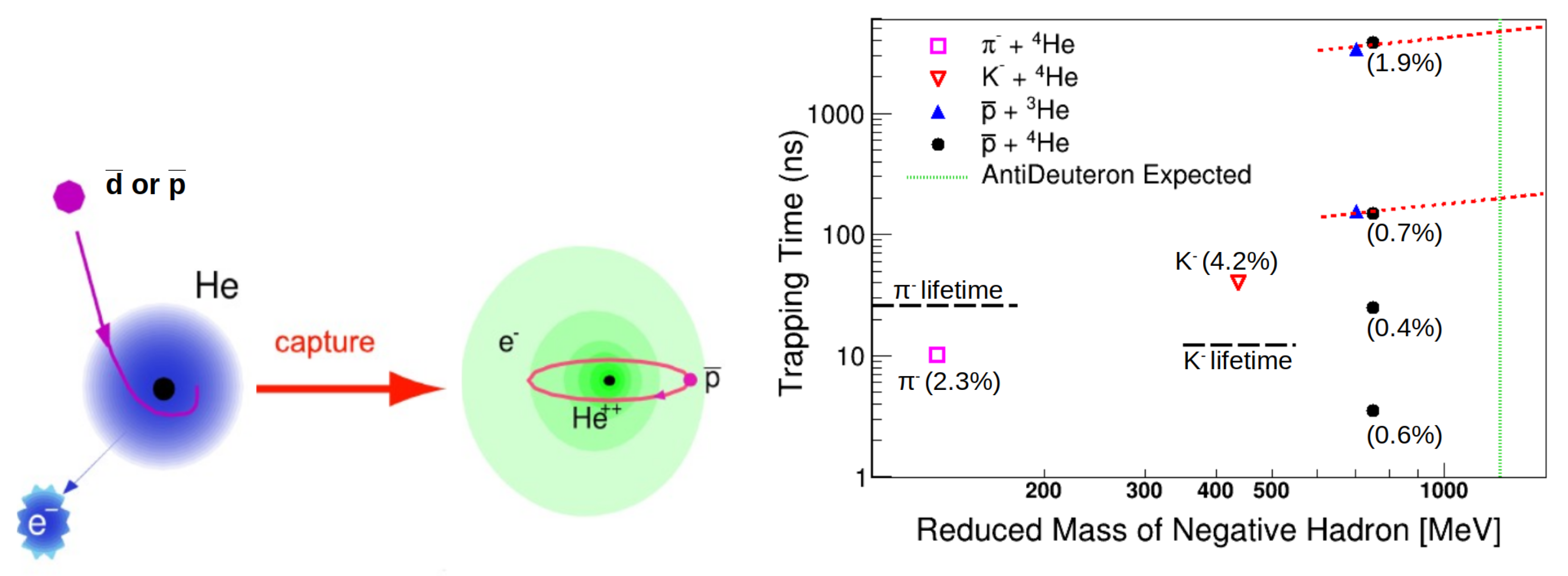
The typical lifetime for stopping antinuclei in matter is of the order of picoseconds. However, since 1991, the existence of long-living (≈µs) metastable states for stopping
in helium targets has been measured [
9,
10,
11]. These metastable states in helium have also been measured for other heavy negative particles such as negative pions and kaons [
12,
13]. The theoretical description of the effect [
11,
14,
15,
16,
17] predicts that the metastable state lifetimes increase as the reduced mass squared of the exotic atom [
18]. Thus, a slightly larger delay is expected for
captured in helium as compared to the
case. The antiprotonic-helium metastable states are well understood, and their existence is already exploited for other fundamental physics measurements like the antiproton-to-electron-mass ratio at the CERN Antiproton Decelerator [
19].
The phenomenology for the formation of metastable states in helium can be summarized following the scheme of
Figure 1.
An exotic metastable atom can be produced when
or
are stopping near an ordinary helium atom. In this case, a capture of the antiparticle from the helium nucleus is possible, and the atom spontaneously removes one of its two electrons. The antiparticle typically is captured in a state with a large principal and angular momentum quantum numbers (
n∼38 for
). Because of the large mass ratio, the orbits of the antinuclei are smaller with respect to the typical size of the electron orbits. However, the annihilation is suppressed by the relatively large principal and angular momentum quantum numbers that imply a small superposition of nucleus-antinucleus wavefunctions. The annihilation probability increases when the bound system de-excites towards the fundamental level. For the He target, the remaining electron cannot provide the (fast) Auger de-excitation, i.e., the main de-excitation process for the Z
antiprotonic atoms. On the other hand, the relatively large size of the orbit of the single remaining electron also suppresses the Stark collisional de-excitation of the inner antiparticle (that is the main de-excitation process for the Protonium,
, naked system). Thus, for antiprotonic-He, the (slow) radiative channel is the main remaining de-excitation process. This metastability is a unique (and well-measured) feature for the He target that is not expected/observed for other target nuclei [
10]. The captured antiproton/antideuteron can thus orbit the He nucleus for a few microseconds before annihilating, providing a few charged pion tracks. This process is expected to happen in the case of a few percent of the captures, and this characteristic delayed annihilation signal in He is a distinctive signature to identify the antimatter nature of the stopping particle that can be used to detect antideuterons in space.
Measurements for liquid and gas helium targets [
9,
10,
11] have shown that about 3.5% of the antiproton annihilations are delayed in several decay components from a few ns to a few µs. A simplified model with two decay components
and
can be adopted to roughly describe the time distribution of delayed annihilations:
where
A ≈ 3.5% is the fraction of delayed annihilation and
F is the fraction of the “
fast” annihilation component.
In
Figure 2, experimental measurements of these parameters at different temperatures and pressures for antiprotonic-He are shown as a function of the helium density. The measurements for highly pressurized helium gas are scarce. However, in principle, handling helium gas at a pressure of 400 bar at room temperature is feasible, and the expected gas density in that condition is just half of the density of liquid helium. For 400 bar helium gas, we expect that roughly half of the delayed annihilations belong to the fast,
ns or to the slow,
µs components. Despite the poor knowledge of these parameters for helium gas at 400 bar, we can evaluate that (63 ± 4)% of delayed annihilations occurs in a time window from 50 ns to 2 µs for antiprotonic-He. Knowing that the delayed annihilation time is proportional to the squared reduced mass of the exotic atom [
18], we can evaluate that ≈50% of
annihilations should occur in the same time window for a 400-bar helium target.
3. Antideuteron Identification with Helium Calorimeters
Helium gas is a fast UV scintillator, with a light yield similar to other fast plastic/liquid scintillators and capable of ∼ns timing performance [
20,
21].
Pressurized helium gas scintillators are currently adopted in fast neutron detection [
21,
22]; however, the gas in these detectors is typically stored in a thick and heavy steel vessel. Therefore, commercially available pressurized helium gas detectors are not suitable for investigating low-energy
that would stop in the thick vessel material. The idea of the PHeSCAMI project is to design a large helium calorimeter (HeCal) using a composite overwrapped pressure vessel (COPV) that would provide a small grammage of the walls, allowing for the detection of
with kinetic energy down to ≈50 MeV/n. A COPV is a pressure-containing vessel, typically composed of a metallic liner, a composite overwrap, and two bosses at the edges. COPVs are commonly manufactured by winding resin-impregnated high tensile strength fiber tape directly onto a cylindrical or spherical metallic liner. The inner liner contains the gas and limits permeation through the tank wall, while the outer fiber overwrap absorbs the stresses generated by the high-pressure gas within. COPVs have been developed for spaceflight due to their high strength and low weight as compared to metallic gas cylinders. They are also used in the automotive industry for hydrogen or compressed natural gas storage. ArianeGroup has developed a space-qualified COPV for helium: working pressure is 400 bar, volume is 300 L, dry mass is 80 kg, and the average vessel grammage is ≈3.5 g/cm
[
23]. A smaller space-qualified HeHPV was developed in the ESA-ARTES program: working pressure is 310 bar, volume is 40 L, dry mass is 8.5 kg, and average grammage is ≈1.5 g/cm
[
24]. To measure the UV scintillation light emitted by the helium stored in the COPV a possible strategy is depicted in
Figure 3a): one of the two bosses of the COPV tank can be equipped with Wavelength Shifting fibers (WLS) that are able to convert the UV scintillation light into visible light and to guide the photons to an external Photomultiplier Tube (PMT).
A possible configuration for a detector prototype of the PHeSCAMI technique is depicted in
Figure 3. The response of a similar detector to
,
and to the main cosmic ray components (p, He, C, e
) has been simulated with the Geant4 11.1.3 package and FTFP-BERT physics list [
25]. The inner part is a ∼20 kg scintillating helium calorimeter (HeCal) where the 400-bar gas is filling the ArianeGroup space-qualified COPV [
23].
The HeCal is surrounded by three layers, made by 4 mm thick plastic scintillator bars, providing velocity measurement () by Time of Flight (ToF) and charge measurement (Z) by ionization energy loss measurement (). It is assumed that with current technology, such a ToF detector is capable of measuring with 5% resolution and deposited energy with 10% resolution. A time resolution of 1 ns and energy resolution of 10% have been assumed in the simulation for the HeCal detector. These assumptions are supported by preliminary measurements on an HeCal prototype (see next sections). Considering the energy loss in the ToF detector and the vessel, a minimum kinetic energy of ∼60 MeV/n is necessary for to reach the He target. On the other hand, with kinetic energy larger than 140 MeV/n would typically cross the 400 bar He active region without stopping inside.
This defines the 60–140 MeV/n energy window of sensitivity for
by this detector configuration.
Figure 3 also shows the typical event topology for a stopping
within the He gas. The antiparticle initially produces three prompt hits (yellow) in the ToF detector and one prompt energy deposit (S1) in the HeCal; these prompt hits occur within 10 ns. This is the typical signal produced by any ionizing particle stopping in the vessel. Then, only for
and
, the antiparticle can be captured in the He metastable states and after a time delay going from several tens of ns to a few µs the annihilation occurs (pink delayed hits in
Figure 3). Typical
multiplicity is 3.0 ± 0.2 for each anti-nucleon annihilation at rest [
26]; therefore, twice the number of delayed out-going tracks is expected for
regarding
. For the same reason, the delayed signal (S2) in the HeCal for
is also expected to have a double amplitude regarding the delayed signal for
. The characteristic temporal structure of S1/S2 signals as measured by HeCal for
is shown in
Figure 4. The time gap from S1 (prompt) to S2 (delayed) is related to the metastability of He capture and is statistically distributed with
O (1 µs). The S1 signal is related to the energy loss in the scintillating He; the amplitude measures the residual particle kinetic energy after the energy losses due to the ToF detector and vessel crossing.
One advantage of the PHeSCAMI approach is that it relies on the relatively simple trigger condition, which is not purely ToF-based, as in the case of the GAPS experiment. Most cosmic rays (90%) are relativistic protons [
27]. Thus, they would deposit ∼10 MeV crossing the HeCal diameter, and this energy is much lower than the energy deposited by stopping
(60–140 MeV/n). Moreover, crossing helium nuclei (∼10% of cosmic rays [
27]) would be identified by six “prompt” hits in the ToF detector with ∼4 MIP (4 × the energy deposited by a Minimum Ionizing Particle). Therefore, a “start trigger” condition can be defined as:
. The “start trigger” would reject most of the crossing protons and a large fraction of helium nuclei, opening a 50 ns–2 µs time gate where delayed annihilation signals are searched for. The delayed annihilation signal provides a relatively large amount of energy deposited in HeCal (due to annihilation), and several hits in the ToF detector are expected due to produced charged pions. Thus, a “stop trigger” condition, enabling the data acquisition and the event storage on disk, can be defined as:
. This provides a strong suppression of the random coincidences due to ordinary cosmic rays casually detected within the 2 µs time gate. A precise identification of
and
is possible in the offline event analysis. In particular,
Figure 5 shows the spectrometric separation power of the “prompt” part of the event.
On the other hand, for the PHeSCAMI technique, also the “delay” HeCal signal, S2, and the reconstruction of the number of charged pions produced in the annihilation (ToF activity classifier [
28]) allow a good separation of
from
, as shown in
Figure 6.
Combining prompt and delayed event information, the PHeSCAMI technique can identify a single over 1000 background in the 60–140 MeV/n range. Considering the expected flux, this technique would be able to test the presence of in cosmic rays down to a flux of 2–3 × 10 (ms sr GeV/n) with less than 1 as background.
4. Test of HeCal Performance with Arktis B-470 Detector
The timing and energy resolutions of the HeCal detector are key parameters for the PHeSCAMI project. Some measurements on a prototype based on the fast neutron detector B-470 Arktis Radiation Detectors [
21,
22,
29] have been conducted at INFN-TIFPA laboratories to test the response of pressurized helium gas as a scintillator.
The Arktis B-470 detector consists of a 5mm thick stainless steel cylindrical vessel filled with (209 bar) pressurized He gas and two Hamamatsu-R580 photomultiplier tubes (PMTs,
38 mm, Q.E. ≈ 27%) installed at the two ends of the vessel (see
Figure 7). The inner wall of the vessel is lined with a wavelength shifter to convert ultraviolet He scintillation to the optical wavelengths for the PMTs.
Performances of this detector for fast neutron identification are extensively studied; however, for the aim of the PHeSCAMI project, a characterization of the response of He scintillation to charged (crossing/stopping) particles is necessary. To allow the detection of the charged particles in the calorimeter avoiding the passage of the particle through the PMT, one PMT of the Arktis B-470 detector was replaced with an array of 8 × Silicon PhotoMultipliers (SensL MicroFJ-60035 6 × 6 mm
Fill Factor 65%); see left panel of
Figure 8. The SiPM circular array is shielded by 20 cm of iron, and a central hole,
1 cm, allows the particles to enter the helium target, crossing only the (≈2.5 cm thick) fused silica optical window.
4.1. Muon Calibration
A preliminary test with muons, µ, from cosmic rays was performed. The B-470 detector was operated in coincidence with two (40 × 8 × 4 mm
) plastic scintillators, placed in a telescopic configuration, to detect crossing µ. The data were acquired with a LeCroy HDO9104-MS oscilloscope by sampling the detector waveforms at 20 Gs/s. The “minimum” energy deposition in the helium volume was obtained for µ transversely crossing the detector diameter (depositing ≈0.26 MeV in 200 bar helium). Conversely, the maximum energy deposition was obtained for µ crossing the whole detector (vertically placed, 250 µ detected in 4 months, depositing ∼3 MeV in 200 bar helium). The muon calibration is analyzed along with the proton calibration to measure the detector performance described in the following sections (
Figure 9,
Figure 10 and
Figure 11).
4.2. Proton Calibration
A test on the proton beam line in the experimental room of the Trento Proton Therapy Facility (Italy) [
30] was pursued to characterize the B-470 detector response to protons in the energy range 70–230 MeV that is the same range of interest for
detection in CR.
The detector was tested with transversely crossing protons (Right Panel of
Figure 7). In particular, for beam energy of 215 MeV, 100 MeV, and 80 MeV, we expect an energy deposit in He of 0.54 MeV, 0.93 MeV, and 1.1 MeV, respectively. Moreover, the B-470 was tested with protons entering longitudinally in the detector through the hollow SiPM array and the fused silica optical window (left panel of
Figure 12). In this latter case, the energy measured by the helium scintillator follows the typical behavior expected for the Bragg peak. (Right Plot of
Figure 12). Two plastic scintillators (4 mm thickness) are placed in front of the detector to provide the DAQ trigger, T
, and behind the detector, to provide a crossing/veto trigger, T
. Waveforms were acquired with a CAEN DT5742B 5 GS/s digitizer based on the DRS4 chip.
4.3. Arktis B-470 Light Collection Efficiency
The measurement of the Arktis B-470 detector response at different transversal positions allows the testing of the effect of position-dependent light collection efficiency. The signal amplitude variation for particles crossing different positions along the tube is shown in
Figure 9. Measurements as a function of the distance from the SiPM side and from the PMT side agree and are superimposed in the left plot of
Figure 9.
From the measured signal amplitudes, the probability of photon detection at each side can be modeled as: where: d is the distance from the photon detector (SiPM or PMT), = 123 ± 2 mm is a photon absorption length scale and = 1 − = 0.063 ± 0.003. The measured value can be attributed mainly to the peculiar B-470 detector geometry. By inverting the efficiency relationship, it is possible to infer the position of the crossing particle with a resolution of 5–10 cm by considering the asymmetry of the signals collected on both sides. Position resolution for particles passing near the SiPM (right) side is worse than the one for particles passing near the PMT (left) side due to the smaller detection surface of the 8xSiPM array (1.9 cm vs. 3 cm considering the 65% SiPM Fill Factor and the 27% PMT Quantum Efficiency).
4.4. Arktis B-470 Energy Resolution
The energy resolution of each side of the B-470 detector was investigated by considering the measured position-dependent collection efficiency (see left panel of
Figure 10).
In particular, the relative energy resolution for each side is shown as a function of the photon collection efficiency corrected Energy:
. For the four runs of longitudinally crossing protons (tagged by the rear veto), a rough approximation,
0.5, was adopted. A simplified resolution model dominated by Poisson statistics was adopted to fit the energy resolutions measured for each side:
(red and blue dotted line in the left panel of
Figure 10). Both sides provide an asymptotic energy resolution of
8%. Moreover, the numbers of collected photoelectrons evaluated at the side (P(d) = 1) are
ph.e/MeV and
ph.e/MeV for SiPM and PMT side, respectively. The ratio
is compatible with the expected (≈1.6) collection efficiency ratio among the two sides (knowing the photodetection surfaces, SiPM Fill Factor and PMT Q.E.).
Finally, in the Right Panel of
Figure 10, the asymmetry distribution of the Energy measured by both detector sides for longitudinal protons with beam Energy of 112 MeV is shown. In this case, a deposited energy of 16 MeV is measured in the helium scintillator. The obtained width of the relative energy difference, ≈4.5%, is reasonably compatible with
as expected from the simplified resolution model.
In summary, there are a lot of unknowns and uncertainties when relating our measurements based on the Arktis B-470 detector to the expected performance of the PHeSCAMI detector. These include the nature of helium gas scintillation (wavelength, photon yield, pressure dependence, etc.), the wavelength shifter used in the Arktis B-470, and the differences in the geometry. Despite these, we feel that our measurements based on the Arktis B-470 detector show that it is plausible to achieve the assumed hypothesis that the HeCal detector would be able to measure energy depositions larger than 10 MeV with an energy resolution better than 10%. It is our future project to study the unknowns and uncertainties mentioned above.
4.5. Arktis B-470 Time Resolution
The time resolution of each side of the B-470 detector was investigated by measuring the time difference between the helium scintillation and the plastic scintillator signals. The time resolution of the plastic scintillator is negligible in this difference. It is observed that the measured time resolution improves for larger signals collected by the detector side.
The red and blue dotted lines in the left panel of
Figure 11 are the fit of a simplified model of time resolution dominated by the Poisson statistics:
. In this model,
can be interpreted as the effective time uncertainty of the single photoelectron, while
is the asymptotic time resolution expected for large signals. The SiPM side provides the worst time resolution:
ns and
ns while for the PMT channel:
ns and
ns. The better timing performance of PMT with respect to the SiPM array is related to the larger photon detection efficiency and the relatively fast single photoelectron signal shape. The asymptotic value of time resolution obtained for the PMT channel suggests that, for this preliminary measurement, the ultimate time resolution is dominated by the typical non-uniform sampling time step, varying from cell to cell, of the CAEN DT5742B 5GS/s digitizer based on the DRS4 chip. As a summary, the time resolution tested with the Arktis B-470 detector confirms the capability of a pressurized helium calorimeter to detect the >50 ns delayed annihilation, i.e., the signature for antinuclei of the PHeSCAMI technique.
5. Scintillation Components of Helium at 200 Bar
Both the slow and fast scintillation components of helium were investigated by sampling the Arktis B-470 signal waveforms at 20 Gs/s with a LeCroy HDO9104-MS oscilloscope. In
Figure 13, the measured scintillation signal, obtained as the average of many different scintillation pulses, is shown.
The signal rise time was inferred by fitting the first part of the sampled waveform with the function:
. The measured
ns confirms that pressurized helium is a suitable scintillator for fast calorimetry (see left plot of
Figure 13). The scintillation decay of helium was described with a three-component model:
where
ns,
ns and
µs are the fast, intermediate and slow scintillation decay times, respectively. The measured relative amplitudes are:
% and
%. The quoted errors for
and
are dominated by the systematic uncertainty related to the possibility of multiple intermediate components. The presence of fast and slow scintillation components in helium was well known, and the ratio
was found to be much larger for nuclear recoils. For this reason, helium scintillators are adopted to identify fast neutrons from gamma rays thanks to the PSD technique [
20,
21,
22,
29]. In this work, we identify a hint for a (so far undetected) small intermediate component (
ns), and we measured a fast decay component (
ns). These measurements confirm that pressurized helium is quite a fast scintillator. In particular, it is known that scintillation decay time in helium is dependent on pressure and gas impurities. In
Figure 14, the lifetime of the fast decay component,
ns, measured at 200 bar is compared with scintillation decay times for helium measured at lower pressure in [
31].
Since our system does not directly measure the UV scintillation light from helium, but only the visible light emitted by the wavelength shifter adopted in the Arktis B-470 detector, both the measured values of the intermediate and fast components could be related to this WLS emission stimulated by a faster UV helium scintillation. Therefore, the measured value of ns should be interpreted as an upper limit for the helium scintillation fast decay time at 200 bar.