Ball-Flight Viewing Duration and Estimates of Passing Height in Baseball
Abstract
:1. Introduction
1.1. Cues for Batting
1.2. Predictions of When a Pitched Ball Will Arrive
1.3. Predictions of Where a Pitched Ball Will Arrive
1.3.1. Internal Models
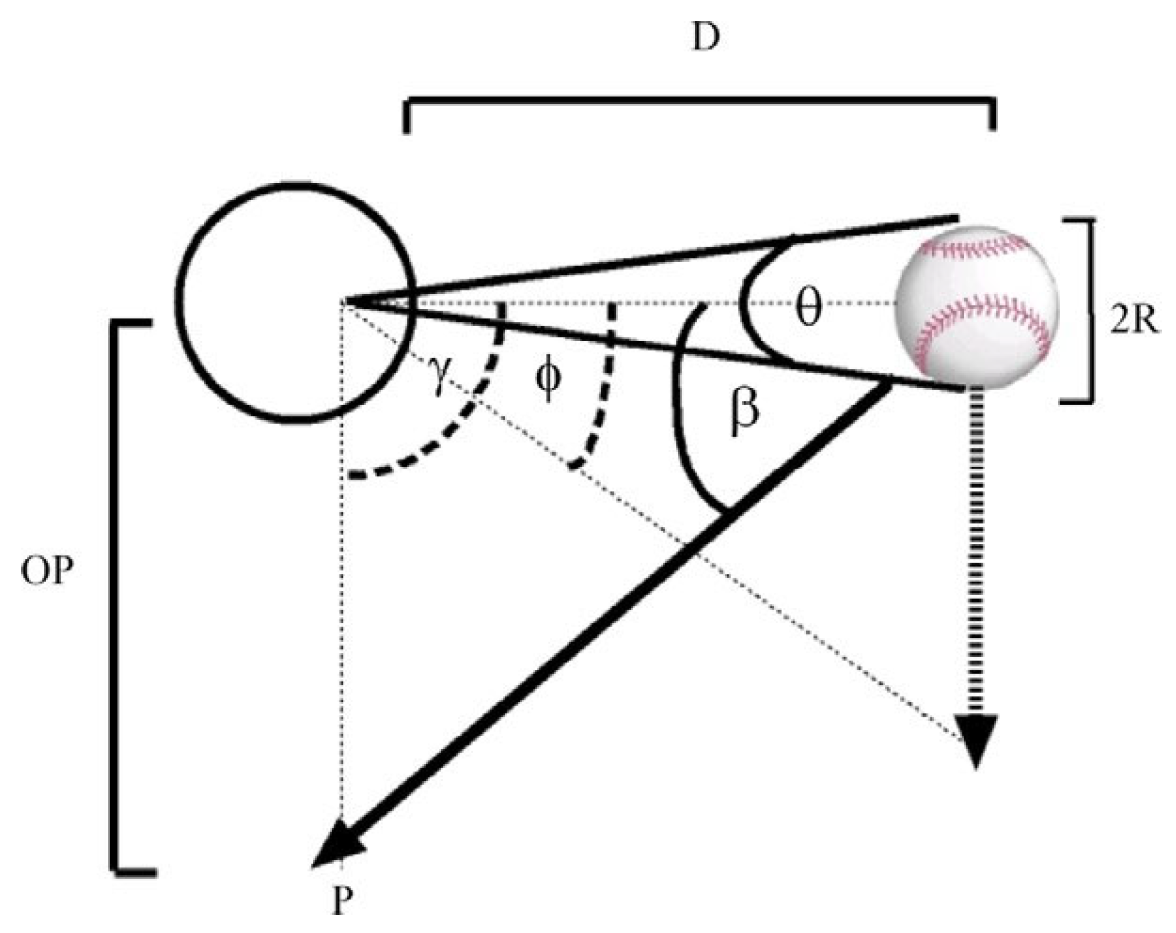
1.3.2. Ball-Flight Cues
2. Materials and Methods
2.1. Subjects
2.2. Equipment
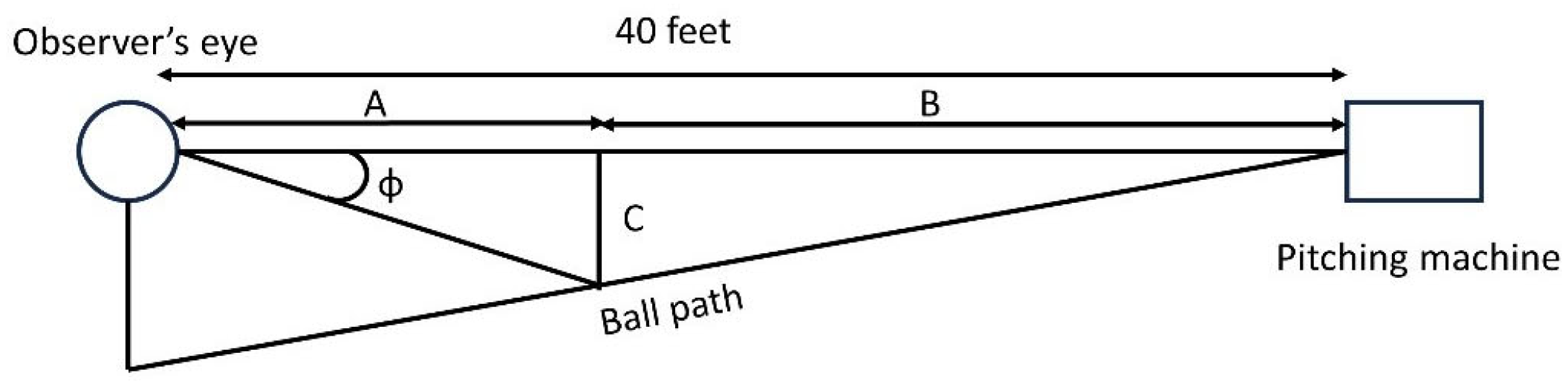
2.3. Experimental Protocol
2.4. Data Analyses
3. Results
3.1. Mean Passing Height Responses
3.2. Accuracy of Mean Passing Heights
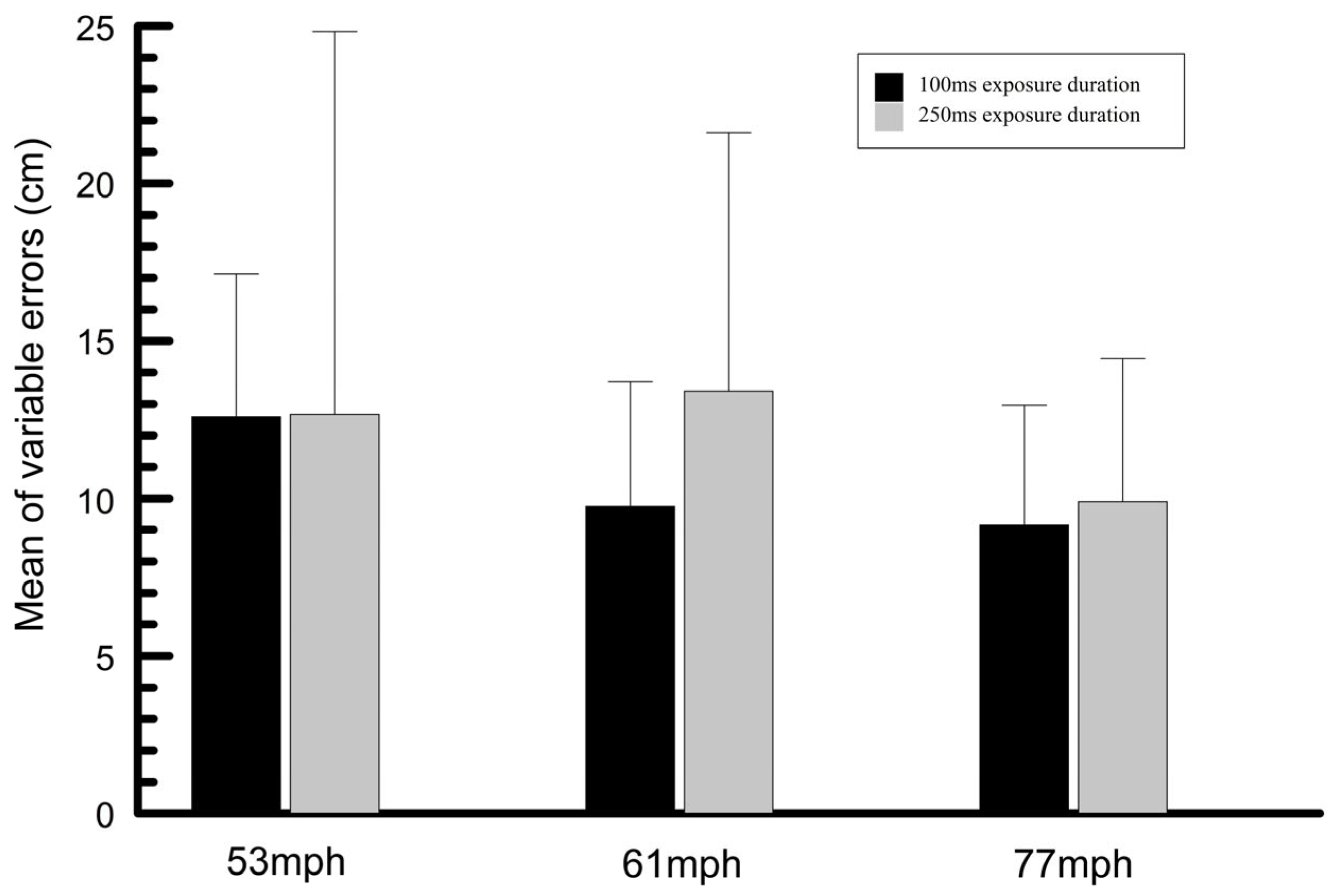
3.3. Mean Variability for Passing Height Responses
3.4. Mean Constant and Variable Passing Height Errors
3.5. Calculations of Expected Passsing Height with Magnus and Drag Forces
3.6. Summary of Results
4. Discussion
4.1. Assessment of Ball-Flight Cues
4.2. Cues Associated with Internal Models
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Subject | Speed 1 (77mph) Exposure 1 (100 ms) Exposure 2 (250 ms) | Speed 2 (61mph) Exposure 1 (100 ms) Exposure 2 (250 ms) | Speed 3 (53mph) Exposure 1 (100 ms) Exposure 2 (250 ms) |
|---|---|---|---|
| A | 99.5 ± 11.17 (60) 93.2 ± 11.06 (50) | 88.5 ± 14.54 (10) 74.5 ± 15.71 (30) | 82.5 ± 12.96 (0) 61 ± 8.43 (0) |
| B | 115.5 ± 7.25 (10) 106 ± 10.22 (50) | 101.5 ± 8.51 (0) 85± 17.48 (10) | 101 ± 7.75 (0) 61 ± 13.9 (0) |
| C | 118.9 ± 9.47 (20) 107.7 ± 7.83 (60) | 93.2 ± 14.97 (0) 82.9 ± 11.62 (10) | 90.3 ± 10.25 (0) 52.1 ± 14.97 (0) |
| D | 115.9 ± 6.19 (20) 100 ± 12.27(60) | 102.6 ± 8.18 (0) 67.1 ± 14.93 (50) | 87.4 ± 20.81 (0) 58.5 ± 12.39 (0) |
| E | 114.6 ± 5.64 (20) 105.8 ± 4.71 (80) | 108 ± 4.57 (0) 94.9 ± 5.45 (0) | 106.7 ± 6.29 (0) 85.4 ± 5.66 (0) |
| F | 116.2 ± 11.77 (30) 88.7 ± 8.82 (40) | 89.7 ± 12.24 (0) 77.6 ± 9.11 (10) | 75.4 ± 17.32 (0) 48.7 ± 11.09 (10) |
| G | 119 ± 3.94 (0) 114.8 ± 5.9 (10) | 98.5 ± 9.44 (0) 90 ± 13.94 (10) | 78 ± 12.06 (0) 75 ± 12.69 (0) |
| H | 84 ± 6.58 (40) 88 ± 4.83 (70) | 74.5 ± 5.99 (10) 69 ± 10.22 (30) | 71.5 ± 7.47 (0) 61 ± 5.68 (0) |
| I | 109.5 ± 11.39 (50) 93.6 ± 10.06 (60) | 101.7 ± 8.59 (0) 71.9 ± 8.03 (40) | 89.8 ± 15.31 (0) 49.1 ± 9.57 (10) |
| J | 117.1 ± 5.26 (10) 110.9 ± 8.18 (50) | 114.7 ± 3.2 (0) 99.5 ± 4.65 (0) | 104.1 ± 5.92 (0) 91.9 ± 7 (0) |
| K | 108.8 ± 10.13 (40) 92.3 ± 8.53 (70) | 93.9 ± 7.42 (0) 78.2 ± 10.46 (10) | 74.7 ± 12.86 (0) 56.3 ± 8.01 (0) |
| L | 106 ± 8.96 (50) 95 ± 8.3 (80) | 102.3 ± 7.82 (0) 75.1 ± 7.08 (20) | 93.8 ± 10.27 (0) 62.8 ± 6.89 (0) |
| M | 100.6 ± 15.13 (50) 98.7 ± 6.31 (90) | 80.1 ± 16.48 (30) 69.9 ± 12.18 (30) | 80 ± 12.27 (0) 51.5 ± 7.11 (0) |
| N | 96.2 ± 19.78 (10) 95.8 ± 9.16 (70) | 98.7 ± 5.81 (0) 72.1 ± 15.62 (20) | 80.7 ± 15.68 (0) 59.2 ± 12.37 (0) |
| O | 102.2 ± 5.87 (80) 97 ± 10.36 (60) | 96.2 ± 8.57 (0) 85.5 ± 9.13 (0) | 93.4 ± 14.99 (0) 86.3 ± 7.38 (0) |
| P | 120.2 ± 7.8 (20) 99.8 ± 10.26 (70) | 107.9 ± 10.77 (0) 72.7 ± 14.14 (30) | 91.3 ± 12.94 (0) 63.5 ± 13.44 (0) |
| Q | 118.7 ± 8.58 (20) 109.5 ± 8.58 (50) | 110 ± 10.65 (0) 84.8 ± 13.53 (10) | 99.6 ± 9.11 (0) 75.3 ± 10.74 (0) |
| R | 88.5 ± 12.7 (60) 84 ± 11.01 (30) | 80 ± 17.48 (30) 70 ± 15.63 (50) | 67 ± 16.02 (10) 43.5 ± 7.09 (10) |
| S | 117.1 ± 5.8 (10) 113.9 ± 7.46 (10) | 114.3 ± 6.88 (0) 103.5 ± 9.2 (0) | 105.5 ± 9.14 (0) 90.1 ± 13.24 (0) |
| T | 116 ± 9.66 (20) 102 ± 20.03 (20) | 109 ± 12.87 (0) 73.5 ± 18.42 (0) | 88 ± 22.39 (0) 73.5 ± 14.35 (0) |
References
- Toole, A.J.; Fogt, N. Review: Head and eye movements and gaze tracking in baseball batting. Optom. Vis. Sci. 2021, 98, 750–758. [Google Scholar] [CrossRef] [PubMed]
- Gray, R. Behavior of college baseball players in a virtual batting task. J. Exp. Psychol. Hum. Percept. Perform. 2002, 28, 1131–1148. [Google Scholar] [CrossRef] [PubMed]
- Gray, R. Review: Approaches to visual-motor control in baseball batting. Optom. Vis. Sci. 2021, 98, 738–749. [Google Scholar] [CrossRef] [PubMed]
- Gray, R.; Regan, D. Accuracy of estimating time to collision using binocular and monocular information. Vis. Res. 1998, 38, 499–512. [Google Scholar] [CrossRef]
- Lee, D.N. A theory of visual control of braking based on information about time-to-collision. Perception. 1976, 5, 437–459. [Google Scholar] [CrossRef]
- Regan, D. Binocular information about time to collision and time to passage. Vis. Res. 2002, 42, 2479–2484. [Google Scholar] [CrossRef] [PubMed]
- Rushton, S.K.; Wann, J.P. Weighted combination of size and disparity: A computational model for timing a ball catch. Nat. Neurosci. 1999, 2, 186–190. [Google Scholar] [CrossRef]
- Yan, J.J.; Lorv, B.; Li, H.; Sun, H.J. Visual processing of the impending collision of a looming object: Time to collision revisited. J. Vis. 2011, 11, 7. [Google Scholar] [CrossRef]
- Tresilian, J.R. Visually timed action: Time-out for ‘tau’? Trends Cogn. Sci. 1999, 3, 301–310. [Google Scholar] [CrossRef]
- Smeets, J.B.; Brenner, E.; Trébuchet, S.; Mestre, D.R. Is judging time-to-contact based on ‘tau’? Perception 1996, 25, 583–590. [Google Scholar] [CrossRef]
- Chang, C.J.; Jazayeri, M. Integration of speed and time for estimating time to contact. Proc. Natl. Acad. Sci. USA 2018, 115, E2879–E2887. [Google Scholar] [CrossRef] [PubMed]
- Aguado, B.; López-Moliner, J. Gravity and known size calibrate visual information to time parabolic trajectories. Front. Hum. Neurosci. 2021, 15, 642025. [Google Scholar] [CrossRef] [PubMed]
- Gómez, J.; López-Moliner, J. Synergies between optical and physical variables in intercepting parabolic targets. Front. Behav. Neurosci. 2013, 7, 46. [Google Scholar] [CrossRef]
- Gray, R.; Regan, D.M. Unconfounding the direction of motion in depth, time to passage and rotation rate of an approaching object. Vis. Res. 2006, 46, 2388–2402. [Google Scholar] [CrossRef]
- Jörges, B.; López-Moliner, J. Gravity as a strong prior: Implications for perception and action. Front. Hum. Neurosci. 2017, 11, 203. [Google Scholar] [CrossRef]
- Delle Monache, S.; Indovina, I.; Zago, M.; Daprati, E.; Lacquaniti, F.; Bosco, G. Watching the effects of gravity. Vestibular cortex and the neural representation of “visual” gravity. Front. Integr. Neurosci. 2021, 15, 793634. [Google Scholar] [CrossRef]
- Nathan, A.M. The effect of spin on the flight of a baseball. Am. J. Phys. 2008, 76, 119–124. [Google Scholar] [CrossRef]
- Bahill, A.T.; Karnavas, W.J. The perceptual illusion of baseball’s rising fastball and breaking curveball. J. Exp. Psychol. Hum. Percept. Perform. 1993, 19, 3–14. [Google Scholar] [CrossRef]
- Bootsma, R.J.; Peper, C.E. Predictive visual information sources for the regulation of action with special emphasis on catching and hitting. In Vision and Motor Control; Proteau, L., Elliott, D., Eds.; North-Holland Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1992; Volume 85, pp. 285–314. [Google Scholar]
- McKee, S.P. A local mechanism for differential velocity detection. Vis. Res. 1981, 21, 491–500. [Google Scholar] [CrossRef]
- Orban, G.A.; de Wolf, J.; Maes, H. Factors influencing velocity coding in the human visual system. Vis. Res. 1984, 24, 33–39. [Google Scholar] [CrossRef]
- Sekuler, A.B. Simple-pooling of unidirectional motion predicts speed discrimination for looming stimuli. Vis. Res. 1992, 32, 2277–2288. [Google Scholar] [CrossRef] [PubMed]
- Rushton, S.K.; Duke, P.A. Observers cannot accurately estimate the speed of an approaching object in flight. Vis. Res. 2009, 49, 1919–1928. [Google Scholar] [CrossRef]
- Thompson, L.; Ji, M.; Rokers, B.; Rosenberg, A. Contributions of binocular and monocular cues to motion-in-depth perception. J. Vis. 2019, 19, 2. [Google Scholar] [CrossRef] [PubMed]
- De Bruyn, B.; Orban, G.A. Human velocity and direction discrimination measured with random dot patterns. Vis. Res. 1988, 28, 1323–1335. [Google Scholar] [CrossRef] [PubMed]
- Delle Monache, S.; Paolocci, G.; Scalici, F.; Conti, A.; Lacquaniti, F.; Indovina, I.; Bosco, G. Interception of vertically approaching objects: Temporal recruitment of the internal model of gravity and contribution of optical information. Front. Physiol. 2023, 14, 1266332. [Google Scholar] [CrossRef] [PubMed]
- Gray, R.; Cañal-Bruland, R. Integrating visual trajectory and probabilistic information in baseball batting. Psychol. Sport Exerc. 2018, 36, 123–131. [Google Scholar] [CrossRef]
- Nakamoto, H.; Fukuhara, K.; Torii, T.; Takamido, R.; Mann, D.L. Optimal integration of kinematic and ball-flight information when perceiving the speed of a moving ball. Front. Sports Act. Living 2022, 4, 930295. [Google Scholar] [CrossRef]
- de la Malla, C.; López-Moliner, J. Predictive plus online visual information optimizes temporal precision in interception. J. Exp. Psychol. Hum. Percept. Perform. 2015, 41, 1271–1280. [Google Scholar] [CrossRef] [PubMed]
- Brantley, J.A.; Körding, K.P. Bayesian integration in professional baseball batters. bioRxiv 2022, 511934. [Google Scholar] [CrossRef]
- Sander, J.; Fogt, N. Estimations of the passing height of approaching objects. Optom Vis Sci. 2022, 99, 274–280. [Google Scholar] [CrossRef]
- Giancoli, D.C. Physics: Principles with Applications, 2nd ed.; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Wong, R.; Laudner, K.; Amonette, W.; Vazquez, J.; Evans, D.; Meister, K. Relationships between lower extremity power and fastball spin rate and ball velocity in professional baseball pitchers. J. Strength Cond. Res. 2023, 37, 823–828. [Google Scholar] [CrossRef] [PubMed]
- Djamovski, V.; Pateras, J.; Chowdhury, H.; Alom, F.; Steiner, T. Effects of seam and surface texture on tennis balls aerodynamics. Procedia Eng. 2012, 34, 140–145. [Google Scholar] [CrossRef]
- Zhao, H.; Warren, W.H. On-line and model-based approaches to the visual control of action. Vis. Res. 2015, 110 Pt B, 190–202. [Google Scholar] [CrossRef]
- Farrow, D.; Abernethy, B. Do expertise and the degree of perception-action coupling affect natural anticipatory performance? Perception 2003, 32, 1127–1139. [Google Scholar] [CrossRef]
- Ranganathan, R.; Carlton, L.G. Perception-action coupling and anticipatory performance in baseball batting. J. Mot. Behav. 2007, 39, 369–380. [Google Scholar] [CrossRef] [PubMed]
- Kalén, A.; Bisagno, E.; Musculus, L.; Raab, M.; Pérez-Ferreirós, A.; Williams, A.M.; Araújo, D.; Lindwall, M.; Ivarsson, A. The role of domain-specific and domain-general cognitive functions and skills in sports performance: A meta-analysis. Psychol. Bull. 2021, 147, 1290–1308. [Google Scholar] [CrossRef] [PubMed]
- Grieve, G.; Besler, Z.; Müller, S.; Spering, M.; Hodges, N.J. Assessing the validity and reliability of a baseball pitch discrimination online task. Int. J. Sport Exerc. Psychol. 2024, 22, 481–505. [Google Scholar] [CrossRef]
- Nasu, D.; Baba, T.; Imamura, T.; Yamaguchi, M.; Kitanishi, Y.; Kashino, M. Virtual reality perceptual training can improve the temporal discrimination ability of swinging during softball batting. Front. Sports Act. Living 2024, 6, 1332149. [Google Scholar] [CrossRef]
- Müller, S.; Abernethy, B. Expert anticipatory skill in striking sports: A review and a model. Res. Q. Exerc. Sport. 2012, 83, 175–187. [Google Scholar] [CrossRef] [PubMed]
- Morris-Binelli, K.; Müller, S. Advancements to the understanding of expert visual anticipation skill in striking sports. Can. J. Behav. Sci. 2017, 49, 262–268. [Google Scholar] [CrossRef]


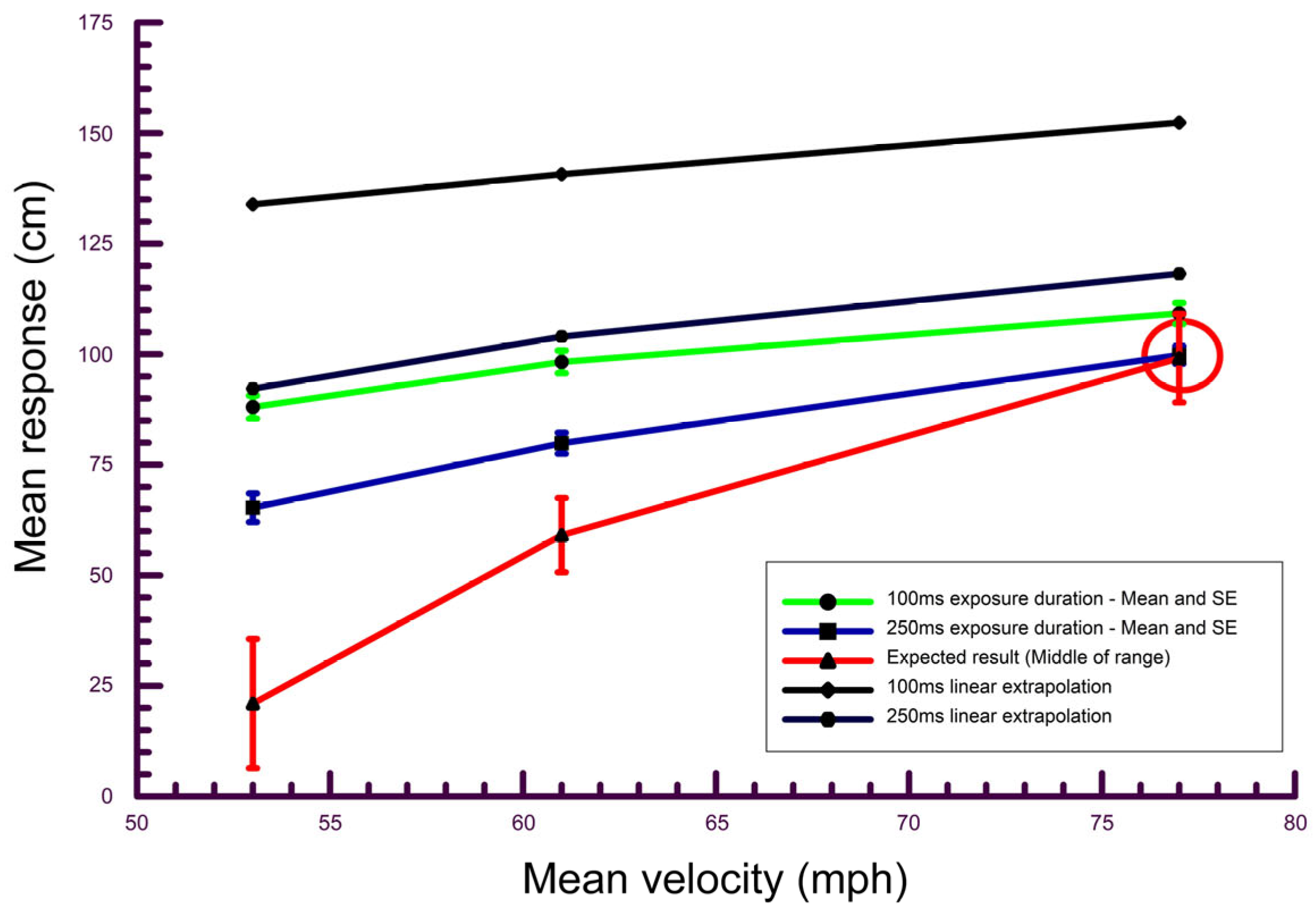
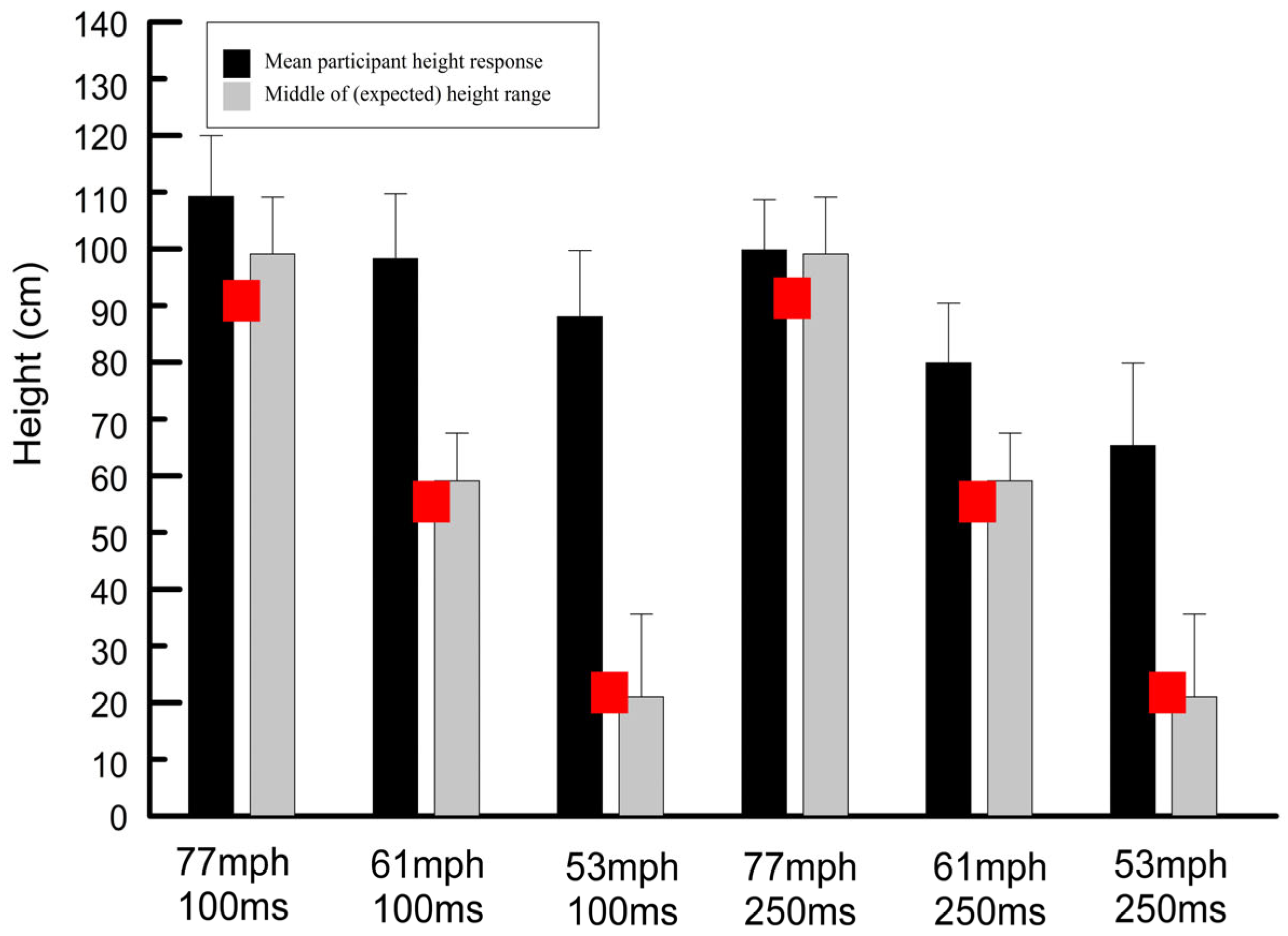

| Exposure Duration | Mean Passing Height Response and Standard Deviation (and Standard Error) (cm From Ground) | Expected Range of Heights (cm Above the Ground) and Midpoint of the Measured Range (cm) | Calculated Height (cm) Using the Equation −1/2 gt2 | Time for Ball to Traverse Total 40 ft Distance | |
|---|---|---|---|---|---|
| Speed 1 (77 mph) | 100 ms | 109.23 ± 10.75 cm (2.40) | 89.1–109.1 cm (99.1 cm) | 90.9 cm | 360.3 ± 7.41 ms |
| 250 ms | 99.84 ± 8.83 cm (1.98) | ||||
| Speed 2 (61 mph) | 100 ms | 98.27 ± 11.41 cm (2.55) | 50.7–67.5 cm (59.1 cm) | 56.9 cm | 446.9 ± 8.75 ms |
| 250 ms | 79.89 ± 10.56 cm (2.36) | ||||
| Speed 3 (53 mph) | 100 ms | 88.04 ± 11.69 cm (2.61) | 6.3–35.6 cm (21.0 cm) | 22.9 cm | 518.5 ± 14.9 ms |
| 250 ms | 65.29 ± 14.58 cm (3.26) |
| Exposure Duration | Mean Percentage of Responses Within the Expected Range | |
|---|---|---|
| Speed 1 (77 mph) | 100 ms | 31.0 ± 21.5% |
| 250 ms | 54.0 ± 22.6% | |
| Speed 2 (61 mph) | 100 ms | 4.0 ± 9.4% |
| 250 ms | 18.0 ± 16.4% | |
| Speed 3 (53 mph) | 100 ms | 0.5 ± 2.2% |
| 250 ms | 1.5 ± 3.7% |
| Calculated Height (cm) Using the Equation −1/2 gt2 | Calculated Height (cm) from Trajectory Calculator (Magnus Force (Top) and Magnus and drag Forces (Bottom)) | Exposure Duration | Mean Height Response and Standard Deviation (and Standard Error) | |
|---|---|---|---|---|
| Speed 1 (77 mph) | 90.9 cm | 116.62 cm 113.81 cm | 100 ms | 109.23 ± 10.75 cm (2.40) |
| 250 ms | 99.84 ± 8.83 cm (1.98) | |||
| Speed 2 (61 mph) | 56.9 cm | 85.10 cm 80.74 cm | 100 ms | 98.27 ± 11.41 cm (2.55) |
| 250 ms | 79.89 ± 10.56 cm (2.36) | |||
| Speed 3 (53 mph) | 22.9 cm | 54.35 cm 48.28 cm | 100 ms | 88.04 ± 11.69 cm (2.61) |
| 250 ms | 65.29 ± 14.58 cm (3.26) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benson, E.; Toole, A.J.; Fogt, N. Ball-Flight Viewing Duration and Estimates of Passing Height in Baseball. Vision 2025, 9, 8. https://doi.org/10.3390/vision9010008
Benson E, Toole AJ, Fogt N. Ball-Flight Viewing Duration and Estimates of Passing Height in Baseball. Vision. 2025; 9(1):8. https://doi.org/10.3390/vision9010008
Chicago/Turabian StyleBenson, Emily, Andrew J. Toole, and Nick Fogt. 2025. "Ball-Flight Viewing Duration and Estimates of Passing Height in Baseball" Vision 9, no. 1: 8. https://doi.org/10.3390/vision9010008
APA StyleBenson, E., Toole, A. J., & Fogt, N. (2025). Ball-Flight Viewing Duration and Estimates of Passing Height in Baseball. Vision, 9(1), 8. https://doi.org/10.3390/vision9010008




