Real-Time Behaviour Planning and Highway Situation Analysis Concept with Scenario Classification and Risk Estimation for Autonomous Vehicles
Abstract
:1. Introduction
- It is also a question of whether the system is performing risk analysis for a predefined, fixed number of possible options or optimising on the entire decision-making area [7]. In our research, we work with the earlier mentioned approach.
- Movement in our own lane
- Overtaking
- Lane changing
- Planning a danger avoidance manoeuvre
2. Materials and Methods
2.1. System Architecture
2.1.1. Perception
2.1.2. Decision Making
2.2. Simulation Environment
2.3. Situation Analysis
2.3.1. Analysing Traffic Density
- the number of vehicles in the given lane per unit length,
- the average longitudinal velocity of the vehicles in the given lane,
- the average longitudinal acceleration of the vehicles in the given lane,
- and the average TIV parameter for the consecutive vehicles in the given lane.
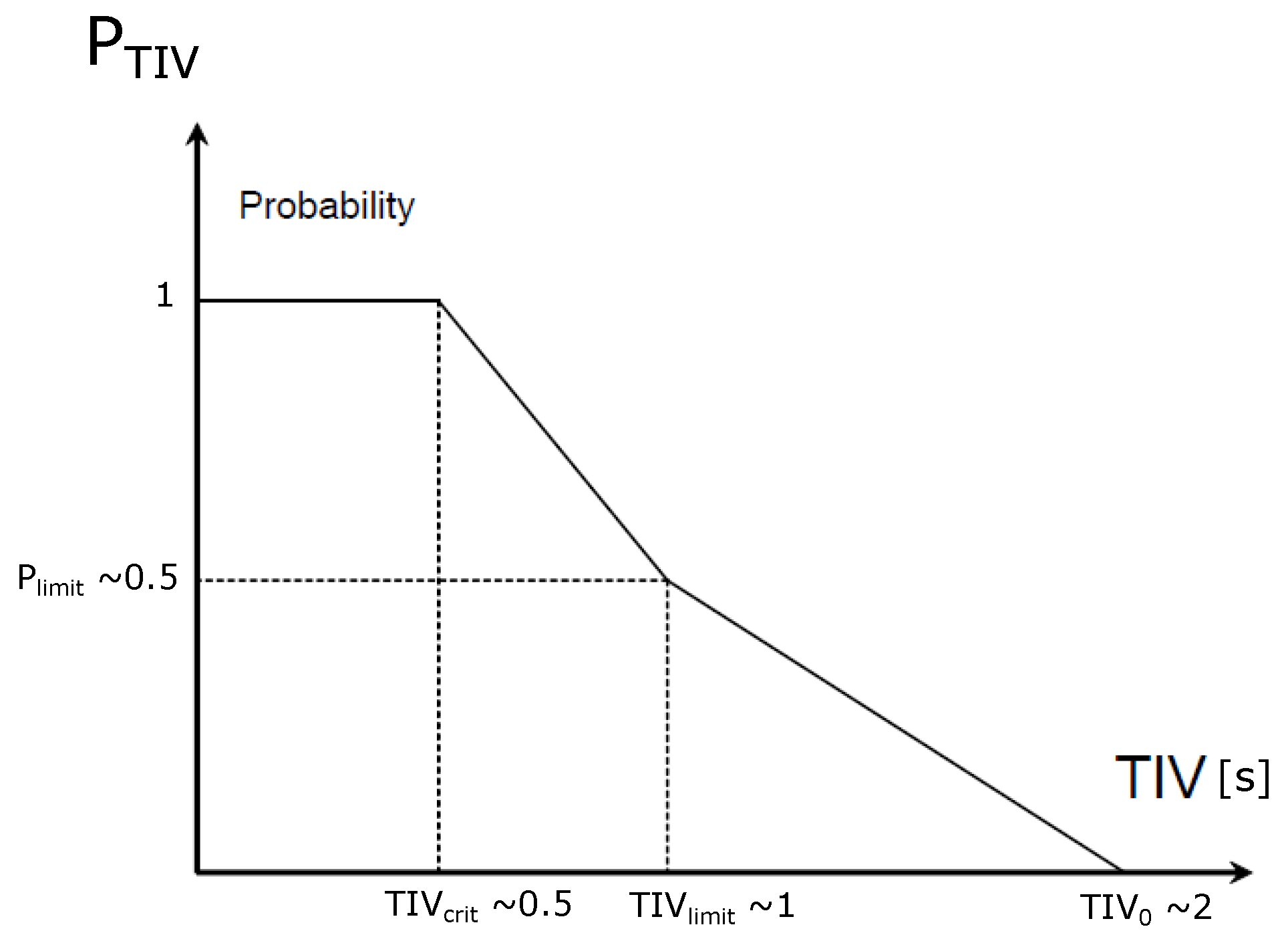
2.3.2. Risk Estimation
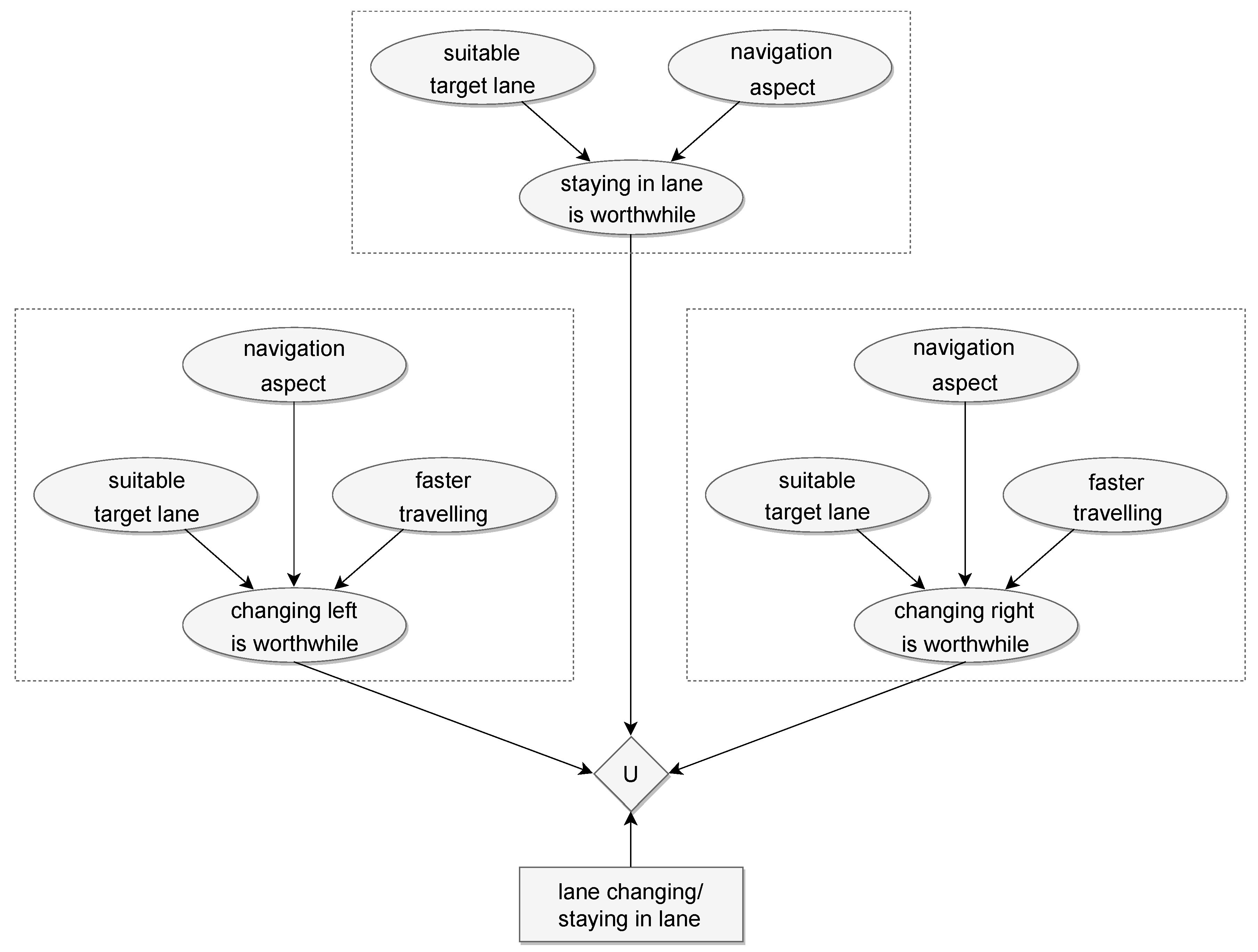
Concept
- If the foreseen distance of a lane’s end is getting significantly close to the ego, all risk values rise related to manoeuvres that are linked to that lane. Basically, the algorithm treats the end of a lane like a still standing object.
- All lane changing manoeuvres should have a risk value of at least one, thus preferring the lane keeping behaviour. As a result, a lane changing manoeuvre will only be performed if the behaviour planning algorithms can find significant benefits for it.
Label Generation
Training Data
- previous real-world measurements,
- virtual measurements from different simulation environments,
- data generated from probability distributions and expert systems.
Neural Network
2.4. Behaviour Planning
- State vector of the vehicle
- -
- Longitudinal and lateral velocity
- -
- Longitudinal and lateral acceleration
- -
- Width and the length of the vehicle
- Environmental sensor data
- -
- Lane information
- -
- Line information (road markings)
- -
- Information about peer vehicles
- ∗
- Position
- ∗
- Longitudinal and lateral velocity
- ∗
- Longitudinal and lateral acceleration
- Output of the risk analysis module
- Output of the situation classifying module
Reasons for Applying Probabilistic Inference
- Perceptions are uncertain: The environmental sensing module gives us uncertain information about the objects around us, so, practically, the input values of the algorithm are probabilistic variables, and they have expected values and deviations.
- All of the inputs of the task cannot be defined: If we want to implement driving with computer software, then we certainly do not know all the parameters that can influence the decisions. There are several reasons for this:
- -
- Laziness: Defining the complete system of causes and effects means too much work.
- -
- Theoretical ignorance: We do not know all of the parameters of driving as an algorithmizable task.
- -
- Practical ignorance: If we knew the whole rule-based system, there would still be several uncertainties surrounding the definition and measurement of the parameters.
- It is close to human thinking: With probabilistic networks, we can provide a solution to a high-level problem with a model which is similar to our thinking, and its graphic visualisation also makes the solution more straightforward.
- It reduces the number of parameters: Several known or unknown parameters can be replaced by a single probability variable. If the number of the parameters seems to be too low, the network can be extended until the operation seems right. The low number of parameters has several advantages:
- -
- Hidden parameters are also considered through the probabilities.
- -
- We do not complicate our algorithm with unnecessary parameters.
- -
- The calculation time can be significantly reduced in real-time applications.
Imagine that, initially, we decide on a lane change only on the basis of two questions: Is the lane next to us empty? Is somebody moving slowly in front of us? If the algorithm says that it is worthwhile to switch with 60% probability, and this is permitted by the rules and the traffic situation, then we made a decision with a very simplified model, but, in most of cases, this would prove to be good. If we add to this description additional variables, then we will be getting closer to the optimal solution, but we are still far from the practically impossible task of treating driving with all of the existing parameters. - The prediction appears in the algorithm: A human driver’s decision is often based on predicting the motions of the peer vehicles. These parameters can be easily grasped through probabilistic variables. Analysing the movement of the objects detected by the sensors, we can give estimates for the near future based on previous measurement data [14]. For example, if a car is passing by at a high speed, it is highly likely that it will not stop suddenly, but if there is a slowed vehicle in front of it, there is a high probability that it will also brake.
- We can make decisions based on probabilistic variables: If a probabilistic network is supplemented by additional node types, we can represent the decision problem with a so-called decision network. The decision network contains information about the state of the agent, and gives us the possible actions and the status that these actions will cause. From this point, the utility of the state can be treated as a problem of maximising a utility function.
Algorithm Design
- The behaviour planner cannot make safety-critical decisions. This means that it can only select points defined in the manoeuvre space which were judged as safe by the risk analyser module (their risk is ranked as low or minimal).
- If the risk analysis module has assigned medium or higher risk values for all of the points in the manoeuvre space, then the decision of the algorithm cannot be based on the conditional probability tables learned before.
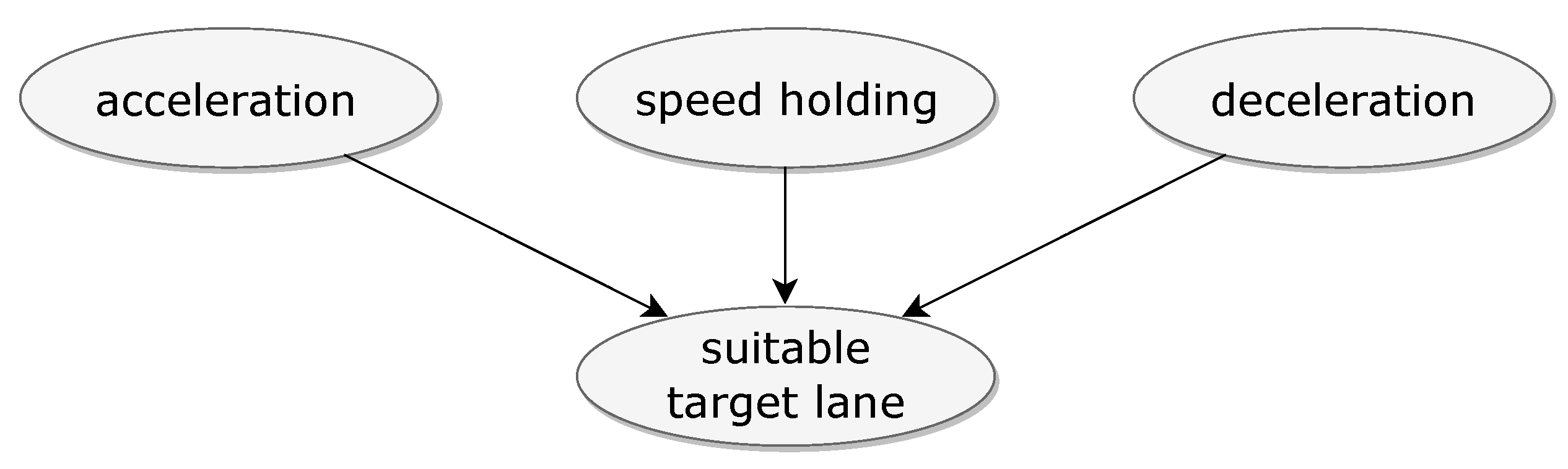
- Longitudinal acceleration
- (a)
- Acceleration
- (b)
- Speed holding
- (c)
- Deceleration
- Lateral action
- (a)
- Lane changing to the left
- (b)
- Staying in our own lane
- (c)
- Lane changing to the right
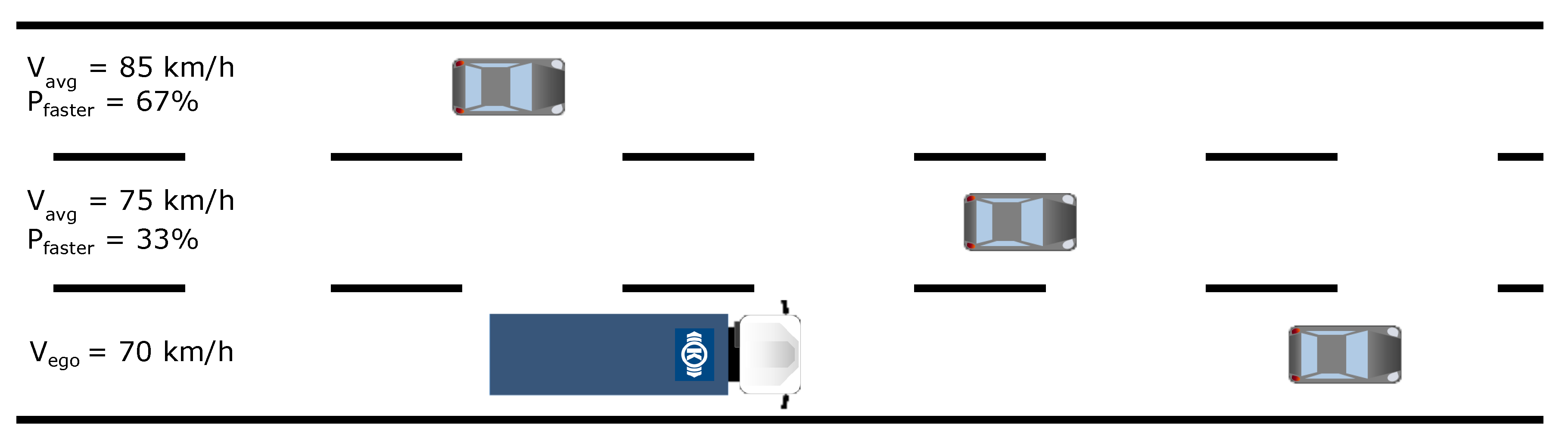
- For navigational reasons
- In the hope of moving faster
- Assign 0% probability to speeds which are not greater than ours.
- Assign 100% probability to speeds which are larger by a given value (for example 15 km/h) than ours.
- Suitability of target lanes which is based on risk calculation.
- Navigation-based lane changing needs.
- Lane changing needs, which can result in faster travelling.
- Movement in our own lane: In the case of heavy-duty commercial vehicles, the most significant part of travelling on the highway is characterised by this situation. The probabilistic network outlined in the previous part (if correctly trained) will mostly keep us in our own lane at the proper speed if it is appropriate for navigational purposes.
- Overtaking: Practically, overtaking means two consecutive lane changes. If the network decides to change and it sees that we can return to our original lane, then it will return. Of course, keeping to the right (or left, in the case of left-hand traffic) must be compelled with different weights in the utility function. Overtaking from the right and zigzag manoeuvres can be prevented by forbidding the lane changes to the right in the hope of moving faster.
- Lane changing: Lane changing differs from movement in our own lane in that it is not caused by traffic but is for a navigational reason, so it is not followed by returning to our original lane. Returning is prevented by a decrease in the original lane’s navigational probabilistic variable.
- Planning a danger avoidance manoeuvre: This situation is different from the others because, in this case, there are no points with an adequate security risk in the manoeuvre space. So, we cannot use the output of the probabilistic network, but we select the safest (or least dangerous) point.
- Tagging measurement data from a simulator and training the network.
- Tagging real measurements.
- Continuous learning during the operation of the system or learning the choices of a human driver.
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- SAE International. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Lefèvre, S.; Vasquez, D.; Laugier, C. A survey on motion prediction and risk assessment for intelligent vehicles. ROBOMECH J. 2014, 1. [Google Scholar] [CrossRef]
- Lytrivis, P.; Thomaidis, G.; Amditis, A. Cooperative path prediction in vehicular environments. In Proceedings of the 2008 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 12–15 October 2008; pp. 803–808. [Google Scholar]
- Aoude, G.S.; Luders, B.D.; Lee, K.K.H.; Levine, D.S.; How, J.P. Threat assessment design for driver assistance system at intersections. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 1855–1862. [Google Scholar]
- Ammoun, S.; Nashashibi, F. Real time trajectory prediction for collision risk estimation between vehicles. In Proceedings of the 2009 IEEE 5th International Conference on Intelligent Computer Communication and Processing, Cluj-Napoca, Romania, 27–29 August 2009; pp. 417–442. [Google Scholar]
- Batz, T.; Watson, K.; Beyerer, J. Recognition of dangerous situations within a cooperative group of vehicles. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 907–912. [Google Scholar]
- Kaempchen, N.; Schiele, B.; Dietmayer, K. Situation assessment of an autonomous emergency brake for arbitrary vehicle-to-vehicle collision scenarios. IEEE Trans. Intell. Transp. Syst. 2009, 10, 678–687. [Google Scholar] [CrossRef]
- Vanholme, B.; Gruyer, D.; Lusetti, B.; Glaser, S.; Mammar, S. Highly Automated Driving on Highways based on Legal Safety. Ph.D. Dissertation, University of Evry-Val-d’Essonne, Évry, France, 2012. [Google Scholar]
- Ulbrich, S.; Maurer, M. Probabilistic Online POMDP Decision Making for Lane Changes in Fully Automated Driving. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems, The Hague, The Netherlands, 6–9 October 2013. [Google Scholar]
- Wei, J.; Dolan, J.M.; Litkouhi, B. A Prediction- and Cost Function-Based Algorithm for Robust Autonomous Freeway Driving. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium University of California, San Diego, CA, USA, 21–24 June 2010. [Google Scholar]
- Ulbrich, S.; Maurer, M. Towards Tactical Lane Change Behavior Planning for Automated Vehicles. In Proceedings of the IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015. [Google Scholar]
- Schnitman, L.; Sobral, A.; Oliveira, L. Highway traffic congestion classification using holistic properties. In Proceedings of the 10th IASTED International Conference on Signal Processing, Pattern Recognition and Applications, Innsbruck, Austria, 12–14 February 2013; Volume 798. [Google Scholar]
- Glaser, S.; Vanholme, B.; Mammar, S.; Gruyer, D.; Nouveliere, L. Maneuver-based trajectory planning for highly autonomous vehicles on real road with traffic and driver interaction. IEEE Trans. Intell. Transp. Syst. 2010, 11, 589–606. [Google Scholar] [CrossRef]
- Bahram, M.; Wolf, A.; Aeberhard, M.; Wollherr, D. A prediction-based reactive driving strategy for highly automated driving function on freeways. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 400–406. [Google Scholar]
- Porikli, F.; Li, X. Traffic congestion estimation using HMM models without vehicle tracking. In Proceedings of the IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004; pp. 188–193. [Google Scholar] [CrossRef]
- Hansson, S.O. Risk. In The Stanford Encyclopedia of Philosophy; Zalta, M.N., Ed.; Etaphysics Research Lab, Stanford University: Stanford, CA, USA, 2018. [Google Scholar]
- Mills, P.J.; Hobbs, C.A. The Probability of Injury to Car Occupants in Frontal and Side Impacts; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1984; Volume 10. [Google Scholar]
- Pride, R.; Giddings, D.; Richens, D.; McNally, D.S. The sensitivity of the calculation of delta-v to vehicle and impact parameters. Accid. Anal. Prev. 2013, 55, 144–153. [Google Scholar] [CrossRef] [PubMed]
- Jurewicz, C.; Sobhani, A.; Woolley, J.; Dutschke, J.; Corben, B. Exploration of vehicle impact speed—Injury severity relationships for application in safer road design. Transp. Res. Procedia 2016, 14, 4247–4256. [Google Scholar] [CrossRef]
- Gennarelli, T.A.; Wodzin, E. The Abbreviated Injury Scale; American Association for Automotive Medicine: Des Plaines, IL, USA, 2005. [Google Scholar]
- Bahouth, G.; Graygo, J.; Digges, K.; Schulman, C.; Baur, P. The benefits and tradeoffs for varied high-severity injury risk thresholds for advanced automatic crash notification systems. Traffic Inj. Prev. 2014, 15 (Suppl. 1), S134–S140. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Vetier, A. Probability Theory; Muegyetemi Kiado: Budapest, Hungary, 2008. [Google Scholar]
- Bayes Server Learning Center. Available online: https://www.bayesserver.com/ (accessed on 15 November 2018).
- Stuart, R.; Peter, N. Artificial Intelligence. A Modern Approach, 2nd ed.; Pearson Education Inc., Prentice Hall: Upper Saddle River, NJ, USA, 2003; p. 07458. ISBN 0137903952. [Google Scholar]
- Nilsson, J.; Silvlin, J.; Brannstrom, M.; Coelingh, E.; Fredriksson, J. If, When, and How to Perform Lane Change Maneuvers on Highways. IEEE Intell. Transp. Syst. Mag. 2016, 8, 68–78. [Google Scholar] [CrossRef]






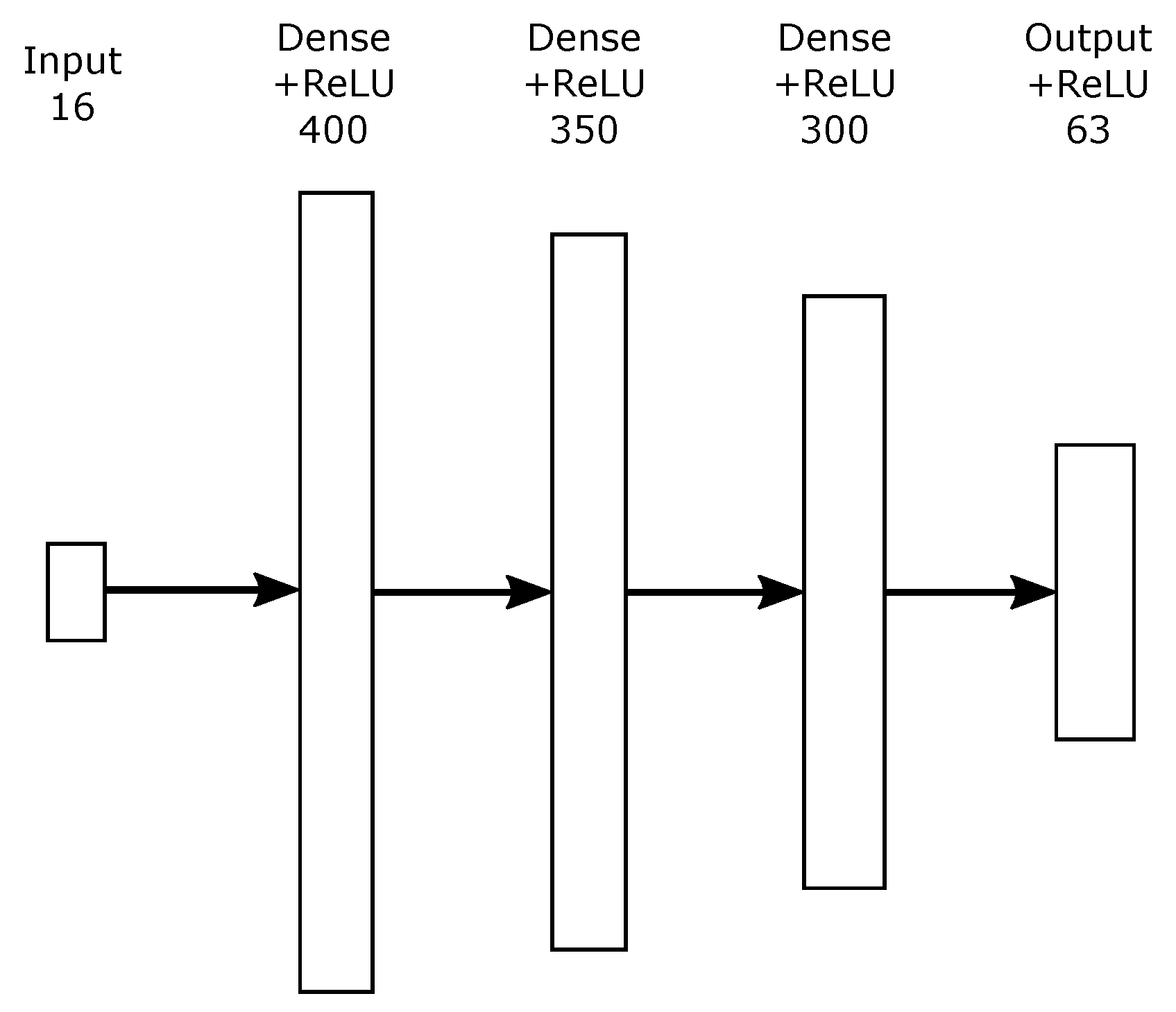





| # | Model Configuration | Epoch | Train Err. | Val. Err. | Test Err. |
|---|---|---|---|---|---|
| 1 | 16-100-63 | 119 | 0.053 | 0.056 | 0.059 |
| 2 | 16-200-63 | 67 | 0.039 | 0.041 | 0.043 |
| 3 | 16-200-150-63 | 19 | 0.021 | 0.030 | 0.025 |
| 4 | 16-400-250-63 | 29 | 0.019 | 0.020 | 0.022 |
| 5 | 16-400-350-300-63 | 39 | 0.016 | 0.017 | 0.019 |
| 6 | 16-80-150-300-600-300-300-63 | 46 | 0.017 | 0.021 | 0.023 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dávid, B.; Láncz, G.; Hunyady, G. Real-Time Behaviour Planning and Highway Situation Analysis Concept with Scenario Classification and Risk Estimation for Autonomous Vehicles. Designs 2019, 3, 4. https://doi.org/10.3390/designs3010004
Dávid B, Láncz G, Hunyady G. Real-Time Behaviour Planning and Highway Situation Analysis Concept with Scenario Classification and Risk Estimation for Autonomous Vehicles. Designs. 2019; 3(1):4. https://doi.org/10.3390/designs3010004
Chicago/Turabian StyleDávid, Bence, Gergő Láncz, and Gergely Hunyady. 2019. "Real-Time Behaviour Planning and Highway Situation Analysis Concept with Scenario Classification and Risk Estimation for Autonomous Vehicles" Designs 3, no. 1: 4. https://doi.org/10.3390/designs3010004
APA StyleDávid, B., Láncz, G., & Hunyady, G. (2019). Real-Time Behaviour Planning and Highway Situation Analysis Concept with Scenario Classification and Risk Estimation for Autonomous Vehicles. Designs, 3(1), 4. https://doi.org/10.3390/designs3010004




