Abstract
Architected cellular materials encompass a wide range of design and performance possibilities. While there has been significant interest in periodic cellular materials, recent emphasis has included consideration of aperiodicity, most commonly in studies of stochastic and graded cellular materials. This study proposes a classification scheme for aperiodic cellular materials, by first dividing the design domain into three main types: gradation, perturbation, and hybridization. For each of these types, two design decisions are identified: (i) the feature that is to be modified and (ii) the method of its modification. Considerations such as combining different types of aperiodic design methods, and modulating the degree of aperiodicity are also discussed, along with a review of the literature that places each aperiodic design within the classification developed here, as well as summarizing the performance benefits attributed to aperiodic cellular materials over their periodic counterparts.
Keywords:
aperiodicity; cellular materials; classification; gradation; perturbation; stochasticity; random; lattice; honeycomb 1. Introduction
Architected cellular materials are an exciting frontier in engineering, enabled by the recent confluence of advances in computational design and additive manufacturing and driven by the wide range of current and potential applications that leverage their often unique properties [1]. Prior to these advances, cellular materials were most commonly categorized into two domains, constrained primarily on account of manufacturability limitations—honeycombs and foams [2,3]. Honeycombs are prismatic cellular structures with a repeating unit cell, typically hexagonal, whereas metal foams are stochastic in nature on account of the limited degree of control of typical manufacturing processes used to fabricate them. With additive manufacturing, however, it is feasible to not just explore other unit cell shapes but also to control a wide range of variables that define how these shapes and the parameters associated with them undergo spatial changes. Key decisions confronting the designer of cellular materials include the selection of a particular unit cell, determination of its size and member thickness, and how both vary spatially, as well as integrating the materials within an arbitrary volume [4].
In principle, an infinite number of cellular materials may be designed and further modified in three-dimensional space. To grapple with this wide variety of possibilities, the authors previously proposed a general classification for cellular materials, which are reproduced here in Figure 1 [5]. This classification scheme primarily focused on providing designers a framework for decoupling cellular material design into three aspects: tessellation of space, identification of elements that form the members within those tessellations, and finally, determining connectivity of the elements. A combination of these three considerations, it was argued, is sufficient to define a unit cell. One of the three options for tessellation was identified as “stochastic,” the intent of which was to address structures such as metal foams. Stochastic cellular materials, however, are strictly speaking a subset of a larger class of cellular materials that one may term as being aperiodic, which is worthy of independent exploration and forms the aim of the current study. Aperiodicity in the context of cellular materials is defined as any intentional deviation in unit cell shape or size across repeating occurrences in space. Thus, this study seeks to expand the classification of cellular materials that do not conform to a periodic, repetitive pattern.
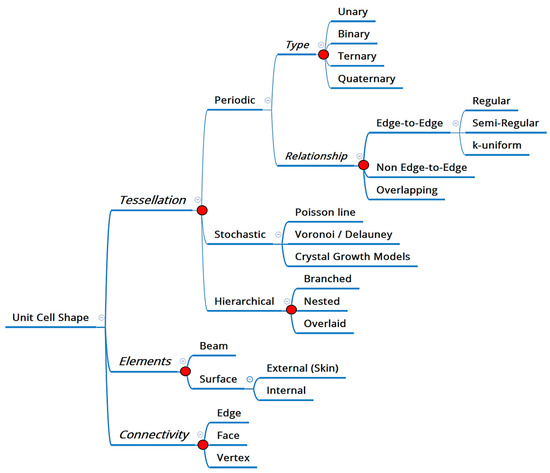
Figure 1.
Classification scheme for architected cellular materials, as first proposed in [5].
The motivation for this research stems from two sources: The first of these is from observations of aperiodicity in natural cellular materials. There is ample evidence in the nature of repeating cellular structures, themselves arising out of symmetry-breaking processes in biology that enhance functionality [6]. However, a deeper study of these natural cellular materials demonstrates that seemingly repetitive patterns indeed possess a degree of aperiodicity including functional gradients [7]. The honeybee’s nest, for example, is typically considered to be a periodic structure consisting of a repeating hexagonal unit cell. However, a well-known feature is that there is variation in this structure, most visible in the differences in cell sizes between worker and drone cells. Additionally, recent research demonstrates that the perceived imperfections in the honeycomb, defined as a deviation from a baseline unit cell, are in fact architectural decisions made by the bees to achieve transitions between different cell sizes [8]. Some of these variations are evident in Figure 2a. Aperiodicity in natural materials extends beyond these subtle variations in size, however, as seen in additional examples for a cross-section of the stem of a sunflower (Figure 2b) and in trabecular bone (Figure 2c), both of which clearly show an overarching aperiodicity that is different from what is observed for the honeycomb in Figure 2a. While it is evident from this observation that these are different, there is no agreed-upon terminology to label these differences, which is what this study seeks to establish.
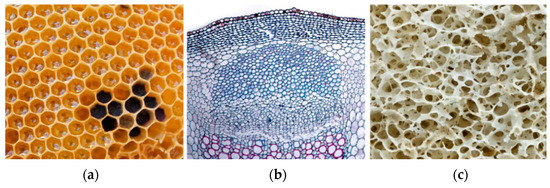
Figure 2.
Three examples of aperiodic architected cellular materials in nature: (a) honeybee nest; (b) cross-section of a sunflower stem; and (c) trabecular bone (attribution for sunflower stem: John Bebbington; for trabecular bone: Patrick Siemer, both images reproduced under Creative Commons-CC BY-NC-SA 2.0).
In addition to these observations, engineering applications leveraging aperiodic cellular materials have traditionally involved metal foams, but there is a growing body of research that explores ideas such as the programmable insertion of defects into periodic cellular materials [9,10], gradation in cell size or thickness [11], and the use of multiple-unit cell shapes and managing transitions between them [12,13]. Several approaches have also been proposed for the design of these aperiodic cellular materials [14], and a selection of these methods, most commonly the Voronoi tessellation, have also been implemented in commercial design software [15]. There is, however, an absence of a classification scheme that brings together the different approaches one may take to designing aperiodic cellular materials.
This work seeks to develop this classification by combining observations in nature and the engineering literature, with ideas developed in the domains of artistic form and design, as presented by Wong in Principles of Form and Design [16]. Section 2 presents the three main types of aperiodic cellular materials, and Section 3 delves into each of these in more detail, elaborating on subtypes. Several assumptions made in demonstrating the different types are expanded upon in Section 4, which also discusses combining different types of aperiodicity and reviews some of the benefits ascribed in the literature to aperiodic cellular materials.
2. Types of Aperiodic Cellular Materials
Periodicity and symmetry are related but different concepts in the context of cellular materials. The former implies the repetition of identical building blocks, the latter is defined as the degree of invariance under transformation. A unit cell itself may have a certain symmetry, but it is its repetitive use in space-filling that gives it periodicity. Deviations from this repetition of identical unit cells are what is termed here as aperiodicity. To develop the first level of classification of aperiodic cellular materials, it is helpful to follow ideas developed for asymmetry. In his influential book, Symmetry, Weyl states that “…seldom is asymmetry merely the absence of symmetry. Even in asymmetric designs one feels symmetry as the norm from which one deviates under the influence of forces of non-formal character” [17]. This idea of asymmetry being defined in relation to a symmetric form is also found elsewhere [16,18]. A similar approach is borrowed to develop a classification of aperiodicity and forms the basis of the first major claim of this study: all aperiodic cellular materials belong to one of the three categories demonstrated in Figure 3: gradation, perturbation, and hybridization, all of which can be derived by the modification of a periodic baseline. A rigorous mathematical proof of this statement is beyond the scope of the present paper. Instead, this high-level classification of all aperiodic cellular materials is arrived at empirically, by observation of structures in nature, as well as a review of the engineering literature.
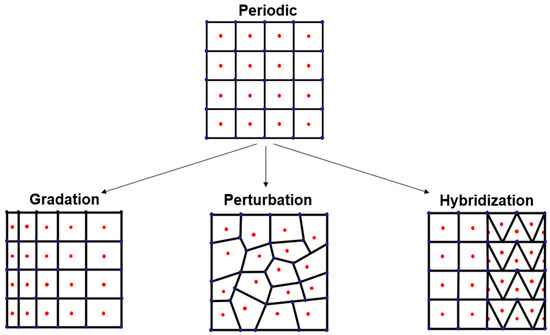
Figure 3.
Aperiodic cellular materials as emergent from a periodic template, with three main types: gradation, perturbation, and hybridization. Red dots indicate cell nuclei, while black lines indicate cell members.
Gradation is the most commonly studied form of aperiodicity in cellular materials and is defined as a prescribed spatial variation in a geometric feature of a unit cell [11]. In Figure 3, the feature being graded is the width of the rectangular unit cell, which increases from left to right. In addition to modulating cell size, it is also possible to spatially prescribe variations in wall thickness, even with discrete step changes in value, as shown in one example from the published literature in Figure 4a [19]. With advances in simulation capabilities, particularly with topology optimization, it is possible to prescribe these gradients in response to a field derived from simulation [20,21]. One such example, using the commercially available nTopology software [15], is shown in Figure 4b.
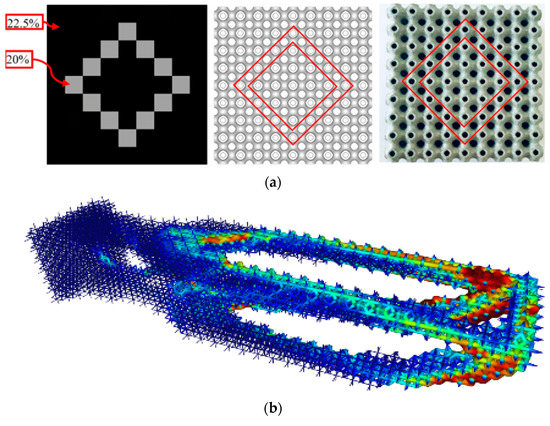
Figure 4.
Two approaches to implementing gradation in prescribed regions: (a) a priori identification of regions with specific relative density targets of 20 and 22.5% shown, reproduced from [19] (CC BY license); (b) simulation-obtained field-driven thickening of lattice struts, with colors corresponding to von-Mises stress (authors’ work).
Crucial to the definition of gradation in the above terms is that the variation is prescribed as a function of distance in one or more directions. This separates gradation from perturbation: The latter addresses variation in geometric features of cells but defines it without reference to spatial coordinates. Voronoi structures, metal foams, and other stochastic forms all fall into this category. In Figure 3, a Voronoi pattern is demonstrated where cell nuclei (red dots indicating centroidal locations) are perturbed and lines are drawn equidistant between pairs of perturbed nuclei. This effect is shown for a Schwarz-P TPMS structure in Figure 5.

Figure 5.
Perturbed shell around a Schwarz-P TPMS structure, from periodic shape (left) to increasing aperiodicity (middle and right) (authors’ work).
Finally, the third level of aperiodicity is termed here as hybridization and refers to cellular materials that are derived from a combination of different cell shapes. In Figure 3, a square unit cell is combined with a triangular unit cell to create a hybrid structure. Hybridization can also involve the programmed introduction of defects onto an existing unit cell pattern, equivalent to a Boolean subtraction. An example of combining unit cells to create a hybrid cellular structure, drawn from the literature, is shown in Figure 6 [22], where two different unit cell types from a class of cellular materials called triply periodic minimal surfaces (TPMSs) are combined into one structure.
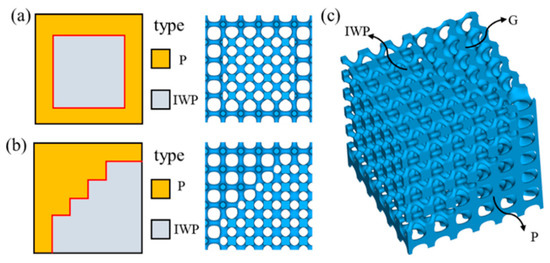
Figure 6.
Two examples of hybridizing cellular materials, shown here for two kinds of TPMS geometries (Schwarz Primitive P, and Schoen IWP), with (a) an embedded transition boundary; (b) curve discretization; and (c) representation in 3D; reproduced from [22] under CC BY-NC-ND.
It is also possible to combine one or more of these types of aperiodic design approaches to generate, for example, a structure with graded randomness [14]. Indeed, this is, in principle, feasible for all subtypes to be discussed in the next section. For the purpose of simplicity, however, these combinations are not included in the classification proposed here but are discussed instead in Section 4.
3. Toward a Comprehensive Classification of Aperiodic Cellular Materials
In the previous section, it was postulated that all aperiodic cellular materials can be classified as being derived from a periodic basis through one of three types of modifications: gradation, perturbation, and hybridization. This section expands upon each of these three main types, to examine subcategories within them with the aim of developing a comprehensive classification scheme, which is shown in its entirety in Appendix A, and available as a mind-map in Supplementary Material. The subcategories are demonstrated using a diagrammatic approach borrowed from Wong [16] and, for simplicity of representation, are limited to two-dimensional designs with the assumption of a periodic square grid as the baseline, as shown in Figure 3.
3.1. Gradation
Gradation is categorized in the context of three separate decisions that the designer has to make. These relate to what is being graded (termed here as a feature), what aspect of the selected feature is being modified (parameter), and finally, how the gradation is prescribed spatially (pattern), as shown in Figure 7. These three pieces of information together constitute a sufficient descriptor of gradation in the context of architected cellular materials: This classification would not apply, for example, to functionally graded materials in which the composition of the material itself is changing. The specification of the classification as a decision tree reduces the number of variations possible since it converts these into a series of dependent decisions as opposed to a selection from a wide list of possibilities. Each of these design decisions is discussed next, with examples.
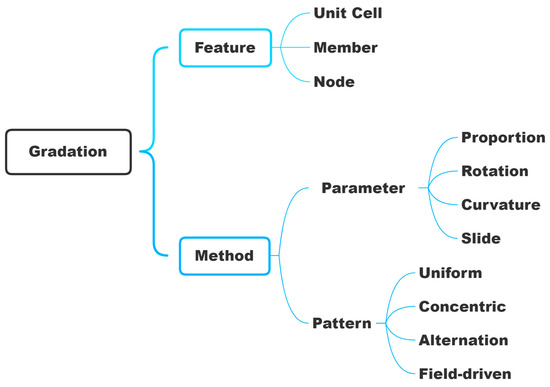
Figure 7.
Gradation is classified as a collection of three levels of decisions (feature, parameter, and pattern), with options selected at each of the three levels.
3.1.1. Feature
Gradation may be applied to each of the three main aspects that define a cellular material: the unit cell, the member (such as the beam or wall), and the nodes at which the members meet. To illustrate this, a particular type of gradation, viz. proportion (discussed next) is demonstrated for each of these three features in Figure 8. The pattern, in this case, is a uniform one-directional pattern, with the proportion increasing from left to right. This particular gradation can be applied either to the unit cell, the beam, or at the node. Each of these has the effect of modifying local relative density but can achieve different outcomes depending on the environment for which it is being developed. While unit cell and member gradation are most common in the literature, modifying nodal curvature has been demonstrated to modulate effective stiffness and redistribute corner stresses [23].
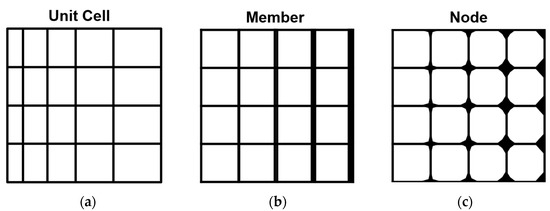
Figure 8.
Gradation may be applied to one of three features: (a) the unit cell, (b) member (such as beams or walls), and (c) node.
3.1.2. Method: Parameter
The second decision in the gradation classification involves the selection of the parameter of gradation. Wong proposes nine different ways of grading structures, of which four are relevant for this classification and are shown in Figure 9. Proportion, rotation, and slide are all demonstrated on the feature level of the unit cell, whereas curvature is demonstrated at the level of the member. In proportion, the feature maintains its overall shape but is altered in size—this was demonstrated for each of the three features in Figure 8—this is the most common form of gradation in the literature on cellular materials. However, it is also possible to apply a rotation to the feature, or curvature, as shown in Figure 9. In rotation, for a unit cell feature, the entire cell is rotated, and the amount of rotation is graded spatially. Curvature distorts the connecting members in such a way that the connections between nodes are no longer linear. Slide, as the name and figure imply, is the movement of the feature along a certain direction in relation to the others. As with the other examples, the amount of slide needs to be graded—mere sliding as seen in brick-laying does not confer gradation.
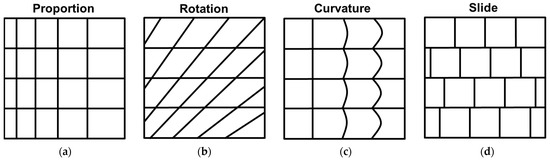
Figure 9.
The four types of gradation proposed: (a) proportion, (b) rotation, (c) curvature, and (d) slide—these are applied at the level of the unit cell, with the exception of the curvature type (c), which is demonstrated at the level of the member.
3.1.3. Method: Pattern
The last step in the classification is to specify how the type of gradation applied to a feature will vary spatially. Four types are proposed: The first three, shown in Figure 10a–c, follow Wong’s principles and are demonstrated for a gradation in proportion as applied to the unit cell. The first of these, in Figure 10a, is the uniform gradation of unit cell proportion, where cell size reduces from top to bottom. The same reduction in cell size is applied from the inside into the outward direction, as shown for the concentric pattern in Figure 10b. Finally, alternation is an instance of gradation that is repeated, as shown in Figure 10c. These transitions in cell shape may be prescribed by a globally defined mathematical function, as opposed to the simplistic demonstrations here. The fourth category of pattern emerges from simulation-driven design approaches, where a field is calculated from a simulation of the response of the structure to its environment, and this field is used to drive specific aspects of a feature. Figure 10d demonstrates this, in principle, by the application of a load, which is then used in simulation to derive stresses locally in beams, and that, in turn, is used to modulate, in this instance, member thickness. A specific example of this is shown in Figure 10d, where lattice beams with higher stresses are thicker (demonstrated in nToplogy). Field-driven design is categorized as a form of gradation since it essentially involves modifying a parameter of interest spatially with an underlying relationship to a metric such as stress or temperature—as such, the only difference is that this relationship is derived from a simulation result.
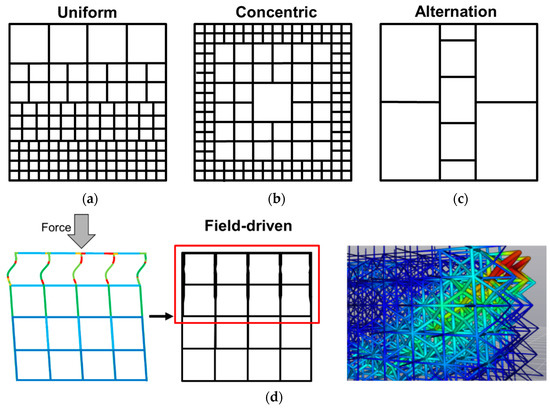
Figure 10.
Different patterns that gradation can be applied with: (a) uniform, (b) concentric, (c) alternation, and (d) field-driven. (a–c) demonstrate the patterns for proportion gradation of the unit cell, while (d) demonstrates this for proportion gradation of the member (in this case, the beams thickness varied as a function of von-Mises stresses, represented by the color contours.
3.2. Perturbation
Perturbation is similar to gradation in that a feature is modified spatially to generate aperiodicity, but it differs in one crucial respect: Perturbation does not require the specification of a direction to the modification. All stochastic cellular materials, including Voronoi structures and most foams, fall in this category. Similar to the classification proposed for gradation, perturbation is specified here as a decision that is made at two levels (the third level in gradation, i.e., pattern, is not applicable here). The proposed classification for perturbation is shown in Figure 11. As seen in gradation, the first level is one of specifying the feature which is to be perturbed, but the second level collects the different methods of perturbation since designed perturbation involves the use of mathematical functions and algorithms to achieve them.
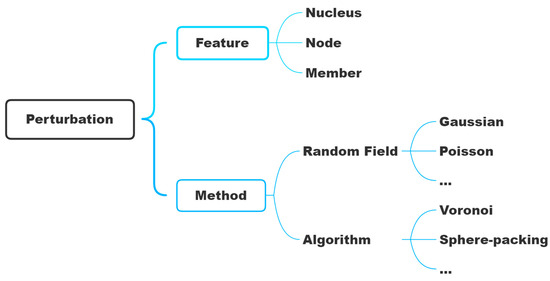
Figure 11.
Classification proposed for perturbation of cellular materials, divided into two decision levels: the feature to which it is applied and the method used to define it.
3.2.1. Feature
Instead of specifying perturbation at the level of the unit cell, as was proposed for gradation, it is more useful to specify it in terms of whether the perturbation is applied at the level of the nucleus or the node, as shown in Figure 12, for structures perturbed using a random number generator. In both cases, perturbation is applied to a point cloud, with the subsequent definition of connectivity driving the definition of the cellular material that forms. Perturbation of the nucleus tends to result in forms that approach the familiar Voronoi tessellation (Figure 12a), whereas nodal perturbation tends to generate more extreme angles, as shown in Figure 12b. Not shown in Figure 12 is the perturbation of the member that connects the nodes—this could either apply to perturbing member thickness, such that each beam has a different thickness, similar to that shown for gradation in Figure 8b, or the members themselves could be perturbed, having variable thickness or curvature within each beam itself [24].
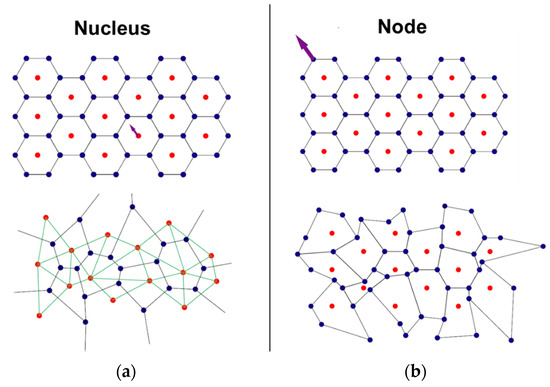
Figure 12.
Two approaches to applying perturbation, at the level of (a) the nucleus and (b) the node, as indicated by the arrows.
3.2.2. Method
Several approaches have been proposed to develop perturbed cellular material designs. This study builds on the arguments summarized by Groth et al. [14], who review different approaches to this problem in the literature, identify methods used for the generation of stochastic lattices using random (strictly speaking, pseudo-random) distributions, and apply them to the coordinates of points in space. Here, two general approaches are first proposed, as shown in Figure 11. The first of these involves the use of a random distribution to define the coordinates of nodes in space [25,26] or to perturb a periodic set of coordinates by randomly generated distances, the latter shown in Figure 12b. The nodes themselves are then connected to create the cellular material, without the imposition of additional rules, with the exception of checks made to ensure members do not cross each other. The second method involves the use of a generating algorithm, such as a Voronoi algorithm that operates on seeding points [27,28,29], or a sphere packing algorithm that uses a nearest-neighbor model to connect nodes [30]. The methods listed in Figure 11 do not represent a complete set—indeed, several different distributions may be used to drive the underlying randomness but are shown here as representing the most common approaches leveraged in the literature. Additionally, in some cases such as for spinodoid cellular material topologies, which are inspired by spinodal decomposition events that occur typically in diffusion-driven phase separation, the structure can emerge from the modeling of equations that govern the underlying kinetics (algorithm), or by the use of Gaussian random fields that approximate them well [31,32].
3.3. Hybridization
The final type of aperiodicity proposed in this paper is hybridization, which involves combining two or more aspects of architected cellular material design into the same structure. As shown in the classification scheme in Figure 13, this could be at the level of the unit cell or the member. Three different methods can be used to combine either of these features.
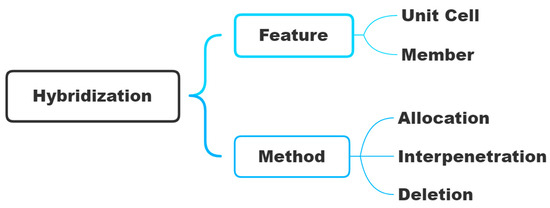
Figure 13.
Classification proposed for the hybridization of cellular materials, divided into two decision levels: the feature to which it is applied and the method used to define it.
3.3.1. Feature
Hybridization most commonly involves the combination of two different unit cell shapes into a larger structure, as demonstrated in Figure 14a and shown previously in Figure 6. Hybridization can also be performed by combining structures with different member types—this is demonstrated for a three-dimensional structure in Figure 14b, in which two different beam-based lattices are combined with a surface-based cellular material. However, this could also apply to beams alone, where different beams have different cross-section shapes. Trabecular bone (Figure 2c) is an example in nature that combines both surface-based foam-like structures with beam-based ones.
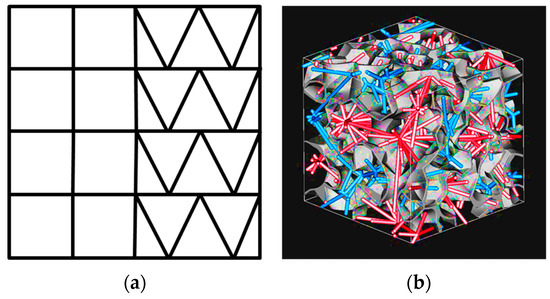
Figure 14.
Two levels of feature selection to which hybridization may be applied: (a) the unit cell or (b) the member (two non-intersecting lattices indicated with different colors, inside a surface-based cellular material).
3.3.2. Method
Three different methods are proposed here that define how the unit cells and/or members may be combined. The most common one in the literature is termed here as allocation. It applies to hybridized structures that have predefined regions assigned for the different cells or beams, with interfaces evident at the boundary of each type. This is the type demonstrated in Figure 6c and Figure 14b and is also shown in Figure 15a. The second method is to combine the two feature sets not by allocating them to different regions spatially but by allowing them to occupy the same space by interpenetrating the shapes, as shown in Figure 14b and Figure 15b. Finally, aperiodicity can also be introduced by deleting cells or members, an example of which is shown in Figure 15c. This latter design is an instance of hybridization since the two features being combined are a filled and an empty member, borrowing from the concept of negative space in art [16,33].
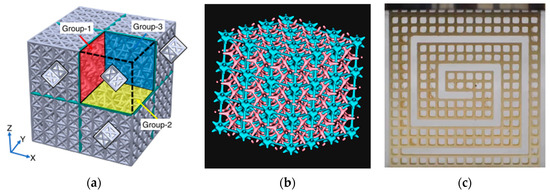
Figure 15.
Three examples representing each of the methods for hybridization: (a) allocation of differently oriented lattices in different groups, from [34], reproduced under CC BY 4.0 license; (b) interpenetrating lattices indicated in different colors; (c) deletion of beams within a periodic square grid, reproduced from [33].
4. Discussion
The above discussion focused on the development of a practical classification scheme for aperiodic cellular materials, with most examples shown for simplified instances. In this section, two aspects that the classification scheme does not directly address are covered, viz. modulating the degree to which the method is applied and combining types in the classification. This is followed by a brief review of aperiodic cellular materials in the literature, highlighting the benefits ascribed to these structures.
4.1. Degree of Aperiodicity
The classification scheme proposed here does not specify the degree to which aperiodicity may be implemented. Within each method driving a feature’s structure is a parameter that can be modulated. One instance of this is demonstrated in Figure 16, which shows how this may equally be applied to two-dimensional (shown here for a square honeycomb) or three-dimensional cellular materials (shown here for a cubic lattice), where the degree of perturbation of the nuclei, which constitute the seeds for a Voronoi algorithm, is changed from zero for a periodic structure to gradually increasing values, with increasing irregularity evident in the resulting shape. While the development and characterization of such structures are well-represented in the literature [35], more research is needed to understand how the degree of aperiodicity influences behaviors of interest.
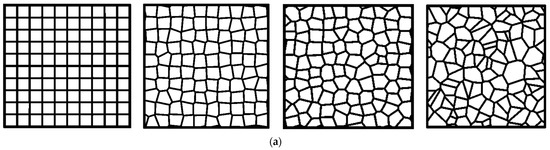
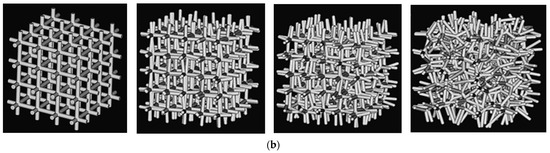
Figure 16.
Increasing degree of aperiodicity applied to (a) a prismatic square grid honeycomb and (b) a cubic lattice.
4.2. Combining Approaches
One of the implications of the classification scheme is that it suggests combinations between different approaches. While some authors have examined this aspect of aperiodicity in the context of cellular materials, there is an opportunity for wider exploration. Gradation, for example, can be applied to perturbation itself [14], where the degree of stochasticity changes spatially, or for enabling transitions between different cell types in hybrid cellular structures [13]. Some examples of combining approaches are shown in Figure 17. Figure 17a shows a gradation of cell size for a Voronoi lattice, while Figure 17b shows gradation in beam deletion, from [33]. Figure 17c demonstrates hybridization and perturbation applied together, where a Voronoi lattice is used to derive a surface- and beam-based cellular material. The latter is then subtracted from the former, giving an unusual shape that appears similar to bone morphology. Combining approaches in this way, therefore, has the potential for exploring new areas of architected material design, as well as for mimicking natural cellular materials more accurately.

Figure 17.
Three examples of combining different methods in the classification: (a) gradation of unit cell size applied to a Voronoi lattice; (b) gradation of beam deletion, from [33]; (c) hybridization of beam- and surface-based elements in a perturbed cellular material.
4.3. Properties
An important aspect of designing aperiodic cellular materials is to accomplish specific performance objectives. For stochastic metal foams, these applications are well-summarized in [3] and are indicative of the wide range of application possibilities for stochastic cellular materials. This paper is, however, concerned with designer-prescribed aperiodicity in cellular structures, as opposed to foams, which arise due to stochasticity inherent in the manufacturing process. Several publications that study such prescribed aperiodicity were reviewed and are summarized in Table 1, showing both the category of classification each body of work falls within as well as listing the key benefits or differences reported for each shape. These benefits must be considered carefully, in particular for perturbed structures, where the benefits may be highly sensitive to the initial random seed. An example of this is shown in Figure 18, from prior research that looked at the effect of stochastic seeds on the tensile response of a beam infilled with Voronoi-based lattices [36]. Figure 18a shows how the effective modulus of the beam (computed as the stiffness of the beam under tension divided by its cross-sectional area, normalized by the modulus of the bulk material [2]) varies across different relative densities for different random generator seeds. An examination of the axial deformation contours of two differently seeded lattices with similar relative densities, shown in Figure 18b, demonstrates how local differences influence overall deformation. While this represents a limited study, it is a cautionary result that uncertainty, when built into the design of aperiodic cellular materials, can translate into performance uncertainty.

Table 1.
Summary of select studies on the behavior of aperiodic architected cellular materials.
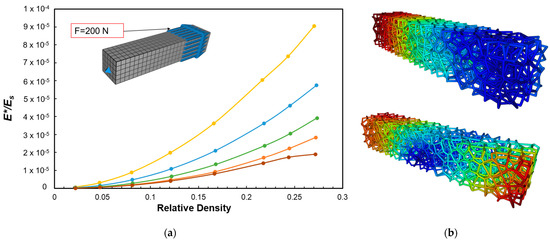
Figure 18.
Effect of different Voronoi seeds on the (a) effective tensile modulus of stochastic lattice-filled beams and (b) axial displacement color contours.
5. Conclusions
This research proposed a classification of aperiodic architected cellular materials. At the highest level, three main types were identified: gradation, perturbation, and hybridization. For each of these three types, a feature (what is modified?) and a method (how is it modified?) were identified as the two key decisions a designer needs to make. Depending on the main type, each of these decisions has different options for the designer to consider. The complete classification enables a more formal discussion of aperiodic cellular materials and also invites future studies to develop their full potential.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/designs6040063/s1, XMind mind map of the entire classification developed in this work is provided (requires the use of XMind software, available at Xmind.net).
Author Contributions
Conceptualization, C.L., D.A. and D.B.; methodology, I.E.R.-C. and D.B.; software-driven design, D.A. and R.S.; figures, I.E.R.-C., D.A. and R.S.; resources, D.B.; writing—original draft preparation, D.B.; writing—review and editing, D.B., I.E.R.-C. and C.L.; supervision, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
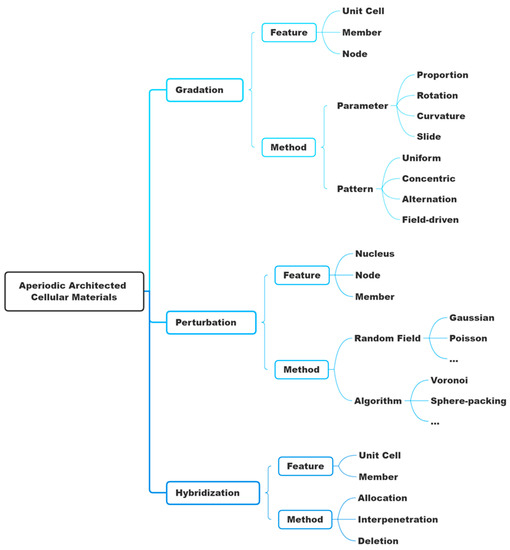
Figure A1.
The complete classification proposed in this work.
References
- du Plessis, A.; Mohammad Javad Razavi, S.; Benedetti, M.; Murchio, S.; Leary, M.; Watson, M.; Bhate, D.; Berto, F. Properties and applications of additively manufactured metallic cellular materials: A review. Prog. Mater. Sci. 2021, 125, 100918. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ashby, M.F.; Evans, A.G.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide; Butterworth Heinemann: Oxford, UK, 2010. [Google Scholar]
- Bhate, D. Four Questions in Cellular Material Design. Materials 2019, 12, 1060. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhate, D.; Penick, C.; Ferry, L.; Lee, C. Classification and Selection of Cellular Materials in Mechanical Design: Engineering and Biomimetic Approaches. Designs 2019, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Bowerman, B. Symmetry breaking in biology. Cold Spring Harb. Perspect. Biol. 2010, 2, a003475. [Google Scholar] [CrossRef]
- Liu, Z.; Meyers, M.A.; Zhang, Z.; Ritchie, R.O. Functional gradients and heterogeneities in biological materials: Design principles, functions, and bioinspired applications. Prog. Mater. Sci. 2017, 88, 467–498. [Google Scholar] [CrossRef]
- Smith, M.L.; Napp, N.; Petersen, K.H. Imperfect comb construction reveals the architectural abilities of honeybees. Proc. Natl. Acad. Sci. USA 2021, 118, e2103605118. [Google Scholar] [CrossRef] [PubMed]
- Restrepo, D.; Mankame, N.D.; Zavattieri, P.D. Programmable materials based on periodic cellular solids. Part I: Experiments. Int. J. Solids Struct. 2016, 100–101, 485–504. [Google Scholar] [CrossRef]
- Restrepo, D.; Mankame, N.D.; Zavattieri, P.D. Programmable materials based on periodic cellular solids. Part II: Numerical analysis. Int. J. Solids Struct. 2016, 100–101, 505–522. [Google Scholar] [CrossRef]
- Rahman, O.; Uddin, K.Z.; Muthulingam, J.; Youssef, G.; Shen, C.; Koohbor, B. Density-Graded Cellular Solids: Mechanics, Fabrication, and Applications. Adv. Eng. Mater. 2022, 24, 2100646. [Google Scholar] [CrossRef]
- Wang, J.; Callanan, J.; Ogunbodede, O.; Rai, R. Hierarchical combinatorial design and optimization of non-periodic metamaterial structures. Addit. Manuf. 2021, 37, 101710. [Google Scholar] [CrossRef]
- Carbon. Enabling Custom Mechanical Responses Using Spatially Varying Lattices; Carbon, Inc.: Redwood City, CA, USA, 2022. [Google Scholar]
- Groth, J.-H.; Anderson, C.; Magnini, M.; Tuck, C.; Clare, A. Five simple tools for stochastic lattice creation. Addit. Manuf. 2022, 49, 102488. [Google Scholar] [CrossRef]
- NTopology. Platform; NTopology Inc.: New York, NY, USA, 2020. [Google Scholar]
- Wong, W. Principles of Form and Design, 1st ed.; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Weyl, H. Symmetry, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Du Sautoy, M. Symmetry: A Journey into the Patterns of Nature; Harper: New York, NY, USA, 2008; ISBN 0060789409. [Google Scholar]
- Al-Ketan, O. Programmed plastic deformation in mathematically-designed architected cellular materials. Metals 2021, 11, 1622. [Google Scholar] [CrossRef]
- Wu, J.; Aage, N.; Westermann, R.; Sigmund, O. Infill Optimization for Additive Manufacturing—Approaching Bone-like Porous Structures. IEEE Trans. Vis. Comput. Graph. 2018, 24, 1127–1140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for Additive Manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Ren, F.; Zhang, C.; Liao, W.; Liu, T.; Li, D.; Shi, X.; Jiang, W.; Wang, C.; Qi, J.; Chen, Y.; et al. Transition boundaries and stiffness optimal design for multi-TPMS lattices. Mater. Des. 2021, 210, 110062. [Google Scholar] [CrossRef]
- Rajeev, A.; Grishin, A.; Agrawal, V.; Santhanam, B.; Goss, D.; Niverty, S.; Cope, G.; Penick, C.A.; Chawla, N.; Shyam, V.; et al. Parametric optimization of corner radius in hexagonal honeycombs under in-plane compression. J. Manuf. Process. 2022, 79, 35–46. [Google Scholar] [CrossRef]
- Storm, J.; Abendroth, M.; Kuna, M. Influence of curved struts, anisotropic pores and strut cavities on the effective elastic properties of open-cell foams. Int. J. Mech. Mater. 2015, 86, 1–10. [Google Scholar] [CrossRef]
- Silva, M.J.; Hayes, W.C.; Gibson, L.J. The Effects of Non-Periodic Microstructure on the Elastic Properties of Two-Dimensional Cellular Solids. Int. J. Mech. Sci. 1995, 37, 1161–1177. [Google Scholar] [CrossRef]
- Zhu, H.X.; Hobdell, J.R.; Windle, A.H. Effects of cell irregularity on the elastic properties of open-cell foams. Acta Mater. 2000, 48, 4893–4900. [Google Scholar] [CrossRef]
- Van der Burg, M.; Shulmeister, V.; Van der Geissen, E.; Marissen, R. On the linear elastic properties of regular and random open-cell foam models. J. Cell. Plast. 1997, 33, 31–54. [Google Scholar] [CrossRef]
- Martínez, J.; Song, H.; Dumas, J.; Lefebvre, S. Orthotropic k-nearest foams for additive manufacturing. ACM Trans. Graph. 2017, 36, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Martínez, J.; Dumas, J.; Lefebvre, S. Procedural voronoi foams for additive manufacturing. ACM Trans. Graph. 2016, 35, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Roberts, A.P.; Garboczi, E.J. Elastic properties of model random three-dimensional open-cell solids. J. Mech. Phys. Solids 2002, 50, 33–55. [Google Scholar] [CrossRef]
- Zheng, L.; Kumar, S.; Kochmann, D.M. Data-driven topology optimization of spinodoid metamaterials with seamlessly tunable anisotropy. Comput. Methods Appl. Mech. Eng. 2021, 383, 113894. [Google Scholar] [CrossRef]
- Kumar, S.; Tan, S.; Zheng, L.; Kochmann, D.M. Inverse-designed spinodoid metamaterials. NPJ Comput. Mater. 2020, 6, 1–10. [Google Scholar] [CrossRef]
- Casanova, L.; Vijayan Anitha, V.; Kadway, N.; Gandhi, A.; Le, T.; Lee, C.; Bhate, D. On the Mechanical Behavior of Additively Manufactured Asymmetric Honeycombs. In Proceedings of the 2018 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2018. [Google Scholar]
- Liu, C.; Lertthanasarn, J.; Pham, M.S. The origin of the boundary strengthening in polycrystal-inspired architected materials. Nat. Commun. 2021, 12, 1–10. [Google Scholar] [CrossRef]
- Sotomayor, O.E.; Tippur, H.V. Role of cell regularity and relative density on elastoplastic compression response of 3-D open-cell foam core sandwich structure generated using Voronoi diagrams. Acta Mater. 2014, 78, 301–313. [Google Scholar] [CrossRef]
- Sharma, R. An Investigation into the Stiffness Response of Lattice Shapes under Various Loading Conditions. Master’s Thesis, Arizona State University, Tempe, AZ, USA, 2019. [Google Scholar]
- Al-Ketan, O.; Lee, D.W.; Rowshan, R.; Abu Al-Rub, R.K. Functionally graded and multi-morphology sheet TPMS lattices: Design, manufacturing, and mechanical properties. J. Mech. Behav. Biomed. Mater. 2020, 102, 103520. [Google Scholar] [CrossRef]
- Maskery, I.; Hussey, A.; Panesar, A.; Aremu, A.; Tuck, C.; Ashcroft, I.; Hague, R. An investigation into reinforced and functionally graded lattice structures. J. Cell. Plast. 2017, 53, 151–165. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Sun, J.; Bai, J. Investigation of functionally graded TPMS structures fabricated by additive manufacturing. Mater. Des. 2019, 182, 108021. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Liu, F.; Li, Z.; Ma, Z.; Ren, Z. Mechanical and energy absorption characteristics of additively manufactured functionally graded sheet lattice structures with minimal surfaces. Int. J. Mech. Sci. 2020, 167, 105262. [Google Scholar] [CrossRef]
- Zhong, M.; Zhou, W.; Xi, H.; Liang, Y.; Wu, Z. Double-level energy absorption of 3d printed tpms cellular structures via wall thickness gradient design. Materials 2021, 14, 6262. [Google Scholar] [CrossRef]
- Shi, X.; Liao, W.; Liu, T.; Zhang, C.; Li, D.; Jiang, W.; Wang, C.; Ren, F. Design optimization of multimorphology surface-based lattice structures with density gradients. Int. J. Adv. Manuf. Technol. 2021, 117, 2013–2028. [Google Scholar] [CrossRef]
- Liebenstein, S.; Sandfeld, S.; Zaiser, M. Size and disorder effects in elasticity of cellular structures: From discrete models to continuum representations. Int. J. Solids Struct. 2018, 146, 97–116. [Google Scholar] [CrossRef] [Green Version]
- Sotomayor, O.E.; Tippur, H.V. Role of cell regularity and relative density on elasto-plastic compression response of random honeycombs generated using Voronoi diagrams. Int. J. Solids Struct. 2014, 51, 3776–3786. [Google Scholar] [CrossRef] [Green Version]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Numerical simulations of 3D open cell structures—Influence of structural irregularities on elasto-plasticity and deformation localization. Int. J. Solids Struct. 2007, 44, 2990–3003. [Google Scholar] [CrossRef] [Green Version]
- Rahman, O.; Koohbor, B. Optimization of energy absorption performance of polymer honeycombs by density gradation. Compos. Part C Open Access 2020, 3, 100052. [Google Scholar] [CrossRef]
- Pham, M.-S.; Liu, C.; Todd, I.; Lertthanasarn, J. Damage-tolerant architected materials inspired by crystal microstructure. Nature 2019, 565, 305–311. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.W.; Abu Al-Rub, R.K. Mechanical properties of additively-manufactured sheet-based gyroidal stochastic cellular materials. Addit. Manuf. 2021, 48, 102418. [Google Scholar] [CrossRef]
- White, B.C.; Garland, A.; Alberdi, R.; Boyce, B.L. Interpenetrating lattices with enhanced mechanical functionality. Addit. Manuf. 2021, 38, 101741. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Z.; Yu, J.; Wang, C. Impact resistance and energy absorption of functionally graded cellular structures. Appl. Mech. Mater. 2011, 69, 73–78. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).