Evaluation of the Compressive Strength of CFRP-Wrapped Circular Concrete Columns Using Artificial Intelligence Techniques
Abstract
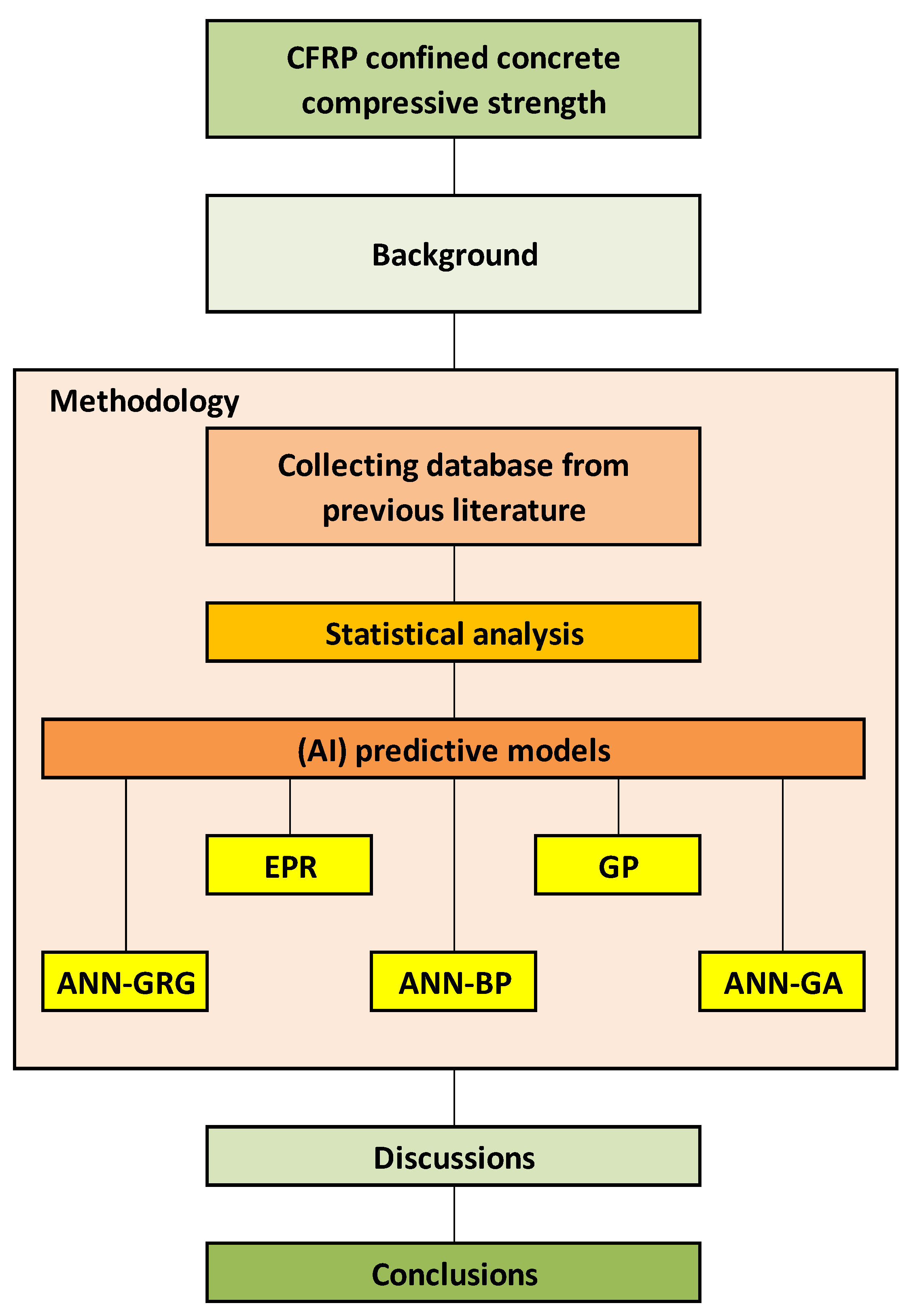
:1. Introduction
2. Methodology
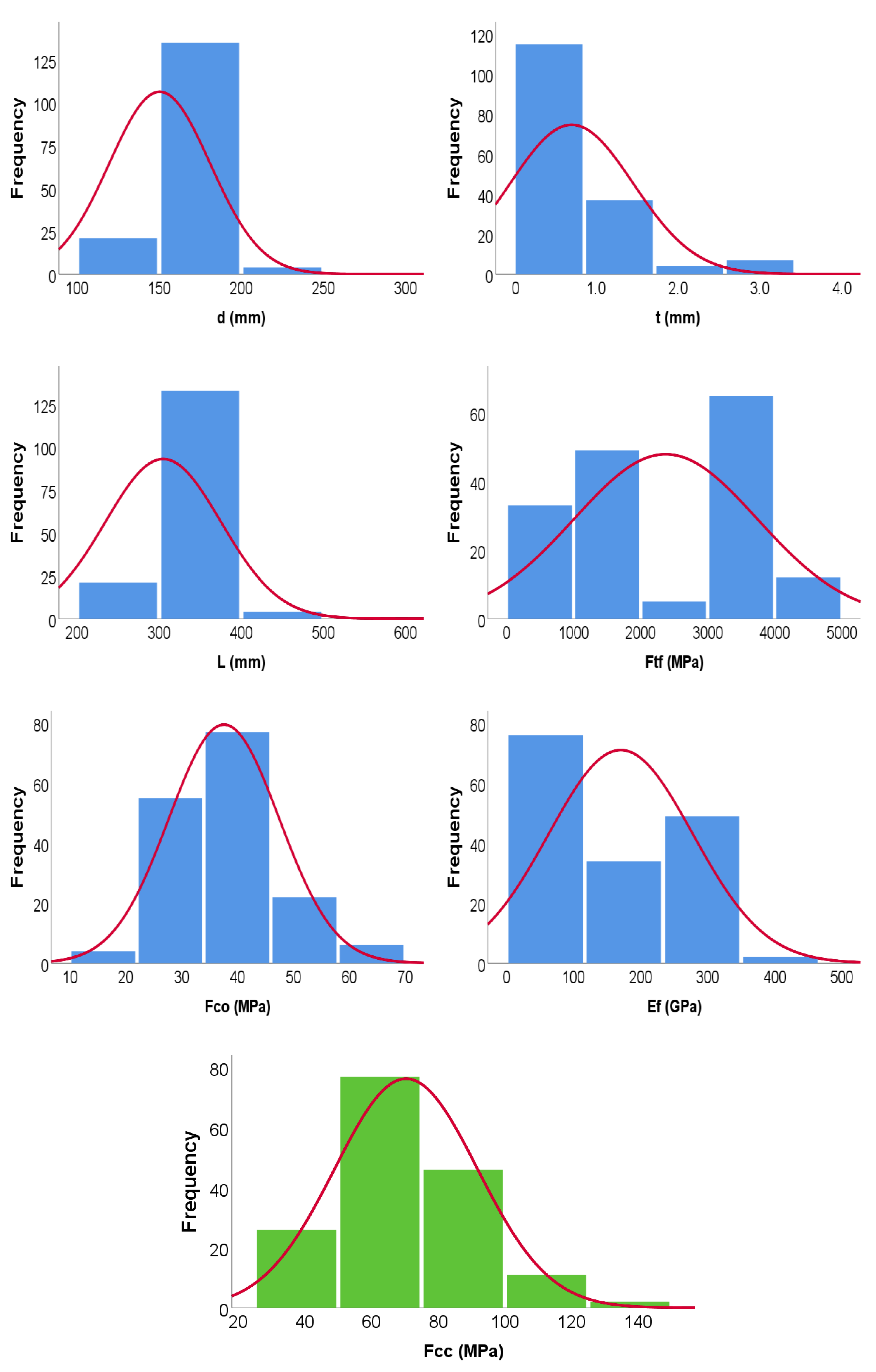
2.1. CFRP Confined/Wrapped Concrete Data Collection
2.2. CFRP Confined/Wrapped Concrete Data Collection
- -
- d specimen diameter (mm);
- -
- L specimen length (mm);
- -
- Fco compression strength of unwrapped concrete cylinder (MPa);
- -
- t the thickness of the used CFRP sheets (mm);
- -
- Ftf tension capacity of the used CFRP sheets (MPa);
- -
- Ef modulus of elasticity of the used CFRP sheets (GPa);
- -
- Fcc compression strength of wrapped concrete cylinder (MPa).
| d | L | Fco | t | Ftf | Ef | Fcc | |
|---|---|---|---|---|---|---|---|
| mm | mm | MPa | mm | MPa | GPa | MPa | |
| Training set | |||||||
| Min. | 100.0 | 200.0 | 18.0 | 0.1 | 365.0 | 19.0 | 36.5 |
| Max. | 300.0 | 610.0 | 63.0 | 5.3 | 4198.0 | 629.6 | 161.3 |
| Avg. | 149.5 | 304.3 | 38.3 | 0.7 | 2374.1 | 173.0 | 71.6 |
| SD | 31.3 | 73.4 | 10.4 | 0.7 | 1353.9 | 109.4 | 22.2 |
| VAR | 0.2 | 0.2 | 0.3 | 1.1 | 0.6 | 0.6 | 0.3 |
| Validation set | |||||||
| Min. | 100.0 | 200.0 | 18.0 | 0.1 | 167.0 | 13.0 | 41.3 |
| Max. | 300.0 | 600.0 | 52.2 | 3.0 | 4198.0 | 420.0 | 129.0 |
| Avg. | 153.3 | 307.0 | 35.1 | 0.7 | 2370.5 | 160.5 | 65.6 |
| SD | 28.0 | 56.0 | 7.0 | 0.8 | 1386.3 | 97.6 | 17.0 |
| VAR | 0.2 | 0.2 | 0.2 | 1.1 | 0.6 | 0.6 | 0.3 |
| d | L | Fco | t | Ftf | Ef | Fcc | |
|---|---|---|---|---|---|---|---|
| d | 1.00 | ||||||
| L | 0.88 | 1.00 | |||||
| Fco | −0.09 | −0.14 | 1.00 | ||||
| t | 0.10 | 0.15 | 0.05 | 1.00 | |||
| Ftf | 0.04 | −0.04 | −0.20 | −0.60 | 1.00 | ||
| Ef | −0.12 | −0.14 | −0.26 | −0.54 | 0.67 | 1.00 | |
| Fcc | −0.08 | −0.10 | 0.26 | 0.30 | 0.13 | −0.01 | 1.00 |
2.3. Predictive Models
3. Results and Discussion
3.1. General Behavior of the Wrapped Concrete Column
3.2. Prediction of Fcc Values
3.2.1. ANN Approaches


| Hidden Layer | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Layer | H (1:1) | H (1:2) | H (1:3) | H (1:4) | H (1:5) | H (1:6) | ||
| (Bias) | 2.298 | 1.054 | 0.046 | −1.003 | 0.171 | 0.160 | ||
| d | −0.755 | 0.023 | −0.576 | 0.460 | −0.086 | 0.269 | ||
| L | −0.119 | −0.022 | 0.113 | 1.274 | 0.488 | 0.383 | ||
| Fco | 0.326 | 0.001 | −0.969 | −0.399 | 0.096 | −1.868 | ||
| t | −1.134 | 0.928 | −0.270 | 0.308 | 0.009 | −0.590 | ||
| Ftf | −0.651 | −0.141 | −0.045 | 0.542 | 0.892 | 0.749 | ||
| Ef | −0.814 | 0.067 | 0.695 | 0.304 | −0.577 | 0.139 | ||
| Output | Hidden Layer | |||||||
| H (1:1) | H (1:2) | H (1:3) | H (1:4) | H (1:5) | H (1:6) | (Bias) | ||
| Fcc | −1.724 | 3.071 | 1.948 | −2.161 | 2.409 | −0.987 | −2.656 | |
| Hidden Layer | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Layer | H (1:1) | H (1:2) | H (1:3) | H (1:4) | H (1:5) | H (1:6) | ||
| (Bias) | −2.118 | −0.155 | 1.590 | 0.088 | 3.604 | −1.593 | ||
| d | −0.325 | 0.173 | −1.436 | 1.302 | 0.182 | −0.595 | ||
| L | −0.480 | 1.432 | −1.026 | 1.526 | −0.724 | 0.103 | ||
| Fco | −0.267 | 0.058 | −0.088 | 0.083 | 0.072 | −1.264 | ||
| t | 1.068 | −2.178 | 3.266 | −0.191 | 3.324 | −0.916 | ||
| Ftf | −1.997 | −0.249 | 0.269 | −0.724 | −0.156 | −2.875 | ||
| Ef | −0.484 | −0.173 | 1.742 | −0.050 | −0.238 | −2.793 | ||
| Output | Hidden Layer | |||||||
| H (1:1) | H (1:2) | H (1:3) | H (1:4) | H (1:5) | H (1:6) | (Bias) | ||
| Fcc | −1.690 | −3.748 | −1.952 | 0.658 | 3.709 | −0.932 | −2.788 | |
| Hidden Layer | ||||||||
|---|---|---|---|---|---|---|---|---|
| Input Layer | H (1:1) | H (1:2) | H (1:3) | H (1:4) | H (1:5) | H (1:6) | ||
| (Bias) | 1.703 | −3.786 | −1.735 | 3.387 | −7.024 | −3.192 | ||
| d | 4.490 | 2.758 | 0.693 | 2.336 | 3.055 | 3.803 | ||
| L | 5.030 | 6.018 | 0.230 | 1.216 | 6.178 | 4.085 | ||
| Fco | −4.781 | −2.707 | 0.062 | −5.521 | −0.220 | 2.318 | ||
| t | −5.914 | −5.006 | −14.219 | −4.898 | 0.185 | 1.355 | ||
| Ftf | 0.126 | 3.619 | 0.918 | −0.835 | 10.729 | 11.586 | ||
| Ef | 0.101 | 2.688 | −1.512 | 0.328 | −6.343 | 1.150 | ||
| Output | Hidden Layer | |||||||
| H (1:1) | H (1:2) | H (1:3) | H (1:4) | H (1:5) | H (1:6) | (Bias) | ||
| Fcc | −3.293 | −6.103 | −12.682 | 3.349 | 6.661 | 6.336 | −6.252 | |
3.2.2. GP Approach
3.2.3. EPR Approach
| GP | ANN-BP | ANN-GRG | ANN-GA | EPR | ||
|---|---|---|---|---|---|---|
| MAE | Training | 6.29 | 3.24 | 3.29 | 3.51 | 4.22 |
| Validation | 5.37 | 3.29 | 2.71 | 3.26 | 3.85 | |
| RMSE | Training | 7.82 | 4.15 | 4.27 | 4.67 | 5.22 |
| Validation | 6.84 | 4.13 | 3.38 | 3.93 | 4.77 | |
| RRMSE % | Training | 10.91 | 5.79 | 5.97 | 6.52 | 7.28 |
| Validation | 10.43 | 6.30 | 5.16 | 5.99 | 7.28 | |
| MAPE% | Training | 9.13 | 4.93 | 4.86 | 5.13 | 6.31 |
| Validation | 8.27 | 5.04 | 4.27 | 4.94 | 5.97 | |
| SSE | Training | 7882 | 2220 | 2356 | 2815 | 3511 |
| Validation | 1635 | 596 | 401 | 540 | 798 | |
| Error % | Training | 10.91 | 5.79 | 5.97 | 6.52 | 7.28 |
| Validation | 10.43 | 6.30 | 5.16 | 5.99 | 7.28 | |
| R2 | Training | 0.878 | 0.966 | 0.963 | 0.956 | 0.945 |
| Validation | 0.843 | 0.944 | 0.962 | 0.950 | 0.924 |

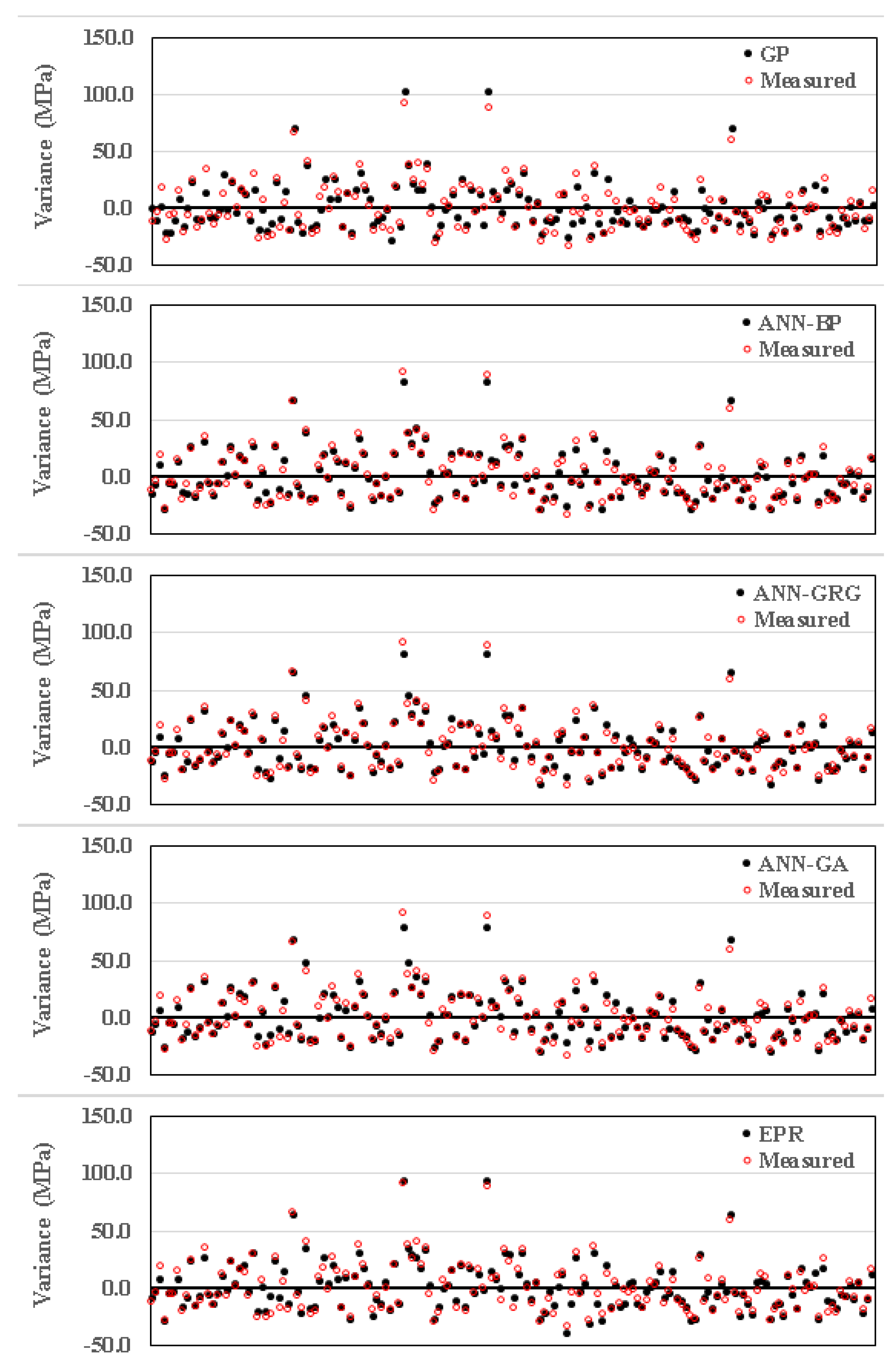

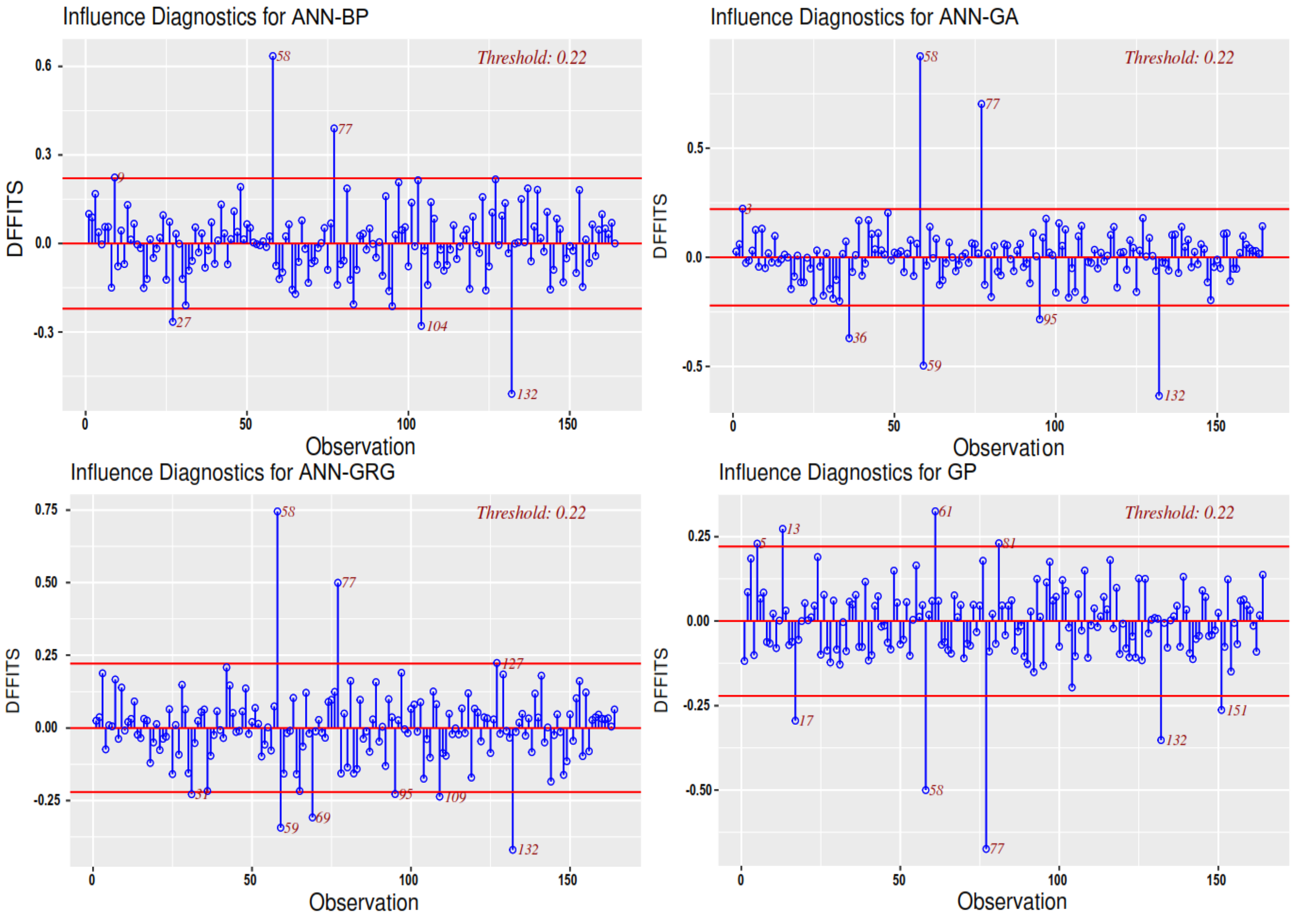
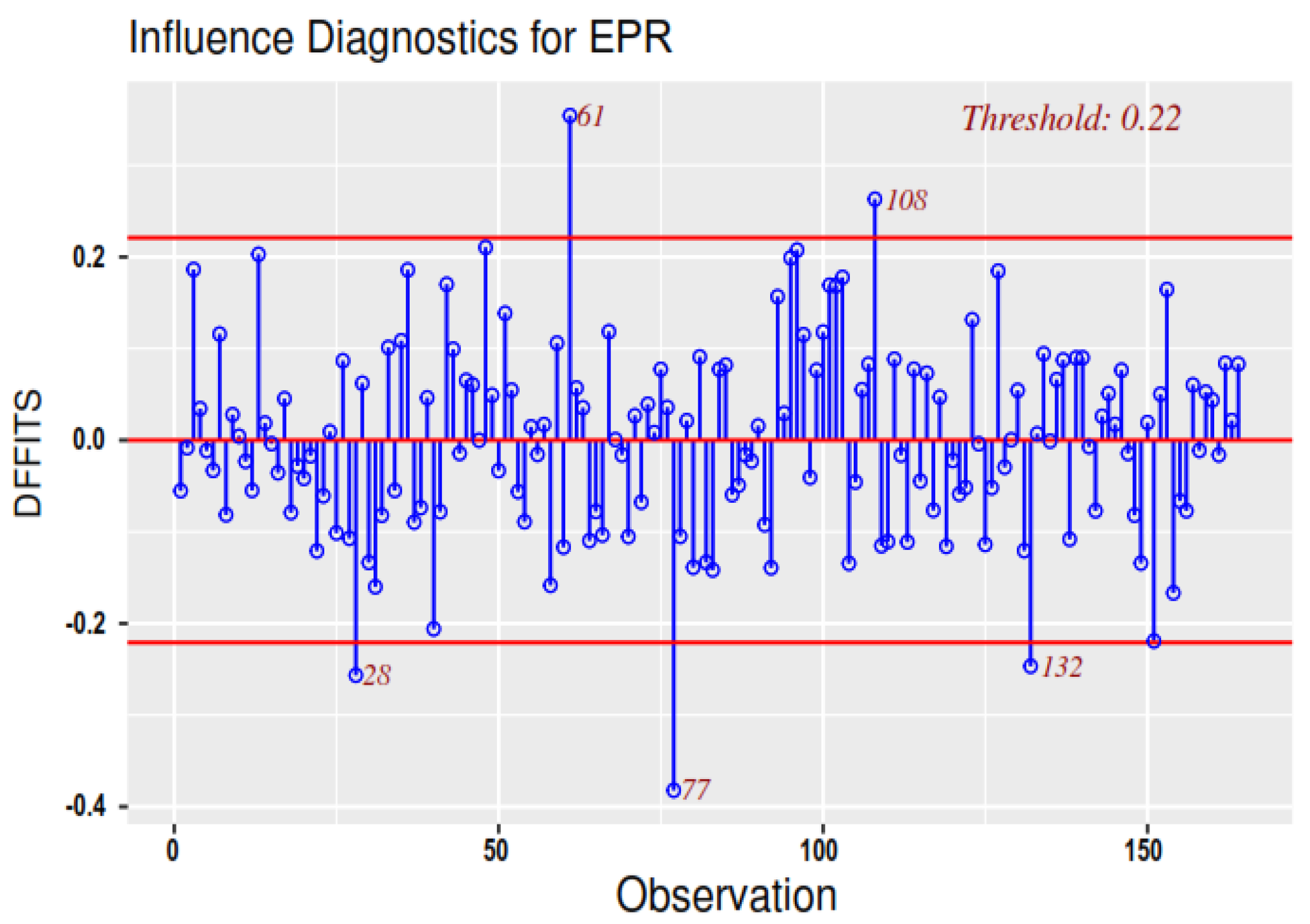
4. Conclusions
- -
- The GP model is the simplest but also the least accurate. Its accuracy is about 90%. The EPR model came next as a more complicated and more accurate model, with an accuracy of about 92.5%. The three ANN models presented more complicated and more accurate models with almost the same level of accuracy (94%).
- -
- The outcomes showed that the training algorithm of the ANN model slightly affected its accuracy. Back propagation (BP) and gradually reduced gradient (GRG) showed almost the same level of accuracy, while the genetic algorithm (GA) showed a lower level of accuracy.
- -
- Although the ANN models are more accurate than the GP and EPR models, the high complexity of the ANN models make them suitable for computerized calculations. On the other hand, the closed-form equations of GP and EPR could be used manually.
- -
- The summation of the absolute weights of each neuron in the input layer of the developed ANN models indicates that FRP properties (t and Ftf) are the most important factors, while the factors of unwrapped compressive strength (Fco) and sample dimensions (d and L) have a much lower influence.
- -
- The modulus of elasticity of CFRP (Ef) was not used in the GP model nor in the EPR model, which indicates its insignificant impact on Fcc compared to other parameters.
- -
- Because the ratio (L/d) is almost constant and equals 2.0 in all the database records, these two parameters are dependent, and they both have the same importance; hence, the appearance of (L) only in the GP model is quite enough for both of them and captures the effect of size on the Fcc.
- -
- Using the GA approach to reduce the possible 28 terms of traditional polynomial regression to only 15 terms was successful without reducing the accuracy.
- -
- All the developed predictive models are valid within the used ranges of input parameters, and they should be verified beyond that.
- -
- Generally, the closed-form equations proposed in this research work became decisive models in designing structural members belonging to this group of concrete columns jacketed with CFRP, with less need for the laboratory.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| d | L | Fco | t | Ftf | Ef | Fcc |
|---|---|---|---|---|---|---|
| mm | mm | Mpa | mm | Mpa | Gpa | Mpa |
| Training set | ||||||
| 152 | 305 | 55.2 | 0.38 | 1577 | 105 | 57.9 |
| 100 | 200 | 25.9 | 0.167 | 3591 | 242 | 66.4 |
| 150 | 300 | 29.2 | 0.33 | 3788 | 225.7 | 88.2 |
| 152 | 305 | 38.6 | 0.31 | 755 | 73.3 | 41.9 |
| 152 | 610 | 26.2 | 2 | 580 | 87.3 | 64 |
| 100 | 200 | 25.9 | 0.167 | 3591 | 242 | 64.8 |
| 152 | 305 | 43.8 | 0.76 | 1577 | 105 | 85 |
| 152 | 305 | 38.6 | 1.22 | 388 | 27.7 | 49.3 |
| 152 | 305 | 55.2 | 0.38 | 1577 | 105 | 62.9 |
| 152 | 305 | 43.8 | 1.14 | 1577 | 105 | 94 |
| 152 | 305 | 35.9 | 0.165 | 4198 | 250.5 | 53.2 |
| 150 | 300 | 34.3 | 1 | 753 | 91 | 59.4 |
| 100 | 200 | 51.9 | 0.22 | 3481 | 230.5 | 104.6 |
| 152 | 305 | 38.6 | 0.92 | 822 | 54 | 64.7 |
| 152 | 305 | 41.1 | 0.165 | 3800 | 250.5 | 55.4 |
| 152 | 305 | 44.2 | 0.22 | 3762 | 260 | 62.9 |
| 152 | 305 | 18 | 5.31 | 513 | 35.9 | 82.23 |
| 160 | 320 | 61.81 | 1 | 450 | 34 | 62.68 |
| 152 | 305 | 43.8 | 1.14 | 1577 | 105 | 92.6 |
| 100 | 200 | 26.3 | 0.22 | 3481 | 230.5 | 70.9 |
| 152 | 305 | 33.7 | 1.14 | 1577 | 105 | 86.2 |
| 160 | 320 | 49.46 | 3 | 450 | 34 | 82.91 |
| 100 | 200 | 25.9 | 0.167 | 3591 | 242 | 63 |
| 150 | 300 | 52.3 | 0.33 | 3788 | 225.7 | 100 |
| 150 | 300 | 25.6 | 0.165 | 3550 | 235 | 43.9 |
| 152 | 305 | 38.6 | 0.92 | 1105 | 77.5 | 76.4 |
| 150 | 300 | 34.3 | 1 | 423 | 37 | 44.2 |
| 100 | 200 | 30.2 | 0.17 | 2716 | 224.6 | 46.6 |
| 152 | 305 | 43.8 | 1.14 | 1577 | 105 | 96.5 |
| 160 | 320 | 49.46 | 1 | 450 | 34 | 52.75 |
| 152 | 305 | 55.2 | 0.76 | 1577 | 105 | 74.6 |
| 100 | 200 | 26.3 | 0.11 | 3481 | 230.5 | 50.7 |
| 152 | 305 | 38 | 1.02 | 3615 | 240.7 | 135.7 |
| 300 | 600 | 24.5 | 0.501 | 3591 | 242 | 63 |
| 150 | 300 | 31.2 | 0.11 | 3481 | 230.5 | 52.4 |
| 152 | 305 | 38 | 0.68 | 3615 | 240.7 | 110.1 |
| 152 | 305 | 38.6 | 0.61 | 660 | 39.9 | 47.1 |
| 152 | 305 | 33.7 | 0.38 | 1577 | 105 | 49.4 |
| 150 | 300 | 45.2 | 0.22 | 3481 | 230.5 | 79.4 |
| 100 | 200 | 30.2 | 0.5 | 2873 | 224.6 | 87.2 |
| 152 | 305 | 35.9 | 0.33 | 4198 | 250.5 | 68.7 |
| 152 | 305 | 34.3 | 0.495 | 4198 | 250.5 | 97.3 |
| 152 | 305 | 43.8 | 0.76 | 1577 | 105 | 84 |
| 152 | 305 | 38.6 | 1.22 | 388 | 27.7 | 52.7 |
| 152 | 305 | 18 | 1.55 | 1353 | 96 | 82.23 |
| 152 | 305 | 38.38 | 0.33 | 795 | 72.4 | 44.87 |
| 152 | 305 | 18 | 2.26 | 978 | 62.5 | 79.49 |
| 152 | 305 | 55.2 | 1.14 | 1577 | 105 | 108 |
| 152 | 305 | 38.6 | 1.22 | 1352 | 95.7 | 89.5 |
| 152 | 305 | 35.9 | 0.33 | 4198 | 250.5 | 71.6 |
| 152 | 305 | 37.7 | 0.11 | 3905 | 260 | 50.3 |
| 100 | 200 | 30.2 | 0.42 | 1285 | 576.6 | 63.3 |
| 152 | 305 | 41.1 | 0.165 | 3800 | 250.5 | 52.6 |
| 150 | 300 | 51.7 | 0.165 | 3788 | 225.7 | 69.2 |
| 152 | 610 | 26.2 | 1 | 580 | 97.1 | 50.6 |
| 152 | 305 | 38.38 | 1.32 | 1352 | 95.7 | 89.48 |
| 150 | 300 | 29.8 | 0.165 | 3550 | 235 | 57 |
| 152 | 305 | 38 | 1.36 | 3615 | 240.7 | 161.3 |
| 152 | 305 | 38 | 0.68 | 3615 | 240.7 | 107.4 |
| 160 | 320 | 63.01 | 3 | 450 | 34 | 94.81 |
| 100 | 200 | 33.7 | 0.33 | 3481 | 230.5 | 109.9 |
| 152 | 305 | 38.6 | 1.22 | 1352 | 95.7 | 89.9 |
| 100 | 200 | 30.2 | 0.67 | 2658 | 224.6 | 104.6 |
| 152 | 305 | 33.7 | 0.76 | 1577 | 105 | 64.6 |
| 160 | 320 | 25.93 | 1 | 450 | 34 | 39.63 |
| 152 | 305 | 33.7 | 0.38 | 1577 | 105 | 47.9 |
| 160 | 320 | 63.01 | 1 | 450 | 34 | 76.21 |
| 152 | 305 | 33.7 | 0.76 | 1577 | 105 | 71.8 |
| 100 | 200 | 26.3 | 0.33 | 3481 | 230.5 | 84.9 |
| 152 | 305 | 43.8 | 0.38 | 1577 | 105 | 52.1 |
| 152 | 305 | 34.3 | 0.495 | 4198 | 250.5 | 90.4 |
| 152 | 305 | 33.7 | 0.38 | 1577 | 105 | 49.7 |
| 152 | 305 | 38.6 | 1.22 | 1352 | 95.7 | 89 |
| 152 | 305 | 44.2 | 0.22 | 3762 | 260 | 65.7 |
| 152 | 305 | 47.6 | 0.33 | 3757 | 250.5 | 85.5 |
| 100 | 200 | 33.7 | 0.11 | 3481 | 230.5 | 69.6 |
| 152 | 305 | 38 | 1.36 | 3615 | 240.7 | 158.5 |
| 152 | 305 | 55.2 | 0.76 | 1577 | 105 | 77.6 |
| 152 | 305 | 43.8 | 0.76 | 1577 | 105 | 79.2 |
| 150 | 300 | 25.6 | 0.33 | 3550 | 235 | 59.6 |
| 150 | 300 | 52.2 | 0.33 | 3788 | 225.7 | 103 |
| 160 | 320 | 61.81 | 3 | 450 | 34 | 93.19 |
| 150 | 300 | 31.3 | 0.165 | 3788 | 225.7 | 52.3 |
| 152 | 305 | 47.6 | 0.33 | 3757 | 250.5 | 85.5 |
| 152 | 305 | 55.2 | 1.14 | 1577 | 105 | 103.3 |
| 152 | 305 | 35.9 | 0.33 | 4198 | 250.5 | 69.9 |
| 152 | 305 | 38.6 | 0.61 | 1047 | 70.6 | 56.5 |
| 100 | 200 | 42 | 0.6 | 1265 | 82.7 | 73.5 |
| 150 | 300 | 34.9 | 0.24 | 1100 | 420 | 40.7 |
| 152 | 305 | 44.2 | 0.11 | 3905 | 260 | 48.1 |
| 300 | 600 | 24.5 | 0.501 | 3591 | 242 | 60.6 |
| 152 | 305 | 35.9 | 0.165 | 4198 | 250.5 | 47.2 |
| 152 | 305 | 38.6 | 0.92 | 1105 | 77.5 | 80.9 |
| 152 | 305 | 47.6 | 0.33 | 3757 | 250.5 | 82.7 |
| 150 | 300 | 23.6 | 0.11 | 3481 | 230.5 | 36.5 |
| 200 | 400 | 22.7 | 0.334 | 3591 | 242 | 66.3 |
| 160 | 320 | 58.24 | 3 | 450 | 34 | 100.41 |
| 100 | 200 | 25.9 | 0.167 | 3591 | 242 | 64.3 |
| 152 | 305 | 38.38 | 0.99 | 1105 | 77.4 | 77.68 |
| 100 | 200 | 30.2 | 0.14 | 1579 | 628.6 | 41.7 |
| 152 | 305 | 55.2 | 1.14 | 1577 | 105 | 106.5 |
| 200 | 400 | 22.7 | 0.334 | 3591 | 242 | 64.3 |
| 152 | 305 | 38.6 | 0.31 | 755 | 73.3 | 47.2 |
| 152 | 305 | 34.3 | 0.495 | 4198 | 250.5 | 82.6 |
| 152 | 305 | 34.3 | 0.165 | 4198 | 250.5 | 50.3 |
| 100 | 200 | 51.9 | 0.11 | 3481 | 230.5 | 75.2 |
| 152 | 305 | 34.3 | 0.165 | 4198 | 250.5 | 56.7 |
| 200 | 400 | 22.7 | 0.334 | 3591 | 242 | 69.1 |
| 152 | 305 | 38.9 | 0.33 | 3754 | 247 | 65.8 |
| 150 | 300 | 52.3 | 0.165 | 3788 | 225.7 | 68 |
| 200 | 400 | 22.7 | 0.334 | 3591 | 242 | 60.1 |
| 152 | 305 | 38.6 | 1.22 | 388 | 27.7 | 52.6 |
| 300 | 600 | 24.5 | 0.501 | 3591 | 242 | 59.4 |
| 152 | 305 | 38.6 | 0.92 | 1105 | 77.5 | 75.8 |
| 150 | 300 | 29.8 | 0.33 | 3550 | 235 | 72.1 |
| 100 | 200 | 33.7 | 0.22 | 3481 | 230.5 | 88 |
| 100 | 200 | 30.2 | 0.28 | 1824 | 629.6 | 56 |
| 150 | 300 | 31.2 | 0.22 | 3481 | 230.5 | 67.4 |
| 152 | 305 | 55.2 | 0.76 | 1577 | 105 | 77 |
| 152 | 305 | 38.38 | 0.66 | 1047 | 138.1 | 59.68 |
| 152 | 305 | 43.8 | 0.38 | 1577 | 105 | 54.7 |
| 152 | 305 | 34.3 | 0.165 | 4198 | 250.5 | 50 |
| 152 | 305 | 38.6 | 0.31 | 755 | 73.3 | 45.5 |
| 150 | 300 | 34.9 | 0.12 | 2600 | 200 | 42.2 |
| 150 | 300 | 51.7 | 0.33 | 3788 | 225.7 | 94.9 |
| 152 | 305 | 55.2 | 0.38 | 1577 | 105 | 58.1 |
| 160 | 320 | 58.24 | 1 | 450 | 34 | 77.51 |
| 152 | 305 | 38.6 | 0.61 | 660 | 39.9 | 50 |
| 150 | 300 | 34.3 | 2.44 | 365 | 19 | 62.5 |
| Validation set | ||||||
| 152 | 305 | 38.9 | 0.33 | 3754 | 247 | 76.8 |
| 300 | 600 | 24.5 | 0.501 | 3591 | 242 | 58.8 |
| 152 | 305 | 38 | 1.02 | 3615 | 240.7 | 129 |
| 160 | 320 | 25.93 | 3 | 450 | 34 | 66.14 |
| 152 | 305 | 37.7 | 0.11 | 3905 | 260 | 48.5 |
| 150 | 300 | 23.6 | 0.33 | 3481 | 230.5 | 64.3 |
| 150 | 300 | 45.2 | 0.11 | 3481 | 230.5 | 59.4 |
| 160 | 320 | 29.51 | 1 | 450 | 34 | 49.88 |
| 100 | 200 | 42 | 0.6 | 1265 | 82.7 | 67.6 |
| 150 | 300 | 31.2 | 0.33 | 3481 | 230.5 | 81.7 |
| 152 | 305 | 38.9 | 0.33 | 3754 | 247 | 79.1 |
| 150 | 300 | 34.9 | 0.24 | 1100 | 420 | 41.3 |
| 152 | 305 | 35.9 | 0.165 | 4198 | 250.5 | 50.4 |
| 152 | 305 | 41.1 | 0.165 | 3800 | 250.5 | 57 |
| 150 | 300 | 34.3 | 2.83 | 167 | 13 | 47.5 |
| 150 | 300 | 31.3 | 0.33 | 3788 | 225.7 | 80.6 |
| 152 | 305 | 38.6 | 0.92 | 822 | 54 | 68.3 |
| 150 | 300 | 23.6 | 0.22 | 3481 | 230.5 | 50.8 |
| 152 | 305 | 33.7 | 1.14 | 1577 | 105 | 82.9 |
| 150 | 300 | 52.2 | 0.165 | 3788 | 225.7 | 66.5 |
| 160 | 320 | 29.51 | 3 | 450 | 34 | 71.35 |
| 152 | 305 | 18 | 2.06 | 1127 | 150 | 70.58 |
| 150 | 300 | 34.9 | 0.12 | 2600 | 200 | 44.3 |
| 152 | 305 | 33.7 | 1.14 | 1577 | 105 | 95.4 |
| 152 | 305 | 43.8 | 0.38 | 1577 | 105 | 48.7 |
| 150 | 300 | 29.2 | 0.165 | 3788 | 34 | 53.8 |
| 152 | 305 | 38.6 | 0.61 | 660 | 39.9 | 47.7 |
| 152 | 305 | 38.6 | 0.92 | 822 | 54 | 67.3 |
| 150 | 300 | 32.2 | 0.165 | 3788 | 225.7 | 61.2 |
| 152 | 305 | 33.7 | 0.76 | 1577 | 105 | 75.2 |
| 152 | 305 | 38.6 | 0.61 | 1047 | 70.6 | 61.9 |
| 100 | 200 | 42 | 0.6 | 1265 | 82.7 | 73.5 |
| 152 | 305 | 44.2 | 0.11 | 3905 | 260 | 51.1 |
| 152 | 305 | 38.6 | 0.61 | 1047 | 70.6 | 60.6 |
| 150 | 300 | 32.2 | 0.33 | 3788 | 225.7 | 85.6 |
References
- Bagheri, M.; Chahkandi, A.; Jahangir, H. Seismic Reliability Analysis of RC Frames Rehabilitated by Glass Fiber-Reinforced Polymers. Int. J. Civ. Eng. 2019, 17, 1785–1797. [Google Scholar] [CrossRef]
- Teng, J.G.; Chen, J.-F.; Yu, T. FRP: Strengthened RC Structures; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; Available online: https://asset-pdf.scinapse.io/prod/1824168954/1824168954.pdf (accessed on 22 May 2022).
- Jahangir, H.; Khatibinia, M.; Kavousi, M. Application of Contourlet Transform in Damage Localization and Severity Assessment of Prestressed Concrete Slabs. J. Soft Comput. Civ. Eng. 2021, 5, 39–68. [Google Scholar] [CrossRef]
- Prado, D.M.; Araujo, I.D.G.; Haach, V.G.; Carrazedo, R. Assessment of Shear Damaged and NSM CFRP Retrofitted Reinforced Concrete Beams Based on Modal Analysis. Eng. Struct. 2016, 129, 54–66. [Google Scholar] [CrossRef]
- Jahangir, H.; Hasani, H.; Esfahani, M.R. Wavelet-Based Damage Localization and Severity Estimation of Experimental RC Beams Subjected to Gradual Static Bending Tests. Structures 2021, 34, 3055–3069. [Google Scholar] [CrossRef]
- Nagender, T.; Parulekar, Y.M.; Selvam, P.; Chattopadhyay, J. Experimental Study and Numerical Simulation of Seismic Behaviour of Corroded Reinforced Concrete Frames. Structures 2022, 35, 1256–1269. [Google Scholar] [CrossRef]
- Huang, Z.; Shen, J.; Lin, H.; Song, X.; Yao, Y. Shear Behavior of Concrete Shear Walls with CFRP Grids under Lateral Cyclic Loading. Eng. Struct. 2020, 211, 110422. [Google Scholar] [CrossRef]
- Xu, T.; Liu, J.; Wang, X.; Guo, Y.; Chen, Y.F. Behaviour of Short CFRP-Steel Composite Tubed Reinforced Normal and High Strength Concrete Columns under Eccentric Compression. Eng. Struct. 2020, 205, 110096. [Google Scholar] [CrossRef]
- Al-Mekhlafi, G.M.; Al-Osta, M.A.; Sharif, A.M. Behavior of Eccentrically Loaded Concrete-Filled Stainless Steel Tubular Stub Columns Confined by CFRP Composites. Eng. Struct. 2020, 205, 110113. [Google Scholar] [CrossRef]
- Soleymani, A.; Esfahani, M.R. Effect of concrete strength and thickness of flat slab on preventing of progressive collapse caused by elimination of an internal column. J. Struct. Constr. Eng. 2019, 6, 24–40. [Google Scholar] [CrossRef]
- Yazeed, S.-A.E.; Abdelsalam, S.A.; Abdelaziz, A.E. CFRP-Strengthened HSS Columns Subject to Eccentric Loading. J. Compos. Constr. 2018, 22, 4018025. [Google Scholar] [CrossRef]
- Zeng, J.J.; Teng, J.G.; Lin, G.; Li, L.J. Large-Scale FRP-Confined Rectangular RC Columns with Section Curvilinearization under Axial Compression. J. Compos. Constr. 2021, 25, 4021020. [Google Scholar] [CrossRef]
- Deng, Z.; Chai, W.; Liu, B.; Hu, Y. Compression Behavior of CFRP–Confined Coral Aggregate Concrete (CCAC) Circular Stub Columns. Case Stud. Constr. Mater. 2022, 16, e00863. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Experimental Analysis on Tensile Strengthening Properties of Steel and Glass Fiber Reinforced Inorganic Matrix Composites. Sci. Iran. 2020, 28, 1152–1166. [Google Scholar] [CrossRef]
- Dundar, C.; Erturkmen, D.; Tokgoz, S. Studies on Carbon Fiber Polymer Confined Slender Plain and Steel Fiber Reinforced Concrete Columns. Eng. Struct. 2015, 102, 31–39. [Google Scholar] [CrossRef]
- Gergely, I.; Pantelides, C.P.; Nuismer, R.J.; Reaveley, L.D. Bridge Pier Retrofit Using Fiber-Reinforced Plastic Composites. J. Compos. Constr. 1998, 2, 165–174. [Google Scholar] [CrossRef]
- Bank, L.C. Progressive Failure and Ductility of FRP Composites for Construction: Review. J. Compos. Constr. 2013, 17, 406–419. [Google Scholar] [CrossRef]
- Chotickai, P.; Tongya, P.; Jantharaksa, S. Performance of Corroded Rectangular RC Columns Strengthened with CFRP Composite under Eccentric Loading. Constr. Build. Mater. 2021, 268, 121134. [Google Scholar] [CrossRef]
- Nematzadeh, M.; Mousavimehr, M.; Shayanfar, J.; Omidalizadeh, M. Eccentric Compressive Behavior of Steel Fiber-Reinforced RC Columns Strengthened with CFRP Wraps: Experimental Investigation and Analytical Modeling. Eng. Struct. 2021, 226, 111389. [Google Scholar] [CrossRef]
- Naser, M.Z.; Hawileh, R.A.; Abdalla, J.A. Fiber-Reinforced Polymer Composites in Strengthening Reinforced Concrete Structures: A Critical Review. Eng. Struct. 2019, 198, 109542. [Google Scholar] [CrossRef]
- Habil, A.; Neaz, S.M.; Hadi, M.N. Experimental Investigation on the Behavior of Hollow-Core Glass Fiber-Reinforced Concrete Columns with GFRP Bars. J. Compos. Constr. 2022, 26, 4021074. [Google Scholar] [CrossRef]
- Al-Nimry, H.; Neqresh, M. Confinement Effects of Unidirectional CFRP Sheets on Axial and Bending Capacities of Square RC Columns. Eng. Struct. 2019, 196, 109329. [Google Scholar] [CrossRef]
- Punurai, W.; Hsu, C.T.T.; Punurai, S.; Chen, J. Biaxially Loaded RC Slender Columns Strengthened by CFRP Composite Fabrics. Eng. Struct. 2013, 46, 311–321. [Google Scholar] [CrossRef]
- Teng, J.G.; Lam, L. Behavior and Modeling of Fiber Reinforced Polymer-Confined Concrete. J. Struct. Eng. 2004, 130, 1713–1723. [Google Scholar] [CrossRef]
- Abd El Fattah, A. New Axial Stress-Strain Model of Square Concrete Columns Confined with Lateral Steel and FRP. Compos. Struct. 2018, 202, 731–751. [Google Scholar] [CrossRef]
- Harajli, M.H. Axial Stress–Strain Relationship for FRP Confined Circular and Rectangular Concrete Columns. Cem. Concr. Compos. 2006, 28, 938–948. [Google Scholar] [CrossRef]
- Lignola, G.P.; Prota, A.; Manfredi, G.; Cosenza, E. Experimental Performance of RC Hollow Columns Confined with CFRP. J. Compos. Constr. 2007, 11, 42–49. [Google Scholar] [CrossRef]
- Sadeghian, P.; Rahai, A.R.; Ehsani, M.R. Experimental Study of Rectangular RC Columns Strengthened with CFRP Composites under Eccentric Loading. J. Compos. Constr. 2010, 14, 443–450. [Google Scholar] [CrossRef]
- Yang, J.; Wang, J.; Wang, Z. Rectangular High-Strength Concrete Columns Confined with Carbon Fiber-Reinforced Polymer (CFRP) under Eccentric Compression Loading. Constr. Build. Mater. 2018, 193, 604–622. [Google Scholar] [CrossRef]
- Quiertant, M.; Clement, J.L. Behavior of RC Columns Strengthened with Different CFRP Systems under Eccentric Loading. Constr. Build. Mater. 2011, 25, 452–460. [Google Scholar] [CrossRef]
- Pan, J.L.; Xu, T.; Hu, Z.J. Experimental Investigation of Load Carrying Capacity of the Slender Reinforced Concrete Columns Wrapped with FRP. Constr. Build. Mater. 2007, 21, 1991–1996. [Google Scholar] [CrossRef]
- Azadeh, P.; Wei, W. Behavior of FRP Jacketed Concrete Columns under Eccentric Loading. J. Compos. Constr. 2001, 5, 146–152. [Google Scholar] [CrossRef]
- Barros, J.A.O.; Varma, R.K.; Sena-Cruz, J.M.; Azevedo, A.F.M. Near Surface Mounted CFRP Strips for the Flexural Strengthening of RC Columns: Experimental and Numerical Research. Eng. Struct. 2008, 30, 3412–3425. [Google Scholar] [CrossRef] [Green Version]
- Fitzwilliam, J.; Bisby, L.A. Slenderness Effects on Circular CFRP Confined Reinforced Concrete Columns. J. Compos. Constr. 2010, 14, 280–288. [Google Scholar] [CrossRef]
- Hadi, M.N.S.; Le, T.D. Behaviour of Hollow Core Square Reinforced Concrete Columns Wrapped with CFRP with Different Fibre Orientations. Constr. Build. Mater. 2014, 50, 62–73. [Google Scholar] [CrossRef] [Green Version]
- Chellapandian, M.; Suriya Prakash, S.; Sharma, A. Strength and Ductility of Innovative Hybrid NSM Reinforced and FRP Confined Short RC Columns under Axial Compression. Compos. Struct. 2017, 176, 205–216. [Google Scholar] [CrossRef]
- Cao, Q.; Li, X.; Zhou, J.; Ma, Z.J. Expansive Concrete Confined by CFRP under Eccentric Compression. Constr. Build. Mater. 2019, 208, 113–124. [Google Scholar] [CrossRef]
- Miyauchi, K.; Inoue, S.; Kuroda, T.; Kobayashi, A. Strengthening effects of concrete column with carbon fiber sheet. Trans. Jpn. Concr. Inst. 2000, 21, 143–150. [Google Scholar]
- Karbhari, V.M.; Gao, Y. Composite Jacketed Concrete under Uniaxial Compression—Verification of Simple Design Equations. J. Mater. Civ. Eng. 1997, 9, 185–193. [Google Scholar] [CrossRef]
- Watanabe, K.; Nakamura, R.; Honda, Y.; Toyoshima, M.; Iso, M.; Fujimaki, T.; Kaneto, M.; Shirai, N. Confinement Effect of FRP Sheet on Strength and Ductility of Concrete Cylinders under Uniaxial Compression. In Proceedings of the Third International Symposium, Sapporo, Japan, 14–16 October 1997; Volume 1, pp. 233–238. [Google Scholar]
- Widiarsa, I.B.R. FRP-Wrapped Square RC Columns under Eccentric Loading. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 2014. [Google Scholar]
- Rochette, P.; Labossière, P. Axial Testing of Rectangular Column Models Confined with Composites. J. Compos. Constr. 2000, 4, 129–136. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, H. Compressive Behavior of Concrete Confined by Carbon Fiber Composite Jackets. J. Mater. Civ. Eng. 2000, 12, 139–146. [Google Scholar] [CrossRef]
- Jiang, T.; Teng, J.G. Analysis-Oriented Stress-Strain Models for FRP-Confined Concrete. Eng. Struct. 2007, 29, 2968–2986. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G.; Cheung, C.H.; Xiao, Y. FRP-Confined Concrete under Axial Cyclic Compression. Cem. Concr. Compos. 2006, 28, 949–958. [Google Scholar] [CrossRef]
- Shehata, I.A.E.M.; Carneiro, L.A.V.; Shehata, L.C.D. Strength of Short Concrete Columns Confined with CFRP Sheets. Mater. Struct. 2002, 35, 50–58. [Google Scholar] [CrossRef]
- Nafees, A.; Javed, M.F.; Khan, S.; Nazir, K.; Farooq, F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Predictive Modeling of Mechanical Properties of Silica Fume-Based Green Concrete Using Artificial Intelligence Approaches: MLPNN, ANFIS, and GEP. Materials 2021, 14, 7531. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.; Farooq, F.; Niewiadomski, P.; Ostrowski, K.; Akbar, A.; Aslam, F.; Alyousef, R. Prediction of Compressive Strength of Fly Ash Based Concrete Using Individual and Ensemble Algorithm. Materials 2021, 14, 794. [Google Scholar] [CrossRef]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive Modeling for Sustainable High-Performance Concrete from Industrial Wastes: A Comparison and Optimization of Models Using Ensemble Learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Perera, R.; Tarazona, D.; Ruiz, A.; Martín, A. Application of Artificial Intelligence Techniques to Predict the Performance of RC Beams Shear Strengthened with NSM FRP Rods. Formulation of Design Equations. Compos. Part B Eng. 2014, 66, 162–173. [Google Scholar] [CrossRef]
- Deifalla, A.; Salem, N.M. A Machine Learning Model for Torsion Strength of Externally Bonded FRP-Reinforced Concrete Beams. Polymers 2022, 14, 1824. [Google Scholar] [CrossRef]
- Liang, M.; Wu, Z.-M.; Ueda, T.; Zheng, J.-J.; Akogbe, R. Experiment and Modeling on Axial Behavior of Carbon Fiber Reinforced Polymer Confined Concrete Cylinders with Different Sizes. J. Reinf. Plast. Compos. 2012, 31, 389–403. [Google Scholar] [CrossRef]
- Bisby, L.; Ranger, M. Axial–Flexural Interaction in Circular FRP-Confined Reinforced Concrete Columns. Constr. Build. Mater. 2010, 24, 1672–1681. [Google Scholar] [CrossRef]
- Wang, L.M.; Wu, Y.F. Effect of Corner Radius on the Performance of CFRP-Confined Square Concrete Columns: Test. Eng. Struct. 2008, 30, 493–505. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Ebid, A.M.; Mahdi, H.A.; Soleymani, A.; Jayabalan, J.; Jahangir, H.; Samui, P.; Singh, R.P. Modeling the Confined Compressive Strength of CFRP-Jacketed Noncircular Concrete Columns Using Artificial Intelligence Techniques. Cogent Eng. 2022, 9, 2122156. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Gnananandarao, T.; Ebid, A.M.; Mahdi, H.A.; Ghadikolaee, M.R.; Al-Ajamee, M. Evaluating the Compressive Strength of Recycled Aggregate Concrete Using Novel Artificial Neural Network. Civ. Eng. J. 2022, 8, 1679–1693. [Google Scholar] [CrossRef]
- Ebid, A.M. 35 Years of (AI) in Geotechnical Engineering: State of the Art. Geotech. Geol. Eng. 2021, 39, 637–690. [Google Scholar] [CrossRef]
- Welsch, R.E.; Kuh, E. Linear Regression Diagnostics; NBER: Cambridge, MA, USA, 1977. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onyelowe, K.C.; Jayabalan, J.; Ebid, A.M.; Samui, P.; Singh, R.P.; Soleymani, A.; Jahangir, H. Evaluation of the Compressive Strength of CFRP-Wrapped Circular Concrete Columns Using Artificial Intelligence Techniques. Designs 2022, 6, 112. https://doi.org/10.3390/designs6060112
Onyelowe KC, Jayabalan J, Ebid AM, Samui P, Singh RP, Soleymani A, Jahangir H. Evaluation of the Compressive Strength of CFRP-Wrapped Circular Concrete Columns Using Artificial Intelligence Techniques. Designs. 2022; 6(6):112. https://doi.org/10.3390/designs6060112
Chicago/Turabian StyleOnyelowe, Kennedy C., Jagan Jayabalan, Ahmed M. Ebid, Pijush Samui, Rahul Pratap Singh, Atefeh Soleymani, and Hashem Jahangir. 2022. "Evaluation of the Compressive Strength of CFRP-Wrapped Circular Concrete Columns Using Artificial Intelligence Techniques" Designs 6, no. 6: 112. https://doi.org/10.3390/designs6060112
APA StyleOnyelowe, K. C., Jayabalan, J., Ebid, A. M., Samui, P., Singh, R. P., Soleymani, A., & Jahangir, H. (2022). Evaluation of the Compressive Strength of CFRP-Wrapped Circular Concrete Columns Using Artificial Intelligence Techniques. Designs, 6(6), 112. https://doi.org/10.3390/designs6060112







