Reliability Analysis of Steel Bridge Girders Strengthened with CFRP Considering the Debonding of Adhesive Layer
Abstract
:1. Introduction
2. Structural Reliability Index and Limit State Function
2.1. Reliability Index
2.2. Strength Limit State Function
2.3. Debonding Limit State Function
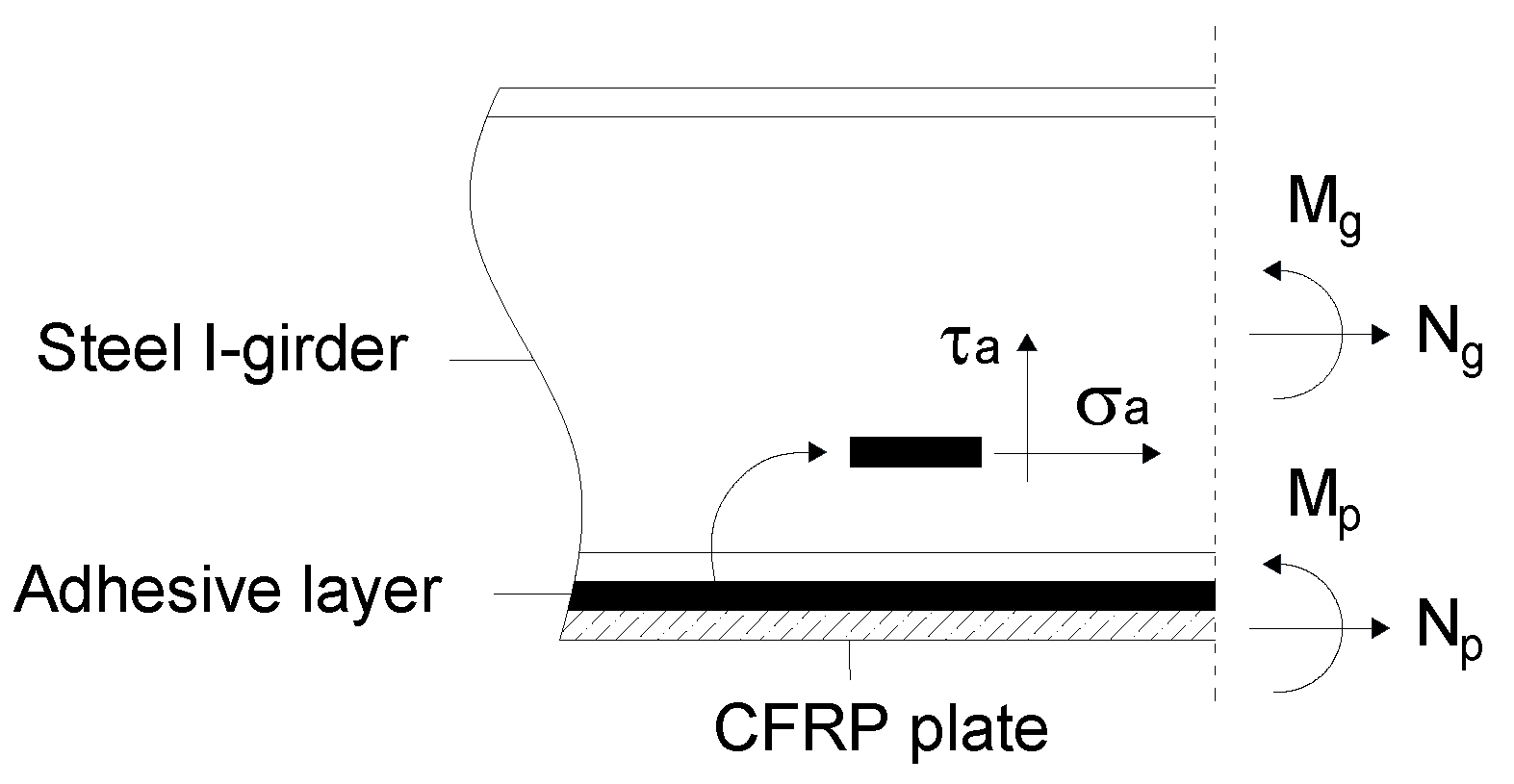
2.3.1. Shear Stress
2.3.2. Peel Stress
2.3.3. Debonding Stress
2.3.4. Margin Function of Debonding Limit State
2.4. System Reliability Model
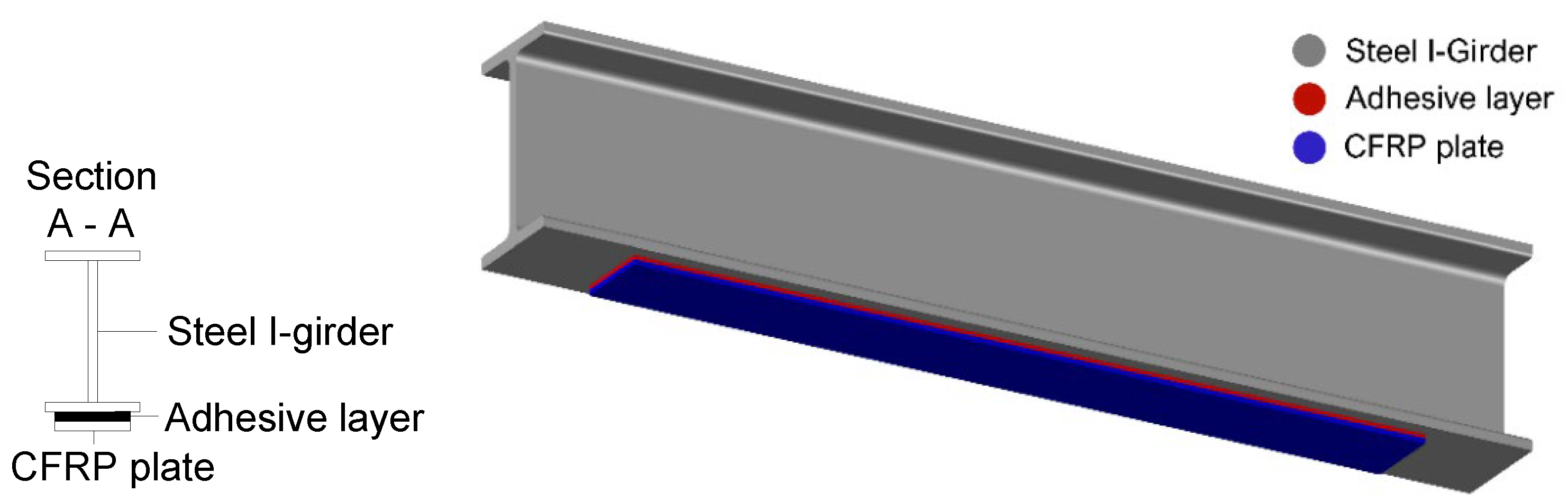
3. Reliability Analysis of CFRP-Strengthened Steel Girders
3.1. Statistical Characteristics
3.1.1. Steel Girders
3.1.2. CFRP Plate
3.1.3. Adhesive
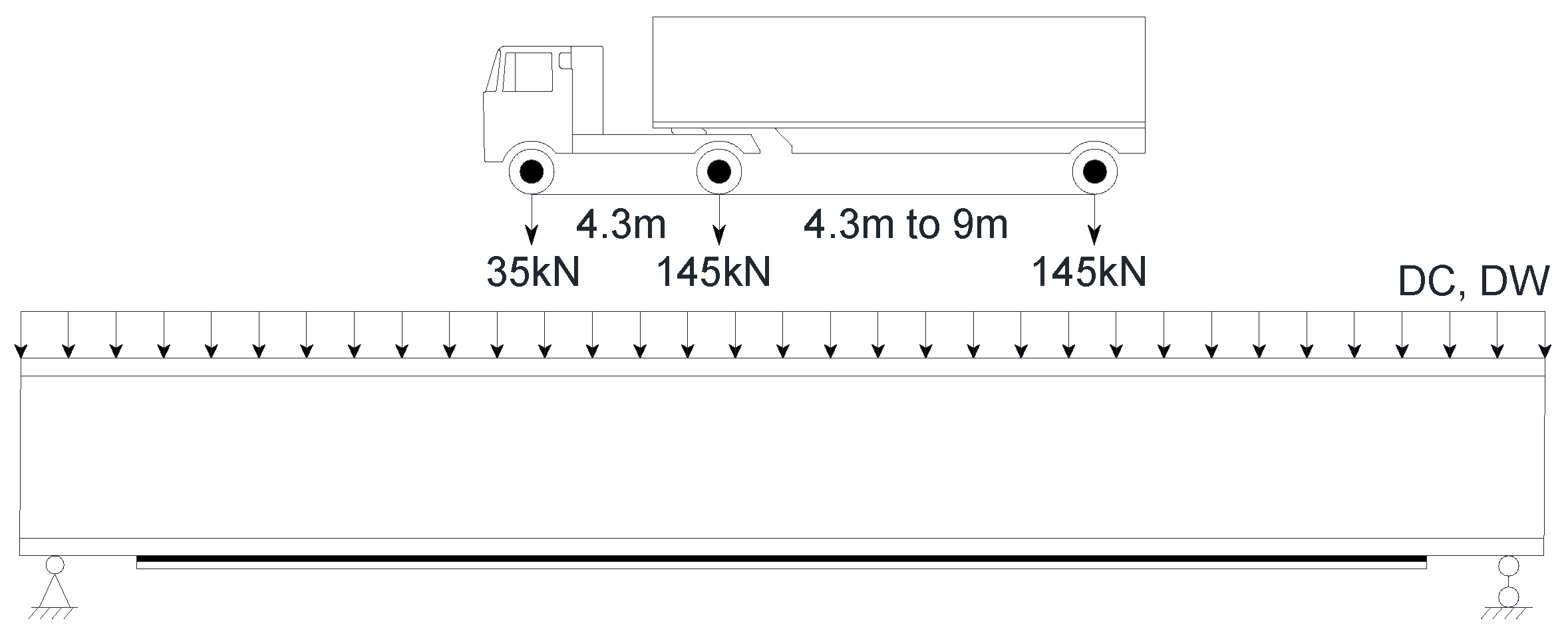
3.2. Structure Reliability Analysis
4. Results and Discussion
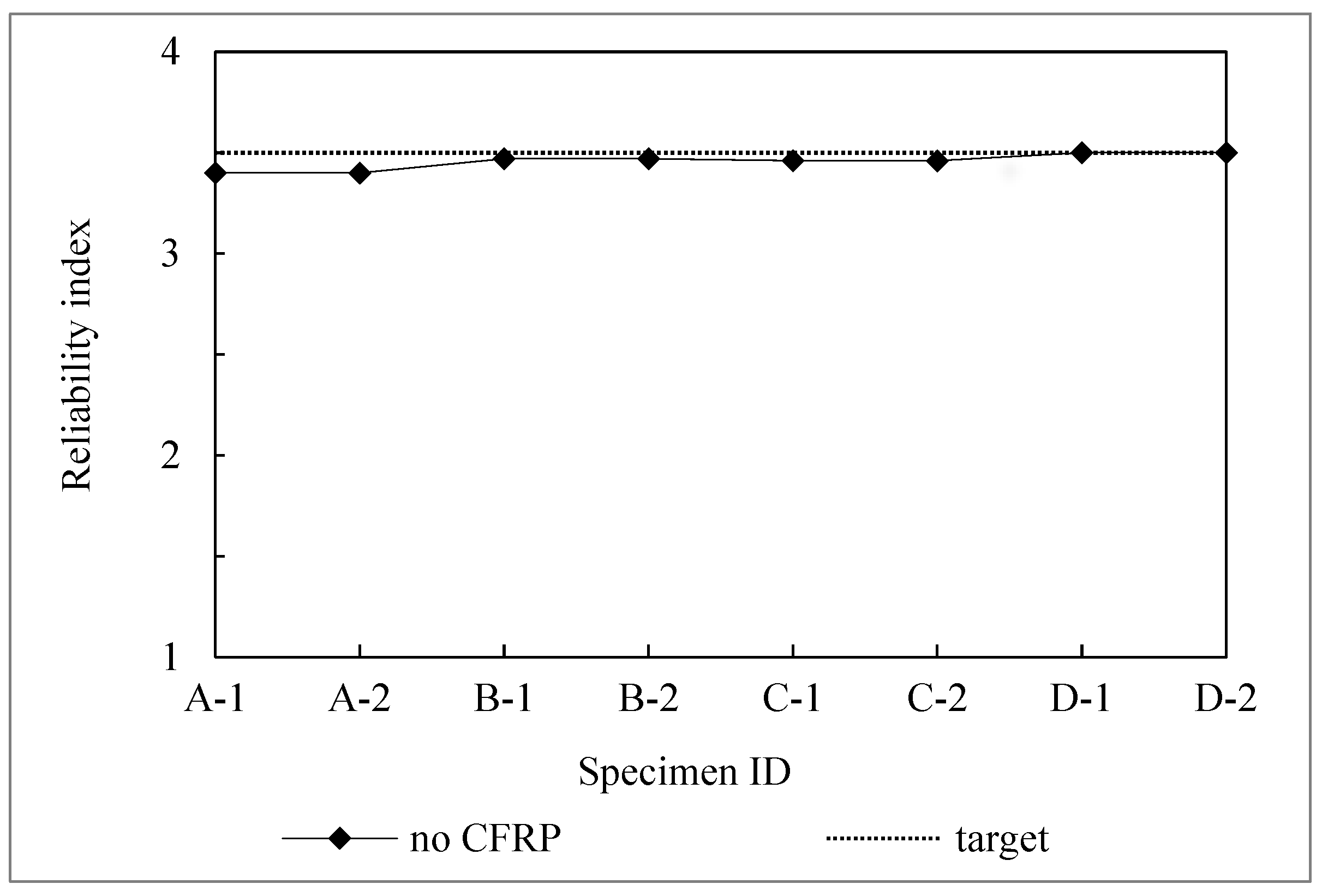
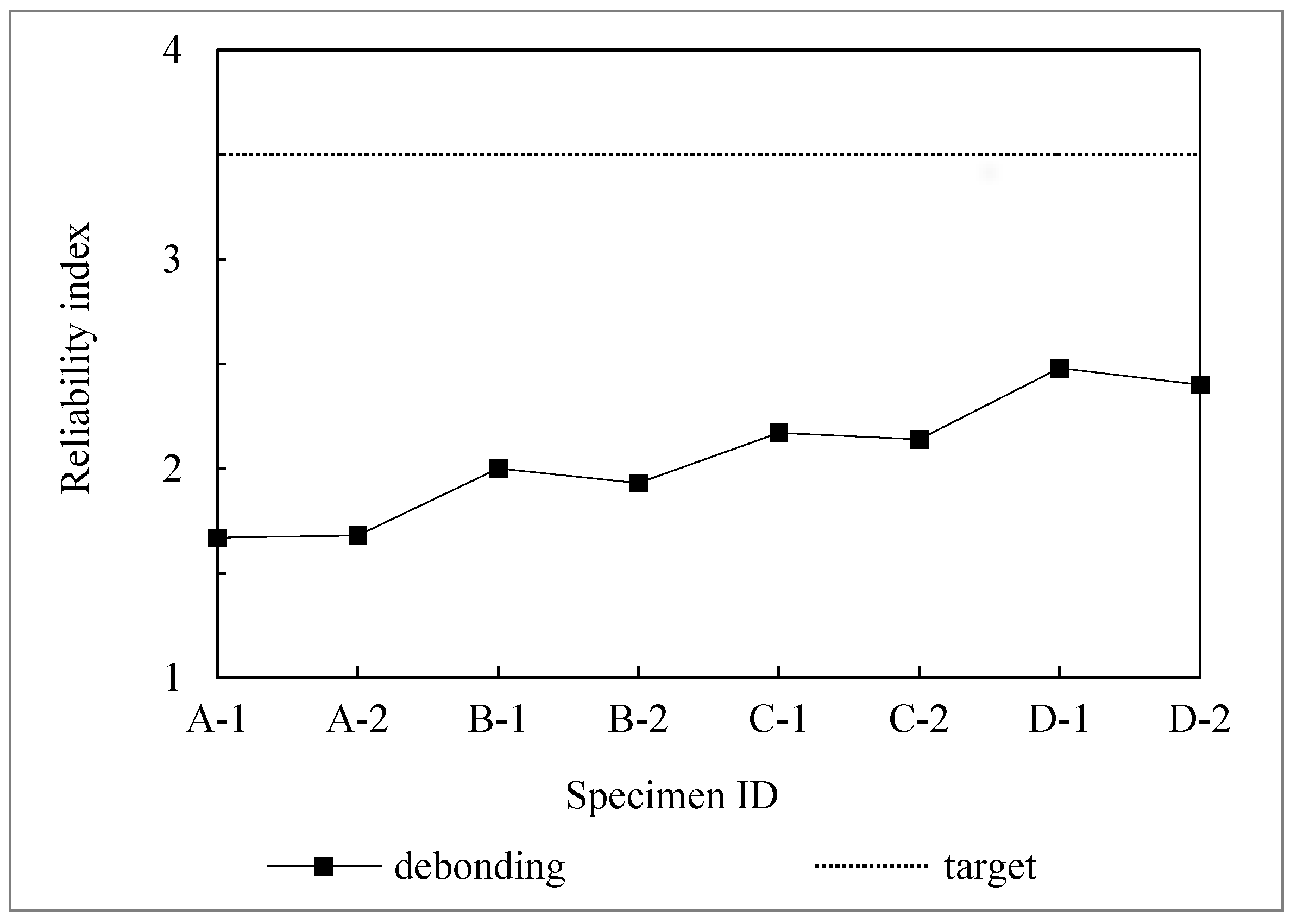
4.1. Reliability Indices of Strength Limit State and Debonding Limit State
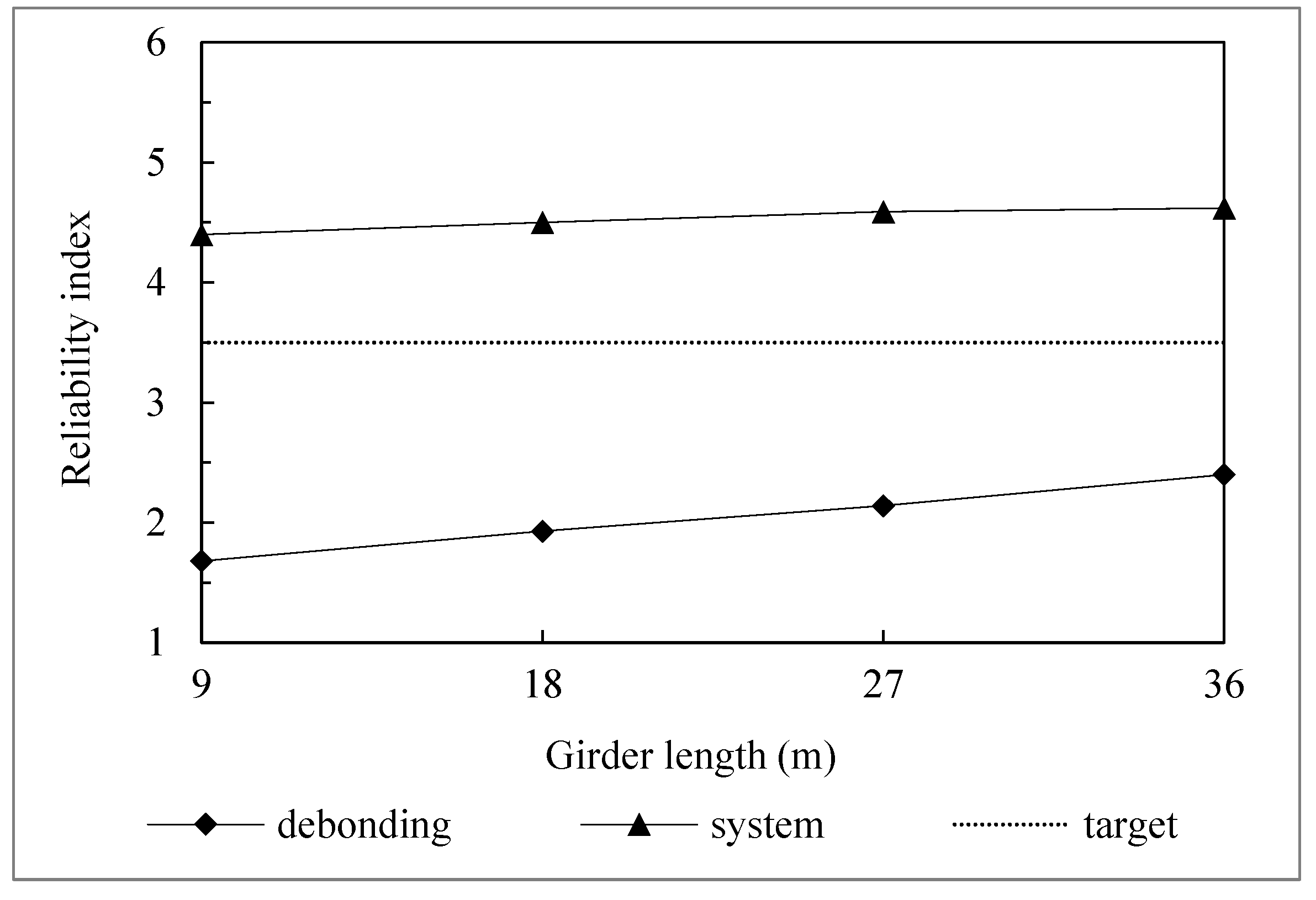
4.2. System Reliability Index of the Strengthened Steel Bridge Girder
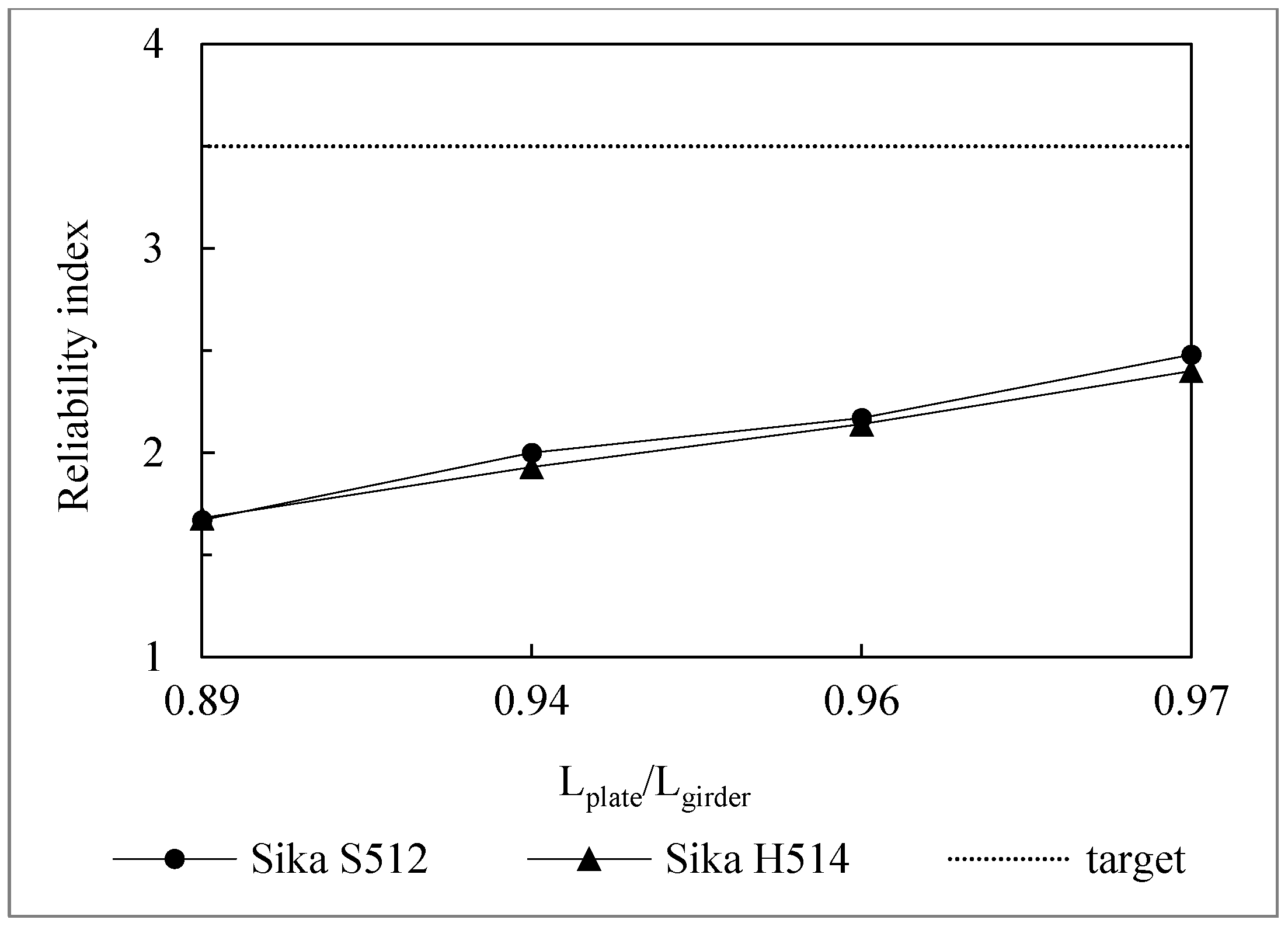
4.3. Effect of the CFRP Plate Length on the Reliability Index
5. Conclusions
- The reliability indices for strengthened steel bridge girders are significantly lower than the target reliability index of 3.5 when considering the debonding of the adhesive layer. The debonding limit state has a substantially lower reliability index than the strength limit state. Hence, debonding limit state should be carefully taken into account when strengthening steel bridge girders using CFRP plates.
- When considering debonding limit state, reliability indices are relatively similar for steel bridge girders reinforced by Sika H514 CFRP plate or Sika S512 CFRP plate. Thus, the reliability index is not significantly affected by the features of the CFRP plate when debonding occurs.
- The tensile strength of the CFRP plate has a substantial impact on the reliability indices of the girders. The higher strength tensile CFRP plates that are used to reinforce the steel bridge girders result in a higher reliability index for the girder.
- The length of the CFRP plate affixed to the steel bridge girder has a considerable impact on its reliability index. As a result, it is critical to ensure that the length of the CFRP plate is as long as possible while strengthening the bridge girder.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bakis, C.E.; Bank, L.C.; Brown, V.L.; Cosenza, E.; Davalos, J.F.; Lesko, J.J.; Machida, A.; Rizkalla, S.H.; Triantafillou, T.C. Fiber-Reinforced Polymer Composites for Construction—State-of-the-Art Review. J. Compos. Constr. 2002, 6, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Colombi, P.; Fava, G. Fatigue behavior of tensile steel/CFRP joints. J. Compos. Constr. 2012, 94, 2407–2417. [Google Scholar]
- Gangarao, H.; Vijay, P. Feasibility Review of FRP Materials for Structural Applications; Technical Report; Constructed Facilities Center Dept. of Civil & Env. Engineering College of Engineering and Mineral Resources West Virginia University: Morgantown, WV, USA.
- Khedmatgozar Dolati, S.S.; Mehrabi, A. NSM FRP Pile-Splice System for Prestressed Precast Concrete Piles. Pract. Period. Struct. Des. Constr. 2022, 27, 04022046. [Google Scholar] [CrossRef]
- Dolati, S.S.K.; Mehrabi, A. FRP sheet/jacket system as an alternative method for splicing prestressed-precast concrete piles. Case Stud. Constr. Mater. 2022, 16, e00912. [Google Scholar]
- Sen, R.; Liby, L.; Mullins, G. Strengthening steel bridge sections using CFRP laminates. Compos. Part B Eng. 2001, 32, 302–322. [Google Scholar] [CrossRef]
- Matta, F.; Karbhari, V.M.; Vitaliani, R. Tensile response of steel/CFRP adhesive bonds for the rehabilitation of civil structures. Struct. Eng. Mech. 2005, 20, 589–608. [Google Scholar] [CrossRef]
- Dawood, M.; Rizkalla, S.; Sumner, E. Fatigue and overloading behavior of steel concrete composite flexural members strengthened with high modulus CFRP materials. J. Compos. Constr. 2007, 11, 659–669. [Google Scholar] [CrossRef] [Green Version]
- Esfahani, M.R.; Kianoush, M.R.; Tajari, A.R. Flexural behavior of reinforced concrete beams strengthened by CFRP sheets. Eng. Struct. 2007, 29, 2428–2444. [Google Scholar] [CrossRef]
- Fernando, D.; Yu, T.; Teng, J.G.; Zhao, X.L. CFRP strengthening of rectangular steel tubes subjected to end bearing loads: Effect of adhesive properties and finite element modeling. Thin-Wall. Struct. 2009, 47, 1020–1028. [Google Scholar] [CrossRef]
- Teng, J.G.; Yu, T.; Fernando, D. Strengthening of steel structures with fiber reinforced polymer composites. J. Constr. Steel Res. 2012, 78, 131–143. [Google Scholar] [CrossRef]
- Jenarthanan, M.P.; Jeyapaul, R. Machinability study of carbon fiber reinforced polymer (CFRP) composites using design of experiment technique. Pigment. Resin Technol. 2014, 43, 35–44. [Google Scholar] [CrossRef]
- Sahin, M.U.; Dawood, M. Experimental investigation of bond between high modulus CFRP and steel at moderately elevated temperatures. J. Compos. Constr. 2016, 20, 04016049. [Google Scholar] [CrossRef]
- Lee, M.S.; Kang, C.G. Determination of forming procedure by numerical analysis and investigation of mechanical properties of steel/CFRP hybrid composites with complicated shapes. Compos. Struct. 2017, 164, 118–129. [Google Scholar] [CrossRef]
- Szewczak, I.; Rozylo, R.; Rzeszut, K. Influence of Mechanical Properties of Steel and CFRP Tapes on the Effectiveness of Strengthening Thin-Walled Beams. Materials 2021, 14, 2388. [Google Scholar] [CrossRef] [PubMed]
- Pawlak, A.M.; Górny, T.; Dopierała, Ł.; Paczos, P. The Use of CFRP for Structural Reinforcement—Literature Review. Metals 2022, 12, 1470. [Google Scholar] [CrossRef]
- Salama, T.; Abd-El-Meguid, A.S. Strengthening Steel Bridge Girders Using CFRP; Technical Report; Department of Civil, Construction, and Environmental Engineering, The University of Alabama at Birmingham: Birmingham, AL, USA, 2010. [Google Scholar]
- Lenwari, A.; Thepchatri, T.; Albrecht, P. Debonding Strength of Steel Beams Strengthened with CFRP Plates. J. Compos. Constr. 2006, 10, 69–78. [Google Scholar] [CrossRef]
- Nozaka, K.; Shield, C.K.; Hajjar, J.F. Effective Bond Length of Carbon-Fiber-Reinforced Polymer Strips Bonded to Fatigued Steel Bridge I-Girders. J. Bridge Eng. 2005, 10, 195–205. [Google Scholar] [CrossRef]
- Stratford, T.; Cadei, J. Elastic analysis of adhesion stresses for the design of a strengthening plate bonded to a girder. Constr. Buil. Mater. 2006, 20, 34–45. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Dawood, M. Reliability analysis of debonding in steel girders strengthened with externally bonded CFRP composites. J. Compos. Constr. 2019, 23, 65–70. [Google Scholar] [CrossRef]
- Schnerch, D.; Dawood, M.; Rizkalla, S.; Summer, E. Propose design guidelines for strengthening steel bridges with FRP materials. Constr. Buil. Mater. 2007, 21, 1001–1010. [Google Scholar] [CrossRef]
- Nowak, A.S.; Collins, K.R. Reliability of Structures, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013; ISBN -13-978-0415675758. [Google Scholar]
- Zhao, X. FRP-Strengthened Metallic Structures; CRC Press: Boca Raton, FL, USA, 2014; ISBN -9781138074330. [Google Scholar]
- Liu, M.; Dawood, M. Reliability analysis of adhesively bonded CFRP-to-steel double lap shear joint with thin outer adherends. Constr. Build. Mater. 2017, 141, 52–63. [Google Scholar] [CrossRef] [Green Version]
- Nowak, A.S. System reliability models for bridge structures. Bull. Pol. Acad. Sci. Tech. Sci. 2004, 52, 321–328. [Google Scholar]
- Stanojev, M.; Stojić, D. Reliability analysis of structures. Archi. Civil Eng. 2014, 12, 265–272. [Google Scholar] [CrossRef]
- Al-Shawaf, A.; Al-Mahaidi, R.; Zhao, X.L. Effect of elevated temperature on bond behaviour of high-modulus CFRP/steel doublestrap joints. Aust. J. Struct. Eng. 2009, 10, 63–74. [Google Scholar] [CrossRef]
- Qureshi, H.J.; Saleem, M.U.; Khurram, N.; Ahmad, J.; Amin, M.N.; Khan, K.; Aslam, F.; Al Fuhaid, A.F.; Arifuzzaman, M. Investigation of CFRP Reinforcement Ratio on the Flexural Capacity and Failure Mode of Plain Concrete Prisms. Materials 2022, 15, 7248. [Google Scholar] [CrossRef]
- Bigaud, D.; Ali, O. Time-variant flexural reliability of RC beams with externally bonded CFRP under combined fatigue-corrosion actions. Reliab. Eng. Syst. Saf. 2014, 131, 257–270. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Xu, H.; Qu, F.; Wang, X.; Shi, Y. A reliability analysis framework with Monte Carlo simulation for weld structure of crane’s beam. AIP Conf. Proc. 2018, 1955, 030024. [Google Scholar]
- Bresson, G.; Jumel, J.; Shanahan, M.E.R.; Serin, P. Statistical aspects of the mechanical behavior of a paste adhesive. Inter J. Adhes. Adhes. 2013, 40, 70–79. [Google Scholar] [CrossRef]
- Wu, C.; Zhao, X.; Hui Duan, W.; Al-Mahaidi, R. Bond characteristics between ultra-high modulus CFRP laminates and steel. Thin-Walled Struct. 2012, 51, 147–157. [Google Scholar] [CrossRef]
- Ferrier, E.; Bigaud, D.; Hamelin, P.; Bizindavyi, L.; Neale, K.W. Fatigue Reliability of External Bonded CFRP Used for Concrete Structure. Mater. Struct. 2005, 38, 39–46. [Google Scholar] [CrossRef]


| Specimen ID | Steel Girder | CFRP Plate | Adhesive | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Girder Length (m) | Girder Height (mm) | Thickness of Web (mm) | Width of Flange (mm) | Thickness of Flange (mm) | Plate Length (m) | Plate Width (mm) | Plate Thickness (mm) | Adhesive Width (mm) | Adhesive Thickness (mm) | |
| A-1 | 9 | 560 | 15 | 320 | 18 | 8 | 320 | 3.0 | 320 | 2.0 |
| B-1 | 18 | 1000 | 20 | 400 | 22 | 17 | 400 | 4.3 | 370 | 2.0 |
| C-1 | 27 | 1500 | 22 | 410 | 24 | 26 | 410 | 5.5 | 340 | 2.0 |
| D-1 | 36 | 1800 | 24 | 500 | 28 | 35 | 500 | 6.2 | 440 | 2.0 |
| Specimen ID | Steel Girder | CFRP Plate | Adhesive | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Girder Length (m) | Girder Height (mm) | Thickness of Web (mm) | Width of Flange (mm) | Thickness of Flange (mm) | Plate Length (m) | Plate Width (mm) | Plate Thickness (mm) | Adhesive Width (mm) | Adhesive Thickness (mm) | |
| A-2 | 9 | 560 | 15 | 320 | 18 | 8 | 320 | 2.7 | 320 | 1.5 |
| B-2 | 18 | 1000 | 20 | 400 | 22 | 17 | 400 | 3.8 | 370 | 1.5 |
| C-2 | 27 | 1500 | 22 | 410 | 24 | 26 | 410 | 4.9 | 340 | 1.5 |
| D-2 | 36 | 1800 | 24 | 500 | 28 | 35 | 500 | 5.5 | 440 | 1.5 |
| CFRP | Tensile Strength (MPa) | E-Modulus (GPa) |
|---|---|---|
| Sika® carbodur® S512 | 2800 a | 165 a |
| Sika® carbodur® H514 | 1500 a | 300 a |
| Adhesive | σa (MPa) | E-Modulus (GPa) |
|---|---|---|
| Sikadur®-30 | 56.5 | 11.2 |
| Parameters | Bias | COV | Distribution |
|---|---|---|---|
| Maximum stress of adhesive layer (σr) | 1.30 | 0.333 | Lognormal |
| Resistance modeling uncertainty (ξr) | 1.20 | 0.221 | Gamma |
| Modulus of the adhesive layer (Ea) | 1.00 | 0.084 | Lognormal |
| Adhesive layer thickness (ta) | 0.93 | 0.098 | Lognormal |
| Bending moment due to self-weight (DC) | 1.03 | 0.080 | Normal |
| Bending moment due to wearing surface load (DW) | 1.00 | 0.250 | Normal |
| Bending moment due to live load (LL) | Varies b | Varies b | Normal |
| Flange width of the steel girder (bf) | 1.00 | 1.5 × 10−3 | Normal |
| Steel girder’s web height (D) | 1.00 | 1.5 × 10−3 | Normal |
| Flange thickness of steel girder (tf) | 1.00 | 1.5 × 10−3 | Normal |
| Web thickness of steel girder (tw) | 1.00 | 1.5 × 10−3 | Normal |
| CFRP tensile strength (fp) | 1.00 | 0.110 | Normal |
| Steel yield strength (fy) | 1.12 | 0.100 | Lognormal |
| Girder Length (m) | Bias | COV | Distribution |
|---|---|---|---|
| 9 | 1.43 | 0.12 | Normal |
| 18 | 1.43 | 0.12 | Normal |
| 27 | 1.42 | 0.12 | Normal |
| 36 | 1.41 | 0.12 | Normal |
| Specimen ID | ꞵ0 | ꞵd | ꞵst |
|---|---|---|---|
| A-1 | 3.40 | 1.67 | 5.63 |
| A-2 | 3.40 | 1.68 | 4.40 |
| B-1 | 3.47 | 2.00 | 5.79 |
| B-2 | 3.47 | 1.93 | 4.50 |
| C-1 | 3.46 | 2.17 | 5.86 |
| C-2 | 3.46 | 2.14 | 4.59 |
| D-1 | 3.50 | 2.48 | 5.93 |
| D-2 | 3.50 | 2.40 | 4.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vo, D.H.; Do, V.H.; Tran, Q.V.; Nguyen, M.H.; Hoang, T.L. Reliability Analysis of Steel Bridge Girders Strengthened with CFRP Considering the Debonding of Adhesive Layer. Designs 2022, 6, 126. https://doi.org/10.3390/designs6060126
Vo DH, Do VH, Tran QV, Nguyen MH, Hoang TL. Reliability Analysis of Steel Bridge Girders Strengthened with CFRP Considering the Debonding of Adhesive Layer. Designs. 2022; 6(6):126. https://doi.org/10.3390/designs6060126
Chicago/Turabian StyleVo, Duy Hung, Viet Hai Do, Quang Vy Tran, Minh Hai Nguyen, and Trong Lam Hoang. 2022. "Reliability Analysis of Steel Bridge Girders Strengthened with CFRP Considering the Debonding of Adhesive Layer" Designs 6, no. 6: 126. https://doi.org/10.3390/designs6060126
APA StyleVo, D. H., Do, V. H., Tran, Q. V., Nguyen, M. H., & Hoang, T. L. (2022). Reliability Analysis of Steel Bridge Girders Strengthened with CFRP Considering the Debonding of Adhesive Layer. Designs, 6(6), 126. https://doi.org/10.3390/designs6060126






