Next Article in Journal
Automated Solar PV Simulation System Supported by DC–DC Power Converters
Previous Article in Journal
Open-Source Vertical Swinging Wood-Based Solar Photovoltaic Racking Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Designs
Volume 7
Issue 2
10.3390/designs7020035
designs-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Design of Electrical Characterization Method for Electroporation-Treated Biological Tissues

by
Patrizia Lamberti
1,
Elisabetta Sieni
2,* and
Raji Sundararajan
3
1
Department of Information and Electrical Engineering and Applied Mathematics, University of Salerno, 84084 Fisciano, Italy
2
Department of Theoretical and Applied Sciences, University of Insubria, 21100 Varese, Italy
3
School of Engineering Technology, Purdue University, Knoy Hall of Technology, West Lafayette, IN 47907, USA
*
Author to whom correspondence should be addressed.
Designs 2023, 7(2), 35; https://doi.org/10.3390/designs7020035
Submission received: 18 January 2023 / Revised: 20 February 2023 / Accepted: 23 February 2023 / Published: 1 March 2023
(This article belongs to the Section Bioengineering Design)
Browse Figures
Versions Notes

Abstract

:
The design of a method to evaluate the efficacy of electroporation-treated (with several pulses) tissues is proposed. This method is based on the application of both the standard and a non-standard electrical characterization of biological tissues, on a platform, containing the samples under test, adopted to have minimal invasive contact measurements. Standard direct current electrical characterization was performed for comparison. For the electroporated tissues (using eight pulses), the electrical behavior of the tissue in working condition, governed by high intensity and short duration square wave stimuli, typically used in electrochemotherapy treatments, is utilized. Both electroporation stimuli application and direct current testing were performed using the same electrodes in parallel plate configuration on the parallelepiped shaped samples. The electrodes were not removed during the designed procedure to reduce the interaction with the tissue under test and the effect of different contact resistances. A finite element analysis-based numerical evaluation of the test cell used in the procedure was also performed, both with a constant and an electric field-dependent electrical conductivity, showing its robustness. The method is tested on potato samples, as an example of a biomaterial, whose electrical conductivity is electric field-dependent. The samples were subjected to a high intensity square wave pulse voltage of 100μs long, in order to evaluate the effect of multiple pulses, as a single protocol parameter. Results indicate the dependency of the electrical conductivity on the electric field strength applied using multiple pulses, and the method is easily scalable and usable as a starting point for evaluating the effect of other protocol parameters.

1. Introduction

Electroporation (EP) is used in practice to permeabilize cell membranes for clinical treatments used for enhanced cancer drug delivery or for the processing of materials in industrial applications, e.g., food treatment , sterilization, etc. [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. It uses a pulsed (8 pulses) electric field, which modifies the arrangement of the bi-lipid layers of the cell membranes to induce the generation of reversible aqueous pores or to induce irreversible damage of the cell membrane, depending on the applied voltage amplitude, number of pulses, pulse length, and frequency [7,15,16,17]. In clinical practice, electrochemotherapy (ECT) uses local electroporation in conjunction with a chemo drug infusion to enhance the drug uptake [18,19], whereas, Irreversible Electroporation (IRE) uses a large number of high voltage pulses [7] to damage irreversibly the cancer cells. ECT is widespread in Europe and in South America, while, IRE is diffused in the USA [20,21,22,23,24]. In ECT, the permeabilization of the cell membrane improves the permeation inside the cells of non-permeant or poorly-permeant drugs. In this condition, the drug is able to damage the cancer cells, while in IRE, the electric field acts directly on the cell viability, destroying the cell membrane [25].
It is well known that the local inhomogeneity of the electrical properties of the tissues influence the electric field distribution. Since the EP effect is strictly dependent on the applied electric field [26,27,28,29], it is of interest to know the electrical properties of various tissues treated. Moreover, in EP, the applied electric field modifies the tissue and its electrical properties, starting from the first pulse. Thus, for every successive pulse (when eight pulses are applied), the tissue properties are quite different at the end than at the beginning [30,31,32,33,34].
In general, when a high strength electric field is applied to a biological tissue, it modifies locally the electrical properties of the treated volume [14,27,31,35,36,37]. Moreover, the biological tissue is a highly complex material. At the microscopic level, it is highly heterogeneous, since the cell volume is divided into various compartments inside and outside the cell membrane with different conductivities depending on the ions dissolved in the medium [38].
Typically, the electrical properties of the tissues were evaluated using standard conditions (SC). For instance, Gabriel et al. performed the evaluation of animal tissues from 10 Hz to GHz using sinusoidal waveform [20]. The values obtained in this way did not include Direct Current (DC) conditions. DC values were extrapolated from the lowest frequency values. In solid materials, DC conductivity is evaluated using a constant voltage and measuring the resulting electrical current in a sample with known geometry. In general, a thin parallelepiped or disk-shaped geometry is used if a 2-point probe method is considered. In this way, the sample resistance is determined by the ratio of voltage to current value, and from the geometry, the conductivity is calculated. This procedure, defined as SC, is suitable for materials for which the electrical properties are invariant with respect to the electric field applied for the testing.
The electrical properties of biological tissues change depending on the electric field intensity [39,40,41]. Therefore, under ECT conditions given by the electrochemotherapy protocol, for which the applied electric field changes in terms of pulse shape, pulse amplitude, number of pulses, and time duration, the tissue properties are different with respect to the ones measured in SC [42]. In general, the electrical conductivity in SC is measured applying a field of few V/cm (e.g., 1–10 V/cm) that does not damage the specimen. However, at working conditions in EP, a higher field, up to 1000 V/cm could be applied in a non-continuous way. If the same voltage is applied to study SC characterization, the specimen could burn out.
In this research, the possibility to evaluate the EP efficacy by exploiting coherently the effect under a Non-Standard test Condition (NSC) is explored. In particular, a method is designed to assess the electrical behavior of the biological material in NSC is established. The derived electrical characteristics are compared with the results obtained by measurements. The proposed method could be used in various conditions for which the application for long time of the working conditions could modify irreversibly the specimen.
The validity of the adopted method is confirmed by using a Finite Element Model (FEM), in which field-dependent electrical properties, derived from NSC condition, are considered.

2. Materials and Methods

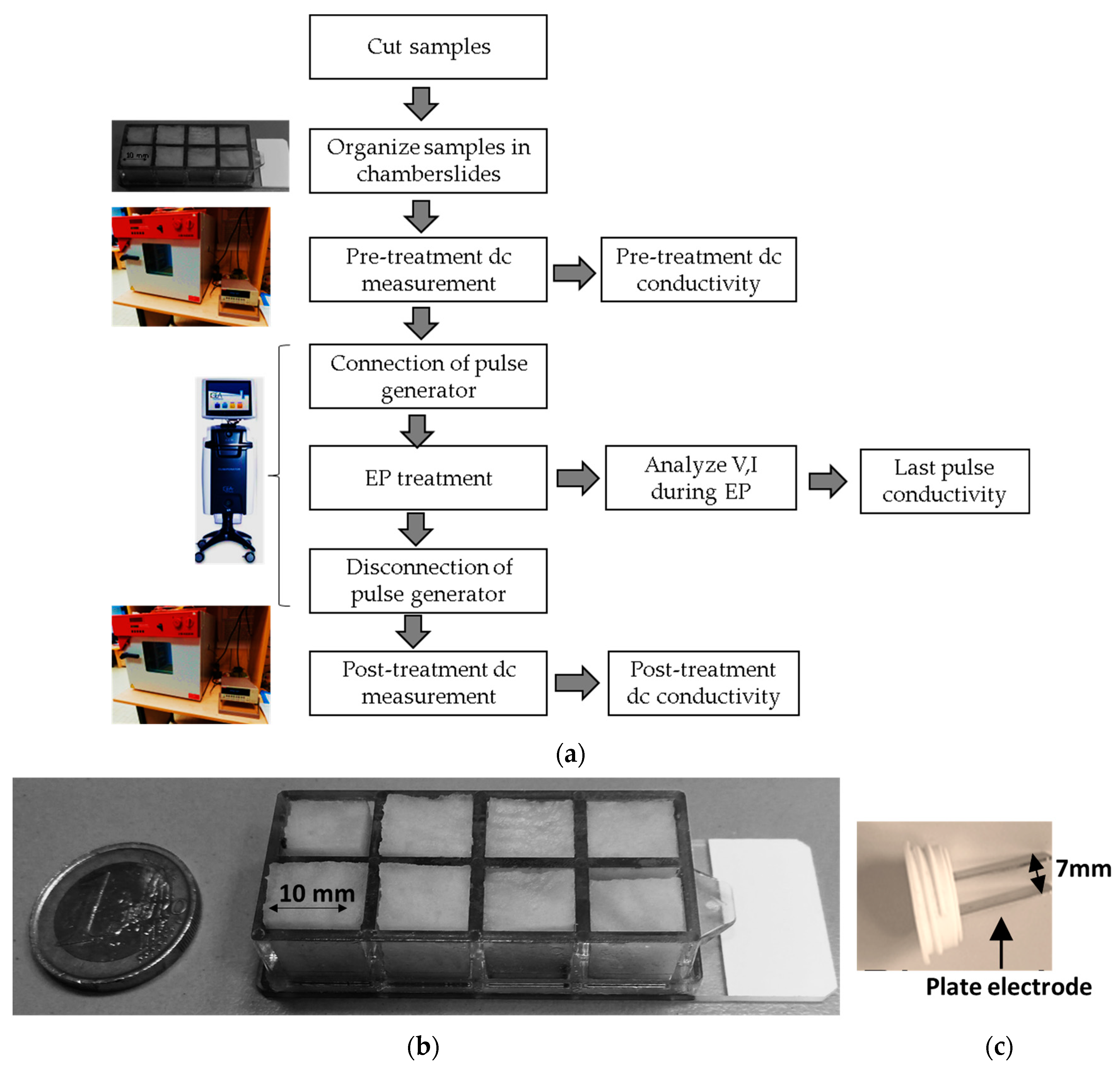
2.1. Procedure for NSC Testing

The proposed method is composed of the following five steps (Figure 1a):
Step 1: Define the NSC protocol to be tested for various parameters
Step 2: Cut samples and organize the chamber slides
Step 3: Perform pre-treatment SC DC measurement of the electrical properties
Step 4: Apply the EP protocol—under NSC (e.g., offline extraction of last-pulses conductivity)
Step 5: Perform post-treatment SC DC measurement of the electrical properties.
The NSC for EP (Step 1) is related to the application of a square voltage pulse, with an amplitude in the order of up to hundreds of V/cm on a specimen, with a thickness of 1 cm (applied electric field from 100 to 1000 V/cm), using a commercial chamber slide, as the sample holder.
The same sample holder was used both for tissue characterization and for treatment protocol application, in order to reduce measurement artifact on the biological tissue.

2.2. Sample Preparation

The potato tubers were purchased in different seasons of one solar year in the local markets in Padova (North-Eastern Italy) and Salerno (South-West Italy). The main experiments were conducted in the months of May and June.
Potato tubers were cut in parallelepiped shape, with size 11 × 9 × 11 mm3 (Step 2). Following, the excess liquid due to the cut had been removed with an absorbent paper and immediately after, the measurements were made—both at the SC (Steps 3 and 5) and at the NSC (Step 4).
A set-up with 8 wells, with a rectangular shape (section 11 × 9 mm and a thickness of 11 mm) as described in [41] was used as the treatment chamber. Figure 1b shows the experimental setup, and Figure 1c shows the parallel plate electrode used for the NSC conductivity evaluation.

2.3. Experimental Measurement of the Conductivity

2.3.1. Under Standard Condition (SC)

The standard DC conductivity evaluation of the potato samples (Steps 3 and 5) was performed using a Keithley 6514 (Tektronix, Inc., Beaverton, OR, USA) Electrometer. If IDC is the current and Vmeas is the voltage between the external electrodes, the resistance of the sample under test is calculated as:
R t e s t = V m e a s I D C
with, test ∈ {pre, post}. To represent the static condition, the instrument was used in the “slow acquisition” mode and each measurement was performed after 5 min of testing. For this, two metallic parallel plane electrodes are applied to the lateral surface of the samples in the chamber slide and the external electrodes of the instrument are connected to that in order to have the same configuration of the pulse generator EPS-01 (manufactured by Igea S.p.A., Carpi, Italy, the device used for ECT in clinics) testing (Figure 2).
Using the parallelepipedal shape of the samples, the SC conductivity is derived from the measured resistance as:
σ SC , test   = 1 R t e s t h S
where, h is the distance between the two metallic electrodes and S is the sample surface area that is interfaced with the electrodes.
The DC conductivity of the untreated and the post-treated samples were collected and used to evaluate the EP efficacy of the protocol adopted between these two measurements. The variation of the conductivity can be used as an indication of the EP protocol efficacy.

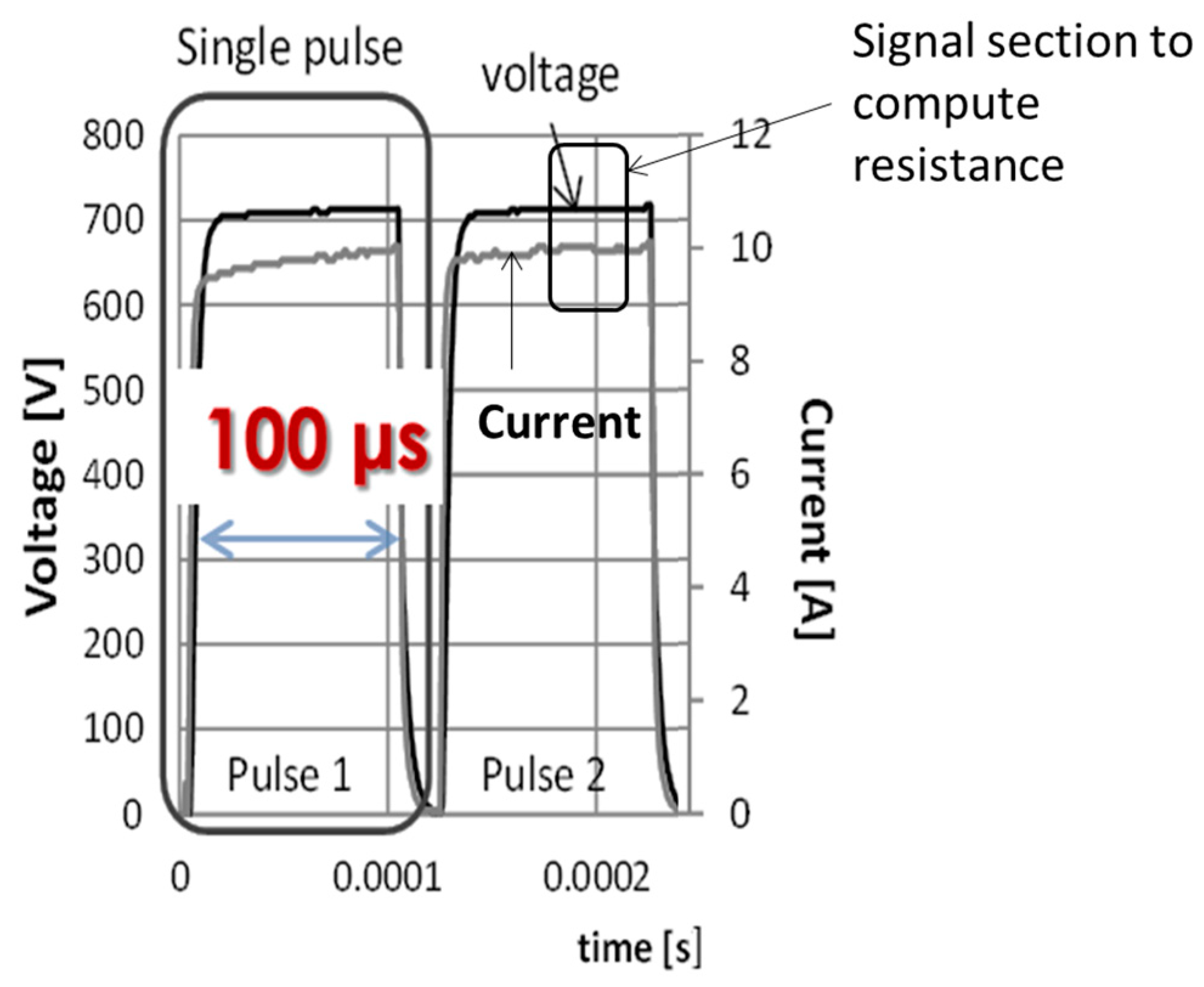
2.3.2. Under Non-Standard Condition (NSC)—Using the Last-Pulse Conductivity of Potato Tuber

The last-pulse conductivity of the potato tuber was evaluated experimentally from the voltage and current values for the last pulse, using Ohm’s law as in [41], and the sample geometry. First, RNSC is derived as:
R N S C = V L P P I L P P
where, VLPP and ILPP are the last pulse plateau values of the voltage and current, at the generator electrodes (Figure 3).
Then, the conductivity, σNSC(xNSC) was obtained by varying the electric field intensity of the standard ECT protocol [43,44], as:
σ N S C ( x N S C ) = 1 R N S C h S
where, S is the cross-sectional area, and h the thickness of the sample that corresponds to the gap of the plate electrodes, and xNSC is the single protocol parameter considered as variable. Equation (4) gives the local conductivity of the sample at the last pulse applied and represents a point value useful to investigate the electroporation.
The standard ECT protocol considers a sequence of 8 voltage pulses at 5000 Hz. Figure 3 shows a sample of the voltage pulses applied and the resultant current pulses recoded.
The voltage pulses show a square shape, and the time duration of the positive voltage is 100 μs. The pulse period is 200 μs and the 0 V part is not stored in the recording system. The voltage was applied using a stainless-steel plate electrode (10 mm × 30 mm = S, that fits the 11 mm of the well depth) with a gap of h = 7 mm. The voltage amplitude was varied from 100 V (electric field E = 143 V/cm) to 1000 V (E = 1430 V/cm). The conductivity was evaluated using Equation (4), with the resistance computed from the recorded voltage and current. Assuming that xNSC = E, the procedure (Step 4) furnishes a point measurement of σNSC(E), that is the offline extraction of last-pulse conductivity evaluation due to this particular NSC.

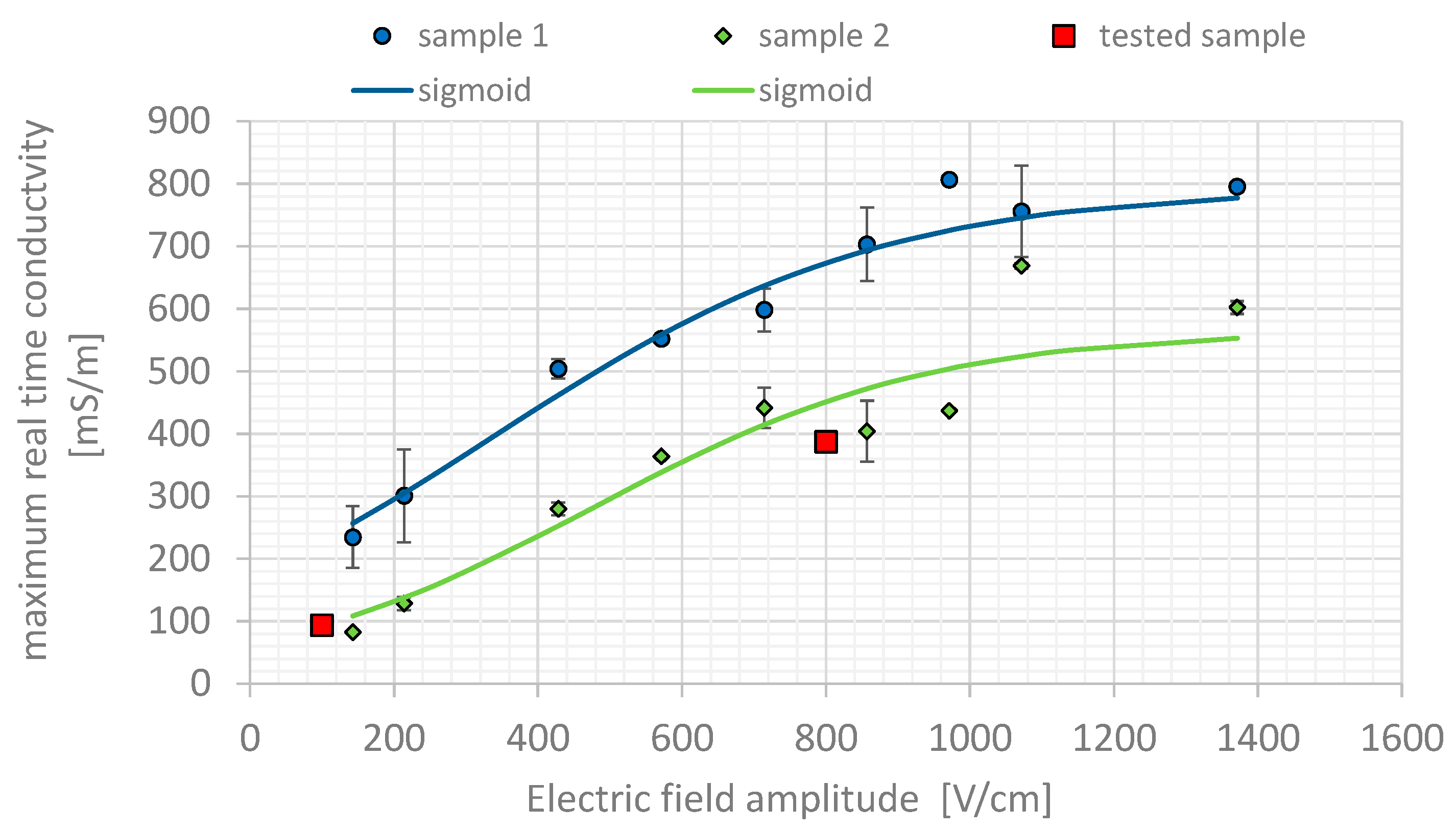
2.3.3. Evaluation of Electrical Characteristics of Potato Tuber in NSC as a Function of Electric Field Strength

The electrical characteristics of the potato tuber in NSC is estimated by computing σNSC(E) as in [40,41] and as proposed in [27,39,40,41,45]:
σ N S C ( E ) = σ 0 + σ 1 − σ 0 2 ( 1 + tan h ( k v ( E − E t h ) ) )
where, σ0 and σ1 (S/m) are the conductivities of the tissue at 0 V/cm (untreated condition), and at the maximum amplitude applied pulsed electric field, for which the conductivity is maximum; kv (cm/V) is a constant and Eth (V/cm) is the electric field at the half of the σ0 − σ1 gap. This is not a conventional DC conductivity, measured for an applied continuous field of constant E amplitude, but the conductivity measured “during” the application of the pulsed electric field, using the maximum value of the voltage (Figure 3) where, the maximum value of the waveform in Figure 3 is fixed to the voltage that generates the electric field strength E. σNSC(E) represents a parameter in NSC, useful to evaluate the electrical behavior of the material in the presence of a voltage, for which a standard DC characterization cannot be performed without irreversibly damaging the specimen.
The measured conductivity, σNSC(E), evaluated at different electric field intensities were used to fit the model given by Equation (5) to find the unknown values of the parameters σ0, σ1, kv and Eth, by means of non-linear least mean square method, as described in [41].

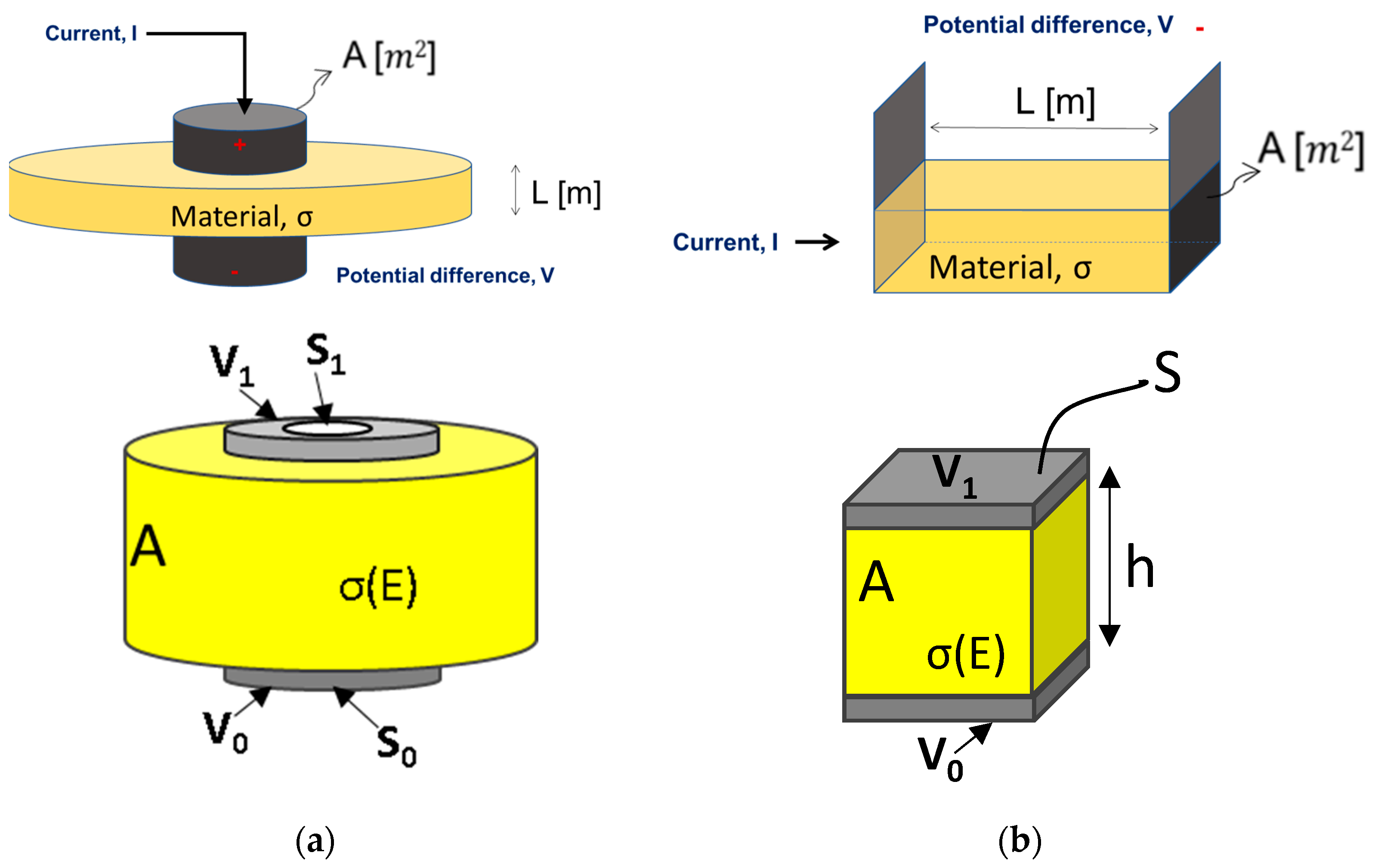
2.4. Finite Element Simulations—Model Setup

2.4.1. Geometry of the Testing Chamber

In order to evaluate the validity of the adopted parallelepiped treatment chamber, FEM models of the two experimental setups were developed (Figure 4a,b). The simulated setup in Figure 4a uses a sample of circular shape, and it corresponds to the standard configuration in dielectric material DC characterization (ASTM-D257 [46]), whereas the simulated setup in Figure 4b uses the treatment chamber considered in this research.

2.4.2. Finite Element Simulations

The Finite Element Analysis (FEA) was performed to compute the electric field applied to the considered volume, labeled A (Figure 4), using stainless-steel plate electrodes, applied to the faced surfaces of the volume under examination, labeled with V0 and V1, and supplied with a constant voltage. Volume A is surrounded by air. The results obtained with the disk-shape model (Figure 4a) were compared with the ones obtained using the cube-shape model (Figure 4b).
For the disk-shape model (Figure 4a), the supply electrodes show a diameter smaller than the one of the volume A, made on a material with the electrical properties of potato. For this model, two geometric conditions for the energizing electrodes, V1-V0 were considered. Moreover, the figures show also S0, S1 and S surfaces to be used in the post-processing evaluation of the electrical conductivity using Equation (4). For the circular-shape model, two conditions were considered: S1-S0 with the same or with smaller diameter electrodes, where V1-V0 are applied.
The electric field intensity, from which the current density and electrical properties were derived, had been computed by means of the Finite Element commercial software (FLUX3D [47] released by Altair Engineering, Inc., Troy, MI, USA).
Using FEA, a conduction problem in DC, i.e., the Laplace equation in the electric scalar potential, V, was solved using the static condition:
∇ ⋅ σ ∇ V = 0
Here, the electrical conductivity σ as a constant or as parameter dependent (σ(E)) was used. A constant potential, V1, on one face and a zero-potential, V0, on the opposite face have been applied (Figure 4 [27,48]) as Dirichlet boundary condition [49,50]. Moreover, on the external boundary, a null tangent condition of electric field lines has been imposed as in [51,52]:
∂ V ∂ n = 0
According to similar applications [27,53,54,55,56] for the evaluation of the electric field in electroporation conditions, the model has been tested for four different fixed conductivity values σ ∈ {2.3, 23, 230, 950} (mS/m), and two V1 values of 100 V (i.e., non electroporation condition) and 700 V (i.e., electroporation condition, considering a plate gap of 7 mm long), corresponding to 143 V/cm or 1000 V/cm electric field intensity, respectively. Moreover, in order to consider the effect of protocol dependent parameter, the previous models were compared in the case of a sample under test, where, conductivity is a function of the local electric field, σ(E), as proposed in [27,39,40,41,45] and given in Equation (5).
For the model in Figure 4, the electrical current is measured “numerically”, utilizing the same electrode used to apply the voltage.
The mesh of the cube-shape model has 1.65 × 106 nodes and 1.2 × 106 cubic elements for a size of 0.25 mm, whereas the disk-shape model has 3.92 × 106 nodes and 2.94 × 106 volume elements for a size of 0.25 × 0.25 mm on the volume in which the current density is evaluated. Both the models have the second-order mesh.

3. Results and Discussion

In order to demonstrate the working of the above procedure, an ECT protocol with a maximum amplitude of 8 pulses of electric field of 100 μs long at 5 kHz, was used as a single parameter effect evaluation. A similar procedure could be used for evaluating other similar parameter protocols.

3.1. Measurements

Evaluation of Conductivity under Pre-, Post-, and during-Treatments.
Table 1 shows the conductivity values of the potato samples measured by means of the cubic applicator in two different conditions: SC and NSC. Here, Group A represents the condition before applying pulses and Group B indicates after the treatment.
SC refers to the standard conductivity measurement (constant current applied for 5 min) before and after the application of eight 100 μs long voltage pulses that generated a pulsed electric field with an intensity of 111 or 889 V/cm (applied voltage 100 V or 800 V at the cube extremities at a distance of 0.9 cm).
NSC refers to the evaluation of the conductivity, such as described in [41], corresponding to the proposed procedure applied on the electrical measurements obtained during the application of the pulsed electric field, i.e., the last-pulse conductivity.
It is to be noted that the measurements of groups A and B are made on the same samples: the first measurement before the application of the electric field (SC-0V), the second measurement after the application of the electric field (SC-100V or SC-800V) and finally, the last value is referred to the online evaluation of the conductivity from the values recorded by the pulse generator (NSC-100V or NSC-800V).
Starting from samples that exhibited about 10 mS/m of conductivity in the pre-treatment condition, the application of a PEF with 100 V amplitude, corresponding to a non-electroporating condition of 111 V/cm (experimental validation in [41]), leads to 13 mS/m. This is not a significant increment as is evidenced by the results on Group A. However, at a higher amplitude of 800 V of applied voltage, corresponding to an electroporating condition of 889 V/cm (experimental validation in [41]), the conductivity increased to almost double the original value in the Group B samples, reaching 20 mS/m, which means that the conductivity of an electroporated tissue measured after the treatment differs from the not-electroporated one of about 54% (i.e., 13 mS/m vs. 20 mS/m).
The NSC estimation of the conductivity is always higher than that of the SC cases; it is less than 10 times the SC value, and up to 20 times in the electroporation condition. These NSC values can be used to describe the local enhancement of the conductivity due to the high-amplitude stress applied as described in the following paragraph. It is considered as possible information to be used for indicating electroporation. The NSC value is about four times that of a non-electroporation condition, showing a very significant variation of 278% between the two groups (i.e., 107 mS/m vs. 404 mS/m).

3.2. Estimated Conductivity for Potato Tissue

Figure 5 shows the conductivity results obtained under NSC, applied on two different types of potatoe tubers to form the codomain or band of possible conductivities values. The data were obtained by applying nine different electric field intensities, each of 8 pulses, using ECT protocol to the tissue samples of same size and shape.
With the increase in electric field intensity, the tissue conductivity also increased as reported in similar experiments. In practice, with the increase in the applied electric field, the tissue experiences electropermeabilization of the cell membranes, and, hence, modifies electrical properties of the tissue [1,3,26,57,58,59,60].
The conductivities, σm1 and σm2, evaluated by Equation (4) and the corresponding resistivities, ρm = 1/σm, are reported in Table 2.
Table 2 also shows the values of the parameters of Equation (5) obtained by fitting the means of least square the reported data as a function of electric field intensity. These interpolating curves are reported as continuous lines in Figure 5, where the red square marks the point measurements corresponding to the experimental data. These measurements are in accordance with a previous evaluation of potatoes conductivities in NSC condition [41].

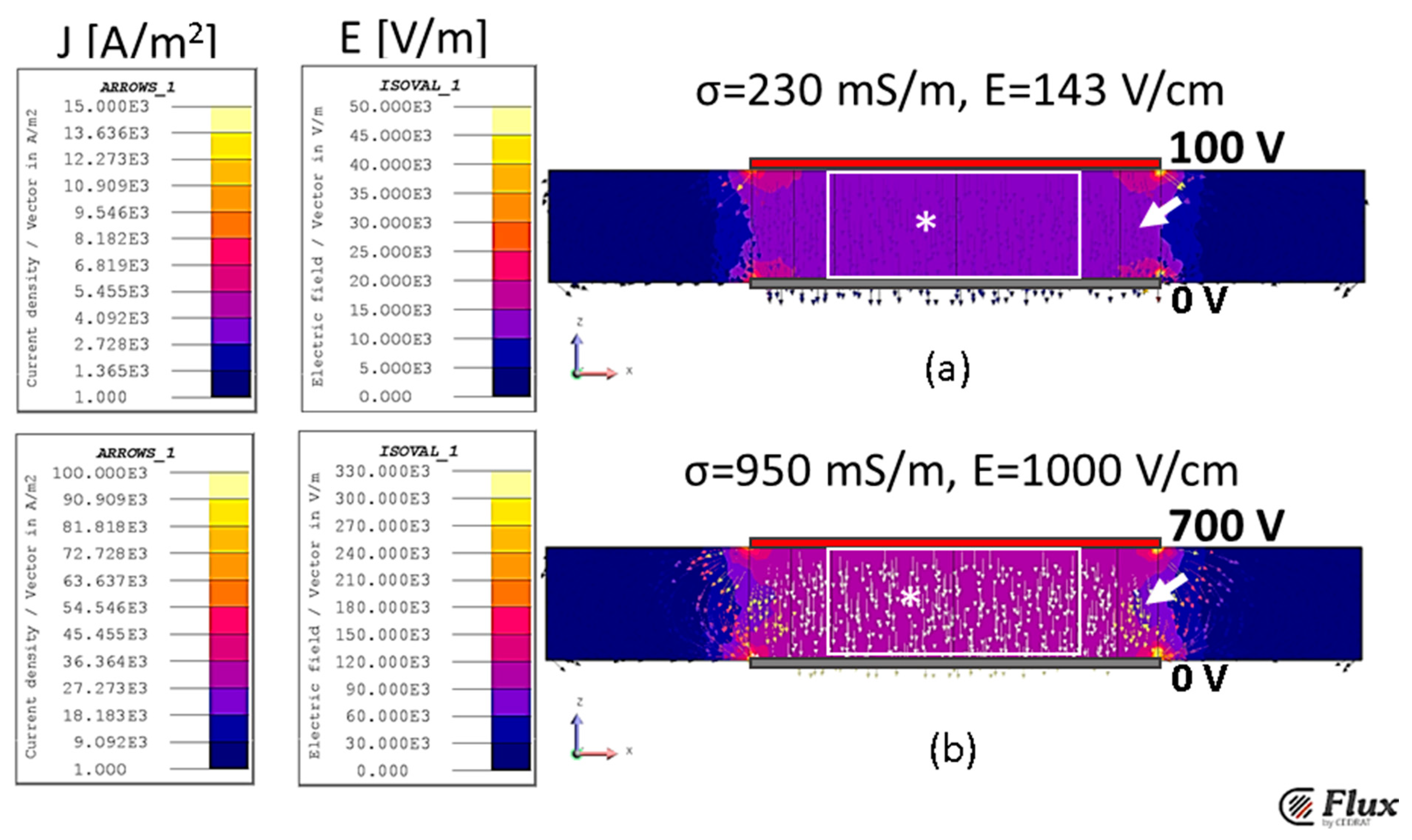
3.3. FEM Validation of the Estimated Conductivity for Potato Tissue

To evaluate the efficacy of the measurement of the treated samples, the conductivities as a function of the electric field strength are used in the FEA. The FEA simulates the electric field in the volume of the sample with disk or cube shape (Figure 4), by considering a field-dependent or a fixed conductivity of the material. Figure 6 illustrates the colored map of the electric field strength in the disk-shape model, with a field dependent conductivity, and Figure 7 shows the results with fixed conductivities (i.e., 230 mS/m and 950 mS/m). Comparing Figure 6 and Figure 7, it appears that the electric field distribution at the boundary of the electrode, as shown by white arrows, is different and in the latter case, it is more homogeneous. The non-uniformity of the electric field in the disk-shape treatment cell reflects the variations of the conductivities in the medium.
In each case, the electric field is uniform in the volume of the rectangles identified with the white star. This volume is internal with respect to the one delimited by the electrodes (red and gray parallel lines). Outside the star volume, the electric field intensity distribution, as evidenced by the white arrow, is not uniform. This fact is less evident in the case for which the applied electric field intensity E is 143 V/cm (Figure 7a). With the cube-shape model, the electric field distribution is more uniform along all the samples and the influence of the field-dependent conductivities is negligible.
Figure 8 shows the current densities (arrows) and electric field distribution (color map) obtained only in the case of fixed conductivities.
If the computed data are used to derive the conductivity, such as in the experimental case (i.e., applied voltage divided by the current density integral on a given surface representing the electrodes using the Equation (4)), different results are obtained for the different adopted models.
Table 3 shows the estimated conductivities by FEA, obtained using Equation (5), and applying 100 or 700 V for the disk and cube-shape models. In the case of disk-shape, two different current measurement surfaces were considered: using the same area of 4.9 × 10−4 m2 (Disk-case A) and a reduced area of 1.8 × 10−4 m2 for Disk-case B, respectively. In the same table, for each case, the fixed conductivity value in the hypothesis of uniform electric field is also reported.
Varying the voltage, the electrical parameter of the material evaluated using Equation (5) is in accordance with the expected conductivity at the corresponding electric field for the Cube and for the Disk-case B. Here, a smaller surface is used for the electric current evaluation, covering a more uniform area for the electric field distribution. On the other hand, the Disk-case A leads to an overestimation of the conductivity up to 15%.
These results indicate that for this particular type of material, for which, the electrical properties depend on the local value of the applied field, the cubic geometry is a more reliable measurement model. In fact, the cubic geometry, for which the boundary conditions impose a discontinuity on the current density, due to a non-conductive media in the surrounding of the tested volume, allows to measure the electrical current inside the analyzed volume, only in the region in which the electric field is uniform, leading to a very accurate conductivity estimation, as confirmed by the last row of Table 3 data.
Using the constant conductivity model, the data in Table 4 shows the results for the disk-shape samples with two different surface areas, confirming the dependence of the accuracy with the surface selection itself.
Table 4 indicates that the estimated conductivities in the disk-shape model are different for Disk-case A and Disk-case B. For the Disk-case A model, the estimated conductivity is less accurate than that of using Disk-case B. In fact, the numerically obtained conductivity in the larger surface electrodes case (Disk-case A) overestimates greater than 21% the 230 mS/m and the 950 mS/m applied values, whereas in the Disk-case B, the overestimation is less than 1%. Moreover, by comparing Table 3 and Table 4, it is possible to observe that the fixed-conductivity model performs worse than the field-dependent conductivity. In particular for the Disk-case A in the field-dependent model (Table 3), the overestimations of the numerical-evaluated conductivities are 15.1% and 7.7%, and the error is also three times higher in the fixed conductivity model (21.5% in Table 4).
The analysis of these data confirms once more that the adoption of a computational area in which the maximum electric field uniformity distribution is mandatory.
Conversely, the cube-shape samples are not affected by this phenomenon, as the simulation results reported in Figure 8. In fact, the FEA results reported in Figure 8 in terms of the colored map of the electric field strength and arrow-plot of the current density show the uniformity of the electric field in all the considered volume. The uniformity is guaranteed for both the lower (230 mS/m) and higher (950 mS/m) conductivity considered as fixed values. If the computed data are used to numerically derive the conductivity in the material, such as in the SC measurement configuration, the cube-shape sample seems robust also if the fix-conductivity model is used.
Table 5 shows the evaluated conductivities for the cube-shape model, obtained from the applied voltage at electrodes and the current flowing through the electrized face evaluated as the integral on the electrode surface of the normal component of the computed current density. The last row shows the very low percentage error evaluated with respect to the true fixed conductivity value reported in the third row.
The data in Table 5 show that in the cube-shape model the percentage error in the estimated conductivity is close to 10−5%, compatible with the numerical approximation error.

4. Conclusions

In this research, we designed a measurement protocol to investigate the effect of electroporation protocol variations on the conductivity of the biological samples. The measurement protocol used include directly measuring on the chamber slide in which the samples are placed. This way, the effect related to the repeated insertion and removal of the measurement electrodes or by the change of the test chamber is minimized.
The proposed protocol was organized in 5 steps.
In step 1, the protocol to be tested and the parameters under investigation are chosen.
In step 2, the samples to be tested were prepared and put inside the treatment chamber, which was also used as measurement chamber.
In step 3, the measurement of the pre-treatment direct current conductivity was conducted with the standard procedure on a cube-shape sample.
In step 4, the pulsed electric field treatment was conducted using the same measuring electrodes but changing the generator. By utilizing the data collected in the generator, the last-pulse conductivity parameter was obtained offline. This parameter is a useful information of the tissue electroporation.
In step 5 (the last step), the measurement of the post-treatment direct current conductivity was conducted, using the standard procedure on the cube-shape samples, always using the same electrodes. The latter has also been used as a ‘measure’ of electroporation.
Potato tissues were used as a representative of biological tissues since its behavior to the applied electric field in terms of electrical conductivity is well-known. The electroporation effect can be evidenced by the fast darkening of the sample after electroporation with respect to untreated samples [41,57]. The samples were treated by a square wave voltage 100 μs long, with high strength (100–800 V in a 1 cm-depth sample), in order to evaluate the effect of a single protocol parameter. This way, we performed experiments, considering both the electroporation and non-electroporation conditions. The comparison between the data obtained under standard and non-standard conditions are consistent (no substantial changes are evidenced in electrical properties in standard conditions, if the sample is not-electroporated). An increase in conductivity is found in the case of exposition of the sample to electroporation.
We also used finite element analysis to validate the disk-shape and the cube-shape chambers in electrical property measurement. The finite element simulations were performed both in the case of a constant and an electric field-dependent conductivity.
Overall, the designed method could be used to study different electroporation protocols, focusing on the effect of one or more parameters. Towards that, this study is a starting point for further investigations on different biological samples.

Author Contributions

Conceptualization, P.L., E.S. and R.S.; methodology, P.L. and E.S.; validation, P.L. and E.S.; investigation, P.L. and E.S.; resources, P.L.; data curation, P.L. and E.S.; writing—original draft preparation, E.S.; writing—review and editing, P.L. and R.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data not available in public database.

Acknowledgments

Authors are grateful to Igea spa, Carpi (MO) Italy for the voltage pulse generator loan. They also thank the networking of the ISEBTT, International Society for Electroporation-Based Technology and Treatments (http://www.electroporation.net/ (accessed on 20 January 2023)), which made possible this research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Angersbach, A.; Heinz, V.; Knorr, D. Effects of Pulsed Electric Fields on Cell Membranes in Real Food Systems. Innov. Food Sci. Emerg. Technol. 2000, 1, 135–149. [Google Scholar] [CrossRef]
  2. Saulis, G. Electroporation of Cell Membranes: The Fundamental Effects of Pulsed Electric Fields in Food Processing. Food Eng. Rev. 2010, 2, 52–73. [Google Scholar] [CrossRef]
  3. Castellví, Q.; Banús, J.; Ivorra, A. 3D Assessment of Irreversible Electroporation Treatments in Vegetal Models. In 1st World Congress on Electroporation and Pulsed Electric Fields in Biology, Medicine and Food & Environmental Technologies; Jarm, T., Kramar, P., Eds.; Springer Singapore: Singapore, 2016; Volume 53, pp. 294–297. ISBN 978-981-287-816-8. [Google Scholar]
  4. Frey, W.; Gusbeth, C.; Sakugawa, T.; Sack, M.; Mueller, G.; Sigler, J.; Vorobiev, E.; Lebovka, N.; Álvarez, I.; Raso, J.; et al. Environmental Applications, Food and Biomass Processing by Pulsed Electric Fields. In Bioelectrics; Akiyama, H., Heller, R., Eds.; Springer: Tokyo, Japan, 2017; pp. 389–476. ISBN 978-4-431-56095-1. [Google Scholar]
  5. Chen, C.; Smye, S.W.; Robinson, M.P.; Evans, J.A. Membrane Electroporation Theories: A Review. Med. Biol. Eng. Comput. 2006, 44, 5–14. [Google Scholar] [CrossRef]
  6. Kotnik, T.; Kramar, P.; Pucihar, G.; Miklavcic, D.; Tarek, M. Cell Membrane Electroporation—Part 1: The Phenomenon. IEEE Electr. Insul. Mag. 2012, 28, 14–23. [Google Scholar] [CrossRef] [Green Version]
  7. Davalos, R.V.; Mir, I.L.M.; Rubinsky, B. Tissue Ablation with Irreversible Electroporation. Ann. Biomed. Eng. 2005, 33, 223–231. [Google Scholar] [CrossRef]
  8. Donsì, G.; Ferrari, G.; Pataro, G. Inactivation Kinetics of Saccharomyces Cerevisiae by Pulsed Electric Fields in a Batch Treatment Chamber: The Effect of Electric Field Unevenness and Initial Cell Concentration. J. Food Eng. 2007, 78, 784–792. [Google Scholar] [CrossRef]
  9. Zhao, W.; Tang, Y.; Lu, L.; Chen, X.; Li, C. Review: Pulsed Electric Fields Processing of Protein-Based Foods. Food Bioprocess Technol. 2014, 7, 114–125. [Google Scholar] [CrossRef]
  10. Delbaere, S.M.; Bernaerts, T.; Vangrunderbeek, M.; Vancoillie, F.; Hendrickx, M.E.; Grauwet, T.; Van Loey, A.M. The Volatile Profile of Brussels Sprouts (Brassica Oleracea Var. Gemmifera) as Affected by Pulsed Electric Fields in Comparison to Other Pretreatments, Selected to Steer (Bio)Chemical Reactions. Foods 2022, 11, 2892. [Google Scholar] [CrossRef]
  11. Bolumar, T.; Rohlik, B.-A.; Stark, J.; Sikes, A.; Watkins, P.; Buckow, R. Investigation of Pulsed Electric Field Conditions at Low Field Strength for the Tenderisation of Beef Topside. Foods 2022, 11, 2803. [Google Scholar] [CrossRef]
  12. Timmermans, R.A.H.; Roland, W.S.U.; van Kekem, K.; Matser, A.M.; van Boekel, M.A.J.S. Effect of Pasteurization by Moderate Intensity Pulsed Electric Fields (PEF) Treatment Compared to Thermal Treatment on Quality Attributes of Fresh Orange Juice. Foods 2022, 11, 3360. [Google Scholar] [CrossRef]
  13. Stühmeier-Niehe, C.; Lass, L.; Brocksieper, M.; Chanos, P.; Hertel, C. Pre-Treatment of Starter Cultures with Mild Pulsed Electric Fields Influences the Characteristics of Set Yogurt. Foods 2023, 12, 442. [Google Scholar] [CrossRef]
  14. Kim, S.-Y.; Lee, B.-M.; Hong, S.-Y.; Yeo, H.-H.; Jeong, S.-H.; Lee, D.-U. A Pulsed Electric Field Accelerates the Mass Transfer during the Convective Drying of Carrots: Drying and Rehydration Kinetics, Texture, and Carotenoid Content. Foods 2023, 12, 589. [Google Scholar] [CrossRef] [PubMed]
  15. Kotnik, T.; Miklavcic, D. Theoretical Evaluation of Voltage Inducement on Internal Membranes of Biological Cells Exposed to Electric Fields. Biophys. J. 2006, 90, 480–491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Probst, U.; Fuhrmann, I.; Beyer, L.; Wiggermann, P. Electrochemotherapy as a New Modality in Interventional Oncology: A Review. Technol. Cancer Res. Treat. 2018, 17, 153303381878532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  17. Mahnič-Kalamiza, S.; Kotnik, T.; Miklavčič, D. Educational Application for Visualization and Analysis of Electric Field Strength in Multiple Electrode Electroporation. BMC Med. Educ. 2012, 12, 102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  18. Mir, L.M. Therapeutic Perspectives of in Vivo Cell Electropermeabilization. Bioelectrochemistry 2001, 53, 1–10. [Google Scholar] [CrossRef] [PubMed]
  19. Mir, L.M.; Orlowski, S. Mechanisms of Electrochemotherapy. Adv. Drug Deliv. Rev. 1999, 35, 107–118. [Google Scholar] [CrossRef] [PubMed]
  20. Zhang, K.; Teoh, J.; Laguna, P.; Dominguez-Escrig, J.; Barret, E.; Ramon-Borja, J.C.; Muir, G.; Bohr, J.; Pelechano Gómez, P.; Ng, C.-F.; et al. Effect of Focal vs Extended Irreversible Electroporation for the Ablation of Localized Low- or Intermediate-Risk Prostate Cancer on Early Oncological Control: A Randomized Clinical Trial. JAMA Surg. 2023. [Google Scholar] [CrossRef]
  21. Masone, M.C. Irreversible Electroporation in Radio-Recurrent Prostate Cancer. Nat. Rev. Urol. 2023, 20, 65. [Google Scholar] [CrossRef]
  22. Batista Napotnik, T.; Polajžer, T.; Miklavčič, D. Cell Death Due to Electroporation—A Review. Bioelectrochemistry 2021, 141, 107871. [Google Scholar] [CrossRef]
  23. Miklavcic, D.; Davalos, R.V. Electrochemotherapy (ECT) and Irreversible Electroporation (IRE)-Advanced Techniques for Treating Deep-Seated Tumors Based on Electroporation. Biomed. Eng. Online 2015, 14, I1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Garcia, P.A.; Rossmeisl, J.H.; Robertson, J.; Ellis, T.L.; Davalos, R.V. Pilot Study of Irreversible Electroporation for Intracranial Surgery. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2009, 2009, 6513–6516. [Google Scholar] [CrossRef]
  25. Miklavčič, D. Handbook of Electroporation; Springer: New York, NY, USA, 2016; ISBN 978-3-319-26779-1. [Google Scholar]
  26. Ivorra, A.; Al-Sakere, B.; Rubinsky, B.; Mir, L.M. In Vivo Electrical Conductivity Measurements during and after Tumor Electroporation: Conductivity Changes Reflect the Treatment Outcome. Phys. Med. Biol. 2009, 54, 5949. [Google Scholar] [CrossRef] [PubMed]
  27. Corovic, S.; Lackovic, I.; Sustaric, P.; Sustar, T.; Rodic, T.; Miklavcic, D. Modeling of Electric Field Distribution in Tissues during Electroporation. BioMed. Eng. OnLine 2013, 12, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Denzi, A.; Strigari, L.; Di Filippo, F.; Botti, C.; Di Filippo, S.; Perracchio, L.; Ronchetti, M.; Cadossi, R.; Liberti, M. Modeling the Positioning of Single Needle Electrodes for the Treatment of Breast Cancer in a Clinical Case. BioMed. Eng. OnLine 2015, 14, S1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  29. Sieni, E.; Sgarbossa, P.; Mognaschi, M.E.; Forzan, M.; Parupudi, T.; Mittal, L.; Camarillo, I.G.; Sundararajan, R. Electric Field Distribution Study in Inhomogeneous Biological Tissues. Int. J. Numer. Model. 2019, 33, e2699. [Google Scholar] [CrossRef]
  30. Kranjc, M.; Bajd, F.; Serša, I.; de Boevere, M.; Miklavčič, D. Electric Field Distribution in Relation to Cell Membrane Electroporation in Potato Tuber Tissue Studied by Magnetic Resonance Techniques. Innov. Food Sci. Emerg. Technol. 2016, 37, 384–390. [Google Scholar] [CrossRef]
  31. Silve, A.; Guimerà Brunet, A.; Al-Sakere, B.; Ivorra, A.; Mir, L.M. Comparison of the Effects of the Repetition Rate between Microsecond and Nanosecond Pulses: Electropermeabilization-Induced Electro-Desensitization? Biochim. Et Biophys. Acta (BBA)—Gen. Subj. 2014, 1840, 2139–2151. [Google Scholar] [CrossRef]
  32. Janositz, A.; Noack, A.-K.; Knorr, D. Pulsed Electric Fields and Their Impact on the Diffusion Characteristics of Potato Slices. LWT—Food Sci. Technol. 2011, 44, 1939–1945. [Google Scholar] [CrossRef]
  33. Jeong, S.; Kim, H.; Park, J.; Kim, K.W.; Sim, S.B.; Chung, J.H. Evaluation of Electroporated Area Using 2,3,5-Triphenyltetrazolium Chloride in a Potato Model. Sci. Rep. 2021, 11, 20431. [Google Scholar] [CrossRef]
  34. López-Alonso, B.; Sarnago, H.; Lucía, Ó.; Briz, P.; Burdío, J.M. Real-Time Impedance Monitoring During Electroporation Processes in Vegetal Tissue Using a High-Performance Generator. Sensors 2020, 20, 3158. [Google Scholar] [CrossRef] [PubMed]
  35. Pliquett, U. Electrical Characterization in Time Domain—Sample Rate and ADC Precision. In 6th European Conference of the International Federation for Medical and Biological Engineering; Lacković, I., Vasic, D., Eds.; IFMBE Proceedings; Springer International Publishing: New York, NY, USA, 2015; Volume 45, pp. 854–857. ISBN 978-3-319-11127-8. [Google Scholar]
  36. Pliquett, U.; Prausnitz, M.R. Electrical Impedance Spectroscopy for Rapid and Noninvasive Analysis of Skin Electroporation. In Electrochemotherapy, Electrogenetherapy, and Transdermal Drug Delivery; Jaroszeski, Mark, J., Heller, R., Gilbert, R., Eds.; Methods in Molecular Medicine; Humana Press: Totowa, NJ, USA, 2000; Volume 37, pp. 377–406. ISBN 978-0-89603-606-2. [Google Scholar]
  37. Pliquett, U.; Langer, R.; Weaver, J.C. Changes in the Passive Electrical Properties of Human Stratum Corneum Due to Electroporation. Biochim. Et Biophys. Acta (BBA)—Biomembr. 1995, 1239, 111–121. [Google Scholar] [CrossRef] [Green Version]
  38. Menegazzo, I.; Mammi, S.; Sgarbossa, P.; Bartolozzi, A.; Mozzon, M.; Bertani, R.; Forzan, M.; Sundararajan, R.; Sieni, E. Time Domain Nuclear Magnetic Resonance (TD-NMR) to Evaluate the Effect of Potato Cell Membrane Electroporation. Innov. Food Sci. Emerg. Technol. 2020, 65, 102456. [Google Scholar] [CrossRef]
  39. Neal, R.E.; Garcia, P.A.; Robertson, J.L.; Davalos, R.V. Experimental Characterization and Numerical Modeling of Tissue Electrical Conductivity during Pulsed Electric Fields for Irreversible Electroporation Treatment Planning. IEEE Trans. Biomed. Eng. 2012, 59, 1076–1085. [Google Scholar] [CrossRef]
  40. Breton, M.; Buret, F.; Krahenbuhl, L.; Leguebe, M.; Mir, L.M.; Perrussel, R.; Poignard, C.; Scorretti, R.; Voyer, D. Non-Linear Steady-State Electrical Current Modeling for the Electropermeabilization of Biological Tissue. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef] [Green Version]
  41. Bernardis, A.; Bullo, M.; Campana, L.G.; Di Barba, P.; Dughiero, F.; Forzan, M.; Mognaschi, M.E.; Sgarbossa, P.; Sieni, E. Electric Field Computation and Measurements in the Electroporation of Inhomogeneous Samples. Open Phys. 2017, 15, 790–796. [Google Scholar] [CrossRef]
  42. Elia, S.; Lamberti, P.; Tucci, V. Influence of Uncertain Electrical Properties on the Conditions for the Onset of Electroporation in an Eukaryotic Cell. IEEE Trans. Nanobiosci. 2010, 9, 204–212. [Google Scholar] [CrossRef]
  43. Marty, M.; Sersa, G.; Garbay, J.R.; Gehl, J.; Collins, C.G.; Snoj, M.; Billard, V.; Geertsen, P.F.; Larkin, J.O.; Miklavcic, D.; et al. Electrochemotherapy—An Easy, Highly Effective and Safe Treatment of Cutaneous and Subcutaneous Metastases: Results of ESOPE (European Standard Operating Procedures of Electrochemotherapy) Study. Eur. J. Cancer Suppl. 2006, 4, 3–13. [Google Scholar] [CrossRef]
  44. Mir, L.M.; Gehl, J.; Sersa, G.; Collins, C.G.; Garbay, J.-R.; Billard, V.; Geertsen, P.F.; Rudolf, Z.; O’Sullivan, G.C.; Marty, M. Standard Operating Procedures of the Electrochemotherapy: Instructions for the Use of Bleomycin or Cisplatin Administered Either Systemically or Locally and Electric Pulses Delivered by the CliniporatorTM by Means of Invasive or Non-Invasive Electrodes. EJC Suppl. 2006, 4, 14–25. [Google Scholar] [CrossRef]
  45. Sel, D.; Cukjati, D.; Batiuskaite, D.; Slivnik, T.; Mir, L.M.; Miklavcic, D. Sequential Finite Element Model of Tissue Electropermeabilization. Biomed. Eng. IEEE Trans. 2005, 52, 816–827. [Google Scholar] [CrossRef] [Green Version]
  46. ASTM 257-14; Standard Test Methods for DC Resistance or Conductance of Insulating Materials. ASTM International: West Conshohocken, PA, USA, 2021.
  47. FLUX (Altair). Available online: https://Altairhyperworks.Com/Product/Flux (accessed on 20 January 2023).
  48. Campana, L.G.; Di Barba, P.; Dughiero, F.; Rossi, C.R.; Sieni, E. Optimal Needle Positioning for Electrochemotherapy: A Constrained Multiobjective Strategy. IEEE Trans. Magn. 2013, 49, 2141–2144. [Google Scholar] [CrossRef]
  49. Meunier, G. (Ed.) The Finite Element Method for Electromagnetic Modeling; ISTE; Wiley: London, UK; Hoboken, NJ, USA, 2008; ISBN 978-1-84821-030-1. [Google Scholar]
  50. Di Barba, P.; Savini, A.; Wiak, S. Field Models in Electricity and Magnetism; Springer: Dordrecht, The Netherlands, 2008; ISBN 978-1-4020-6842-3. [Google Scholar]
  51. Ongaro, A.; Pellati, A.; Caruso, A.; Battista, M.; De Terlizzi, F.; De Mattei, M.; Fini, M. Identification of in Vitro Electropermeabilization Equivalent Pulse Protocols. Technol. Cancer Res. Treat. 2011, 10, 465–473. [Google Scholar] [CrossRef]
  52. Ongaro, A.; Campana, L.G.; De Mattei, M.; Di Barba, P.; Dughiero, F.; Forzan, M.; Mognaschi, M.E.; Pellati, A.; Rossi, C.R.; Bernardello, C.; et al. Effect of Electrode Distance in Grid Electrode: Numerical Models and In Vitro Tests. Technol. Cancer Res. Treat. 2018, 17, 153303381876449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Corovic, S.; Zupanic, A.; Miklavcic, D. Numerical Modeling and Optimization of Electric Field Distribution in Subcutaneous Tumor Treated With Electrochemotherapy Using Needle Electrodes. Plasma Sci. IEEE Trans. 2008, 36, 1665–1672. [Google Scholar] [CrossRef] [Green Version]
  54. Pavselj, N.; Miklavcic, D. Numerical Models of Skin Electropermeabilization Taking Into Account Conductivity Changes and the Presence of Local Transport Regions. Plasma Sci. IEEE Trans. 2008, 36, 1650–1658. [Google Scholar] [CrossRef] [Green Version]
  55. Čorović, S.; Županič, A.; Kranjc, S.; Al Sakere, B.; Leroy-Willig, A.; Mir, L.M.; Miklavčič, D. The Influence of Skeletal Muscle Anisotropy on Electroporation: In Vivo Study and Numerical Modeling. Med. Biol. Eng. Comput. 2010, 48, 637–648. [Google Scholar] [CrossRef] [Green Version]
  56. Kos, B.; Zupanic, A.; Kotnik, T.; Snoj, M.; Sersa, G.; Miklavcic, D. Robustness of Treatment Planning for Electrochemotherapy of Deep-Seated Tumors. J. Membr. Biol. 2010, 236, 147–153. [Google Scholar] [CrossRef]
  57. Ivorra, A.; Mir, L.M.; Rubinsky, B. Electric Field Redistribution Due to Conductivity Changes during Tissue Electroporation: Experiments with a Simple Vegetal Model. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; Dössel, O., Schlegel, W.C., Eds.; IFMBE Proceedings. Springer: Berlin Heidelberg, Germany, 2010; Volume 25/13, pp. 59–62, ISBN 978-3-642-03894-5. [Google Scholar]
  58. Laufer, S.; Ivorra, A.; Reuter, V.E.; Rubinsky, B.; Solomon, S.B. Electrical Impedance Characterization of Normal and Cancerous Human Hepatic Tissue. Physiol. Meas. 2010, 31, 995. [Google Scholar] [CrossRef]
  59. Miklavčič, D.; Pavšelj, N.; Hart, F.X. Electric Properties of Tissues. In Wiley Encyclopedia of Biomedical Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; ISBN 978-0-471-74036-0. [Google Scholar]
  60. Teissié, J.; Eynard, N.; Gabriel, B.; Rols, M.P. Electropermeabilization of Cell Membranes. Adv. Drug Deliv. Rev. 1999, 35, 3–19. [Google Scholar] [CrossRef]
Designs 07 00035 g001 550
Figure 1. Flowchart of the proposed method (a), experimental set-up used for the evaluation of the electrical conductivity of the potato tissue (b), and the plate electrode used for the NSC characterization (c).
Figure 1. Flowchart of the proposed method (a), experimental set-up used for the evaluation of the electrical conductivity of the potato tissue (b), and the plate electrode used for the NSC characterization (c).
Designs 07 00035 g001
Designs 07 00035 g002 550
Figure 2. Samples under DC standard test.
Figure 2. Samples under DC standard test.
Designs 07 00035 g002
Designs 07 00035 g003 550
Figure 3. Voltage pulse shape applied and the resultant current pulse for the evaluation of the conductivity. (Note: only the positive part of the pulse is recorded. The 0 V part of the pulse is omitted to reduce memory space).
Figure 3. Voltage pulse shape applied and the resultant current pulse for the evaluation of the conductivity. (Note: only the positive part of the pulse is recorded. The 0 V part of the pulse is omitted to reduce memory space).
Designs 07 00035 g003
Designs 07 00035 g004 550
Figure 4. Schematic of the measurement set-ups and correspondent FEM models for (a) disk-shape model and (b) cube-shape model, with electrodes.
Figure 4. Schematic of the measurement set-ups and correspondent FEM models for (a) disk-shape model and (b) cube-shape model, with electrodes.
Designs 07 00035 g004
Designs 07 00035 g005 550
Figure 5. Conductivity as a function of the applied voltage in a PEF simulation scheme evaluated during the treatment.
Figure 5. Conductivity as a function of the applied voltage in a PEF simulation scheme evaluated during the treatment.
Designs 07 00035 g005
Designs 07 00035 g006 550
Figure 6. Electric field intensity and current density in the potato volume in the disk case with electric conductivity depending on electric field strength for different applied voltages, (a) 100 V, (b) 700 V.
Figure 6. Electric field intensity and current density in the potato volume in the disk case with electric conductivity depending on electric field strength for different applied voltages, (a) 100 V, (b) 700 V.
Designs 07 00035 g006
Designs 07 00035 g007 550
Figure 7. Electric field intensity and current density in the potato volume in the disk case with constant electric conductivity for different applied voltages, (a) 143 V/cm, (b) 1000 V/cm.
Figure 7. Electric field intensity and current density in the potato volume in the disk case with constant electric conductivity for different applied voltages, (a) 143 V/cm, (b) 1000 V/cm.
Designs 07 00035 g007
Designs 07 00035 g008 550
Figure 8. Electric field intensities and current densities in the potato volume and air surrounding in the cubic case when a fixed-conductivity material property is considered-the behavior for the lower (230 mS/m) (left) and for the higher (950 mS/m) (right).
Figure 8. Electric field intensities and current densities in the potato volume and air surrounding in the cubic case when a fixed-conductivity material property is considered-the behavior for the lower (230 mS/m) (left) and for the higher (950 mS/m) (right).
Designs 07 00035 g008
Table
Table 1. Conductivity [mS/m] measurements using the cubic applicator.
Table 1. Conductivity [mS/m] measurements using the cubic applicator.
ConditionGroup AGroup B
0 VStd-Dev100 VStd-Dev0 VStd-Dev800 VStd-Dev
SC [mS/m]110.92131.9101.5200.35
NSC [mS/m]--1070.14--40489
Table
Table 2. Conductivity as a function of the applied voltage and parameter obtained fitting the model using Equation (5).
Table 2. Conductivity as a function of the applied voltage and parameter obtained fitting the model using Equation (5).
E [Vcm−1]σm1 [Sm−1]Std (σm1) [Sm−1]σm2 [Sm−1]Std (σm2) [Sm−1]
#1143234.50.0582.80.000
#2214396.70.04128.60.010
#3429487.90.00280.20.011
#4571621.20.10364.10.000
#5714700.80.07441.30.033
#6857669.40.10404.10.049
#7971938.10.10436.50.028
#81071979.50.02668.60.004
#91371867.10.00602.10.010
σ0[mSm−1]100--1-
σ1[mSm−1]960--570-
Eth[Vcm−1]480--489.6-
kv[cm/V]0.00190--0.00204-
Table
Table 3. Conductivity estimation using the FEA and assessment of the error of estimation for disk and cube-shape model with field-dependent electrical conductivity.
Table 3. Conductivity estimation using the FEA and assessment of the error of estimation for disk and cube-shape model with field-dependent electrical conductivity.
Disk-Case ADisk-Case BCube
Voltage [V]100700100700100700
Current [A]1.8650.230.5816.830.339.81
σ(E) [mS/m]σ (143 V/cm) 230σ (1000 V/cm) 950σ (143 V/cm) 230σ (1000 V/cm) 950σ (143 V/cm) 230σ (1000 V/cm) 950
R [Ω]53.913.9172.341.6304.373.5
h [m]7 × 10−37 × 10−37 × 10−37 × 10−37 × 10−37 × 10−3
S [m2]4.9 × 10−44.9 × 10−41.8 × 10−41.8 × 10−41 × 10−41 × 10−4
ρm [Ωm]3.81.04.31.14.31.1
σm [mS/m]2651023230952230952
error [%]−15.1−7.70.0−0.20.0−0.2
Table
Table 4. Conductivity estimation using the FEA, using the hypothesis of fixed conductivity medium and assessment of the error of estimation for disk-shape model with variable measurement electrode.
Table 4. Conductivity estimation using the FEA, using the hypothesis of fixed conductivity medium and assessment of the error of estimation for disk-shape model with variable measurement electrode.
Disk-Case ADisk-Case B
Voltage [V]100700100700
Current [A]1.9656.660.5816.82
σ [mS/m]230950230950
R [Ω]51.012.4171.941.6
h [m]7 × 10−37 × 10−37 × 10−37 × 10−3
S [m2]4.9 × 10−44.9 × 10−41.8 × 10−41.8 × 10−4
ρm [Ωm]3.5780.8994.3381.051
σm [mS/m]2801154231952
error [%]−21.5−21.5−0.2−0.2
Table
Table 5. Conductivity estimation using the FEM and assessment of the error of estimation for the cube-shape model.
Table 5. Conductivity estimation using the FEM and assessment of the error of estimation for the cube-shape model.
Cube–Case Model
Voltage [V]100700
Current [A]0.339.50
σ(E) [mS/m]230950
R [Ω]304.373.7
h [m]7 × 10−37 × 10−3
S [m2]1 × 10−41 × 10−4
ρm [Ωm]4.351.05
σm [mS/m]230950
error [%]6.08 × 10−5−4 × 10−5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Lamberti, P.; Sieni, E.; Sundararajan, R. Design of Electrical Characterization Method for Electroporation-Treated Biological Tissues. Designs 2023, 7, 35. https://doi.org/10.3390/designs7020035

AMA Style

Lamberti P, Sieni E, Sundararajan R. Design of Electrical Characterization Method for Electroporation-Treated Biological Tissues. Designs. 2023; 7(2):35. https://doi.org/10.3390/designs7020035

Chicago/Turabian Style

Lamberti, Patrizia, Elisabetta Sieni, and Raji Sundararajan. 2023. "Design of Electrical Characterization Method for Electroporation-Treated Biological Tissues" Designs 7, no. 2: 35. https://doi.org/10.3390/designs7020035

APA Style

Lamberti, P., Sieni, E., & Sundararajan, R. (2023). Design of Electrical Characterization Method for Electroporation-Treated Biological Tissues. Designs, 7(2), 35. https://doi.org/10.3390/designs7020035

Article Metrics

Back to TopTop