Automated Solar PV Simulation System Supported by DC–DC Power Converters
Abstract
1. Introduction
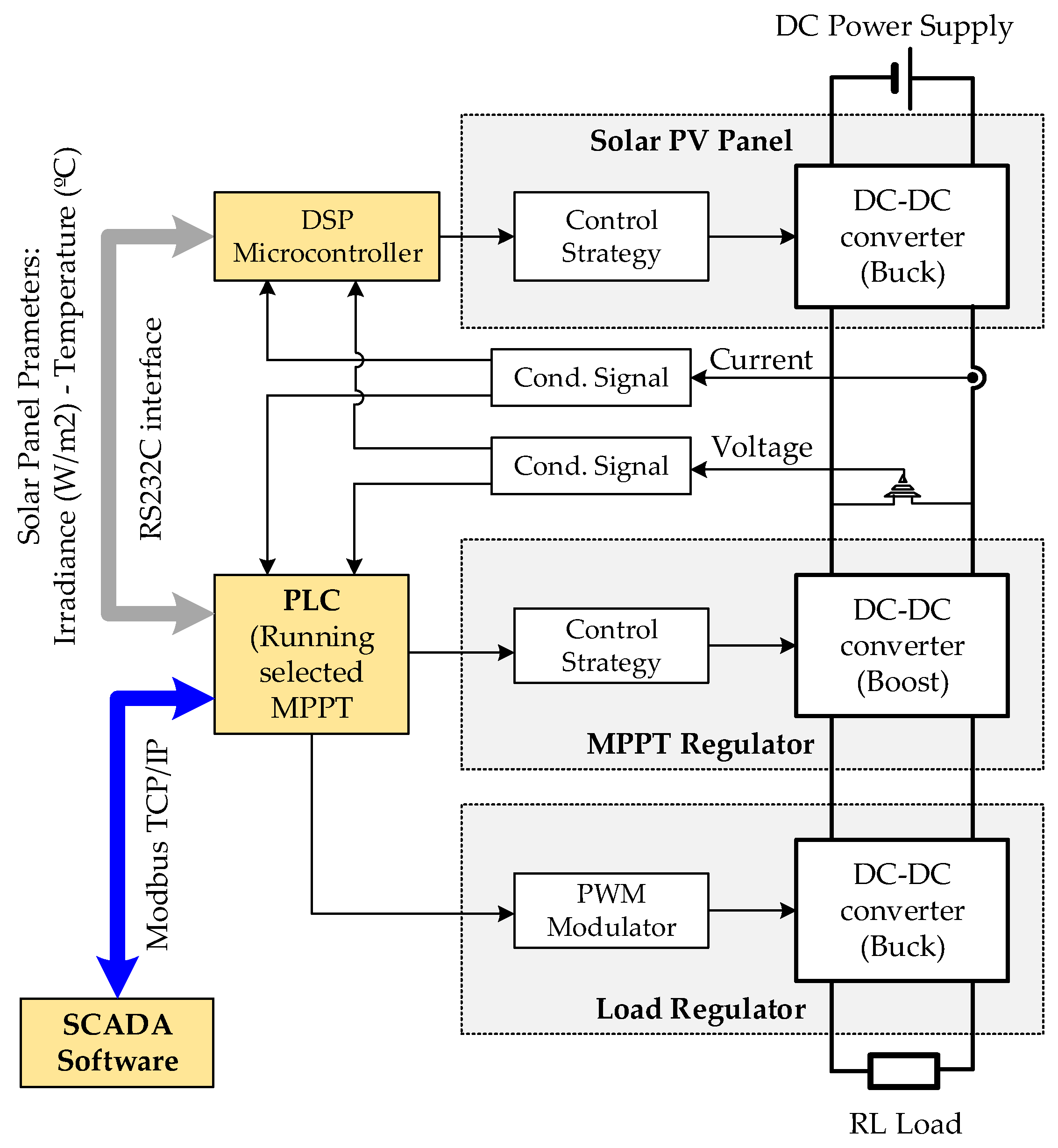
2. Description of the Proposed System
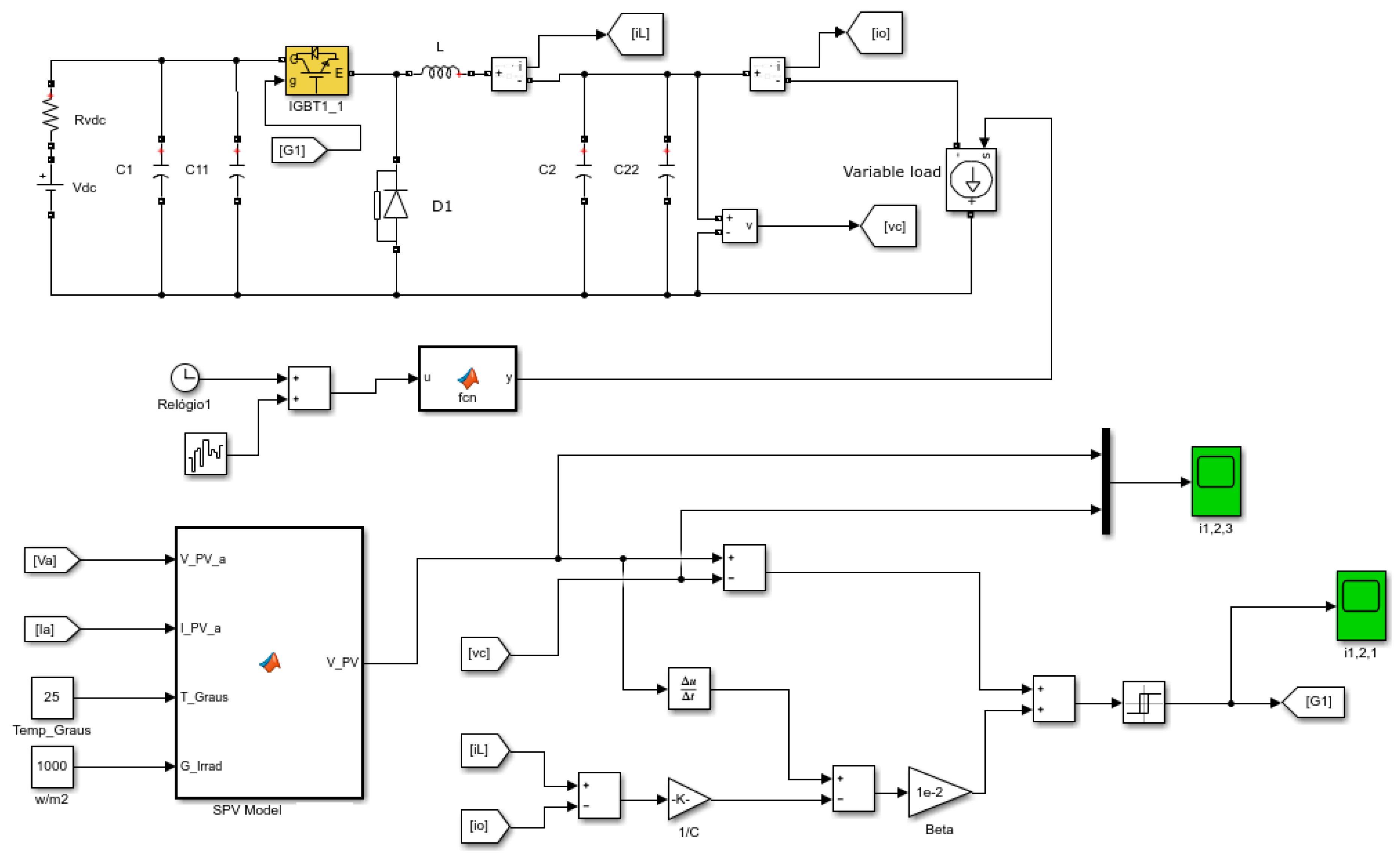
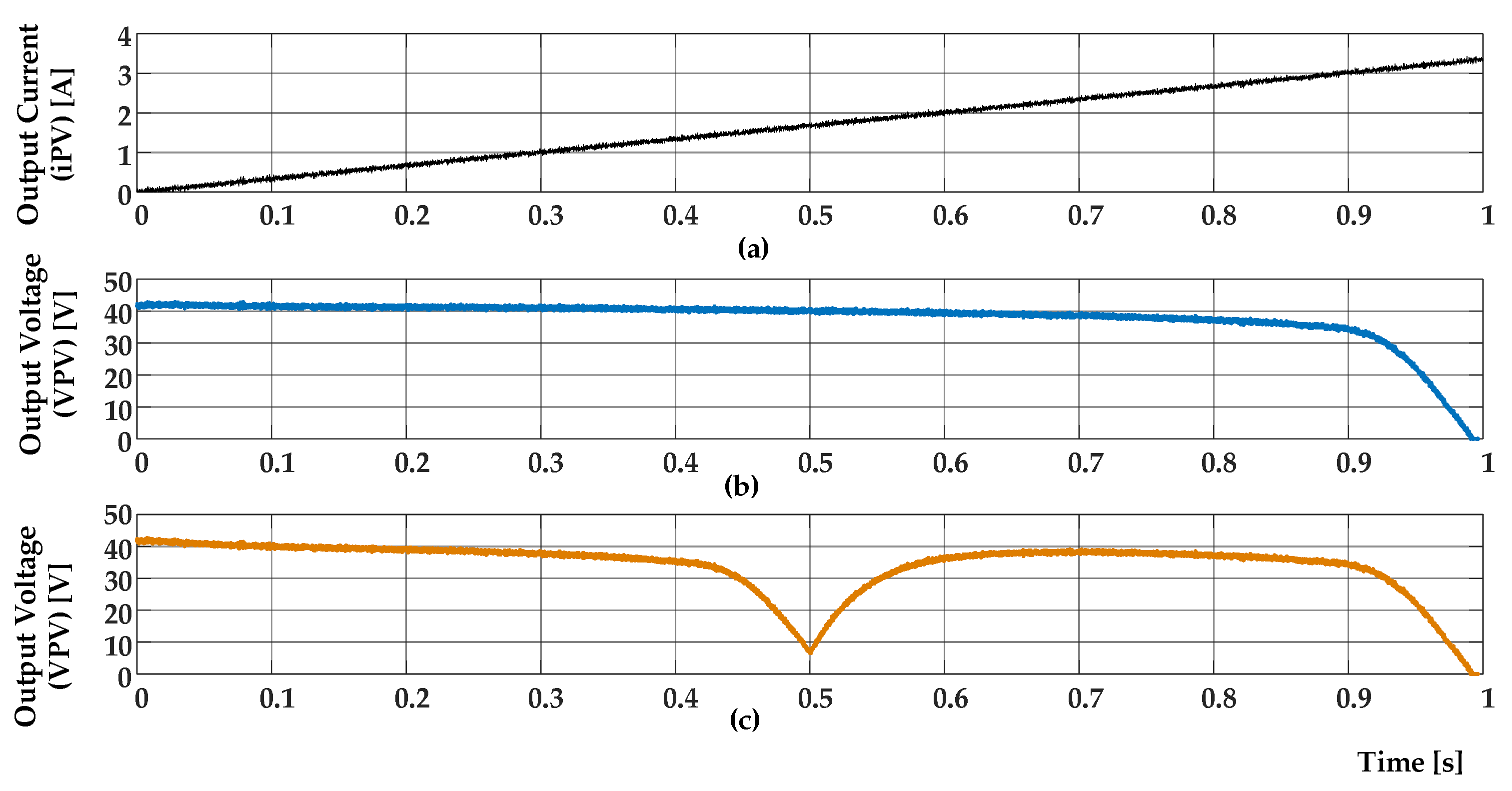
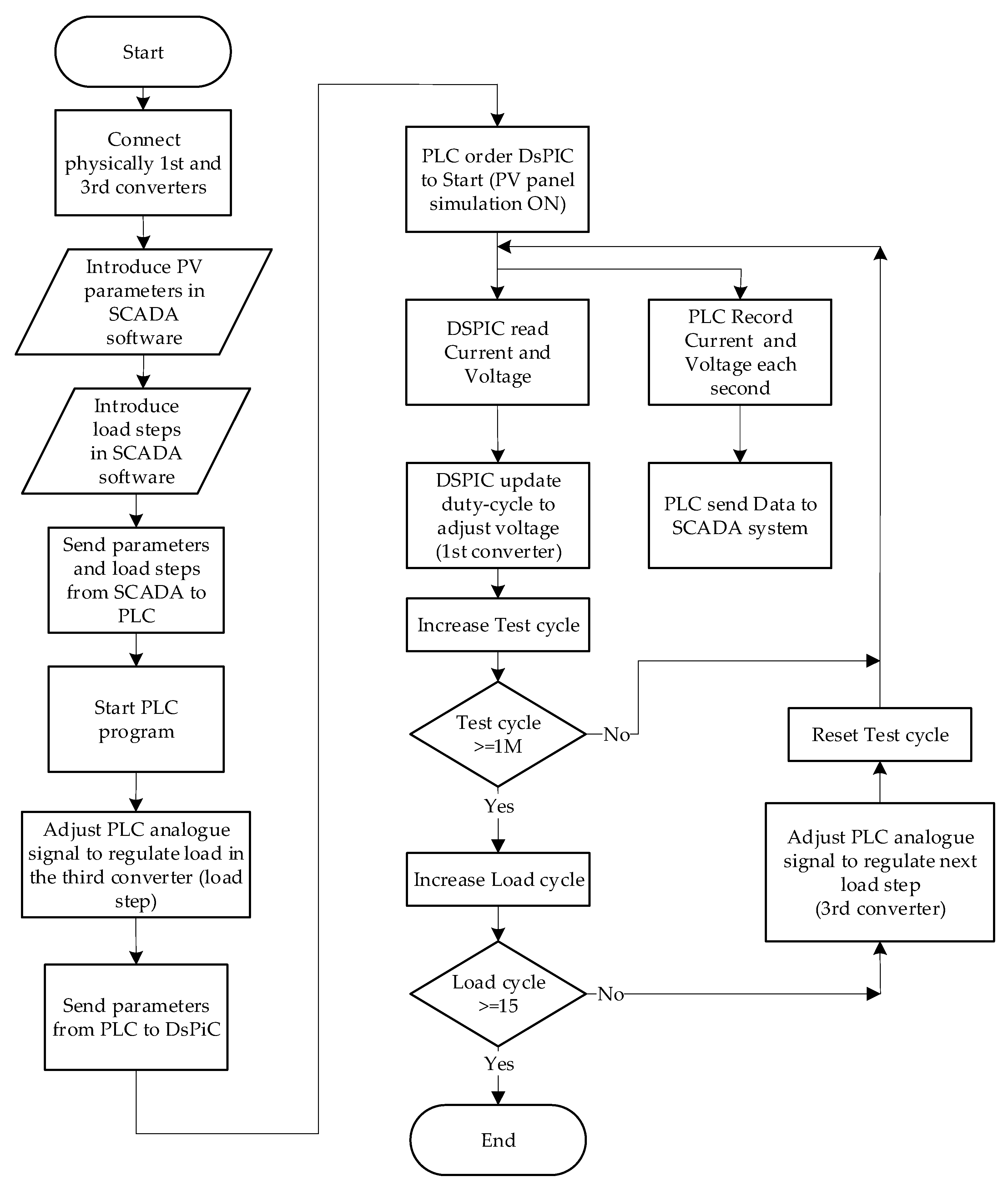
2.1. Mode I—Test and Emulate Characteristic I-V Curves
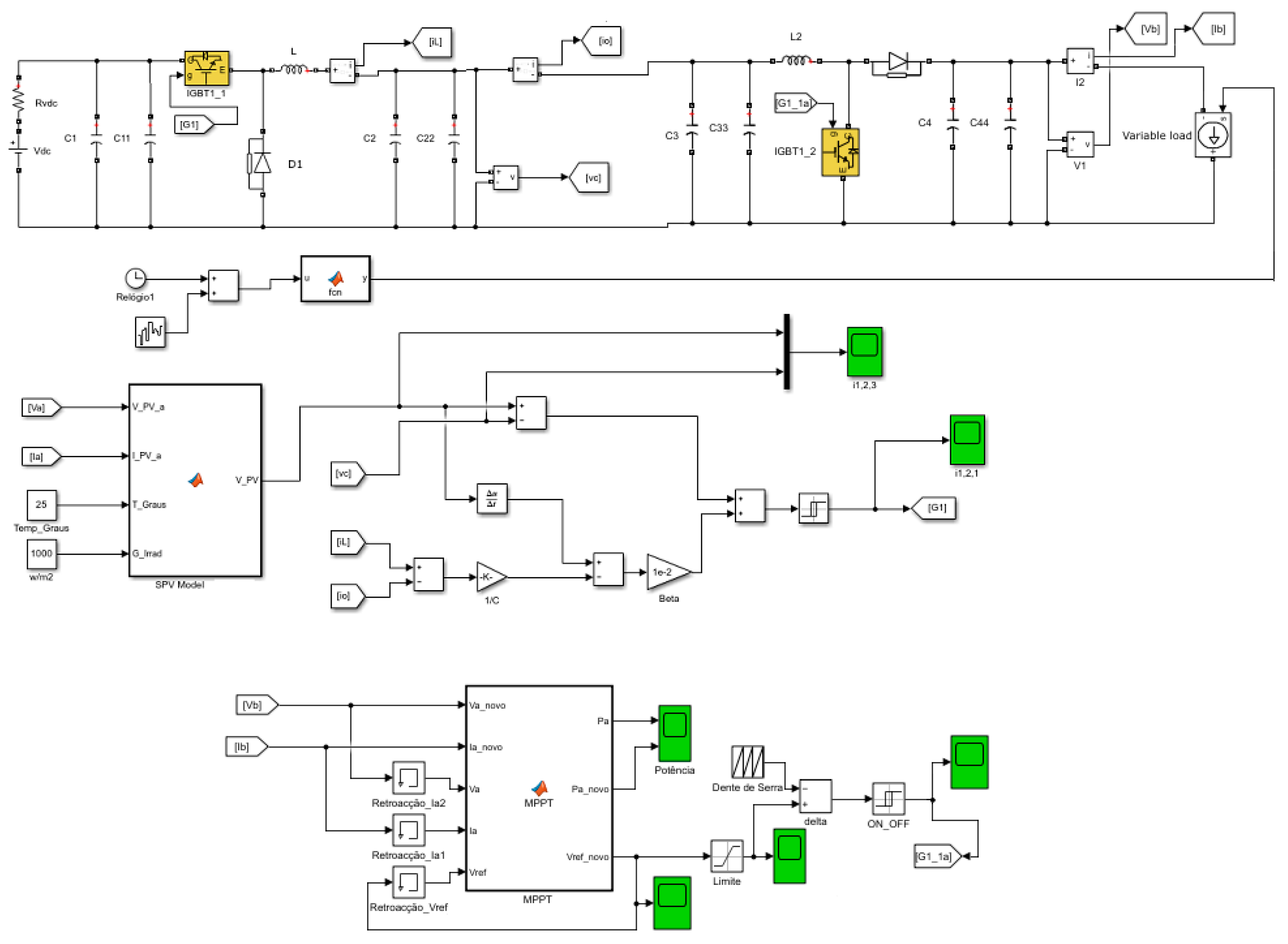
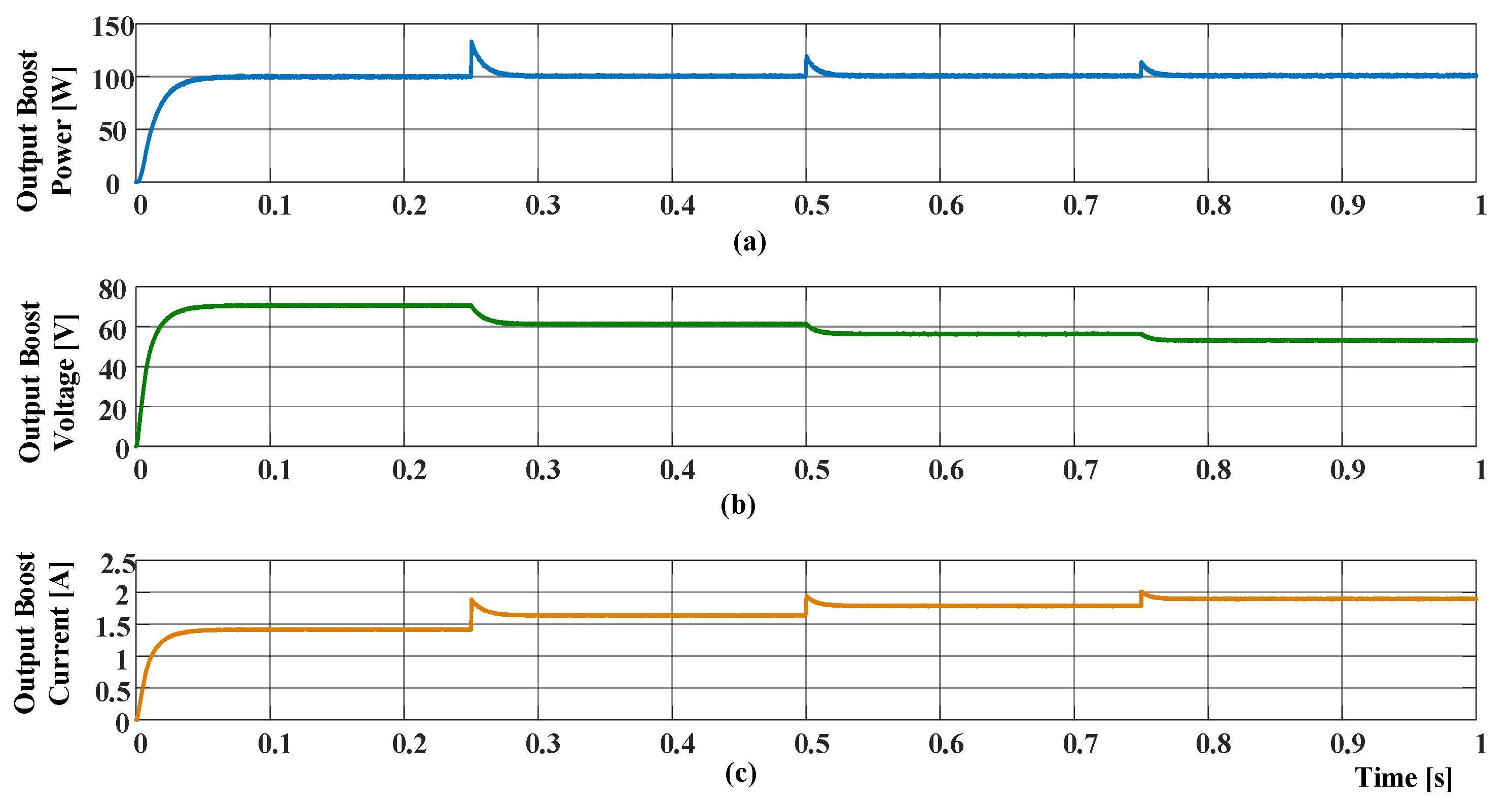
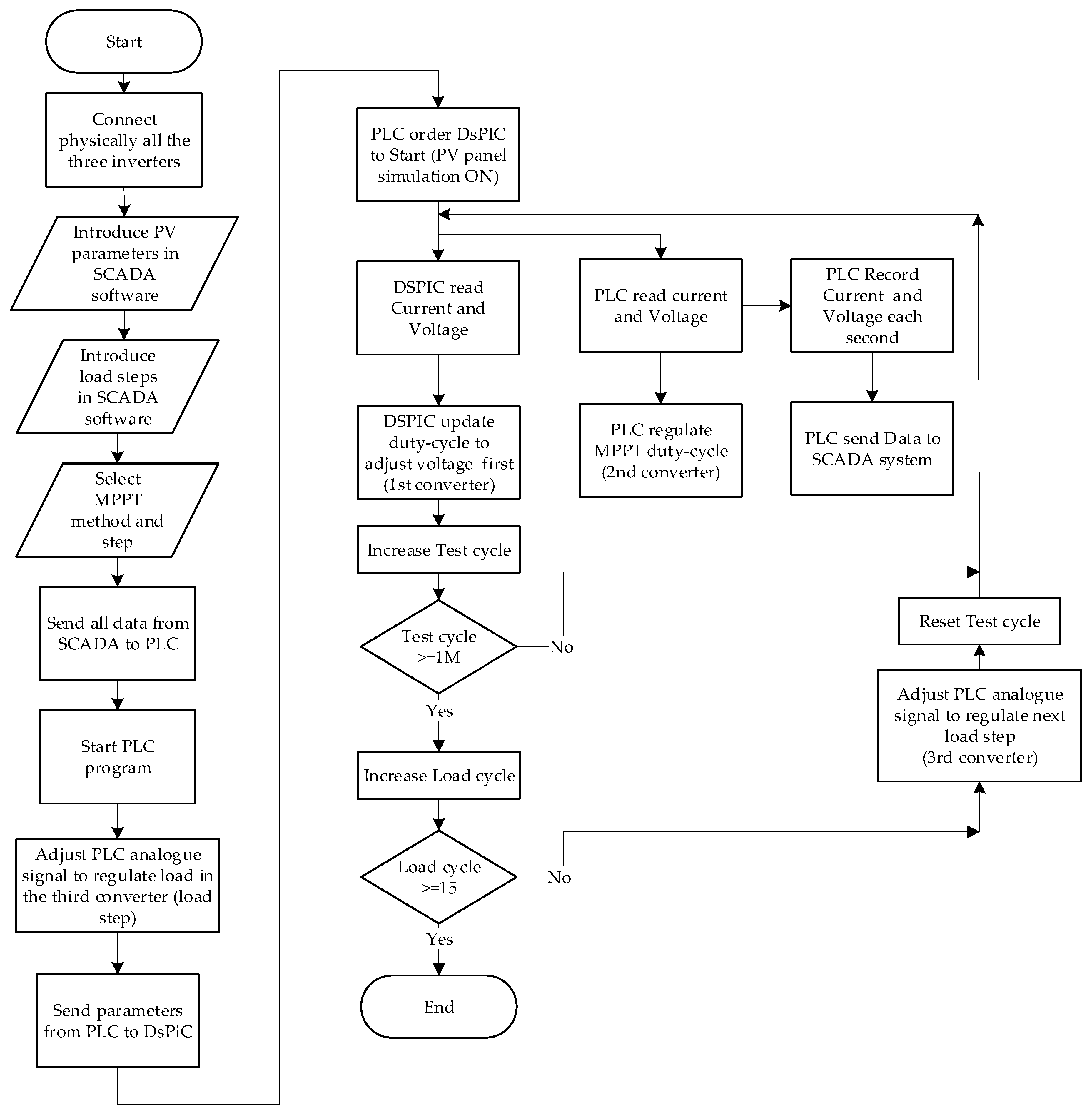
2.2. Mode II—MPPT Test Mode
2.3. Converters Design
- Input voltage VDC;
- Minimum output voltage VOUT(min);
- Maximum output current IOUT(max).
2.4. Mathematical Model
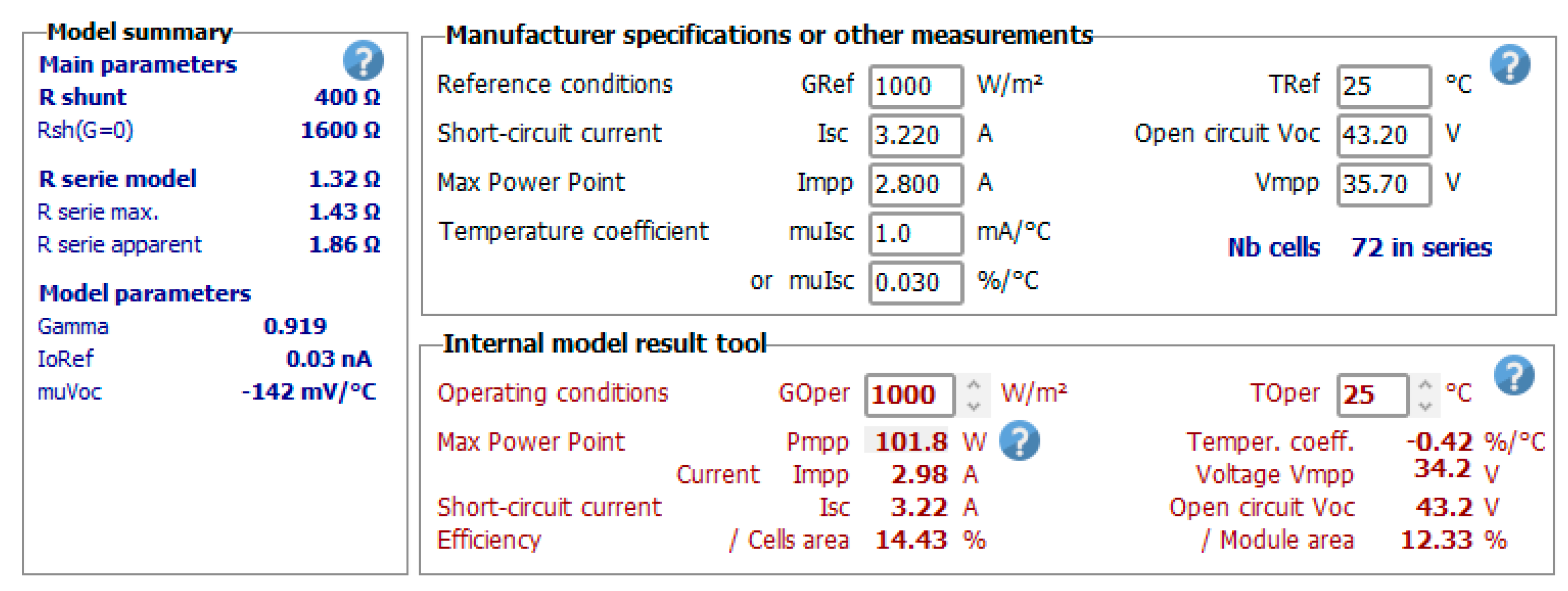
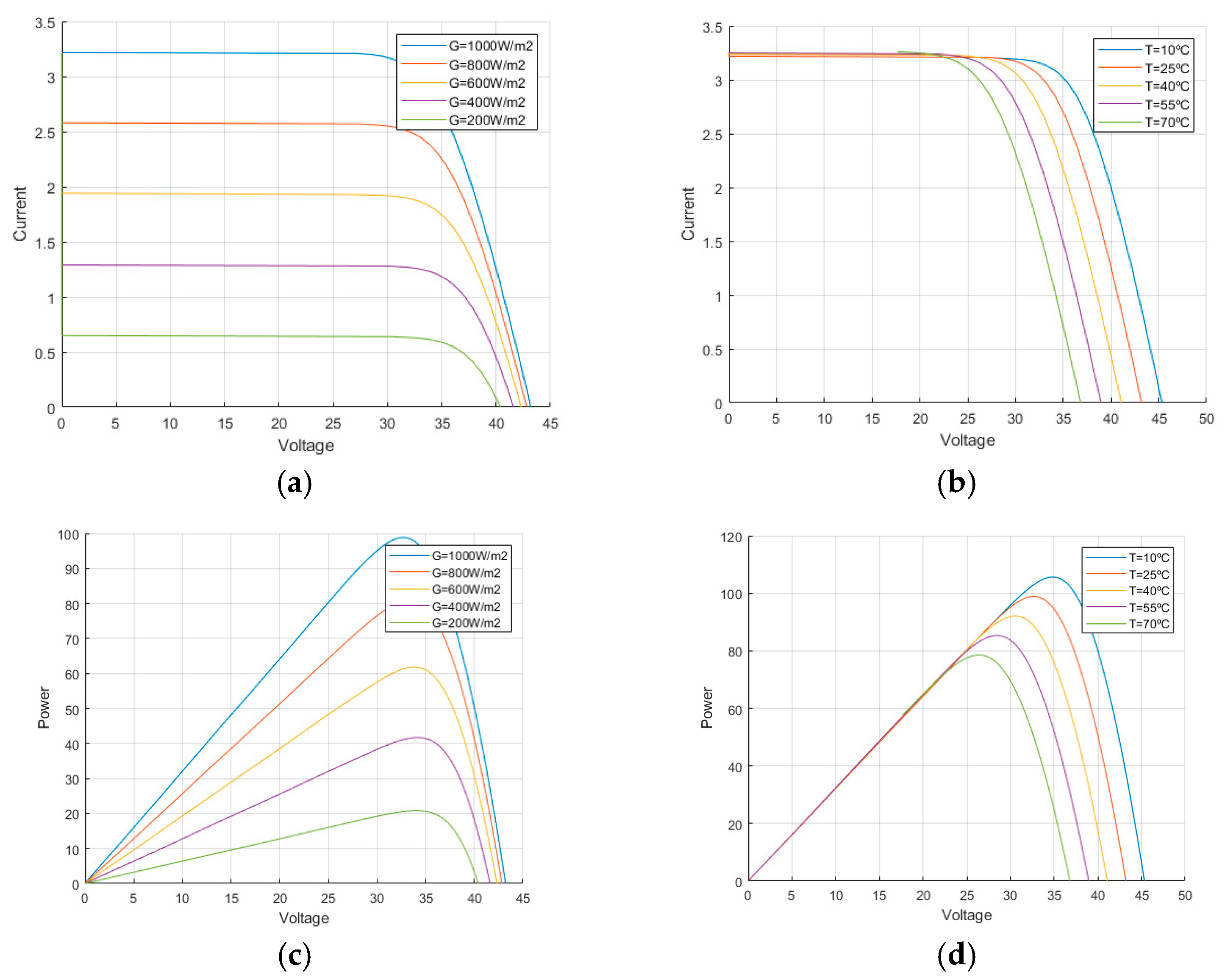
3. SPV Model Adopted
4. Control of the SPV Panel Simulator
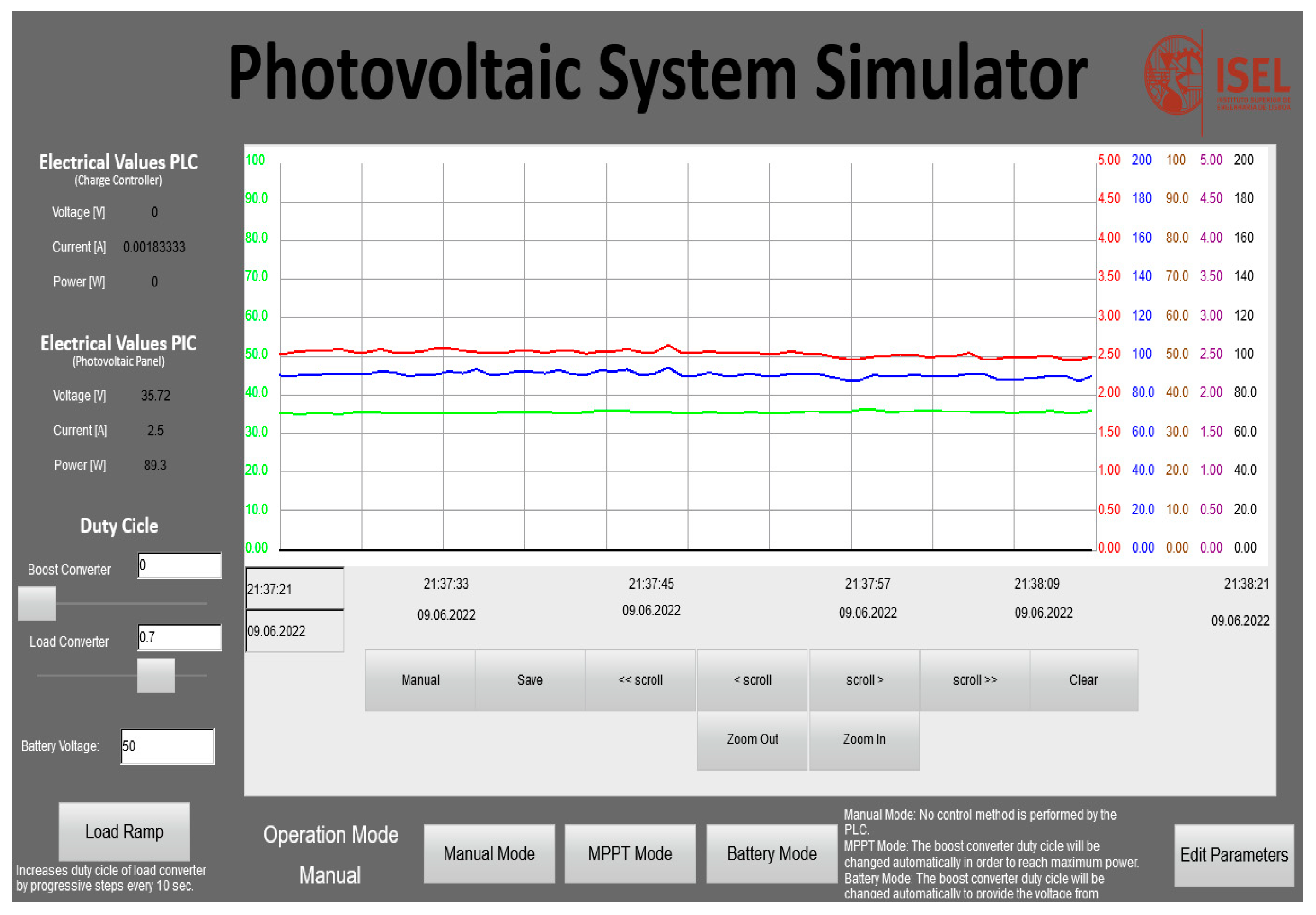
5. Simulation Results
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baena-Moreno, F.M.; Rodríguez-Galán, M.; Vega, F.; Alonso-Fariñas, B.; Arenas, L.F.V.; Navarrete, B. Carbon capture and utilization technologies: A literature review and recent advances. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 41, 1403–1433. [Google Scholar] [CrossRef]
- IEA. International Energy Agency Report. Global Energy Review. 2021. Available online: https://www.iea.org/reports/global-energy-review-2021 (accessed on 10 January 2023).
- Renewables 2021 Global Status Report—A Comprehensive Annual Overview of the State of Renewable Energy, REN21. 2021. Available online: https://ren21.net/gsr-2021/ (accessed on 10 January 2023).
- Zampirolli, F.A.; Josko, J.F.M.B.; Venero, M.L.F.; Kobayashi, G.; Fraga, F.J.; Goya Savegnago, D.H.R. An experience of automated assessment in a large-scale introduction programming course. Comput. Appl. Eng. Educ. 2021, 29, 1284–1299. [Google Scholar] [CrossRef]
- Osamnia, M.; Okada, H.; Berena, A.J.; Ueno, H.; Chunwijitra, S. A novel automated course generation system embedded in the online lecturing platform for higher education. Comput. Appl. Eng. Educ. 2016, 24, 586–598. [Google Scholar] [CrossRef]
- Basheer, S.; Saleh AlLuhaidan, A.; Mathew, R.M. A secured smart automation system for computer labs in engineering colleges using the internet of things. Comput. Appl. Eng. Educ. 2020, 29, 339–349. [Google Scholar] [CrossRef]
- Chinnasamy, J.; Shankar Ramesh Babu, K.; Chenniappan, M.; Rathinasamy, P. A workbench for motion control experiments using programmable automation controllers in industrial automation laboratory at Kongu Engineering College. Comput. Appl. Eng. Educ. 2018, 26, 566–576. [Google Scholar] [CrossRef]
- Gangwar, P.; Tripathi, R.P.; Singh, A.K. Solar photovoltaic tree: A review of designs, performance, applications, and challenges. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 1–28. [Google Scholar] [CrossRef]
- Hishikawa, Y.; Doi, T.; Higa, M.; Yamagoe, K.; Ohshima, H.; Takenouchi, T.; Yoshita, M. Voltage-Dependent Temperature Coefficient of the I–V Curves of Crystalline Silicon Photovoltaic Modules. IEEE J. Photovolt. 2018, 8, 48–53. [Google Scholar] [CrossRef]
- Mann, S.; Fadel, E.; Schoenholz, S.S.; Cubuk, E.D.; Johnson, S.G.; Romano, G. ∂PV: An end-to-end differentiable solar-cell simulator. Comput. Phys. Commun. 2022, 272, 108232. [Google Scholar] [CrossRef]
- Khalid, M.S.; Abido, M.A. A novel and accurate photovoltaic simulator based on seven-parameter model. Electr. Power Syst. Res. 2014, 116, 243–251. [Google Scholar] [CrossRef]
- Ünlü, M.; Çamur, S. A simple Photovoltaic simulator based on a one-diode equivalent circuit model. In Proceedings of the 4th International Conference on Electrical and Electronic Engineering (ICEEE), Ankara, Turkey, 8–10 April 2017; pp. 33–36. [Google Scholar] [CrossRef]
- Shannan, N.M.A.A.; Yahaya, N.; Singh, B. Single-diode model and two-diode model of PV modules: A comparison. In Proceedings of the IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 29 November–1 December 2013; pp. 210–214. [Google Scholar] [CrossRef]
- Hosseini, H.S.M.; Keymanesh, A.A. Design and construction of photovoltaic simulator based on dual-diode model. Sol. Energy 2016, 137, 594–607. [Google Scholar] [CrossRef]
- Singh, B.; Singla, M.K.; Nijhawan, P. Parameter estimation of four diode solar photovoltaic cell using hybrid algorithm. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 4597–4613. [Google Scholar] [CrossRef]
- Sousa, S.; Onofre, M.; Antunes, T.; Branco, C.; Maia, J.; Rocha, J.I.; Pires, V.F. Implementation of a low-cost data acquisition board for photovoltaic arrays analysis and diagnostic. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013; pp. 1084–1088. [Google Scholar] [CrossRef]
- Roncero-Clemente, C.; Romero-Cadaval, E.; Minambres, V.M.; Guerrero-Martinez, M.A.; Gallardo-Lozano, J. PV Array Emulator for Testing Commercial PV Inverters. Elektron. Ir Elektrotechnika 2013, 19, 71–75. [Google Scholar] [CrossRef]
- Bun, L.; Raison, B.; Rostaing, G.; Bacha, S.; Rumeau, A.; Labonne, A. Development of a real time photovoltaic simulator in normal and abnormal operations. In Proceedings of the IECON 2011-37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 867–872. [Google Scholar] [CrossRef]
- Kahoul, N.; Houabes, M.; Neçaibia, A. A comprehensive simulator for assessing the reliability of a photovoltaic painel peak power tracking system. Front. Energy 2015, 9, 170–179. [Google Scholar] [CrossRef]
- Subsingha, W. Real-time Photovoltaic Simulator Using Current Feedback Control. Energy Procedia 2016, 89, 160–169. [Google Scholar] [CrossRef]
- Tang, K.H.; Chao, K.H.; Chao, Y.W.; Chen, J.P. Design and Implementation of a Simulator for Photovoltaic Modules. Int. J. Photoenergy 2012, 6, 368931. [Google Scholar] [CrossRef]
- Qi, H.; Bi, Y.; Wu, Y. Development of a photovoltaic array simulator based on buck convertor. In Proceedings of the International Conference on Information Science Electronics and Electrical Engineering, Sapporo, Japan, 26–28 April 2014; pp. 14–17. [Google Scholar] [CrossRef]
- Cordeiro, A.; Foito, D.; Pires, V.F. A PV panel simulator based on a two quadrant DC/DC power converter with a sliding mode controller. In Proceedings of the International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 928–932. [Google Scholar] [CrossRef]
- Zhang, W.; Kimball, J.W. DC–DC Converter Based Photovoltaic Simulator with a Double Current Mode Controller. IEEE Trans. Power Electro. 2018, 33, 5860–5868. [Google Scholar] [CrossRef]
- Chakraborty, I.; Sekaran, S.; Pradhan, S.K. An enhanced DC-DC boost converter based stand-alone PV-Battery OFF-Grid system with voltage balancing capability for fluctuating environmental and load conditions. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 8247–8265. [Google Scholar] [CrossRef]
- Ahmad, R.; Murtaza, A.F.; Sher, H.A. Power tracking techniques for efficient operation of photovoltaic array in solar applications—A review. Renew. Sustain. Energy Rev. 2019, 101, 82–102. [Google Scholar] [CrossRef]
- De Brito, M.A.; Galotto, L.; Sampaio, L.P.; e Melo, G.D.A.; Canesin, C.A. Evaluation of the Main MPPT Techniques for Photovoltaic Applications. IEEE Trans. Ind. Electron. 2013, 60, 1156–1167. [Google Scholar] [CrossRef]
- Khodair, D.; Motahhir, S.; Mostafa, H.H.; Shaker, A.; Munim, H.A.E.; Abouelatta, M.; Saeed, A. Modeling and Simulation of Modified MPPT Techniques under Varying Operating Climatic Conditions. Energies 2023, 16, 549. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G.; El-Sharkawy, I.I.; Radwan, A.; Memon, S. Influence of a Hybrid MPPT Technique, SA-P&O, on PV System Performance under Partial Shading Conditions. Energies 2023, 16, 577. [Google Scholar] [CrossRef]
- Asif, R.M.; Siddique, M.A.; Rehman, A.U.; Sadiq, M.T.; Asad, A. Modified Fuzzy Logic MPPT for PV System under Severe Climatic Profiles. Pak. J. Eng. Technol. 2021, 4, 49–55. [Google Scholar] [CrossRef]
- Siddique, M.A.B.; Khan, M.A.; Asad, A.; Rehman, A.U.; Asif, R.M.; Rehman, S.U. Maximum Power Point Tracking with Modified Incremental Conductance Technique in Grid-Connected PV Array. In Proceedings of the 2020 5th International Conference on Innovative Technologies in Intelligent Systems and Industrial Applications (CITISIA), Sydney, Australia, 25–27 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 978-0792372707. [Google Scholar]
- Available online: https://www.pvxchange.com/Solar-Modules/JA-Solar/JAM60S21-365-MR_1-996000354 (accessed on 10 January 2023).
- Asif, R.M.; Ur Rehman, A.; Ur Rehman, S.; Arshad, J.; Hamid, J.; Tariq Sadiq, M.; Tahir, S. Design and analysis of robust fuzzy logic maximum power point tracking based isolated photovoltaic energy system. Eng. Rep. 2020, 2, e12234. [Google Scholar] [CrossRef]
- Soon, J.J.; Low, K.S. Optimizing Photovoltaic Model for Different Cell Technologies Using a Generalized Multidimension Diode Model. IEEE Trans. Ind. Electron. 2015, 62, 6371–6380. [Google Scholar] [CrossRef]
- Gao, W.; Hung, J.C. Variable structure control of nonlinear systems: A new approach. IEEE Trans. Ind. Electron. 1993, 40, 45–55. [Google Scholar] [CrossRef]
- Silva, J.F.; Pinto, S.F. Advanced Control of Switching Power Converters. In Power Electronics Handbook, 4th ed.; Rashid, H.M., Ed.; Butterworth-Heinemann: Oxford, UK, 2018; Chapter 35; ISBN 978-0128114070. [Google Scholar]
- Ang, S.; Oliva, A.; Griffiths, G.; Harrison, R. Power-Switching Converters, 3rd ed.; CRC Press, Taylor & Francis Group: New York, NY, USA, 2011; ISBN 978-1439815335. [Google Scholar]
- Pires, V.F.; Martins, J.F.; Hao, C. Dual-Inverter for Grid Connected Photovoltaic System: Modelling and Sliding Mode Control. Sol. Energy 2012, 86, 2106–2115. [Google Scholar] [CrossRef]
- Mérida, J.; Aguilar, L.T.; Dávila, J. Analysis and synthesis of sliding mode control for large scale variable speed wind turbine for power optimization. Renew. Energy 2014, 71, 715–728. [Google Scholar] [CrossRef]
- Pires, V.F.; Silva, J.F. Teaching nonlinear modeling, simulation, and control of electronic power converters using MATLAB/SIMULINK. IEEE Trans. Educ. 2002, 45, 253–261. [Google Scholar] [CrossRef]
- PVSYST. 2022. Available online: https://www.pvsyst.com/ (accessed on 10 January 2023).
- Pvxchange. 2022. Available online: https://www.pvxchange.com/Solar-Modules/Schott-Solar/ASE-100-GT-FT-100W_1-992500269-1 (accessed on 10 January 2023).
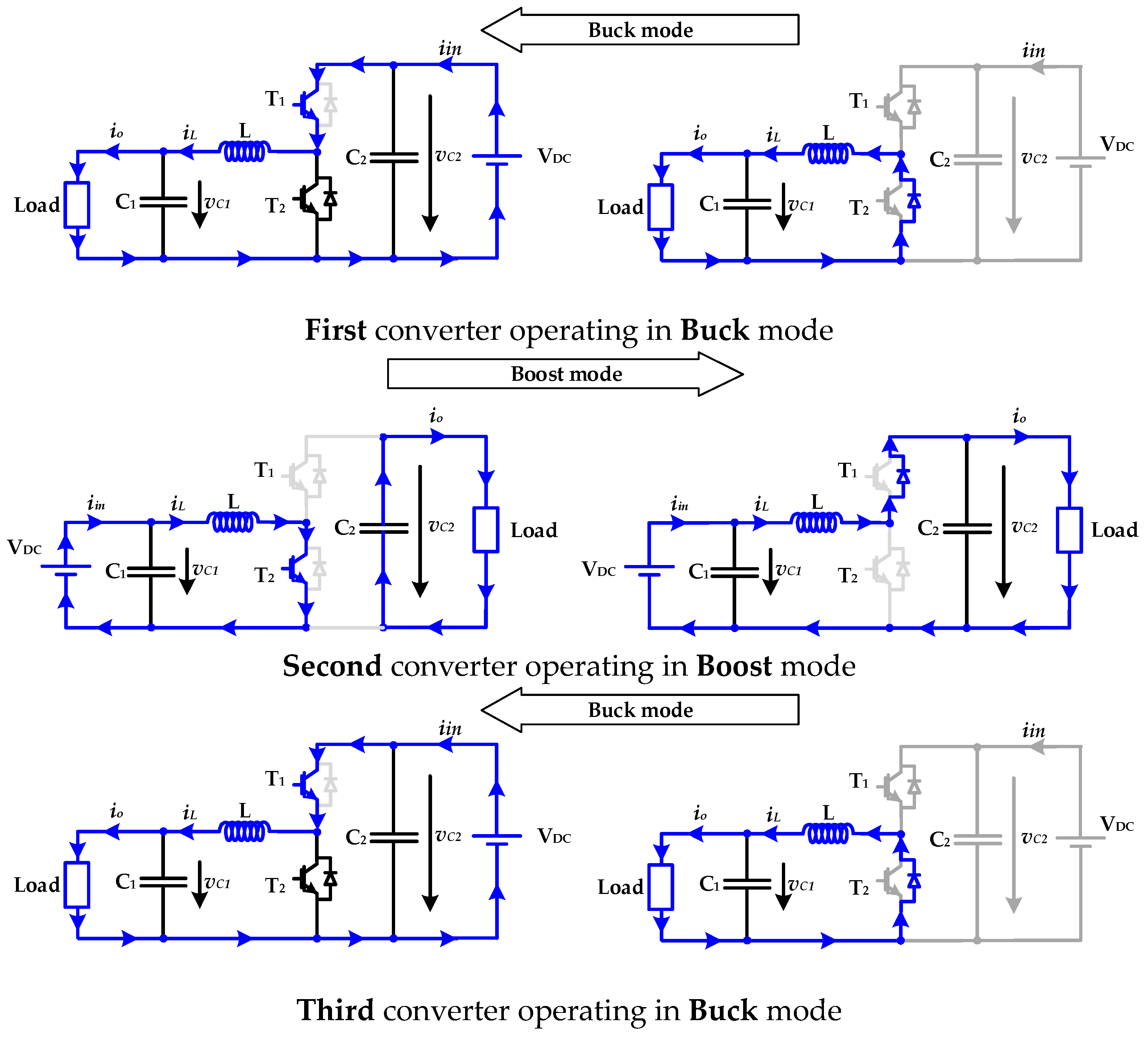





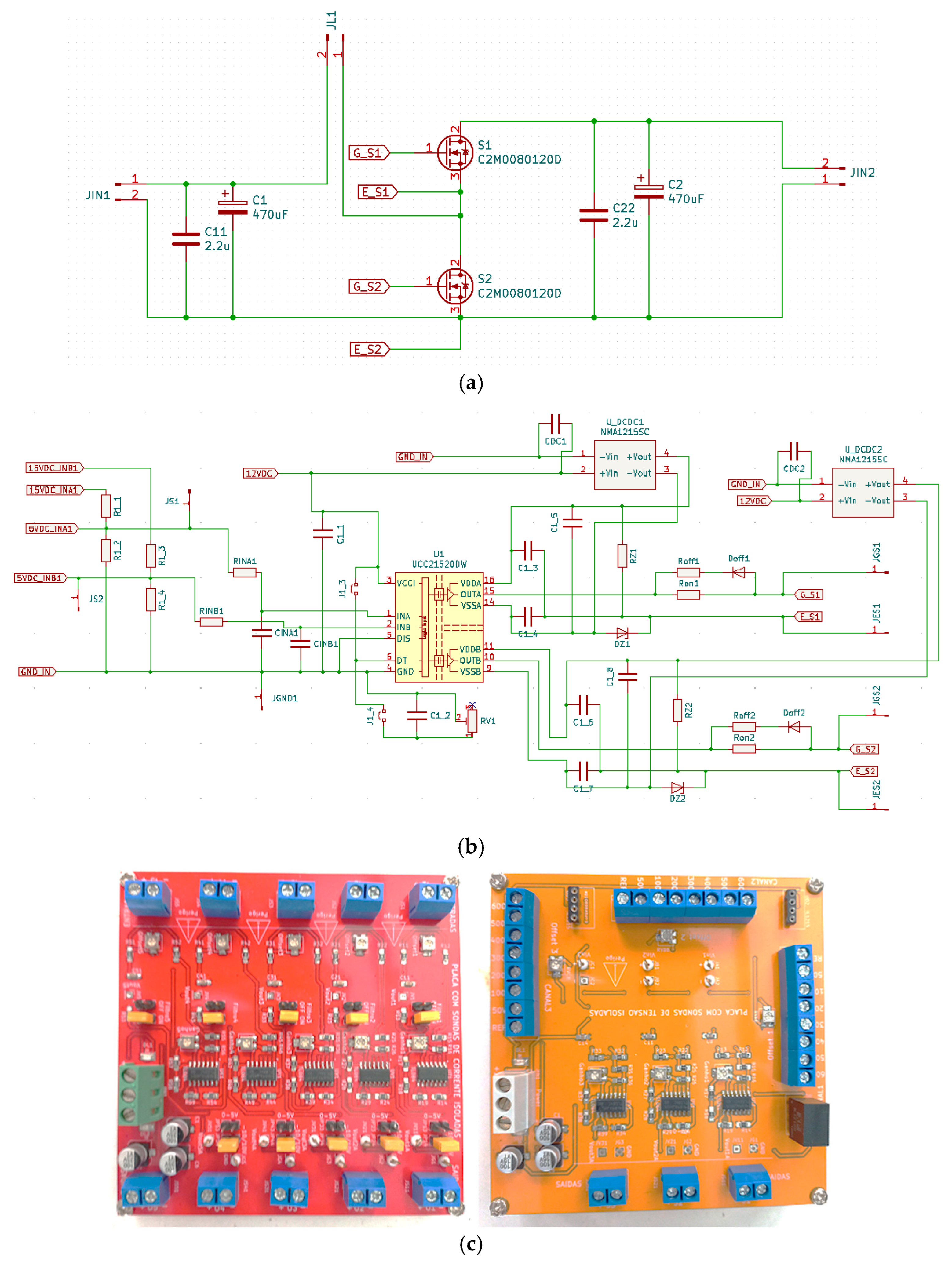

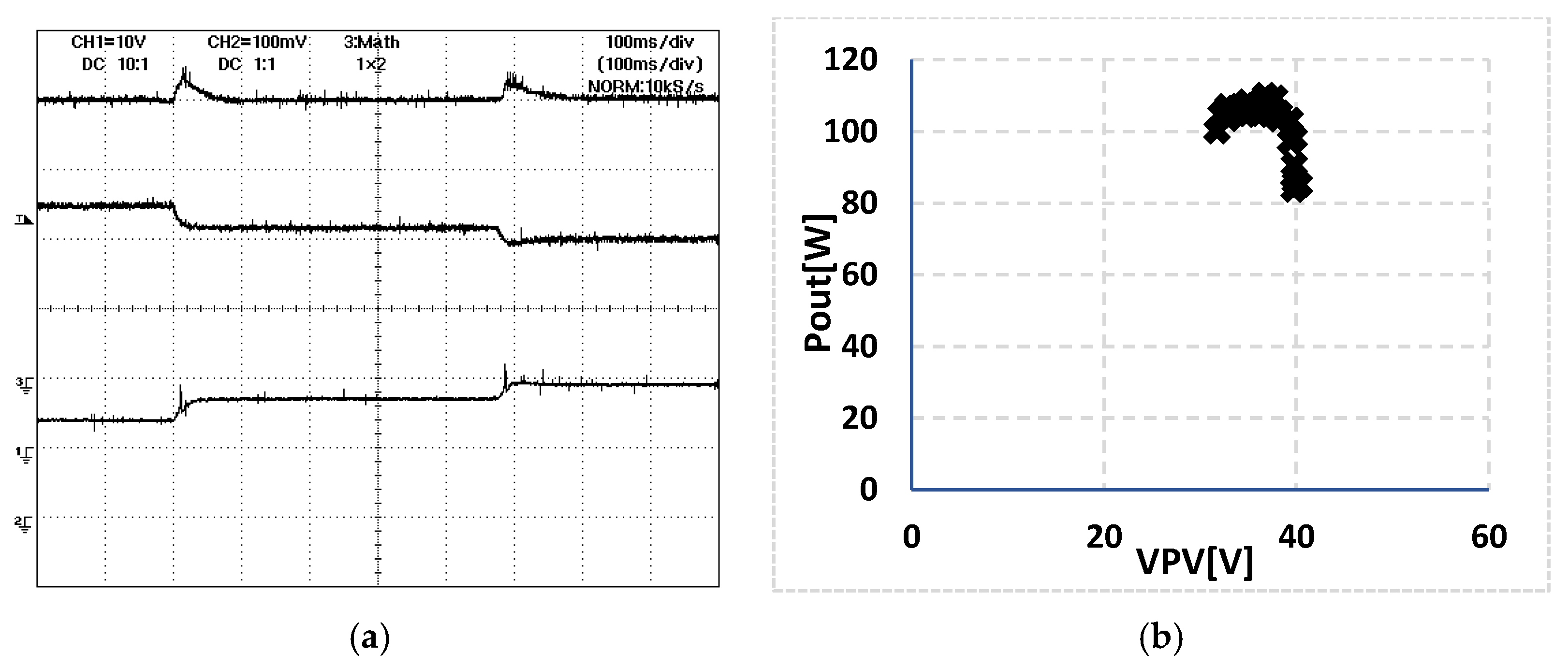




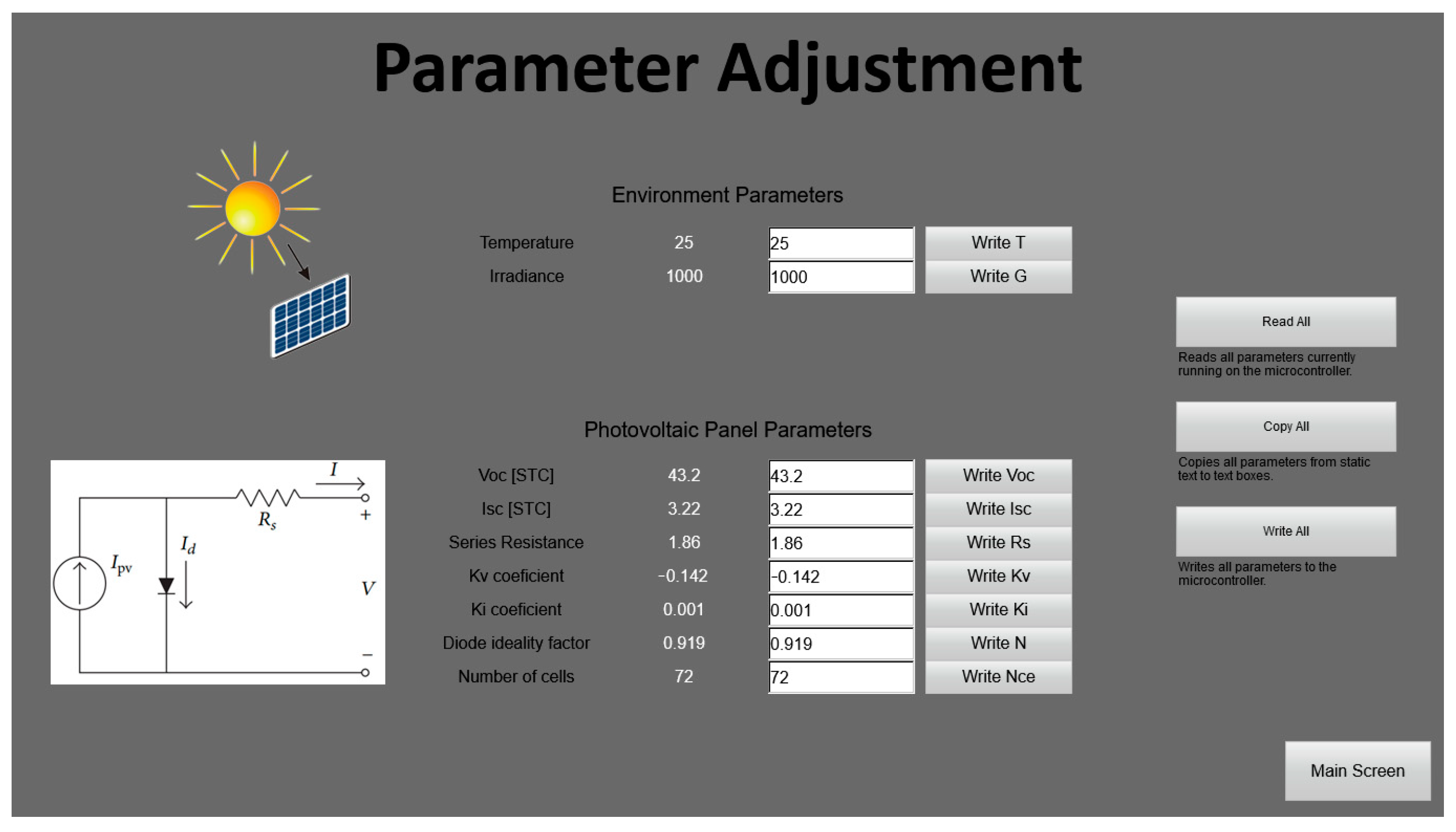
| Operation Mode | Converter Used | Topology | Description |
|---|---|---|---|
| Mode I (SPV panel mode) | 1st converter connected in series with… | Buck mode | Simulate the I-V PV curves |
| 3rd converter | Buck mode | Simulate a variable load (Fixed load with variable voltage) | |
| Mode II (MPPT test mode) | 1st converter connected in series with… | Buck mode | Simulate the I-V PV characteristics |
| 2nd converter connected in series with… | Boost mode | Simulate the MPPT algorithm | |
| 3rd converter | Buck mode | Simulate a variable load (Fixed load with variable voltage) |
| Parameter | Value |
|---|---|
| Voltage at MPP | 33.6 V |
| Current at MPP | 10.75 A |
| Power at MPP | 365 W |
| Open-circuit voltage | 41.13 V |
| Short-circuit current | 11.3 A |
| Parameter | Value |
|---|---|
| Inductors | L = 1 mH |
| Capacitors | C1 = C2 = 470 μF |
| Input Voltage (first converter) | VDC = 60 V |
| Voltage at MPP | 34.2 V |
| Current at MPP | 2.98 A |
| Power at MPP | 10.8 W |
| Open-circuit voltage | 42.2 V |
| Short-circuit current | 3.22 A |
| Equivalent shunt resistor | 400 Ω |
| Equivalent series resistor | 1.32 Ω |
| Power switches | Ron = 10−3 |
| Diodes | Ron = 10−3 Ω; Vf = 0.8V |
| Load (last converter) | R = 100 Ω; L = 0.5 mH; |
| Component or Circuit | Value |
|---|---|
| Inductors | L = 1 mH (manually created) |
| Capacitors | EPCOS–C1 = C2 = 470 μF, 200 V |
| Power Devices | C2M0080120D SiC MOSFET (1200 V; 36 A) with freewheel diode |
| Filtering capacitors | 2.2 μF, 400 V |
| Isolated drive circuits | TI–UCC21520DW |
| Auxiliary Isolated power sources | Murata–NMA1215SC |
| Main Power Source | Wanptek–100VDC; 20 A. |
| DSP device | Microchip DSPIC30F4012 |
| DAC device | Microchip 12-bits MCP4922 |
| PLC | Phoenix Contact–ACX-1050-PN |
| Current sensors | ACHS7122; Current range: ±20A; Sensitivity: 100 mV/A; Primary conductor resistance: 0.7 mΩ; Bandwidth: 80 kHz; Total output error of ±1.5% |
| Voltage sensors | AMC1100; ±250 mV input voltage range optimized for shunt resistors; Offset error: 1.5 mV; Input bandwidth: 60 kHz min; Fixed gain: 8 (0.5% Accuracy). |
| Configuration Statements | Value |
|---|---|
| %Oscillator | |
| #pragma config FPR | FRC_PLL16 %Primary Oscillator Mode (FRC |
| #pragma config FOS | PRI %Oscillator Source (Primary Oscillator) |
| #pragma config FCKSMEN | CSW_FSCM_OFF %Clock Switching and Monitor |
| %Watchdog | |
| #pragma config FWPSB | WDTPSB_16 %WDT Prescaler B (1:16) |
| #pragma config FWPSA | WDTPSA_512 %WDT Prescaler A (1:512) |
| #pragma config WDT | WDT_OFF %Watchdog Timer (Disabled) |
| %Voltage Protection | |
| #pragma config FPWRT | PWRT_64 %POR Timer Value (64 ms) |
| #pragma config BODENV | BORV42 %Brown Out Voltage (4.2 V) |
| #pragma config BOREN | PBOR_ON %PBOR Enable (Enabled) |
| #pragma config MCLRE | MCLR_EN % Master Clear Enable (Enabled) |
| %Code protection | |
| #pragma config GWRP | GWRP_OFF %General Code Segment Write Protect |
| #pragma config GCP | CODE_PROT_OFF %General Segment Code Protection |
| %Programming | |
| #pragma config ICS | ICS_PGD %Comm Channel Select (Use PGC/EMUC) |
| Type | Variable |
|---|---|
| float | VT |
| float | n |
| float | VOC_STC |
| float | ISC_STC |
| float | IO |
| float | RS |
| float | RT |
| float | VOC |
| float | ISC |
| float | Ki |
| float | Kv |
| float | dT |
| float | T |
| float | G |
| float | Ncell |
| float | VPVref |
| float | VPV |
| float | VPVref5V |
| float | IPV |
| integer | VPVrefWord |
| integer | DataReceived = 0 |
| char | buffer (80) |
| char | rxbuffer (80) |
| char | rxbuffer2 (80) |
| Characteristics | Solution | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [11] | [12] | [14] | [15] | [16] | [17] | [18] | [19] | [20] | [21] | [22] | [23] | Proposed | |
| New SPV model | Yes | No | No | Yes | No | No | No | No | No | No | No | No | No |
| Model Accuracy | Good | Med. | Good | Good | Low | Med. | Med. | Med. | Med. | Med. | Low | Med. | medium |
| Simulations results | Yes | Yes | Yes | Yes | Yes | No | No | No | Yes | Yes | Yes | Yes | Yes |
| Experimental results | No | Yes | Yes | No | Yes | Yes | Yes | Yes | No | Yes | Yes | Yes | Yes |
| Hardware developed | No | No | Yes | No | Yes | Yes | No | Yes | No | Yes | Yes | Yes | Yes |
| New MPPT algorithm | No | No | No | No | No | No | No | No | No | No | No | No | No |
| Any MPPT algorithm included | No | No | No | No | No | No | No | Yes | No | No | No | No | Yes |
| Complexity implementation | Med. | Low | Low | Med. | Low | Med. | Low | Low | Low | Low | Low | Low | Med. |
| Automated tests | No | No | Yes | No | No | No | Yes | Yes | No | No | No | No | Yes |
| SCADA/HMI interface | No | No | Yes | No | Yes | No | Yes | No | No | No | No | No | Yes |
| Hardware Cost | *NA | Low | High | *NA | Low | High | High | Low | *NA | Low | Low | Low | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordeiro, A.; Chaves, M.; Gâmboa, P.; Barata, F.; Fonte, P.; Lopes, H.; Pires, V.F.; Foito, D.; Amaral, T.G.; Martins, J.F. Automated Solar PV Simulation System Supported by DC–DC Power Converters. Designs 2023, 7, 36. https://doi.org/10.3390/designs7020036
Cordeiro A, Chaves M, Gâmboa P, Barata F, Fonte P, Lopes H, Pires VF, Foito D, Amaral TG, Martins JF. Automated Solar PV Simulation System Supported by DC–DC Power Converters. Designs. 2023; 7(2):36. https://doi.org/10.3390/designs7020036
Chicago/Turabian StyleCordeiro, Armando, Miguel Chaves, Paulo Gâmboa, Filipe Barata, Pedro Fonte, Hélio Lopes, Vítor Fernão Pires, Daniel Foito, Tito G. Amaral, and João Francisco Martins. 2023. "Automated Solar PV Simulation System Supported by DC–DC Power Converters" Designs 7, no. 2: 36. https://doi.org/10.3390/designs7020036
APA StyleCordeiro, A., Chaves, M., Gâmboa, P., Barata, F., Fonte, P., Lopes, H., Pires, V. F., Foito, D., Amaral, T. G., & Martins, J. F. (2023). Automated Solar PV Simulation System Supported by DC–DC Power Converters. Designs, 7(2), 36. https://doi.org/10.3390/designs7020036










