Fault Tree Analysis for Robust Design
Abstract
1. Introduction
1.1. Design Optimization Background
1.2. Fault Tree Analysis (FTA) Background
1.3. Purpose and Outline
2. Materials and Methods
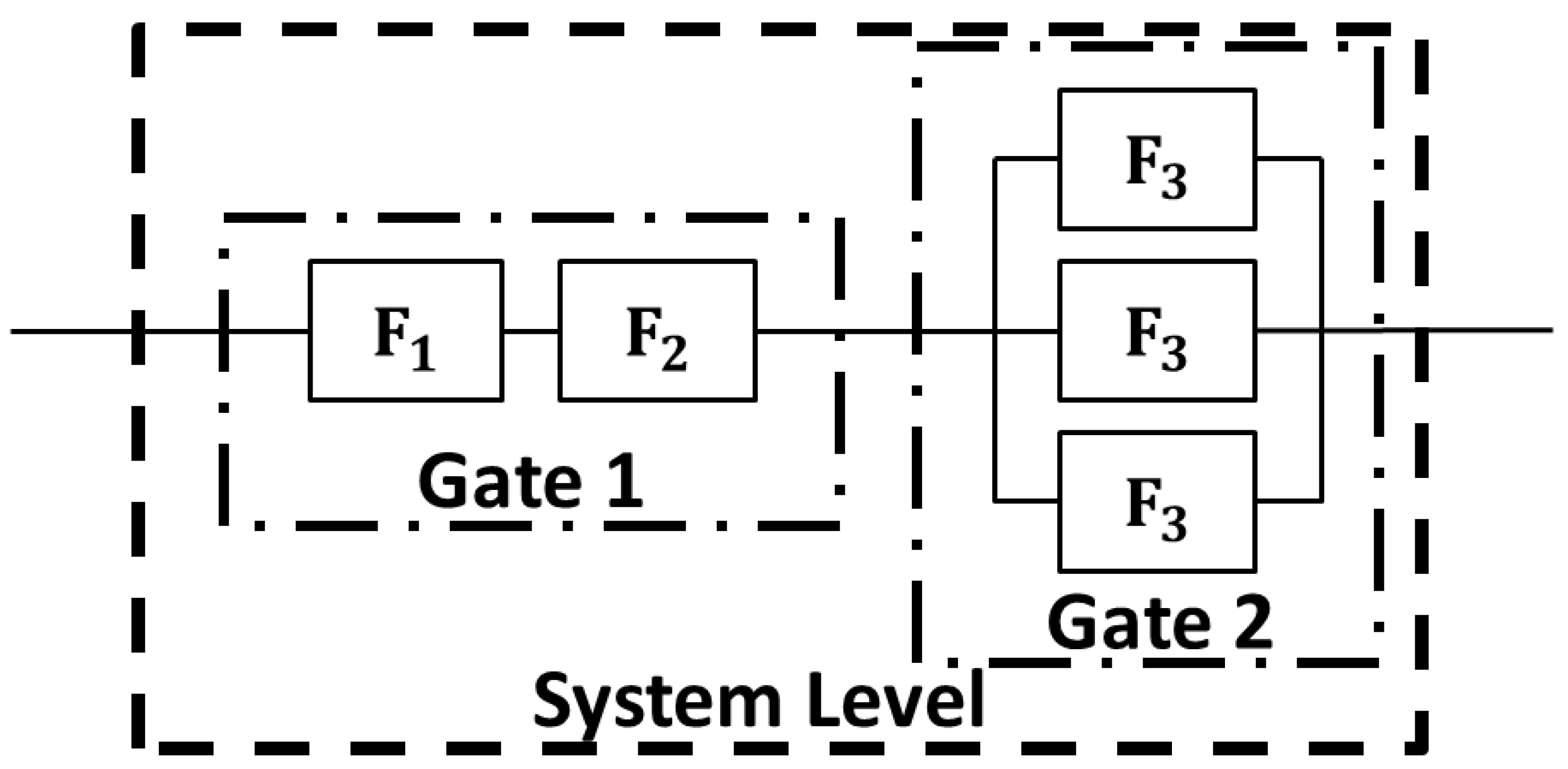
2.1. Parallel Circuit Configuration: A Demonstrative Example
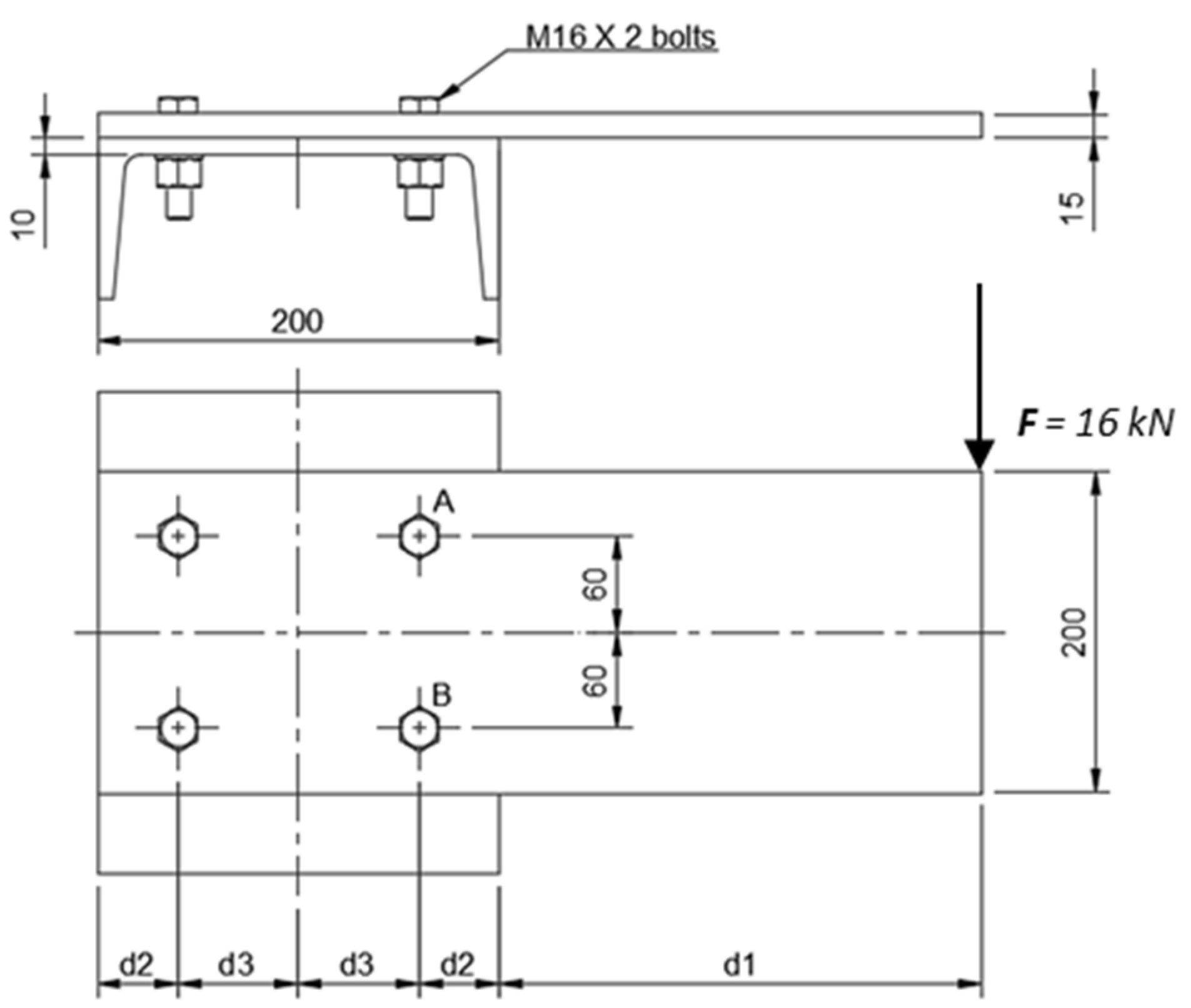
2.2. A Bolted Plate Design Problem and Deterministic Design Optimization
2.3. Robust Design and Reliability Index-Based Design Optimization
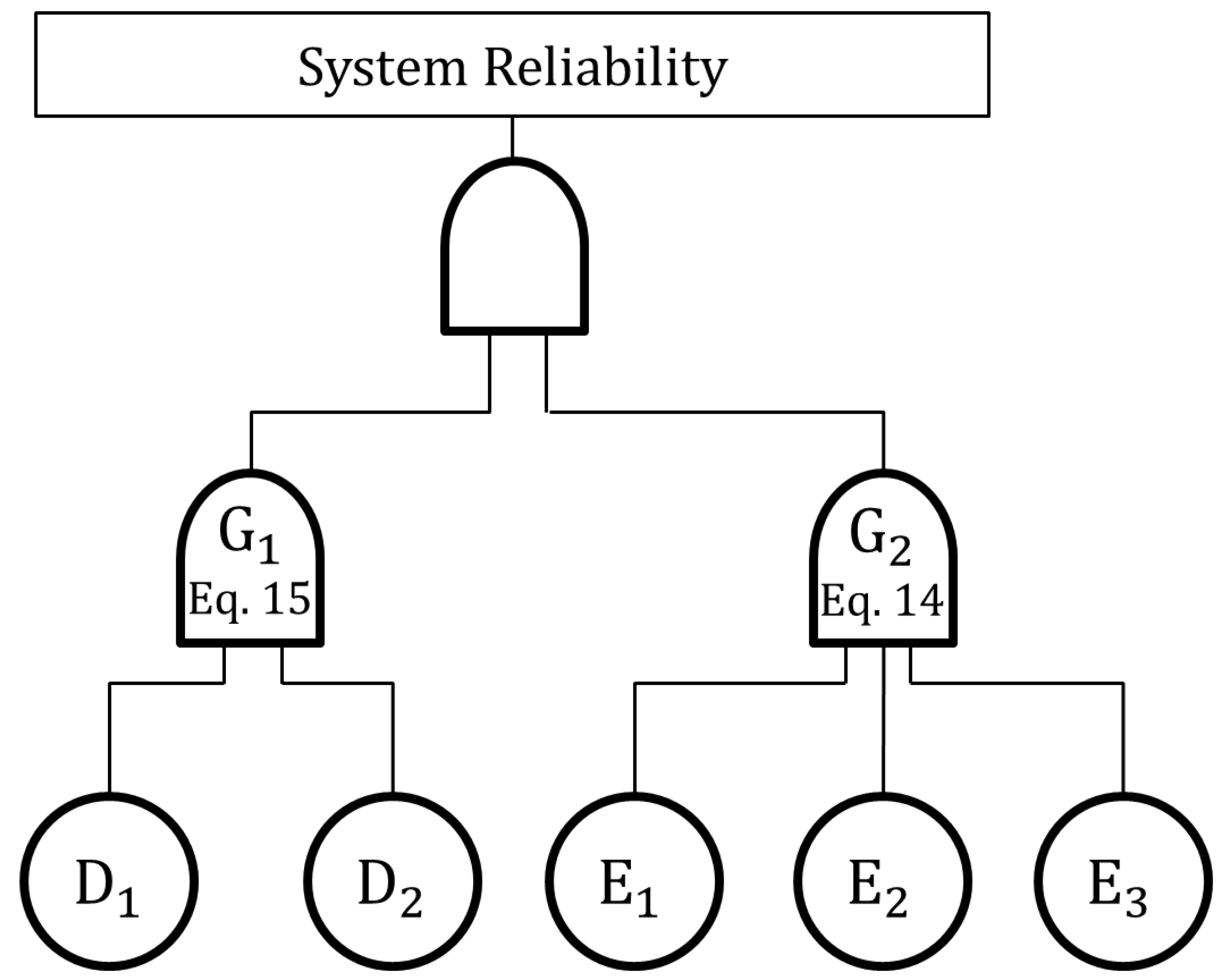
2.4. Robust Design with System Failures Built by FTA
2.4.1. Case 1: System Reliability with “and” Gate
2.4.2. Case 2: System Reliability with “or” Gate
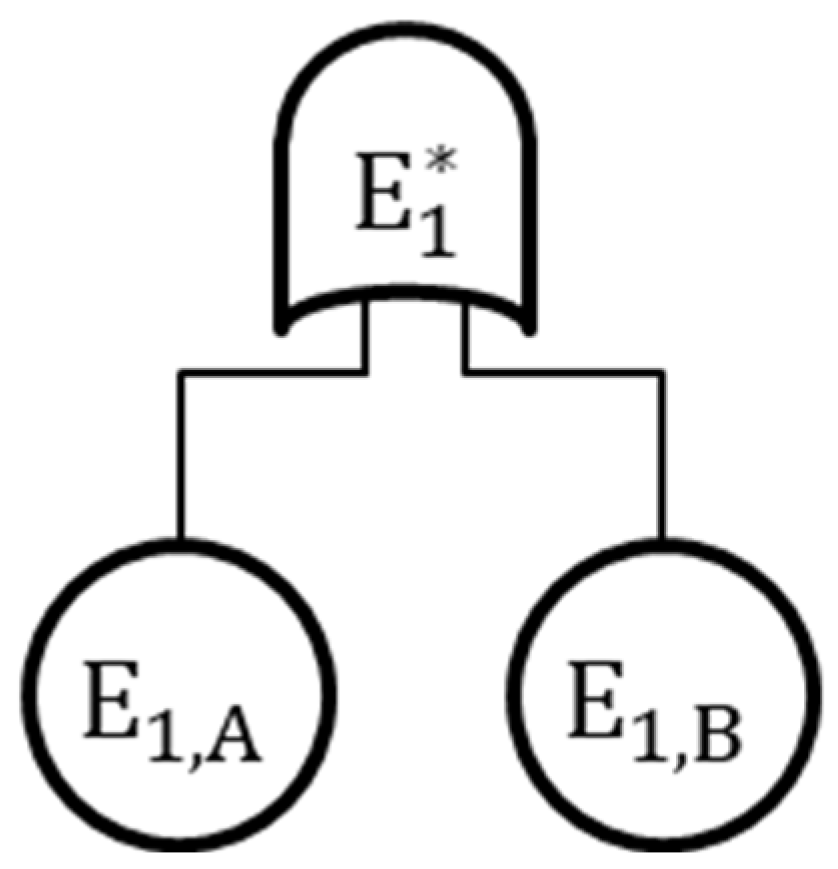
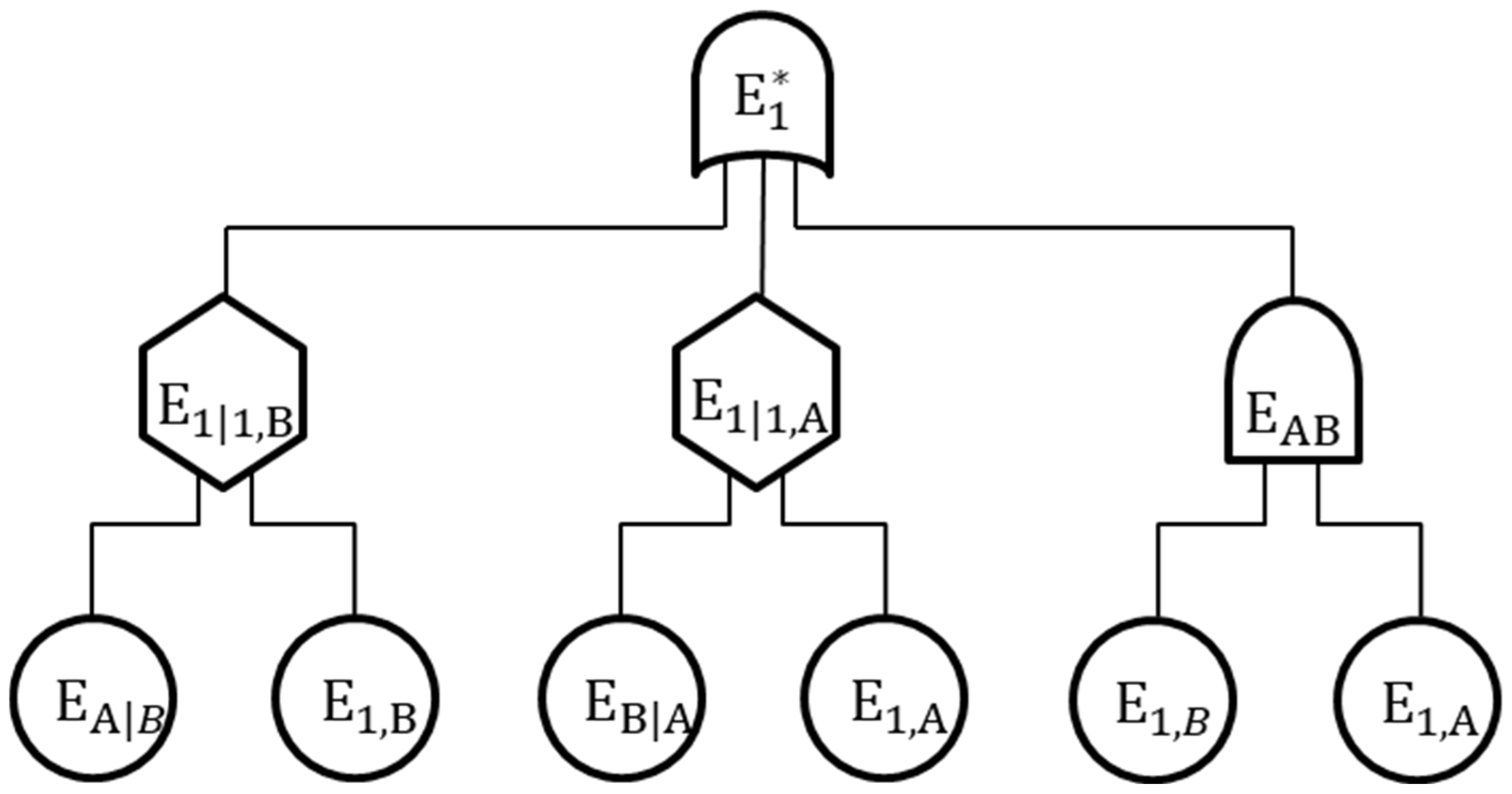
2.4.3. Case 3: System Reliability with “Inhibit” Gate
2.5. Post-Optimality Design Sensitivity Analysis
3. Numerical Results
3.1. Robust Design Optimization
- Deterministic Design Optimization: Equations (2)–(4).
- Robust Design with Reliability-Indices: Equations (11)–(13).
- Robust Design with “and” Gate: Equations (15)–(17).
- Robust Design with “or” Gate: Equations (22)–(24).
- Robust Design with “Inhibit” Gate: Equations (28)–(30).
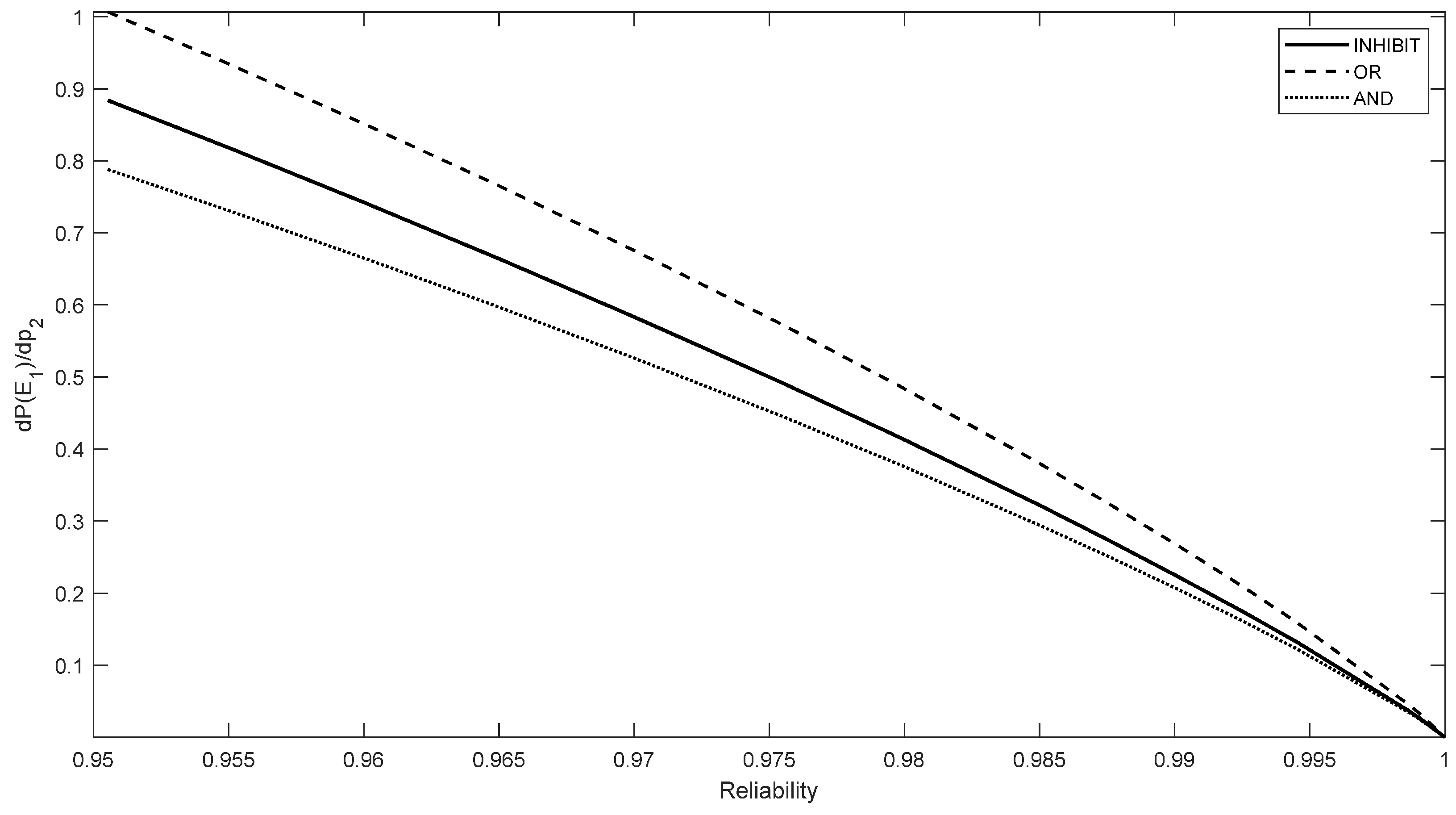
3.2. Post-Optimality Sensitivity Analysis
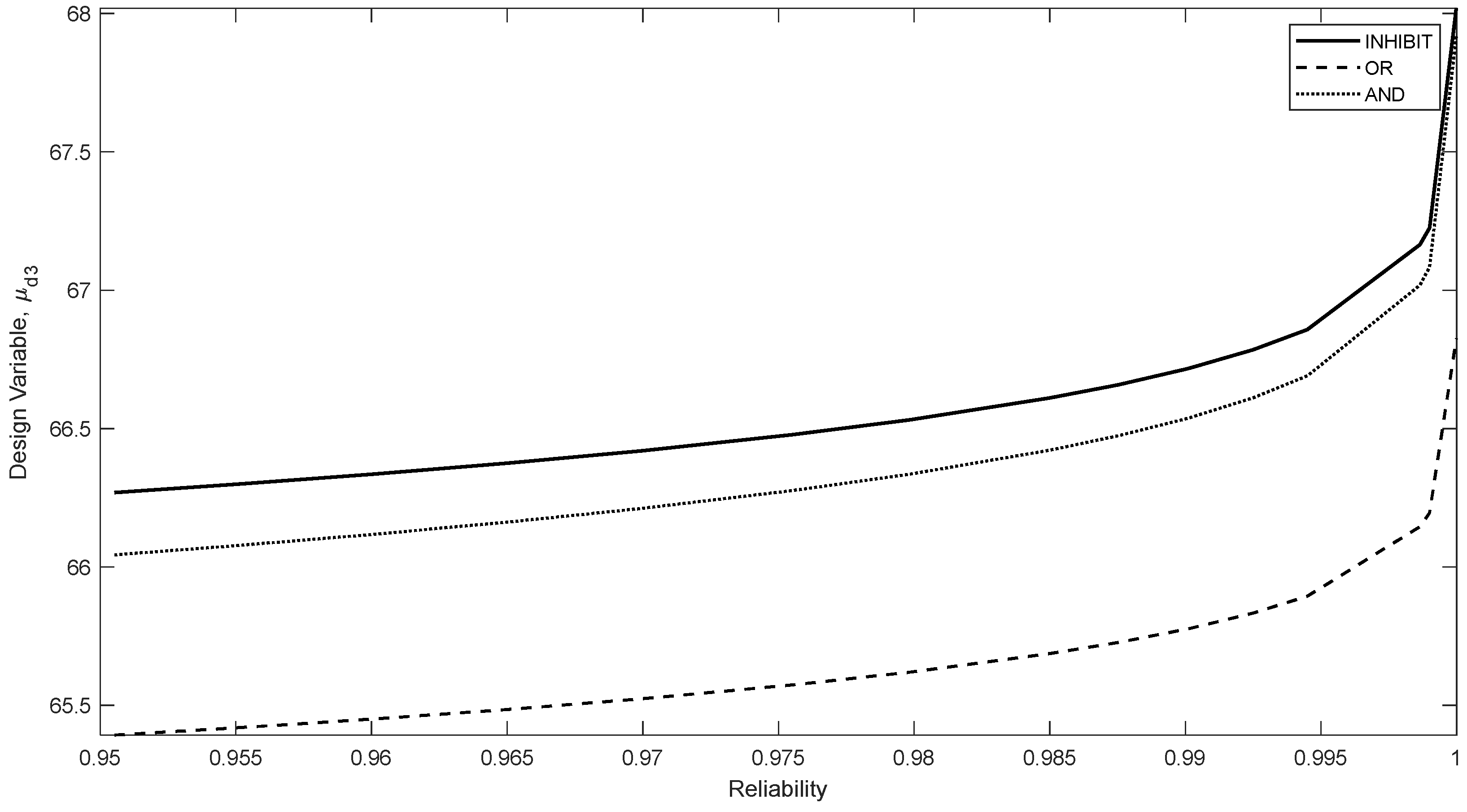
3.3. Design Evolution by Increasing System Reliability
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Haldar, A.; Mahadevan, A. Probability, Reliability and Statistical Methods in Engineering Design; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Ghanem, R.; Spanos, P. Stochastic Finite Elements—A Spectral Approach, 1st ed.; Springer: New York, NY, USA, 1991. [Google Scholar]
- Isukapalli, S.S.; Roy, A.; Georgopoulos, P.G. Efficient Sensitivity/Uncertainty Analysis Using the Combined Stochastic Response Surface Method and Automated Differentiation: Application to Environmental and Biological Systems. Risk Anal. 2000, 20, 591–602. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener--Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Kim, N.H.; Wang, H.; Queipo, V. Efficient Shape Optimization under Uncertainty using Polynomial Chaos Expansions and Local Sensitivities. AIAA J. 2006, 44, 1112–1116. [Google Scholar] [CrossRef][Green Version]
- Huang, B.; Du, X. A Robust Design Method using Variable Transformation and Gauss-Hermite Integration. Int. J. Numer. Meth. Eng. 2006, 66, 1841–1858. [Google Scholar] [CrossRef]
- Kamiński, M. Potential Problems with Random Parameters by the Generalized Perturbation-Based Stochastic Finite Element Method. Comput. Struct. 2010, 88, 437–445. [Google Scholar] [CrossRef]
- Navarro-Quiles, A.; Laudani, R.; Giovanni, G. A New Stochastic Method Based on the Taylor Expansion to Compute Response Probability Densities of Uncertain Systems. Int. J. Numer. Meth. Eng. 2023, 124, 1111–1127. [Google Scholar] [CrossRef]
- Moustapha, M.; Sudret, B.; Bourinet, J.-M.; Guillaume, B. Quantile-Based Optimization under Uncertainties Using Adaptive Kriging Surrogate Models. Struct. Multidiscip. Optim. 2016, 54, 1403–1421. [Google Scholar] [CrossRef]
- Ren, X.; Rahman, S. Stochastic Design Optimization Accounting for Structural and Distributional Design Variables. Eng. Comput. 2018, 35, 2654–2695. [Google Scholar] [CrossRef]
- Xu, H.; Rahman, S. A Generalized Dimension-Reduction Method for Multidimensional Integration in Stochastic Mechanics. Int. J. Numer. Meth. Eng. 2004, 61, 1992–2019. [Google Scholar] [CrossRef]
- Rahman, S. A Polynomial Dimensional Decomposition for Stochastic Computing. Int. J. Numer. Meth. Eng. 2008, 76, 2091–2116. [Google Scholar] [CrossRef]
- Barthelemy, J.-F.M.; Sobieszczanski-Sobieski, J. Extrapolation of Optimum Design Based on Sensitivity Derivatives. AIAA J. 1983, 21, 797–799. [Google Scholar] [CrossRef]
- Barthelemy, J.-F.M.; Sobieszczanski-Sobieski, J. Optimum Sensitivity Derivatives of Objective Functions in Nonlinear Programming. AIAA J. 1983, 21, 913–915. [Google Scholar] [CrossRef]
- Tu, J.; Choi, K.K. A New Study on Reliability-Based Design Optimization. J. Mech. Des. 1999, 121, 557–564. [Google Scholar] [CrossRef]
- Hou, G.J.-W. A Most Probable Point-Based Method for Reliability Analysis, Sensitivity Analysis, and Design Optimization; NASA/CR-2004-213002; National Aeronautics and Space Administration, NASA Langley Research Center: Hampton, VA, USA, 2004. Available online: https://ntrs.nasa.gov/citations/20040045166 (accessed on 8 November 2024).
- Youn, B.D.; Choi, K.K. Hybrid Analysis Method for Reliability-Based Design Optimization. J. Mech. Des. 2003, 125, 221–232. [Google Scholar] [CrossRef]
- Du, X.; Chen, W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design. J. Mech. Des. 2004, 126, 225–233. [Google Scholar] [CrossRef]
- Yang, R.J.; Gu, L. Experience with Approximate Reliability Based Optimization Method. Struct. Multidisc. Optim. 2004, 26, 152–159. [Google Scholar] [CrossRef]
- Gumbert, C.R.; Newman, P.A.; Hou, G.J.-W. High-Fidelity Computational Optimization for 3-D Flexible Wings: Part II—Effect of Random Geometric Uncertainty on Design. Optim. Eng. 2005, 6, 139–156. [Google Scholar] [CrossRef]
- Cho, T.M.; Lee, B.C. Reliability-Based Design Optimization Using Convex Linearization and Sequential Optimization and Reliability Assessment Method. Struct. Saf. 2011, 33, 42–50. [Google Scholar] [CrossRef]
- Doltsinis, I.; Kang, Z. Robust Design of Structures Using Optimization Methods. Comput. Methods Appl. Mech. Eng. 2004, 193, 2221–2237. [Google Scholar] [CrossRef]
- Zhang, W.; Kang, Z. Robust Shape and Topology Optimization Considering Geometric Uncertainties with Stochastic Level Set Perturbation. Int. J. Numer. Meth. Eng. 2017, 110, 31–56. [Google Scholar] [CrossRef]
- Meng, D.; Yang, H.; Yang, S.; Zhang, Y.; De Jesus, A.M.P.; Correia, J.; Fazeres-Ferradosa, T.; Macek, W.; Branco, R.; Zhu, S.P. Kriging-Assisted Hybrid Reliability Design and Optimization Of Offshore Wind Turbine Support Structure Based On A Portfolio Allocation Strategy. Ocean Eng. 2024, 295, 116842. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; De Jesus, A.M.P.; Fazeres-Ferradosa, T.; Zhu, S.P. A Novel Hybrid Adaptive Kriging And Water Cycle Algorithm For Reliability-Based Design And Optimization Strategy: Application In Offshore Wind Turbine Monopile. Comput. Methods Appl. Mech. Eng. 2023, 412, 116083. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, B.; Lu, F. A Reliability-Based Robust Design Optimization Method for Rolling Bearing Fatigue under Cyclic Load Spectrum. Mathematics 2023, 11, 2843. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, B.; Lu, F. An Adaptive Kriging-Based Fourth-Moment Reliability Analysis Method for Engineering Structures. Appl. Sci. 2024, 14, 3247. [Google Scholar] [CrossRef]
- Liao, H.; Elsayed, E.A. Optimization of System Reliability Robustness Using Accelerated Degradation Testing. In Proceedings of the 51st Annual Reliability and Maintainability Symposium, Alexandria, VA, USA, 24–27 January 2005. [Google Scholar] [CrossRef]
- Babonneau, F.; Gilbert, D.; Piller, O.; Vial, J.P. Robust Optimal Design of a Tree-based Water Distribution Network with Intermittent Demand. Eur. J. Oper. Res. 2024, 319, 834–844. [Google Scholar] [CrossRef]
- Wang, C.; Fan, H.; Qiang, X. A Review of Uncertainty-Based Multidisciplinary Design Optimization Methods Based on Intelligent Strategies. Symmetry 2023, 15, 1875. [Google Scholar] [CrossRef]
- Veyna, U.; Blasco, X.; Pajares, A. Strategy for Obtaining Robust Solutions in Multi-objective Design with Uncertainties. Appl. Math. Model. 2025, 138, 115767. [Google Scholar] [CrossRef]
- Shahraki, A.F.; Noorossana, R. Reliability-Based Robust Design Optimization: A General Methodology Using Genetic Algorithm. Comput. Ind. Eng. 2014, 74, 199–207. [Google Scholar] [CrossRef]
- Ortmeier, F.; Reif, W. Safety Optimization: A Combination of Fault Tree Analysis and Optimization Techniques. In Proceedings of the International Conference on Dependable Systems and Networks, Florence, Italy, 28 June–1 July 2004. [Google Scholar] [CrossRef]
- Krasich, M. Fault Tree Analysis for Product Reliability Improvement. In Proceedings of the Annual Reliability and Maintainability Symposium, Alexandria, VA, USA, 24–27 January 2005. [Google Scholar]
- Baig, A.A.; Ruzli, R.; Buang, A.B. Reliability Analysis Using Fault Tree Analysis: A Review. Int. J. Chem. Eng. Appl. 2013, 4, 169–173. [Google Scholar] [CrossRef]
- Ruijters, E.; Stoelinga, M. Fault Tree Analysis: A Survey of the State-of-the-Art in Modeling, Analysis and Tools. Comput. Sci. Rev. 2015, 15–16, 29–62. [Google Scholar] [CrossRef]
- Andrews, J.; Tolo, S. Dynamic and Dependent Tree Theory (D2T2): A Framework for The Analysis of Fault Trees with Dependent Basic Events. Reliab. Eng. Syst. Saf. 2023, 230, 108959. [Google Scholar] [CrossRef]
- Martinez, J.; Eguia, A.; Urretavizcaya, I.; Negro, P.L. Fault Tree Analysis and Failure Modes and Effects Analysis for Systems with Artificial Intelligence: A Mapping Study. In Proceedings of the IEEE 7th International Conference on System Reliability and Safety, Bologna, Italy, 22–24 November 2023; pp. 464–473. [Google Scholar] [CrossRef]
- Shao, T.; Lin, Z.; Krishnamurty, S.; Grosse, I.R.; Osterwell, L.J. Automated Fault Tree Analysis for Engineering Design Optimization. In Proceedings of the ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Volume 5: 6th International Conference on Multibody Systems, Nonlinear Dynamics, and Control, Parts A, B, and C, Las Vegas, NV, USA, 4–7 September 2007; pp. 589–598. [Google Scholar] [CrossRef]
- Sun, J.; Bathgate, K.; Zhang, Z. Bayesian Network-Based Resilience Assessment of Interdependent Infrastructure Systems under Optimal Resource Allocation Strategies. Resilient Cities Struct. 2024, 2, 46–56. [Google Scholar] [CrossRef]
- Sezer, S.I.; Ceylan, B.O.; Akyuz, E.; Gardoni, P. Improved Z-Number and Fault Tree Analysis to Predict the Risk of Air Pollution due to Ship Boiler Operation. Mar. Pollut. Bull. 2024, 206, 116801. [Google Scholar] [CrossRef]
- Sun, H.; Li, H.; Fan, F.; Wang, P.; Yin, F.; Liang, Z. Waste Smartphone Disassembly Fault Detection Based upon Fuzzy Set Fault Tree Analysis. Procedia CIRP 2022, 105, 553–558. [Google Scholar] [CrossRef]
- Li, F.; Meng, G.; Sha, L.; Zhou, L. Robust Optimization Design for Fatigue Life. Finite Elem. Anal. Des. 2011, 47, 1186–1190. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Yan, Q.; Hu, Y.; Wang, C.; Luo, W.; Cai, B. A Dynamic Failure Analysis Methodology for Fault Diagnosis of Fatigue Cracks of Subsea Wellhead Connectors with Material Aging. Process Saf. Environ. Prot. 2022, 159, 36–52. [Google Scholar] [CrossRef]
- Arsic, D.; Kirin, S.; Nikolic, R.; Nikolic, R.; Arsic, A.; Radovic, L. Probabilistic Approach and Fault-Tree Analysis for Increased Bucket Wheel Excavator Welded Joints Reliability. Procedia Struct. Integr. 2022, 42, 189–195. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design, 11th ed.; McGraw Hill: New York, NY, USA, 2020. [Google Scholar]
- Belegundu, A.D.; Chandrupatlia, T.R. Optimization Concepts and Applications in Engineering, 3rd ed.; Cambridge University Press: New York, NY, USA, 2019. [Google Scholar]

| Symbol | Name | Equation |
|---|---|---|
 | AND | |
 | OR | |
 | INHIBIT |
| Method | |||||
|---|---|---|---|---|---|
| RD | MC | ||||
| Deterministic | 64.8332 | 319.6463 | - | - | - |
| Robust Design | 66.0437 | 332.5874 | (13.7859, 0.1298) | 0.9505 | 0.9483 |
| “and” Gate | 66.0437 | 332.5874 | (13.7859, 0.1298) | 0.9505 | 0.9483 |
| “or” Gate | 65.3925 | 331.285 | (13.8994, 0.1317) | 0.7776 | 0.7760 |
| “Inhibit” Gate | 66.2687 | 333.0374 | (13.7470, 0.1291) | 0.9505 | 0.9468 |
| Methods | Lagrange Multiplier | Post Optimality SA, | |||
|---|---|---|---|---|---|
| 95.053% to 95.994% | , 14 to 13.9 | 95.053% to 95.994% | , 14 to 13.9 | ||
| Deterministic | 11.2439 | - | 1.1244 | - | 1.1316 |
| Robust Design | 1.4593 | 0.1459 | 1.1245 | 0.1458 | 1.2018 |
| “and” Gate | 14.2637 | 0.1343 | 1.1251 | 0.1458 | 1.1313 |
| “or” Gate | 11.1726 | 0.1050 | 1.1244 | 0.114 | 1.1317 |
| “Inhibit” Gate | 12.7206 | 0.1197 | 1.1246 | 0.1303 | 1.1317 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
DeGroff, J.; Hou, G.J.-W. Fault Tree Analysis for Robust Design. Designs 2025, 9, 19. https://doi.org/10.3390/designs9010019
DeGroff J, Hou GJ-W. Fault Tree Analysis for Robust Design. Designs. 2025; 9(1):19. https://doi.org/10.3390/designs9010019
Chicago/Turabian StyleDeGroff, Jonathan, and Gene Jean-Win Hou. 2025. "Fault Tree Analysis for Robust Design" Designs 9, no. 1: 19. https://doi.org/10.3390/designs9010019
APA StyleDeGroff, J., & Hou, G. J.-W. (2025). Fault Tree Analysis for Robust Design. Designs, 9(1), 19. https://doi.org/10.3390/designs9010019







