Development and Dynamic Numerical Evaluation of a Lightweight Sports Helmet Using Topology Optimization and Advanced Architected Materials
Abstract
:1. Introduction
- Lightweight sports helmet with relatively low-cost materials, i.e., PA12;
- Additively manufactured sports helmet with enhanced structural integrity and increased energy absorption capability utilizing only one construction material;
- Significant reduction in probability of injury from impact compared to a solid helmet;
- Further improvement of the helmet’s energy absorption performance by filling the porosity of the structure with foam material (polyurethane foam).
2. Materials and Methods
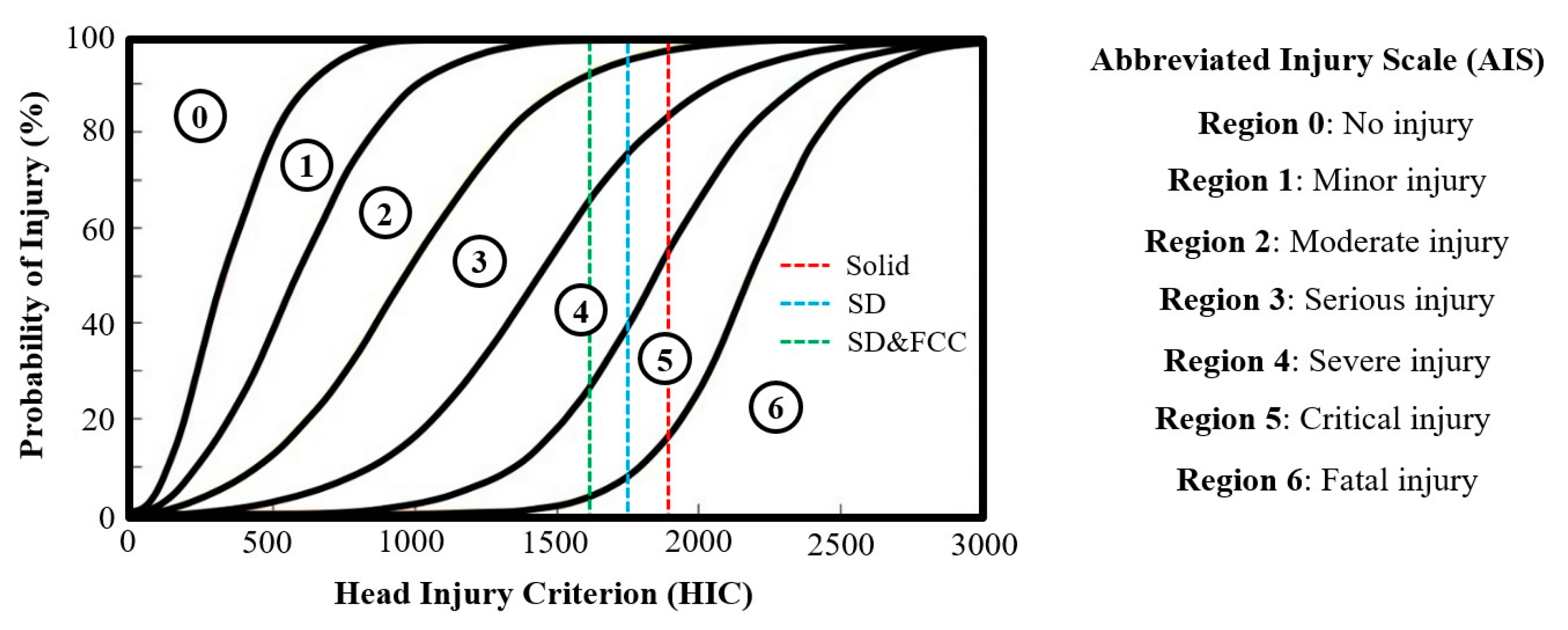
2.1. HIC Evaluation
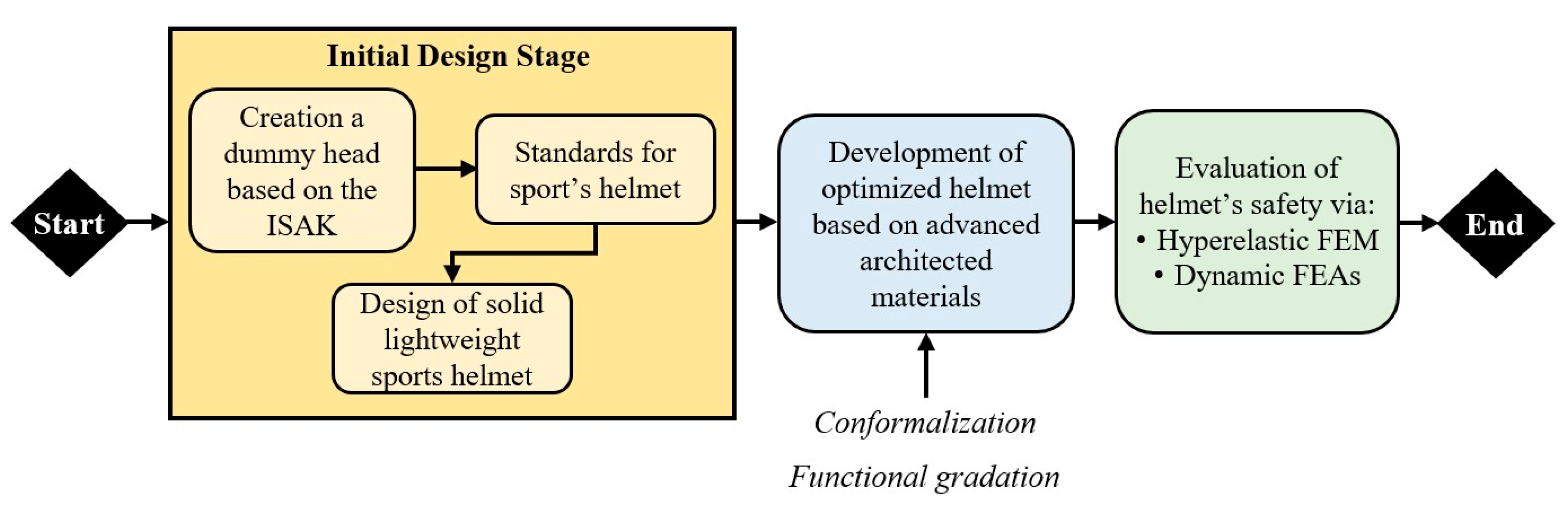
2.2. Design Process of the Sport’s Helmet
2.3. Evaluation Methodology
3. Results
3.1. Final Design of the Helmet
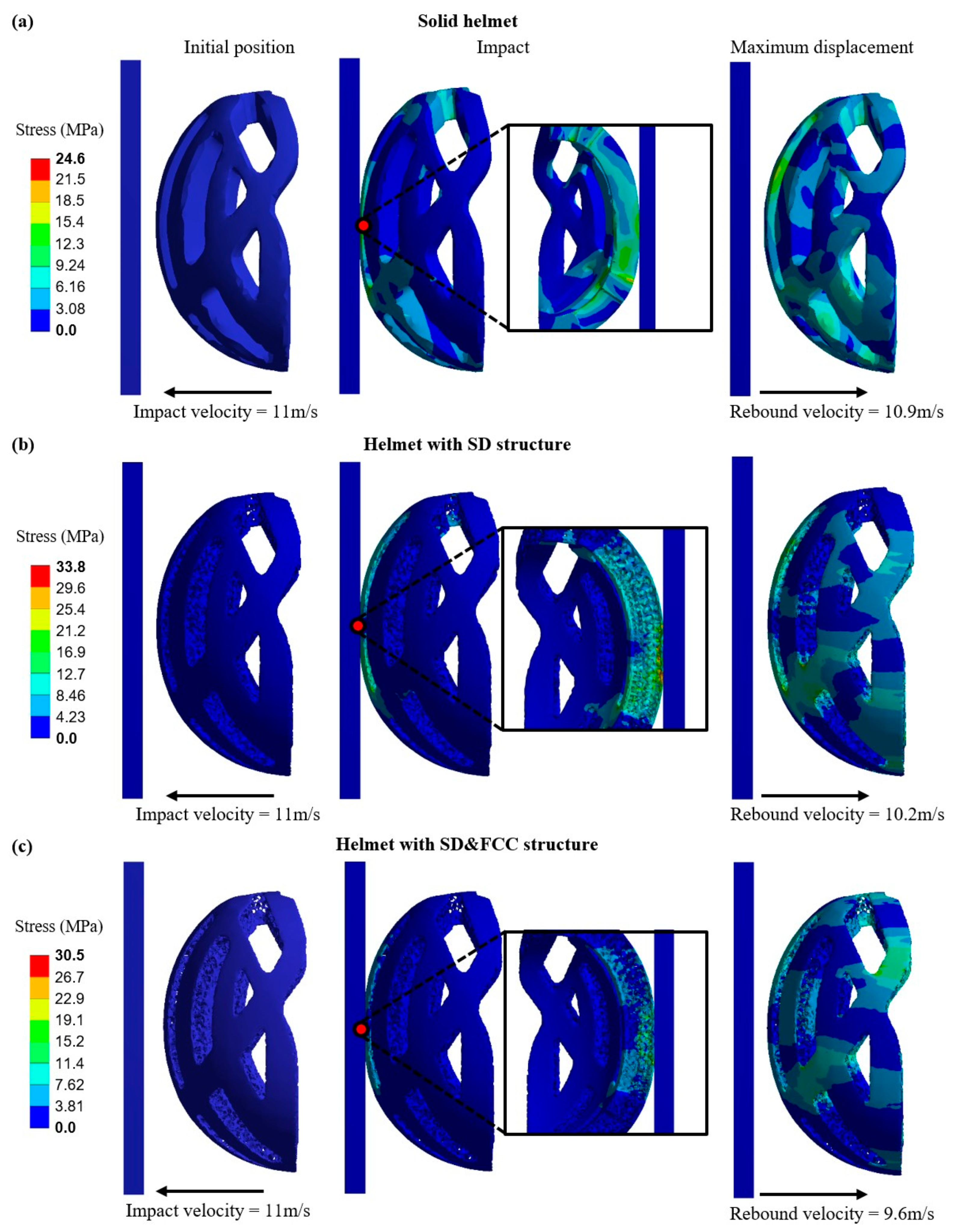
3.2. Dynamic FEA Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gennarelli, T.A.; Wodzin, E. AIS 2005: A contemporary injury scale. Injury 2006, 37, 1083–1091. [Google Scholar] [CrossRef] [PubMed]
- Henn, H.W. Crash Tests and the Head Injury Criterion. Teach. Math. Its Appl. Int. J. IMA 1998, 17, 162–170. [Google Scholar] [CrossRef]
- Nellippallil, A.B.; Berthelson, P.R.; Peterson, L.; Prabhu, R.K. Chapter 10—Robust concept exploration of driver’s side vehicular impacts for human-centric crashworthiness. In Multiscale Biomechanical Modeling of the Brain; Prabhu, R., Horstemeyer, M., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 153–176. [Google Scholar] [CrossRef]
- Mustafa, H.; Pang, T.Y.; Perret-Ellena, T.; Subic, A. Finite Element Bicycle Helmet Models Development. Procedia Technol. 2015, 10, 91–97. [Google Scholar] [CrossRef]
- Willinger, R.; Deck, C.; Halldin, P.H.; Otte, D. Towards advanced bicycle helmet test methods. In Proceedings of the International Cycling Safety Conference 2014, Göteborg, Sweden, 18–19 November 2014. [Google Scholar]
- Fernandes, F.A.O.; de Sousa, R.J.A. Finite element analysis of helmeted oblique impacts and head injury evaluation with a commercial road helmet. Struct. Eng. Mech. 2013, 48, 661–679. [Google Scholar] [CrossRef]
- Dao, P.N.; Nguyen, Q.P.; Vu, M.H. Adaptive optimal coordination control of perturbed Bilateral Teleoperators with variable time delays using Actor–Critic Reinforcement Learning algorithm. Math. Comput. Simul. 2025, 229, 151–175. [Google Scholar] [CrossRef]
- Guo, Y.; Dong, H.; Yinglin Ke, Y. Stiffness-oriented posture optimization in robotic machining applications. Robot. Comput. Integr. Manuf. 2015, 35, 69–76. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Wu, B.; Chen, X.; Ren, X.; Xie, Y.M. A novel bio-inspired helmet with auxetic lattice liners for mitigating trau-matic brain injury. Smart Mater. Struct. 2023, 32, 105020. [Google Scholar] [CrossRef]
- Li, S.; Xiao, Z.; Zhang, Y.; Li, Q.M. Impact analysis of a honeycomb-filled motorcycle helmet based on coupled head-helmet modelling. Int. J. Mech. Sci. 2021, 199, 106406. [Google Scholar] [CrossRef]
- Greer, J.R.; Deshpande, V.S. Three-dimensional architected materials and structures: Design, fabrication, and mechanical be-havior. MRS Bull. 2019, 44, 750–757. [Google Scholar] [CrossRef]
- Baroutaji, A.; Sajjia, M.; Olabi, A.-G. On the Crashworthiness Performance of Thin-Walled Energy Absorbers: Recent Advances and Future Developments. Thin-Walled Struct. 2017, 118, 137–163. [Google Scholar] [CrossRef]
- Novak, N.; Al-Ketan, O.; Krstulović-Opara, L.; Rowshan, R.; Abu Al-Rub, R.K.; Vesenjak, M.; Ren, Z. Quasi-Static and Dynamic Compressive Behaviour of Sheet TPMS Cellular Structures. Compos. Struct. 2021, 266, 113801. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Bakir, M.; Abu Al-Rub, R.K.; Bergström, J.S.; Sobh, N.A.; Jasiuk, I. Mechanical Properties of 3D Printed Polymeric Cellular Materials with Triply Periodic Minimal Surface Architectures. Mater. Des. 2017, 122, 255–267. [Google Scholar] [CrossRef]
- Abou-Ali, A.M.; Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R. Mechanical Re-sponse of 3D Printed Bending-Dominated Liga-ment-Based Triply Periodic Cellu-lar Polymeric Solids. J. Mater. Eng. Perform. 2019, 28, 2316–2326. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Karalekas, D.; Tzetzis, D. Architected Materials for Additive Manufacturing: A Comprehensive Review. Materials 2022, 15, 5919. [Google Scholar] [CrossRef] [PubMed]
- Hayes, W.C.; Erickson, M.S.; Power, E.D. Forensic Injury Biomechanics. Annu. Rev. Biomed. Eng. 2007, 9, 55–86. [Google Scholar] [CrossRef]
- Pheasant, S.; Haslegrave, C.M. Bodyspace: Anthropometry, Ergonomics and the Design of Work, 3rd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis: London, UK, 2018. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Kostavelis, I.; Tzovaras, D.; Tzetzis, D. Effective mechanical properties of additive manufactured triply periodic minimal surfaces: Experimental and finite element study. Int. J. Adv. Manuf. Technol. 2022, 121, 7169–7189. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Tzetzis, D. Development of Novel Additive Manufactured Hybrid Architected Materials and Investigation of their Mechanical Behavior. Mech. Mater. 2023, 176, 104525. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Y.M.; Wu, X.; Wang, Z.; Li, Q.; Zhou, S. On hybrid cellular materials based on triply periodic minimal surfaces with extreme mechanical properties. J. Mater. Des. 2019, 183, 108109. [Google Scholar] [CrossRef]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for Functionally Graded Lattice Structures Derived Using Topology Optimisation for Additive Manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Yang, L.; Mertens, R.; Ferrucci, M.; Yan, C.; Shi, Y.; Yang, S. Continuous Grad-ed Gyroid Cellular Structures Fabricated by Se-lective Laser Melting: Design, Manufacturing and Mechanical Properties. Mater. Des. 2019, 162, 394–404. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Kyriakidis, I.F.; Tzimtzimis, E.K.; Pechlivani, E.M.; Tsongas, K.; Tzetzis, D. Development of 4D-Printed Arterial Stents Utilizing Bioinspired Architected Auxetic Materials. Biomimetics 2025, 10, 78. [Google Scholar] [CrossRef] [PubMed]
- Abueidda, D.W.; Abu Al-Rub, R.K.; Dalaq, A.S.; Lee, D.-W.; Khan, K.A.; Ja-siuk, I. Effective Conductivities and Elastic Moduli of Novel Foams with Triply Periodic Minimal Surfaces. Mech. Mater. 2016, 95, 102–115. [Google Scholar] [CrossRef]
- Renaud, C.; Cros, J.-M.; Feng, Z.-Q.; Yang, B. The Yeoh Model Applied to the Modeling of Large Deformation Contact/Impact Problems. Int. J. Impact Eng. 2009, 36, 659–666. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Kostavelis, I.; Tzovaras, D.; Tzetzis, D. Effective Mechanical Properties of Additive Manufac-tured Strut-Lattice Structures: Experimental and Finite Element Study. Adv. Eng. Mater. 2021, 24, 2100879. [Google Scholar] [CrossRef]





| Level | Severity | Type of Injury |
|---|---|---|
| 0 | None | No injury |
| 1 | Minor | Superficial injury |
| 2 | Moderate | Reversible injury, medical attention required |
| 3 | Serious | Reversible injury, and hospitalization required |
| 4 | Severe | Life-threatening, not fully recoverable without care |
| 5 | Critical | Non-reversible injury, not fully recoverable even with medical care |
| 6 | Fatal | Unsurvivable injury |
| Design | Total Elements | Minimum Edge Length |
|---|---|---|
| Solid | 129,200 | 0.15 mm |
| SD | 412,278 | 0.12 mm |
| SD–FCC | 444,808 | 0.15 |
| Properties | Values |
|---|---|
| Density | 0.95 g/cm3 |
| Elastic modulus | 938 ± 30 MPa |
| Yield strength | 22.7 ± 0.5 MPa |
| Ultimate tensile strength | 31.8 ± 0.5 MPa |
| Elongation at break | 10% ± 1% |
| Design | Average Acceleration (gs) | Impact Duration (s) | HIC | FOS | Weight (kg) |
|---|---|---|---|---|---|
| Solid | 89.33 | 0.025 | 1885 | 0.93 | 1.67 |
| SD | 86.47 | 1738 | 0.68 | 0.86 | |
| SD–FCC | 84.02 | 1618 | 0.76 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kladovasilakis, N.; Tsongas, K.; Pechlivani, E.M.; Tzetzis, D. Development and Dynamic Numerical Evaluation of a Lightweight Sports Helmet Using Topology Optimization and Advanced Architected Materials. Designs 2025, 9, 28. https://doi.org/10.3390/designs9020028
Kladovasilakis N, Tsongas K, Pechlivani EM, Tzetzis D. Development and Dynamic Numerical Evaluation of a Lightweight Sports Helmet Using Topology Optimization and Advanced Architected Materials. Designs. 2025; 9(2):28. https://doi.org/10.3390/designs9020028
Chicago/Turabian StyleKladovasilakis, Nikolaos, Konstantinos Tsongas, Eleftheria Maria Pechlivani, and Dimitrios Tzetzis. 2025. "Development and Dynamic Numerical Evaluation of a Lightweight Sports Helmet Using Topology Optimization and Advanced Architected Materials" Designs 9, no. 2: 28. https://doi.org/10.3390/designs9020028
APA StyleKladovasilakis, N., Tsongas, K., Pechlivani, E. M., & Tzetzis, D. (2025). Development and Dynamic Numerical Evaluation of a Lightweight Sports Helmet Using Topology Optimization and Advanced Architected Materials. Designs, 9(2), 28. https://doi.org/10.3390/designs9020028









