Guidelines for Design and Additive Manufacturing Specify the Use of Surgical Templates with Improved Accuracy Using the Masked Stereolithography Technique in the Zygomatic Bone Region

Abstract

The zygomatic bone area experiences frequent mechanical damage in the middle craniofacial region, including the orbital floor. The orbital floor bone is very thin, ranging from 0.74 mm to 1.5 mm. Enhancing digitization, reconstruction, and CAD modeling procedures is essential to improving the visualization of this structure. Achieving a homogeneous surface with high manufacturing accuracy is crucial for developing precise surgical models and tools for creating titanium mesh implants to reconstruct the orbital floor geometry. This article improved the accuracy of reconstruction and CAD modeling using the example of the development of a prototype implant to replace the zygomatic bone and a tool to form the geometry of the titanium mesh within the geometry of the orbital floor. The masked stereolithography (mSLA) method was used in the model manufacturing process because it is low-cost and highly accurate. Two manufacturing modes (standard and ultra-light) were tested on an Anycubic Photon M3 Premium 3D printer to determine which mode produced a more accurate representation of the geometry. To verify the geometric accuracy of the manufactured models, a GOM Scan1 structured light scanner was used. In the process of evaluating the accuracy of the model preparation, the maximum deviation, mean deviation, range and standard deviation were determined. The maximum deviations for anatomical structures created using the normal mode ranged from ±0.6 mm to ±0.7 mm. In contrast, models produced with the ultra-light mode showed deviations of ±0.5 mm to ±0.6 mm. Furthermore, the results indicate that the ultra-light mode offers better surface accuracy for die and stamp models. More than 70% of the surface of the models is within the deviation range of ±0.3 mm, which is sufficient for planning surgical procedures. However, the guidelines developed in the presented publication need to optimize the CAD process and select 3D-printing parameters to minimize deviations, especially at the edges of manufactured models.

1. Introduction

The craniofacial bone includes the zygomatic bone. The zygomatic bone is a significant part of the skull structure, giving the face shape and form. It helps protect the orbital region, including the eyeball, from injury. The zygomatic bone joins with other facial bones, such as the temporal, maxillary, and cuneiform bones, to form the complex structure of the facial skeleton. It is one of the bones most frequently subjected to mechanical trauma [1]. Injuries and diseases of the skeletal system in this area result in altered facial appearance, malocclusion, and problems with the essential functions of chewing food, which, in the long term, leads to eating disorders [2,3]. These factors all contribute to deteriorations in the patient’s mental and physical state. It is, therefore, essential to undertake treatment and reconstruction of the resulting bone defect. The surgical reconstruction of the zygomatic bone area is very complex, as it requires the implant to be accurately matched to the defect [4,5]. Autogenous grafts are the gold standard in treating zygomatic bone defects [6,7]. They are used in cases of extensive fractures resulting in the loss of a large portion of bone [4]. This procedure is associated with the possibility of additional swelling and complications at the site of bone harvesting for grafting. The geometry of the graft itself also has to be manually adjusted to the size and shape of the defect [8]. This considerably lengthens the procedure, and the final result upon fitting the graft into the defect is not ideal [9]. For this reason, 3D-printing methods are being used more and more frequently to manufacture models of craniofacial anatomical structures, as models made using these methods are individually adapted and prepared for a specific patient [10]. This ensures that they are precisely matched to the defect, significantly reducing the time it takes to perform the procedure and the occurrence of postoperative complications [11].

The entire process of reconstructing the geometry within the region encompassing the zygomatic bone is possible due to the integration of tomographic measurement systems, digital data-editing software, and modern manufacturing methods [12,13,14]. Despite obtaining a complete geometry of the anatomical structure, it must be borne in mind that at each stage of the measurement process, reconstruction, computer-aided design (CAD) modeling, and manufacturing errors are created that significantly affect the geometric accuracy of the completed model [15,16,17]. The accuracy of the representation of the geometry of anatomical structures is mainly affected by the digitization stage [16,17] and the processing of volumetric data [18,19]. Multi-detector and cone tomographies are most commonly used in the diagnostic process of the craniofacial region [12,20]. Based on the collected Digital Imaging and Communications in Medicine (DICOM) data, a segmentation and geometry reconstruction is achieved using computer-aided design software. At this stage, the segmentation process plays the most crucial role in the method and the parameters used to extract the anatomical structure from the DICOM data, as well as in the geometry reconstruction methods [16,19]. In developing the geometry of an anatomical structure and a surgical template or implant, it is necessary to use additional CAD modeling software. Most often, hybrid modeling combining solid and surface modeling is used [20,21]. The gold standard uses mirroring and Boolean methods to model zygomatic bone defect geometry in a CAD environment [12]. However, the uncontrolled accuracy of monitoring when using stereolithography (STL) file-processing methods and the CAD-based creation of surgical templates and implant constructs generate additional geometry errors in the final digital model [21].

The choice of manufacturing method also influences the accuracy of reconstructions of the geometry of the anatomical structure [22,23]. A physical model can be obtained using subtractive methods [24] or molding methods [25]. However, due to the complex geometry of the models of anatomical structures within the zygomatic bone area, it is challenging, time-consuming, and thus costly to produce them using, among other things, subtractive methods. Therefore, additive methods are an ideal alternative for creating such models [26,27]. To date, material extrusion (MEX) [12,13,28], vat photopolymerization (VPP) [29], powder bed fusion (PBF) [13,20], and material jetting (MJ) [20] methods are most commonly used to produce models of anatomical structures and surgical templates within the zygomatic bone. Unfortunately, the methods listed also have limitations. These are due to the cost of manufacturing the models and, in some cases, the quality of the manufactured models. Actually, it is becoming increasingly common to manufacture models using masked stereolithography (mSLA) technology, which is a VPP method [30]. SLA technology is becoming increasingly recognized as it has a operating cost than digital-light-processing (DLP) and provides excellent reproduction of details, which is beneficial for high-precision applications [31]. This is a hybrid 3D-printing method combining the advantages of stereolithography (SLA) and DLP. Instead of a projector, as in DLP, mSLA uses an LCD array that masks the UV light emitted by the LED array, allowing the entire resin layer to cure simultaneously [30]. According to the literature review, this method’s models are mainly used to produce electronic circuits [32,33]. The application of this method in the medical industry has also been noted. Previous research has primarily evaluated the applicability of the models in terms of assessing the materials available for this technology in the broader sense of bioengineering [34,35]. However, a study on the usefulness of mSLA technology in producing models of anatomical structures and instruments to support surgical procedures is still lacking. One of the possible anatomical areas in which the mSLA method could find a place is the area of the zygomatic bone. This is an area subject to frequent complex mechanical trauma. The bony structure of the zygomatic bone also includes the area of the orbital floor bone. The orbital floor bone is very thin and varies between 0.74 mm and 1.5 mm [36]. To obtain a more accurate visualization of this bony structure, it is necessary not only to develop a more precise digitization, reconstruction, and CAD modeling procedure, but also to obtain a final homogeneous surface with a high degree of manufacturing accuracy, which will allow for the precise development of models for surgery planning [21,37,38] and tools that enable the formation of implants in the form of a titanium mesh for the reconstruction of the orbital floor geometry.

Based on the literature review, guidelines should be established to enhance the accuracy of the reconstruction and CAD modeling of the zygomatic bone. The goal is to create digital models of anatomical structures resembling real geometries. Additionally, due to the significant advantages of the mSLA method in producing precision models, it is worth testing this method in the context of producing models of anatomical structures to verify the obtained geometrical accuracy. The study may significantly extend the applicability of the mSLA method in manufacturing models of anatomical structures, where the high-precision matching of models to each other is required, as is the case within the zygomatic bone area.

2. Materials and Methods

A study was conducted between the F. Chopin University Clinical Regional Hospital in Rzeszów, specifically within the Department of Maxillofacial Surgery, and Rzeszów University of Technology. From 2022 to 2023, 23 patients were involved in the study. This article focuses on two of the most clinically significant cases of patients who experienced injuries from a traffic accident. In the first patient’s case, a significant portion of the zygomatic bone was damaged. In the second patient’s case, the geometry of the left orbital floor was damaged in a non-standard manner. This was due to significant bone loss of the orbital floor. Diagnostic data were obtained using a Discovery CT750 HD multidetector tomograph from GE Medical Systems. The imaging of the craniofacial region was conducted at the University Clinical Hospital Fryderyk Chopin in Rzeszów. The following scanning protocol is commonly used:

• Scan type: helical;
• Beam collimation: 40 mm;
• Detector configuration: 64 × 0.625 mm;
• Tube settings: 120 kV;
• Slice thickness: 1.25 mm;
• Matrix size: 512 × 512.

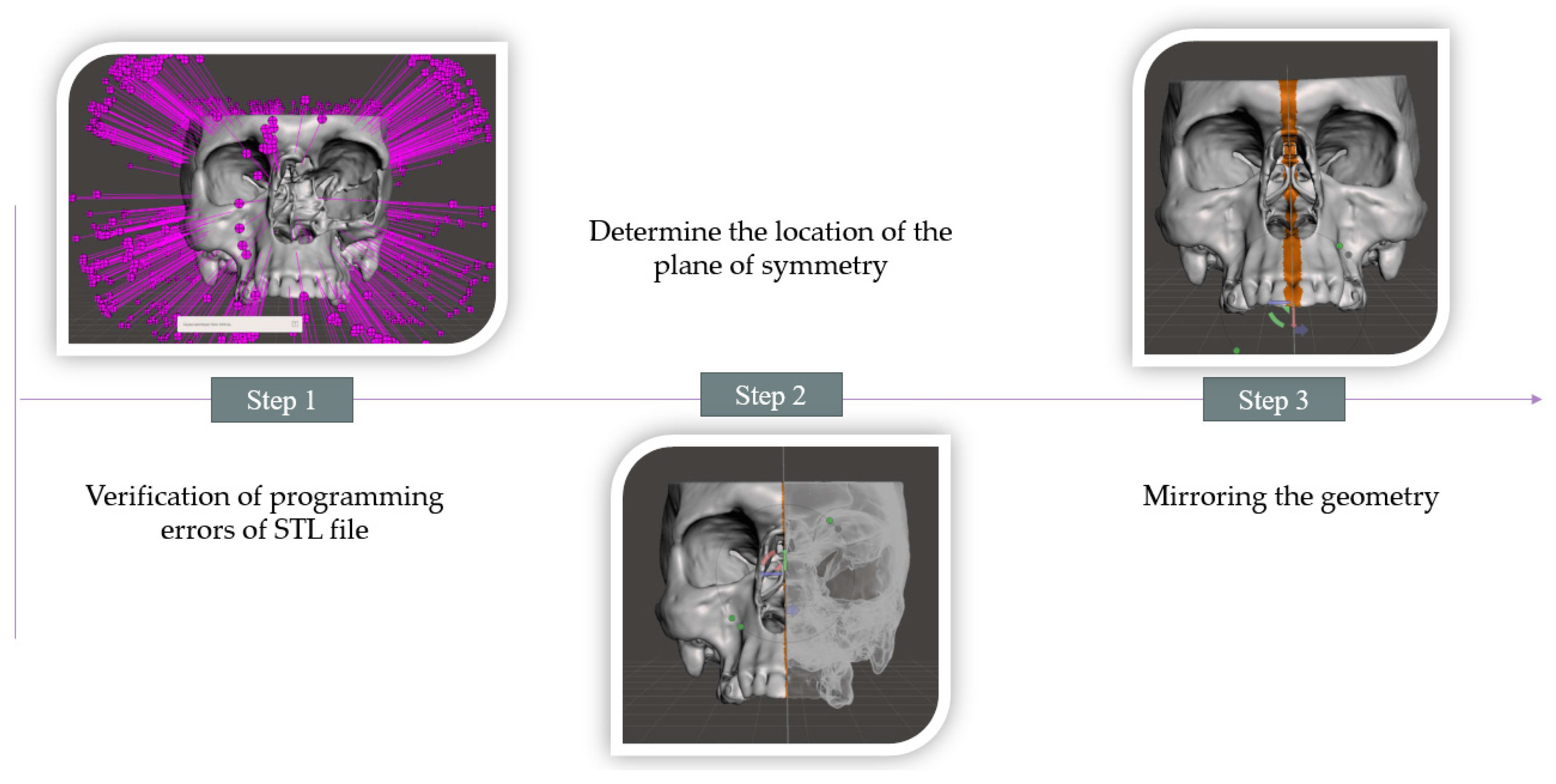
2.1. Process of Digital Processing, Segmentation, and 3D Reconstruction of DICOM Data

This protocol achieves high-resolution DICOM data, with voxel dimensions characterized by an isotropic structure of 0.6 mm × 0.6 mm × 0.625 mm. However, a significant influence of the volume-averaging artifact was observed. Its influence significantly impeded the accurate reconstruction of bone structures within the zygomatic bone region. This artifact occurs when a single voxel encompasses multiple tissue types, leading to contrast distortion, particularly in structures with low contrast. While using a thinner CT layer can address this issue, it also increases the radiation dose, posing a danger to the patient. A safer approach is to perform digital processing on the already-collected DICOM data to improve the accuracy of the 3D model of the anatomical structure (Figure 1).

The first step in this process involved applying an interpolation technique to the DICOM data, specifically using a bilinear method [39]. This method analyzes the gray shade values of the four nearest pixels adjacent to the newly calculated pixel. Bilinear interpolation determines the gray shade value of the new pixel by taking the arithmetic average of the four neighboring pixels, as described in Equation (1):

$$k\left(x\right)=\left\{\begin{array}{c}1-\left|x\right|; \left|x\right|<1\\ 0;otherwise\end{array}\right.,$$

(1)

The interpolation process significantly enhanced the spatial resolution of the data, reducing the voxel size to 0.1 mm × 0.1 mm × 0.1 mm. Using the reformatted DICOM data, we reconstructed the bone structures in the region, including the zygomatic bone, using the 3D Slicer software. The modeling of the bone structures began by importing a sequence of 2D images into the program’s workspace. In the next step, we carried out the segmentation process using a thresholding method [16,18]. To improve the accuracy of the segmentation, we focused on determining the thresholds by averaging the gray shade values of pixels only within the zygomatic bone area instead of across the entire craniofacial region. The average pixel gray value within the zygomatic bone area was 248 HU, with a standard deviation of 81 HU. The mean value and standard deviation of the lower segmentation threshold was established in the context of the 23 patients studied. This procedure avoided artificially increasing the volume of segmented anatomical structures due to the incorrect selection of segmentation thresholds. The marching cubes algorithm was utilized to visualize the 3D model [40,41]. This algorithm divides space into cubes, each encompassing one or more voxels. The values of the nodes at each corner of the designated cube are then compared against a specified iso-value. Depending on whether a node’s value is higher or lower than the iso-value, polygons are generated to represent the iso-surface that intersects the cube. The marching cubes method, like any algorithm, has its limitations. These limitations mainly arise from errors that occur during the reconstruction process of the 3D STL model. Common issues include incorrect triangle orientations, duplicated edges and vertices, and duplicated triangles. To prepare models for 3D-printing, it is crucial to eliminate these errors. If these corrections are not made, it can lead to challenges in dividing the facet surface into 3D-print layers, making it difficult or even impossible to create a model of bone structures using the additive method. We used the triangle mesh editing tools in Meshmixer software to correct programming errors. During the generation of the triangle mesh, chord, and angular deviations occur, particularly in areas with rapid changes in the curvature radii. To minimize these errors, we employed an optimization process to enhance the facet structure by compacting the triangle mesh in regions of high surface complexity. This approach significantly improved the mapping quality of the model geometry. The procedure optimization consisted of two steps:

• The surface is smoothed by moving the nodes on which the triangle mesh is spanned. Each node is moved to the average position of its neighbors by applying the Laplace function. The function is the sum of the squares of the lengths of edges sharing a common node (2):

$$f(x,y)={\displaystyle \sum _{i=0}^k\left({\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2\right)}$$

(2)

• k is the number of neighboring nodes; the position of new nodes is determined using Formula (3):

$$x^{\prime }={\displaystyle \frac{1}{k}}{\displaystyle \sum _{i=1}^k{x}_i}{y}^{\prime }={\displaystyle \frac{1}{k}}{\displaystyle \sum _{i=1}^k{y}_i}$$

(3)

• Triangle densities are created in regions of high complexity, and reducing the number of triangles in flatter areas using the isotropic surface remashing algorithm.

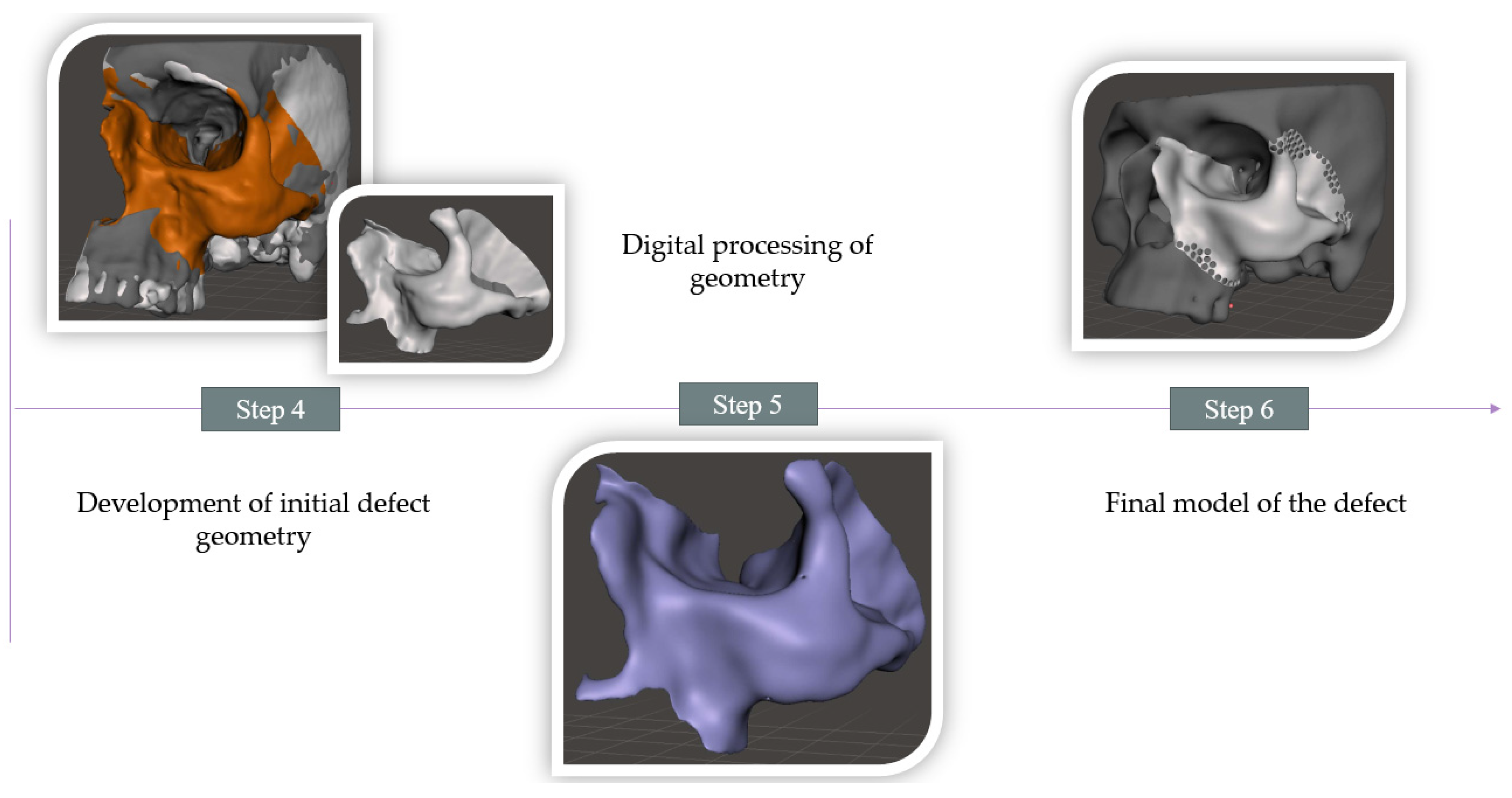
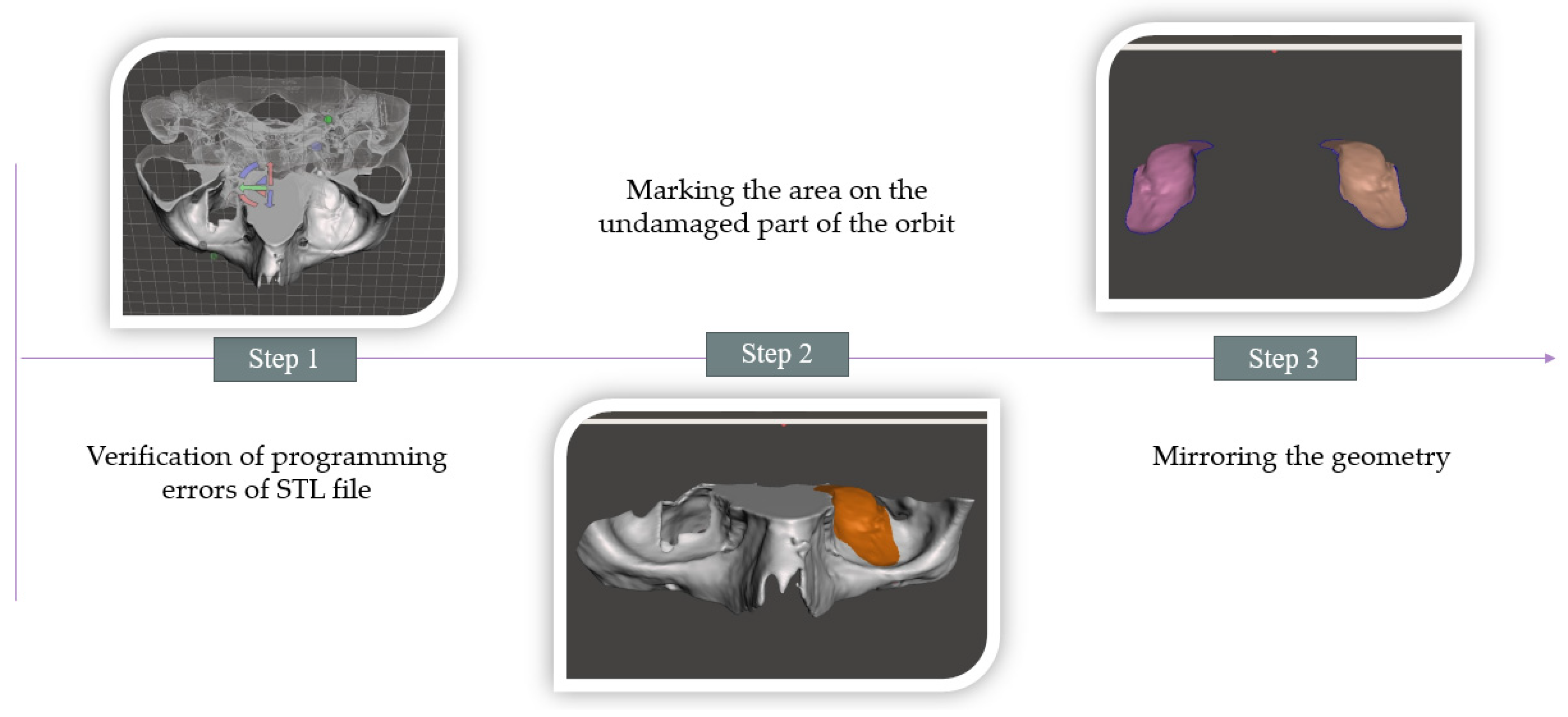
2.2. Procedure for Modeling a Defect in the Zygomatic Bone Area

The process of modeling a defect in the zygomatic bone is presented in Figure 2. After verifying programming errors, the plane of symmetry was developed. Based on this, the skull model was divided into two separate parts. Then, the right (undamaged) part was mirrored onto the left (damaged) part. The mirroring operation was carried out by setting the mirror plane’s angle and selecting the direction of the mirrored part. The damaged part of the skull was visualized so that a visualization of the common edge was obtained, which formed the basis for the zygomatic bone fragment containing the defect. The edges were smoothed on the selected part of the surface, and then a preliminary separation of the geometry covering the defect area was carried out. After the surfaces were disconnected, the newly created geometry was given a thickness, and its surface was smoothed, obtaining a preliminary version of the defect. After smoothing the edges of the defect, it was reapplied to the rest of the skull to eliminate overlapping surface fragments. This procedure aimed to improve the accuracy of the defect’s fit to the skull. The developed model was then examined for any discontinuities arising from the standard edge-extraction process. In the final step, the defect’s geometry was refined by modeling holes within the model geometry. This aim of this procedure was to develop a model structure that would allow the defect to grow more quickly into the bone structure.

2.3. Development of a Tool to Form the Geometry of a Mesh Implant to Reconstruct an Orbital Floor Defect

The geometry of the defect in the right orbit was modeled using data from the left, undamaged orbit (Figure 3). Initially, the model generated through the segmentation and reconstruction process from DICOM data was imported into Meshmixer. After verifying the STL file for programming errors, an area of the geometry from the undamaged orbit was selected as a starting point for further modeling.

At this stage, the goal was to adjust the size of the marked area so that it would resemble the size of the damaged area in the right orbit. The selected part of the orbit was then extracted and separated from the rest of the model. This extracted fragment underwent a mirror image operation. To ensure it matched the area of the orbital defect, further editing, including smoothing the edges, was performed on the extracted area. Once the final geometry of the defect was established, the surface modeling process began. The die and stamp model was developed to create the geometry of the implant using CATIA software. After importing the geometry from the previous modeling stage in STL format, it was converted into a surface model using the Automatic Surface Reconstruction function. At this stage, the primary surface-matching parameters were defined: Mean Surface Deviation was set to 0.025 mm and the Surface Detail parameter was specified to include 20,000 elements. Additionally, attention was paid to the Target Ratio parameter, which determines the percentage of the STL model surface coverage by the generated surface; this was set to 100%. An edge outline was created using a Spline curve in the following step. This edge outline underwent the Spline drawing process, which produced a surface model. This surface model was then transformed into a solid model in the next step. The entire modeling process resulted in a die model that accurately represents the geometry of the orbital floor. The next step was to create a stamp model based on the geometry of the die model. In the first step, the attitude edge of the earlier model was dropped onto the created plane. Based on the dropped sketch, a Pad operation was applied to pull it out in the specified direction, thus creating a new solid. The next step was to trim the newly created solid so that its geometry corresponded to the die model. To achieve this, the Boolean Remove tool in the Part Design module could be used for logical operations on solids. This procedure allowed for the precise subtraction of one solid from another. The die model was a negative to cut off the corresponding stamp elements. As a result, a stamp model was created that perfectly matched the geometry of the die, which is crucial for the precise formation of the geometry of the orbital floor implant.

2.4. Additive Manufacturing of Designed Models Using the mSLA Method

The models were manufactured using an Anycubic Photon M3 Premium 3D printer using the mSLA method. The process began by filling the 3D printer with Siraya Tech liquid resin. Next, the models’ manufacturing parameters were established, focusing on normal and ultra-light modes (

Table 1. Applied 3D-printing parameters.

	Parameter	Value
Basic parameters	Layer Thickness	0.050 mm
	Light-Off Delay	2 s
	Exposure Time	2.4 s
	Lift Distance	2.5 mm
	Lift Speed	45 mm/min
	Retract Speed	240 mm/min
Normal mode	Tip Diameter	0.6 mm
	Tip Length	3 mm
	Diameter	1.3 mm
Ultra-light mode	Tip Diameter	0.3 mm
	Tip Length	2 mm
	Diameter	1 mm

). The Lychee Slicer program generated a support material to ensure the stability of the model and minimize deformations due to its complex geometry.

After defining the model’s layers, the 3D-printing process started (Figure 4). The mSLA method relies on curing photopolymer resin with UV light, which is directed through a mask using an LCD. Once the first layer is cured, the working platform on which the models are being built rises slightly, allowing the next layer to be manufactured. This cycle of exposing the resin and lifting the platform continues until all the models are complete.

After the 3D-printing process, the models and supports remained attached to the working platform. The models were then removed from the platform and placed in a special container filled with alcohol. This rinsing process lasted 4 min to eliminate any remaining resin on their surfaces. Next, the models underwent a precision cleaning of the printed supports. This involved using pliers to cut off the supports close to the model’s surface and plastic cutters for more precise removal. The final processing step included rinsing the models once again in alcohol for another 4 min and exposing them to ultraviolet light. The completed models were then placed on a rotating platform within a multifunctional device from Anycubic, which was used for drying and curing the manufactured objects. The models were exposed for 2 min in one position, after which they were rotated and exposed again for another 2 min in a second position. As a result of the 3D-printing and post-processing steps, fully processed models were obtained.

3. Results

Before measurements, models made from Siraya Tech resin had smooth and glossy surfaces that could cause reflections and glare, leading to measurement errors when digitizing their geometry. To address this issue, the manufactured models were sprayed with a thin layer of AESUB Blue aerosol to create a matte finish on the surface before data acquisition. After the measurement, the powder layer disappeared within a few minutes, eliminating the need for additional cleaning of the models. In the measurement process, we used an optical measurement system, GOM Scan1 with GOM Professional software using blue structured light, to conduct geometric accuracy tests (Figure 5). This measurement method is based on trigonometric triangulation and projects a light pattern onto an object. An LCD projector emits this pattern. Then, two cameras slightly offset from the projector will examine the shape of the light pattern and calculate the distance from each point in the field of view.

Parameters were utilized to acquire the highest measurement resolution with the GOM Scan1 system during the measurement (

Table 2. Established measurement parameters for the GOM Scan 1.

Parameters	Value
Pixel-resolution cameras	5,000,000
Measuring area	100 mm × 65 mm × 400 mm
Min. point resolution	0.037 mm
Number of points per scan	5,000,000
Number of rotations of the measuring table	13

). During the measurement process, the orientations of the skull model and the zygomatic bone defect model were adjusted twice to achieve a complete and accurate 3D scan. The models were measured in a single orientation on the measuring table for the geometry measurement of the stamp and die. The measuring table facilitated the measurement process by performing 13 rotations around its axis, allowing for comprehensive geometry data collection for all models.

The accuracy of the manufactured model was verified using GOM Inspect software. This involved comparing the nominal model created during the RE design stage with the model generated during the measurement stage using the GOM Scan1 optical system. The comparison was conducted using the best-fit method, achieving an accuracy of 0.001 mm. As a result of the model adjustments, three-dimensional maps of the geometry, mapping model deviations obtained using two modes, normal and ultra-light (Figure 6, Figure 7 and Figure 8), were developed. In addition, statistical results were developed for the model of the skull part and the modeled defect of the zygomatic bone (

Table 3. Statistical parameters assessing the accuracy of the skull model and the model of the zygomatic bone defect in normal mode.

Parameters	Cranial Model	Defect of the Zygomatic Bone
Maximum deviation [mm]	2.016	2.226
Minimum deviation [mm]	−1.903	−1.092
Range [mm]	3.919	3.318
Mean deviation [mm]	−0.014	−0.047
Standard deviation [mm]	0.277	0.340

and

Table 4. Statistical parameters assessing the accuracy of the model of the skull part and the defect of the zygomatic bone in ultra-light mode.

Parameters	Cranial Model	Defect of the Zygomatic Bone
Maximum deviation [mm]	1.802	1.197
Minimum deviation [mm]	−1.673	−1.209
Range [mm]	3.475	2.406
Mean deviation [mm]	−0.004	−0.024
Standard deviation [mm]	0.242	0.290

), as well as for the model of the stamp and die (

Table 5. Statistical parameters assessing the accuracy of the model of the stamp and the die manufactured in normal mode and in the ultra-light mode.

Parameters	Stamp Model	Die Model	Type of Mode
Maximum deviation [mm]	0.827	0.687	Normal
Minimum deviation [mm]	−1.394	−1.396
Range [mm]	2.211	2.082
Mean deviation [mm]	0.009	−0.014
Standard deviation [mm]	0.341	0.230
Maximum deviation [mm]	0.547	0.727	Ultra-light
Minimum deviation [mm]	−1.443	−0.696
Range [mm]	1.990	1.423
Mean deviation [mm]	0.020	0.045
Standard deviation [mm]	0.259	0.193

).

Based on the statistical results, the skull model was manufactured within a deviation range of ±0.56 mm for the normal mode while the prototype implant of zygomatic bone geometry was within a deviation range of ±0.68 mm. Notably, over 70% of the surfaces of the models fell within the deviation range of ±0.3 mm, which is considered acceptable for planning procedures in the craniofacial region. The most significant positive deviations in the skull model were primarily found in the temporal bone area. Conversely, the most substantial negative deviations were noted mainly at the edges of the completed skull model, particularly in the upper jaw region. Most positive and negative deviations were located at the model’s edges for the prototype implant, where the missing zygomatic bone was replaced, especially in the areas corresponding to the designed mesh. Additionally, deviations of approximately 0.3 mm were observed in the frontal process area, lateral surface, and orbital floor geometry. Based on the statistical results obtained for the ultra-light mode, the skull model was manufactured with a deviation range of ±0.48 mm, while the implant prototype of zygomatic bone geometry was within a ±0.58 mm range. Notably, over 70% of the surfaces of both models fell within the deviation ranges of ±0.25 mm for the skull and ±0.29 mm for the implant prototype. Deviations over the ±0.3 mm range occurred at the edges and in the area of the designed mesh, as observed in normal mode. An additional group of negative deviations was observed in the skull model compared to the model created in normal mode. This group of negative deviations was primarily located in the temporal bone area, frontal bone area, and along the edges of the model. Conversely, the upper jaw area noted the most significant positive deviations. For the prototype implant designed to replace the lost zygomatic bone, the most significant positive and negative deviations were also found at the model’s edges, particularly in the areas of the designed mesh. Positive deviations of 0.3 mm were observed at similar locations on the implant prototype’s surface, particularly in the frontal process area, lateral surface, and orbital floor geometry. Considering the statistical results obtained for the die and stamp model, the positive and negative deviation areas are comparable for both modes. In addition, the die model has a better surface quality for both methods than the stamp model. Higher deviation values were obtained for the normal mode. For normal mode, the deviation range for the stamp model was within ±0.68 mm, and for the ultra-light mode, the deviations were within ±0.52 mm. When using the die model, the maximum deviations were within ±0.46 mm for normal mode and ±0.4 mm for the ultra-light mode. 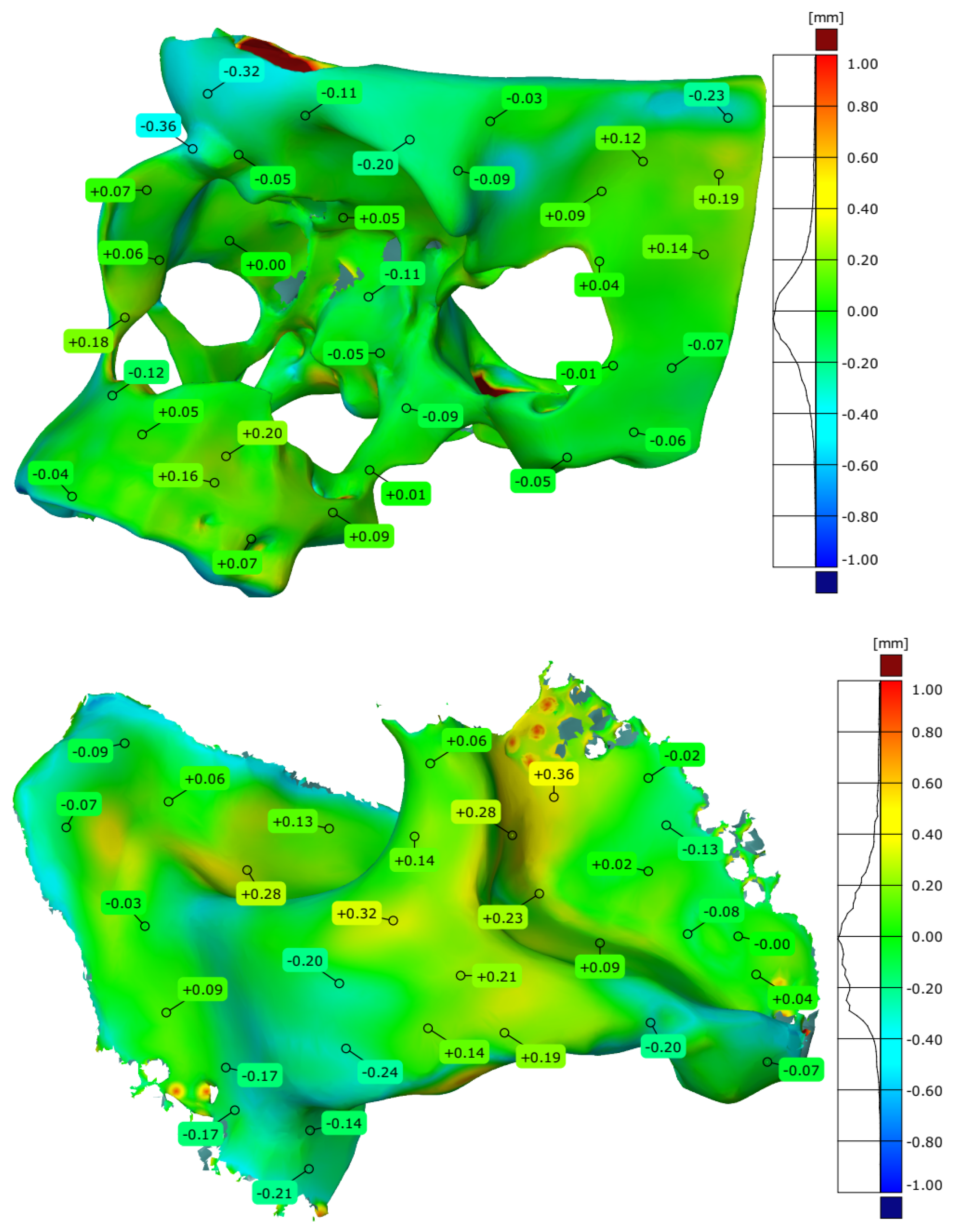It is worth adding that more than 70% of the surface of the models was within the deviation range of ±0.3 mm, which is sufficient for planning surgical procedures.

4. Discussion

Designing and manufacturing a model of an anatomical structure for surgical procedures is a complex task, particularly in the craniofacial area, which contains bony tissues with intricate geometries. Recent advancements in coordinate measuring systems, data processing software, and modern manufacturing techniques have helped to solve this challenge through a process known as reverse engineering. However, errors can occur at various stages—from measuring the patient to creating the final model—that can significantly impact the accuracy of the surgical procedure. Notably, significant errors arise when digitizing geometry. The diagnostic data of the zygomatic bone area most often derive from multidetector CT scanners. High-resolution measurements are necessary to reconstruct the damaged area of the zygomatic bone, including the orbit. This is partly because the orbital floor bone is fragile, and its thickness varies between 0.74 mm and 1.5 mm [36]. High-resolution DICOM data are essential in correctly establishing the diagnosis and especially useful for creating reliable reconstructions and treatment-planning [21,37,38]. Unfortunately, due to the limitations of multidetector tomographic measurement systems, it is often difficult to obtain very high-resolution data. Thus, based on the obtained DICOM data, difficulties arise with the overall segmentation process and reconstruction of the geometry of the zygomatic bone, particularly the orbital floor. It is also necessary to pay attention to the accuracy of manufacturing models using additive methods. MEX methods are most commonly used in manufacturing models of the craniofacial region [14,22]. However, these methods also have their limitations due to, among other things, the use of layer thicknesses close to or higher than 0.1 mm and the anisotropic surface properties obtained during 3D-printing. These factors significantly degrade the geometric accuracy of the obtained models. In addition, using a layer thickness with a value close to the thickness of the orbital floor bone can make it much more difficult or impossible to achieve this part of the geometry at the manufacturing stage. Therefore, when manufacturing models of the craniofacial region, significant detail is often required. Among other dental models, VPP methods are used [42]. These allow for models to be made with a layer thickness of less than 0.1 mm while obtaining a surface with essentially isotropic properties. Therefore, it is essential to develop solutions to ensure the final model closely reflects the anatomical structure.

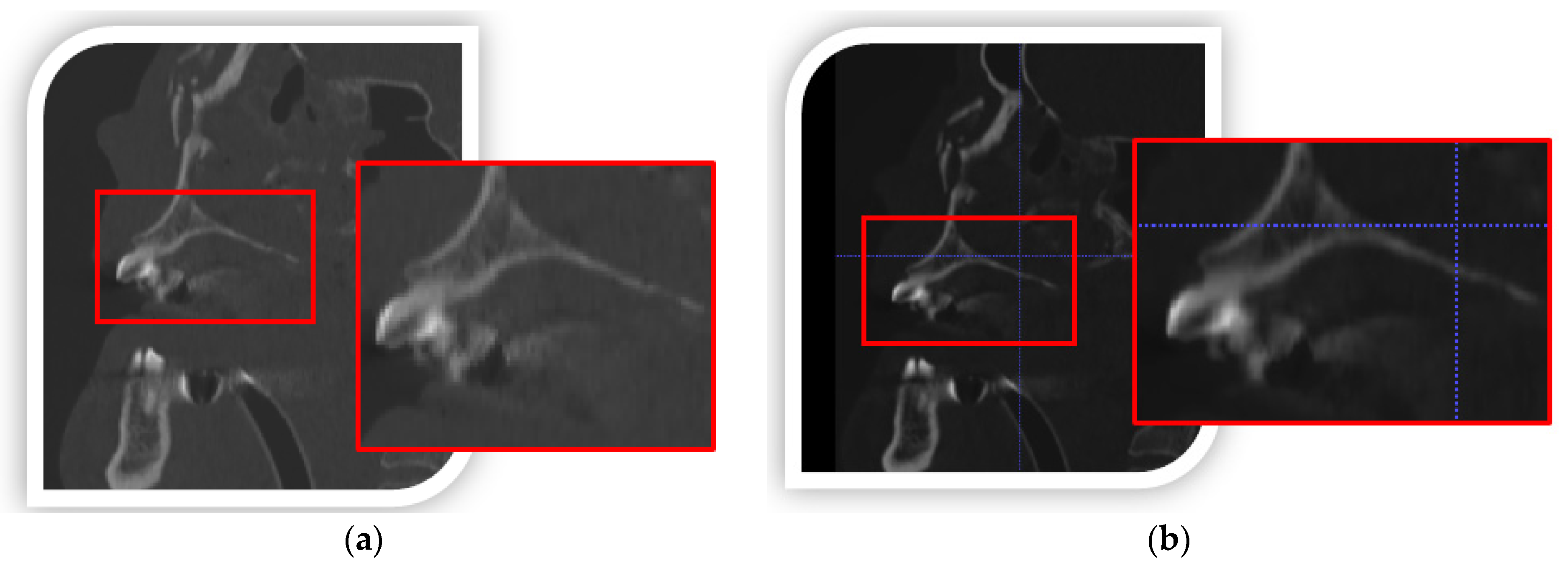
4.1. Methods to Improve Accuracy in the Numerical Processing of DICOM Data

Most diagnoses use data from multi-detector CT systems to identify injuries or diseases affecting bone structures. The quality of the resulting DICOM data is primarily influenced by spatial and contrast resolution [17,43]. These factors are determined by various parameters, including the design of the diagnostic system and its calibration quality. Low spatial and contrast resolutions can significantly impede the accurate segmentation of bone structures. This issue can be addressed by implementing a measurement protocol that enhances accuracy; however, such procedures may pose risks to the patient’s health and, in some cases, their life. For this reason, research to improve accuracy using previously collected DICOM data is ongoing. The authors presented procedures for removing measurement noise, which mainly arises from within the implant area that is to be diagnosed [44,45,46]. In addition, depending on the quality of the obtained DICOM data, they focus on procedures for smoothing or sharpening the edges of segmented structures [47,48,49]. The article’s authors implemented a digital data-processing technique to enhance the quality of the image and extract essential information. The use of an interpolation method significantly improved the contrast resolution of the DICOM data, which also helped minimize the measurement noise. Additionally, this method increased the spatial resolution of the image by digitally generating extra pixels based on the intensity values of neighboring pixels (Figure 9). As a result, the issue of volume-averaging that previously complicated the accurate assignment of pixels to segmented bone tissue was significantly reduced.

A segmentation process was carried out on the digitally processed image. This process involves extracting a selected bone structure from the entire volumetric data set. Several methods are currently used to obtain segmented outlines of anatomical structures. Among the best-known are Global Thresholding [50], Edge Detection [51], Region Growing [52], and machine learning methods [53,54]. However, as with most automatic or semi-automatic methods, it is impossible to accurately determine segmentation thresholds using these methods. This problem of determining accurate HU values is still a significant challenge in modeling anatomical structures [18,50]. The authors of the presented article focused on using the local thresholding method. Narrowing the segmentation area and using the interpolation method significantly improved the selection of a more accurate value of the lower threshold against which the middle part of the craniofacial was separated. Thus, the digital model was not artificially increased or decreased in volume during the segmentation process. Various reconstruction methods are used in the literature to depict the three-dimensional model. In the current publications, two main groups, contour-based and Voxel-based, are considered. More often, however, the voxel-based method is used to reconstruct the geometry of anatomical structures. This is because this method does not generate too many programming errors in the structure of the 3D-STL model. For this reason, the authors of the presented publication used the Marching Cubes algorithm, one of the voxel-based methods, to develop a 3D representation of the anatomical structure using DICOM data [40,41].

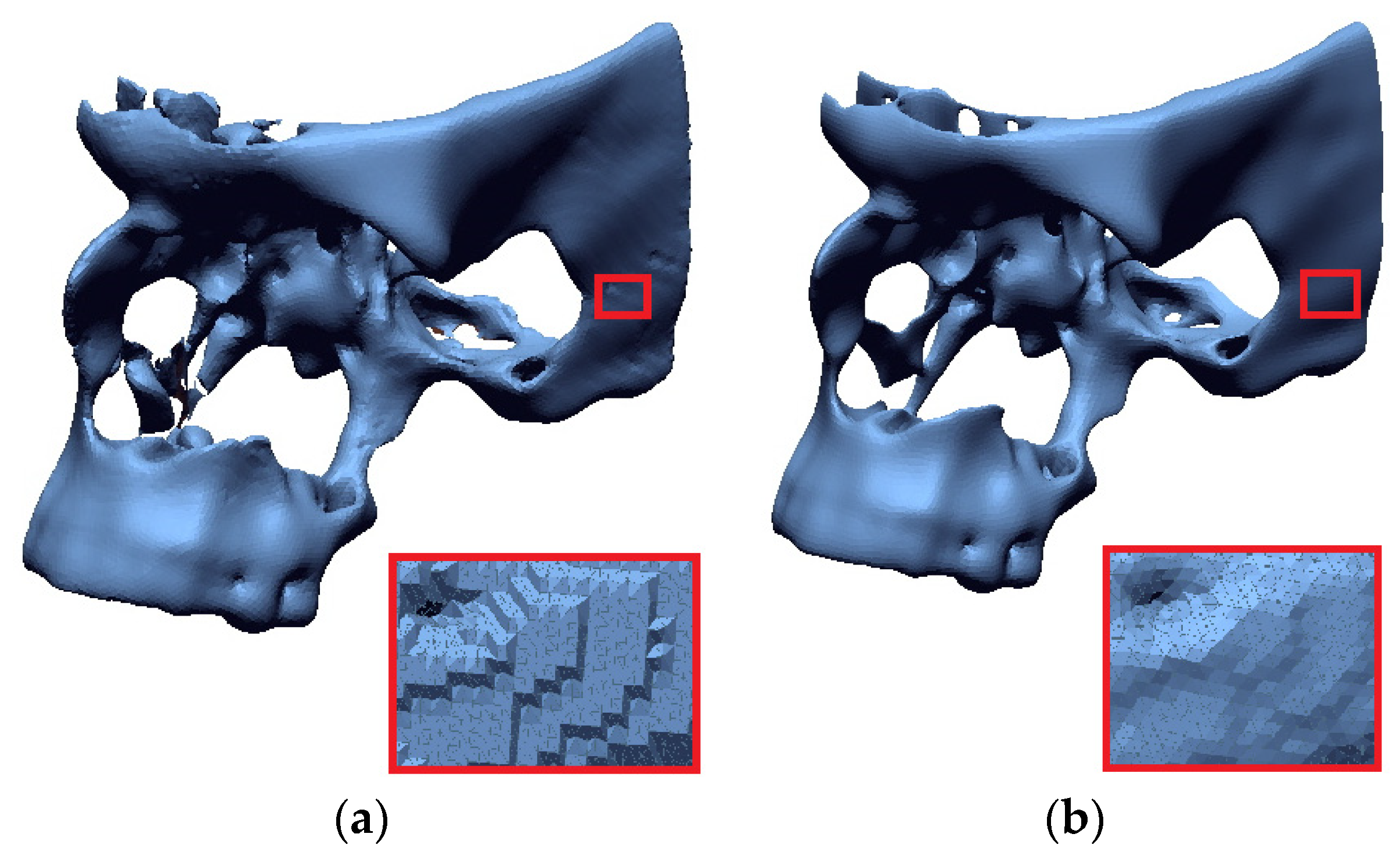
4.2. Methods to Improve Accuracy in the Numerical Processing of 3D-STL Models

The marching cubes method, like any algorithm, has its limitations. The quality of the transformation from segmented contours to a faceted surface primarily depends on the layer thickness obtained during tomographic imaging. When the CT layer thickness is significantly larger than the pixel dimensions, gaps can appear in the triangle mesh in some regions of the reconstructed geometry. These gaps result from insufficient diagnostic data, hindering adjacent contours’ smooth merging. Also, errors were observed in the triangle mesh structure during geometry reconstruction. The most common issues included incorrectly oriented triangles, duplicated edges and vertices, and duplicated triangles. In certain situations, a triangle mesh transformation process known as remeshing is necessary [55]. This process can involve various quality indicators for the triangle mesh, such as shape modifications, size, diversity, solution error, or a combination of these factors. There are two primary approaches to triangle mesh processing: parameterization techniques [56,57] and mesh adaptation strategies [58,59]. The most commonly used parameterization techniques include linear [60], non-linear [61], and hybrid methods [62]. In the referenced publication, the authors used the hybrid method. This approach involved optimizing the facet structure by compacting the triangle mesh in areas with high surface complexity, thereby minimizing the errors. (Figure 10). This approach significantly improved the quality of the model’s geometry.

The CAD modeling process focuses on commonly used surface modeling methods and uses functions for mirroring and Boolean functions [63,64]. Appropriate functions are essential, as their configuration can affect the accuracy of the final 3D-CAD model [65]. During the modeling process, it is especially crucial to accurately determine the plane of symmetry on the reconstructed geometries of the anatomic structure models. This procedure significantly shortens the modeling process. One of the crucial steps in preparing data for 3D-printing is converting the developed 3D-CAD models to STL format. During the tessellation process, thousands or even millions of triangles are often created to accurately approximate the curvilinear surface. The resulting differences in mapping accuracy are described by angular and chordal deviations [66,67]. If a smaller value is used for the angular deviation and chord, a 3D-STL model with higher accuracy and a more significant number of triangles will be generated. This generally results in more time being required to carry out the CAD software tessellation process and divide the STL model into print layers. Therefore, it was necessary during the development of the final 3D-STL models to adjust the export parameters in terms of the resolution of the 3D printer in order to not duplicate the errors in the tessellation process when manufacturing the model using the mSLA additive method. In the case of the presented article, the authors assumed that the value of the chord deviation should be 10 times smaller than the resolution of the 3D print. In addition, when selecting the value of the angular deviation, it was determined that it should be no greater than 10 degrees. This ensured sufficient accuracy for the 3D-STL model generation in areas characterized by, among other things, variable radii of curvature.

4.3. Research on Assessing the Accuracy of Models Produced via mSLA Additive Manufacturing

By selecting the appropriate technological parameters during the model’s manufacturing, the surface geometry is modified to meet specific technical conditions, ensuring optimal operating performance. The technological evaluation of surface texture is also crucial for objects created using additive methods. Based on research findings in the literature, the accuracy of geometric representation in the mSLA method is significantly influenced by the layer thickness, exposure time, and orientation model in the 3D printer space [68]. Additionally, surface roughness is affected by layer thickness and the object’s orientation within the 3D printer space [68]. Additionally, one study [69] observed that exposure time plays an important role in most output measures. However, the studies in the publications were conducted on simple test samples and not on models depicting anatomical structures. In a recent publication [70], attention was drawn to the accuracy of anatomical structure models within the knee joint and the designed reaction templates created using the mSLA method. These models were created using Siraya Tech Fast resin. The bone models and a surgical guide were manufactured with a layer thickness of 0.05 mm, and the exposure times for each layer were consecutively set to 1.8 s. Regarding geometric accuracy, the results for anatomical models and surgical templates were in the ±0.6 mm deviation range. However, the aforementioned publications did not pay attention to yet another research aspect concerning the influence of the method of generating the support material. The use of any 3D-printing method significantly impacts the quality of the surface reproduction. The article presented here examines two modes of generating the support material: normal mode and ultra-light mode. The ultra-light mode produces more accurate models than those created in normal mode. This improvement is attributed to the reduced density and thickness of the supports in the ultra-light mode, which reduces support marks and makes their removal easier (Figure 11).

In both modes, the most significant positive and negative deviation values were found in the areas of the mesh designed for the implant prototype model. Given the established parameters for 3D-printing, producing a CAD-designed mesh using the mSLA method with the recommended geometric accuracy of ±0.3 mm is impossible. If there is considerable negative deviation along the edges of the models, this may be linked to the resin’s exposure time. A shorter exposure time means more resin in that area remains uncured, leading to shrinkage of the outer outlines. Additionally, mapping more complex surfaces with the mSLA method can pose challenges. The LCD matrix of the 3D printer produces more accurate images for lines parallel to the X- and Y-axes, whereas lines at an angle are prone to what is known as “step error.” Therefore, further research is needed to optimize the parameters used to manufacture models of anatomical structures using the mSLA method.

5. Conclusions

Thanks to the development of coordinate measuring systems, digital data processing methods, and modern manufacturing methods, it is now possible to develop models of anatomical structures, surgical templates, and implants for planning surgical procedures. Designing and manufacturing models for surgical procedures is not a simple task. At each stage of the measurement, reconstruction, CAD modeling, and manufacturing process, geometry errors arise, significantly hindering the development of a final model tailored to a specific patient. In the paper presented here, the following methods were developed to improve geometric accuracy within the zygomatic bone at different stages:

• DICOM data-processing increased spatial and contrast resolution by using a data interpolation process. In addition, the segmentation process used a local thresholding method, which more precisely determined the lower threshold for segmenting bone structures within the zygomatic bone area. Through the use of remeshing methods, the quality of the facet area was significantly increased,
• During CAD modeling, special attention was paid to tessellation, that is, converting the model from CAD to STL format. The values of chordal and angular deviation were adjusted so that errors made during data export were not duplicated in the process of manufacturing the model using the additive method,
• The thinnest layer thickness used in the mSLA method was applied during manufacturing. The recommended model orientation within the 3D printer’s workspace was also utilized. The study evaluated two methods for generating the support material. The results indicated that the ultra-light mode produced a more accurate geometrical model. This was attributed to the reduced amount of support material generated during the model’s execution, which made the mechanical removal of supports easier during the post-processing stage.

However, the guidelines developed in the presented publication related to the reconstruction process, design, and manufacture using the mSLA method of surgical templates require further improvement. They relate to optimizing the CAD process and selecting 3D-printing parameters to minimize deviations, especially at the edges of models of anatomical structures.