Accounting for Healthcare-Seeking Behaviours and Testing Practices in Real-Time Influenza Forecasts
Abstract
:1. Introduction
2. Results
2.1. Relating Flutracking Trends to the General Population in 2014–2016
- “Now-casts”: How well forecasts predicted the observation for the forecasting date itself.
- “Next 2 weeks”: How well forecasts predicted observations 1–2 weeks after the forecasting date.
- “Next 4 weeks”: How well forecasts predicted observations 1–4 weeks after the forecasting date.
- “Next 6 weeks”: How well forecasts predicted observations 1–6 weeks after the forecasting date.
2.2. Incorporating Flutracking Trends into 2017 Forecasts
3. Discussion
3.1. Principal Findings
3.2. Study Strengths and Weaknesses
3.3. Meaning and Implications
4. Materials and Methods
4.1. Flutracking Survey Data
4.2. Estimating the Probability of an Influenza Test, Given ILI Symptoms
4.3. Influenza Surveillance Data
4.4. Forecasting Methods
4.5. Forecast Performance
4.6. Availability of Materials and Methods
Author Contributions
Funding
Acknowledgments
- Robin Gilmour and Nathan Saul. Communicable Disease Branch, Health Protection New South Wales, New SouthWales.
- Frances A. Birrell, AngelaWakefield, and Mayet Jayloni. Epidemiology and Research Unit, Communicable Diseases Branch, Prevention Division, Department of Health, Queensland.
- Lucinda J. Franklin, Nicola Stephens, Janet Strachan, Trevor Lauer, and Kim White. Communicable Diseases Section, Health Protection Branch, Regulation Health Protection and Emergency Management Division, Victorian Government Department of Health and Human Services, Victoria.
- Avram Levy and Cara Minney-Smith. PathWest Laboratory Medicine WA, Department of Health, Western Australia.
Conflicts of Interest
Abbreviations
| CDNA | Communicable Diseases Network Australia |
| ILI | Influenza-like illness |
| RT-PCR | Reverse transcription polymerase chain reaction |
| SEIR | Susceptible, exposed, infectious, recovered |
Appendix A. Forecasting Methods
| Meaning | Value | |
|---|---|---|
| Force of infection | Equation (A5) | |
| Basic reproduction number | ||
| Inverse of the incubation period (days) | ||
| Inverse of the infectious period (days) | ||
| Seasonal modulation of | ||
| Time of the first infection (days) | ||
| Number of particles (simulations) | ||
| Minimum number of effective particles | ||
| Observation period (days) | 7 | |
| k | Dispersion parameter | 100 |
| Background observation probability | Equation (A10) | |
| Estimated background observation rate | see Table A2 | |
| Observation probability | see Table A2 | |
| N | Population size | see Table A2 |
| City | Year | Peak Size | Peak Timing | N | ||
|---|---|---|---|---|---|---|
| Brisbane | 2012 | 510 | 12 August | |||
| 2013 | 140 | 1 September | ||||
| 2014 | 509 | 24 August | 28 | 0.003 | 2,308,700 | |
| 2015 | 986 | 23 August | 48 | 0.003 | 2,308,700 | |
| 2016 | 544 | 4 September | 46 | 0.003 | 2,308,700 | |
| 2017 | 1346 | 27 August | 40 | 0.003 | 2,308,700 | |
| Melbourne | 2012 | 360 | 15 July | |||
| 2013 | 417 | 25 August | ||||
| 2014 | 691 | 24 August | 36 | 0.00275 | 4,108,541 | |
| 2015 | 1329 | 30 August | 73 | 0.00275 | 4,108,541 | |
| 2016 | 975 | 4 September | 62 | 0.00275 | 4,108,541 | |
| 2017 | 3962 | 10 September | 79 | 0.00275 | 4,108,541 | |
| Perth | 2012 | 351 | 15 July | |||
| 2013 | 106 | 15 September | ||||
| 2014 | 199 | 24 August | 10 | 0.002 | 1,900,000 | |
| 2015 | 170 | 23 August | 20 | 0.002 | 1,900,000 | |
| 2016 | 221 | 14 August | 14 | 0.002 | 1,900,000 | |
| 2017 | 94 | 10 September | 5 | 0.002 | 1,900,000 | |
| Sydney | 2012 | 535 | 1 July | |||
| 2013 | 855 | 1 September | ||||
| 2014 | 1989 | 17 August | 38 | 0.0076 | 4,921,000 | |
| 2015 | 2933 | 23 August | 75 | 0.0076 | 4,921,000 | |
| 2016 | 2884 | 4 September | 138 | 0.0076 | 4,921,000 | |
| 2017 | 8798 | 20 August | 139 | 0.0076 | 4,921,000 |
References
- Reed, C.; Chaves, S.S.; Daily Kirley, P.; Emerson, R.; Aragon, D.; Hancock, E.B.; Butler, L.; Baumbach, J.; Hollick, G.; Bennett, N.M.; et al. Estimating Influenza Disease Burden from Population-Based Surveillance Data in the United States. PLoS ONE 2015, 10, e0118369. [Google Scholar] [CrossRef] [PubMed]
- Biggerstaff, M.; Alper, D.; Dredze, M.; Fox, S.; Fung, I.C.H.; Hickmann, K.S.; Lewis, B.; Rosenfeld, R.; Shaman, J.; Tsou, M.H.; et al. Results from the centers for disease control and prevention’s predict the 2013–2014 Influenza Season Challenge. BMC Infect. Dis. 2016, 16, 357. [Google Scholar] [CrossRef] [PubMed]
- Moss, R.; Zarebski, A.; Dawson, P.; McCaw, J.M. Retrospective forecasting of the 2010–14 Melbourne influenza seasons using multiple surveillance systems. Epidemiol. Infect. 2017, 145, 156–169. [Google Scholar] [CrossRef] [PubMed]
- Riley, P.; Ben-Nun, M.; Turtle, J.A.; Linker, J.; Bacon, D.P.; Riley, S. Identifying factors that may improve mechanistic forecasting models for influenza. bioRxiv 2017, 172817. [Google Scholar] [CrossRef] [Green Version]
- Ben-Nun, M.; Riley, P.; Turtle, J.; Bacon, D.; Riley, S. National and Regional Influenza-Like-Illness Forecasts for the USA. bioRxiv 2018, 309021. [Google Scholar] [CrossRef] [Green Version]
- Biggerstaff, M.; Johansson, M.; Alper, D.; Brooks, L.C.; Chakraborty, P.; Farrow, D.C.; Hyun, S.; Kandula, S.; McGowan, C.; Ramakrishnan, N.; et al. Results from the second year of a collaborative effort to forecast influenza seasons in the United States. Epidemics 2018. [Google Scholar] [CrossRef] [PubMed]
- Cope, R.C.; Ross, J.V.; Chilver, M.; Stocks, N.P.; Mitchell, L. Characterising seasonal influenza epidemiology using primary care surveillance data. PLoS Comput. Biol. 2018, 14, e1006377. [Google Scholar] [CrossRef]
- Cope, R.C.; Ross, J.V.; Chilver, M.; Stocks, N.P.; Mitchell, L. Connecting surveillance and population-level influenza incidence. bioRxiv 2018, 427708. [Google Scholar] [CrossRef]
- Moss, R.; Fielding, J.E.; Franklin, L.J.; Stephens, N.; McVernon, J.; Dawson, P.; McCaw, J.M. Epidemic forecasts as a tool for public health: interpretation and (re)calibration. Aust. N. Z. J. Public Health 2018, 42, 69–76. [Google Scholar] [CrossRef]
- Moss, R.; Zarebski, A.E.; Dawson, P.; Franklin, L.J.; Birrell, F.A.; McCaw, J.M. Anatomy of a seasonal influenza epidemic forecast. Commun. Dis. Intell. 2019. accepted. [Google Scholar]
- Funk, S.; Bansal, S.; Bauch, C.T.; Eames, K.T.; Edmunds, W.J.; Galvani, A.P.; Klepac, P. Nine challenges in incorporating the dynamics of behaviour in infectious diseases models. Epidemics 2015, 10, 21–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moran, K.R.; Fairchild, G.; Generous, N.; Hickmann, K.; Osthus, D.; Priedhorsky, R.; Hyman, J.; Del Valle, S.Y. Epidemic Forecasting is Messier Than Weather Forecasting: The Role of Human Behavior and Internet Data Streams in Epidemic Forecast. J. Infect. Dis. 2016, 214, S404–S408. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, L.; Ross, J.V. A data-driven model for influenza transmission incorporating media effects. R. Soc. Open Sci. 2016, 3, 160481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reich, N.G.; Brooks, L.; Fox, S.; Kandula, S.; McGowan, C.; Moore, E.; Osthus, D.; Ray, E.L.; Tushar, A.; Yamana, T.; et al. Forecasting seasonal influenza in the US: A collaborative multi-year, multi-model assessment of forecast performance. bioRxiv 2018, 397190. [Google Scholar] [CrossRef]
- Kandula, S.; Yamana, T.; Pei, S.; Yang, W.; Morita, H.; Shaman, J. Evaluation of mechanistic and statistical methods in forecasting influenza-like illness. J. R. Soc. Interface 2018, 15. [Google Scholar] [CrossRef] [PubMed]
- Moss, R.; McCaw, J.M.; Cheng, A.C.; Hurt, A.C.; McVernon, J. Reducing disease burden in an influenza pandemic by targeted delivery of neuraminidase inhibitors: Mathematical models in the Australian context. BMC Infect. Dis. 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Carlson, S.J.; Dalton, C.B.; Durrheim, D.N.; Fejsa, J. Online Flutracking Survey of Influenza-like Illness during Pandemic (H1N1) 2009, Australia. Emerg. Infect. Dis. 2010, 16, 1960–1962. [Google Scholar] [CrossRef] [Green Version]
- Carlson, S.J.; Dalton, C.B.; Butler, M.T.; Fejsa, J.; Elvidge, E.; Durrheim, D.N. Flutracking weekly online community survey of influenza-like illness annual report 2011 and 2012. Commun. Dis. Intell. 2013, 37, E398–E406. [Google Scholar]
- Dalton, C.B.; Carlson, S.J.; McCallum, L.; Butler, M.T.; Fejsa, J.; Elvidge, E.; Durrheim, D.N. Flutracking weekly online community survey of influenza-like illness: 2013 and 2014. Commun. Dis. Intell. 2015, 39, E361–E368. [Google Scholar]
- Dalton, C.B.; Carlson, S.J.; Durrheim, D.N.; Butler, M.T.; Cheng, A.C.; Kelly, H.A. Flutracking weekly online community survey of influenza-like illness annual report, 2015. Commun. Dis. Intell. 2016, 40, E512–E520. [Google Scholar]
- Department of Health. Australian Influenza Surveillance Report: 2017 Season Summary; Technical Report; Australian Government: Canberra, Australia, 2017.
- Scutti, S. ‘Australian flu’: It’s Not from Australia. CNN. 2018. Available online: https://edition.cnn.com/2018/02/02/health/australian-flu-became-global/index.html (accessed on 5 October 2018).
- Moss, R.; Zarebski, A.; Dawson, P.; McCaw, J.M. Forecasting influenza outbreak dynamics in Melbourne from Internet search query surveillance data. Influenza Other Respir. Viruses 2016, 10, 314–323. [Google Scholar] [CrossRef] [Green Version]
- Zarebski, A.E.; Dawson, P.; McCaw, J.M.; Moss, R. Model selection for seasonal influenza forecasting. Infect. Dis. Model. 2017, 2, 56–70. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Ibuka, Y.; Chapman, G.B.; Meyers, L.A.; Li, M.; Galvani, A.P. The dynamics of risk perceptions and precautionary behavior in response to 2009 (H1N1) pandemic influenza. BMC Infect. Dis. 2010, 10, 296. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.D.M.; Stephenson, N.; Lohm, D.; Waller, E.; Flowers, P. Beyond resistance: Social factors in the general public response to pandemic influenza. BMC Public Health 2015, 15, 436. [Google Scholar] [CrossRef] [PubMed]
- De Angelis, D.; Presanis, A.M.; Birrell, P.J.; Tomba, G.S.; House, T. Four key challenges in infectious disease modelling using data from multiple sources. Epidemics 2015, 10, 83–87. [Google Scholar] [CrossRef] [Green Version]
- Presanis, A.M.; Pebody, R.G.; Paterson, B.J.; Tom, B.D.M.; Birrell, P.J.; Charlett, A.; Lipsitch, M.; De Angelis, D. Changes in severity of 2009 pandemic A/H1N1 influenza in England: A Bayesian evidence synthesis. BMJ 2011, 343, d5408. [Google Scholar] [CrossRef] [PubMed]
- Birrell, P.J.; De Angelis, D.; Presanis, A.M. Evidence synthesis for stochastic epidemic models. Stat. Sci. 2018, 33, 34–43. [Google Scholar] [CrossRef]
- van Noort, S.P.; Codeço, C.T.; Koppeschaar, C.E.; van Ranst, M.; Paolotti, D.; Gomes, M.G.M. Ten-year performance of Influenzanet: ILI time series, risks, vaccine effects, and care-seeking behaviour. Epidemics 2015, 13, 28–36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baltrusaitis, K.; Santillana, M.; Crawley, A.W.; Chunara, R.; Smolinski, M.; Brownstein, J.S. Determinants of Participants’ Follow-Up and Characterization of Representativeness in Flu Near You, A Participatory Disease Surveillance System. JMIR Public Health Surveill. 2017, 3, e18. [Google Scholar] [CrossRef] [PubMed]
- Chretien, J.P.; George, D.; Shaman, J.; Chitale, R.A.; McKenzie, F.E. Influenza forecasting in human populations: A scoping review. PLoS ONE 2014, 9, e94130. [Google Scholar] [CrossRef] [PubMed]
- Nsoesie, E.O.; Brownstein, J.S.; Ramakrishnan, N.; Marathe, M.V. A systematic review of studies on forecasting the dynamics of influenza outbreaks. Influenza Other Respir. Viruses 2014, 8, 309–316. [Google Scholar] [CrossRef] [PubMed]
- Priedhorsky, R.; Osthus, D.; Daughton, A.R.; Moran, K.R.; Culotta, A. Deceptiveness of internet data for disease surveillance. arXiv, 2017; arXiv:1711.06241v1. [Google Scholar]
- Domnich, A.; Panatto, D.; Signori, A.; Lai, P.L.; Gasparini, R.; Amicizia, D. Age-Related Differences in the Accuracy of Web Query-Based Predictions of Influenza-Like Illness. PLoS ONE 2015, 10, e0127754. [Google Scholar] [CrossRef]
- Fielding, J.E.; Regan, A.K.; Dalton, C.B.; Chilver, M.B.N.; Sullivan, S.G. How severe was the 2015 influenza season in Australia? Med. J. Aust. 2016, 204, 60–61. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rowe, S.L. Infectious diseases notification trends and practices in Victoria, 2011. Vic. Infect. Dis. Bull. 2012, 15, 92–97. [Google Scholar]
- Dalton, C.B.; Carlson, S.J.; Butler, M.T.; Elvidge, E.; Durrheim, D.N. Building Influenza Surveillance Pyramids in Near Real Time, Australia. Emerg. Infect. Dis. 2013, 19, 1863–1865. [Google Scholar] [CrossRef] [PubMed]
- Jeffreys, H. The Theory of Probability; OUP Oxford: Oxford, UK, 1998. [Google Scholar]
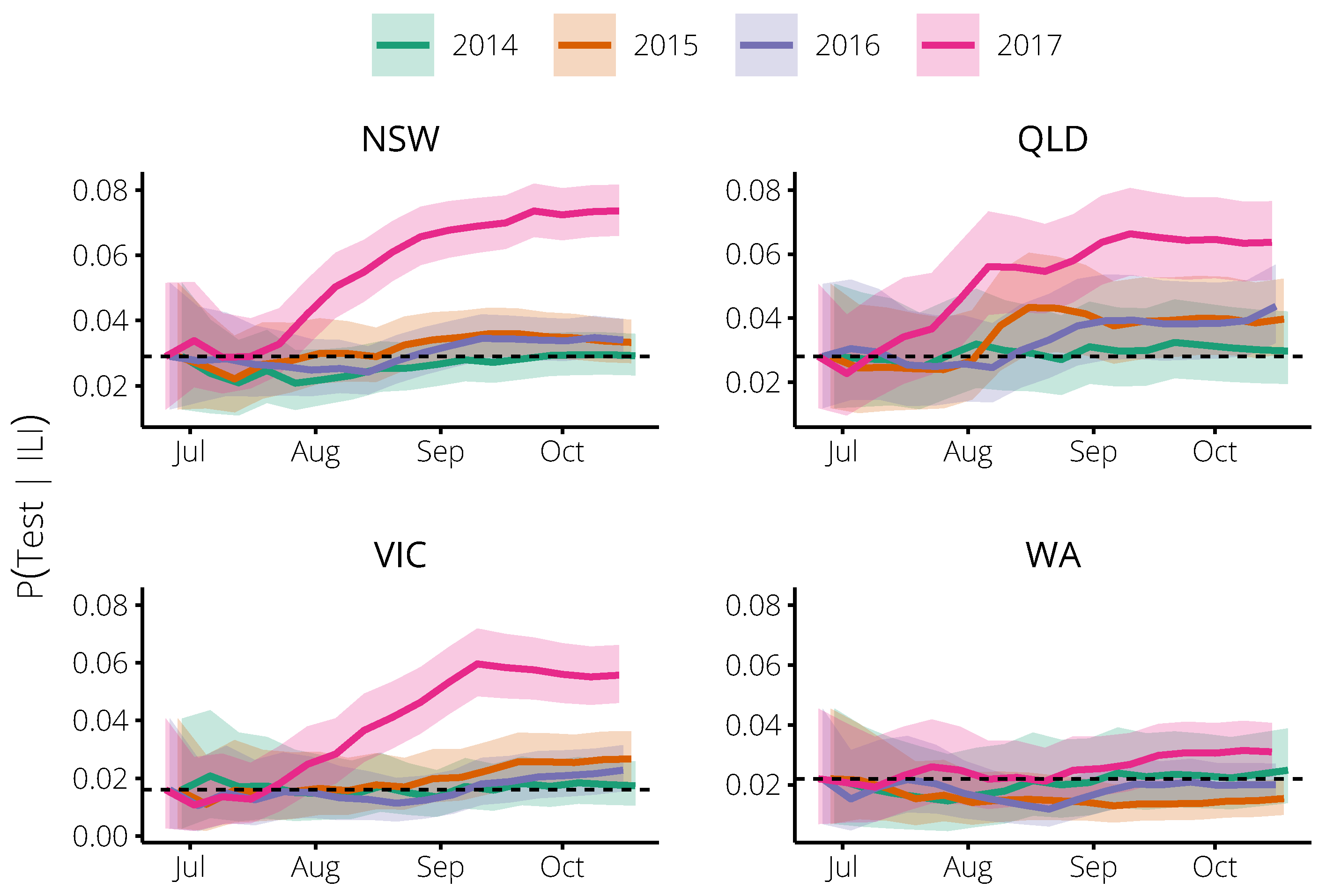
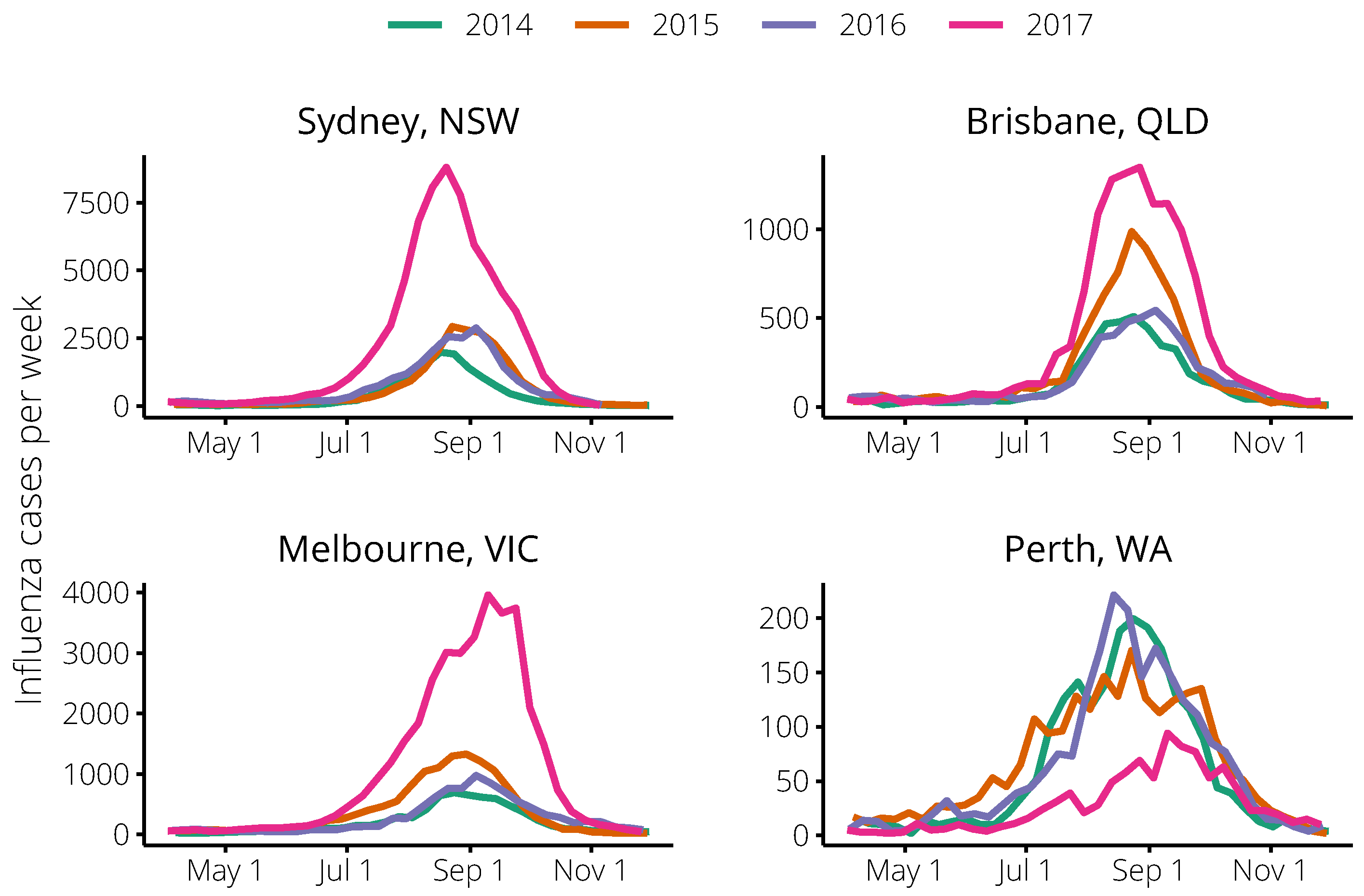






| State | Year | Completed Surveys | Participants with ILI | Reported Tests | Influenza Cases |
|---|---|---|---|---|---|
| NSW | 2014 | 6311 | 146 | 3 | 15,100 |
| 2015 | 7242 | 155 | 4 | 23,324 | |
| 2016 | 8439 | 178 | 5 | 25,613 | |
| 2017 | 9405 | 218 | 14 | 71,752 | |
| Vic | 2014 | 2815 | 64 | 1 | 7627 |
| 2015 | 3348 | 68 | 2 | 13,566 | |
| 2016 | 3894 | 75 | 1 | 10,276 | |
| 2017 | 4712 | 104 | 5 | 37,739 | |
| Qld | 2014 | 1736 | 36 | 1 | 5020 |
| 2015 | 2180 | 46 | 2 | 8084 | |
| 2016 | 2481 | 50 | 2 | 5844 | |
| 2017 | 2822 | 68 | 4 | 13,365 | |
| WA | 2014 | 1039 | 24 | 1 | 2302 |
| 2015 | 3804 | 88 | 1 | 2515 | |
| 2016 | 3511 | 90 | 2 | 2399 | |
| 2017 | 3541 | 72 | 2 | 1087 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moss, R.; Zarebski, A.E.; Carlson, S.J.; McCaw, J.M. Accounting for Healthcare-Seeking Behaviours and Testing Practices in Real-Time Influenza Forecasts. Trop. Med. Infect. Dis. 2019, 4, 12. https://doi.org/10.3390/tropicalmed4010012
Moss R, Zarebski AE, Carlson SJ, McCaw JM. Accounting for Healthcare-Seeking Behaviours and Testing Practices in Real-Time Influenza Forecasts. Tropical Medicine and Infectious Disease. 2019; 4(1):12. https://doi.org/10.3390/tropicalmed4010012
Chicago/Turabian StyleMoss, Robert, Alexander E. Zarebski, Sandra J. Carlson, and James M. McCaw. 2019. "Accounting for Healthcare-Seeking Behaviours and Testing Practices in Real-Time Influenza Forecasts" Tropical Medicine and Infectious Disease 4, no. 1: 12. https://doi.org/10.3390/tropicalmed4010012
APA StyleMoss, R., Zarebski, A. E., Carlson, S. J., & McCaw, J. M. (2019). Accounting for Healthcare-Seeking Behaviours and Testing Practices in Real-Time Influenza Forecasts. Tropical Medicine and Infectious Disease, 4(1), 12. https://doi.org/10.3390/tropicalmed4010012





