Assessing the Impact of Relapse, Reinfection and Recrudescence on Malaria Eradication Policy: A Bifurcation and Optimal Control Analysis
Abstract
:1. Introduction
2. Mathematical Model Formulation and Parameter Estimation
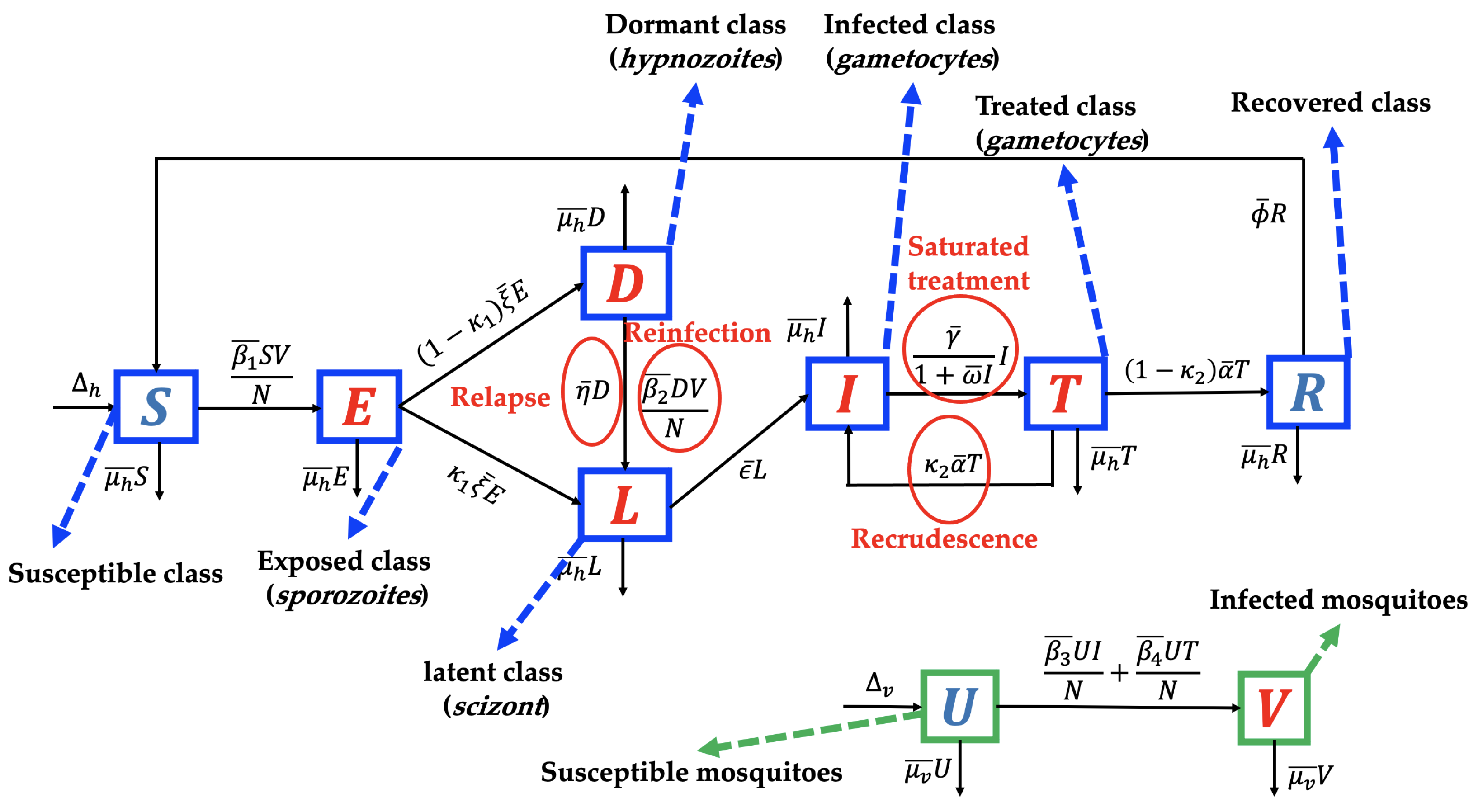
2.1. The Mathematical Model
2.2. Parameter Estimation
3. Mathematical Analysis
3.1. Non-Dimensional Model
3.2. Malaria-Free Equilibrium and the Basic Reproduction Number
- 1.
- Model without recurrence. When all recurrence phenomena are not involved in the model, i.e., , and , then the transmission diagram in Figure 1 is reduced to the transmission diagram in Figure 4.Using the parameter transformation in Supplementary Section S1, the basic reproduction number of the malaria model using transmission diagram in Figure 4 is given byTo give further interpretation of , Equation (6) can be rewritten as follows:It is clear to see that is a result of multiplication between the number of new infected humans, new infected mosquitoes, and the lifetime of the exposed and latent classes. It can be seen that the saturated parameter of the treatment term does not appear in .
- 2.
- Model with reinfection only. When the malaria model in the transmission diagram in Figure 1 includes reinfection only, without relapse and recrudescence, then the transmission diagram becomes that depicted in Figure 5.Calculating the basic reproduction number of the non-dimensional form of the model from the transmission diagram in Figure 5, we haveIt can be seen that , which means that reinfections do not change the standard basic reproduction number.
- 3.
- Model with relapse only. With the same approach as before, when reinfection and recrudescence are not involved, and . Based on this, the transmission diagram in Figure 1 changes to Figure 6.The basic reproduction number of a non-dimensional model based on transmission diagram in Figure 6 is given bySince , we can conclude that the existence of relapse phenomena reduces the standard basic reproduction number . This reduction was due to the dormant period experienced by infected individuals in the hypnozoite phase, which made them unable to directly infect healthy mosquitoes. As previously mentioned, malaria infection by Plasmodium Vivax and Ovale can result in a long dormant period of up to 2–3 years.
- 4.
- Model with recrudescence only. When relapse and reinfection are not involved in the original model (Equation (S1) in the Supplementary File), then we have . Hence, the transmission diagram in Figure 1 is reduced to the one in Figure 7.The basic reproduction number of the non-dimensional model based on transmission diagram in Figure 7 is given byIt can be seen that since , we may conclude that recrudescence will increase the standard basic reproduction number.
- The basic reproduction number when all recurrence phenomena are constructed as a multiplication between infection in humans, infection in mosquitoes, lifetime period of class e, and the ratio between the in- and outflow of class l. We call this basic reproduction number the standard basic reproduction number.
- The existence of reinfection phenomena does not change the size of the standard basic reproduction number. It means that increasing reinfection the rate will not affect the size of the standard basic reproduction number. However, it will increase the endemic size and the possibility for the existence of multiple endemic conditions in the environment. We discuss this in the next section of this article.
- The existence of relapse phenomena will reduce the size of the standard basic reproduction number. This is highly related to the duration of the dormant period of the hypnozoite inside the human body.
- The existence of recrudescence phenomena will increase the size of the standard basic reproduction number.
3.3. Existence of the Endemic Equilibrium
4. Bifurcation Analysis
5. Global Sensitivity Analysis
6. Optimal Control Problem
6.1. Characterization of the Optimal Control Problem
- Use of a bed net. Use of bed net is reportedly successful in reducing malaria incidence worldwide [58]. Bed nets provide protection to humans from the bite of a mosquito. Let us assume represents the proportion of the human population who use a bed net. Hence, and represent the total human population who use and do not use a bed net, respectively. The successful transmission rate for humans who use bed nets now read as , where presents the efficacy of bed nets in reducing the number of successful bites. Note that in a smaller represents a bed net with better quality. Based on this assumption, the total number of new infections for non-users of bed nets in susceptible populations is given byand the total number of new infections for the bed net users is given byTherefore, total of new infections in the susceptible population is given byNote that if the entire human population used a bed net and the quality of the bed net could provide 100% protection against mosquitoes’ bites , then no infections would occur in the field (in this case, we have ). On the other hand, if all humans used a bed net but the efficacy level (protection from mosquito bites) is not 100%, then there is still a possibility that new infections occur, which given byFurthermore, when not all humans use a bed net, but the efficacy level of the bed net is 100%, then the total number of new infections is given byA similar approach is applied to the reinfection term and the new infection in mosquito population term, which involve and . Note that when , the infection term is reduced into the standard model in Equation (S1) of the Supplementary File.For the sake of simplification, we use another interpretation of bed net use, the term , as follows. The term can be rewritten as where represents the effective bed net utilization rate. If or (equivalently) , then the bed net is useless, and regardless of the number of people who use the bed net, there will not be any impact on malaria prevention. In contrast, if , which is equivalent to the condition , then the bed net can always provide protection to humans from mosquito bites. The larger the utilization rate , the stronger the impact of bed net usage in the malaria prevention program. Therefore, instead of using the expression as in (13), we use the following expression to show the impact of bed net usage
- Hospitalization. In endemic malaria areas, hospitalization is the most frequently used outbreak control effort. However, this effort is difficult to execute continuously at a high intensity. Therefore, instead of using the constant hospitalization rate of , we use the new term , which represents the time-dependent treatment rate.
- Fumigation. For many types of vector-borne disease, including malaria, vector control programs are the most common intervention to control the spread of the disease. Hence, we introduce as the additional death rate of the mosquito population due to fumigation, where the intervention depends on time.
6.2. Optimal Control Characterization
6.3. Optimal Control Simulation
6.3.1. Strategy 1. Single Intervention: Use of Bed Net Only
6.3.2. Strategy 2. Single Intervention: Use of Hospitalization Only
6.3.3. Strategy 3. Single Intervention: Use of Fumigation Only
6.3.4. Strategy 4. Double Intervention: Combination of Hospitalization and Fumigation
7. Cost-Effectiveness Analysis
8. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, D.L.; Bathle, K.E.; Hay, S.I.; Barker, C.M.; Scott, T.W.; McKenzie, F.E. Ross, Macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog. 2012, 8, e1002588. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. World Malaria Report 2020: 20 Years of Global Progress and Challenges, 1st ed.; World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Ghosh, M.; Lashari, A.A.; Li, X.Z. Biological control of malaria: A mathematical model. Appl. Math. Comput. 2013, 219, 7923–7939. [Google Scholar] [CrossRef]
- Aldila, D.; Angelina, M. Optimal control problem and backward bifurcation on malaria transmission with vector bias. Heliyon 2021, 7, e06824. [Google Scholar] [CrossRef] [PubMed]
- Woldegerima, W.; Ouifki, R.; Banasiak, J. Mathematical analysis of the impact of transmission–blocking drugs on the population dynamics of malaria. Appl. Math. Comput. 2021, 400, 126005. [Google Scholar] [CrossRef]
- Adedeji, E.O.; Ogunlana, O.O.; Fatumo, S.; Beder, T.; Ajamma, Y.; Koenig, R.; Adebiyi, E. Anopheles metabolic proteins in malaria transmission, prevention and control: A review. Parasites Vectors 2020, 13, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Hyde, J.E. Drug-resistant malaria an insight. FEBS J. 2007, 274, 4688–4698. [Google Scholar] [CrossRef] [PubMed]
- Birx, M.; de Souza, M.; Nkengasong, J. Laboratory challenges in the scaling-up of HIV, TB, and malaria programs: The interaction of health and laboratory systems, clinical research and service delivery. Am. J. Clin. Pathol. 2009, 131, 849–851. [Google Scholar] [CrossRef] [PubMed]
- Price, R.; von Seidlein, L.; Valecha, N.; Nosten, F.; Baird, J.; White, N. Global extent chloroquine–resistant Plasmodium vivax: A systematic review and meta–analysis. Lancet Infect. Dis. 2014, 14, 982–991. [Google Scholar] [CrossRef]
- Douglas, N.; Nosten, F.; Ashley, E.; Phaiphun, L.; Vught, M.V.; Singhasivanon, P.; White, N.; Price, R. Plasmodium vivax Recurrence Following Falciparum and Mixed Species Malaria: Risk Factors and Effect of Antimalarial Kinetics. Clin. Infect. Dis. 2019, 52, 612–620. [Google Scholar] [CrossRef] [PubMed]
- Lawpoolsri, S.; Sattabongkot, J.; Sirichaisinthop, J.; Cui, L.; Kiattibutr, K.; Rachaphaew, N.; Suk–uam, K.; Khamsiriwatchara, A.; Kaewkungwal, J. Epidemiological profiles of recurrent malaria episodes in an endemic area along the Thailand-Myanmar border: A prospective cohort study. Malar. J. 2019, 18, 124. [Google Scholar] [CrossRef]
- Ross, R. The Prevention of Malaria; Dutton: New York, NY, USA, 1910. [Google Scholar]
- Macdonald, G. The epidemiology and control of malaria. In Epidemiology and Control of Malaria; Oxford University Press: Oxford, UK, 1957. [Google Scholar]
- Tumwiine, J.; Mugisha, J.; Luboobi, L. A mathematical model for the dynamics of malaria in a human host and mosquito vector with temporary immunity. Appl. Math. Comput. 2007, 189, 1953–1965. [Google Scholar] [CrossRef]
- Traore, B.; Koutou, O.; Sangare, B. A global mathematical model of malaria transmission dynamics with structured mosquito population and temperature variations. Nonlinear Anal. Real World Appl. 2021, 53, 103081. [Google Scholar] [CrossRef]
- Tumwiine, J.; Mugisha, J.; Luboobi, L. A host-vector model for malaria with infective immigrants. J. Math. Anal. Appl. 2010, 36, 139–149. [Google Scholar] [CrossRef]
- Handari, B.; Vitra, F.; Ahya, R.; S, T.N.; Aldila, D. Optimal control in a malaria model: Intervention of fumigation and bed nets. Adv. Differ. Equ. 2019, 2019, 497. [Google Scholar] [CrossRef]
- Wan, H.; Zhu, H. The impact of resource and temperature on malaria transmission. J. Biol. Syst. 2012, 20, 285–302. [Google Scholar] [CrossRef]
- Li, J.; teng, Z.; Zhang, L. Stability and bifurcation in a vector-bias model of malaria transmission with delay. Math. Comput. Simul. 2014, 152, 15–34. [Google Scholar] [CrossRef]
- Aldila, D. A superinfection model on malaria transmission: Analysis on the invasion basic reproduction number. Commun. Math. Biol. Neurosci. 2021, 2021, 30. [Google Scholar] [CrossRef]
- Fatmawati; Herdicho, F.F.; Windarto; Chukwu, W.; Tasman, H. An optimal control of malaria transmission model with mosquito seasonal factor. Results Phys. 2021, 25, 104238. [Google Scholar]
- Tasman, H.; Purwati, U.D.; Herdicho, F.F.; Chukwu, C.W. An optimal control problem of malaria model with seasonality effect using real data. Commun. Math. Biol. Neurosci. 2021, 2021, 66. [Google Scholar]
- Handari, B.D.; Ramadhani, R.A.; Chukwu, C.W.; Khoshnaw, S.H.A.; Aldila, D. An Optimal Control Model to Understand the Potential Impact of the New Vaccine and Transmission-Blocking Drugs for Malaria: A Case Study in Papua and West Papua, Indonesia. Vaccines 2022, 10, 1174. [Google Scholar] [CrossRef]
- Olaniyi, S.; Mukamuri, M.; Okosun, K.O.; Adepoju, O.A. Mathematical analysis of a social hierarchy-structured model for malaria transmission dynamics. Results Phys. 2022, 34, 104991. [Google Scholar] [CrossRef]
- Niger, A.; Gumel, A. Mathematical analysis of the role of repeated exposure on malaria transmission dynamics. Differ. Equ. Dyn. Syst. 2008, 16, 251–287. [Google Scholar] [CrossRef]
- Chamcod, F.; Beier, J. Modeling Plasmodium vivax: Relapses, treatment, seasonality, and G6PD deficiency. J. Theor. Biol. 2013, 316, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, M.; Olaniyi, S.; Obabiyi, O. Mathematical analysis of reinfection and relapse in malaria dynamics. Appl. Math. Comput. 2020, 373, 125044. [Google Scholar] [CrossRef]
- Wang, S.; Hu, L.; Nie, L. Global dynamics and optimal control of an age-structure Malaria transmission model with vaccination and relapse. Chaos Solitons Fractals 2021, 150, 111216. [Google Scholar] [CrossRef]
- Abimbade, S.F.; Olaniyi, S.; Ajala, O.A. Recurrent malaria dynamics: Insight from mathematical modelling. Eur. Phys. J. Plus Vol. 2022, 137, 1–16. [Google Scholar] [CrossRef]
- Castillo–Chavez, C.; Song, B. Dynamical Models of Tuberculosis and Their Applications. Math. Biosci. Eng. 2014, 1, 361–404. [Google Scholar] [CrossRef]
- Ndoen, E.; Wild, C.; dale, P.; Sipe, N.; Dale, M. Mosquito Longevity, Vector Capacity, and Malaria Incidence in West Timor and Central Java, Indonesia. Int. Sch. Res. Not. 2012, 2012, 143863. [Google Scholar] [CrossRef]
- Douamba, Z.; Dao, N.; Zohoncon, T.; Bisseye, C.; Compaore, T.; Kafando, J.; Sombie, B.; Ouermi, D.; Djigma, F.; Ouedraogo, P.; et al. Mother-to-Children Plasmodium falciparum Asymptomatic Malaria Transmission at Saint Camille Medical Centre in Ouagadougou, Burkina Faso. Malar. Res. Treat. 2014, 2014, 390513. [Google Scholar] [CrossRef]
- Ouedraogo, A.; Tiono, A.; Diarra, A.; Bougouma, E.; Nebie, I.; Konate, A.; Sirima, S. Transplacental Transmission of Plasmodium falciparum in a Highly Malaria Endemic Area of Burkina Faso. J. Trop. Med. 2012, 2012, 109705. [Google Scholar] [CrossRef]
- Center for Disease Control and Prevention. Malaria. 2019. Available online: https://www.cdc.gov/malaria/about/disease.html (accessed on 28 July 2021).
- The World Bank. Hospital Beds (per 1000 People). 2017. Available online: https://data.worldbank.org/indicator/SH.MED.BEDS.ZS (accessed on 28 July 2021).
- Chamberlain, R.; Sudia, W. Mechanism of transmission of viruses by mosquitoes. Annu. Rev. Entomol. 1961, 6, 371–390. [Google Scholar] [CrossRef]
- Ngonghala, C.; Del Valle, S.; Zhao, R.; Mohammed-Awel, J. Quantifying the impact of decay in bed-net efficacy on malaria transmission. J. Theor. Biol. 2014, 363, 247–261. [Google Scholar] [CrossRef] [Green Version]
- Chu, C.; White, N. Management of relapsing Plasmodium vivax malaria. Expert Rev. Anti-Infect. Ther. 2016, 14, 885–900. [Google Scholar] [CrossRef]
- White, M.; Shirreff, G.; Karl, S.; Ghani, A.; Mueller, I. Variation in relapse frequency and the transmission potential of Plasmodium vivax malaria. Proc. R. Soc. B Biol. Sci. 2016, 283, 20160048. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhao, Y.; Li, S. Fast and Slow dynamics of Malaria model with relapse. Math. Biosci. 2013, 246, 94–104. [Google Scholar] [CrossRef]
- Jackson, Y.; Chappuis, F.; Loutan, L.; Taylor, W. Malaria treatment failures after artemisinin-based therapy in three expatriates: Could improved manufacturer information help to decrease the risk of treatment failure? Malar. J. 2006, 5, 81. [Google Scholar] [CrossRef]
- Duong, M.; Pham, O.K.N.; Nguyen, P.; Nguyen, V.; Nguyen, P. Predictors of treatment failures of plasmodium falciparum malaria in Vietnam: A 4-year single-centre retrospective study. Malar. J. 2021, 20, 205. [Google Scholar] [CrossRef] [PubMed]
- Chitnis, N.; Hyman, J.; Cushing, J. Determining Important Parameters in the Spread of Malaria Through the Sensitivity Analysis of a Mathematical Model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef] [PubMed]
- Ngonghala, C.; Mohammed-Awel, J.; Zhao, R.; Prosper, O. Interplay between insecticide-treated bed-nets and mosquito demography: Implications for malaria control. J. Theor. Biol. 2016, 397, 179–192. [Google Scholar] [CrossRef]
- Chowell, G. Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts. Infect. Dis. Model. 2017, 2, 379–398. [Google Scholar] [CrossRef]
- Gumel, A.B.; Iboi, E.A.; Ngonghala, C.N.; Elbasha, E.H. A primer on using mathematics to understand COVID-19 dynamics: Modeling, analysis and simulations. Infect. Dis. Model. 2021, 6, 148–168. [Google Scholar] [CrossRef] [PubMed]
- Aldila, D. Analyzing the impact of the media campaign and rapid testing for COVID-19 as an optimal control problem in East Java, Indonesia. Chaos Solitons Fractals 2020, 141, 110364. [Google Scholar] [CrossRef] [PubMed]
- Aldila, D.; Samiadji, B.M.; Simorangkir, G.M.; Khosnaw, S.H.A.; Shahzad, M. Impact of early detection and vaccination strategy in COVID-19 eradication program in Jakarta, Indonesia. BMC Res. Notes 2021, 14, 132. [Google Scholar] [CrossRef]
- Chukwu, C.; Fatimawati. Modelling fractional-order dynamics of COVID-19 with environmental transmission and vaccination: A case study of Indonesia. AIMS Math. 2022, 7, 4416–4438. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- Mushanyu, J.; Chukwu, W.; Nyabadza, F.; Muchatibaya, G. Modelling the potential role of super spreaders on COVID-19 transmission dynamics. medRxiv 2021. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Wu, J.; Dhingra, R.; Gambhir, M.; Remais, J.V. Sensitivity analysis of infectious disease models: Methods, advances and their application. J. R. Soc. Interface 2013, 10, 20121018. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Adi, Y.A. Understanding the effects of individual awareness and vector controls on malaria transmission dynamics using multiple optimal control. Chaos Solitons Fractals 2021, 153, 111476. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Anggriani, N.; Messakh, J.J.; Djahi, B.S. Estimating the reproduction number and designing the integrated strategies against dengue. Results Phys. 2021, 27, 104473. [Google Scholar] [CrossRef]
- Chukwu, C.W.; Nyabadza, F. Modelling the potential role of media campaigns on the control of Listeriosis. Math. Biosci. Eng. 2021, 18, 7580–7601. [Google Scholar] [CrossRef] [PubMed]
- Steinhardt, L.C.; Jean, Y.S.; Impoinvil, D.; Mace, K.E.; Wiegand, R.; Huber, C.S.; Fils Alexandre, J.S.; Frederick, J.; Nkurunziza, E.; Jean, S.; et al. Effectiveness of insecticide-treated bednets in malaria prevention in Haiti: A case-control study. Lancet 2017, 5, E96–E103. [Google Scholar] [CrossRef]
- Agusto, F.B.; Del-Valle, S.Y.; Blayneh, K.W.; Ngonghala, C.N.; Goncalves, M.J.; Li, N.; Zhao, R.; Gong, H. The impact of bed-net use on malaria prevalence. J. Theor. Biol. 2013, 320, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; CRC Press: Boca Raton, FL, USA, 1987. [Google Scholar]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Buonomo, B.; Della Marca, R. Optimal bed net use for a dengue disease model with mosquito seasonal pattern. Math. Methods Appl. Sci. 2018, 41, 573–592. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, Y.; Zhang, X. Dynamic analysis of a malaria reaction-diffusion model with periodic delays and vector bias. Math. Biosci. Eng. 2022, 19, 2538–2574. [Google Scholar] [CrossRef]
- Leung, S.; Windbichler, N.; Wenger, E.A.; Bever, C.A.; Selvaraj, P. Population replacement gene drive characteristics for malaria elimination in a range of seasonal transmission settings: A modelling study. Malar. J. 2022, 21, 226. [Google Scholar] [CrossRef] [PubMed]
- Kirakoya-Samadoulougou, F.; De Brouwere, V.; F, F.A.; Ouedraogo, M.; Ye, Y. Assessing the effect of seasonal malaria chemoprevention on malaria burden among children under 5 years in Burkina Faso. Malar. J. 2022, 21, 143. [Google Scholar] [CrossRef] [PubMed]














| Par | Description | Units | Interval Values | Baseline Value | Ref. |
|---|---|---|---|---|---|
| Recruitment rate of human population | Estimated | ||||
| Average probability of successful transmission rate from mosquito to human in S | Fitted | 0.062 | Fitted | ||
| Average probability of successful transmission rate from mosquito to human in D due to reinfection | Fitted | 0.06 | Fitted | ||
| Intrinsic incubation rate of E | [34,37] | ||||
| Transition from L to D after incubation period and ready to attack red blood cells | [34] | ||||
| Rate of relapse | [38,39] | ||||
| Proportion of exposed individuals who do not experience a dormant period | - | 0.7 | Estimated | ||
| Natural human death rate | [34] | ||||
| Treatment rate | Fitted | ||||
| Recovery rate | [27,40] | ||||
| Half-saturation parameter | Estimated | ||||
| Proportion of treated individuals who experience recrudescence (treatment failure) | - | 0.19 | [41,42] | ||
| Rate of loss of natural immunity in human population | [43] | ||||
| Recruitment rate of mosquito population | Estimated | ||||
| Average probability of successful transmission rate in mosquito after biting I individuals | Fitted | 0.048 | Fitted | ||
| Average probability of successful transmission rate in mosquito after biting T individuals | Fitted | 0.048 | Fitted | ||
| Natural mosquitoes’ death rate | [44] |
| Strategies | Optimal Controls | Total Averted Infection | Total Cost |
|---|---|---|---|
| 1 | 1.4963 | ||
| 3 | 18.4577 | ||
| 2 | 765.5569 | ||
| 4 | 773.8898 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tasman, H.; Aldila, D.; Dumbela, P.A.; Ndii, M.Z.; Fatmawati; Herdicho, F.F.; Chukwu, C.W. Assessing the Impact of Relapse, Reinfection and Recrudescence on Malaria Eradication Policy: A Bifurcation and Optimal Control Analysis. Trop. Med. Infect. Dis. 2022, 7, 263. https://doi.org/10.3390/tropicalmed7100263
Tasman H, Aldila D, Dumbela PA, Ndii MZ, Fatmawati, Herdicho FF, Chukwu CW. Assessing the Impact of Relapse, Reinfection and Recrudescence on Malaria Eradication Policy: A Bifurcation and Optimal Control Analysis. Tropical Medicine and Infectious Disease. 2022; 7(10):263. https://doi.org/10.3390/tropicalmed7100263
Chicago/Turabian StyleTasman, Hengki, Dipo Aldila, Putri A. Dumbela, Meksianis Z. Ndii, Fatmawati, Faishal F. Herdicho, and Chidozie W. Chukwu. 2022. "Assessing the Impact of Relapse, Reinfection and Recrudescence on Malaria Eradication Policy: A Bifurcation and Optimal Control Analysis" Tropical Medicine and Infectious Disease 7, no. 10: 263. https://doi.org/10.3390/tropicalmed7100263








