Estimating Dengue Transmission Intensity in China Using Catalytic Models Based on Serological Data
Abstract
1. Introduction
1.1. Current Status of Dengue
1.2. Dengue Data and Modelling
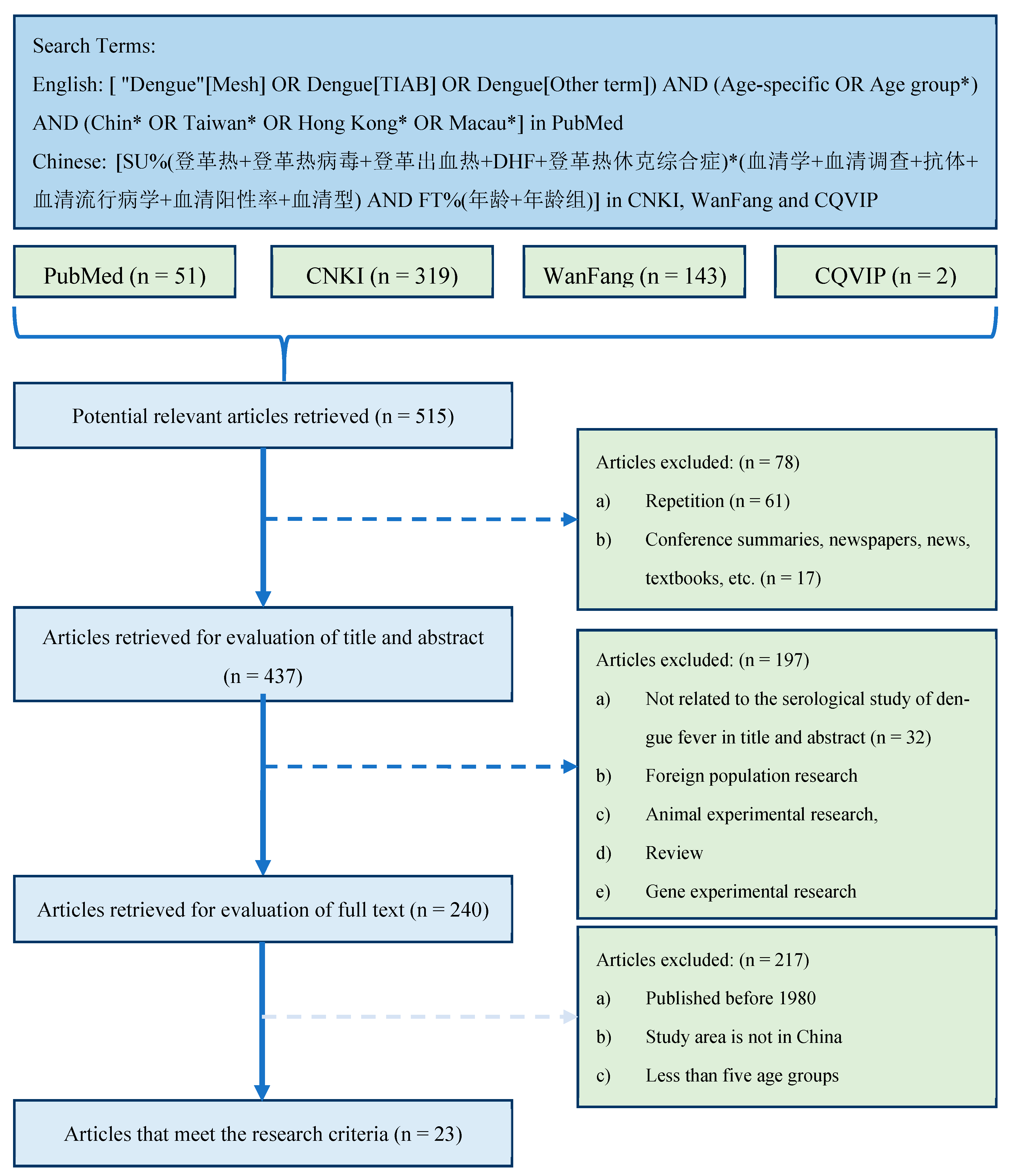
2. Materials and Methods
2.1. Literature Search and Data
2.2. Dengue Models
2.2.1. Model A: Constant Force of Infection
2.2.2. Model B: Antibody Protection Decay
2.2.3. Models That Include Threshold Age
2.3. Inference Method
2.4. Negative Log-Likelihood (-LnL)
2.5. Estimation of Basic Reproduction Number (R0)
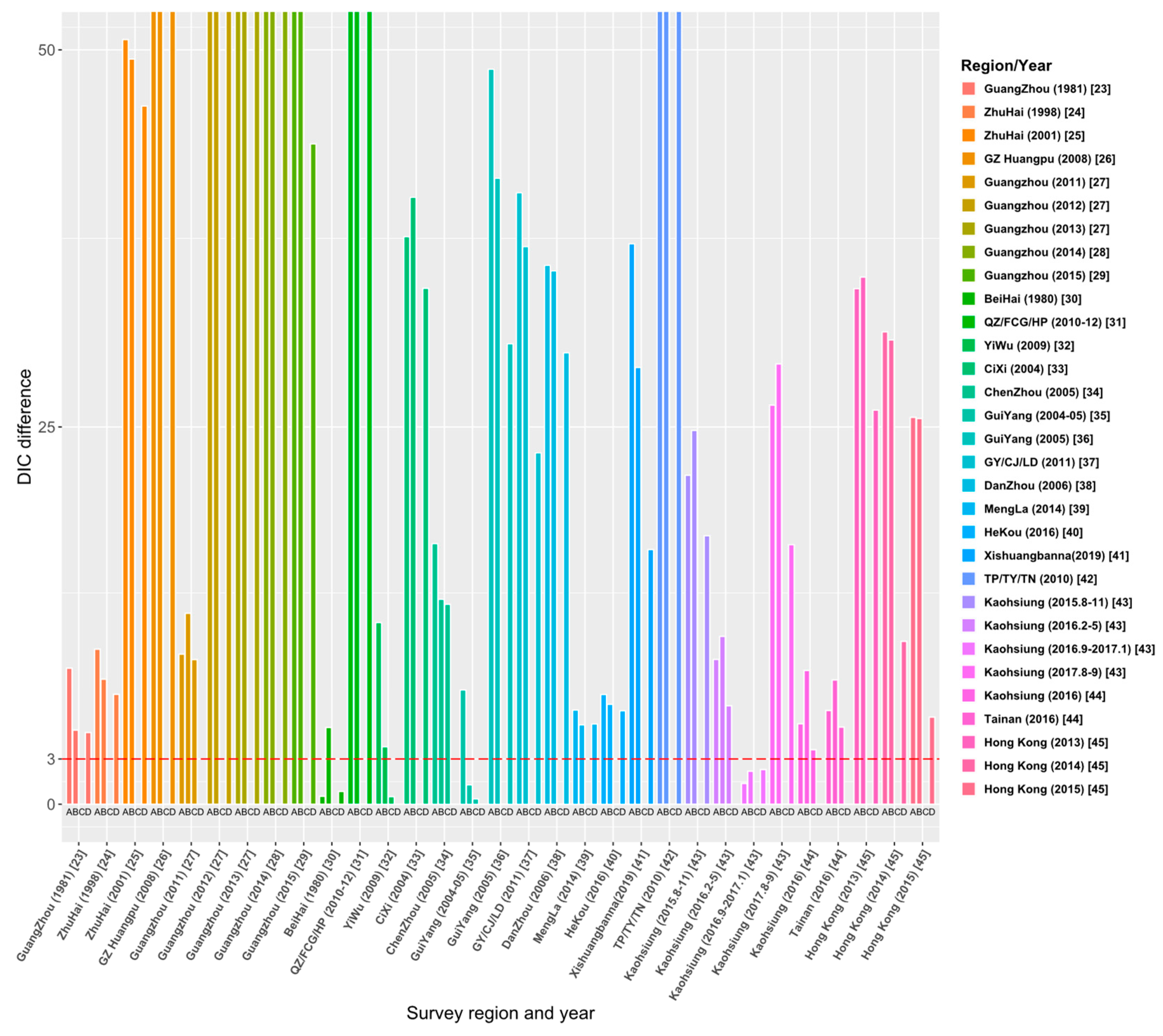
2.6. Deviation Information Criterion (DIC) and Model Selection
3. Results
3.1. Model Comparison and Selection
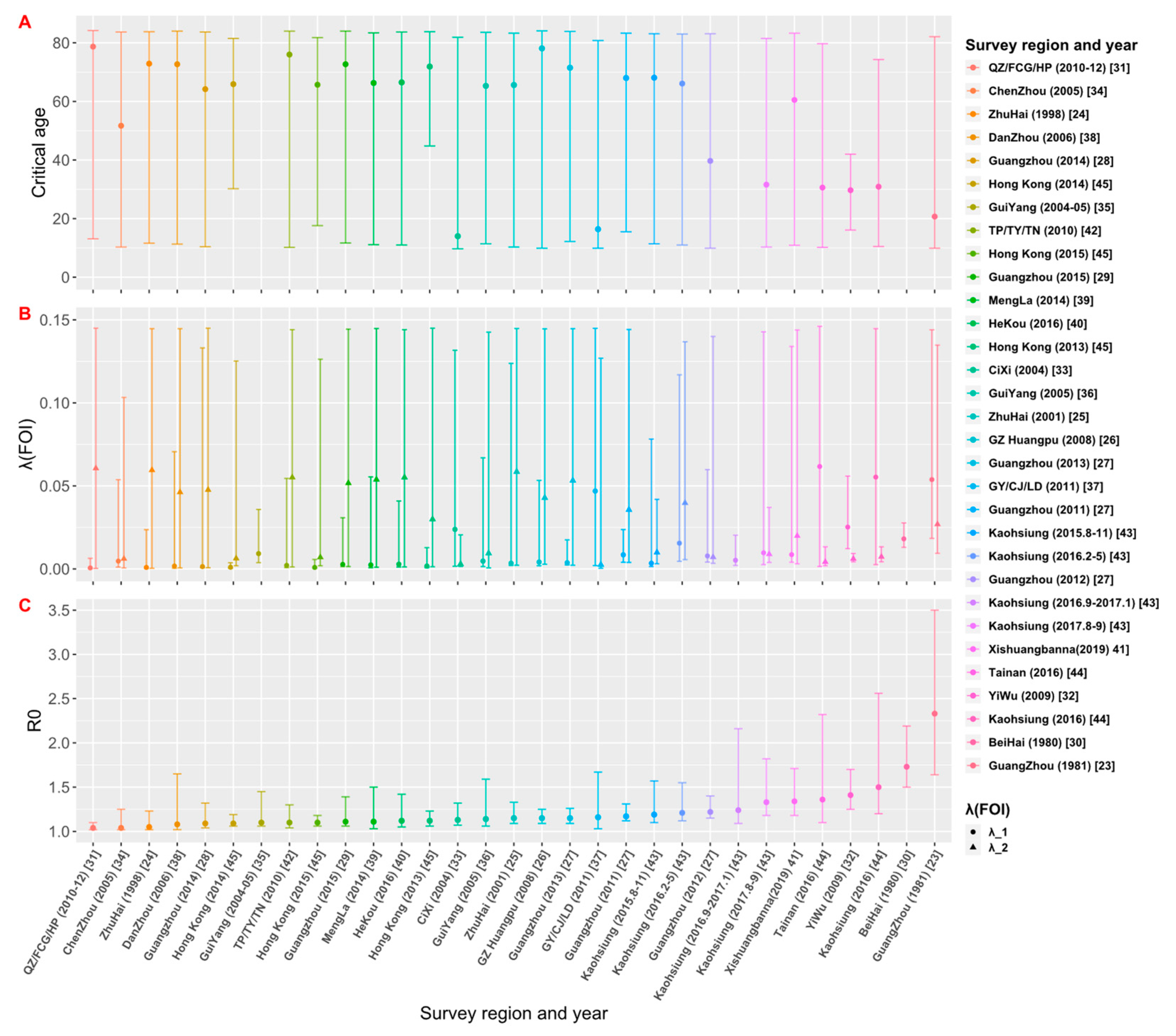
3.2. Estimates of FOI and R0
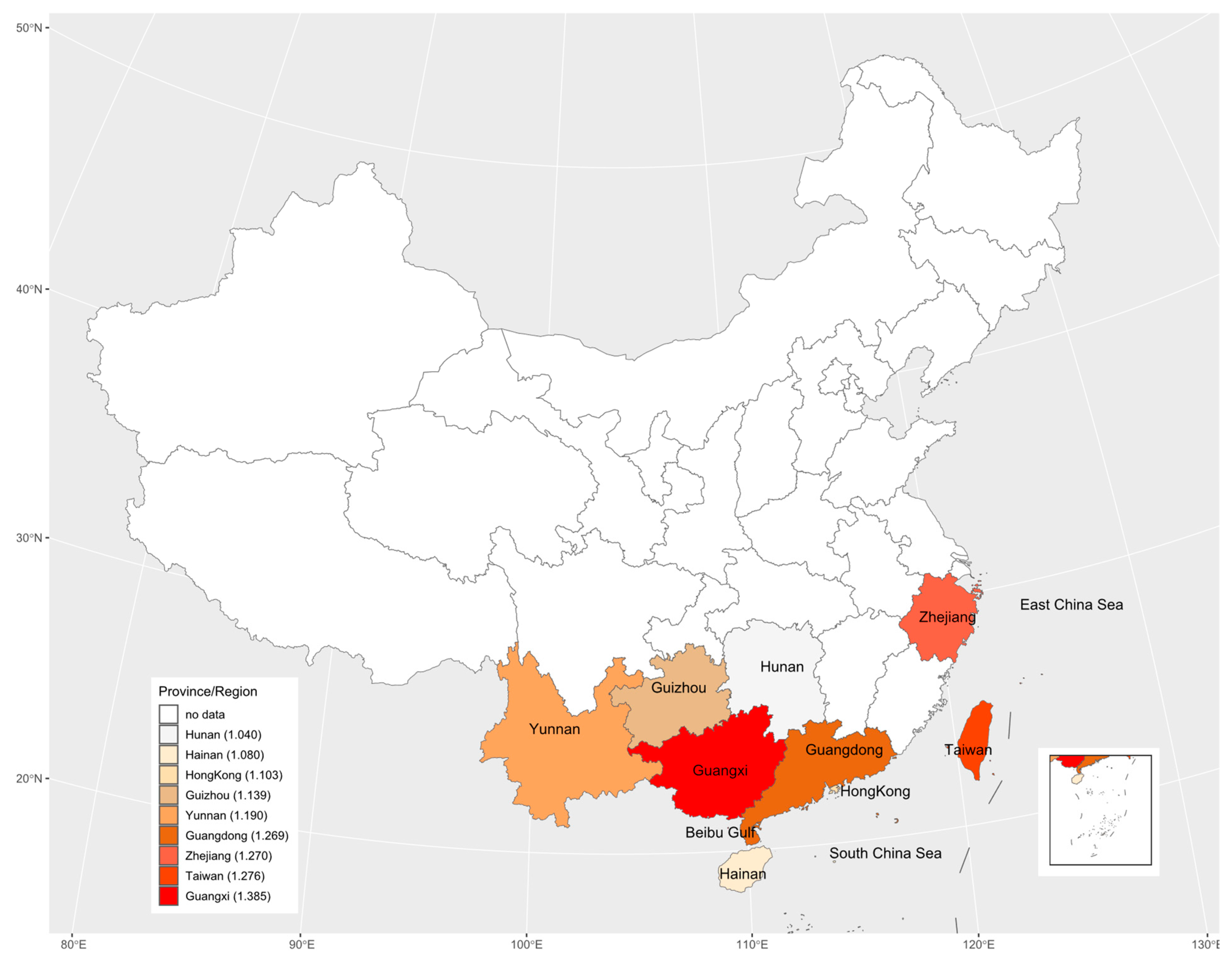
3.3. Time-Space Comparison
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization (WHO). Dengue: Guidelines for Diagnosis, Treatment, Prevention and Control: New Edition; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- World Health Organization (WHO). Accelerating Work to Overcome the Global Impact of Neglected Tropical Diseases; World Health Organization: Geneva, Switzerland, 2007; Volume 7, p. 596. [Google Scholar]
- World Health Organization. Dengue and Severe Dengue, 10 January 2022. Available online: https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe-dengue (accessed on 22 October 2022).
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Huang, Y.; Zhang, X.; Xiong, L.; Li, Y.; Zhang, R. Epidemiology and genotyping of dengue fever in Shenzhen City in 2018. Chin. J. Infect. Dis. 2020, 38, 342–347. [Google Scholar] [CrossRef]
- Wu, T.; Qin, N.; Zhang, J.; Wang, W.; Li, J. Dengue fever epidemic risk in Tianjin from 2009 to 2015. Mod. Prev. Med. 2016, 43, 1925–1927+1943. [Google Scholar]
- Cai, Y.; Liu, S.; Wei, Y.; Han, X.; Han, Z.; Zhang, Y.; Xu, Y.; Qi, S.; Li, Q. Epidemic characteristics and prevention and control Strategies of imported Dengue fever in Hebei province from 2011 to 2018. Pract. Prev. Med. 2022, 27, 798–801. [Google Scholar]
- Li, H.; Jiang, J.; Do, L.; Chen, Z.; Chen, S.; Li, J.; Liu, H. Emergency monitoring and analysis of the epidemiological characteristics and vectors of a dengue fever outbreak in Mengla County in 2018. J. Parasit. Biol. 2020, 15, 83–85+90. [Google Scholar] [CrossRef]
- Feng, S.; Guan, J.; Chen, J.; Rao, Q.; Sun, Q. Clinical and laboratory characteristics of 96 cases of dengue fever in Qiyang County, Hunan Province, China in 2018. Chin. J. Biol. 2020, 33, 423–428+433. [Google Scholar]
- Dai, B.; Wang, F.; Pan, J.; Han, C.; Huang, K. Epidemic characteristics and treatment effect of the first dengue fever outbreak in Hubei Province. J. Public Health Prev. Med. 2020, 31, 62–65. [Google Scholar] [CrossRef]
- Ning, D.; Sun, J.; Peng, Z.; Wu, D. The epidemiological situation and epidemiological characteristics of dengue fever in Guangdong Province. South China Prev. Med. 2017, 43, 368–372. [Google Scholar]
- Cai, W.; Jing, Q.; Liu, W.; Chen, C. Analysis of epidemiological characteristics of local dengue fever cases in Guangzhou from 2015 to 2019. South China Prev. Med. 2020, 46, 138–140. [Google Scholar]
- Yang, J.; Chen, M.; Wang, H.; Zhang., S. Analysis of epidemiological characteristics of dengue fever outbreak in Fuzhou in 2016. Chin. Trop. Med. 2017, 17, 795–797+805. [Google Scholar]
- Mai, G.; He, Y.; Chen, Z. Analysis of the epidemiological characteristics of dengue antibody positive in Gaoming District, Foshan City from 2015 to 2019. Public Health Prev. Med. 2020, 31, 122–124. [Google Scholar]
- World Health Organization (WHO). Global Strategy for Dengue Prevention and Control, 2012–2020; World Health Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Grenfell, B.T.; Anderson, R.M. The estimation of age-related rates of infection from case notifications and serological data. J. Hyg. 1985, 95, 419–436. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control (Oxford Science Publications); OUP Oxford: Oxford, UK, 1992. [Google Scholar]
- Ferguson, N.M. Mathematical prediction in infection. Medicine 2009, 37, 507–509. [Google Scholar] [CrossRef]
- Imai, N.; Dorigatti, I.; Cauchemez, S.; Ferguson, N.M. Estimating dengue transmission intensity from sero-prevalence surveys in multiple countries. PLoS Negl. Trop. Dis. 2015, 9, e0003719. [Google Scholar] [CrossRef]
- Thai, K.T.; Nagelkerke, N.; Phuong, H.L.; Nga, T.T.; Giao, P.T.; Hung, L.Q.; Binh, T.Q.; Nam, N.V.; De Vries, P.J. Geographical heterogeneity of dengue transmission in two villages in southern Vietnam. Epidemiol. Infect. 2010, 138, 585–591. [Google Scholar] [CrossRef] [PubMed]
- Gordon, A.; Kuan, G.; Mercado, J.C.; Gresh, L.; Avilés, W.; Balmaseda, A.; Harris, E. The Nicaraguan pediatric dengue cohort study: Incidence of inapparent and symptomatic dengue virus infections, 2004–2010. PLoS Negl. Trop. Dis. 2013, 7, e2462. [Google Scholar] [CrossRef]
- Endy, T.P.; Chunsuttiwat, S.; Nisalak, A.; Libraty, D.H.; Green, S.; Rothman, A.L.; Vaughn, D.W.; Ennis, F.A. Epidemiology of inapparent and symptomatic acute dengue virus infection: A prospective study of primary school children in Kamphaeng Phet, Thailand. Am. J. Epidemiol. 2002, 156, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Liang, J.; Lin, Z. Survey of dengue anti-antibody level in population after dengue fever epidemic in Guangzhou. Guangzhou Med. J. 1983, 20–25. [Google Scholar]
- Li, Z.; Zhang, J.; Ma, H. Surveillance of Dengue Fever Antibody Levels in People in Zhuhai Port Area. Chin. J. Front. Health Quar. 1999, 22, 141–143. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, H.; Lin, G.; Zeng, W.; Tu, C.; Ye, L.; Zhao, J.; Yao, R. Analysis of dengue antibody levels and related factors in different populations. Mod. Prev. Med. 2002, 29, 694–695. [Google Scholar] [CrossRef]
- Zheng, X.; Wu, Y.; Zhang, M.; He, A.; Li, Z.; Qu, Z.; Zhan, X. Sero-epidemiological Investigation of Dengue Fever in Guangzhou. J. Trop. Med. 2009, 9, 1397–1399+1404. [Google Scholar]
- Cao, Y.; Jiang, L.; Xu, Y.; Jing, Q.; Cao, Q.; Di, B.; Yang, Z. Monitoring and analysis of dengue fever serum antibody levels in Guangzhou from 2011 to 2013. South China J. Prev. Med. 2015, 41, 364–366. [Google Scholar] [CrossRef]
- Li, S.; Liao, Q.; Liang, Y.; Chen, J.; You, R.; Xiong, H.; Huang, K.; Rong, X. Study on the risk of dengue virus transmission by blood transfusion in Guangzhou area. Guangdong Med. J. 2017, 38, 1064–1067. [Google Scholar] [CrossRef]
- Jing, Q.; Li, Y.; Liu, J.; Jiang, L.; Chen, Z.; Su, W.; Birkhead, G.S.; Lu, J.; Yang, Z. Dengue Underestimation in Guangzhou, China: Evidence of Seroprevalence in Communities with No Reported Cases Before a Large Outbreak in 2014. Open Forum Infect. Dis. 2019, 6, ofz256. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Ai, C.; Li, C.; Wen, Y.; Liu, Y.; Xia, H. Epidemiological surveillance of dengue fever in Beihai City, Guangxi. J. Mil. Med. Sci. 1985, 38, 387–392. [Google Scholar]
- Zhou, K.; Chen, M.; Tan, Y.; Mo, Y.; Bi, Y. Serological surveillance of healthy population in Guangxi dengue surveillance sites. J. Appl. Prev. Med. 2013, 19, 236–237. [Google Scholar] [CrossRef]
- Sun, J.; Luo, S.; Lin, J.; Chen, J.; Hou, J.; Fu, T.; Lv, H.; Chen, Z.; Cong, L.; Ling, F.; et al. Inapparent infection during an outbreak of dengue fever in Southeastern China. Viral Immunol. 2012, 25, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Cen, D.; Wu, J.; Xu, Y. Application of Serum Bank in the Investigation and Analysis of Dengue Fever Antibody Level. Chin. Prev. Med. 2007, 8, 734–735. [Google Scholar] [CrossRef]
- Gao, L.; Xiao, J.; Zhang, H.; Duan, L.; Liu, F.; Dai, D.; Li, J.; Deng, Z. Sero-epidemiology investigation of dengue fever in Chenzhou. South China J. Prev. Med. 2007, 33, 34–35. [Google Scholar] [CrossRef]
- Gao, R.; Zhou, X.; Zhou, C.; Han, Y.; Luo, J.; Qin, J. Serological Epidemiological Research on Dengue Virus Antibodies among Personnel at Guiyang Port. Chin. J. Front. Health Quar. 2006, 29 (Suppl. S1), 57–59. [Google Scholar] [CrossRef]
- Tian, H.; Han, Y.; Dai, A.; Fu, D.; Zhou, Y.; Zhou, N.; Gao, R. The Investigation of the Population Infected with Dengue Virus at Guiyang Port and other Close Areas. J. Travel Med. Sci. 2007, 13, 28–29. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, J.; Tang, G.; Zhuang, Y.; Yun, C.; Fu, L. Investigation on Dengue Fever Infection among Healthy Population in Some Counties and Cities in Guizhou Province. Guizhou Med. J. 2013, 37, 164–165. [Google Scholar] [CrossRef]
- Jin, Y.; Sun, L.; Zeng, X.; Wu, W.; Ma, Y.; Su, X.; Lao, S.; Chen, Y.; Li, Z. Sero-epidemiological survey and analysis on dengue fever in Hainan Province. China Trop. Med. 2007, 7, 2007–2008. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, Y.; Ji, R.; Luo, Z.; Zhang, Q.; Zhou, L.; Yang, X. Serological surveillance on arboviral diseases among exit-entry population at Sino-Laos port. Chin. J. Front. Health Quar. 2016, 39, 180–182. [Google Scholar] [CrossRef]
- Pu, L.; Chen, J.; Zhang, Q.; Zhang, C.; Li, Z.; Liu, W.; Wu, Z. Aedes surveillance and dengue fever serological survey at Sino-Vietnam Hekou-Laocai ports. Chin. J. Front. Health Quar. 2018, 41, 255–257+268. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Lu, S.; Dong, J.; Xu, H.; Zhang, Q.; Weng, R.; Yin, Y.; He, R.; Fang, P.; et al. Epidemiological survey and screening strategy for dengue virus in blood donors from Yunnan Province. BMC Infect. Dis. 2021, 21, 104. [Google Scholar] [CrossRef]
- Lee, Y.H.; Hsieh, Y.C.; Chen, C.J.; Lin, T.Y.; Huang, Y.C. Retrospective Seroepidemiology study of dengue virus infection in Taiwan. BMC Infect. Dis. 2021, 21, 96. [Google Scholar] [CrossRef]
- Tsai, J.J.; Liu, C.K.; Tsai, W.Y.; Liu, L.T.; Tyson, J.; Tsai, C.Y.; Lin, P.C.; Wang, W.K. Seroprevalence of dengue virus in two districts of Kaohsiung City after the largest dengue outbreak in Taiwan since World War II. PLoS Negl. Trop. Dis. 2018, 12, e0006879. [Google Scholar] [CrossRef]
- Pan, Y.H.; Liao, M.Y.; Chien, Y.W.; Ho, T.S.; Ko, H.Y.; Yang, C.R.; Chang, S.F.; Yu, C.Y.; Lin, S.Y.; Shih, P.W.; et al. Use of seroprevalence to guide dengue vaccination plans for older adults in a dengue non-endemic country. PLoS Negl. Trop. Dis. 2021, 15, e0009312. [Google Scholar] [CrossRef]
- Lee, P.; Yeung, A.C.M.; Chen, Z.; Chan, M.C.W.; Sze, K.H.; Chan, P.K.S. Age-specific seroprevalence of dengue infection in Hong Kong. J. Med. Virol. 2018, 90, 1427–1430. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Donnelly, C.A.; Anderson, R.M. Transmission dynamics and epidemiology of dengue: Insights from age-stratified sero-prevalence surveys. Philos Trans. R. Soc. Lond. B Biol. Sci. 1999, 354, 757–768. [Google Scholar] [CrossRef] [PubMed]
- Becker, N.G. Martingale methods for the analysis of epidemic data. Stat. Methods Med. Res. 1993, 2, 93–112. [Google Scholar] [CrossRef] [PubMed]
- Muench, H. Catalytic Models in Epidemiology; Harvard University Press: Cambridge, MA, USA; London, UK, 1959. [Google Scholar] [CrossRef]
- Salje, H.; Lessler, J.; Endy, T.P.; Curriero, F.C.; Gibbons, R.V.; Nisalak, A.; Nimmannitya, S.; Kalayanarooj, S.; Jarman, R.G.; Thomas, S.J.; et al. Revealing the microscale spatial signature of dengue transmission and immunity in an urban population. Proc. Natl. Acad. Sci. USA 2012, 109, 9535–9538. [Google Scholar] [CrossRef]
- Reich, N.G.; Shrestha, S.; King, A.A.; Rohani, P.; Lessler, J.; Kalayanarooj, S.; Yoon, I.K.; Gibbons, R.V.; Burke, D.S.; Cummings, D.A. Interactions between serotypes of dengue highlight epidemiological impact of cross-immunity. J. R. Soc. Interface 2013, 10, 20130414. [Google Scholar] [CrossRef] [PubMed]
- OhAinle, M.; Balmaseda, A.; Macalalad, A.R.; Tellez, Y.; Zody, M.C.; Saborío, S.; Nuñez, A.; Lennon, N.J.; Birren, B.W.; Gordon, A.; et al. Dynamics of dengue disease severity determined by the interplay between viral genetics and serotype-specific immunity. Sci. Transl. Med. 2011, 3, 114ra128. [Google Scholar] [CrossRef]
- Gibbons, R.V.; Kalanarooj, S.; Jarman, R.G.; Nisalak, A.; Vaughn, D.W.; Endy, T.P.; Mammen, M.P., Jr.; Srikiatkhachorn, A. Analysis of repeat hospital admissions for dengue to estimate the frequency of third or fourth dengue infections resulting in admissions and dengue hemorrhagic fever, and serotype sequences. Am. J. Trop. Med. Hyg. 2007, 77, 910–913. [Google Scholar] [CrossRef]
- Puschnik, A.; Lau, L.; Cromwell, E.A.; Balmaseda, A.; Zompi, S.; Harris, E. Correlation between dengue-specific neutralizing antibodies and serum avidity in primary and secondary dengue virus 3 natural infections in humans. PLoS Negl. Trop. Dis. 2013, 7, e2274. [Google Scholar] [CrossRef]
- Lai, C.Y.; Williams, K.L.; Wu, Y.C.; Knight, S.; Balmaseda, A.; Harris, E.; Wang, W.K. Analysis of cross-reactive antibodies recognizing the fusion loop of envelope protein and correlation with neutralizing antibody titers in Nicaraguan dengue cases. PLoS Negl. Trop. Dis. 2013, 7, e2451. [Google Scholar] [CrossRef]
- Katzelnick, L.C.; Montoya, M.; Gresh, L.; Balmaseda, A.; Harris, E. Neutralizing antibody titers against dengue virus correlate with protection from symptomatic infection in a longitudinal cohort. Proc. Natl. Acad. Sci. USA 2016, 113, 728–733. [Google Scholar] [CrossRef]
- Guzman, M.G.; Alvarez, M.; Rodriguez-Roche, R.; Bernardo, L.; Montes, T.; Vazquez, S.; Morier, L.; Alvarez, A.; Gould, E.A.; Kouri, G.; et al. Neutralizing antibodies after infection with dengue 1 virus. Emerg. Infect. Dis. 2007, 13, 282–286. [Google Scholar] [CrossRef]
- Zhang, X.S.; Xiong, H.; Chen, Z.; Liu, W. Importation, Local Transmission, and Model Selection in Estimating the Transmissibility of COVID-19: The Outbreak in Shaanxi Province of China as a Case Study. Trop. Med. Infect. Dis. 2022, 7, 227. [Google Scholar] [CrossRef]
- R Core Team. R: A language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 25 December 2022).
- National Bureau of Statistics of China. Census Data. Available online: http://www.stats.gov.cn/tjsj/pcsj/ (accessed on 25 December 2022).
- The Red and Black Population Database. Ranking of Each Province by Region. Available online: https://www.hongheiku.com/ (accessed on 25 December 2022).
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.; Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 64. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Inference; Springer: New York, NY, USA, 1998. [Google Scholar]
- Imai, N.; Dorigatti, I.; Cauchemez, S.; Ferguson, N.M. Estimating Dengue Transmission Intensity from Case-Notification Data from Multiple Countries. PLoS Negl. Trop. Dis. 2016, 10, e0004833. [Google Scholar] [CrossRef] [PubMed]
- Fine, P.; Eames, K.; Heymann, D.L. “Herd immunity”: A rough guide. Clin. Infect. Dis. 2011, 52, 911–916. [Google Scholar] [CrossRef] [PubMed]
- Waggoner, J.J.; Balmaseda, A.; Gresh, L.; Sahoo, M.K.; Montoya, M.; Wang, C.; Abeynayake, J.; Kuan, G.; Pinsky, B.A.; Harris, E. Homotypic Dengue Virus Reinfections in Nicaraguan Children. J. Infect. Dis. 2016, 214, 986–993. [Google Scholar] [CrossRef]
- Williams, M.; Mayer, S.V.; Johnson, W.L.; Chen, R.; Volkova, E.; Vilcarromero, S.; Widen, S.G.; Wood, T.G.; Suarez-Ognio, L.; Long, K.C.; et al. Lineage II of Southeast Asian/American DENV-2 is associated with a severe dengue outbreak in the Peruvian Amazon. Am. J. Trop. Med. Hyg. 2014, 91, 611–620. [Google Scholar] [CrossRef]
- Forshey, B.M.; Reiner, R.C.; Olkowski, S.; Morrison, A.C.; Espinoza, A.; Long, K.C.; Vilcarromero, S.; Casanova, W.; Wearing, H.J.; Halsey, E.S.; et al. Incomplete Protection against Dengue Virus Type 2 Re-infection in Peru. PLoS Negl. Trop. Dis. 2016, 10, e0004398. [Google Scholar] [CrossRef] [PubMed]
- Rico-Hesse, R. Dengue virus virulence and transmission determinants. Curr. Top. Microbiol. Immunol. 2010, 338, 45–55. [Google Scholar] [CrossRef]
- Cummings, D.A.T.; Iamsirithaworn, S.; Lessler, J.T.; McDermott, A.; Prasanthong, R.; Nisalak, A.; Jarman, R.G.; Burke, D.S.; Gibbons, R.V. The Impact of the Demographic Transition on Dengue in Thailand: Insights from a Statistical Analysis and Mathematical Modeling. PLoS Med. 2009, 6, e1000139. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.T.; Takahashi, S.; Salje, H.; Garcia-Carreras, B.; Anderson, K.; Endy, T.; Thomas, S.; Rothman, A.L.; Klungthong, C.; Jones, A.R.; et al. Assessing the role of multiple mechanisms increasing the age of dengue cases in Thailand. Proc. Natl. Acad. Sci. USA 2022, 119, e2115790119. [Google Scholar] [CrossRef]
- Doherty, J.A. Final report and recommendations from the National Notifiable Diseases Working Group. Can. Commun. Dis. Rep. 2006, 32, 211–225, Erratum in Can. Commun. Dis. Rep. 2008, 34, 24–25(In English and French). [Google Scholar] [PubMed]
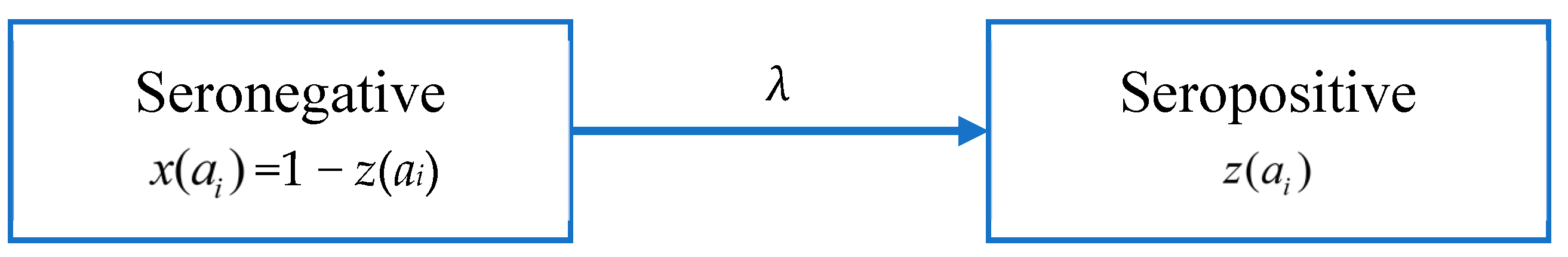


| Survey Region | Reference | Survey Year | Age Range | No. of Samples | No. of Positives | Testing Method | * Circulating Serotype | Source of Sample Population |
|---|---|---|---|---|---|---|---|---|
| Guangdong Province | ||||||||
| Guangzhou | Huang Y et al. [23] | 1981 | 5–50+ | 174 | 86 | HI | DENV-1,2,3,4 | Herd |
| Zhuhai | Li Z et al. [24] | 1998 | 10–60+ | 374 | 4 | ELISA | NA | Herd |
| Zhuhai | Yang Z et al. [25] | 2001 | 10–50+ | 558 | 51 | ELISA | NA | Herd |
| # GZ Huangpu | Zheng X et al. [26] | 2008 | 0–71+ | 324 | 55 | ELISA/RT-PCR | NA | Herd |
| Guangzhou | Cao Y et al. [27] | |||||||
| 2011 | 0–60+ | 2075 | 200 | ELISA | NA | Hospital/CDC | ||
| 2012 | 0–60+ | 1201 | 192 | ELISA | NA | Hospital/CDC | ||
| 2013 | 0–60+ | 1235 | 124 | ELISA | NA | Hospital/CDC | ||
| Guangzhou | Li S et al. [28] | 2014 | 18–60 | 4000 | 131 | ELISA/PCR | DENV-1,2 | Blood Donation Center |
| Guangzhou | Jing Q et al. [29] | 2015 | 0–60+ | 850 | 56 | ELISA/IFA test | DENV-1,2,3,4 | Herd |
| Guangxi Province | ||||||||
| Beihai | Tian X et al. [30] | 1980 | 0–40 | 435 | 116 | HI | DENV-2 | Sentinel Hospital |
| $ QZ/FCG/HP | Zhou K et al. [31] | 2010–2012 | 0–79 | 1800 | 37 | ELISA | NA | Herd |
| Zhejiang Province | ||||||||
| Yiwu | Sun J et al. [32] | 2009 | 0–80+ | 365 | 102 | ELISA | DENV-3 | Herd |
| Cixi | Cen D et al. [33] | 2004 | 0–80+ | 520 | 35 | IFA | NA | Herd |
| Hunan Province | ||||||||
| Chenzhou | Gao L et.al. [34] | 2005 | 0–80+ | 488 | 7 | ELISA | NA | Herd |
| Guizhou Province | ||||||||
| Guiyang | Gao R et al. [35] | 2004–2005 | 0–50+ | 2281 | 197 | ELISA | NA | Herd |
| Guiyang | Tian H et al. [36] | 2005 | 0–60+ | 755 | 55 | ELISA | NA | Herd |
| & GY/CJ/LD | Jiang W et al. [37] | 2011 | 5–60+ | 530 | 11 | ELISA | NA | Herd |
| Hainan Province | ||||||||
| Danzhou | Jin Y et al. [38] | 2006 | 0–60+ | 431 | 7 | ELISA | NA | Herd |
| Yunnan Province | ||||||||
| Mengla | Lu Y et al. [39] | 2014 | 0–60 | 182 | 3 | ELISA | NA | Health Checkup Center |
| Hekou | Pu L et al. [40] | 2016 | 0–60 | 203 | 9 | ELISA/ RT-PCR | NA | Health Checkup Center |
| Xishuangbanna | Li L et al. [41] | 2019 | 18–60 | 2254 | 484 | ELISA | NA | Blood Donation Center |
| Taiwan Province | ||||||||
| % TP/TY/TN | Lee YH et al. [42] | 2010 | 0–70+ | 1308 | 44 | ELISA | NA | Herd |
| Kaohsiung | Tsai JJ et al. [43] | |||||||
| 2015.8–11 | 0–89 | 417 | 48 | ELISA | DENV-1,2 | Herd | ||
| 2016.2–5 | 0–89 | 294 | 36 | ELISA | DENV-1,2 | Herd | ||
| 2016.9–2017.1 | 0–59 | 226 | 23 | ELISA | DENV-1,2 | Herd | ||
| 2017.8–9 | 20–89 | 153 | 28 | ELISA | DENV-1,2 | Herd | ||
| Kaohsiung and Tainan | Pan YH et al. [44] | |||||||
| Kaohsiung | 2016 | 40–80+ | 1498 | 595 | ELISA | DENV-1,2,3, | Herd | |
| Tainan | 2016 | 40–80+ | 2603 | 291 | ELISA | DENV-1,2,3,4 | Herd | |
| Hong Kong | Lee P et al. [45] | |||||||
| 2013 | 1–66+ | 700 | 24 | ELISA | NA | Hospital | ||
| 2014 | 1–66+ | 700 | 32 | ELISA | NA | Hospital | ||
| 2015 | 1–66+ | 700 | 31 | ELISA | NA | Hospital |
| Survey Region | Reference | Survey Year | Acrit (95% CrI) | λ (95% CrI) Year−1 | R0 (95% CrI) | α (95% CrI) Year−1 | Applicable Model | |
|---|---|---|---|---|---|---|---|---|
| Guangdong Province | λ1 | λ2 | ||||||
| Guangzhou | Huang Y et al. [23] | 1981 | 20.7 (9.9, 82.1) | 0.0538 (0.0184, 0.1440) | 0.0269 (0.0094, 0.1348) | 2.33 (1.64, 3.50) | — | Model C |
| Zhuhai | Li Z et al. [24] | 1998 | 72.9 (11.6, 83.8) | 0.0009 (0.0003, 0.0236) | 0.0595 (0.0004, 0.1447) | 1.05 (1.02, 1.23) | — | Model C |
| Zhuhai | Yang Z et al. [25] | 2001 | 65.6 (10.3, 83.3) | 0.0034 (0.0021, 0.1238) | 0.0585 (0.0022, 0.1448) | 1.15 (1.09, 1.33) | — | Model C |
| # GZ Huangpu | Zheng X et al. [26] | 2008 | 78.1 (9.9, 84.1) | 0.0041 (0.0019, 0.0533) | 0.0428 (0.0028, 0.1446) | 1.15 (1.09, 1.25) | — | Model C |
| Guangzhou | Cao Y et al. [27] | 2011–2013 | ||||||
| 2011 | 68.0 (15.5, 83.3)(15.5, 83.3) | 0.0085 (0.0040, 0.0237) | 0.0356 (0.0039, 0.1442) | 1.17 (1.12, 1.31) | 0.04 (0.00, 0.10) | Model D | ||
| 2012 | 39.7 (9.9, 83.1) | 0.0078 (0.0041, 0.0598) | 0.0071 (0.0034, 0.1400) | 1.22 (1.15, 1.40) | — | Model C | ||
| 2013 | 71.5 (12.2, 83.9) | 0.0037 (0.0024, 0.0175) | 0.0532 (0.0022, 0.1447) | 1.15 (1.09, 1.26) | — | Model C | ||
| Guangzhou | Li S et al. [28] | 2014 | 64.2 (10.4, 83.7) | 0.0014 (0.0007, 0.1331) | 0.0476 (0.0007, 0.1450) | 1.09 (1.04, 1.32) | — | Model C |
| Guangzhou | Jing Q et al. [29] | 2015 | 72.7 (11.7, 84.0) | 0.0027 (0.0014, 0.0308) | 0.0517 (0.0014, 0.1444) | 1.11 (1.06, 1.39) | — | Model C |
| Guangxi Province | ||||||||
| Beihai | Tian X et al. [30] | 1980 | — | 0.0181 (0.0130, 0.0277) | 1.73 (1.50, 2.19) | — | Model A | |
| $ QZ/FCG/HP | Zhou K et al. [31] | 2010–2012 | 78.7 (13.1, 84.2) | 0.0006 (0.0003, 0.0064) | 0.0606 (0.0003, 0.1450) | 1.04 (1.02, 1.10) | — | Model C |
| Zhejiang Province | ||||||||
| Yiwu | Sun J et al. [32] | 2009 | 29.7 (16.1, 42.0) | 0.0252 (0.0122, 0.0559) | 0.0061 (0.0043, 0.0093) | 1.41 (1.25, 1.70) | — | Model C |
| Cixi | Cen D et al. [33] | 2004 | 14.0 (9.7, 81.9) | 0.0238 (0.0016, 0.1317) | 0.0029 (0.0015, 0.0205) | 1.13 (1.07, 1.32) | — | Model C |
| Hunan Province | ||||||||
| Chenzhou | Gao L et al. [34] | 2005 | 51.7 (10.3, 83.7) | 0.0047 (0.0011, 0.0537) | 0.0061 (0.0006, 0.1033) | 1.04 (1.02, 1.25) | 0.08 (0.02, 0.10) | Model D |
| Guizhou Province | ||||||||
| Guiyang | Gao R et al. [35] | 2004–2005 | — | 0.0092 (0.0038, 0.0358) | 1.10 (1.06, 1.45) | 0.08 (0.02, 0.10) | Model B | |
| Guiyang | Tian H et al. [36] | 2005 | 65.3 (11.4, 83.6) | 0.0047 (0.0014, 0.0669) | 0.0094 (0.0006, 0.1426) | 1.14 (1.06, 1.59) | — | Model C |
| & GY/CJ/LD | Jiang W et al. [37] | 2011 | 16.4 (9.9, 80.8) | 0.0469 (0.0020, 0.1449) | 0.0025 (0.0004, 0.1269) | 1.16 (1.03, 1.67) | — | Model C |
| Hainan Province | ||||||||
| Danzhou | Jin Y et al. [38] | 2006 | 72.7 (11.3, 84.0) | 0.0017 (0.0004, 0.0706) | 0.0462 (0.0006, 0.1447) | 1.08 (1.02, 1.65) | — | Model C |
| Yunnan Province | ||||||||
| Mengla | Lu Y et al. [39] | 2014 | 66.3 (11.1, 83.4) | 0.0024 (0.0007, 0.0554) | 0.0538 (0.0010, 0.1448) | 1.11 (1.03, 1.50) | — | Model C |
| Hekou | Pu L et al. [40] | 2016 | 66.5 (11.0, 83.7) | 0.0028 (0.0011, 0.0409) | 0.0551 (0.0012, 0.1441) | 1.12 (1.05, 1.42) | — | Model C |
| Xishuangbanna | Li L et al. [41] | 2019 | 60.5 (10.9, 83.3) | 0.0086 (0.0040, 0.1340) | 0.0199 (0.0031, 0.1439) | 1.34 (1.18, 1.71) | — | Model C |
| Taiwan Province | ||||||||
| % TP/TY/TN | Lee YH et al. [42] | 2010 | 76.0 (10.2, 84.0) | 0.0021 (0.0008, 0.0545) | 0.0551 (0.0012, 0.1441) | 1.10 (1.04, 1.30) | — | Model C |
| Kaohsiung | Tsai JJ et al. [43] | 2015–2017 | ||||||
| 2015.8–11 | 68.1 (11.4, 83.1) | 0.0034 (0.0014, 0.0782) | 0.0099 (0.0031, 0.0419) | 1.19 (1.10, 1.57) | — | Model C | ||
| 2016.2–5 | 66.1 (11.0, 83.0) | 0.0155 (0.0046, 0.1169) | 0.0397 (0.0056, 0.1368) | 1.21 (1.12, 1.55) | 0.07 (0.01, 0.10) | Model D | ||
| 2016.9–2017.1 | — | 0.0052 (0.0021, 0.0203) | 1.24 (1.09, 2.16) | — | Model A | |||
| 2017.8–9 | 31.6 (10.3, 81.5) | 0.0097 (0.0026, 0.1428) | 0.0089 (0.0039, 0.0370) | 1.33 (1.18, 1.82) | — | Model C | ||
| Kaohsiung and Tainan | Pan YH et al. [44] | 2016 | ||||||
| Kaohsiung | 30.9 (10.5, 74.3) | 0.0553 (0.0026, 0.1447) | 0.0073 (0.0043, 0.0133) | 1.50 (1.20, 2.56) | — | Model C | ||
| Tainan | 30.6 (10.2, 79.7) | 0.0617 (0.0015, 0.1461) | 0.0042 (0.0019, 0.0133) | 1.36 (1.10, 2.32) | — | Model C | ||
| Hong Kong | Lee P et al. [45] | 2013–2015 | ||||||
| 2013 | 71.9 (44.8, 83.8) | 0.0017 (0.0008, 0.0128) | 0.0299 (0.0013, 0.1450) | 1.12 (1.06, 1.23) | — | Model C | ||
| 2014 | 65.9 (30.2, 81.5) | 0.0010 (0.0005, 0.0037) | 0.0063 (0.0019, 0.1252) | 1.09 (1.06, 1.19) | — | Model C | ||
| 2015 | 65.7 (17.6, 81.8) | 0.0009 (0.0005 0.0057) | 0.0070 (0.0019, 0.1263) | 1.10 (1.06, 1.18) | — | Model C | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Li, H.; Chen, Z.; Xiong, H.; Li, Z.; Wei, T.; Liu, W.; Zhang, X.-S. Estimating Dengue Transmission Intensity in China Using Catalytic Models Based on Serological Data. Trop. Med. Infect. Dis. 2023, 8, 116. https://doi.org/10.3390/tropicalmed8020116
Li N, Li H, Chen Z, Xiong H, Li Z, Wei T, Liu W, Zhang X-S. Estimating Dengue Transmission Intensity in China Using Catalytic Models Based on Serological Data. Tropical Medicine and Infectious Disease. 2023; 8(2):116. https://doi.org/10.3390/tropicalmed8020116
Chicago/Turabian StyleLi, Ning, Haidong Li, Zhengji Chen, Huan Xiong, Zhibo Li, Tao Wei, Wei Liu, and Xu-Sheng Zhang. 2023. "Estimating Dengue Transmission Intensity in China Using Catalytic Models Based on Serological Data" Tropical Medicine and Infectious Disease 8, no. 2: 116. https://doi.org/10.3390/tropicalmed8020116
APA StyleLi, N., Li, H., Chen, Z., Xiong, H., Li, Z., Wei, T., Liu, W., & Zhang, X.-S. (2023). Estimating Dengue Transmission Intensity in China Using Catalytic Models Based on Serological Data. Tropical Medicine and Infectious Disease, 8(2), 116. https://doi.org/10.3390/tropicalmed8020116






