Design and Commissioning of a Combustor Simulator Combining Swirl and Entropy Wave Generation

Abstract

Modern aero-engine combustion chambers burn a lean and premixed mixture, generating a turbulent flame which involves large heat-release fluctuations, thus producing unsteady temperature phenomena commonly referred to as entropy waves (EWs). Furthermore, to enhance the fuel air mixing, combustion air is swirled, leading to vorticity disturbances. These instabilities represent one of the biggest challenges in gas turbine design. In this paper, the design and testing of a novel entropy wave generator (EWG) equipped with a swirler generator (SG) are described. The novel EWG will be used in future works on the high-speed test rig at Politecnico di Milano to study the combustor–turbine interaction. The paper shows the process of the EWG geometry and layout. The EWG is able to produce an engine-representative EW, the extreme condition is at the maximum frequency of 110 Hz, a peak-to-valley temperature value of 20 °C and swirling angles of ±25° are measured. By virtue of these results, the proposed system outperforms other EWG devices documented in the literature. Furthermore, the addition of a swirling generator makes this device one of a kind.

1. Introduction

In order to match the strict regulations on pollutant emissions, modern aero-engines feature a lean premixed combustion to limit combustion temperature, and hence NO_x production. This type of combustion involves a complex evolution of the front flame that results in a strong heat release unsteadiness. These temperature fluctuations are commonly referred to as entropy waves. Furthermore, a strong swirl motion is imposed on the combustor flow to enhance air–fuel mixing. The combination of the swirl motion and entropy wave makes the design of the first turbine stages challenging: this unsteadiness complicates the aerodynamics, hence they have a role in the definition of the stage performance [1,2]; they are responsible for the production of entropy noise [3,4,5,6] and have an effect on the heat transfer [7,8], which implies modification in the blade cooling system. All these phenomena acknowledge that combustor instabilities still exist at the turbine inlet. Both Sattelmayer [9] and Morgans et al. [10] have developed models to predict entropy wave advection. Sattelmayer [9] states that entropy waves are diffused by the flow turbulence, whereas in [10], the authors demonstrate that entropy wave dispersion from combustor to turbine is weak and the entropy wave strength is preserved at the combustor exit. Furthermore, Semlitsch et al. [11] have demonstrated by means of a computational study that swirl also persists at the combustor exit.

Commonly, turbine test facilities feature inlet air that is uniform and without any of the aforementioned disturbances. However, if the turbine efficiency and performance have to be analyzed, combustor non-uniformities cannot be disregarded. It is possible to account for these effects by implementing a combustor simulator in the turbine facility. Some combustor simulators are already documented in the literature. Bake et al. [12] developed an entropy wave generator (EWG) to study indirect combustion noise, without considering the harsh environment created by combustion. According to the same idea, the EWG proposed in [13] was designed, where only temperature perturbations were generated while vorticity perturbations were possibly imposed by tilting the injector axis with respect to the turbine axial direction. In [14], the only example of a combustor simulator featuring swirl and hot streaks implemented in a rotating turbine test facility is described. Another example of an EWG is described in [15].

The purpose of this paper is to describe and discuss a novel combustor simulator and its design process. The simulator delivers engine representative conditions in terms of swirl motion and entropy wave, making possible to carry out both turbine stage investigations and studies on the combustor–turbine interaction. The device also locally increases the flow turbulence at the stator inlet. In [16], the authors show how severe the impact of turbulence on turbine stage efficiency is, hence, the ability to simulate a combustor turbulence closer to that of a real engine is a plus that few experimental test rigs exploit. A rough estimate of the EWG turbulence intensity is found by calculating the standard deviation with respect to the phase averaged value (STD) of the total pressure. The novel EWG, by the authors’ knowledge, is the first documented in the literature that combines the production of an entropy wave with a swirl motion able to represent the harsh combustor-produced environment.

The paper is organized into two main sections. In the first, corresponding to Section 2, the EWG layout and the main facilities used are described. This section introduces the measuring instruments used to characterize the disturbance produced by the EWG. The second main section (Section 3) presents the results of the EWG tests that are divided into two experimental campaigns: one carried out in a wind tunnel nozzle, where different EWG layouts and swirl generators (SGs) are tested to find the best solution, and the second done in the turbine test rig, where the definitive EWG is tested.

2. Materials and Methods

In this section, the combustor simulator, the wind tunnel and the measurement techniques are described. A description of the turbine test facility is proposed in [17]. Here, the results are discussed for an operating condition, called OP3 in [17], that exploits a stage expansion ratio of 1.4 with a flow Mach number approaching the stator of 0.14.

2.1. Combustor Simulator

The layout of the combustor simulator is shown in Figure 1. For each EWG, a set of automotive fuel injectors for methane-fueled engines (labeled valve dispenser in Figure 1) feeds alternatively two different ducts with electrical heaters installed: one branch has the electrical heater switched on this is referred to as “hot duct”) and the other has the heater switched off (“cold duct”). This geometry ensures the same pressure losses in the two branches. A bypass valve is placed on the hot duct so that, when opened, the device works as a hot streak generator bypassing the valve dispenser. The two ducts are coupled in the injector head which injects the alternating hot–cold air in the turbine streamwise direction. In order to simulate the real aero-engine turbine inlet flow, at the injector outlet, a swirl generator is placed.

The EWG supply air temperature is measured by a T-type thermocouple, its total pressure by a Kulite XT190 pressure transducer (full-scale 50 psi, Kulite, Leonia, NJ, USA). A calibrated nozzle is used to calculate the mass flow rate. A pressure drop exists between the upstream and the downstream section of this device and, whenever the device is calibrated, the flowrate can be determined from the measured pressure difference and from the knowledge of fluid conditions. This pressure drop is measured by a Kulite XT190 transducer (full-scale 10 psi, Kulite, Leonia, NJ, USA). Downstream of the electric heater, a K-type thermocouple is placed and used to control the power supply of the heater. The pressure difference between the heater inlet and the turbine static pressure is measured by a Kulite XT190 (full-scale 50 psi, Kulite, Leonia, NJ, USA) and it is used as a safety control since if this pressure difference is negative, the heater is switched off. A Kulite XT190 transducer (Kulite, Leonia, NJ, USA), featuring a full scale of 10 psi, measures the pressure in the cold duct and this pressure signal is used as a trigger signal to phase average the unsteady measurements.

All transducers are specifically calibrated featuring a max uncertainty of 0.05% of the transducer range.

2.1.1. Valves

Automotive methane injectors are used because of their high reliability, the high frequency achievable (110 Hz) and the consistent mass flow rate delivered (1.5 dm³/s at 2 bar inlet pressure). These devices are driven by pulse width modulation (PWM), specifically in-house built. Each PWM circuit requires two relays (Figure 2) that are controlled by means of an Arduino board. Valve frequency can be set by the operator at the beginning of each test. The two relays, S1 and S2 (Figure 2), are properly controlled to provide a current peak, needed to open the valve (both S1 and S2 are closed), and a lower current (S1 closed and S2 open) able to maintain the opening of the valve. Each valve has its own circuit so, by opening/closing the relay S1, the hot and cold branches are alternatively opened.

2.1.2. Electric Heater

The electric heater used is shown in Figure 3 (maximum power of 600 W). The advantages of such a device are its robustness and low pressure losses. A power regulator, which reads as a controlling input the K-thermocouple placed downstream of the electrical wires, allows to set the outlet heater temperature. Due to the thermal resistance of the components, the heater has a constraint on the maximum increase in temperature between the inlet and outlet, which is 400 K. Therefore, with the feeding air at ambient conditions, the maximum achievable temperature at the heater outlet is about 700 K.

2.1.3. Swirler

A modern aero-engine features an high degree of swirl angles with magnitudes up to ±40° [7,14]. In order to match this target, three different swirler generators are tested in the wind tunnel. With reference to Figure 4, the first (type A) features a tangential case positioned at the EWG outlet that is coaxial with the turbine main flow; the second (type B) and third (type C) solutions both have a vaned case device placed at the injector outlet. Type B and C have the same blade angles (inlet 20° and outlet 40°), but they differ in the swirler geometry: in type B, the blades act on the turbine main flow, while the EW is injected undisturbed in the turbine axial direction; in type C, the blades work with both the turbine main flow and part of the EWG injected air, and the remaining portion is injected axially.

Figure 4 also shows the scale model of the three geometries, highlighting the different flow portion that is put in rotation (red in Figure 4 represents the injected EW, blue the cold mainstream turbine flow). Another difference concerns the casing and the injector geometries: both type A and B have an injector stem diameter of 4 mm and a 13 mm case diameter; type C has an injector stem diameter of 10 mm and a case inner diameter of 15.4 mm. The larger the injector stem diameter, the higher the EW mass flow, given the same expansion ratio available; therefore, type C can inject the highest EW mass flow.

2.2. Wind Tunnel

The combustor simulator has been tested in a wind tunnel featuring the same flow properties of the turbine test rig inlet. The experimental facility available at Laboratory of Fluid Machines (LFM) for this purpose is a blow-down wind tunnel. A Pitot tube measures the flow total pressure of the wind tunnel and a J thermocouple measures the reservoir temperature. The ambient pressure is read by a reference manometer, hence the core flow Mach number can be determined by assuming an isentropic expansion in the convergent nozzle. This assumption is consistent because the measuring area is far from the wall where there is no influence of boundary layer. The Mach number is set to 0.14: it corresponds to the turbine test rig Mach number upstream of the turbine stage where the EWG is placed.

Measuring probes are moved in a Cartesian reference system (x,y,z), as shown in Figure 5. The x and y axes define, respectively, the probe horizontal and vertical positioning with respect to the EWG, while the z axis defines the distance between the injector and the probe. Measurements are performed at a z position such that the distance between the measuring plane and the swirler outlet section is the same as the distance between the turbine stator leading edge and the swirler outlet (50 mm). Therefore, the results shown in the wind tunnel experimental campaign are what is expected at the turbine stator inlet.

2.3. Measuring Instruments

This section briefly introduces the main measuring instruments used to characterize the flow generated by the EWG. The steady flow field is measured by means of a 5-hole probe properly calibrated. However, since the EW is inherently unsteady, in addition to the 5-hole probe, a fast Pitot tube (uncertainty ±80 Pa) is used to verify that the 5-hole probe steady total pressure matches the unsteady value and to obtain the STD of the total pressure upstream the stator. Its description and usage can be found in [13]. The temperature disturbance produced is measured with a S-type thermocouple able to measure up to the maximum EWG frequency, which is 110 Hz.

2.3.1. 5-Hole Probe

A 5-hole probe is chosen to detect the aerodynamic field produced by the EWG. The yaw angle is defined as the angle between the projection of the velocity vector on a plane perpendicular to the 5-hole stem axis and the axial direction. The pitch angle is the angle between the axial direction and the velocity projection on a plane which contains the probe axis and the probe tip.

Generally, a 5-hole probe is calibrated in the range of about ±25° in both yaw and pitch because this range works with no (or weak) flow separation on the pressure taps. However, given the actual swirler design, the aforementioned range is too limited and for this a proper calibration has to be performed in order to extend it. This is done only for the yaw angle because, due to a mechanical constraint when calibrating the probe, the pitch angle cannot be larger than +22°. Therefore, the yaw angle range is increased up to ±44° by defining three different calibration matrixes on the basis of the yaw angle value: “Right matrix” is defined by yaw angles from 16° to 44°, “Central matrix” from −26° to 26° and “Left matrix” between −44° and −16°. The matrixes overlap to avoid unwanted bouncing from one matrix to the other at boundary angles, thus also ensuring convergence in these critical regions. The calibration coefficients are defined as follows:

Left (Yaw = −44° : −16 °)	Central (Yaw = −26° : 26 °)	Right (Yaw = 16° : 44 °)
$K_{yaw}=\frac{p_{s,ref}-p_r}{p_{t,ref}-p_{s,ref}}$	$K_{yaw}=\frac{p_l-p_r}{p_{t,ref}-p_{s,ref}}$	$K_{yaw}=\frac{p_l-p_{s,ref}}{p_{t,ref}-p_{s,ref}}$
$K_{ps}=\frac{p_{s,ref}-0.25\left(p_l+p_r+p_u+p_d\right)}{p_{t,ref}-p_{s,ref}}$
$K_{pt}=\frac{p_{t,ref}-p_t}{p_{t,ref}-p_{s,ref}}$
$K_{pitch}=\frac{p_u-p_d}{p_{t,ref}-p_{s,ref}}$

where:

• $p_{t,ref}$ = reference upstream total pressure
• $p_{s,ref}$ = reference downstream static pressure
• $p_t$ = central pressure
• $p_u$ = pitch, up pressure
• $p_d$ = pitch, down pressure
• $p_l$ = yaw, left pressure
• $p_r$ = yaw, right pressure

During the probe application, the five taps pressure are read and, by an iterative procedure, the main flow quantities (static and total pressure, yaw and pitch angles) are calculated using the central matrix. Therefore, the iterative method, which is able to extrapolate, gives an angle outcome even if the angle is out of the range defined for the central matrix; if the angle is inside the range, the result is considered correct, otherwise the procedure is repeated using the matrix (the left or the right one) where the computed angle lies. The 5-hole probe has an uncertainty of 0.5° for the flow angles and of 50 Pa for pressures. Uncertainties are computed following the procedure shown in [18].

2.3.2. Fast Thermocouple

Thermal inertia of a thermocouple is the most critical parameter when high-frequency measurements are foreseen: the higher the frequency to be detected, the smaller the thermal inertia has to be. Therefore, to minimize thermal inertia, the thermocouple junction has to be directly exposed to the flow without any shell to protect it and the sensitive junction has to be the smallest possible. For the purpose of this research, a S-type thermocouple with a 25.4 µm diameter junction is suitable (uncertainty ±0.3 K). This kind of thermocouple is in-house built and calibrated in the LFM shock tube facility.

Figure 6 shows the calibration results. The response of the probe matches with a first order instrument response: the dynamic behavior follows a first order derivative equation. If the initial and the final values, as well as the time constant, are experimentally determined, then the transfer function is known.

The green and red lines are, respectively, the measured temperature and pressure. The interpolated temperature (blue line) is fitted by a fourth order interpolating curve. By means of the shock equations, the ideal shock temperature can be calculated (black line in Figure 6). The first order time constant is defined as the time that the interpolated line needs to reach 63.2% of the step shock temperature. Therefore, as the $\tau$ is known, the first order instrument response (purple line) is defined. The probe has a response time $\tau =0.0038\mathrm{ms}$, hence it is appropriate to measure the entropy wave generated in this experimental campaign which has a maximum frequency of 110 Hz. The transfer function is then calculated and used to correct the measured output response. Such a technique is commonly referred to as frequency compensation and allows to extend the instrument frequency range.

3. Results

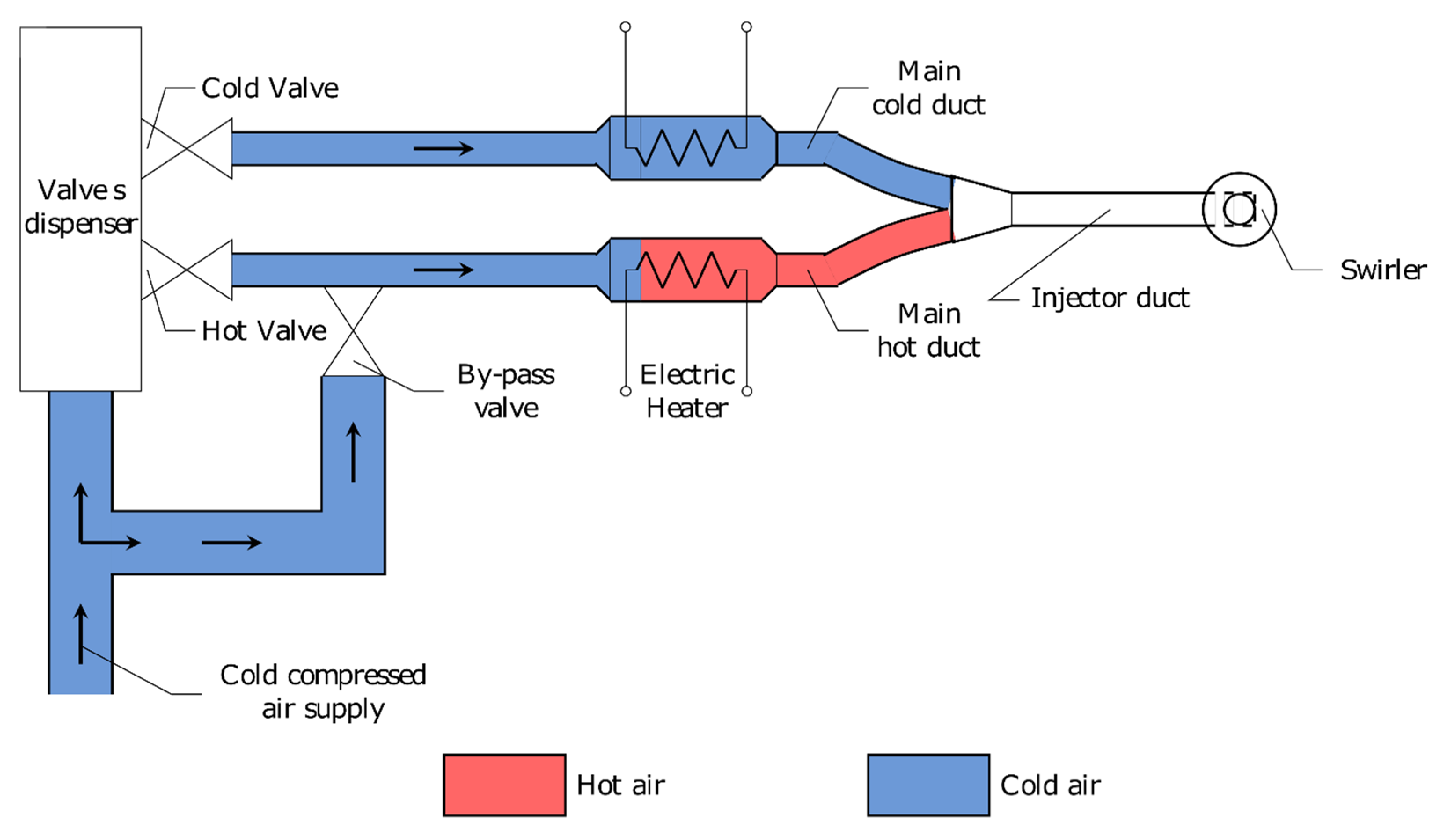
In this section, first, the results of the wind tunnel experimental campaign are shown. Before performing experiments, the wind tunnel flow uniformity and repeatability were checked. For each test shown in this paper, the repeatability was assessed by repeating each test at least twice. The last subsection shows the definitive EWG injector layout and its results in the turbine test rig.

3.1. Aerodynamic Field

The outcomes of the three swirler devices are discussed here. The main difference between the devices is the amount of swirled flow (Figure 4): type A has a tangential geometry which turns only the EW; type B injects the EW axially and the swirler blades act on the mainstream air; in type C, both the mainstream and partially the EW are swirled. In all the figures shown in this subsection, the point (0,0) represents the core of the vortex. The injector is placed horizontally so its stem is located at about Y = 0 and on the positive X.

The results shown in Figure 7 and Figure 8 lead us to discard the type A solution: despite the easy manufacturing, the aerodynamic flow field is not symmetrical, i.e., the vortex is strongly stretched in the X direction. Furthermore, the total pressure field has a complex pattern (Figure 8a), so the resulting flow cannot be considered representative of a combustor outlet flow. Type B is more symmetrical than type A, however, the strong axial jet leads to a distortion of the total pressure field (Figure 8b): for this reason, it is not considered as representative of the flow released by a combustor [19,20]. Type C has the highest angles (Figure 7c) and all the requirements to be considered combustor representative. The low-pressure core (Figure 8c) is unavoidable if a high degree of swirl is expected [21], as happens in aero-engine combustors [19].

Besides the geometry, a second important parameter is the feeding pressure. Its level is set as a tradeoff between the EW penetration in the mainstream and the viscous dissipation between the axial jet and the surrounding swirled flow. The feeding pressure also has an impact on the temperature field and specifically on the temperature fluctuation, as will be described in the next subsection.

For the type C swirler, the aerodynamic flow field is weakly influenced by the feeding pressure, as shown in Figure 9. A higher feeding pressure (Figure 9a,c) increases the jet axial velocity and the viscous dissipation between the axial jet and the surrounding swirling flow; this implies slightly lower pitch and yaw angles than the case with a smaller feeding pressure (Figure 9b,d). However, besides these small differences, in both cases, pitch and yaw angles are in the range of ±25°; so far, the best feeding pressure will be chosen on the basis of temperature outcomes.

3.2. Temperature Field

This experimental campaign is carried out by means of the fast response 25 µm thermocouple, already described in the measuring instruments section. Entropy waves are inherently unsteady as they are generated through the alternative opening and closing of the two valves which feed the hot and the cold ducts. The unsteadiness makes very critical the interaction between the hot and the cold flows in the injector section where they join. In fact, given the same expansion ratio, the hot stream is faster than the cold one, leading to a mixing between the two streams, that unfortunately is unavoidable. Hence, to optimize the peak temperature, different layouts are tested to minimize the mixing and the heat dissipation: basically, the idea is to delay the hot and cold stream joining and to increase the thermal insulation.

A simplified model has been developed to investigate the mixing process between hot and cold flows and to find the parameters which minimize it. Using a quasi-steady assumption, the injector is modeled as a fixed volume which is fed by a square wave $T_{EW}$, which is the entropy wave produced by the alternating opening and closing of the hot and cold valves. The two temperature levels of $T_{EW}$ represent the hot and cold streams; the peak is the temperature measured at the electric heater outlet; the trough is the cold stream temperature equal to the ambient one. At each time step $dt$, the square wave fills the volume entirely in its height and depth and of an amount $dL=dx/L$ along its length, where $dx=v dt$ where $v$ is the flow velocity and $L$ is the volume length. Therefore, every $dt$, a new mass $dm=\frac{dx \left(T_{EW}\left(t\right)\right)}{L \left(T_{eq}\left(t-dt\right)\right)}$ at temperature $T_{EW}\left(t\right)$ enters in the volume, while the same $dm$ leaves it at a temperature equal to the equilibrium temperature at the previous time step $T_{eq}\left(t-dt\right)$ (Figure 10). Therefore, the equilibrium temperature is calculated by solving the power balance applied on the volume surfaces:

$$T_{eq}\left(t\right)=T_{eq}\left(t-dt\right)+T_{EW}\left(t\right)dm-T_{eq}\left(t-dt\right)dm$$

(1)

The volume equilibrium temperature evolution in time is shown for 10 and 110 Hz in Figure 11. The model outcomes state that at the lower frequency, the mixing is negligible since the maximum and minimum volume temperature at equilibrium correspond to the squared wave ones. The mixing has the only effect of producing a time shift in achieving the settled temperatures. However, moving at the higher frequency, mixing becomes more severe and the volume temperature fluctuates between two values that are not the wave maximum and minimum. Since the hotter the flow, the lower the density, the equilibrium temperature at 110 Hz is always far from the EW hot temperature (Equation (1)).

It has to be noted that in the experimental measurements, these temperature values will not be achieved because the EW is not exactly a square wave since valves do not open and close instantaneously; the measurements are carried out 50 mm downstream of the injector outlet section, hence, thermal dissipation reduces the peak temperature.

The yellow line in Figure 11 show the effect of a volume reduction: decreasing the volume by reducing the injector length, the system promptness increases.

Considering the previous conclusion, different layouts are designed and tested in order to obtain the best thermal performance (Figure 12). These tests are carried out without the swirler generator since the analysis focuses on finding the best thermal insulation and layout which maximize the peak-to-valley temperature fluctuation. However, on the basis of the aerodynamic campaign previously discussed, it has to be noted that the different layouts in Figure 12 have different injector dimensions that make the devices suitable for different swirler generators: layouts A and B have a longer injector length and a smaller stem diameter (5 mm, 4 mm outer and inner diameters, respectively) which can be equipped with SG type B; layouts C and D have a shorter injector length and a larger stem diameter (external diameter of 10 mm and internal of 8 mm) and so they are designed for SG type C (hot and cold tubes have 4 mm outer and 3 mm inner diameter).

Layouts A and B have a longer injector length, therefore, the flow is mixed far from the injector outlet. The difference between them regards the thermal insulation: layout A has no insulation, layout B has a coaxial stainless steel cylinder filled with stone wool. Layouts C and D delay the mixing process as much as possible and shorten the length where the mixing can occur, as suggested by the previous quasi-steady state analysis. While in layout C, both the hot and the cold ducts enter parallelly in the injector and only the hot duct is insulated, in layout D, both the hot and the cold ducts are insulated and they have an angle of ±10° with respect to the injector axis. The insulation for these two cases is made wrapping the tubes in a stone wool shell. In layout D, the stone wool is also at the injector inlet to separate the two ducts.

In Figure 13, the different layout outcomes are compared. Layouts A and B are fed with a pressure of 0.3 bar_g, layouts C and D with 0.5 bar_g. This difference in the pressure values is justified by the lower pressure required by SG type B to obtain an engine representative aerodynamic flow field; on the contrary, a higher pressure is needed by SG type C. Therefore, the comparison is made given the same outlet aerodynamic conditions and with the heater outlet temperature set at 670 K.

Since in layouts A and B, the injector length is longer than in layouts C and D, the mixing process is huge, as confirmed by the high valley temperature (see gray and red lines). Furthermore, the addition of the thermal insulation in layout B increases both the peak and valley temperature, but the peak-to-valley value is reduced because the trough temperature increases more than the peak one. The shorter the duct where the hot and cold flows are forced together, the lower the mixing intensity and the interaction between the EW and the walls. Therefore, in layout D, the best peak-to-valley value is achieved: both hot and cold flows are close to their injected condition at 10 Hz (Figure 13a). Nevertheless, layout C, which also features a lower injector length looks worse because bad insulation between hot–cold ducts is designed. At 100 Hz in this layout, the results show that hot–cold phasing at the injector head failed so that peaks and valleys collapse to the mean value and there is no repeatability. At 100 Hz, the general trend in all configurations shows a strong reduction of the peak-to-valley values due to a more severe mixing.

To conclude, the best layout which guarantees the highest peak-to-valley temperature value is layout D. Moreover, considering that SG type C is chosen as the best device to produce a good aerodynamic flow field, layout D equipped with swirler generator type C is the final EWG layout. Furthermore, the larger injector diameter allows us to generate a larger EW perturbation in space.

As for the pressure effect, Figure 14 shows the average peak-to-valley temperature in X direction, which is consistent with the radial coordinates in the turbine test rig for layout D with SG type C with a feeding pressure of 0.5 and 0.75 bar_g at 10 Hz and with a heater temperature of 670 K. The results clearly show the strong improvement obtained by increasing the pressure: the EW penetration increases, and its thermal power as well, due to the flow rate increase ($\dot{Q}=\dot{m}∆T$). Therefore, having already proved that a pressure increase has negligible effects on the aerodynamic flow field, the best pressure is chosen as the one able to provide the highest temperature perturbation; finally, p = 0.75 bar_g is chosen as the one able to provide the operating conditions closest to the engine ones for both aerodynamic and thermal flow fields.

3.3. Definitive EWG and Turbine Inlet Measurements

The previous analysis brings us to the selection of the best geometry of the EWG in terms of SG and layout to minimize mixing and thermal dissipation. Figure 15 shows the final EWG geometry. The device is 3D printed in a cobalt-chrome alloy. This material has similar thermal properties to the stainless steel used in the previous devices. The hot–cold tubes are connected with the EWG by means of straight manifolds. Due to space constraints, the hot and cold tubes have an angle of 2° with respect to the injector axis instead of 10° as in layout D.

The EWG is placed upstream of the turbine test rig to simulate the combustor unsteadiness that occurs in the first stage aero-engine turbine. The investigation of these effects on the turbine aerodynamics will be the subject of future works. On the contrary, the main features of the unsteadiness produced by the novel EWG are described in this section. Figure 16 shows the measuring plane location with respect to the injector axis, the injector outlet section and the stator leading edge. Probes are mounted on a linear stepping motor that moves them in the radial direction. The ring hosting the EWG is moved circumferentially; the coupled movement of probes and EWG allows for the coverage of the whole measuring plane.

There are spots for 11 injectors on the turbine test rig, making it possible to have one injector per two stator blades (i.e., there are 22 stator blades). To carry out the aerodynamic and thermal assessment of the EWG, only three injectors are mounted for the sake of simplicity. Measurements are done on the central of the three injectors, thus guaranteeing the periodicity. However, if in future experimental campaigns, stage efficiency or acoustic measurements are investigated, all 11 injectors will be mounted to guarantee the whole annular periodicity.

Figure 17 shows the peak-to-valley variation of the temperature profile in a valve period. It refers to a condition of 110 Hz, which is a period of about 9 ms. In the data reduction, the period is divided into 100 frames; Figure 17 shows frames at 1%, 20%, 40%, 60%, 80% and 100% of the period.

The best peak to valley is 25 K, the highest difference in temperature between the injected EW and the undisturbed flow is 70 K. These results show a good performance of the novel entropy wave generator compared with already documented ones [12,13]. When reducing the frequency to 10 Hz, the peak-to-valley value increases up to 75 K at the measuring plane location.

Figure 18 shows the total pressure measurements and velocity field performed with a steady 5-hole probe, thus neglecting at this measuring step the EWG-induced pressure fluctuations. The total pressure pattern highlights the main features of a high swirled flow: a core of low total pressure which is recovered moving outward radially. The central upper part of the contour shows a low total pressure region caused by the injector stem wake and boundary layer at the turbine casing. The two high total pressure regions (red circles in the figure) are the injected hot and cold streams in the EWG. The reasons for this discrepancy between total pressure fields shown in Figure 8 and Figure 18, that refer respectively to nozzle and turbine experiments, are twofold. In the wind tunnel experimental campaign, measurements are carried out at a distance representative of the stator position, i.e., 50 mm downstream of the swirler exit (Figure 16). When the EWG is applied on the turbine test facility, measurements are performed at 33.2 mm, hence the two cold–hot flows are not yet fully mixed with the main flow. Secondly, the feeding pressure is tuned to high values because the turbine mainstream has a higher pressure (1.4 bar) than the wind tunnel flow, which has an ambient pressure.

Figure 19 shows the mass weighted average of the velocity profile along the radial coordinate in a cylindrical system of reference centered in the vortex core (white point in Figure 18). The axial velocity is the lowest at the vortex center (radius = 0 mm) and increases linearly up to a radius of 6 mm. At 6 mm the axial velocity has a plateau; the injector wake is significant and modifies the axial velocity trend. At higher radii, the wake weight is smaller and so the axial velocity increases again up to 45 m/s, which is approximately the undisturbed axial velocity.

The tangential velocity flow field follows a common vortex pattern: the core has zero tangential velocity, then it increases rapidly to a 3 mm radius according to a forced vortex trend. For higher radii, it decreases slowly following something like a free vortex structure until it reaches the zero-value component that means undisturbed flow. The field vorticity is positive for radii lower than 5 mm, negative from 5 to 8 mm and null elsewhere, evidencing an irrotational vortex structure. Vorticity becomes negative due to an interaction in the region close to the hub between the swirled flow and the mainstream that makes the flow turn counterclockwise (Figure 18).

Finally, a fast Pitot pressure probe [13] is used to measure the unsteady total pressure field. The results are comparable to the steady total pressure field measured by the 5-hole probe. This was expected when the EWG was designed; lot of efforts were made to reduce differences in the pressure drop across the hot and cold ducts. The only unavoidable unsteadiness in the total pressure regards the two red circled zones shown in Figure 18, that follow the valve frequency (not shown in the paper for the sake of brevity). Therefore, the fast Pitot tube results confirm that the two regions correspond to the hot or cold flows that are not yet fully mixed with the main flow. The STD value, as a percentage of the mean total pressure, is shown in Figure 20. The results show that there is an increase from 0.6% in the freestream to 3.3% in the region perturbed by the EW. According to [22,23], this quantity can be considered as an estimate of the turbulence level, whose specific characterization will be the subject of a future study.

4. Discussion

This paper has shown the design process of a novel entropy wave generator. The performances of this device are shown, both in a simplified environment and in the turbine test rig, where it will be applied. The analysis focuses on the aerodynamic and thermal properties.

To the authors’ knowledge, the novel EWG is the only one documented in the literature able to produce engine representative entropy wave (or hot streak) disturbances combined with swirl motion. The EWG’s main advantage is its versatility: it can be mounted on test rigs requiring only a few modifications, i.e., a hole to host the injector. To gain this versatility, the injector has a stem that produces a wake and makes the flow pattern produced slightly asymmetric. However, as shown in the wind tunnel experimental campaigns, the injector wake is fully recovered at a position representative of the stator inlet section. Furthermore, this device is able to produce an entropy wave which is a temperature fluctuation perturbation, or a hot streak which is also swirled. In the literature, few devices able to combine hot streak and swirled motion are documented and none combine entropy wave and swirl, notwithstanding that both features are unavoidable if the combustor–turbine interaction is under study.

At the highest frequency tested (i.e., 110 Hz), a temperature fluctuation of 25 K and a maximum difference between the EW and the freestream of 75 K are obtained. As discussed in this work, the frequency decrease allows us to increase the temperature fluctuation. Moreover, the typical swirled structure is produced, characterized by angles with magnitudes around 25°.

The purpose of this paper is to share the design methodology and to show the flow field pattern injected upstream of the LFM turbine test rig, as applied in future investigations on the combustor–stage interaction. It is worth remembering that the combustor–turbine interaction has a huge impact on the definition of performance, aerodynamics, acoustics and cooling of first turbine blades; studies on these issues are made possible only by the usage of a proper EWG to simulate combustor outlet flows. Another characteristic that needs to be further investigated is the turbulence intensity of the EW, which is object of future investigations by hot-wire anemometry.