Experimental Study of the Leakage Flow in an Axial-Flow Fan at Variable Loading †
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Experimental Facility
2.2. Measurement Procedure and Data Processing Technique
3. Experimental Results
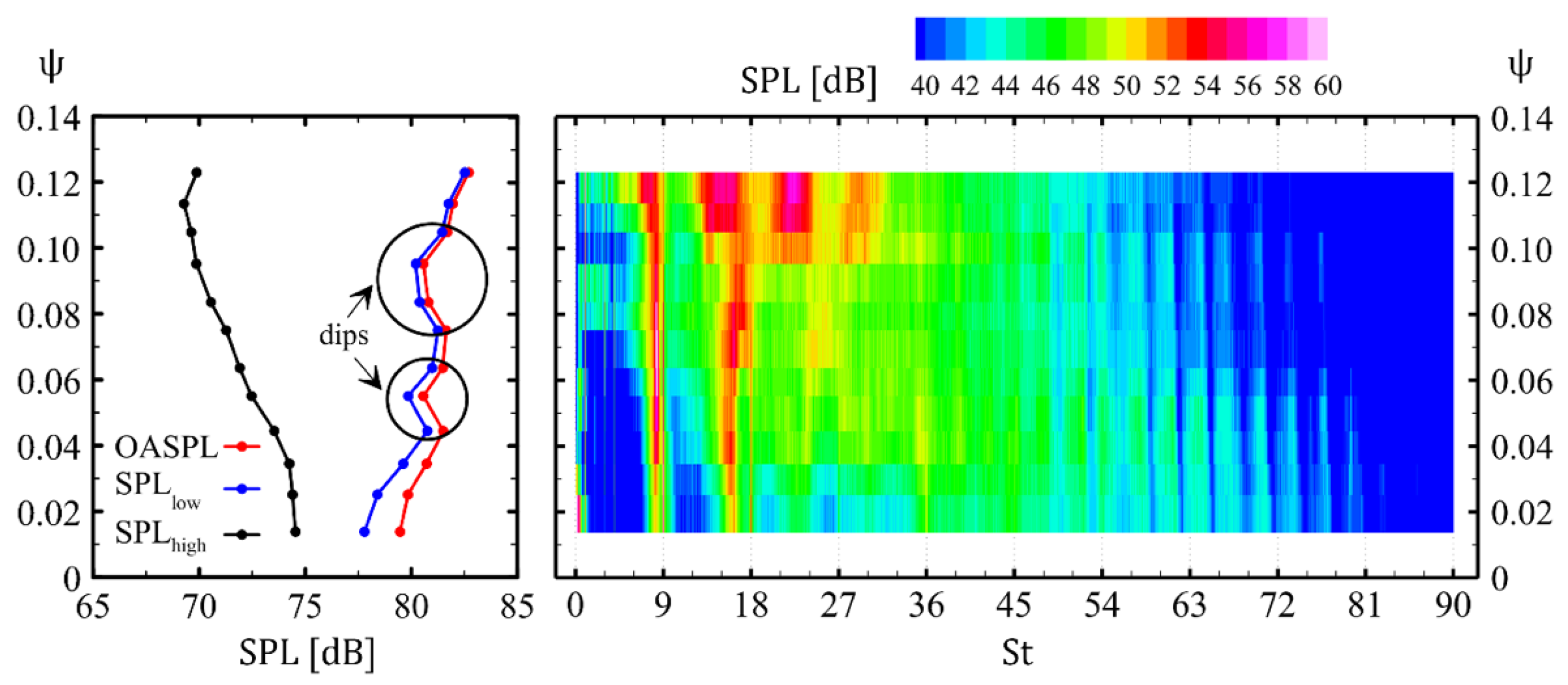
3.1. Previous Measurements
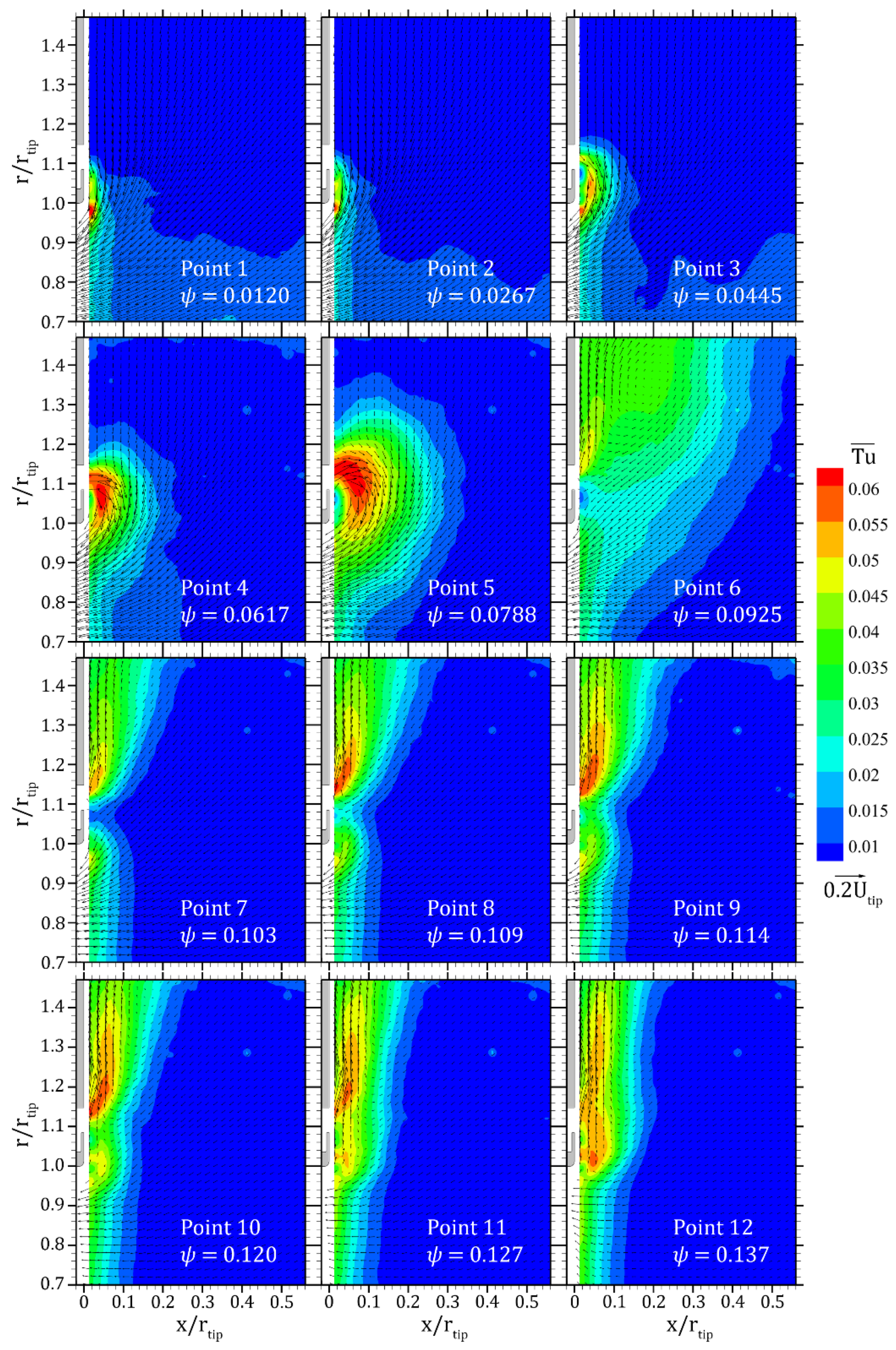
3.2. General Trend of the Time-Averaged Flow Field
- (1)
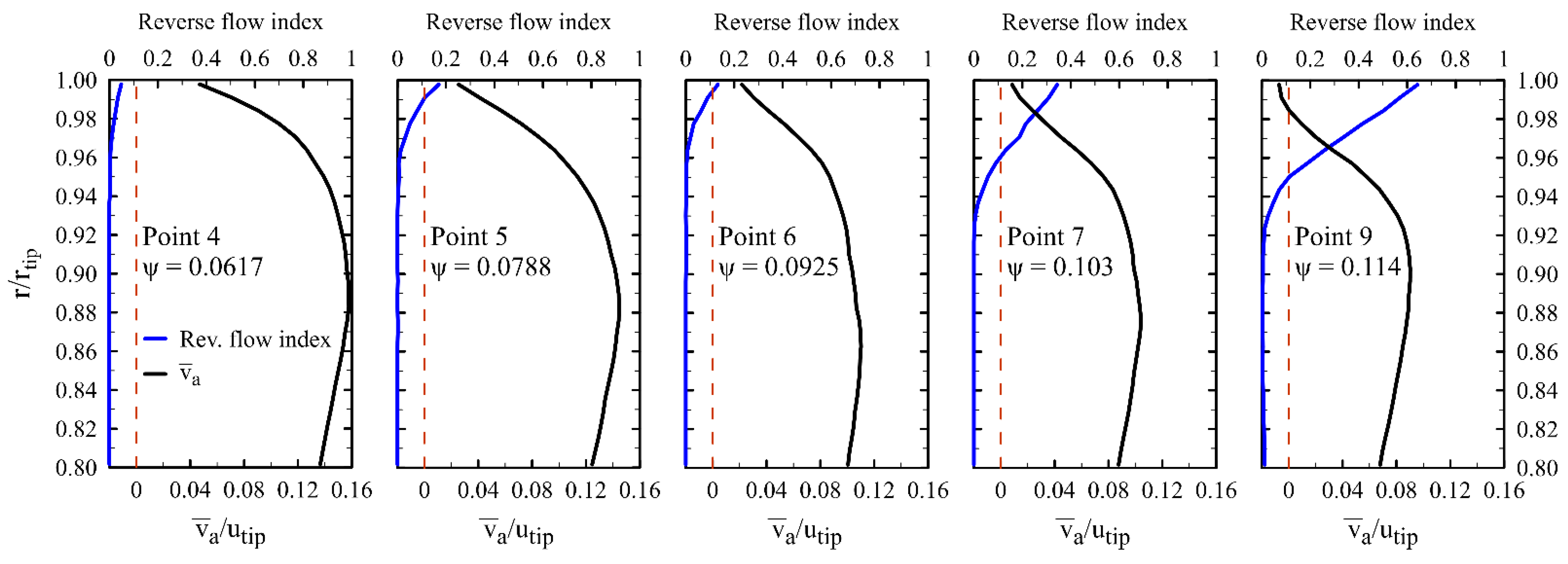
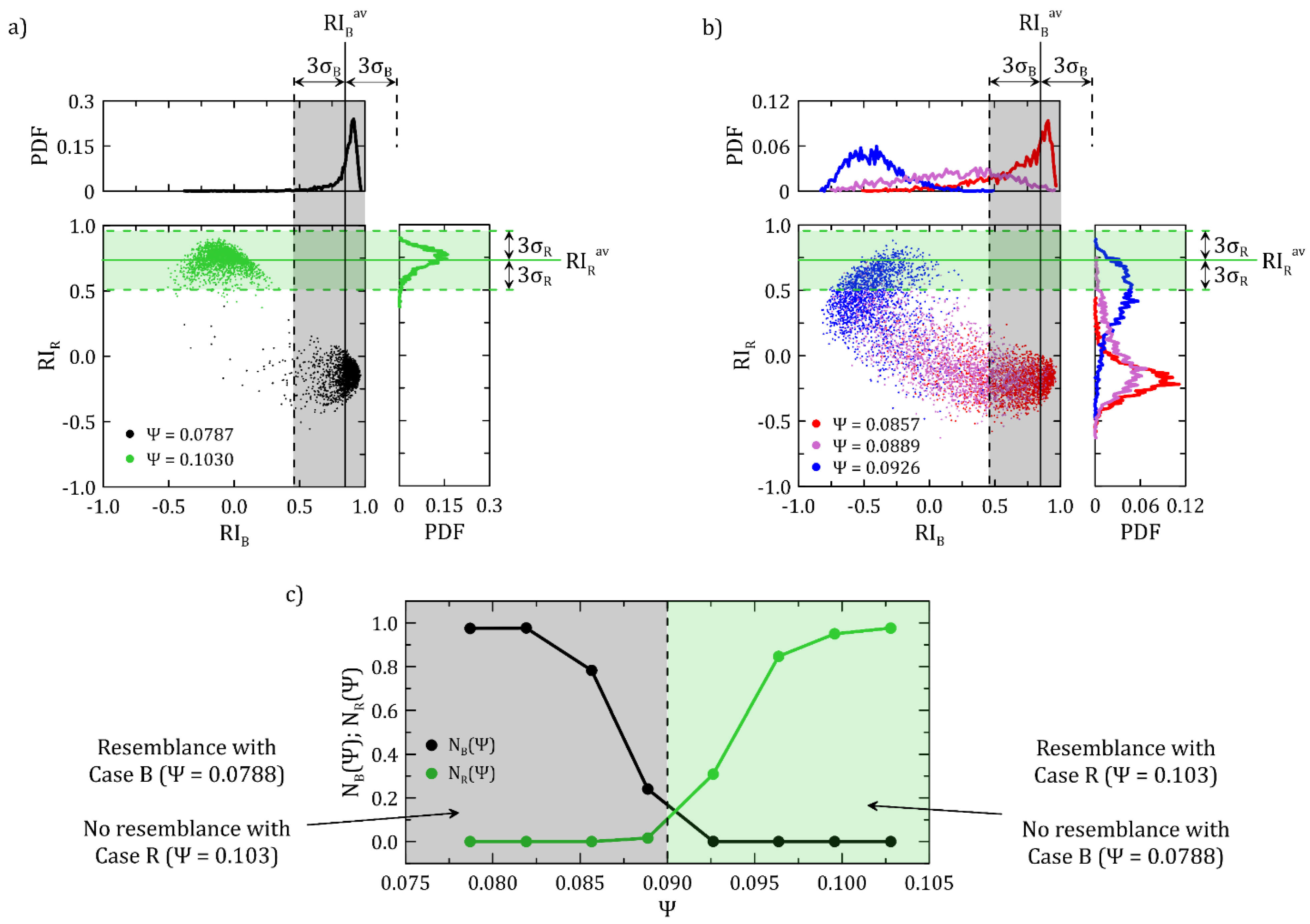
- Below the design (points 1–5), a recirculation bubble attached to the ring lip may be clearly detected at 0.0788, and it is also present at 0.0617; at the interface between the leakage flow and the main one, high values are present. At 0.0617, the high stripe in front of the rotor lip suggests that the bubble should be present. At very low , that is at points 1 and 2, no bubble may be identified; should it be present, it would be very thin since the measurement domain extends up to 3 mm from the ring lip, but, likely, the leakage flow is attached to it. In all of the cases, due the limited extension of the bubble, the flow leaving the gap is reingested by the rotor within a short distance;
- (2)
- At 0.0925 (point 6), the design operating point is approached and the flow pattern has an important change: the gap flow becomes centrifugal and a large separated-flow zone appears instead of the separation bubble attached to the ring. The center of such a zone is located away from the panel wall and at radial locations far from the ring; small values are attained in the gap flow;
- (3)
- Beyond the design conditions (i.e., at 0.103–0.109, points 7 and 8), the leakage flow remains radial with large values; the velocity direction, together with the absence of a center of the recirculation zone, indicates that the leakage flow leaves the measurement domain before turning towards the rotor and being eventually reingested. The large- zone is still present in front of the blade;
- (4)
- As further increases (i.e., at 0.114–0.137, points 9 and 10), the features of the leakage flow are qualitatively unchanged, but the flow at the blade tip clearly modifies as it streams along the ring lip. It points radially outwards and then mixes with the leakage flow; at some locations . At large and low ( 0.127–0.137, points 11 and 12), the flow deteriorates: it probably separates in the lower part of the blade span as at small , and part of it leaves the rotor from the blade tip area consistently with the negative ; the remainder recirculates through the gap. Such a behavior may also be related to the radial breakdown of the flow downstream of the rotor, e.g., see Milanese et al. [22]. However, such operating points are of limited interest since the rotor efficiency is very small.
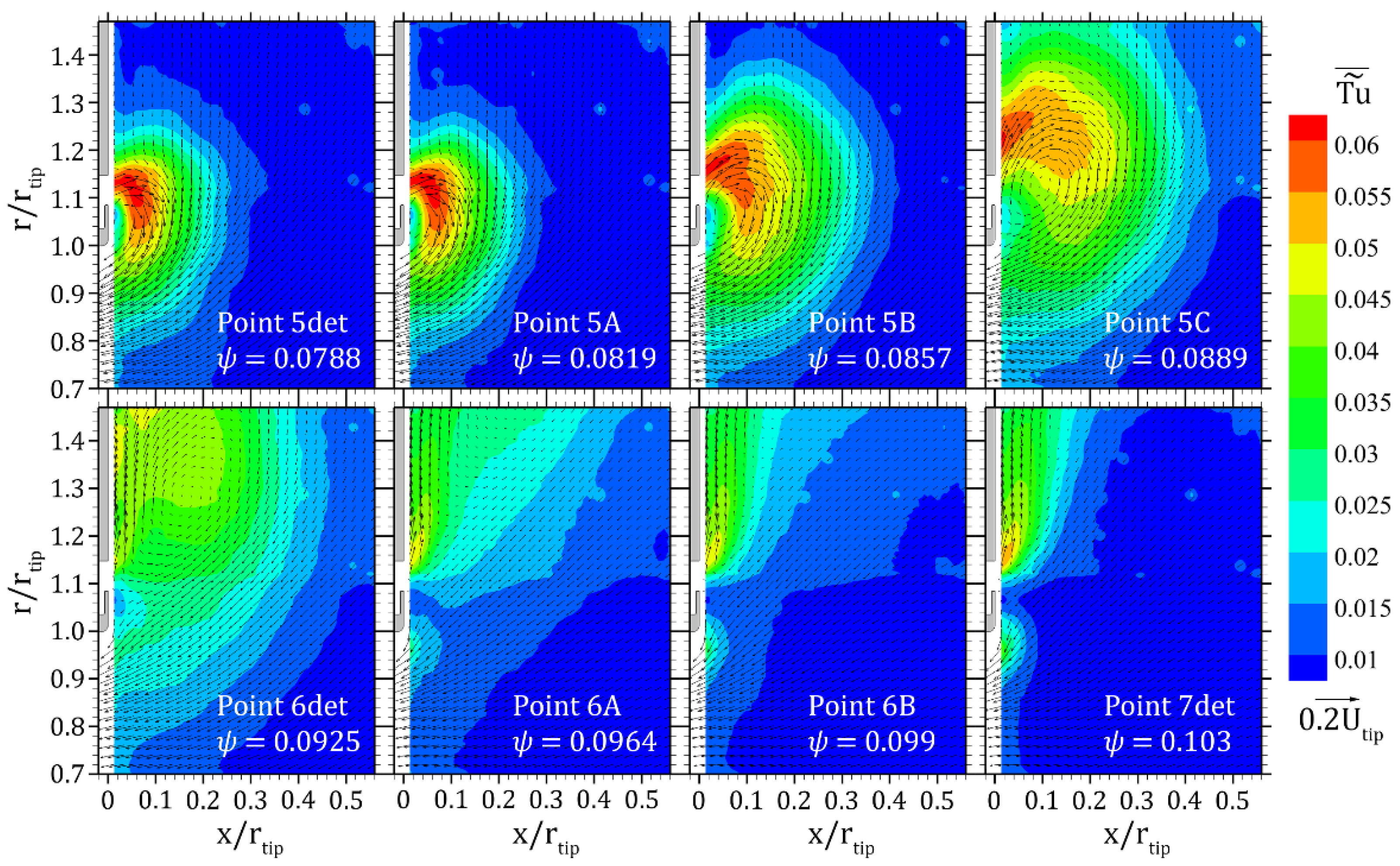
3.3. Flow Pattern Modification about Ψ ≅ 0.09
4. Conclusions
- (1)
- A detailed description of the evolution of the leakage flow as a function of the loading.
- (2)
- A detailed analysis of the flow pattern transition that, for the present geometry, takes place about the design operating point.
- (3)
- The establishment of a correspondence between leakage flow and SPL growth.
- (4)
- Further evidence of the existence of a flow reversal at the blade tip has been provided.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| OASPL | overall sound pressure level, ref. 20 μPa |
| N | percentage of instantaneous flow fields similar to the reference one |
| Q | volume flow rate |
| r | radial coordinate |
| SPL | sound pressure level spectrum, ref. 20 μPa |
| SPLlow | sound pressure level in the range 6 < St < 90, ref. 20 μPa |
| SPLhigh | sound pressure level in the range 90 < St < 300, ref. 20 μPa |
| RI | resemblance index |
| St | Strouhal number (frequency normalized with Ω/60) |
| Tu | |
| peripheral speed of the blade | |
| components of the absolute velocity | |
| x | axial coordinate |
| Δp | pressure rise through the rotor (static outlet minus total inlet) |
| tangential (azimuthal) coordinate | |
| ρ0 | air density |
| Ω | rotational speed (expressed in rev/min) |
| Superscripts | |
| related to the ensemble average | |
| related to the time average | |
| related to non-periodic instantaneous fluctuations | |
| Subscripts | |
| B | related to the reference case with recirculation bubble |
| R | related to the reference case with radial leakage flow |
| tip | related to the blade tip |
References
- Carassale, L.; Cattanei, A.; Mazzocut Zecchin, F.; Moradi, M. Leakage flow flutter in a low-speed axial-flow fan with shrouded blades. J. Sound Vib. 2020, 475, 115275. [Google Scholar] [CrossRef]
- Longhouse, R. Control of tip-vortex noise of axial flow fans by rotating shrouds. J. Sound Vib. 1978, 58, 201–214. [Google Scholar] [CrossRef]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F.; Milanese, G.; Parodi, D. An experimental investigation on the tip leakage noise in axial-flow fans with rotating shroud. J. Sound Vib. 2016, 375, 115–131. [Google Scholar] [CrossRef]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F. Leakage Noise and Related Flow Pattern in a Low-Speed Axial Fan with Rotating Shroud. Int. J. Turbomach. Propuls. Power 2019, 4, 17. [Google Scholar] [CrossRef] [Green Version]
- Fukano, T.; Takamatsu, Y.; Kodama, Y. The effects of tip clearance on the noise of low pressure axial and mixed flow fans. J. Sound Vib. 1986, 105, 291–308. [Google Scholar] [CrossRef]
- Fukano, T.; Jang, C.-M. Tip clearance noise of axial flow fans operating at design and off-design condition. J. Sound Vib. 2004, 275, 1027–1050. [Google Scholar] [CrossRef]
- Piellard, M.; Coutty, B.; Le Goff, V.; Vidal, V.; Pérot, F. Direct Aeroacoustics Simulation of Automotive Engine Cooling Fan System: Effect of Upstream Geometry on Broadband Noise. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014. AIAA Paper 2014–2455. [Google Scholar]
- Magne, S.; Moreau, S.; Berry, A. Subharmonic tonal noise from backflow vortices radiated by a low-speed ring fan in uniform inlet flow. J. Acoust. Soc. Am. 2015, 137, 228–237. [Google Scholar] [CrossRef] [PubMed]
- Moreau, S.; Sanjose, M. Sub-harmonic broadband humps and tip noise in low-speed ring fans. J. Acoust. Soc. Am. 2016, 139, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Zenger, F.J.; Renz, A.; Becher, M.; Becker, S. Experimental investigation of the noise emission of axial fans under distorted inflow conditions. J. Sound Vib. 2016, 383, 124–145. [Google Scholar] [CrossRef]
- Na, G.-D.; Kameier, F.; Springer, N.; Mauß, M.; Paschereit, C.O. URANS Simulations and Experimental Investigations on Unsteady Aerodynamic Effects in the Blade Tip Region of a Shrouded Fan Configuration. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. ASME Paper GT2017-6. [Google Scholar]
- Canepa, E.; Cattanei, A.; Jafelice, F.; Mazzocut Zecchin, F.; Parodi, D. Effect of rotor deformation and blade loading on the leakage noise in low-speed axial fans. J. Sound Vib. 2018, 433, 99–123. [Google Scholar] [CrossRef]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F.; Parodi, D. Large-scale unsteady flow structures in the leakage flow of a low-speed axial fan with rotating shroud. Exp. Therm. Fluid Sci. 2019, 102, 1–19. [Google Scholar] [CrossRef]
- Zhu, T.; Lallier-Daniels, D.; Sanjose, M.; Moreau, S.; Carolus, T. Rotating coherent flow structures as a source for narrowband tip clearance noise from axial fans. J. Sound Vib. 2018, 417, 198–215. [Google Scholar] [CrossRef]
- Hussain AK, M.F.; Reynolds, W.C. The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 1970, 41, 241–258. [Google Scholar] [CrossRef]
- Grant, I. Particle image velocimetry: A review. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1997, 211, 55–76. [Google Scholar] [CrossRef]
- Prasad, A.K.; Adrian, R.J.; Landreth, C.C.; Offutt, P.W. Effect of resolution on the speed and accuracy of particle image velocimetry interrogation. Exp. Fluids 1992, 13, 105–116. [Google Scholar] [CrossRef]
- Liu, K.; Haworth, D.C. Development and Assessment of POD for Analysis of Turbulent Flow in Piston Engines. In Proceedings of the SAE 2011 World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2011. SAE Technical Paper: 2011-01-0830. [Google Scholar]
- Willman, C.; Scott, B.; Stone, R.; Richardson, D. Quantitative metrics for comparison of in-cylinder velocity fields using particle image velocimetry. Exp. Fluids 2020, 61, 62. [Google Scholar] [CrossRef] [Green Version]
- Hanson, D.B. Spectrum of rotor noise caused by atmospheric turbulence. J. Acoust. Soc. Am. 1974, 56, 110–126. [Google Scholar] [CrossRef]
- Majumdar, S.J.; Peake, N. Noise generation by the interaction between ingested turbulence and a rotating fan. J. Fluid Mech. 1998, 359, 181–216. [Google Scholar] [CrossRef]
- Milanese, G.; Cravero, C. Analysis of the Design Bounds in Performance Limits for Industrial Axial Flow Fans. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual, Online, 21–25 September 2020. ASME Paper no. GT2020-16058. [Google Scholar]

| First Set of Measurements | Ψ | Set of Detailed Measurements | Ψ |
|---|---|---|---|
| 1 | 0.0120 | - | - |
| 2 | 0.0267 | - | - |
| 3 | 0.0445 | - | - |
| 4 | 0.0617 | - | - |
| 5 | 0.0788 | 5det | 0.0788 |
| - | - | 5A | 0.0819 |
| - | - | 5B | 0.0857 |
| - | - | 5C | 0.0889 |
| 6 | 0.0925 | 6det | 0.0925 |
| - | - | 6A | 0.0964 |
| - | - | 6B | 0.0996 |
| 7 | 0.103 | 7det | 0.103 |
| 8 | 0.109 | - | - |
| 9 | 0.114 | - | - |
| 10 | 0.120 | - | - |
| 11 | 0.127 | - | - |
| 12 | 0.137 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Canepa, E.; Cattanei, A.; Moradi, M.; Nilberto, A. Experimental Study of the Leakage Flow in an Axial-Flow Fan at Variable Loading. Int. J. Turbomach. Propuls. Power 2021, 6, 40. https://doi.org/10.3390/ijtpp6040040
Canepa E, Cattanei A, Moradi M, Nilberto A. Experimental Study of the Leakage Flow in an Axial-Flow Fan at Variable Loading. International Journal of Turbomachinery, Propulsion and Power. 2021; 6(4):40. https://doi.org/10.3390/ijtpp6040040
Chicago/Turabian StyleCanepa, Edward, Andrea Cattanei, Mehrdad Moradi, and Alessandro Nilberto. 2021. "Experimental Study of the Leakage Flow in an Axial-Flow Fan at Variable Loading" International Journal of Turbomachinery, Propulsion and Power 6, no. 4: 40. https://doi.org/10.3390/ijtpp6040040
APA StyleCanepa, E., Cattanei, A., Moradi, M., & Nilberto, A. (2021). Experimental Study of the Leakage Flow in an Axial-Flow Fan at Variable Loading. International Journal of Turbomachinery, Propulsion and Power, 6(4), 40. https://doi.org/10.3390/ijtpp6040040





