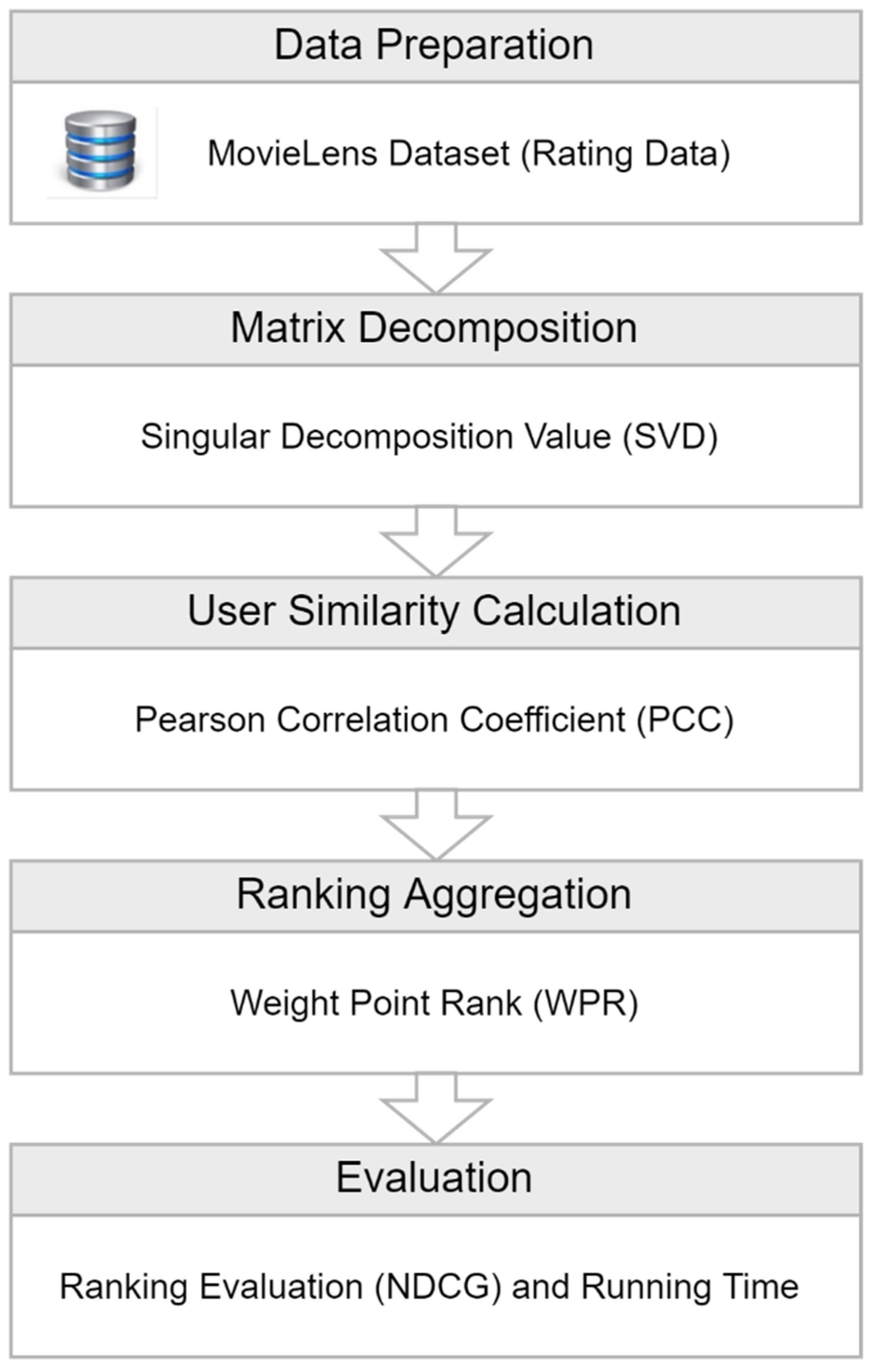
This section starts from the baseline algorithms subsection that presents several ranking algorithms compared with the proposed algorithm. Next, the experimental setting subsection represents the design of our experiments, and the experiment results subsection describes the performance comparison between the proposed method (SVD-WPR) and the previous methods (BordaRank, WP-Rank, and SVD-Borda). The performance comparison of these methods employs two evaluation metrics: ranking evaluation (NDCG) and running time. Finally, the discussion subsection reveals the experiment results’ findings and this research’s shortcomings.
4.2. Experimental Setting
Our experiment divided the dataset into training and testing data to evaluate the performance of the proposed SVD-WPR algorithm. We applied the five-fold cross-validation that separated 80% of training data and 20% of testing data, which refers to many previous studies [
6,
32,
33,
34,
35,
36]. In this five-fold cross-validation process, this study obtained five training data (train1, train2, train3, train4, and train5) and five testing data (test1, test2, test3, test4, and test5). The number of factors (
f) equals 50 to obtain the decomposed matrixes using SVD. We also set the fixed number of neighborhoods contributing to the ranking aggregation process at 50.
We compared our proposed SVD-WPR algorithm with other ranking-oriented collaborative filtering algorithms, i.e., BordaRank, WP-Rank, and SVD-Borda. The NDCG@1, NDCG@3, NDCG@5, and NDCG@10 become the evaluation metric in each testing data.
This study utilized the computer specifications of Processor 11th Gen Intel® Core™ i7-1165G7 @ 2.80 GHz, 1690 MHz (4 Core), and Memory of 16 GB. The algorithms in Python were running under Microsoft Windows 7.
4.3. Experimental Results
This subsection aims to compare the performance of the proposed SVD-WPR algorithm with the other three ranking algorithms (i.e., BordaRank, WP-Rank, and SVD-Borda). Our experiment employed the ranking accuracy and running time metrics to evaluate these algorithms’ performances. The ranking accuracy metric used NDCG, which considered the Top-N items on each ranking list. The performance comparison of these algorithms utilized five iterations. The first iteration applied the train1 and test1 datasets, and the second iteration used the train2 and test2 datasets and continued until the fifth iteration.
Table 6 shows the NDCG scores comparison of each algorithm in the MovieLens 100K dataset. The number after the ranking accuracy metric (NDCG) tells the prediction position, which shows the Top-
N item ranking. For example, NDCG@5 means how accurately the algorithm has predicted the 5th ranking for the set of users in the MovieLens 100K dataset. The values in this table are average NDCG scores obtained from five iterations of testing data. The bolded values show the best results among the compared algorithms. The scale of the NDCG score is [−1, 1], with the number 1 presenting the optimal ranking.
Based on
Table 6, an increment in the top recommended items (Top-
N items) will increase the average NDCG scores in all algorithms. It shows that the number of Top-
N items affects the algorithm’s performance. The average NDCG scores for BordaRank, WP-Rank, SVD-Borda, and SVD-WPR are 0.5676, 0.5897, 0.6720, and 0.7390, respectively. The SVD-WPR algorithm obtains the highest NDCG scores in all the top recommended items. This algorithm gives users a more relevant ranking than the other three algorithms. Compared with SVD-Borda, WP-Rank, and Borda, the SVD-WPR algorithm increases NDCG scores by an average of 10.21%, 27.11%, and 32.32%, respectively. For better readability,
Figure 4 illustrates the average NDCG scores of the four algorithms graphically.
By evaluating the ranking accuracy using NDCG,
Figure 4 shows the four algorithms’ NDCG scores increase with an increasing number of recommended items. It indicates that the number of recommended items affects the performance of algorithms. Compared with BordaRank and WP-Rank, the NDCG scores of SVD-Borda and SVD-WPR are far ahead of the small number of recommended items (@Top-
N = 1, 3, and 5). Meanwhile, at the larger number of recommended items (@Top-
N = 10), the NDCG scores of SVD-Borda and SVD-WPR are not far ahead compared to the NDCG scores of BordaRank and WP-Rank. It shows that the matrix decomposition process using SVD affects the accuracy ranking significantly in the small number of recommended items. The NDCG@10 scores represent the highest score in all algorithms. It denotes that the more items that are recommended, the more relevant items there will be.
With the same number of recommended items, the SVD-WPR algorithm is always higher than the other three algorithms, which means that this algorithm generates the most relevant item ranking. It happens because SVD-WPR applied the rating prediction using a matrix decomposition and involved similar users in ranking aggregation. The increase in NDCG in SVD-Borda shows the smallest; on the other hand, the results of NDCG in SVD-WPR are not far ahead of the ranking accuracy of SVD-Borda. The SVD-Borda algorithm also applies a matrix decomposition to predict ratings. It is good to mention that the matrix decomposition using SVD can generate more accurate recommended items compared to the ranking algorithm without a matrix decomposition. In all conditions of the number of recommended items, SVD-WPR performs the highest NDCG scores, which means that the proposed method performs better than the three previous methods.
This experiment also calculated the running time to evaluate how the SVD process affected the running time of ranking algorithms.
Table 7 compares the average running time in each ranking algorithm using the MovieLens 100K dataset. We evaluate four conditions of Top-
N items in this running time comparison. These four conditions are @Top-1, @Top-3, @Top-5, and @Top-10, which state the number of the top recommended items. The bolded values show the fastest running time among these ranking algorithms. The average values show the running time mean in four conditions of @Top-
N. Please note that the experiment’s running time combines training and recommendation times.
Based on
Table 7, an increment in the number of top recommended items (Top-
N items) needs more time to generate recommendations. The average running time for BordaRank, WP-Rank, SVD-Borda, and SVD-WPR are 18.759 s, 18.785 s, 5.270 s, and 5.283 s, respectively. The results show that the SVD-Borda consumes the least time. However, the running time speed is virtually similar to SVD-WPR (only a 0.013 s difference or slower by 0.25% from SVD-Borda). It shows that the SVD-WPR is still competitive compared to SVD-Borda in running time performance. Nevertheless, the SVD-WPR can outperform the baseline algorithms (SVD-Borda, WP-Rank, and BordaRank) regarding ranking accuracy, as shown in
Table 6. In addition, SVD-WPR still consumes less time compared to the BordaRank and WP-Rank.
Compared with BordaRank and WP-Rank, the SVD-WPR reduced the running time with a decreased average running time of 13.476 s (or 2.551 faster than the BordaRank) and 13.502 s (or 2.556 faster than the WP-Rank). The results show that the matrix decomposition using SVD can accelerate the running time of these algorithms. For better readability,
Figure 5 illustrates the average running time of each algorithm graphically using the MovieLens 100K.
Based on
Figure 5, the running time of the ranking algorithms with SVD (SVD-Borda and the SVD-WPR) is faster than those without SVD (BordaRank and WP-Rank). It shows that the performance of running time employing matrix decomposition is better than without the matrix decomposition process. In other words, the matrix decomposition process helps speed up the running time to generate a recommendation. Compared to SVD-Borda, our proposed SVD-WPR algorithm requires a greater average running time of 0.013 s. This is because the SVD-WPR utilizes the ranking aggregation algorithm, which is more complex than SVD-Borda, to optimize the recommended items ranking. As compensation, the recommended items produced by SVD-WPR are more accurate than those generated by SVD-Borda (see
Table 6).
4.4. Discussion
This paper proposes a recommendation algorithm that incorporates the ranking-based collaborative filtering and matrix factorization method to overcome the scalability problem in the ranking aggregation algorithm. The ranking-based collaborative filtering employs the weight point rank algorithm to aggregate user preferences in the neighborhood. Meanwhile, the matrix factorization method utilizes singular value decomposition (SVD) to predict the unrated rating.
We compare the performance of our proposed algorithm with the three previous ranking-based algorithms (i.e., BordaRank, WP-Rank, and SVD-Borda) using the benchmark dataset (MovieLens 100K). We evaluate two metrics (i.e., ranking accuracy and running time) to compare the performance of these algorithms. The ranking accuracy metric employs normative discounted cumulative gain (NDCG). The NDCG scale is [−1.1], where the number 1 denotes the perfect ranking. Meanwhile, running time comparison is simple; the faster, the better.
The experimental results show that incorporating the ranking aggregation and matrix decomposition algorithms can improve the ranking performance by increasing an average NDCG by 32.32%, 27.3%, and 10.21% compared to BordaRank, WP-Rank, and SVD-Borda algorithms, respectively. In addition, the proposed algorithm can reduce the running time by 13.489 s and 13.502 s compared to BordaRank and WP-Rank, but consumes less time (0.013 s) than SVD-Borda. The results show that the SVD-WPR significantly increases in ranking accuracy and can speed up the running time compared to the ranking aggregation algorithms without matrix decomposition (BordaRank and WP-Rank). The more accurate results of SVD-WPR are caused by the ranking aggregation algorithm using the product weighting and predicting the unrated rating before determining the neighborhood users. Furthermore, the speed of running time in SVD WPR occurs because this algorithm applies a smaller matrix dimension to calculate user similarity (using a user–factor matrix resulting from matrix decomposition).
The proposed approach is independent of the field of application. Consequently, other applications can apply the proposed recommendation algorithm, such as book and transportation recommendations. The application domains only require explicit rating data, i.e., the value entered by the user directly when accessing the chosen item. It becomes the advantage of our proposed algorithm.
We also evaluate the performance of SVD-WPR in another dataset (i.e., MovieLens 1M). The average NDCG values for SVD-WPR are 0.8932 based on testing with MovieLens 1M datasets. The average NDCG values by 0.6765, 0.6887, and 0.7326 for baseline algorithms (BordaRank, WPR, and SVD-Borda). The test results on a larger dataset reveals that SVD-WPR performs better than the baseline algorithms (BordaRank, WPR, and SVD-Borda), improving NDCG by 30.03%, 29.69%, and 21.92%, respectively. Additionally, the larger dataset (MovieLens 1M) produces higher NDCG than MovieLens 100K. It demonstrates that the SVD-WPR generates a highly relevant ranking in a larger dataset, which is advantageous for our research.
Recently, several studies [
37,
38,
39] also offered various recommendation algorithms to enhance performance. A study in [
37] applied a ranking aggregation algorithm that combined the clustering and Copeland method to reduce the victory frequency with defeat frequency in the pairwise contest. The experiment using MovieLens 100K obtains the average NDCG score is 0.5649. The result has lower NDCG compared to our proposed algorithm (SVD-WPR). It means that the SVD-WPR is superior to Copeland. In addition, the study conducted by [
38] suggested an enhanced group recommender system (GRS) by exploiting preference relation (PR), known as GRS-PR. Their experiment result shows that the NDCG@10 average in MovieLens 100K is 0.5519. Based on this result, our proposed algorithm (SVD-WPR) still outperforms GRS-PR by improving the NDCG score to 0.2384. It becomes the advantage of our proposed method to generate relevance of item ranking.
Furthermore, Pujahari and Sisodia [
39] utilize matrix factorization-based preference relation to obtain the predicted rating and then applies the graph aggregation method to aggregate the group member’s preferences. Their recommendation algorithm is known as PR-GA-GRS. The experiment using MovieLens 1M yields the NDCG@10 average is 0.5718. This NDCG result is lower than the NDCG result using SVD-WPR, showing that the SVD-WPR also outperforms the PR-GA-GRS.
Although the proposed SVD-WPR algorithm can overcome data sparsity and scalability, reduce running time, and increase recommendation performance in NDCG scores, the SVD-WPR still has shortcomings. During the implementation of our proposed algorithm, one limitation may arise when the dataset drastically increases. The limitation occurs since the singular value decomposition’s factorization process becomes computationally expensive. Meanwhile, the burden of our proposed algorithm is that the user similarity for determining the neighborhood users depends on selecting the number of factors in matrix decomposition. For the ranking aggregation process, we also set a fixed number of neighborhoods (50 in this case). Thus, it needs to explore the optimal number of factors and neighborhoods for processing the ranking aggregation to achieve more accurate results and faster execution time.