Two-Stage PNN–SVM Ensemble for Higher Education Admission Prediction

Abstract

In this paper, we investigate the methods used to evaluate the admission chances of higher education institutions’ (HEI) entrants as a crucial factor that directly influences the admission efficiency, quality of education results, and future students’ life-long trajectories. Due to the conditions of uncertainty surrounding the decision-making process that determines the admission of entrants and the inability to independently assess the probability of potential outcomes, we propose the application of the machine learning (ML) model as an algorithm that provides decision-making support. The proposed model includes the support vector machine (SVM) stacking ensemble, which expands the input data set obtained using the Probabilistic Neural Network (PNN). The basic algorithms include four SVM ensemble methods with different kernel functions and Logistic Regression (LR) as a meta-algorithm. We evaluate the accuracy of the developed model in three stages: comparison with existing ML methods; comparison with a single-based model that comprises it; and comparison with a similar stacking model and with other types of ensembles (boosting, begging). The results of the designed two-stage PNN–SVM ensemble model provided an accuracy of 94% and possessed acquired superiority in the comparison stages. The obtained results enable the use of the presented model in the subsequent stages of the development of an intellectual support system for decision making regarding entrants’ admission.

1. Introduction

Today, the admission process is a critical component of educational institutions’ activity. In order to strengthen HEIs’ autonomy and social responsibility, one of their priorities is searching for and implementing information technology (IT) innovations that provide effective results. The rapid development of IT, particularly in the field of artificial intelligence (AI), increases the need to constantly investigate the most effective technological solutions to be utilized in different stages of education. It should be emphasized that in order to ensure the quality of higher education, the results of the admission process must meet the needs of both the HEI itself and the other stakeholders, entrants, and society.

One of the critical moments during the admission process is the entrant’s choice of a specific program; the method by which a student selects the HEI and, alternately, the institution selects a student to admit significantly affects the success of both sides. However, today, many factors could make this task more complicated, particularly those that follow:

• an increasing amount of information coming from various HEI or government institutions (complex admission standards for entrants, and a wide range of educational institutions and programs) could complicate how the HEI is perceived and processed by entrants;
• the specific rules of separate HEIs, the complexity of the admission process and annual updates to the admission requirements often confront entrants;
• the risk of entrants getting stuck in the “area of limited information” that is caused by the popularity of certain fields in the labor market (it is difficult to expertly assess the demand for specialists and the labor market trends that change every year); entrants’ uncertainty associated with the inability to independently and accurately assess the success of admission;
• the consequences of final decisions that directly affect future students and their self-realization—education success, employment, and HEI ranking.

As a result, in most cases, entrants are not fully knowledgeable, so they are not ready to choose a program expertly and consciously. HEI entrants cannot use their previous experience, because of its insufficiency, so they rely on their perception and understanding of the general information that is available regarding the admission process. Since all entrants are direct subjects in the education market, the results of their choices are significant and need to be supported in order to achieve effective admission process results.

The current methods and tools used by leading HEIs that aim to support entrants with admission-related information nowadays involve a few main aspects: official websites (programs lists and descriptions, admission requirements, promotional materials); online applications to HEIs (provides all stages, including payment); online/offline specialist consultations (a human impact factor makes them less effective); and commercial software solutions designed to aid the admission management process (problems of privacy and data security, high purchase cost, and difficulties in regard to supporting them makes them unsuitable in many cases). As we can see, these tools do not provide enough support for entrants’ decision making.

A proper evaluation of the chances of entrants’ admission success could support entrant’s decision-making process regarding their choice of education program and, at the same time, save their time and financial costs. Such a prediction of an entrant’s admission will also have a positive impact on the planning and management processes of HEIs.

One possible way to solve this task is to build a specific intellectual information system to support the decision-making process. The advantages of ML include its ability to naturally extend traditional statistical approaches that focus primarily on predictions, to automatically identify patterns within data, and perform the tasks that we aim to investigate in this paper. Based on our previous research results and an analysis of the existing studies, with the aim of achieving high accuracy, low time consumption, and the ability to implement it in future studies, this paper evaluates a new hybrid model that can be used to predict the admission chances of HEI entrants.

2. Related Work

ML and AI more broadly have great current and future potential for implementation in almost all aspects of the education process. However, an analysis of the latest research on ways in which to support decision-making using ML methods shows us that most of them are designed for existing students. This could be explained by the fact that HEIs have flexible curricula and offer a wide list of elective courses, so they use educational data to build possible recommendations and decision-making algorithms.

In addition, there is much ML-based research on decision making and its application in program selection, but it generally aims to support HEI managers. In this case, prediction primarily aids in the understanding of enrollment trends and could influence future strategy and resource decisions. For example, the purpose of such studies was to define the future enrollment trends [1], investigate a statistical model that can be used to better forecast international undergraduate student enrollment at the institutional level [2], identify applicants with a higher tendency to enroll [3], predict student enrollment behavior and predict the students who are at high risk of dropping out [4].

Some papers have focused on predicting the entrant’s admission success. These authors have emphasized the relevance of admission prediction because it will help entrants save their time and money, promote successful study and employment, and reduce the risk of exclusion [5,6,7,8,9,10]. Various methods of intellectual data analysis have been used to extrapolate patterns and new knowledge from the collected data. The authors have also used common ML methods to compare different regression algorithms [5,7], including Association Rule Mining [6] and gradient boosting regressor [9]. These studies were performed in accordance with the needs of undergraduate [6,10] or graduate students [5,7,8,9]. The researchers used data sets that contained the previous year’s admission results [5,6], students’ data [7,8,9,10], or current user’s data. The authors also emphasized the importance of cleaning, preparing data, and the feature selection process.

Intending to improve research results, the authors emphasized the relevance of such tasks in the future, including expanding datasets and using neural networks as another plausible model, instead of single regression models.

However, the existing works in most cases do not provide comparative results with other methods or the authors’ previous studies. In addition, the authors do not consider the application of the researched models in building a software solution that supports applicants. As an essential key component in many data mining applications, neural networks have emerged as being particularly effective in higher education-related tasks. Researchers have used neural networks in the study of engineering student retention prediction [11], have determined the education quality by classifying the students’ achievements [12] and have predicted entrants’ academic performance at the university in order to support them in the admission decision-making process [13]. Other work has investigated classification patterns using the k-nearest neighbors algorithm (k-NNN), artificial neural networks (ANNs), and the Naïve Bayes method. The experiment showed that the ANNs demonstrated the best accuracy and precision [14]. The methods used in these works were defined as practical result detection algorithms with a high accuracy and efficiency.

The results of modern research using ML algorithms testify to the effectiveness of ensemble methods. This approach has become a primary development direction in ML in various subject areas [15].

In one study, the authors applied a new ensemble technique for classifying the multi-class hyperspectral honey dataset, and mitigated a vital drawback of these tree-based methods: they cannot correct for misclassification. This ensemble performed better than the benchmark one-vs-rest SVM across all the feature reduction techniques. However, the authors defined some disadvantages, such as a slow training and testing time [16].

Another paper presented the effective results of applying an ensemble approach in a deep learning-based method for dynamic security assessment. The SVM ensemble was used in the base of the stacked de-noising auto-encoder. The ensemble-boosting learning increased the SVM classifier’s accuracy [17].

To provide high accuracy, another paper presented a new, stacking-based General Regression Neural Network ensemble model with a Successive Geometric Transformations Model and a neural-like structure as a meta-algorithm. A comparison with several known predictors showed the best result of the proposed model [18].

The existing research supports the use of an ensemble approach when building ML models for different tasks and data subject areas. However, existing studies in the educational domain still have certain disadvantages, particularly the lack of comparison with other methods, low accuracy, and missing indicators that affect the admission outcome (incomplete data or their low quality). Therefore, finding and researching the most effective methods and models for solving this task is still necessary. In addition, an analysis of the literature demonstrates that most available research does not explore the combination of different methods. Therefore, this work investigates the possibility of improving the accuracy of predicting the success of admission to an HEI by using a two-stage proposed model.

3. Materials and Methods

This section describes the data set, methods, and modeling process used in more detail.

3.1. Base Models

PNNs are a group of ANNs obtained from Bayesian calculations and the nucleus density method. PNNs often learn more quickly than many neural network models. Its training time, resistance to noise, simple structure, and training manner make this type widely used in modern research and various applications [19].

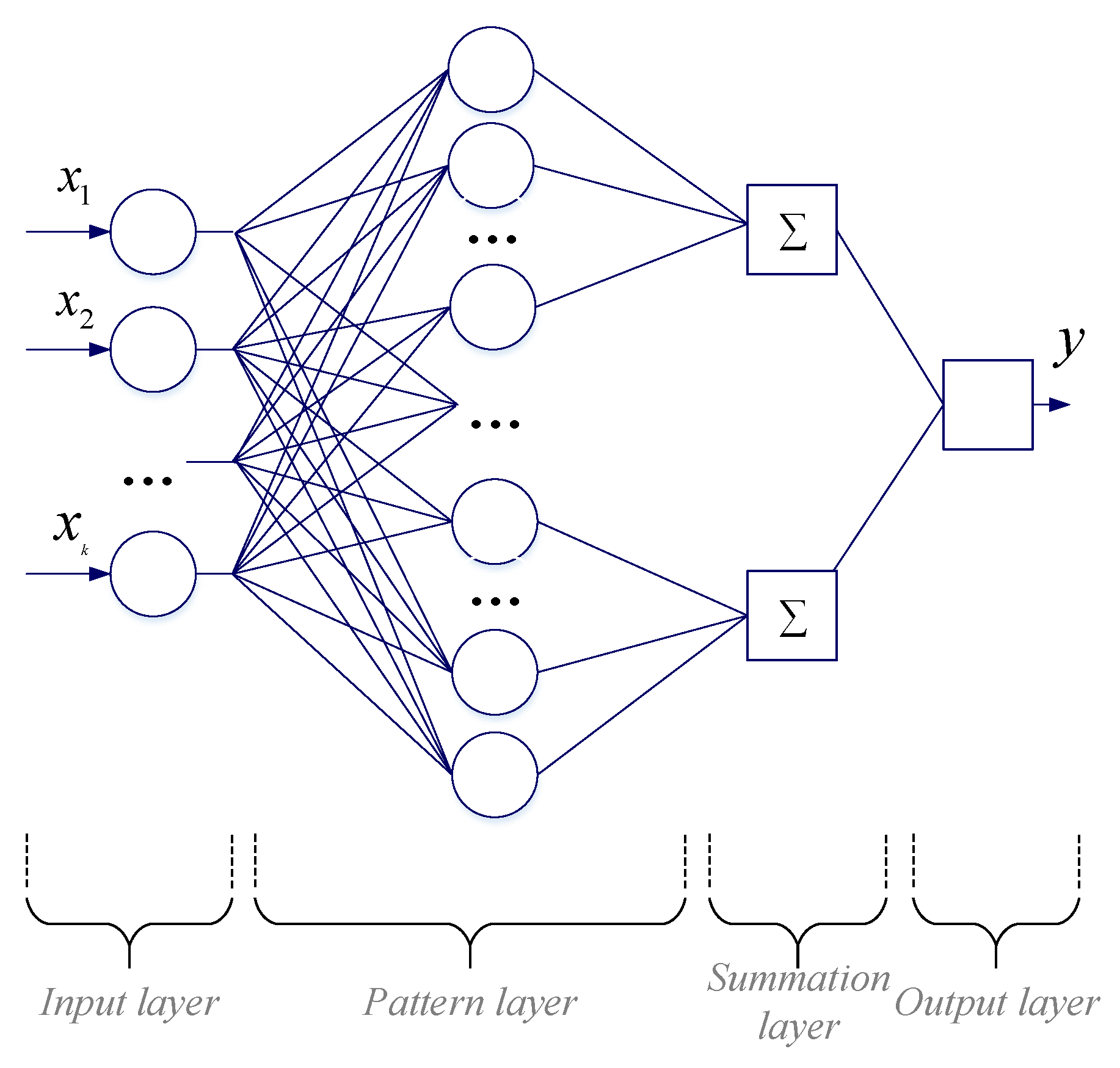
According to the PNN topology, there is no need for massive back-propagation training computations. Instead, each data pattern is represented with a unit that measures the similarity of the input patterns to the data pattern. The point is that the PNN learns to estimate the probability density function. Its output is considered the model’s expected value at a given point in the input space. The output layer of the PNN estimates the probability of an element belonging to a particular class. The PNN topology is presented in Figure 1. A complete analysis and mathematical explanation are presented in [20].

Today, PNNs are widely used in order to solve various issues that researchers have attempted to address. PNNs facilitate the smooth and accurate classification of complex models with arbitrary solution boundary shapes [20].

Another ML method that we used in this research is SVM. It is one of the most common ML methods used for classification, regression, or the detection of outliers. This method shows high efficiency in binary classification (when the data have exactly two classes) [21]. Compared with other statistical learning algorithms, SVM implementation often provides a high level of performance, especially when using high-dimensionality data or data with a small number of training examples [16,17].

SVM is a powerful algorithm that finds the best possible decision boundary and separates the data points of different classes in a high-dimensional feature space. To implement SVM, the data points are first mapped to a higher dimensional feature space using a kernel function. In the feature space, SVM finds the best decision boundary that maximizes the margin between the classes. Once the decision boundary is found, SVM can predict the class of new data points by determining which side of the decision boundary they lie on. SVM is a powerful algorithm that can handle large datasets and works well with both linearly separable and non-linearly separable data. A classical SVM application mathematical theory is explained in [22].

The advantage of this method is also universality. Different kernel functions provide processing data through a set of mathematical functions. The kernel plays an essential role in classification and is used to analyze some patterns in a particular data set. Different algorithmic implementations of SVM can use different types of kernel functions. The most popular are Linear, Sigmoid, Polynomial, Radial Basis Function (RBF), Gaussian kernel, and Bessel function kernel. It is worth noting that the accuracy of the classifier, to some extent, depends on the choice of specific kernels [23]. Since this method shows good results in binary classification, we chose it as the basic algorithm of the ensemble model. To build the ensemble method, we used SVM and LR, also considering previous studies’ results. After investigating the effectiveness of different ML-based classifiers in solving the prediction task, these methods showed the highest accuracy [24]. The LR assumes that the relationship between the input features and the output variable is linear on the logit scale and estimates the coefficients of the linear equation using maximum likelihood estimation. LR is a statistical model commonly used for binary classification tasks to predict whether an observation belongs to one of two classes. Despite its simplicity, LR can achieve high performance on a wide range of classification problems.

3.2. The Proposed Ensemble Model

In this work, the stacking ensemble of the SVM, with the expansion of the input data set via PNN, was implemented. The main idea of such a hybrid approach is to use the summation layer of the PNN topology as a tool for pre-processing data for further use. The processed data set is added to each relevant vector of the initial training and test data samples. This scheme ensures an expansion of the input data space via the probability of the data belonging to each class, which theoretically should increase the probability of the correct result in the classification tasks based on the ML algorithm. In addition, the ensemble method is used as one of the ways to increase the accuracy of the prediction results. We propose Logistic Regression for a meta-algorithm as it is effective and relatively fast compared to other algorithms, making it suitable for real-time applications. We use SVM, as it is one of the most commonly used algorithms in current research and was the most accurate in our previous investigation classification method [24].

Given the possibilities of the methods described above, in this study, we presented a heterogeneous ensemble of SVM with four different kernels, with the expansion of the input data set using PNN and LR as a meta-algorithm.

The essence of the ensemble method is the simultaneous application of several basic algorithms. In this method, algorithms can be taught in parallel, which provides an opportunity to improve the results’ accuracy. Several approaches to building ensemble algorithms exist, such as stacking, boosting, and bagging. Boosting is the continuous application of each model, with each subsequent one correcting the errors of the previous one. The basic algorithms are learned in parallel using the bagging ensemble method, and the final results are aggregated. When using stacking, several different algorithms are trained, and at their outputs, the meta-algorithm gives the final result. The stacking ensemble method is used in this work. The scheme of the proposed model is shown in Figure 2.

Therefore, the model works as follows. In the first stage, we use PNN on the initial data set. As a result, we obtain an additional set of probabilities from the PNN’s summation layer, which increases the features of the initial data set. Next, the extended data set is processed using a heterogeneous stacking ensemble.

3.3. Dataset Description

The effectiveness of the chosen method was evaluated based on a real dataset of admissions to HEIs. It includes information about the admission results of 29 universities. This data set is freely available, which is the main reason for its use in this work. It can be downloaded from [25]. Because of the importance of data preprocessing, we chose this well-prepared dataset, which included all the necessary procedures for data processing, selecting essential attributes, and preparing them for further intellectual analysis. Some dataset statistics are presented in

Table 1. Features statistic.

Feature/Statistic Indicator	Mean	Median	Dispersion	Min	Max
GRE score	313.70	314	0.02	287	338
GRE score quant	162.43	163	0.03	142	170
GRE score verbal	151.27	151	0.03	135	170
English test score (TOELF)	97.344	103	0.245	0	120
Undergraduate score	2.9418	3	0.1607	10.6	3.94
Working experience	17.16	15	0.96	0	132
Paper published	0.74	0	1.65	0	3

. The following are mentioned in the table: mean—the average or the most common value in a collection of numbers; median—the middle value of a set of numbers; dispersion—the extent to which a distribution is stretched or squeezed; and minimum and maximum values of the featured dataset.

In total, 1653 observations in this data set did not contain gaps. That is why the specified data set was used to test the developed method in its current form.

3.4. Performance Indicators

Performance evaluation of the designed two-stage PNN–SVM ensemble model was conducted using the following indicators:

$$\mathrm{Accuracy}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{FP}+\mathrm{TN}+\mathrm{FN}},$$

(1)

$$\mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}},$$

(2)

$$\mathrm{Recall}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}},$$

(3)

$$\mathrm{F}1-\mathrm{score}=2\times \frac{(\mathrm{Recall}\times \mathrm{Precision})}{(\mathrm{Recall}+\mathrm{Precision})},$$

(4)

where TP represents true positive observations, TN represents true negatives observations, FP represents false positive observations, and FN represents false negatives observations.

The basic and commonly described intuitive metric used for model evaluation is accuracy, which defines the number of correct predictions divided by the total number of predictions multiplied by 100. It is defined as the ratio of the number of correct predictions to the total number of predictions made by the model. It evaluates how accurately the model can predict the class according to a problem statement.

Precision provides a measure of accuracy for positive predictions, and it could be applicable to a wide range of ML tasks, including binary classification, multi-class classification, and even regression. This makes it a flexible metric that can be used in various contexts.

Recall is a commonly used performance metric for classification models. It is a crucial performance metric that measures how well a model identifies positive instance recall measures and the proportion of actual positive instances that the model correctly identifies, i.e., the ratio of true positives to the sum of true positives and false negatives [26].

The F1-score metric combines precision and recall metrics to provide a single score that reflects the model’s overall performance. The main advantage is that the F1-score combines other metrics into a single one, capturing many aspects simultaneously.

3.5. Optimal Parameters of Ensemble Members

The smooth factor is the only parameter of PNN selection that is necessary for the exact work of a neural network of this type. Therefore, in Figure 3, the dependence of the PNN accuracy values on the change in this parameter is shown (in the range from 0.01 to 0.3 with a step of 0.01). As shown in Figure 3, the highest accuracy value of the PNN is obtained at a smooth factor of 0.03. A further increase in the value of this indicator does not change the accuracy of the PNN. Therefore, a value of 0.03 was used during the pre-processing of a given data set in order to obtain a set of probabilities belonging to one of the two classes of the original attribute of the task.

All the SVMs (SVM with different kernels) of the stacking ensemble worked on the following parameters: cost = 1, regression loss epsilon = 0.1, numerical tolerance = 0.001, and the number of iterations = 10,000. Only the core of the method changed. It should be noted that when comparing the work of the developed ensemble with single-based SVMs, the same parameters of their work were used.

4. Results

The modeling of the stacking ensemble was based on an extended data set. It is formed by adding to the initial data set the probabilities of belonging to each of the two classes of the task (whether the entrant entered or not) due to the outputs of the summation layer PNN. Thus, the new data set contained not 7, but 9 input attributes. This is the first stage of the developed method. The grid-search method was used to select the optimal operating parameters of each ML method (details are presented in Appendix A).

A stacking ensemble of four SVMs with different kernels was used in the second stage. To objectively assess the behavior of the developed ensemble on the independent data, we used ten-fold cross-validation. This procedure provides more reliable results and allows us to conclude a specific generalization of the studied model.

The results of the ensemble based on Equations (1)–(4) are summarized in

Table 2. The results of the designed two-stage PNN–SVM ensemble model.

Model	Accuracy	F1-Score	Precision	Recall
Designed two-stage PNN–SVM ensemble model	0.940	0.939	0.940	0.940

.

In addition to the numerical results of the accuracy of the developed method, Figure 4 shows the quality of classification in visual form; this is in the form of ROC curves for two classes (get admission or not).

An error curve, the so-called ROC curve, was used to visualize the research results (Figure 4). The ROC curve plots the true positive rate (sensitivity) against the false positive rate (specificity) for each individual class. Accordingly, the studied classifier, whose ROC curve is located above and to the left of the graph, demonstrates greater accuracy.

5. Comparisons and Discussion

The comparison of the model efficiency in this work was carried out in three stages. In the first stage, there was a comparison with the existing ML methods, which are most widely used in the existing literature. The second experiment compared the developed ensemble with a single-based model that formed it. Finally, the third experiment demonstrated the comparison results with a similar stacking model and other types of ensembles (boosting, begging).

5.1. Comparison with Existing Machine Learning Algorithms

The aim of this experiment was to compare the designed two-stage PNN–SVM ensemble model with the neural network and classical ML algorithms:

• classical PNN;
• Neural Network;
• SVM with RBF kernel;
• LR;
• Stochastic gradient descent (SGD);
• Decision Tree;
• Naïve Bayes;
• kNN.

Existing methods were simulated using the “Orange” software package [27]. “Orange” is a tool for data visualization, ML, and open-source data analysis. It is equipped with a visual programming interface for fast and high-quality data analysis and interactive data visualization. Software “Orange” includes a wide array of tools that are suitable for demonstrating such an investigation.

It should be noted that all of these methods used the original data set (without extension using PNN). The results of the experiment are summarized in

Table 3. Comparison of the accuracy of the model with classical ML methods.

Model	Accuracy	F1-Score	Precision	Recall
Designed two-stage PNN–SVM ensemble model	0.940	0.939	0.940	0.940
SVM (RBF-kernel)	0.699	0.676	0.683	0.699
LR	0.689	0.649	0.674	0.689
Neural Network	0.681	0.667	0.665	0.681
SGD	0.678	0.643	0.656	0.678
Decision Tree	0.673	0.666	0.662	0.673
Naïve Bayes	0.666	0.67	0.676	0.666
kNN	0.657	0.617	0.626	0.657
Classical PNN	0.664	0.677	0.692	0.664

.

5.2. Comparison with All Single-Based Ensemble Members

The purpose of this phase was to compare the designed two-stage PNN–SVM ensemble model with its single-based members: PNN [28], which is the basis of the first stage of the developed method; and SVM with RBF, sigmoid, polynomial and linear kernels separately, which used the extended dataset. In

Table 4. Comparison of the accuracy of the designed two-stage PNN–SVM ensemble model with its single-based members.

Model	Accuracy	F1-Score	Precision	Recall
Designed two-stage PNN–SVM ensemble model	0.940	0.939	0.940	0.940
SVM (RBF-kernel)	0.938	0.937	0.938	0.938
SVM (linear kernel)	0.938	0.938	0.938	0.938
SVM (polynomial kernel)	0.935	0.935	0.936	0.935
SVM (sigmoid kernel)	0.914	0.914	0.914	0.914
PNN from [28] *	0.68	0.68	0.67	0.68

* a PNN in this case used the initial dataset, but all other methods used the extended dataset.

, the results of such a comparison are summarized.

5.3. Comparison with Other Ensemble-Based Approaches

This experiment demonstrates the advantages of the developed ensemble in comparison with other ensemble methods:

• stacking of SVMs with different kernels;
• Random Forest algorithm;
• AdaBoost classifier.

All three existing ensemble methods belong to different groups of ensemble construction: stacking, begging, and boosting. It should be noted that the simulation of their work took place on the initial data set. The simulation results are summarized in

Table 5. Comparison of the accuracy of the designed two-stage PNN–SVM ensemble model with other ensemble-based classifiers.

Model	Accuracy	F1-Score	Precision	Recall
Designed two-stage PNN–SVM ensemble model	0.940	0.939	0.940	0.940
Random Forest	0.703	0.695	0.693	0.703
AdaBoost	0.655	0.654	0.654	0.655
Stacking of SVMs with different kernels	0.706	0.680	0.693	0.706

.

5.4. Discussion

According to the research goal, the proposed model results provide high accuracy. The three-stage experiment proves that our model is more accurate than other ML methods, a single-based model that comprises the proposed model and the other ensemble methods. In addition to the numerical results, Figure 5 presents the classification accuracy using the ROC curves of the two classes (get admission or not) of the accuracy of the last experimental stage.

In addition, these results are more accurate in comparison with the previous authors’ investigations. The numerical results show a higher accuracy than our previous implementation of ML-based classifiers for HEI entrants’ admission prediction.

The high accuracy of the model is a prerequisite for building an effective information system. This is also facilitated by the greater reliability of intellectual analysis due to using an ensemble of ML methods, compared to single-based ML algorithms.

The need to make a choice appears every year before entrants of each HEI. At the same time, many variables can affect students’ decision success. As previous studies show, additional research requires a data collection and analysis stage to be used in such a system. The sources of data that were used in the research of other authors are the results of surveys, information about student performance, and (or) historical information about applicants from previous years of admission. However, there is still the problem of considering the crucial parameters of the data set when using specific methods.

Thus, studying a set of independent traits that may affect the results of prediction in each case is also extremely important. This direction will be a subject of a future work.

6. Conclusions

In this research, we considered the need to support the program decision-making process of HEI entrants during admission. As one of the ways to increase the effectiveness of admission results, we investigated the possibility of evaluating entrants’ chances of being admitted to an HEI. Reviewing previous research allowed us to highlight some tendencies in implementing IT systems that aim to support the entrant’s needs. However, existing studies still have certain disadvantages, so we aimed to investigate another model that could accurately predict the entrant’s success more accurately.

A heterogeneous stacking ensemble of the SVM with the expansion of the input data set via PNN was used to investigate the prediction of the entrant’s chances of being admitted through a binary classification task. The basic algorithms of the stacking ensemble were SVM with four different kernels: linear, sigmoid, polynomial, and RBF. We chose Logistic Regression as a meta-algorithm. In the first stage, we used PNN to obtain two additional data vectors. Then, the extended data set was processed using a heterogeneous stacking ensemble.

The results of the designed two-stage PNN–SVM ensemble model provide an accuracy = 0.940, which is the highest value when compared with other studied methods. The obtained results show that the proposed model could be used at the subsequent stages of building an information system that supports HEI entrants’ decision-making process. In addition, the contribution of this study is that it demonstrates the possibility of implementing such a model for the prediction task. This could help other experts who aim to implement IT systems in higher education or other areas.

For a wider and more effective evaluation of the proposed model, our future work will involve testing other datasets that include HEI admission results. We aim to perform all necessary intellectual analysis process stages in order to evaluate the proposed model on another dataset. Further research on a feature selection model is especially important regarding the outcome of prediction and recommendation in each case. These studies will contribute to the effectiveness of building an intelligent system to support entrants’ decision making.