Semantic Non-Negative Matrix Factorization for Term Extraction
Abstract
:1. Introduction
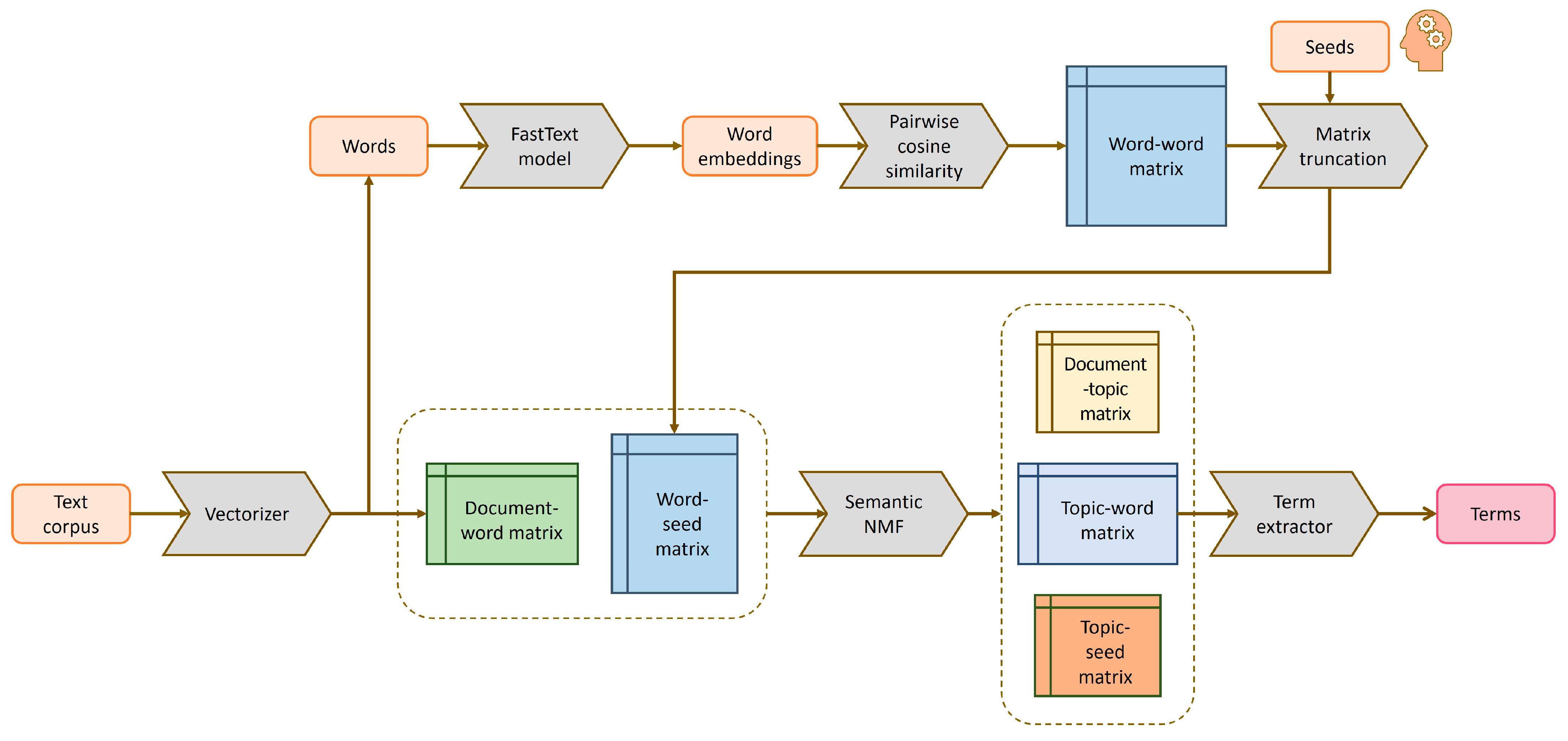
- Novel semantic NMF method for term extraction: We introduced a novel unsupervised method for automatic term extraction that utilizes the semantic NMF algorithm.
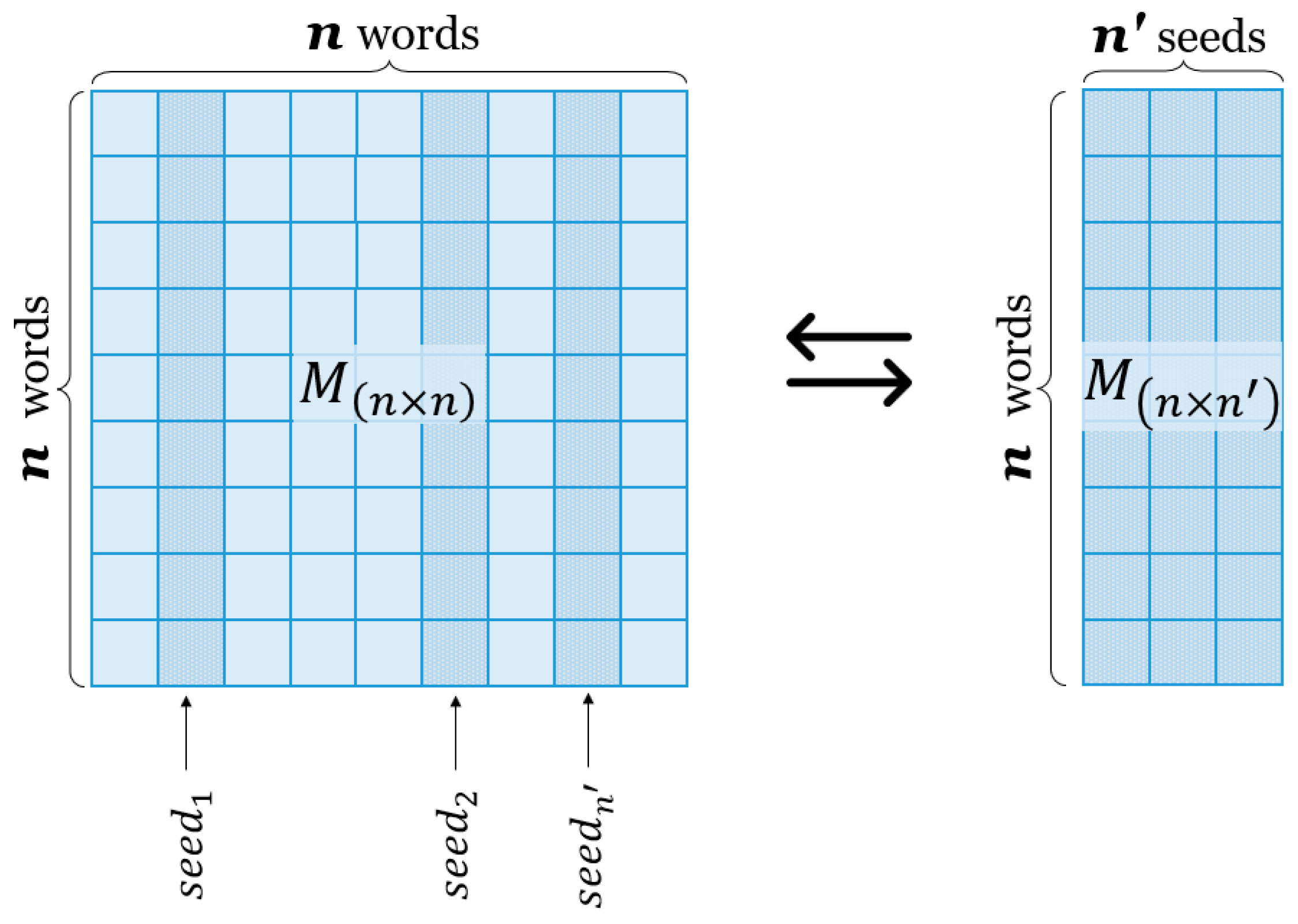
- Novel construction of the word–word matrix using seed words: We proposed a novel way to construct the word–word matrix, a cornerstone of semantic NMF, by introducing the concept of domain seeds. In fact, we replaced the word–word matrix with a word–seed submatrix.
- Development of annotated datasets: We generated two datasets, each consisting of 1000 sentences from the Geography & History and National Heroes domains, and manually annotated them for both term extraction and document clustering/classification tasks. We made these datasets freely available.
2. Related Work
3. Methodology
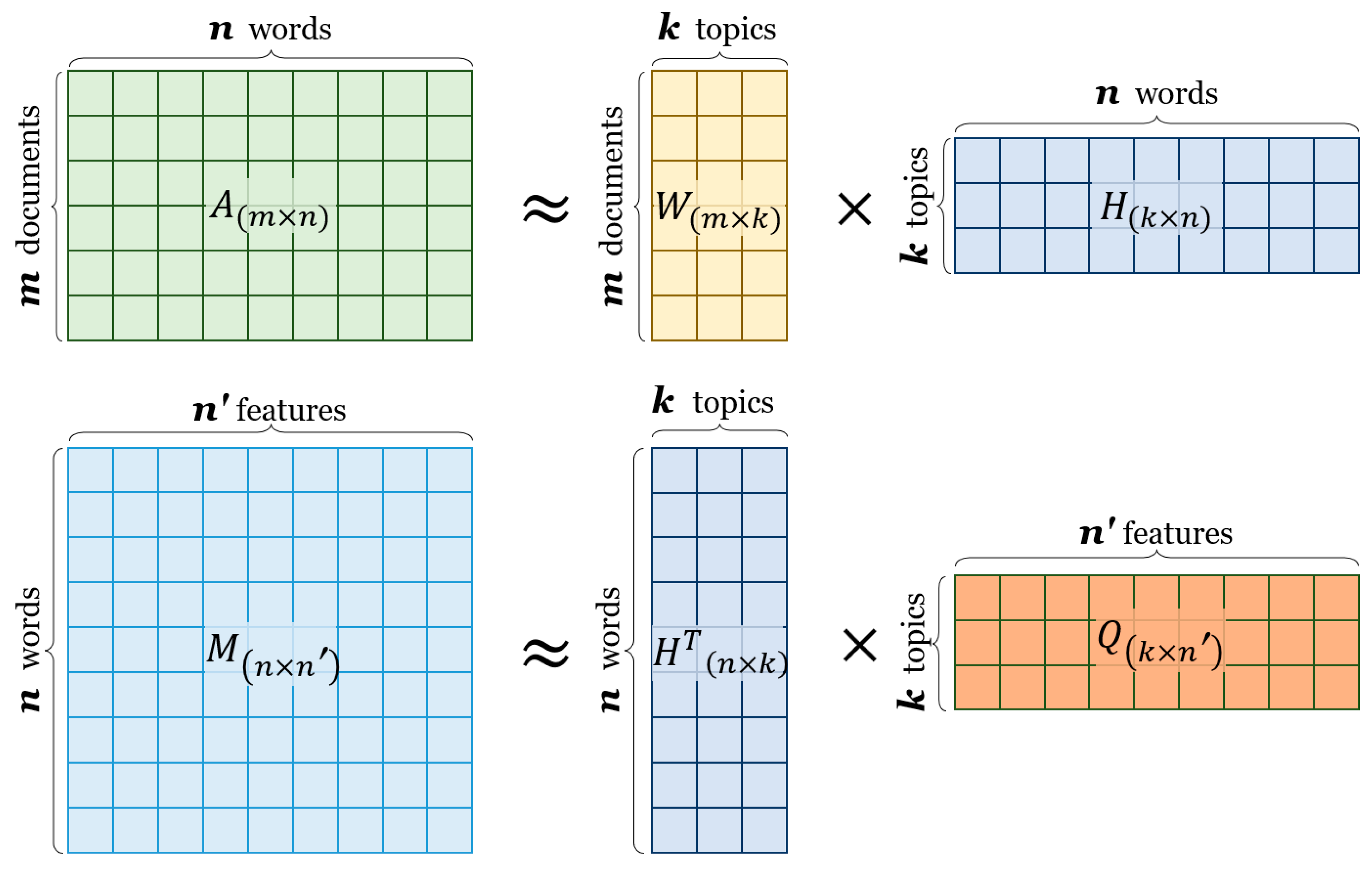
- The creation of the document–word matrix. This matrix represents the distribution of words across the documents in the corpus. Each entry in the matrix reflects the frequency of a word’s occurrence in a specific document, providing a foundational data structure for further analysis.
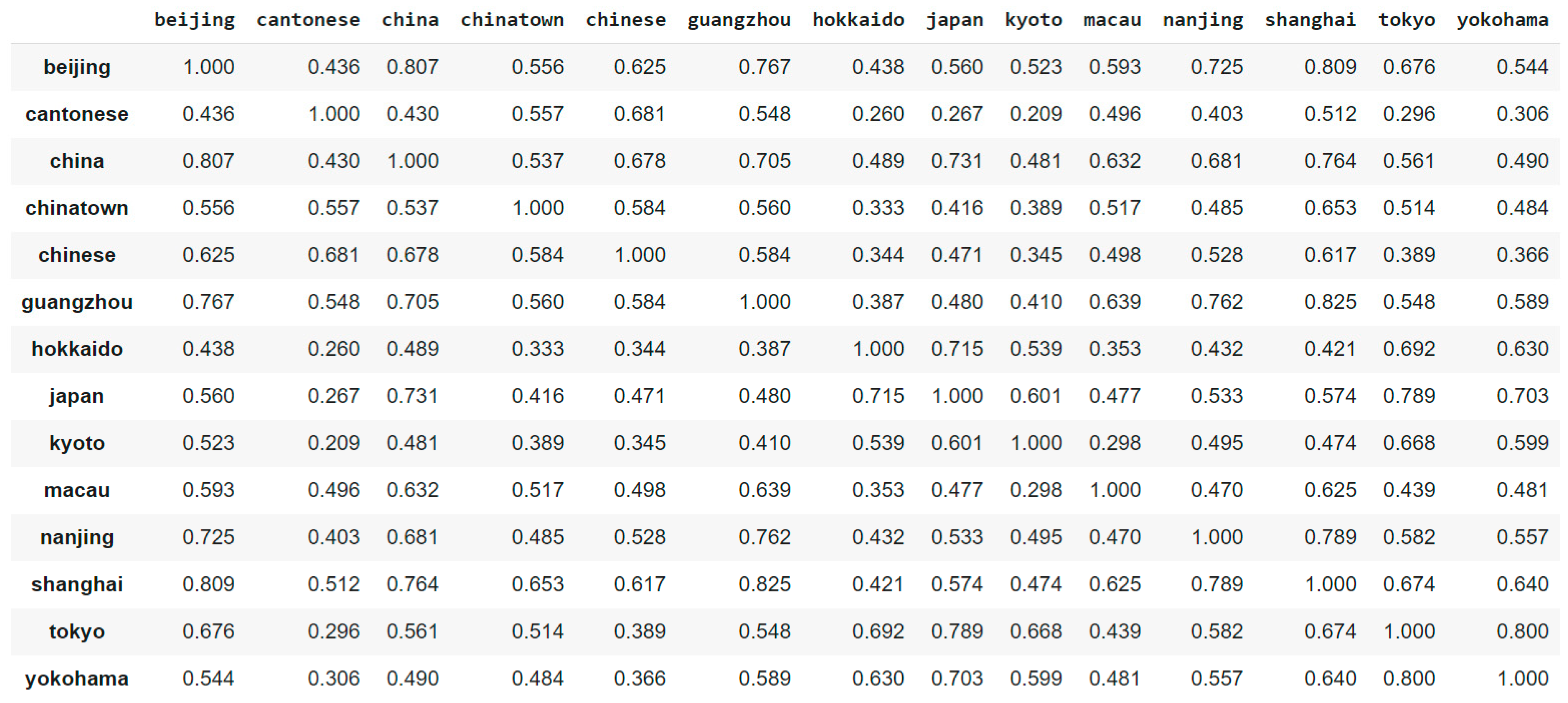
- The creation of the word–seed matrix. This matrix is formed by calculating pairwise cosine similarities between the embeddings of words and predefined seed words. Seed words are selected by a domain expert based on their relevance to the domain, helping to anchor the semantic space around key concepts.
- The joint factorization of the created matrices. The document–word and word–seed matrices are jointly factorized to produce a semantically refined topic–word matrix. This step applies the semantic NMF algorithm and allows for a deeper, more meaningful extraction of topics that are semantically coherent.
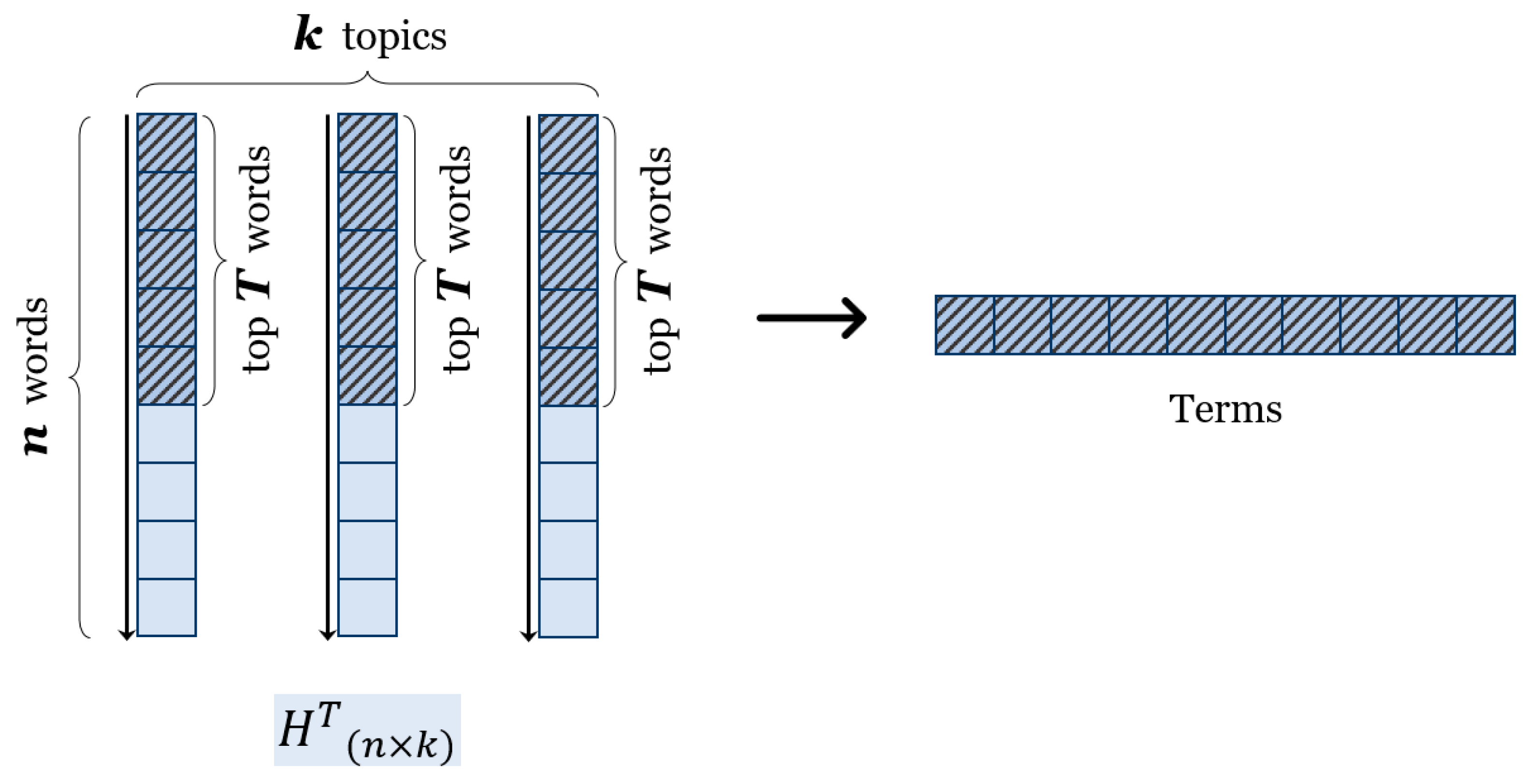
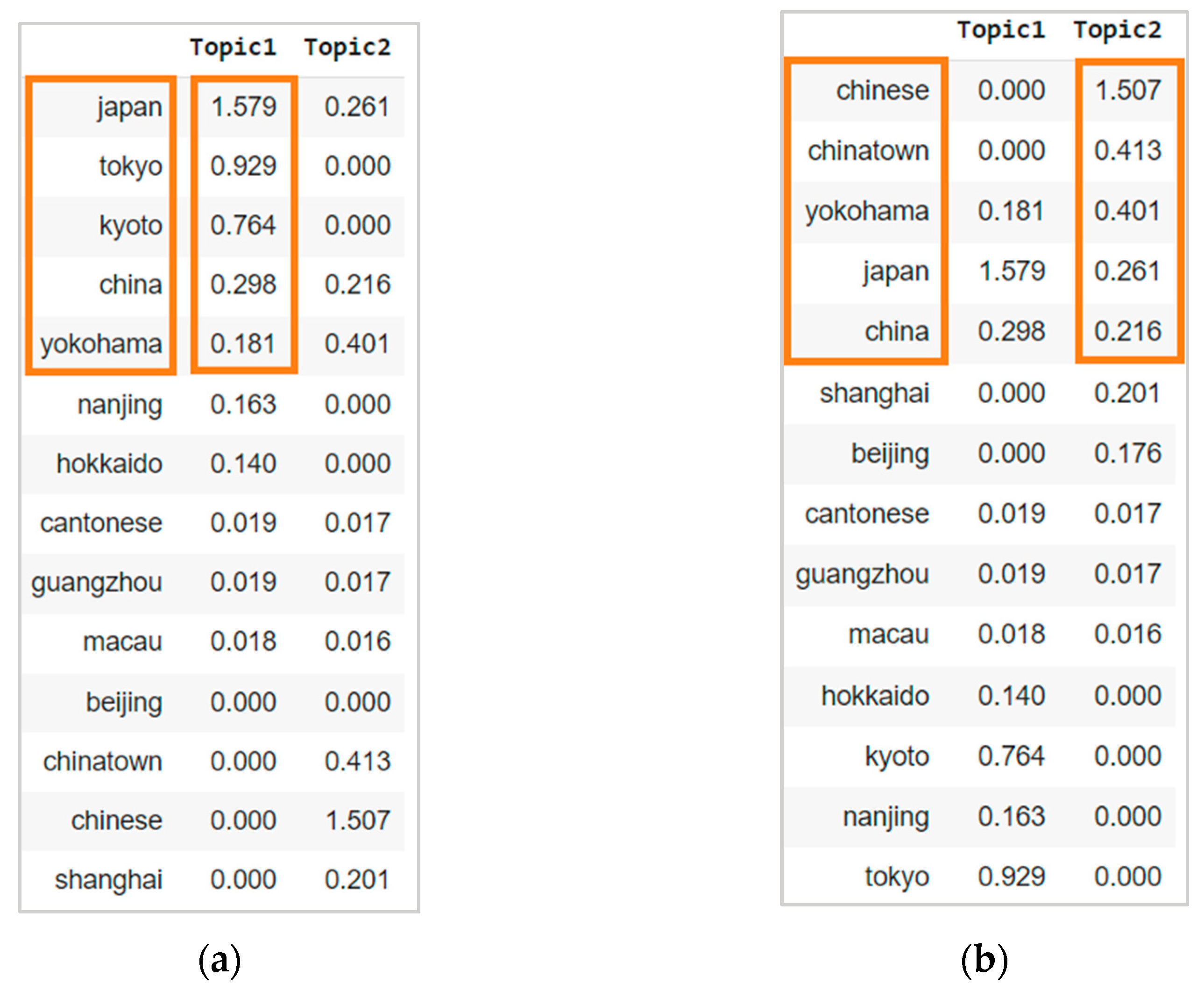
- The extraction of most relevant terms. From each topic in the resulting topic–word matrix, the most relevant terms are extracted. These terms are identified based on their weighted contribution to each topic, highlighting the terms that best define and represent the underlying topics within the domain.
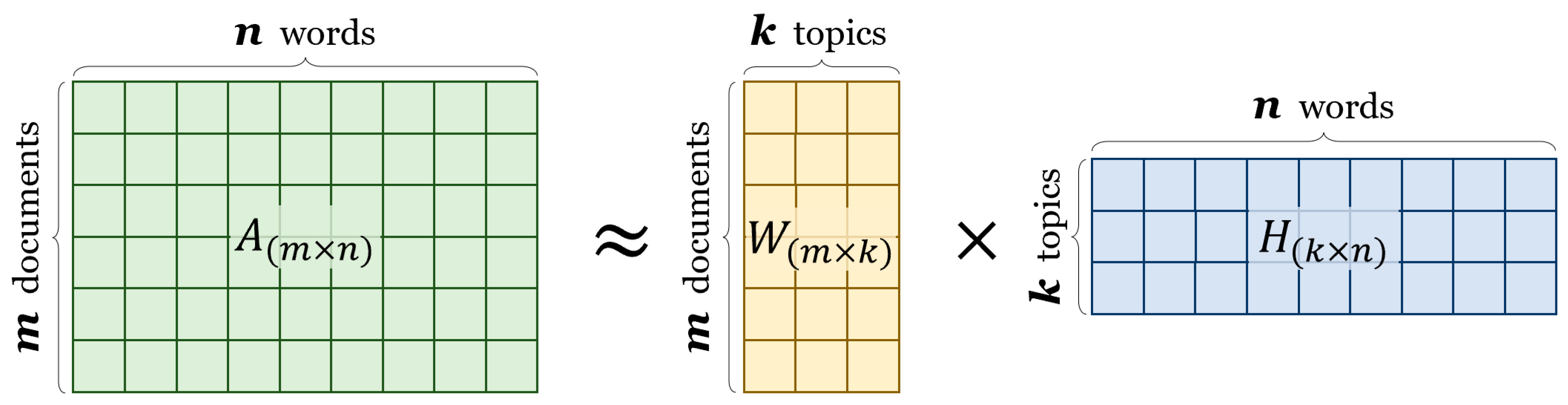
3.1. Standard NMF for Term Extraction
3.2. Semantic NMF for Term Extraction
3.3. Constructing the Word–Seed Matrix for Semantic NMF
4. Experiments and Results
4.1. Datasets
4.2. Experimental Settings
- Number of seeds.
- Number of topics (k).
- Regularization parameter (λ).
- Number of top words extracted from each topic (T).
4.2.1. Selection of the Number of Seeds
4.2.2. Selection of the Number of Topics k
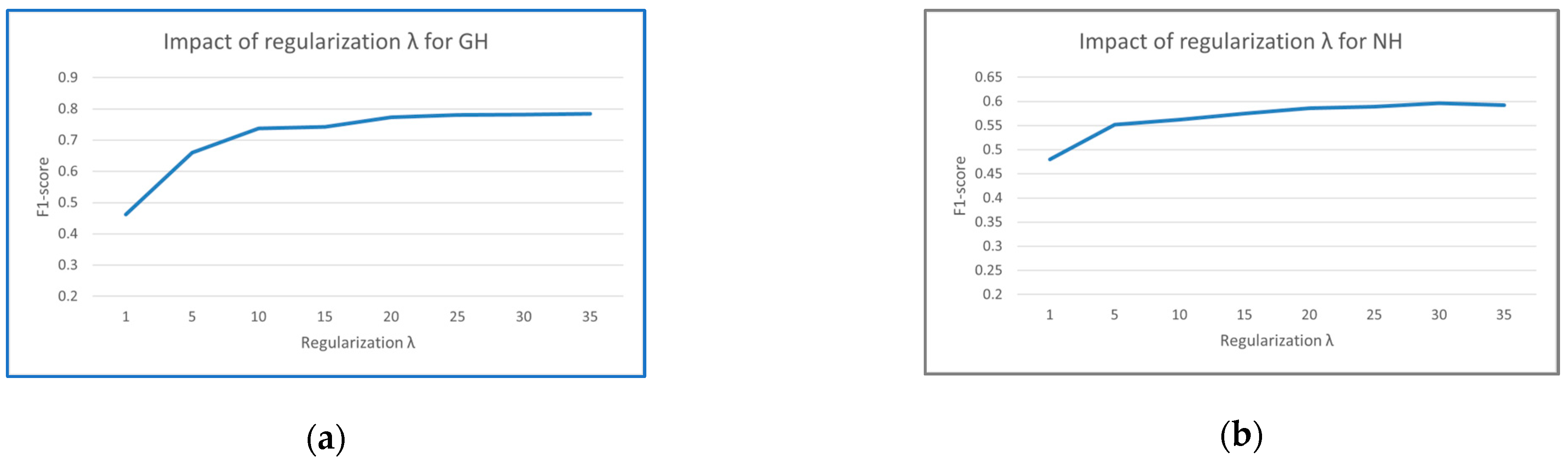
4.2.3. Selection of the Regularization Parameter λ
4.2.4. Selection of the Number of Top Words T
4.3. Baselines
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
|---|---|
| NMF | non-negative matrix factorization |
| BERT | bidirectional encoder representations from transformers |
| KeyBERT | keyword extraction technique that leverages bidirectional encoder representations from transformers |
| BERTopic | bidirectional encoder representations from transformers for topic modeling |
| NLP | natural language processing |
| SSNMF | semi-supervised non-negative matrix factorization |
| SeNMFk | semantic non-negative matrix factorization/semantic assisted non-negative matrix |
| TF-IDF | term frequency–inverse document frequency |
| SeNMFk-SPLIT | semantic non-negative matrix factorization—SPLIT |
| GNMF | guided non-negative matrix factorization |
| GSSNMF | guided semi-supervised non-negative matrix factorization |
| ML | must link |
| CL | cannot link |
| GH | Geography & History |
| NH | National Heroes |
Appendix A. Ablation Study of Number of Topics k, Regularization Parameter λ, Number of Extracted Top Words T and Number of Seeds
| Dataset | Number of Topics k | Regularization λ | Number of Seeds | Number of Extracted Words | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|---|
| GH | 2 | 30 | 30 | 1000/764 | 0.573 | 0.952 | 0.716 |
| 3 | 30 | 30 | 999/707 | 0.617 | 0.948 | 0.747 | |
| 4 | 30 | 30 | 1000/651 | 0.654 | 0.926 | 0.767 | |
| 5 | 30 | 30 | 1000/661 | 0.64 | 0.92 | 0.755 | |
| 6 | 30 | 30 | 996/684 | 0.611 | 0.909 | 0.731 | |
| 7 | 30 | 30 | 994/665 | 0.626 | 0.904 | 0.74 | |
| 8 | 30 | 30 | 1000/653 | 0.632 | 0.898 | 0.742 | |
| 9 | 30 | 30 | 999/575 | 0.704 | 0.88 | 0.783 | |
| 10 | 30 | 30 | 1000/579 | 0.718 | 0.904 | 0.801 | |
| 11 | 30 | 30 | 990/626 | 0.66 | 0.898 | 0.761 | |
| 12 | 30 | 30 | 996/626 | 0.655 | 0.891 | 0.755 | |
| 13 | 30 | 30 | 988/648 | 0.63 | 0.887 | 0.736 | |
| 14 | 30 | 30 | 994/601 | 0.676 | 0.883 | 0.765 | |
| 15 | 30 | 30 | 990/611 | 0.661 | 0.878 | 0.754 | |
| 16 | 30 | 30 | 992/618 | 0.629 | 0.846 | 0.722 | |
| 17 | 30 | 30 | 986/594 | 0.66 | 0.852 | 0.744 | |
| 18 | 30 | 30 | 990/592 | 0.632 | 0.813 | 0.711 | |
| 19 | 30 | 30 | 988/590 | 0.632 | 0.811 | 0.71 | |
| 20 | 30 | 30 | 1000/579 | 0.63 | 0.793 | 0.703 | |
| NH | 2 | 30 | 30 | 1000/498 | 0.5 | 0.523 | 0.511 |
| 3 | 30 | 30 | 999/610 | 0.462 | 0.592 | 0.519 | |
| 4 | 30 | 30 | 1000/917 | 0.447 | 0.861 | 0.589 | |
| 5 | 30 | 30 | 1000/705 | 0.44 | 0.651 | 0.525 | |
| 6 | 30 | 30 | 996/625 | 0.509 | 0.668 | 0.578 | |
| 7 | 30 | 30 | 994/757 | 0.46 | 0.731 | 0.564 | |
| 8 | 30 | 30 | 1000/697 | 0.482 | 0.706 | 0.573 | |
| 9 | 30 | 30 | 999/697 | 0.492 | 0.721 | 0.585 | |
| 10 | 30 | 30 | 1000/632 | 0.516 | 0.685 | 0.588 | |
| 11 | 30 | 30 | 990/757 | 0.448 | 0.712 | 0.55 | |
| 12 | 30 | 30 | 996/715 | 0.487 | 0.731 | 0.584 | |
| 13 | 30 | 30 | 988/733 | 0.475 | 0.731 | 0.576 | |
| 14 | 30 | 30 | 994/745 | 0.454 | 0.71 | 0.554 | |
| 15 | 30 | 30 | 990/728 | 0.47 | 0.718 | 0.568 | |
| 16 | 30 | 30 | 992/731 | 0.453 | 0.695 | 0.548 | |
| 17 | 30 | 30 | 986/720 | 0.454 | 0.687 | 0.547 | |
| 18 | 30 | 30 | 990/709 | 0.461 | 0.687 | 0.552 | |
| 19 | 30 | 30 | 988/732 | 0.445 | 0.685 | 0.54 | |
| 20 | 30 | 30 | 1000/659 | 0.483 | 0.668 | 0.56 |
| Dataset | Regularization λ | Number of Topics k | Number of Seeds | Number of Extracted Words | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|---|
| GH | 1 | 10 | 30 | 1000/627 | 0.4 | 0.546 | 0.462 |
| 5 | 10 | 30 | 1000/695 | 0.548 | 0.828 | 0.66 | |
| 10 | 10 | 30 | 1000/650 | 0.629 | 0.889 | 0.737 | |
| 15 | 10 | 30 | 1000/640 | 0.638 | 0.887 | 0.742 | |
| 20 | 10 | 30 | 1000/595 | 0.686 | 0.887 | 0.773 | |
| 25 | 10 | 30 | 1000/595 | 0.692 | 0.896 | 0.781 | |
| 30 | 10 | 30 | 1000/591 | 0.695 | 0.893 | 0.782 | |
| 35 | 10 | 30 | 1000/593 | 0.696 | 0.898 | 0.784 | |
| NH | 1 | 10 | 30 | 1000/299 | 0.622 | 0.391 | 0.48 |
| 5 | 10 | 30 | 1000/521 | 0.528 | 0.578 | 0.552 | |
| 10 | 10 | 30 | 1000/598 | 0.505 | 0.634 | 0.562 | |
| 15 | 10 | 30 | 1000/634 | 0.503 | 0.67 | 0.575 | |
| 20 | 10 | 30 | 1000/708 | 0.49 | 0.729 | 0.586 | |
| 25 | 10 | 30 | 1000/689 | 0.498 | 0.721 | 0.589 | |
| 30 | 10 | 30 | 1000/692 | 0.503 | 0.731 | 0.596 | |
| 35 | 10 | 30 | 1000/692 | 0.5 | 0.727 | 0.592 |
| Dataset | Extracted Top Words T | Regularization λ | Number of Topics k | Number of Seeds | Number of Extracted Words | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|---|---|
| GH | 50 | 30 | 10 | 30 | 500/398 | 0.854 | 0.739 | 0.793 |
| 60 | 30 | 10 | 30 | 600/455 | 0.807 | 0.798 | 0.802 | |
| 70 | 30 | 10 | 30 | 700/498 | 0.777 | 0.841 | 0.808 | |
| 80 | 30 | 10 | 30 | 800/539 | 0.742 | 0.87 | 0.801 | |
| 90 | 30 | 10 | 30 | 900/581 | 0.711 | 0.898 | 0.793 | |
| 100 | 30 | 10 | 30 | 1000/613 | 0.68 | 0.907 | 0.777 | |
| 110 | 30 | 10 | 30 | 1100/642 | 0.659 | 0.92 | 0.768 | |
| 120 | 30 | 10 | 30 | 1200/673 | 0.633 | 0.926 | 0.752 | |
| 130 | 30 | 10 | 30 | 1300/704 | 0.608 | 0.93 | 0.735 | |
| 140 | 30 | 10 | 30 | 1400/746 | 0.582 | 0.943 | 0.72 | |
| 150 | 30 | 10 | 30 | 1500/766 | 0.569 | 0.948 | 0.711 | |
| 160 | 30 | 10 | 30 | 1600/800 | 0.546 | 0.95 | 0.694 | |
| 170 | 30 | 10 | 30 | 1700/826 | 0.531 | 0.954 | 0.683 | |
| 180 | 30 | 10 | 30 | 1800/865 | 0.509 | 0.957 | 0.664 | |
| 190 | 30 | 10 | 30 | 1900/901 | 0.491 | 0.961 | 0.65 | |
| 200 | 30 | 10 | 30 | 2000/936 | 0.473 | 0.963 | 0.635 | |
| NH | 50 | 30 | 10 | 30 | 500/464 | 0.506 | 0.494 | 0.5 |
| 60 | 30 | 10 | 30 | 600/496 | 0.538 | 0.561 | 0.549 | |
| 70 | 30 | 10 | 30 | 700/514 | 0.535 | 0.578 | 0.556 | |
| 80 | 30 | 10 | 30 | 800/577 | 0.51 | 0.618 | 0.558 | |
| 90 | 30 | 10 | 30 | 900/634 | 0.494 | 0.658 | 0.564 | |
| 100 | 30 | 10 | 30 | 1000/688 | 0.483 | 0.697 | 0.57 | |
| 110 | 30 | 10 | 30 | 1100/734 | 0.473 | 0.729 | 0.574 | |
| 120 | 30 | 10 | 30 | 1200/776 | 0.464 | 0.756 | 0.575 | |
| 130 | 30 | 10 | 30 | 1300/818 | 0.454 | 0.779 | 0.573 | |
| 140 | 30 | 10 | 30 | 1400/857 | 0.443 | 0.798 | 0.57 | |
| 150 | 30 | 10 | 30 | 1500/813 | 0.458 | 0.782 | 0.577 | |
| 160 | 30 | 10 | 30 | 1600/848 | 0.45 | 0.803 | 0.577 | |
| 170 | 30 | 10 | 30 | 1700/881 | 0.442 | 0.817 | 0.573 | |
| 180 | 30 | 10 | 30 | 1800/912 | 0.431 | 0.826 | 0.566 | |
| 190 | 30 | 10 | 30 | 1900/942 | 0.426 | 0.842 | 0.566 | |
| 200 | 30 | 10 | 30 | 2000/968 | 0.419 | 0.853 | 0.562 |
| Dataset | Number of Seeds | Regularization λ | Number of Topics k | Number of Extracted Words | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|---|
| GH | 20 | 30 | 10 | 1000/624 | 0.631 | 0.857 | 0.727 |
| 21 | 30 | 10 | 1000/598 | 0.664 | 0.863 | 0.75 | |
| 22 | 30 | 10 | 1000/613 | 0.635 | 0.846 | 0.725 | |
| 23 | 30 | 10 | 1000/627 | 0.632 | 0.861 | 0.729 | |
| 24 | 30 | 10 | 1000/611 | 0.668 | 0.887 | 0.762 | |
| 25 | 30 | 10 | 1000/556 | 0.718 | 0.867 | 0.785 | |
| 26 | 30 | 10 | 1000/583 | 0.69 | 0.874 | 0.771 | |
| 27 | 30 | 10 | 1000/625 | 0.659 | 0.896 | 0.759 | |
| 28 | 30 | 10 | 1000/577 | 0.719 | 0.902 | 0.8 | |
| 29 | 30 | 10 | 1000/614 | 0.679 | 0.907 | 0.777 | |
| 30 | 30 | 10 | 1000/613 | 0.68 | 0.907 | 0.777 | |
| NH | 20 | 30 | 10 | 1000/691 | 0.47 | 0.683 | 0.557 |
| 21 | 30 | 10 | 1000/728 | 0.442 | 0.676 | 0.535 | |
| 22 | 30 | 10 | 1000/712 | 0.426 | 0.637 | 0.51 | |
| 23 | 30 | 10 | 1000/714 | 0.431 | 0.647 | 0.518 | |
| 24 | 30 | 10 | 1000/656 | 0.485 | 0.668 | 0.562 | |
| 25 | 30 | 10 | 1000/762 | 0.419 | 0.67 | 0.515 | |
| 26 | 30 | 10 | 1000/744 | 0.458 | 0.716 | 0.559 | |
| 27 | 30 | 10 | 1000/658 | 0.473 | 0.653 | 0.549 | |
| 28 | 30 | 10 | 1000/771 | 0.454 | 0.735 | 0.561 | |
| 29 | 30 | 10 | 1000/832 | 0.431 | 0.754 | 0.549 | |
| 30 | 30 | 10 | 1000/632 | 0.516 | 0.685 | 0.588 |
References
- QasemiZadeh, B. Investigating the Use of Distributional Semantic Models for Co-Hyponym Identification in Special Corpora. Ph.D. Thesis, National University of Ireland, Galway, Ireland, 2015. [Google Scholar]
- Drouin, P.; Grabar, N.; Hamon, T.; Kageura, K.; Takeuchi, K. Computational terminology and filtering of terminological information: Introduction to the special issue. Terminology 2018, 24, 1–6. [Google Scholar]
- Fusco, F.; Staar, P.; Antognini, D. Unsupervised Term Extraction for Highly Technical Domains. arXiv 2022, arXiv:2210.13118. [Google Scholar]
- Lang, C.; Wachowiak, L.; Heinisch, B.; Gromann, D. Transforming term extraction: Transformer-based approaches to multilingual term extraction across domains. Find. Assoc. Comput. Linguist. ACL-IJCNLP 2021, 2021, 3607–3620. [Google Scholar]
- Terryn, A.R.; Hoste, V.; Lefever, E. HAMLET: Hybrid adaptable machine learning approach to extract terminology. Terminol. Int. J. Theor. Appl. Issues Spec. Commun. 2021, 27, 254–293. [Google Scholar] [CrossRef]
- Hazem, A.; Bouhandi, M.; Boudin, F.; Daille, B. Cross-lingual and cross-domain transfer learning for automatic term extraction from low resource data. In Proceedings of the Thirteenth Language Resources and Evaluation Conference, Marseille, France, 20–25 June 2022; pp. 648–662. [Google Scholar]
- Vukovic, R.; Heck, M.; Ruppik, B.M.; van Niekerk, C.; Zibrowius, M.; Gašić, M. Dialogue term extraction using transfer learning and topological data analysis. arXiv 2022, arXiv:2208.10448. [Google Scholar]
- Qin, Y.; Zheng, D.; Zhao, T.; Zhang, M. Chinese terminology extraction using EM-based transfer learning method. In Computational Linguistics and Intelligent Text Proceedings of the 14th International Conference, CICLing 2013, Samos, Greece, 24–30 March 2013; Part I; Springer: Berlin/Heidelberg, Germany, 2013; pp. 139–152. [Google Scholar] [CrossRef]
- Nugumanova, A.; Akhmed-Zaki, D.; Mansurova, M.; Baiburin, Y.; Maulit, A. NMF-based approach to automatic term extraction. Expert Syst. Appl. 2022, 199, 117179. [Google Scholar] [CrossRef]
- Febrissy, M.; Salah, A.; Ailem, M.; Nadif, M. Improving NMF clustering by leveraging contextual relationships among words. Neurocomputing 2022, 495, 105–117. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Proceedings of the Neural Information Processing Systems (NIPS), Denver, CO, USA, 1 January 2000; pp. 556–562. [Google Scholar]
- Gao, J.; He, D.; Tan, X.; Qin, T.; Wang, L.; Liu, T.Y. Representation degeneration problem in training natural language generation models. arXiv 2019, arXiv:1907.12009. [Google Scholar]
- Grootendorst, M. KeyBERT: Minimal keyword extraction with BERT. Zenodo. 2020. Version 0.8.0. Available online: https://zenodo.org/records/8388690 (accessed on 29 April 2024).
- Grootendorst, M. BERTopic: Neural topic modeling with a class-based TF-IDF procedure. arXiv 2022, arXiv:2203.05794. [Google Scholar]
- Lee, H.; Yoo, J.; Choi, S. Semi-supervised nonnegative matrix factorization. IEEE Signal Process. Lett. 2009, 17, 4–7. [Google Scholar] [CrossRef]
- Shen, B.; Makhambetov, O. Hierarchical semi-supervised factorization for learning the semantics. J. Adv. Comput. Intell. Intell. Inform. 2014, 18, 366–374. [Google Scholar] [CrossRef]
- Vangara, R.; Skau, E.; Chennupati, G.; Djidjev, H.; Tierney, T.; Smith, J.P.; Bhattarai, M.; Stanev, V.G.; Alexandrov, B.S. Semantic nonnegative matrix factorization with automatic model determination for topic modeling. In Proceedings of the 2020 19th IEEE International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 14–17 December 2020; pp. 328–335. [Google Scholar] [CrossRef]
- Vangara, R.; Bhattarai, M.; Skau, E.; Chennupati, G.; Djidjev, H.; Tierney, T.; Smith, J.P.; Stanev, V.G.; Alexandrov, B.S. Finding the number of latent topics with semantic non-negative matrix factorization. IEEE Access 2021, 9, 117217–117231. [Google Scholar] [CrossRef]
- Eren, M.E.; Solovyev, N.; Bhattarai, M.; Rasmussen, K.Ø.; Nicholas, C.; Alexandrov, B.S. SeNMFk-split: Large corpora topic modeling by semantic non-negative matrix factorization with automatic model selection. In Proceedings of the 22nd ACM Symposium on Document Engineering, San Jose, CA, USA, 20–23 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Budahazy, R.; Cheng, L.; Huang, Y.; Johnson, A.; Li, P.; Vendrow, J.; Wu, Z.; Molitor, D.; Rebrova, E.; Needell, D. Analysis of Legal Documents via Non-negative Matrix Factorization Methods. arXiv 2021, arXiv:2104.14028. [Google Scholar]
- Vendrow, J.; Haddock, J.; Rebrova, E.; Needell, D. On a guided nonnegative matrix factorization. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 3265–32369. [Google Scholar] [CrossRef]
- Li, P.; Tseng, C.; Zheng, Y.; Chew, J.A.; Huang, L.; Jarman, B.; Needell, D. Guided semi-supervised non-negative matrix factorization. Algorithms 2022, 15, 136. [Google Scholar] [CrossRef]
- Kuang, D.; Yun, S.; Park, H. SymNMF: Nonnegative low-rank approximation of a similarity matrix for graph clustering. J. Glob. Optim. 2015, 62, 545–574. [Google Scholar] [CrossRef]
- Jia, Y.; Liu, H.; Hou, J.; Kwong, S. Semisupervised adaptive symmetric non-negative matrix factorization. IEEE Trans. Cybern. 2020, 51, 2550–2562. [Google Scholar] [CrossRef] [PubMed]
- Jing, L.; Yu, J.; Zeng, T.; Zhu, Y. Semi-supervised clustering via constrained symmetric non-negative matrix factorization. In Proceedings of the Brain Informatics: International Conference, Macau, China, 4–7 December 2012; pp. 309–319. [Google Scholar] [CrossRef]
- Gadelrab, F.S.; Haggag, M.H.; Sadek, R.A. Novel semantic tagging detection algorithms based non-negative matrix factorization. SN Appl. Sci. 2020, 2, 54. [Google Scholar] [CrossRef]
- Esposito, F. A review on initialization methods for nonnegative matrix factorization: Towards omics data experiments. Mathematics 2021, 9, 1006. [Google Scholar] [CrossRef]
- Wild, S.; Curry, J.; Dougherty, A. Improving non-negative matrix factorizations through structured initialization. Pattern Recognit. 2004, 37, 2217–2232. [Google Scholar] [CrossRef]
- Nannen, V. The Paradox of Overfitting. Master’s Thesis, Faculty of Science and Engineering, Rijksuniversiteit Groningen, Groningen, The Netherlands, 2003. Available online: https://fse.studenttheses.ub.rug.nl/id/eprint/8664 (accessed on 9 May 2024).
- Pascual-Montano, A.; Carazo, J.M.; Lehmann, D.; Pascual-Marqui, R.D. Nonsmooth nonnegative matrix factorization (nsNMF). IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 403–415. [Google Scholar] [CrossRef]
- Christopher; Manning, D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar] [CrossRef]
- Bojanowski, P.; Grave, E.; Joulin, A.; Mikolov, T. Enriching word vectors with subword information. Trans. Assoc. Comput. Linguist. 2017, 5, 135–146. [Google Scholar] [CrossRef]
- Lopes, L.; Vieira, R.; Fernandes, P. Domain term relevance through tf-dcf. In Proceedings of the 2012 International Conference on Artificial Intelligence (ICAI), Las Vegas, NV, USA, 16–19 July 2012. [Google Scholar]







| docID | Words in Document | In c = China? | |
|---|---|---|---|
| Training set | 1 | Chinese Beijing Chinese | Yes |
| 2 | Chinese Chinese Shanghai | Yes | |
| 3 | Chinese Macao | Yes | |
| 4 | Tokyo Japan Chinese | No | |
| Test set | 5 | Chinese Chinese Chinese Tokyo Japan | ? |
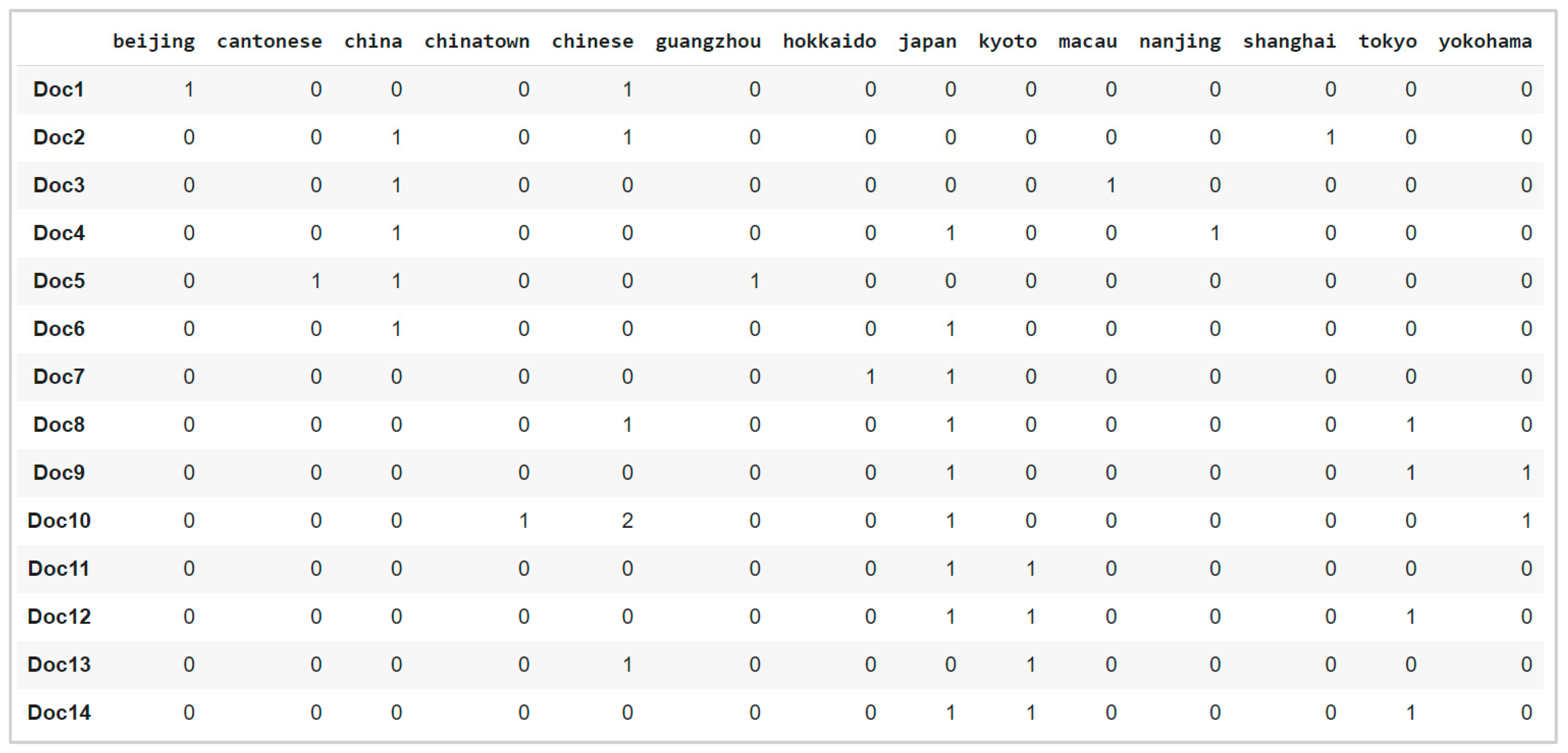
| No. | Document |
|---|---|
| 1 | Beijing, an ancient Chinese capital, is located 75 km away from the Great Wall of China. |
| 2 | Although Shanghai is not the capital of China, it is the main Chinese metropolis. |
| 3 | Macau, an autonomous territory, uniquely blends its rich cultural heritage within China, showcasing a distinct yet harmonious identity. |
| 4 | Nanjing, being a significant center for Buddhism in China, contributed to the spread of Buddhism to Japan. |
| 5 | Guangzhou, a major city in Southern China, is famed for its modern architecture and rich Cantonese heritage. |
| 6 | Over centuries, China and Japan have had extensive cultural exchanges. |
| 7 | Hokkaido, the northern island of Japan, is renowned for its stunning landscapes. |
| 8 | In Tokyo, the technology sector, known for its innovation and advancement, collaborates with Chinese expertise, contributing to the shared progress of Japan and its global partners. |
| 9 | Yokohama is the second largest city in Japan after Tokyo, with a population of 3.7 million people. |
| 10 | Yokohama Chinatown, notable for being the largest Chinese enclave in Japan, boasts a wide array of Chinese restaurants known for their exquisite cuisine. |
| 11 | Kyoto, once the capital of Japan, is celebrated for its historic temples and traditional culture. |
| 12 | Kyoto, the ancient capital of Japan before Tokyo, is renowned for its rich historical and cultural heritage. |
| 13 | Many temples and buildings in Kyoto were influenced by Chinese architecture. |
| 14 | Tokyo is a bustling metropolis, while Kyoto is a serene historical haven, both embodying diverse charm of Japan. |
| Country | GH Dataset | NH Dataset |
|---|---|---|
| China | Macau, an autonomous territory, uniquely blends its rich cultural heritage within China, showcasing a distinct yet harmonious identity. | During Confucius’s lifetime, he traveled across various Chinese states, offering advice to rulers, which later formed the basis of Confucianism. |
| Egypt | Lake Nasser was created by the construction of the Aswan High Dam across the Nile River in southern Egypt in the 1960s. | Osiris was one of the most important gods in ancient Egyptian religion, associated with kingship, death, and the afterlife. |
| Greece | Greece is known as the cradle of Western civilization, with a rich history that spans thousands of years. | In Athens, the philosopher Socrates challenged traditional notions of ethics and wisdom, sparking intellectual revolutions across Greece. |
| Iran | Tehran serves as the political, cultural, economic, and industrial center of Iran | Omar Khayyam’s contributions to mathematics and astronomy were highly regarded in cities like Nishapur, Isfahan, and Baghdad, where he studied and worked. |
| Japan | Yokohama is the second largest city in Japan after Tokyo, with a population of 3.7 million people. | Miyazaki’s love for nature is evident in many of his films, drawing inspiration from the lush forests of Yakushima Island. |
| Kazakhstan | The Irtysh is one of the longest rivers in Asia, flowing through China, Kazakhstan, and Russia. | Abai, the great Kazakh poet, was born in the village located in the Semey region of Kazakhstan. |
| Mongolia | The Gandan Monastery, located in Ulaanbaatar, is one of Mongolia’s most important Buddhist monasteries and a center for religious and cultural activities. | Subutai’s military genius made him one of the most feared and respected commanders of his time, leaving a legacy in Mongol and military history. |
| Russia | The Volga River is the longest river in Europe, flowing through central Russia for over 3500 km. | Turgenev’s masterpiece, “Fathers and Sons”, reflects the tensions between generations and the changing social landscape of 19th-century Russia. |
| Turkey | The capital and second-largest city of Turkey is Ankara. | Sultan Suleiman was born in 1494 in Trabzon, a city located on the northeastern coast of Turkey. |
| Uzbekistan | Khiva is an ancient city located in the western part of Uzbekistan, in the region of Khorezm. | Khiva, located along the Silk Road, was a hub of trade and exchange, influencing Al-Khwarizmi’s understanding of geography and navigation. |
| Country | GH Dataset | NH Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| Number of Sentences | Average Length of Sentences | Number of Terms Occurrences | Number of Unique Terms | Number of Sentences | Average Length of Sentences | Number of Terms Occurrences | Number of Unique Terms | |
| China | 100 | 20 | 302 | 85 | 100 | 20 | 166 | 40 |
| Egypt | 100 | 21 | 294 | 58 | 100 | 22 | 118 | 36 |
| Greece | 100 | 21 | 283 | 65 | 100 | 22 | 123 | 54 |
| Iran | 100 | 17 | 281 | 66 | 100 | 22 | 171 | 63 |
| Japan | 100 | 20 | 235 | 46 | 100 | 19 | 131 | 35 |
| Kazakhstan | 100 | 17 | 390 | 62 | 100 | 22 | 143 | 59 |
| Mongolia | 100 | 18 | 360 | 59 | 100 | 23 | 174 | 57 |
| Russia | 100 | 26 | 295 | 72 | 100 | 21 | 152 | 58 |
| Turkey | 100 | 17 | 271 | 57 | 100 | 20 | 161 | 46 |
| Uzbekistan | 100 | 23 | 436 | 83 | 100 | 22 | 226 | 47 |
| Total | 1000 | - | 3147 | 653/461 | 1000 | - | 1183 | 495/476 |
| GH Dataset | NH Dataset | |||
|---|---|---|---|---|
| Word | Frequency | Word | Frequency | |
| 1 | City | 136 | Born | 159 |
| 2 | Located | 119 | City | 116 |
| 3 | Known | 115 | Ancient | 99 |
| 4 | River | 102 | One | 81 |
| 5 | Ancient | 99 | Known | 71 |
| 6 | One | 93 | Located | 58 |
| 7 | Region | 90 | Around | 52 |
| 8 | Sea | 90 | Chinese | 51 |
| 9 | Cultural | 88 | Legacy | 48 |
| 10 | Including | 79 | Kazakh | 48 |
| Class (Country) | GH Dataset | NH Dataset | ||
|---|---|---|---|---|
| 2 Seed Words per Class | 3 Seed Words per Class | 2 Seed Words per Class | 3 Seed Words per Class | |
| China | China, Beijing | China, Beijing, Shanghai | Confucius, Mao | Confucius, Mao, Laozi |
| Egypt | Egypt, Cairo | Egypt, Cairo, Alexandria | Cleopatra, Osiris | Cleopatra, Osiris, Imhotep |
| Greece | Greece, Athens | Greece, Athens, Olympus | Zeus, Socrates | Zeus, Socrates, Aristotle |
| Iran | Iran, Isfahan | Iran, Tehran, Isfahan | Omar, Avicenna | Omar, Avicenna, Hafez |
| Japan | Japan, Tokyo | Japan, Kyoto, Tokyo | Toyoda, Hokusai | Toyoda, Hokusai, Hanyu |
| Kazakhstan | Kazakh, Almaty | Kazakh, Almaty, Astana | Abai, al-Farabi | Abai, al-Farabi, Tomyris |
| Mongolia | Mongolia, Ulaanbaatar | Mongolia, Ulaanbaatar, Gobi | Chingis, Chagatai | Chingis, Chagatai, Kublai |
| Russia | Russia, Moscow | Russia, Moscow, Petersburg | Pushkin, Gagarin | Pushkin, Gagarin, Lomonosov |
| Turkey | Turkey, Istanbul | Turkey, Istanbul, Ankara | Suleiman, Erdogan | Suleiman, Erdogan, Ataturk |
| Uzbekistan | Uzbek, Tashkent | Uzbek, Tashkent, Samarkand | al-Khwarizmi, Babur | al-Khwarizmi, Babur, Navoi |
| Setup | Regularization λ | Number of Seeds | Use of Anti-Seeds | ||
|---|---|---|---|---|---|
| 1 | 10 | 30 | 70 | 20 | No |
| 2 | 10 | 30 | 70 | 30 | No |
| 3 | 10 | 30 | 70 | 20 | Yes |
| 4 | 10 | 30 | 70 | 30 | Yes |
| Dataset | Baseline Methods | Number of Extracted Words | Number of True Terms | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| GH | Standard NMF | 700/440 | 462 | 29.8 | 28.5 | 29.1 |
| BERTopic | 700/495 | 42.6 | 45.9 | 44.2 | ||
| KeyBERT | 2000/633 | 52 | 71.5 | 60.2 | ||
| NH | Standard NMF | 700/488 | 476 | 19.1 | 19.5 | 19.3 |
| BERTopic | 700/568 | 25.7 | 30.7 | 28 | ||
| KeyBERT | 2000/853 | 44.9 | 80.5 | 57.6 |
| Dataset | Setup | Number of Extracted Words | Number of True Terms | Precision | Recall | F1-Score |
|---|---|---|---|---|---|---|
| GH | 1 (20 + no) | 700/406 | 462 | 77.8 | 68.7 | 73 |
| 2 (30 + no) | 700/459 | 80 | 79.8 | 79.9 | ||
| 3 (20 + yes) | 700/371 | 84.4 | 68 | 75.3 | ||
| 4 (30 + yes) | 700/453 | 80.8 | 79.6 | 80.2 | ||
| NH | 1 (20 + no) | 700/585 | 476 | 46.7 | 57.4 | 51.5 |
| 2 (30 + no) | 700/609 | 48.1 | 61.6 | 54 | ||
| 3 (20 + yes) | 700/526 | 51.9 | 57.4 | 54.5 | ||
| 4 (30 + yes) | 700/551 | 52.5 | 60.7 | 56.3 |
| Approach | GH | NH | ||||
|---|---|---|---|---|---|---|
| Precision | Recall | F1-Score | Precision | Recall | F1-Score | |
| Semantic NMF | 80.8 | 79.6 | 80.2 | 47.4 | 77.7 | 58.9 |
| KeyBERT | 52 | 71.5 | 60.2 | 44.9 | 80.5 | 57.6 |
| Standard NMF | 29.8 | 28.5 | 29.1 | 17.2 | 48.9 | 25.5 |
| BERTopic | 42.6 | 45.9 | 44.2 | 22.3 | 49.2 | 30.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nugumanova, A.; Alzhanov, A.; Mansurova, A.; Rakhymbek, K.; Baiburin, Y. Semantic Non-Negative Matrix Factorization for Term Extraction. Big Data Cogn. Comput. 2024, 8, 72. https://doi.org/10.3390/bdcc8070072
Nugumanova A, Alzhanov A, Mansurova A, Rakhymbek K, Baiburin Y. Semantic Non-Negative Matrix Factorization for Term Extraction. Big Data and Cognitive Computing. 2024; 8(7):72. https://doi.org/10.3390/bdcc8070072
Chicago/Turabian StyleNugumanova, Aliya, Almas Alzhanov, Aiganym Mansurova, Kamilla Rakhymbek, and Yerzhan Baiburin. 2024. "Semantic Non-Negative Matrix Factorization for Term Extraction" Big Data and Cognitive Computing 8, no. 7: 72. https://doi.org/10.3390/bdcc8070072
APA StyleNugumanova, A., Alzhanov, A., Mansurova, A., Rakhymbek, K., & Baiburin, Y. (2024). Semantic Non-Negative Matrix Factorization for Term Extraction. Big Data and Cognitive Computing, 8(7), 72. https://doi.org/10.3390/bdcc8070072






