Survey on Coverage Path Planning with Unmanned Aerial Vehicles
Abstract
:1. Introduction
1.1. UAV Classification
1.2. Overview of the Existing Surveys
1.3. Motivation of This Review
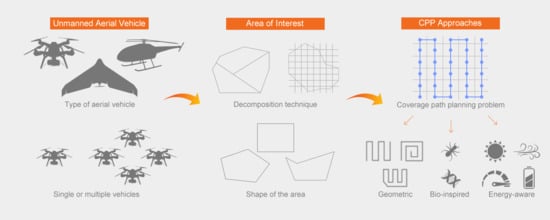
2. Coverage Path Planning
2.1. Area of Interest
2.2. Cellular Decomposition
2.3. Performance Metrics
2.4. Information Availability
3. No Decomposition
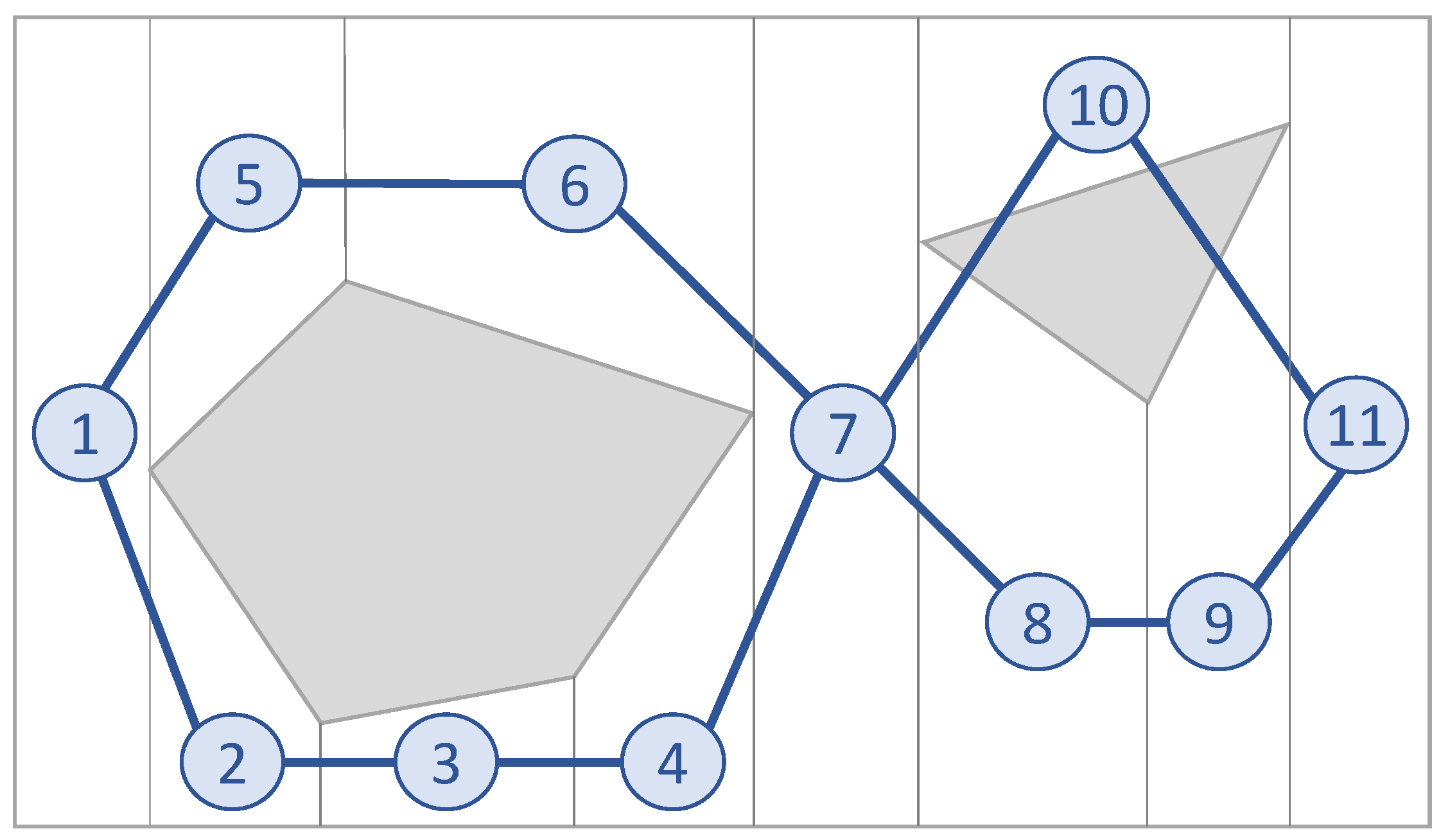
4. Exact Cellular Decomposition
4.1. Single Strategies
4.2. Cooperative Strategies
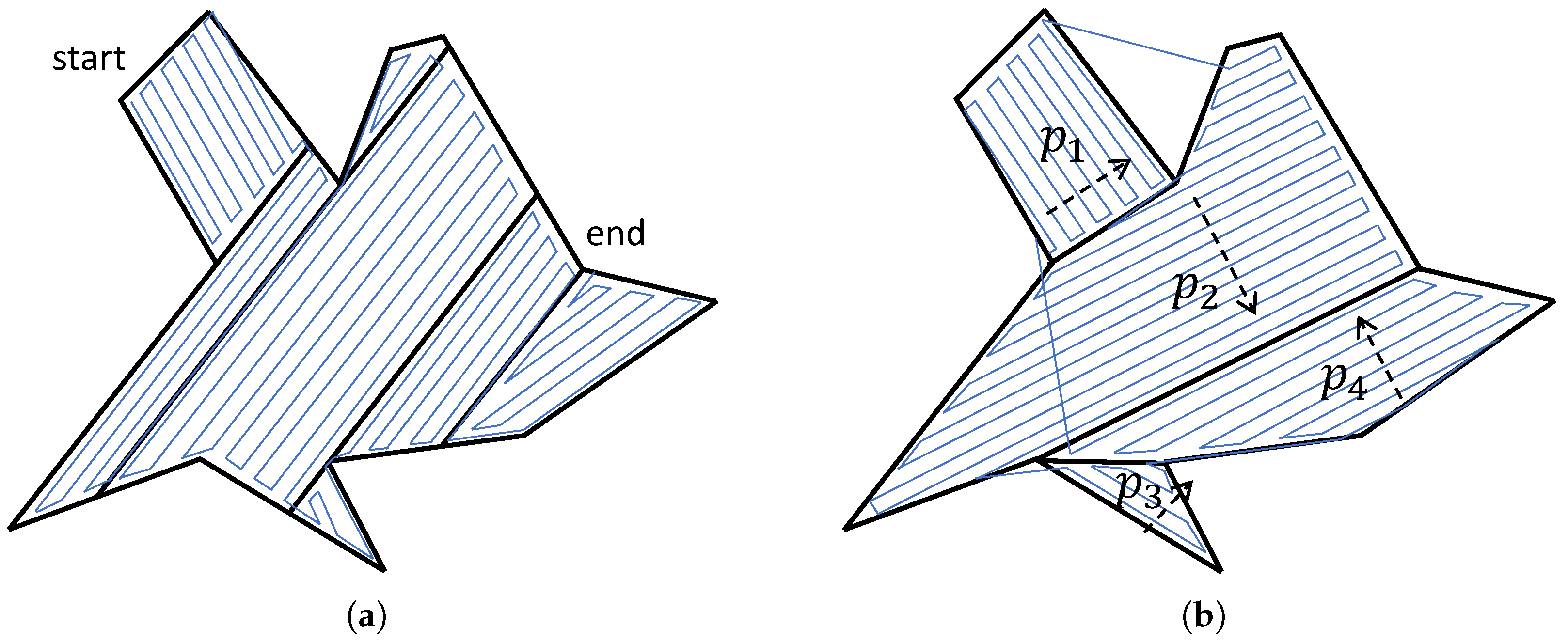
4.2.1. Back-and-Forth
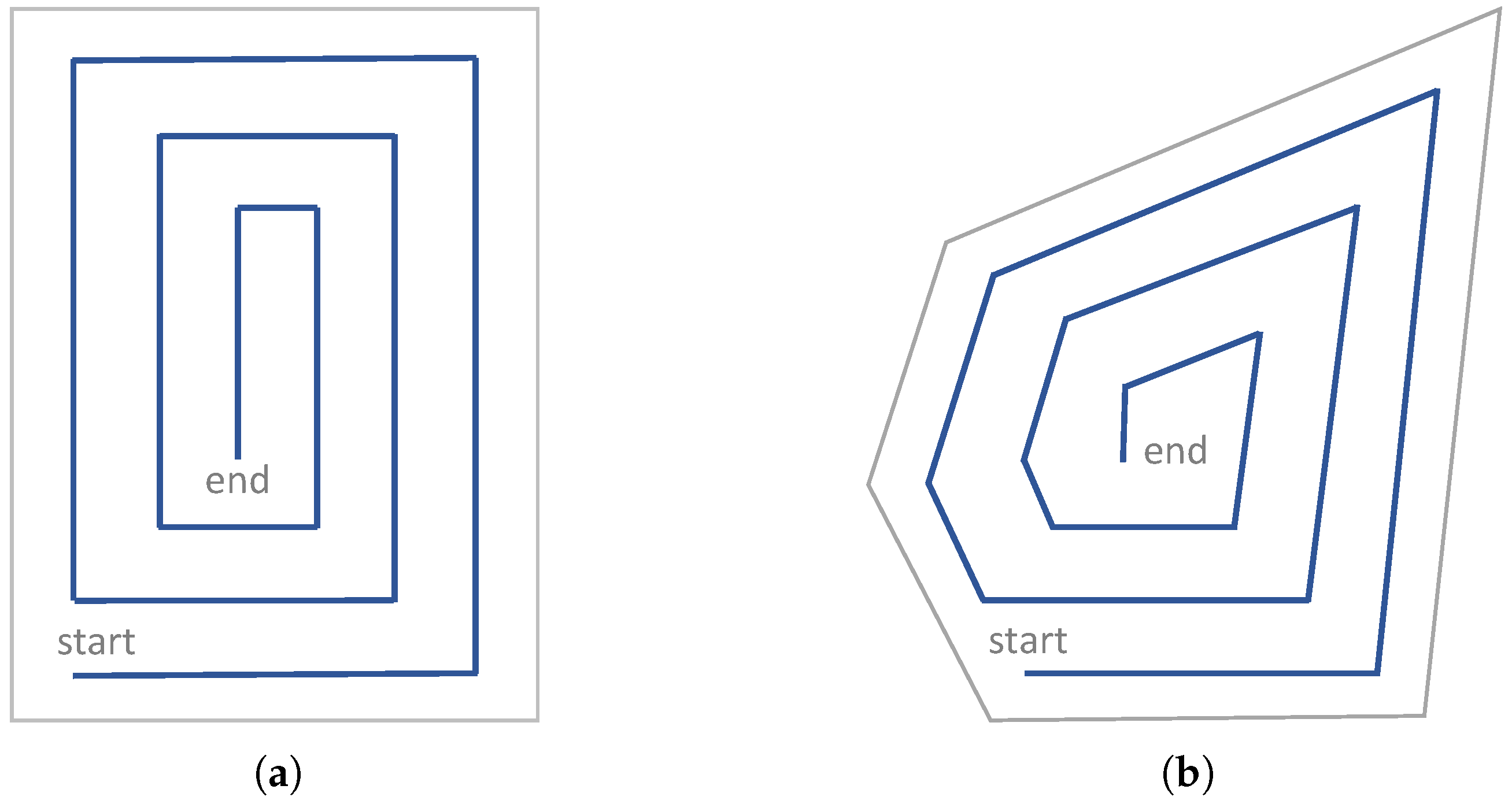
4.2.2. Spiral
4.2.3. Line Formation
4.2.4. Decentralized Technique
4.2.5. Local Priority
5. Approximate Cellular Decomposition
5.1. Full Information
5.2. Partial Information
5.2.1. Pheromone-Based Methods
5.2.2. Real-Time Search Methods
5.2.3. Random Walk
5.2.4. Cellular Automata
5.2.5. Coverage with Uncertainty
5.2.6. Genetic Algorithm
5.2.7. Ant Colony Optimization
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Basilico, N.; Carpin, S. Deploying Teams of Heterogeneous UAVs in Cooperative Two-level Surveillance Missions. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 610–615. [Google Scholar]
- Lottes, P.; Khanna, R.; Pfeifer, J.; Siegwart, R.; Stachniss, C. UAV-Based Crop and Weed Classification for Smart Farming. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3024–3031. [Google Scholar]
- Cesetti, A.; Frontoni, E.; Mancini, A.; Ascani, A.; Zingaretti, P.; Longhi, S. A visual global positioning system for unmanned aerial vehicles used in photogrammetric applications. J. Intell. Robot. Syst. 2011, 61, 157–168. [Google Scholar] [CrossRef]
- Maza, I.; Caballero, F.; Capitán, J.; Martínez-de Dios, J.R.; Ollero, A. Experimental results in multi-UAV coordination for disaster management and civil security applications. J. Intell. Robot. Syst. 2011, 61, 563–585. [Google Scholar] [CrossRef]
- Pham, H.X.; La, H.M.; Feil-Seifer, D.; Deans, M. A Distributed Control Framework for A Team of Unmanned Aerial. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6648–6653. [Google Scholar]
- Renzaglia, A.; Reymann, C.; Lacroix, S. Monitoring the Evolution of Clouds with UAVs. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 278–283. [Google Scholar]
- Guerrero, J.A.; Bestaoui, Y. UAV path planning for structure inspection in windy environments. J. Intell. Robot. Syst. 2013, 69, 297–311. [Google Scholar] [CrossRef]
- Chang, W.; Yang, G.; Yu, J.; Liang, Z.; Cheng, L.; Zhou, C. Development of A Power Line Inspection Robot with Hybrid Operation modes. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September; pp. 973–978.
- Choset, H. Coverage for robotics—A survey of recent results. Ann. Math. Artif. Intell. 2001, 113–126. [Google Scholar] [CrossRef]
- Barrientos, A.; Colorado, J.; del Cerro, J.; Martinez, A.; Rossi, C.; Sanz, D.; Valente, J. Aerial remote sensing in agriculture: A practical approach to area. J. Field Robot. 2011, 28, 667–689. [Google Scholar] [CrossRef]
- Alvarenga, J.; Vitzilaios, N.I.; Valavanis, K.P.; Rutherford, M.J. Survey of unmanned helicopter model-based navigation and control techniques. J. Intell. Robot. Syst. 2015, 80, 87–138. [Google Scholar] [CrossRef]
- Kanellakis, C.; Nikolakopoulos, G. Survey on computer vision for UAVs: Current developments and trends. J. Intell. Robot. Syst. 2017, 87, 141–168. [Google Scholar] [CrossRef]
- Saeed, A.S.; Younes, A.B.; Islam, S.; Dias, J.; Seneviratne, L.; Cai, G. A Review on the Platform Design, Dynamic Modeling and Control of Hybrid UAVs. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 806–815. [Google Scholar]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Hoffer, N.V.; Coopmans, C.; Jensen, A.M.; Chen, Y. A survey and categorization of small low-cost unmanned aerial vehicle system identification. J. Intell. Robot. Syst. 2014, 74, 129–145. [Google Scholar] [CrossRef]
- Goerzen, C.; Kong, Z.; Mettler, B. A survey of motion planning algorithms from the perspective of autonomous UAV guidance. J. Intell. Robot. Syst. 2010, 57, 65. [Google Scholar] [CrossRef]
- Dadkhah, N.; Mettler, B. Survey of motion planning literature in the presence of uncertainty: Considerations for UAV guidance. J. Intell. Robot. Syst. 2012, 65, 233–246. [Google Scholar] [CrossRef]
- Kanistras, K.; Martins, G.; Rutherford, M.J.; Valavanis, K.P. A Survey of Unmanned Aerial Vehicles (UAVs) for Traffic Monitoring. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 221–234. [Google Scholar]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef] [Green Version]
- Gautam, A.; Sujit, P.; Saripalli, S. A Survey of Autonomous Landing Techniques for UAVs. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 1210–1218. [Google Scholar]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef] [Green Version]
- Juliá, M.; Gil, A.; Reinoso, O. A comparison of path planning strategies for autonomous exploration and mapping of unknown environments. Autonomous Robots 2012, 33, 427–444. [Google Scholar] [CrossRef]
- McFerran, D.; Swider, M. The Best Drone 2018: DJI, Parrot and More for Beginners and Pros. Available online: https://www.techradar.com/news/best-drones (accessed on 9 August 2018).
- Di Franco, C.; Buttazzo, G. Energy-Aware Coverage Path Planning of UAVs. In Proceedings of the IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Vila Real, Portugal, 8–10 April 2015; pp. 111–117. [Google Scholar]
- Di Franco, C.; Buttazzo, G. Coverage path planning for UAVs photogrammetry with energy and resolution constraints. J. Intell. Robot. Systems 2016, 1–18. [Google Scholar] [CrossRef]
- Ware, J.; Roy, N. An Analysis of Wind Field Estimation and Exploitation for Quadrotor Flight in the Urban Canopy Layer. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1507–1514. [Google Scholar]
- Kakaes, K.; Greenwood, F.; Lippincott, M.; Dosemagen, S.; Meier, P.; Wich, S. Drones and Aerial Observation: New Technologies for Property Rights, Human Rights, and Global Development: A Primer; New America: Washington, DC, USA, 2015; pp. 6–103. [Google Scholar]
- Sampaio, P.A.; da Silva Sousa, R.; Rocha, A.N. Reducing the range of perception in multi-agent patrolling strategies. J. Intell. Robot. Syst. 2018, 91, 219–231. [Google Scholar] [CrossRef]
- Öst, G. Search Path Generation with UAV Applications Using Approximate Convex Decomposition. Master’s Thesis, Linköpings Universitet, Linköpings, Sweden, 2012. [Google Scholar]
- Xu, A.; Viriyasuthee, C.; Rekleitis, I. Optimal Complete Terrain Coverage Using An Unmanned Aerial Vehicle. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2513–2519. [Google Scholar]
- Artemenko, O.; Dominic, O.J.; Andryeyev, O.; Mitschele-Thiel, A. Energy-Aware Trajectory Planning for the Localization of Mobile Devices Using an Unmanned Aerial Vehicle. In Proceedings of the 2016 25th International Conference on Computer Communication and Networks (ICCCN), Waikoloa, HI, USA, 1–4 August 2016; pp. 1–9. [Google Scholar]
- Valente, J.; Sanz, D.; Del Cerro, J.; Barrientos, A.; de Frutos, M.Á. Near-optimal coverage trajectories for image mosaicing using a mini quad-rotor over irregular-shaped fields. Prec. Agric. 2013, 14, 115–132. [Google Scholar] [CrossRef]
- Li, D.; Wang, X.; Sun, T. Energy-optimal coverage path planning on topographic map for environment survey with unmanned aerial vehicles. Electron. Lett. 2016, 52, 699–701. [Google Scholar] [CrossRef]
- Maza, I.; Ollero, A. Multiple UAV cooperative searching operation using polygon area decomposition and efficient coverage algorithms. In Distributed Autonomous Robotic Systems 6; Springer: Berlin, Germany, 2007; pp. 221–230. [Google Scholar]
- Torres, M.; Pelta, D.A.; Verdegay, J.L.; Torres, J.C. Coverage path planning with unmanned aerial vehicles for 3D terrain reconstruction. Expert Syst. Appl. 2016, 55, 441–451. [Google Scholar] [CrossRef]
- Nattero, C.; Recchiuto, C.T.; Sgorbissa, A.; Wanderlingh, F. Coverage Algorithms for Search and Rescue with UAV Drones. In Proceedings of the Workshop of the XIII AI*IA Symposium on Artificial Intelligence, Pisa, Italy, 10–12 December 2014. [Google Scholar]
- Oborne, M. Mission Planner-Ground Station. Available online: http://planner.ardupilot.com (accessed on 15 October 2015).
- Andersen, H.L. Path Planning for Search and Rescue Mission Using Multicopters. Master’s Thesis, Institutt for Teknisk Kybernetikk, Trondheim, Norway, 2014. [Google Scholar]
- Coombes, M.; Chen, W.H.; Liu, C. Boustrophedon Coverage Path Planning for UAV Aerial Surveys in Wind. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1563–1571. [Google Scholar]
- Cabreira, T.M.; Di Franco, C.; Ferreira, P.R., Jr.; Buttazzo, G.C. Energy-Aware Spiral Coverage Path Planning for UAV Photogrammetric Applications. IEEE Robot. Autom. Lett. 2018, 3, 3662–3668. [Google Scholar] [CrossRef]
- Forsmo, E.J.; Grøtli, E.I.; Fossen, T.I.; Johansen, T.A. Optimal Search Mission with Unmanned Aerial Vehicles Using Mixed Iintege rLinear Programming. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 253–259. [Google Scholar]
- Ahmadzadeh, A.; Keller, J.; Pappas, G.; Jadbabaie, A.; Kumar, V. An Optimization-Based Approach to Time-Critical Cooperative Surveillance and Coverage with UAVs. In Experimental Robotics; Springer: Berlin, Germany, 2008; pp. 491–500. [Google Scholar]
- Jiao, Y.S.; Wang, X.M.; Chen, H.; Li, Y. Research on the Coverage Path Planning of UAVs for Polygon Areas. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; pp. 1467–1472. [Google Scholar]
- Li, Y.; Chen, H.; Er, M.J.; Wang, X. Coverage path planning for UAVs based on enhanced exact cellular decomposition method. Mechatron. Spec. Issue Dev. Auton. Unmanned Aer. Veh. 2011, 21, 876–885. [Google Scholar] [CrossRef]
- Levcopoulos, C.; Krznaric, D. Quasi-Greedy Triangulations Approximating the Minimum Weight Triangulation. Journal of Algorithms 1998, 27, 303–338. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.H. Optimal Line-sweep-based Decompositions for Coverage Algorithms. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; Volume 1, pp. 27–32. [Google Scholar]
- Coombes, M.; Fletcher, T.; Chen, W.H.; Liu, C. Optimal polygon decomposition for UAV survey coverage path planning in wind. Sensors 2018, 18, 2132. [Google Scholar] [CrossRef] [PubMed]
- Xu, A.; Viriyasuthee, C.; Rekleitis, I. Efficient complete coverage of a known arbitrary environment with applications to aerial operations. Auton. Robots 2014, 36, 365–381. [Google Scholar] [CrossRef]
- Choset, H.; Pignon, P. Coverage Path Planning: The Boustrophedon Cellular Decomposition. In Field and Service Robotics; Springer: Berlin, Germany, 1998; pp. 203–209. [Google Scholar] [Green Version]
- Kallmann, M.; Bieri, H.; Thalmann, D. Fully Dynamic Constrained Delaunay Triangulations. In Geometric Modeling for Scientific Visualization; Springer: Berlin, Germany, 2004; pp. 241–257. [Google Scholar] [Green Version]
- Balampanis, F.; Maza, I.; Ollero, A. Area Decomposition, Partition and Coverage with Multiple Remotely Piloted Aircraft Systems Operating in Coastal Regions. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 275–283. [Google Scholar]
- Balampanis, F.; Maza, I.; Ollero, A. Area partition for coastal regions with multiple UAS. J. Intell. Robot. Syst. 2017, 88, 751–766. [Google Scholar] [CrossRef]
- Rineau, L. CGAL—2D Conforming Triangulations and Meshes—2.5 Optimization of Meshes with Lloyd. Available online: https://doc.cgal.org/latest/Mesh_2/index.html#secMesh_2_optimization (accessed on 15 August 2018).
- Balampanis, F.; Maza, I.; Ollero, A. Coastal areas division and coverage with multiple UAVs for remote sensing. Sensors 2017, 17, 808. [Google Scholar] [CrossRef]
- Balampanis, F.; Maza, I.; Ollero, A. Spiral-like Coverage Path Planning for Multiple Heterogeneous UAS Operating in Coastal Regions. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 617–624. [Google Scholar]
- Vincent, P.; Rubin, I. A Framework and Analysis for Cooperative Search Using UAV Swarms. In Proceedings of the A Framework and Analysis for Cooperative Search Using UAV Swarms, Nicosia, Cyprus, 14–17 March 2004; pp. 79–86. [Google Scholar]
- Acevedo, J.J.; Arrue, B.C.; Maza, I.; Ollero, A. Cooperative large area surveillance with a team of aerial mobile robots for long endurance missions. J. Intell. Robot. Syst. 2013, 70, 329–345. [Google Scholar] [CrossRef]
- Acevedo, J.J.; Arrue, B.C.; Maza, I.; Ollero, A. Distributed approach for coverage and patrolling missions with a team of heterogeneous aerial robots under communication constraints. Int. J. Adv. Robot. Syst. 2013, 10. [Google Scholar] [CrossRef]
- Acevedo, J.J.; Arrue, B.C.; Diaz-Bañez, J.M.; Ventura, I.; Maza, I.; Ollero, A. One-to-one coordination algorithm for decentralized area partition in surveillance missions with a team of aerial robots. J. Intell. Robot. Syst. 2014, 74, 269–285. [Google Scholar] [CrossRef]
- Araujo, J.; Sujit, P.; Sousa, J.B. Multiple UAV Area Decomposition and Coverage. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA), Singapore, 16–19 April 2013; pp. 30–37. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Nam, L.; Huang, L.; Li, X.; Xu, J. An Approach for Coverage Path Planning for UAVs. In Proceedings of the 2016 IEEE 14th International Workshop on Advanced Motion Control (AMC), Auckland, New Zealand, 22–24 April 2016; pp. 411–416. [Google Scholar]
- Bouzid, Y.; Bestaoui, Y.; Siguerdidjane, H. Quadrotor-UAV Optimal Coverage Path Planning in Cluttered Environment with A Limited Onboard Energy. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 979–984. [Google Scholar]
- Valente, J.; Cerro, J.D.; Barrientos, A.; Sanz, D. Aerial coverage optimization in precision agriculture management: A musical harmony inspired approach. Comput. Electron. Agric. 2013, 99, 153–159. [Google Scholar] [CrossRef] [Green Version]
- Sadat, S.A.; Wawerla, J.; Vaughan, R.T. Recursive Non-Uniform Coverage of Unknown Terrains for UAVs. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1742–1747. [Google Scholar]
- Sadat, S.A.; Wawerla, J.; Vaughan, R. Fractal Trajectories for Online Non-Uniform Aerial Coverage. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2971–2976. [Google Scholar]
- Santamaria, E.; Segor, F.; Tchouchenkov, I. Rapid Aerial Mapping with Multiple Heterogeneous Unmanned Vehicles. In Proceedings of the 10th International Conference on Information Systems for Crisis Response and Management (ISCRAM), Baden-Baden, Germany, 12–15 May 2013. [Google Scholar]
- Segor, F.; Bürkle, A.; Partmann, T.; Schönbein, R. Mobile Ground Control Station for Local Surveillance. In Proceedings of the 2010 Fifth International Conference on Systems, Menuires, France, 11–16 April 2010; pp. 152–157. [Google Scholar]
- Pfeifer, R.; Lungarella, M.; Iida, F. Self-organization, embodiment, and biologically inspired robotics. Science 2007, 318, 1088–1093. [Google Scholar] [CrossRef]
- Floreano, D.; Mattiussi, C. Bio-Inspired Artificial Intelligence: Theories, Methods, and Technologies; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Albani, D.; Nardi, D.; Trianni, V. Field Coverage and Weed Mapping by UAV Swarms. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 4319–4325. [Google Scholar]
- Zelenka, J.; Kasanicky, T. Insect Pheromone Strategy for the Robots Coordination. Appl. Mech. Mater. 2014, 613, 163–171. [Google Scholar] [CrossRef]
- Zelenka, J.; Kasanicky, T. Insect Pheromone Strategy for the Robots Coordination: Reaction on Loss Communication. In Proceedings of the 2014 IEEE 15th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 19–21 November 2014; pp. 79–83. [Google Scholar]
- Zelenka, J.; Kasanicky, T. Outdoor UAV Control and Coordination System Supported by Biological Inspired Method. In Proceedings of the 2014 23rd International Conference on Robotics in Alpe-Adria-Danube Region (RAAD), Smolenice, Slovakia, 3–5 September 2014; pp. 1–7. [Google Scholar]
- Paradzik, M.; İnce, G. Multi-Agent Search Strategy Based on Digital Pheromones for UAVs. In Proceedings of the 24th IEEE Signal Processing and Communication Application Conference (SIU), Zonguldak, Turkey, 16–19 May 2016; pp. 233–236. [Google Scholar]
- Trujillo, M.M.; Darrah, M.; Speransky, K.; DeRoos, B.; Wathen, M. Optimized Flight Path for 3D Mapping of An Area with Structures Using A Multirotor. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 905–910. [Google Scholar]
- Cheng, C.T.; Fallahi, K.; Leung, H.; Chi, K.T. Cooperative Path Planner for UAVs Using ACO Algorithm with Gaussian Distribution Functions. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 173–176. [Google Scholar]
- Kuiper, E.; Nadjm-Tehrani, S. Mobility Models for UAV Group Reconnaissance Applications. In Proceedings of the 2006 International Conference on Wireless and Mobile Communications (ICWMC’06), Bucharest, Romania, 29–31 July 2006; p. 33. [Google Scholar]
- Rosalie, M.; Danoy, G.; Chaumette, S.; Bouvry, P. From Random Process to Chaotic Behavior in Swarms of UAVs. In Proceedings of the 6th ACM Symposium on Development and Analysis of Intelligent Vehicular Networks and Applications, Malta, Malta, 13–17 November 2016. [Google Scholar]
- Khan, A.; Yanmaz, E.; Rinner, B. Information Merging in Multi-UAV Cooperative Search. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 3122–3129. [Google Scholar]
- Lim, S.; Bang, H. Waypoint planning algorithm using cost functions for surveillance. Int. J. Aeronaut. Space Sci. 2010, 11, 136–144. [Google Scholar] [CrossRef]
- Popović, M.; Hitz, G.; Nieto, J.; Sa, I.; Siegwart, R.; Galceran, E. Online Informative Path Planning for Active Classification Using UAVs. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5753–5758. [Google Scholar]
- Popovic, M.; Vidal-Calleja, T.; Hitz, G.; Sa, I.; Siegwart, R.; Nieto, J. Multiresolution mapping and informative path planning for UAV-based terrain monitoring. arXiv, 2017; arXiv:1703.02854. [Google Scholar]
- Ramasamy, M.; Ghose, D. Learning-Based Preferential Surveillance Algorithm for Persistent Surveillance by Unmanned Aerial Vehicles. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 1032–1040. [Google Scholar]
- Ramasamy, M.; Ghose, D. A heuristic learning algorithm for preferential area surveillance by unmanned aerial vehicles. J. Intell. Robot. Syst. 2017, 88, 655–681. [Google Scholar] [CrossRef]
- Koenig, S.; Liu, Y. Terrain Coverage with Ant Robots: A Simulation Study. In Proceedings of the Fifth International Conference on Autonomous Agents, Montreal, QC, Canada, 28 May–1 June 2001; pp. 600–607. [Google Scholar]
- Sauter, J.A.; Matthews, R.; Van Dyke Parunak, H.; Brueckner, S.A. Performance of Digital Pheromones for Swarming Vehicle Control. In Proceedings of the Fourth International Joint Conference On Autonomous Agents and Multiagent Systems, Utrecht, The Netherlands, 25–29 July 2005; pp. 903–910. [Google Scholar]
- Famouri, M.; Hamzeh, A. A New Complete Heuristic Approach for Ant Rendezvous Problem. In Proceedings of the 2014 4th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 29–30 October 2014; pp. 364–369. [Google Scholar]
- Koenig, S.; Simmons, R.G. Easy and Hard Testbeds for Real-Time Search Algorithms. In Proceedings of the Thirteenth National Conference on Artificial Intelligence (AAAI/IAAI), Portland, OR, USA, 4–8 August 1996; Volume 1, pp. 279–285. [Google Scholar]
- Cannata, G.; Sgorbissa, A. A minimalist algorithm for multirobot continuous coverage. IEEE Trans. Robot. 2011, 27, 297–312. [Google Scholar] [CrossRef]
- Pirzadeh, A.; Snyder, W. A Unified Solution to Coverage and Search in Explored and Unexplored Terrains Using Indirect Control. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 2113–2119. [Google Scholar]
- Korf, R.E. Real-time heuristic search. Artif. Intell. 1990, 42, 189–211. [Google Scholar] [CrossRef] [Green Version]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An Open-Source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 17 May 2009; Volume 3, p. 5. [Google Scholar]
- Piaggio, M.; Sgorbissa, A.; Zaccaria, R. Programming Real-time Distributed Multiple Robotic Systems. In Robot Soccer World Cup; Springer: Berlin, Germany, 1999; pp. 412–423. [Google Scholar]
- Lim, S.; Bang, H. Waypoint Guidance of Cooperative UAVs for Intelligence, Surveillance, and Reconnaissance. In Proceedings of the 2009 IEEE International Conference on Control and Automation, Christchurch, New Zealand, 9–11 December 2009; pp. 291–296. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis With Applications to Biology, Control, and Artificial Intelligence; U Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Darrah, M.; Trujillo, M.M.; Speransky, K.; Wathen, M. Optimized 3D Mapping of A Large Area with Structures Using Multiple Multirotors. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 716–722. [Google Scholar]
- Hayat, S.; Yanmaz, E.; Brown, T.X.; Bettstetter, C. Multi-Objective UAV Path Planning for Search and Rescue. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Piscataway, NJ, USA, 29 May–3 June 2017; pp. 5569–5574. [Google Scholar]
- Rosalie, M.; Dentler, J.E.; Danoy, G.; Bouvry, P.; Kannan, S.; Olivares-Mendez, M.A.; Voos, H. Area Exploration with A Swarm of UAVs Combining Deterministic Chaotic Ant Colony Mobility with Position MPC. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1392–1397. [Google Scholar]
- Rohmer, E.; Singh, S.P.; Freese, M. V-REP: A Versatile and Scalable Robot Simulation Framework. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1321–1326. [Google Scholar]
- Acevedo, J.J.; Arrue, B.C.; Maza, I.; Ollero, A. Distributed Cooperation of Multiple UAVs for Area Monitoring Missions. In Motion and Operation Planning of Robotic Systems; Springer: Berlin, Germany, 2015; pp. 471–494. [Google Scholar]










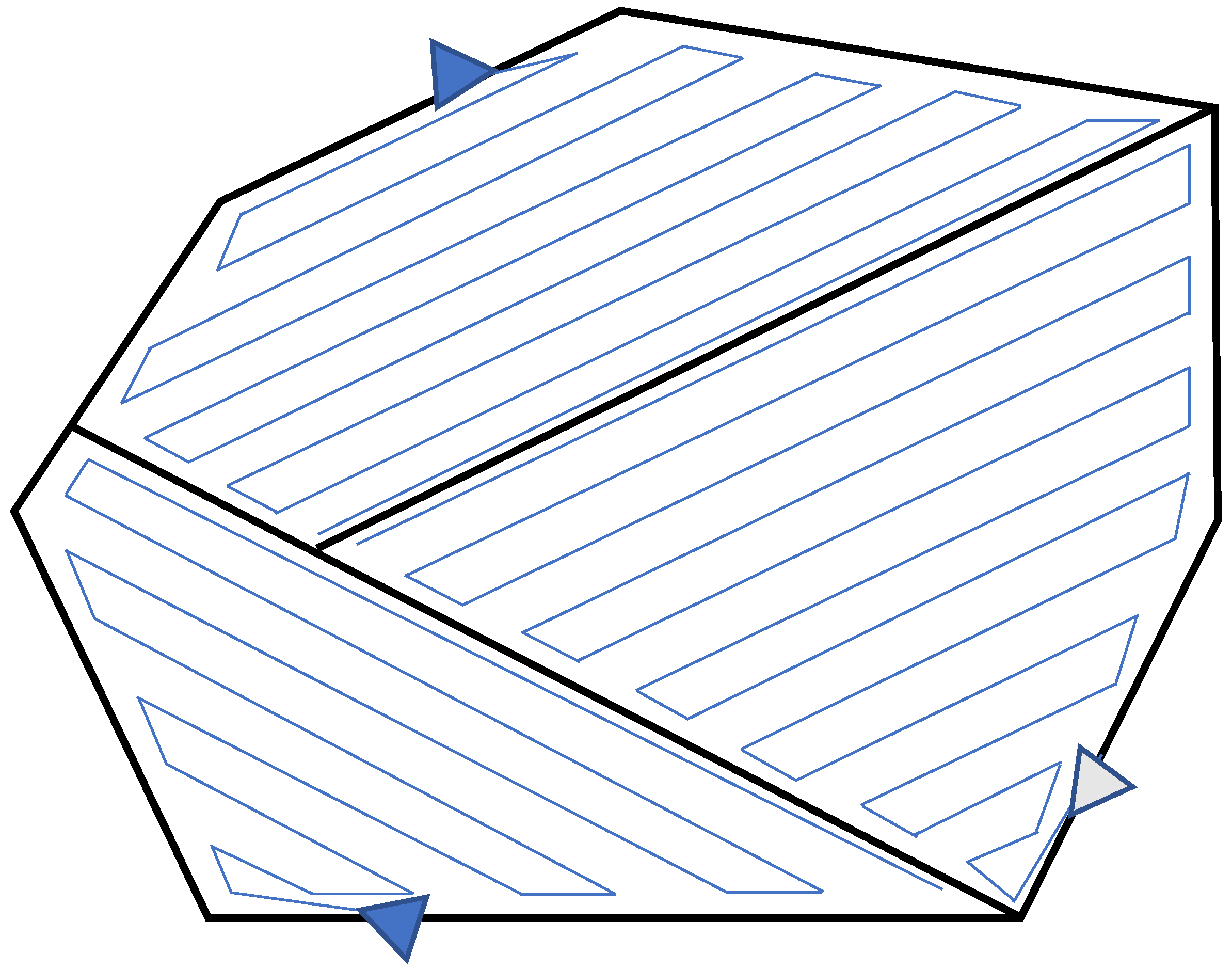






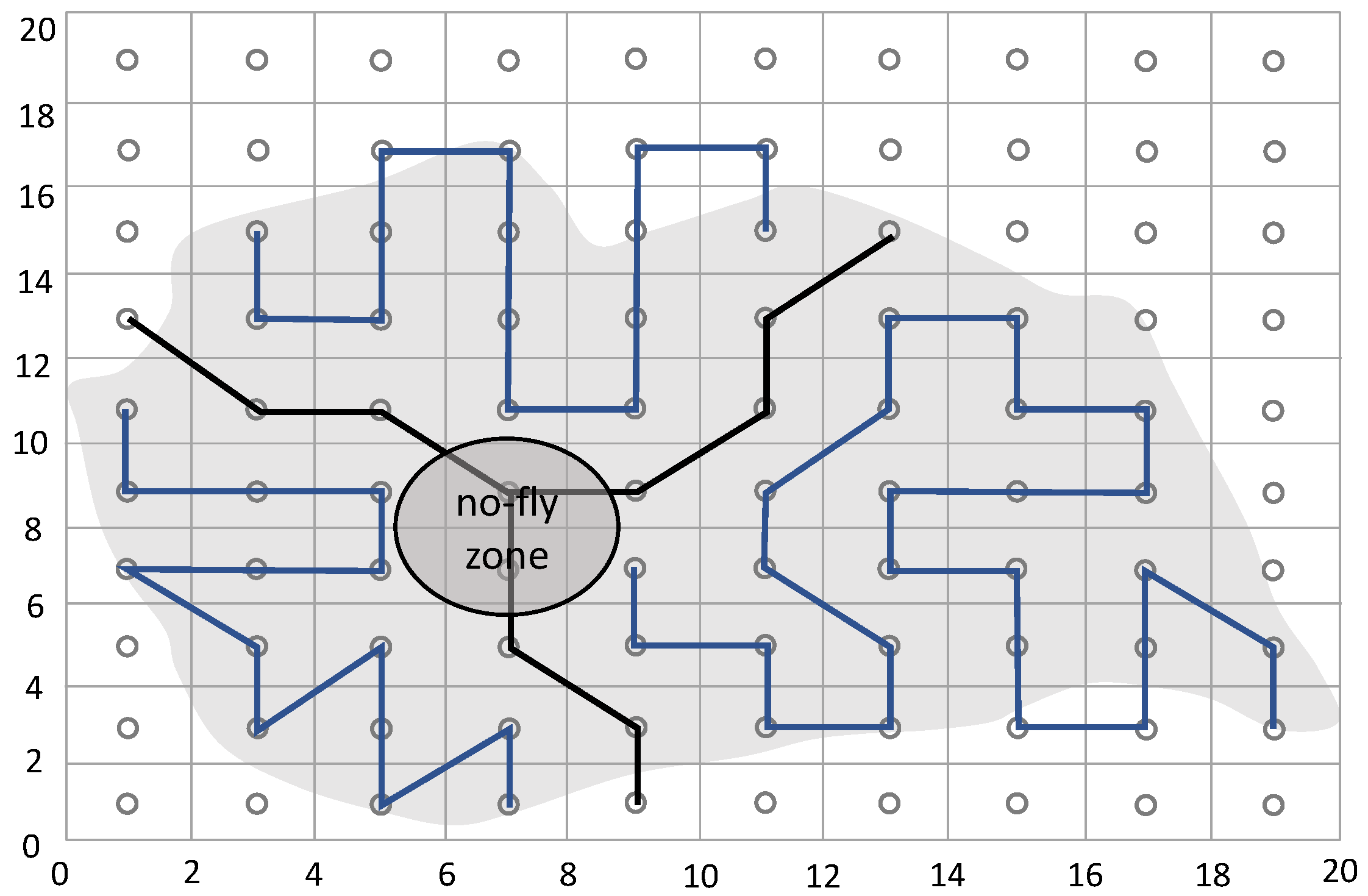










| Approach | Ref. | Shape of the area | Performance metrics | Single/ Multiple | Type |
|---|---|---|---|---|---|
| Back-and-Forth, Square, Sector Search, Barrier Patrol | [38] | Rectangular | Fixed and mobile target detection; Coverage rate | Single | RW |
| Back-and-Forth | [39] | Polygonal | Flight time | Single | FW |
| Energy-aware Back-and-Forth | [25] | Polygonal | Energy consumption | Single | RW |
| Energy-aware Spiral | [40] | Polygonal | Energy consumption | Single | RW |
| Three-stage Energy-aware | [33] | 3D Topology | Energy consumption | Single | RW |
| Smoothing algorithms: E-MoTA e I-MoTA | [31] | Regular Grid | Energy consumption; Mission time; Level of localization accuracy | Single | Both |
| Mixed Integer Linear Programming (MILP) | [41] | Rectangular | Flight time | Multiple | FW |
| Circular | [42] | Rectangular | Coverage rate; time | Multiple | FW |
| Approach | Ref. | Online/ Offline | Shape of the area | Performance metrics | Single/ Multiple | Type |
|---|---|---|---|---|---|---|
| Back-and-Forth | [43,44] | Offline | Polygonal | Number of turning maneuvers | Single | Both |
| Back-and-Forth | [35] | Offline | Polygonal | Number of turning maneuvers; Path length | Single | RW |
| Back-and-Forth | [30,48] | Offline/ Online | Irregular | Path length; Coverage time | Single | FW |
| Back-and-Forth and Spiral | [29] | Offline | Polygonal | Path length | Single | FW |
| Back-and-Forth | [34] | Offline | Polygonal | Number of turning maneuvers | Multiple | RW |
| Spiral | [51,52,54,55] | Offline | Polygonal | Path length | Multiple | FW |
| Back-and-Forth (Line Formation) | [56] | Offline | Rectangular | Target detection; Search time, number of UAVs and information exchange | Multiple | RW |
| One-to-one coordination (Decentralized Technique) | [57,58,59] | Online | Irregular | Interval of visits; Information latency | Multiple | Both |
| Back-and-Forth/Zamboni (Local Priority) | [60] | Offline | Polygonal | Number of turning maneuvers; uncertainty | Multiple | FW |
| Approach | Ref. | Online/Offline | Shape of the area | Performance metrics | Single/Multiple | Type |
|---|---|---|---|---|---|---|
| Gradient-based approach | [32] | Offline | Irregular/Regular Grid | Coverage time | Single | RW |
| Wavefront Algorithm and Cubic Interpolation | [62] | Offline | Irregular/Regular Grid | Path length; Number of turning maneuvers | Single | RW |
| Multi-RTT* Fixed Node (RRT*FN) and Genetic Algorithm (GA) | [63] | Offline | Regular Grid | Path length | Single | RW |
| Wavefront Algorithm | [10] | Offline | Irregular/Regular Grid | Position and altitude errors; Wind disturbances; Mission, flight and configuration times; Path length | Multiple | RW |
| Harmony Search | [64] | Offline | Irregular/Regular Grid | Number of turning maneuvers | Multiple | RW |
| Breadth-First strategy, Depth-First, and Shortcut Heuristic | [65] | Online | Square | Total distance of coverage | Single | RW |
| Hilbert space-filling curves | [66] | Online | Square | Total distance of coverage | Single | RW |
| Long straight-lines algorithm | [67] | Offline | Irregular/Grid related to the sensor | Total distance; Number of turns; Number of jumps between cells | Multiple | RW |
| Edge Counting and PatrolGRAPH* | [36] | Online | Graph Grid | Path length; Robots distance average | Multiple | RW |
| Reinforced Random Walk | [71] | Online | Rectangular | Coverage time; Global detection efficiency | Multiple | RW |
| Cellular Automata | [72,73,74] | Online | Regular Grid | Exploration time with/without barriers | Multiple | RW |
| Waypoint planning with uncertainty | [81] | Online | Rectangular | Certainty of information points | Multiple | Both |
| Information merging for cooperative search | [80] | Online | Rectangular | Target localization | Multiple | RW |
| Fixed-horizon with CMA-ES | [82,83] | Online | Rectangular | Entropy; Classification rate | Multiple | RW |
| Learning-based Preferential Surveillance Algorithm (LPSA) | [84,85] | Online | Regular Grid | Distribution of visits; Target localization; Threat avoidance | Single | Both |
| Back-and-Forth | [75] | Online | Regular Grid | Total distance; Coverage rate; Redundancy rate | Multiple | RW |
| Genetic Algorithm (GA) | [76] | Offline/Online | Polygonal/Regular Grid | Path length | Single | RW |
| GA with flood fill algorithm | [97] | Offline/Online | Polygonal/Regular Grid | Path length | Multiple | RW |
| Multi-Objective Path Planning with GA | [98] | Offline/Online | Rectangular | Mission Completion Time | Multiple | RW |
| Chaotic Ant Colony Optiomization to Coverage | [79,99] | Offline/Online | Regular Grid | Coverage rate; Recent coverage ratio; Fairness (coverage distribution); Connectivity (UAVs distribution) | Multiple | RW |
| ACO with Gaussian distribution functions | [77] | Online | 3D Regular Grid | Path length and rotation angle; Inclination and area overlapping rate | Multiple | Both |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabreira, T.M.; Brisolara, L.B.; Ferreira Jr., P.R. Survey on Coverage Path Planning with Unmanned Aerial Vehicles. Drones 2019, 3, 4. https://doi.org/10.3390/drones3010004
Cabreira TM, Brisolara LB, Ferreira Jr. PR. Survey on Coverage Path Planning with Unmanned Aerial Vehicles. Drones. 2019; 3(1):4. https://doi.org/10.3390/drones3010004
Chicago/Turabian StyleCabreira, Tauã M., Lisane B. Brisolara, and Paulo R. Ferreira Jr. 2019. "Survey on Coverage Path Planning with Unmanned Aerial Vehicles" Drones 3, no. 1: 4. https://doi.org/10.3390/drones3010004