Drone Swarms in Fire Suppression Activities: A Conceptual Framework

Abstract

The recent huge technological development of unmanned aerial vehicles (UAVs) can provide breakthrough means of fighting wildland fires. We propose an innovative forest firefighting system based on the use of a swarm of hundreds of UAVs able to generate a continuous flow of extinguishing liquid on the fire front, simulating the effect of rain. Automatic battery replacement and extinguishing liquid refill ensure the continuity of the action. We illustrate the validity of the approach in Mediterranean scrub first computing the critical water flow rate according to the main factors involved in the evolution of a fire, then estimating the number of linear meters of active fire front that can be extinguished depending on the number of drones available and the amount of extinguishing fluid carried. A fire propagation cellular automata model is also employed to study the evolution of the fire. Simulation results suggest that the proposed system can provide the flow of water required to fight low-intensity and limited extent fires or to support current forest firefighting techniques.

1. Introduction

Forest environments, woods and green areas constitute a natural resource for human life. Unfortunately, they are progressively risking increased impoverishment and destruction [1]. Wildfires represent the most serious and prevalent threat to Mediterranean forests, causing erosion and chemical alteration of the soil, and climate changes [2,3]; they are a particularly complex phenomenon, influenced by numerous interdependent variables, some of which are constantly evolving in time. Slash-and-burn practices have always been used worldwide by humans for land management to adapt the territories for agricultural and residential activities [4]. In the past few decades, there has been a countertrend to an ever-increasing abandonment of rural lands that has led to a re-colonization of many woodlands and shrublands. These richer rural landscape conditions have caused an increase of fire hazards, wildfire frequency, incidence and magnitude, and dangerous consequences involving people, infrastructure, and natural environment; as a result, the issue of forest firefighting has become increasingly important [5].

The protection of forests is implemented through the management of wildfires following a three-step process: prevention, detection, and suppression [6], and involves fire brigades, civil protection, police force, and volunteers. Prevention activities consist in the execution of all actions aimed at mitigating the risk of fire and its consequent damages, in order to make the natural environment safer and to achieve the objectives of ecosystem management. Prevention interventions, aiming at reducing the potential causes of fire ignition, may consist of fire treatment: preventive silviculture techniques, prescribed fire, interventions on firebreaks, and access roads to the forest [7].

The suppression phase includes both direct and indirect attack [8]. Generally, the first strategic approach is the direct attack, usually chosen for small or large fires of low-to-medium intensity. It consists in actions performed directly against the flames at the immediate edge of the fire front or strictly parallel to it; it is commonly associated with the use of water as the main extinguishing component. In emergencies, direct attack may also involve cooling with chemical additives mixed with water to increase suppression effectiveness. Retardant additives are inorganic salts, mainly ammonium phosphates, which inhibit the flame combustion and slow down fire progression when the water used for their diffusion has evaporated [9]. Ground suppression forces are equipped with different vehicles and firefighting systems, e.g., pumps, bulldozers, tankers with different water capacities, which are employed depending on the nature of the fire [6,10].

Aerial support is another important firefighting tool capable of providing an increasing amount of extinguishing liquid. Among the types of aircraft are helicopters, single-engine tankers, fixed-wing water-scooping aircrafts, and large multi-engine tankers. These aircrafts differ in cost, flight speed, flight distance, response time, maneuverability, tank capacity, and type and effectiveness of the liquid, e.g., water, suppressant or retardant that can be delivered [11]. In case of significant water sources in the surrounding area, planes and helicopters can collect water and drop it on both the front and the central part of the fire to counteract its evolution. As a result, airborne resources have enhanced the effectiveness of the initial attack, as they reach the fires rapidly, even in inaccessible locations. As a consequence of the proximity to the sea, tanker planes (e.g., Canadair) and helicopters are widely used in Mediterranean European countries [2]. Aviation fire resources are able to create containment lines before the arrival of ground crews and also provide punctual protection for structures and other threatened assets.

The main disadvantage of direct attack is the risk to human life due to the short distance from the fire: firefighters risk entrapments [12] and are exposed to heat, smoke and flames during operations when conducting fire control actions directly adjacent to the edge of the fire [13]. Drawbacks are also present with regard to the use of firefighting aviation: for safety reasons, in certain countries, Canadair missions can only be carried out during the day and allows to perform a limited number of drops, given the need after each intervention to refuel at an appropriate nearby place. Furthermore, the costs of these strategies have been examined in literature. Aerial firefighting has a high cost of purchasing, operating and maintaining aircraft, and staff training [11].

When the intensity of a fire makes direct attack unsafe and wildfire behavior exceeds the firefighter’s capacity of extinction, a proactive approach is needed. Indirect attack consists in anticipating the flames, building impermeable firelines along a predetermined route at varying safe separation distances from the advancing fire. Advanced firefighting organizations plan extinction operations, identifying appropriate and safety areas where they can organize indirect attack: build effective and distant fire control lines with burnout or backburn actions [14]. As previously mentioned, a second phase should follow prevention and precede suppression with direct and indirect attacks: the detection phase, i.e., the identification and monitoring of an actual fire in progress [15]. A fire of limited size is known to be easier to control and extinguish than a fire that has already spread. In this context, unmanned aerial vehicles (UAVs) are valuable tools for faster fire detection.

During the twentieth century, the UAVs, generically called drones, were exclusively used for military applications, whereas in the last few years, their use in civil applications has increased. Both research institutions and universities, as well as industry, have shown a growing interest in studying this technology. Promising applications include surveillance, precision farming, inspection of potentially dangerous sites, and environmental monitoring. The use of UAVs has also risen in forest fire prevention and detection [16,17].

In the United States, the “John D. Dingell, Jr. Conservation, Management, and Recreation Act”, a law enacted in 2019, pushes federal agencies to expand the use of drones in managing and fighting wildfires [18]. Small unmanned aerial systems are generally employed in three stages: fire search, fire confirmation, and fire observation [19]. They have a short reaction time and flexibility of use, and they reach locations that are inaccessible and dangerous for humans. In addition, thanks to their view from above using video or thermal cameras, the UAVs are able to help fire brigade in reconstructing overviews of an incident [20] and can provide data on chemical measurements, when equipped with appropriate technical sensors. Civil protection and firefighters equip themselves with drones to track vegetation and areas at risk and to carry out evaluations and interventions based on images and data transmitted in real time by drones flying over the burning area. The main limitations of this use are the difficulty of going beyond a sporadic monitoring that does not allow a continuity in time (both the phase of data acquisition and processing must be done manually by an operator) and the impossibility of acting promptly to alert in case of an outbreak of fire. Generally, the overflight of drones takes place with the fire in progress to estimate the extent and direction of propagation of the flames. Recent technological advances in UAV field have increased the possibility to provide real time and high-quality information to end-users. On this issue, in [21], an algorithm for estimating the fire propagation is proposed with the aim of enabling intelligent and long-lasting coordination of UAVs to support firefighters. In [19], the authors show how multiple aerial vehicles with on-board infrared or visual camera, can collaborate to automatically obtain information about the evolution of the fire front shape and other parameters. The system in [22] is developed to help fire experts in indirect attack, by planning flights to reach previously inaccessible terrain and deliver ignition spheres to light prescribed fires.

Unfortunately, there are still few studies in the literature that suggest the use of UAVs not only for the prevention and monitoring of forest fires, but also with the aim of extinguishing them [15,23]. For instance, [24,25] and [26] promote the idea of using such technology in firefighting applications, especially in areas difficult to reach by humans. The first propose a fleet of self-organized drones, carrying $120 \mathrm{kg}$ of water each, with a coordination mechanism based on a forgetful particle swarm algorithm; the second present a rotary wing UAV equipped with a payload drop mechanism that can carry firefighting spheres and release them against fires. [27] proposes the use of drones carrying extinguishing balls as a supplement to traditional firefighting methods. With regard to high temperatures, in [28], the authors propose an aerial robot made of fire-resistant material in order to prevent the risk of damage to electronic equipment directly exposed to flames. In [29], instead, a new lithium-ion battery design is developed with the purpose of handling the ultrahigh thermal shock in UAVs.

In this paper, we propose an innovative method based on the use of a swarm of collaborative UAVs able to transport large quantities of fractionated extinguishing liquid and to release it on fire fronts, simulating rain effect (see Figure 1). This system is designed not only for the detection of a fire, but also for its suppression, in cooperation with the resources previously introduced, i.e., aerial forces and ground crews, with the aim of reducing the risk for human life. The aim of this work is to estimate as robustly as possible the impact of drones’ use in fighting forest fires, which are a complex phenomenon dependent on many factors. While the literature on fire models is extensive, there is a limited number of articles considering how the fire front is modified by the action of firefighting equipment. The most established existing theories are therefore used here, rather than proposing new methods that would also need a validation phase.

First, a drone system that manages a swarm of UAVs and satisfies some requirements is introduced. Then, its effectiveness in suppressing or at least containing a low-intensity wildland fire is studied. For this purpose, the critical water flow rate, i.e., the rate of water application required to arrest a certain number of linear meters of active fire front, is estimated based on fire parameters such as flame length, wind speed, moisture content, active flame depth, fireline intensity, etc. Plant species typically present in the Mediterranean scrubland, which do not give rise to flames of excessive height, are chosen. Therefore, it is not strictly necessary to take into account the percentage of water that cannot reach the fire due to the foliage of the trees. Then, assumed that the drone system is positioned at a certain distance from the fire depending on various surrounding conditions, the number of drones necessary to assure such flow of water is computed. Finally, the implementation of a fire cellular automata propagation model allows to predict how the fire front subjected to the action of drones is modified over time.

The paper is organized as follows. In Section 2, we introduce the system, the equations to obtain the critical water flow rate and the number of linear meters arrested. We also describe the cellular automata model. In Section 3, we present calculation and simulation results. Concluding remarks and conclusions are given in Section 4.

2. Materials and Methods

2.1. Description of the Drone Swarm System

The present paper intends to provide a conceptual framework, assuming that a drone swarm system has to meet a number of requirements in order to be used effectively in firefighting: (i) it has to ensure operational continuity without downtime for a high number of hours (virtually even H24); (ii) it has to be able to automatically replace exhausted batteries and insert them into a charging circuit, given the limited battery duration of the current drones (just over half an hour); (iii) it has to allow for multiple refills of the drones with an appropriate extinguishing liquid placed in containers docked to drones. It mainly consists of a support unit that manages the drone swarm (henceforth called platform) that can be easily moved and positioned close to the fire front. In addition, drones exposed to possible high temperatures have to be assembled with fire-resistant materials.

A system that satisfies these requirements has considerable advantages in fighting forest fires: it can be used both day and night and in low visibility conditions, unlike common aircraft; it does not require the availability of a water basin in the vicinity; it can be used continuously until the alarm ceases, since the automatic battery change, the continuous charging system, and the complete automation of the payload switch (containing the extinguishing liquid), virtually ensure a H24 duration; it can be used in areas not directly accessible by firefighting equipment and in areas with complex orography; it is a precision system because the concerned area and the flight plan can be accurately programmed; it is a flexible system in which the area of intervention can be modified in real time as the fire conditions evolve; it does not put at risk the lives of aircraft pilots that often have to operate in conditions of considerable danger.

On the other hand, the practical implementation of such a system is certainly not easy and requires a high degree of technology. Moreover, the amount of water transported by a drone is obviously significantly reduced compared to the volume of water of a firefighting aircraft [30]. At the same time, however, a large number of drones can guarantee a temporal continuity and uniformity of diffusion that an aircraft is unable to obtain due to the timing of provision. According to [31], intense evaporation is required to effectively extinguish forest fires, while a large percentage of the water discharged in large volumes from aircraft does not contribute efficiently to fire suppression because it has insufficient time to evaporate. It is also conceivable to equip drones with a system to create a polydisperse droplet water flow. In [32,33], it is shown that a water supply distributed over time and space can decrease the amount of water required to extinguish a forest fire. A drone system could therefore create the so-called rain effect, i.e., the release of small quantities of firefighting liquid by drizzling it over the fire or the surrounding vegetation, instead of dropping the liquid in a concentrated manner. This method, both theoretically and experimentally, is acknowledged as being particularly effective in domestic and/or industrial firefighting systems (fire sprinkler systems) [34].

Moreover, multiple strategies are possible: either directing the action of drones directly on the flames, or on an adjacent area, so as to prevent the spread of flames to particularly sensitive areas, for example occupied by inhabited areas or installations at high risk. Moreover, the solution could be perfectly applicable in case of hotspots, i.e., pre-fire and post-fire outbreaks and burning embers, identifying these areas with drones carrying thermal cameras. These situations generally do not require the intervention of air tankers, and in the meantime the hotspots are often difficult to reach by fire brigades.

At the moment, the cost of the system compared to the current firefighting tools cannot be estimated, as it depends on many factors, primarily the implementation choices and the cost of drones. However, in recent years, the price of UAVs has been decreasing continuously thanks to significant technological advancement in the field, with costs expected to decrease even further.

A drone system involves the use of a platform that manages drones and changes their batteries and payloads. Such a platform can be considered as a base station for drones. Drone base stations are gaining popularity mainly for their use in video surveillance and inspections [35]. In the field of forest firefighting, there is very little literature concerning the use of drone base stations. Among them we mention the charging base designed in [17] for fire surveillance, equipped with an upper sliding door and a vertically moving bed for take-off and landing maneuvers.

The aim of this work is to investigate if a management system of a drone swarm fulfilling the requirements (i)–(iii) is able to generate a sufficient flow of extinguishing liquid to effectively fight a low-intensity and limited extent forest fire. We hypothesize that each drone can carry from 5 to 50 L of water. This assumption is plausible considering the characteristics of some manufactured drones reported in

Table 1. Technical specifications of some multirotor drones. Maximum practical use payload < 30 kg.

Drone	Company	Type	Weight (kg)	Dimensions (mm)	Folded Dimensions (mm)	Propeller/ Rotor Number	Speed (km/h)	Payload (kg)	Flight Time (min)	Website
PD6B-type2	Prodrone	hexacopter	19.5 (4 batteries included)	L 1874 W 2060 H 474	L 1348 W 600 H 474	6	max 60	No payload	35	prodrone.com
								10	15
								20 (practical use)	10
GD-40X	Gryphon	X8 octocopter	12 (dry weight) 40 (max takeoff weight)	D 1400	D 1000 detachable arms retractable gear	8 (4 + 4) coaxial propellers	max 50 avg 40	No payload	50	gryphondynamics.co.kr
								22–25	24
Vulcan D8	Vulcan	X8 octocopter	16 (dry weight) max 55	L 1400 W 1150 D 1670	L 1400 W 400 h 500	8 (4 + 4) coaxial propellers	max 80 avg 30/40	No payload	>30	vulcanuav.com
								10	22
								20	14
Griff 135	Griff Aviation	X8 octocopter	max takeoff weight 135	L 2410 W 2260 H 470	L 1440 W 770 H 470	8 (4 + 4) coaxial propellers	—	No payload	>30	griffaviation.com
								30 (max 50)	25–30

W width, L length, H height, D diameter, Dry weight: no payload, no battery.

and

Table 2. Larger and heavier drones. Cargo Air Vehicles and Passenger Autonomous Air Vehicles.

Drone	Company	Type	Speed (km/h)	Payload (kg)	Website
Pegasus 120	Israel’s Aeronautics	octacopter	80	45	cp-aeronautics.com
Altinay Albatros	Altinay	CAV	-	50–100–150	altinay-advanced.com
EHANG 216	Ehang AAV	AAV	130	220	ehang.com
Griff 300	Griff Aviation	X8 octocopter	60 (avg 50)	226	griffaviation.com

. Drones with features similar to those in Table 1, which have the ability to manage flights with payload between 20 and 30 kg, show how road transport of the considered drones is feasible. Their number depends on the folded dimensions of the UAVs considered. Assuming a 12-ton truck, with length 7.20 m, width 2.4 m, height 2.35 m and payload of 5540 kg, its truck box of size 6200 × 2500 × 2400 mm is capable of housing 80–96 drones of the average size of those shown in the Table 1 (e.g., Vulcan D8 and GD-40x, respectively), with additional space left over for the internal management mechanisms of the drones (e.g., conveyor rollers). Moreover, a standard 40 ft container with useful internal dimensions of length 12 m, width 2.33 m, height 2.35 m and maximum load weight 26,500 kg can hold up to 160 drones of size 1400 × 500 × 500 mm, or about 128 transportable folded drones of 700 × 700 × 500 mm, while still ensuring a handling margin for the outflow of drones.

In addition, with UAVs able to carry up to 50 L of water, as shown in Table 2, it is conceivable assuming that drones are located in a hangar a few tens of kilometers away from the fire area, while platforms with payload availability (batteries and extinguishing liquid) are placed closer to the area affected by the fire. In this way, instead of being transported by trucks, larger and heavier drones could reach autonomously the platforms where they would find the recharge and payload needed for firefighting.

Concerning the batteries, the datasheet of the GD-40X drone indicates a 12S LiPo battery (22,000 mAh or 30,000 mAh). Today, this type of battery can provide 25 C. The letter “C” in Li-Po cells indicates the capacity, i.e., the maximum current intensity that the battery is able to deliver safely, which means that a 22,000 mAh battery with 25 C is able to deliver 550 A. The recommended recharging time is about one hour/one hour and a half.

The current implemented architecture does not provide for individual communication between drones of the swarm (e.g., no mesh network). The communication between platform and drones is based on a hierarchy connection architecture, where a central intelligence, i.e., the platform/base station, is able to communicate directly with each single drone during refueling, assigning them their respective flight plans. The platform holds information about battery level, flight position, altitude, speed, and send path plans to multiple UAVs. In this way, the drone swarm is well organized and coordinated in a simultaneous flight and with a controlled and efficient path planning. The platform could provide connectivity to drones through the wireless networking infrastructure of 4G/5G [36]. These high-speed wireless technologies, which are designed for broadband cellular networks, could also enable the platform to remotely control the drones and transmit-receive data from them in real-time. Technical implementations of the system and drone swarm management on the fire front will be analyzed in future papers. Developing of control strategies, insights into the networking capabilities, and collaboration between drones to ensure motion safety, efficiency, and avoiding collision [25,37,38] will be extensively evaluated.

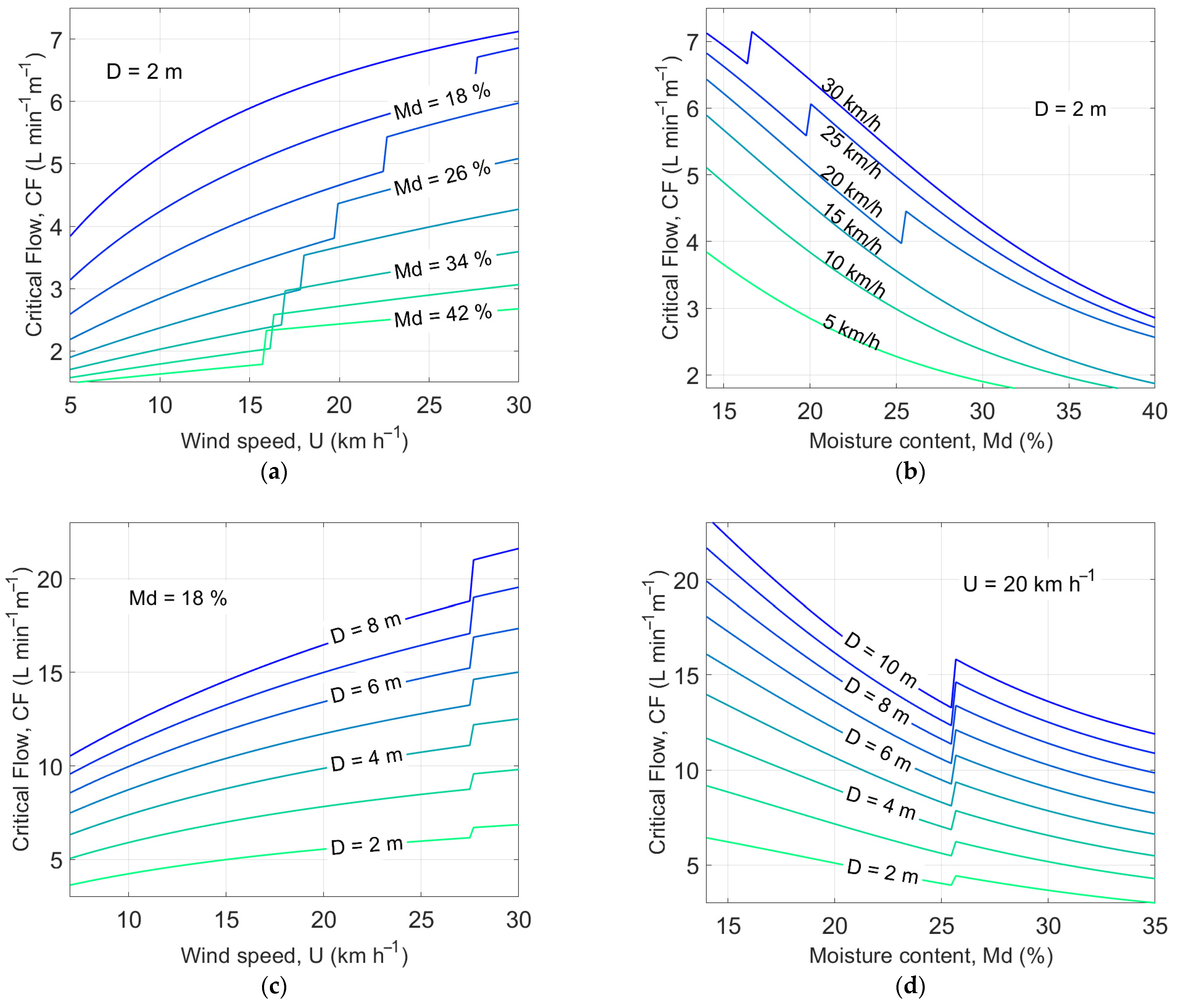
2.2. Calculation of Critical Water Flow Rate CF as Function of Flame Length

The main substance used to suppress wildfires is water, thanks to its high availability, low cost and great extinguishing capacity [39]. In order to test the validity and effectiveness of using a large number of drones to contain and extinguish forest fires, it is essential to estimate the critical water flow rate ($CF$), which is the rate of water application required to arrest a certain number of linear meters of active fire front or, if the water is sufficient, to completely extinguish a wildfire. Once this value has been determined according to the different fire parameters, it is then feasible to compute the number of drones required, knowing the amount of water carried by each drone. It is also possible to reverse the calculation, i.e., to compute the number of meters of active fire front contained by a given number of drones and platforms.

$CF$ mainly depends on the fireline intensity, which can be computed either as a function of flame length or as a function of rate of spread. Moreover, $CF$ can be estimated per unit area or per linear meters of active fire front. In this section, it is calculated as flux over square meter of burning surface and as a function of flame length, while in Section 2.3 it will be evaluated over linear meters of active fire front and depending on the rate of spread, which in turn relies on the main factors of the fire as wind speed, moisture content, etc.

The literature contains a number of works predicting $CF$ to extinguish a wildland fire within an infinite period of time available [40,41]. These articles are based on models obtained by physical considerations and by experimental data collected in databases of thousands of fires. In this paper, we use the Hansen’s approach [40] based on the Fire Point theory [42,43] in which the energy balance at the fuel surface when water is applied is given by:

$$\left(f \Delta H_c-L_v\right) {\dot{m}}_{cr}^{″}+{\dot{q}}_E^{″}-{\dot{q}}_L^{″}-{\dot{q}}_{water}^{″}= 0$$

(1)

where $f$ is the heat release fraction transferred back to the fuel surface by convection and radiation, $\Delta H_c$ is the effective heat of combustion (${\mathrm{kJ} \mathrm{kg}}^{-1})$, $L_v$ is the heat of gasification of the fuel (${\mathrm{kJ} \mathrm{kg}}^{-1})$, ${\dot{m}}_{cr}^{″}$ is the mass burning rate per unit area of the fuel at the critical point (${\mathrm{kg} \mathrm{m}}^{-2}{ \mathrm{s}}^{-1})$, ${\dot{q}}_E^{″}$ is the external heat flux (${\mathrm{kW} \mathrm{m}}^{-2})$, ${\dot{q}}_L^{″}$ and ${\dot{q}}_{water}^{″}$ are the heat loss from the surface and the heat loss due to the water vaporization (${\mathrm{kW} \mathrm{m}}^{-2})$, respectively.

Using Spalding’s B Number theory [44], ${\dot{m}}_{cr}^{″}$ is computed as:

$${\dot{m}}_{cr}^{″}= \frac{h}{c_p} \ln \left(1+\frac{Y_{O_2} \Delta H_{R,O_2} }{\varphi \Delta H_c}\right)$$

(2)

where $h$ is the convective heat transfer coefficient (${\mathrm{kW} \mathrm{m}}^{-2})$, $c_p$ is the specific heat of air at constant pressure (${\mathrm{kJ} \mathrm{kg}}^{-1}{ \mathrm{K}}^{-1})$, $Y_{O_2}$ the oxygen mass fraction, $\Delta H_{R,O_2}$ the heat of combustion per unit mass of oxygen consumed (${\mathrm{kJ} \mathrm{kg}}^{-1})$, and $\varphi$ is the fractional convective heat loss from the flame required to quench the flame.

The heat loss due to water vaporization is given by [40]:

$${\dot{q}}_{water}^{″}={\eta }_{water}\hspace{1em}{\dot{m}}_{water,cr}^{″}\hspace{1em}{L}_{v,water}$$

(3)

where ${\eta }_{water}$ is the efficiency of water application, $L_{v,water}$ is the enthalpy change of water at 283 K and water vapour at 373 K (${\mathrm{kJ} \mathrm{kg}}^{-1})$, and ${\dot{m}}_{water,cr}^{″}$ is the critical water application rate (${\mathrm{kg} \mathrm{m}}^{-2}{ \mathrm{s}}^{-1})$. Then, replacing (3) in (1) and $f$ by $\varphi$, the critical flow rate $CF$ necessary to extinguish a burning surface is expressed as (${\mathrm{L} \mathrm{m}}^{-2}{ \mathrm{s}}^{-1})$:

$$CF:=m_{water,cr}^{″}= \frac{1 }{{\eta }_{water} L_{v,water}}(\left(\varphi \Delta H_c-L_v\right) {\dot{m}}_{cr}^{″}+{\dot{q}}_E^{″}-{\dot{q}}_L^{″})$$

(4)

The expression of ${\dot{q}}_E^{″}$ is given by:

$${\dot{q}}_E^{″}= {\dot{q}}_{E,rad}^{″}+ {\dot{q}}_{E,conv}^{″}$$

(5)

The first term ${\dot{q}}_{E,rad}^{″}$ is the incident flame radiation per unit area and is given by [40]:

$${\dot{q}}_E^{″}= \frac{r_c I }{2 L_f+D} \varphi \tau$$

(6)

where $r_c$ is the radiative component per unit length of fire front, $I$ the fireline intensity $\left({\mathrm{kW} \mathrm{m}}^{-1}\right)$, i.e., the heat release rate per unit length of fire front,$L_f$ the flame length $\left(\mathrm{m}\right)$, $D$ the depth of active combustion zone ($\mathrm{m})$, and $\tau$ the atmospheric transmissivity. The second term ${\dot{q}}_{E,conv}^{″}$ represents the convective heat transfer and has to be taken into account in the case of large wind speed, high-intensity fires, or steep terrain [40]. Since in this application low-intensity fires and flat terrain are considered, ${\dot{q}}_{E,conv}^{″}$ is different from zero only when the flame angle $A$, i.e., the angle between the flame and the unburned fuel ahead, is lower than ${30}^{°}$ [40]. In accordance with [40,45,46], $A$ is computed by numerically solving the following system of two nonlinear equations:

$$\{\begin{array}{l}\tan \left(90-A\right)-1.22 \sqrt{U^2/\left(g H_f\right)}=0\\ H_f-L_f\sin A=0\end{array}$$

(7)

where $H_f$ ($\mathrm{m})$ is the flame tip height, $U$ is the mean horizontal wind speed and $g$ is the gravity acceleration (${\mathrm{m} \mathrm{s}}^{-2})$. Therefore, the expression of ${\dot{q}}_{E,conv}^{″}$ is given by:

$${\dot{q}}_{E,conv}^{″}=\{\begin{array}{ll}h \left(T_g- T_{fuel}\right)& if A<{30}^{°}\\ 0& if A\ge {30}^{°}\end{array}$$

(8)

where $T_g$, $T_{fuel}$ ($\mathrm{K})$ are gas and fuel surface temperatures, respectively.

The heat loss from the surface ${\dot{q}}_L^{″}$ is given by:

$${\dot{q}}_L^{″}={\dot{q}}_{L,rad}^{″}+{\dot{q}}_{L,conv}^{″}$$

(9)

where radiative ${\dot{q}}_{L,rad}^{″}$ heat loss is:

$${\dot{q}}_{L,rad}^{″}=\mathsf{\epsilon } \sigma \left(T_{fuel}^4- T_a^4\right)$$

(10)

and convective ${\dot{q}}_{L,conv}^{″}$ heat loss is:

$${\dot{q}}_{L,conv}^{″}=h \left(T_{fuel}- T_a\right)$$

(11)

The coefficient $\mathsf{\epsilon }$ represents the fuel emissivity, $\sigma$ the Stefan-Boltzmann constant (${\mathrm{W} \mathrm{m}}^{-2}{ \mathrm{K}}^{-4})$,${ \mathrm{T}}_{\mathrm{a}}$ ($\mathrm{K})$ the ambient temperature. Finally, using Byram relation [40], fireline intensity $I$ can be expressed as a function of flame length $L_f$, and it corresponds in low-intensity surface fires to:

$$I=259.833 L_f^{2.174}$$

(12)

It is therefore possible to calculate the critical flow rate as the flame length varies, using Equation (4).

2.3. Critical Water Flow Rate CF as Function of Wind Speed and Moisture Content

In this subsection we calculate the variation of CF as a function of wind speed and moisture content (instead of flame length as in Section 2.2) and considering the linear meters of active fire front, instead of the square meters of burning surface. For this purpose, Equation (12) for fireline intensity is replaced by the formula based on the rate of spread [41,47]:

$$I=\frac{\Delta H_c W RoS}{36}$$

(13)

where $W$ is the total fuel load considering fine fuels typically less than 6 mm in diameter [41] and $RoS$ is the rate of spread of the fire front. Among the various types of $RoS$ is chosen Fernandes’ rate of spread [48], which is suitable for low-intensity fires:

$$RoS=0.06 a U^b\exp \left(-c{M}_d\right)$$

(14)

where $U$ is the wind speed measured at 2 $\mathrm{m}$ above ground level in ${\mathrm{km} \mathrm{h}}^{-1}$, $a$, $b$, and $c$ are parameters obtained experimentally by non-linear regression analysis for Mediterranean scrub, and $M_d$ is the moisture content percentage of the elevated dead fuels. In experimental studies, $M_d$ is determined by weighing samples of vegetation before and after drying them, which means that the formula depends on the type of vegetation. Differently from [48], the rate is multiplied here by 0.06 to be expressed in ${\mathrm{km} \mathrm{h}}^{-1}$. Using Equations (4), (13) and (14), the $CF$ required to extinguish $1 \mathrm{m}$ section of active head fire front is obtained as a function of wind speed $U$ and moisture content $M_d$. Moreover, $m_{water,cr}^{″}$ is multiplied by 60 s and by the flame depth $D$ (i.e., the width of continuous flaming behind the leading fire edge) to obtain the water flow rate in linear meters instead of square meters (${\mathrm{L} \mathrm{m}}^{-1}{\min }^{-1}$):

$$CF:=60 D m_{water,cr}^{″}= 60 D \frac{1 }{{\eta }_{water} L_{v,water}}\left(\left(\varphi \Delta H_c-L_v\right) {\dot{m}}_{cr}^{″}+{\dot{q}}_E^{″}-{\dot{q}}_L^{″}\right)$$

(15)

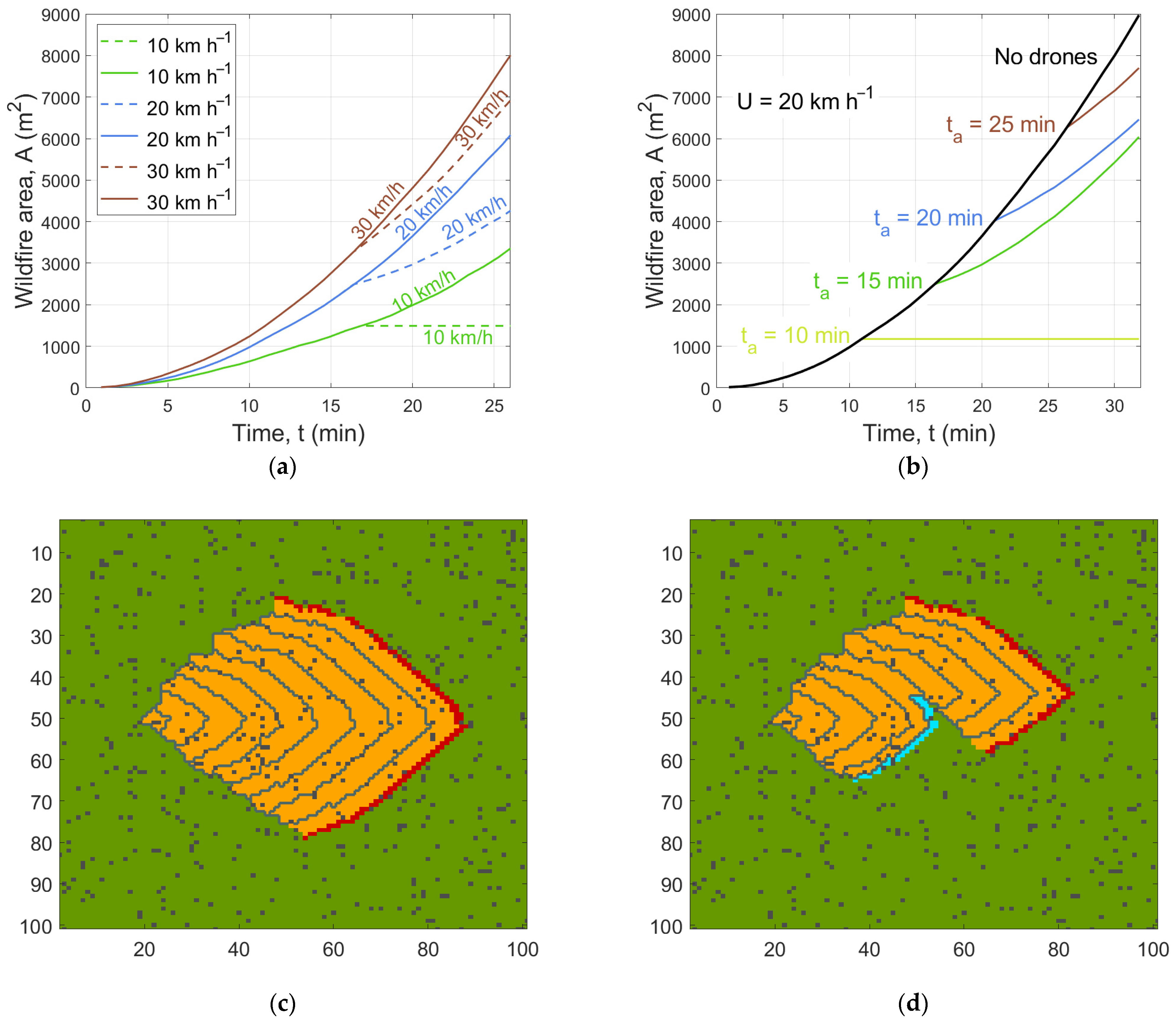
2.4. Impact of Drones on the Evolution of the Active Fire Front

On the basis of the critical water flow rate $CF$, it is then possible to estimate the number of linear meters of active fire front that can be extinguished as the fire parameters (i.e., flame length, wind speed, moisture content, and active flame depth) vary. The platform is assumed to be positioned at a certain distance from the fire depending on various boundary conditions, such as wind direction, terrain orography, presence of roads.

A certain time interval is also required to automatically switch the battery and the payload (the extinguishing liquid) carried by each drone; this timespan can vary from a minimum of a few seconds to a maximum of one minute. A short time is also required for the liquid to be released on the fire by each drone. Since in this work we do not describe how these technical features would be effectively implemented, we consider them in a single variable: the time interval $\Delta t$ ($\min$) in which a drone arrives on the platform, is charged with a new payload, takes off, reaches the active fire front, releases the liquid, and lands back on the platform.

The liquid carried by each drone is identified by $L_d$ ($\mathrm{L}$). As introduced in Section 2.1, it is reasonable to assume $L_d$ to be between 5 and 50 $\mathrm{L}$. In fact, the proposed system concerns the use of a large number of small-sized drones carrying a limited amount of liquid, in contrast to self-guided vehicles similar to current firefighting aircraft with a capacity of thousands of liters. Moreover, each platform is capable of handling a number $n_d$ of drones, ensuring battery replacement and liquid refilling for each drone. Once these variables are introduced, the water flow that a platform assure in the unit of time is easy to estimate. Each drone is able to deliver $n_h$ discharges of extinguishing liquid per hour corresponding to:

$$n_h= \frac{60 \left(\min \right)}{\Delta t \left(\min \right)}$$

(16)

Therefore, a platform, which manages $n_d$ drones, is designed to deliver $n_h^{tot}$ discharges of extinguishing liquid per hour:

$$n_h^{tot}=n_h n_d$$

(17)

and to spread $L_h^{tot}$ of liquid equal to:

$$L_h^{tot}=L_d n_h^{tot} \left({\mathrm{L} \mathrm{h}}^{-1}\right)$$

(18)

Dividing this value by 60 (min), it is possible to estimate the drone flow rate ($DF$), i.e., the amount of liquid that one platform spreads each minute:

$$DF=\frac{L_h^{tot}}{60} \left({\mathrm{L} \min }^{-1}\right)$$

(19)

Replacing in Equation (19) the expression of the variables stated in Equations (16)–(18), we obtain the flow rate that the platform handling $n_d$ drones spreads per minute:

$$DF= \frac{ L_{d }{n}_d}{\Delta t}\hspace{1em}\left({\mathrm{L} \min }^{-1}\right)$$

(20)

For instance, a platform with $n_d=$ 120 drones, each carrying $L_d= 20$ L of fire extinguishing liquid and completing a round trip in $\Delta t=6$ min, ensures a flow of $400 \left({\mathrm{L} \min }^{-1}\right)$. Once calculated the continuous flow that a platform can guarantee and the flow rate necessary to extinguish one linear meter of active fire front, it is possible to estimate the number $m_f$ of linear meters that can be extinguished:

$$m_f= \frac{DF}{CF} \left(\mathrm{m}\right)$$

(21)

or equivalently:

$$m_f= \frac{L_{d }{n}_d}{\Delta t CF} \left(\mathrm{m}\right)$$

(22)

Since the calculation of linear meters does not take into account the time required to ensure the flow of extinguishing liquid, drones are assumed to continue to provide such flow throughout the duration of the fire.

2.5. Estimate of the Drones Required to Extinguish a Specified Number of Linear Meters of Active Fire Front

Considering the total or partial extent of the fire front whose propagation is to be prevented, it is possible to determine the number of drones required. It is assumed to have drones carrying $L_d$ L of extinguishing liquid and to locate the platform such that the time interval required for a drone to reach the fire, release the liquid onto it, and return to the platform is $\Delta t$ ($\min$). Depending on the fire parameters, wind, moisture content, etc., the requested water flow rate changes and consequently the required number of drones. The drone flow rate $D{F}_r$ required to extinguish $m_r$ of active fire front is:

$$D{F}_r=m_r CF \left({\mathrm{L} \min }^{-1}\right)$$

(23)

since $CF$ is the flow rate for 1 linear meter. Therefore, replacing (23) in (20), we obtain the number $n_r$ of drones required:

$$n_r= \frac{ CF \Delta t m_r}{ L_d}$$

(24)

For instance, in a fire with a moisture content of $18\%$ and a wind speed of 10 ${\mathrm{km} \mathrm{h}}^{-1}$, to extinguish 70 m of active front with drones carrying 30 L and completing a loop in $\Delta t=6 \min$, the number of required drones is 60.

2.6. Cellular Automata Model for Studying the Effect of the UAV Platform on Fire Evolution

In the previous subsections, we estimated the number of linear meters of active front arrested using one or more platforms handling a given number of drones with extinguishing liquid. In this subsection, we introduce a fire propagation model in order to simulate the evolution of a fire and subsequently to study the fire behavior under the platform containment action in Section 3.2.

Forest fires are a particularly complex phenomenon, influenced by numerous interdependent variables, some of which are constantly evolving in time. Risk assessment, propagation, and effect models are the three categories in which fire models are grouped by [49]. The objective of forest fire simulation is therefore to improve prevention and control operations: assessment of the attack surface, prediction of the evolution of the fire front, preventive mobilization of rescue teams, and containment of the front-line and fire extinction. In our case, in order to prove the effectiveness of using a coordinated system of drones, among all models of fire evolution, we choose a cellular automata model.

Cellular automata (CA) are mathematical idealizations of physical systems, represented by connected and organized elements that interact with each other and constitute a single entity with the external world. The definition of the physical environment determines the universe upon which the CA is modelled. Physical quantities vary on a finite set of discrete values [50], depicted in grids (two- or three-dimensional lattices) that evolve at discrete time intervals, according to stochastic rules. Every single cell has a finite state characterized by one or more variables and the respective numerical values. Cell states vary according to a local transition function applied to all cells in the lattice, updated synchronously and simultaneously. Specifically, the state of a cell $\left(i,j\right)$, at a given time $t$, depends only on a transition function and on the state of the cell itself and of neighboring ones at the previous discrete time step.

CA have proven their strength in predicting macroscopic and complex dynamics using simple rules that define the physics of a phenomenon on a microscopic grid scale. For this reason, CA models emerge as a useful choice for modelling the complex behavior of wildfire spread [51]. In several researches, CA have been applied to simulate fire spread for the purpose of assisting firefighters in identifying fire suppression tactics and in planning policies for fire risk management [52,53]. They can also be easily integrated with digital data from geographic information systems (GIS) or other sources including local meteorological data [54,55,56].

CA can be identified by the geometry of the regular cell arrangement, i.e., square or hexagonal cells in two-dimensional case [57,58], and the number of neighboring cells taken into account: four neighbors in the case of the Von Neumann neighborhood, eight neighbors in the Moore neighborhood [59]. In [60], the authors present a novel algorithm for wildfire simulation through CA, which is able to effectively mitigate the problem of distorted fire shapes, allowing spread directions that are not constrained to the few angles imposed by the lattice of cells and the neighborhood size.

In the present paper, the CA model introduced in [61,62] is utilized to simulate the evolution and the consequent confinement of a wildfire thanks to the action of one or more platforms of drones. It consists in a square-meshed grid represented as a two-dimensional matrix, easily simulating a forest area. Each cell is generally defined by a finite number of evolving states. Four states characterize the system:

• $State=0$. The cell cannot catch fire (empty cell). This state could describe cells corresponding to parts of the territory in which there is no vegetation that can burn.
• $State=1$. The cell contains live fuel, not yet burned (tree cell).
• $State=2$. The cell contains material that is burning (burning cell).
• $State=3$. The cell contains completely burned fuel (burned cell).
• $State=4$. The cell has a continuous flow of water that provides fire extinction ($CF$ computed in Section 2.2 and Section 2.3) thanks to the action of the drones.

Each cell is subject to local rules that guide the evolution of the spread of the fire. At each discrete time step $t$ of the simulation, the following rules are applied to elements $\left(i,j\right)$ of the state matrix (and therefore to all cells):

• $Rule 1$ states that an empty cell $\left(i, j, t\right)$ maintains the same state without burning at next time step.
• $Rule 2$ states that if a cell contains vegetation fuel and there was at least one neighboring cell burning at the previous time step such that $\left(i\pm 1,j\pm 1,t-1\right)=2$, it can catch fire with a probability $P_{burn}$ greater than a certain threshold. As the wind speed increases, we also consider next-nearest cells as in [63,64]. In particular, we add two layers of cells for wind at $25{ \mathrm{km} \mathrm{h}}^{-1}$ and three for wind at $35{ \mathrm{km} \mathrm{h}}^{-1}$.
• $Rule 3$ determines that a cell that is burning at the present moment will be completely burned at the next one. In subsequent times, it will no longer be able to spread the fire.
• $Rule 4$ implies that a previously burned cell remains burned.

Due to the square grid based on Moore neighborhood, fire can spread to the eight adjacent cells, i.e., horizontally, perpendicularly, and diagonally.

In the following, all the probabilities are computed as in [61,62]. The rule 2 implies that when a cell ignites at the current time, the next instant the fire may spread to nearby cells containing unburned fuel with a $P_{burn}$ probability:

$$p_{burn}=p_0\left(1+p_{veg}\right)\left(1+p_{den}\right) p_w p_s p_m$$

(25)

$p_{burn}$ is a function of several variables that affect fire propagation, such as fuel properties, wind conditions, and topography. The probability $p_0$ measures the chance that a cell in the neighborhood of a burning one will catch fire, supposing flat terrain and no wind conditions. The other probability factors are related to the vegetation typology, to the density and humidity of fuel in each single cell, to the wind blowing over the total area, and to the landscape altitude. Vegetation is considered as a combustible material composed of a set of solid particles distributed in the environment; a density, a typology and a percentage of humidity characterize it. Three density categories are present in the model, sparse, normal, and dense, and each of them corresponds to a $p_{den}$ value. Two types of fuel were chosen, grassland and shrubland, corresponding to the typical vegetative plants of the Mediterranean environment.

The probability due to the moisture content of vegetation is given by

$$p_m=\exp \left(-b{M}_d\right)$$

(26)

adopting Equation (14) given in [48]. It links the rate of spread to the moisture content $M_d$ and to the coefficient $b$, determined by regressive analysis from experimental data.

The wind-effect probability $p_w$ takes into account both wind speed and direction and is calculated using the following empirical relation:

$$p_w=\exp \left(c_{1}U\right)\exp \left(U c_2\left(\cos \theta -1\right)\right)$$

(27)

where $\theta$ is the angle between the spreading direction of the fire and the direction of the wind, $U$ the wind speed, and $c_1$ and $c_2$ constant values. The probability related to the effect of ground elevation is a function of a parameter derived from experimental data and of the slope angle ${\theta }_s$:

$$p_s=\exp \left(a_s{\theta }_s\right)$$

(28)

where $a_s$ is a parameter and ${\theta }_s$ is calculated using

$${\theta }_s={\tan }^{-1}\left[\frac{E_1-E_2}{d}\right]$$

(29)

where $E_1$ and $E_2$ are the altitude of the two adjacent cells, and $d$ is taken equal to $L$ or $\sqrt{2} L$ depending on whether the cell being considered is adjacent or diagonally located to the burning cell.

3. Results and Discussion

3.1. Critical Flow Rate and Fire Front Linear Meters Arrested by Drones

In Section 2, the critical flow rate $CF$ is computed as a function of the fire intensity $I$, which can be evaluated by using the flame length $L_f$ (Equations (4) and (12)) or the rate of spread $RoS$ depending on wind speed and moisture content (Equations (13)–(15)). The computation of $CF$ is valid for various fuel models, but some of the coefficients depend on the vegetation chosen.

Table 3. CF parameters (parameters used to compute the critical water flow rate).

Symbol	Parameter	Value	References
$\Delta H_c$	effective heat of combustion	19,500${ \mathrm{kJ} \mathrm{kg}}^{-1}$	[65]
$L_v$	heat of gasification of the fuel	1800 ${\mathrm{kJ} \mathrm{kg}}^{-1}$	[40]
$h$	convective heat transfer coefficient	20 ${\mathrm{kW} \mathrm{m}}^{-2}$	[40]
$c_p$	specific heat of air at constant pressure	1 ${\mathrm{kJ} \mathrm{kg}}^{-1}{ \mathrm{K}}^{-1}$	[40]
$Y_{O_2}$	oxygen mass fraction	0.233	[40]
$\Delta H_{R,O_2}$	heat of combustion per unit mass of oxygen consumed (Genista salzmannii)	13,480 ${\mathrm{kJ} \mathrm{kg}}^{-1}$	[66]
$\varphi$	fractional convective heat loss	0.3	[40]
${\eta }_{water}$	efficiency of water application	0.7	[40]
$L_{v,water}$	enthalpy change of water	2640 ${\mathrm{kJ} \mathrm{kg}}^{-1}$	[40]
$\tau$	atmospheric transmissivity	1	[40]
$r_c$	radiative component per unit length of fire front (Erica arborea)	0.20	[67]
$\mathsf{\epsilon }$	fuel emissivity	0.6	[40]
$\sigma$	Stefan-Boltzmann constant	$5.67·{\mathrm{W} \mathrm{m}}^{-2}{ \mathrm{K}}^{-4}$	[40]
$T_{fuel}$	fuel surface temperature (Cistus monspeliensis)	693 $\mathrm{K}$	[68]
$T_g$	gas temperature	800 $\mathrm{K}$	[69]
$T_a$	ambient temperature	293 $\mathrm{K}$	[40]
$W$	total fuel load	15 ${\mathrm{tha}}^{-1}$	[41]
$D$	active flame depth	$2 \mathrm{m}$	[40,41]

and

Table 4. Critical flow rate parameters (parameters have been computed in [68]).

Parameter	Symbol	Value
Rate of spread parameters	$a$	3.258
	$b$	0.958
	$c$	0.111

show the coefficients used with their bibliographic references. For parameters depending on the type of vegetation was selected the Mediterranean scrub, while in Hansen’s paper [40] coefficients are referred to Pinus pinaster.

The results obtained by the $CF$ calculation are displayed in Figure 2 and Figure 3. In Figure 2, the critical flow rate at low and high intensity (corresponding to $L_f$ lower and higher that $3.3 \mathrm{m}$, respectively [40,41]), and wind speed at $0$ and $10{ \mathrm{m} \mathrm{s}}^{-1}$ is displayed. Figure 3 shows the $CF$ (${\mathrm{L} \mathrm{m}}^{-1}{\min }^{-1}$) required to extinguish $1 \mathrm{m}$ section of active head fire front as a function of wind speed $U$, moisture content $M_d$, and active flame depth $D$. Two of these factors vary, while the third is maintained fixed. As expected, $CF$ is directly proportional to wind speed and active flame depth and inversely proportional to moisture content. The discontinuities in the curves are due to the computation of ${\dot{q}}_{E,conv}^{″}$ as the angle $A$ varies in Equation (7).

Then, we show the results of the computation of the number of linear meters of active fire front that can be extinguished by drones as the fire parameters vary. Concerning the time interval $\Delta t$ necessary to a drone for complete a round trip, it was chosen $\Delta t=6 \min .$ Based on the drone speeds shown in Table 1, it can be estimated that drones can fly at approximately $35 {\mathrm{km} \mathrm{h}}^{-1}\simeq 583 {\mathrm{m} \min }^{-1}$ at full load and $50 {\mathrm{km} \mathrm{h}}^{-1}\simeq 833 {\mathrm{m} \min }^{-1}$ after discharging water. As an example, with a platform positioned $1.5 \mathrm{km}$ away from the fire front, drones would spend 4.37 min travelling to the fire front and returning to the platform. A $\Delta t$ equal to 6 min (including time to change battery/payload and time to discharge water) is assumed to remain fairly cautious, but even lower values are possible if the platform is located against the wind close to the active fire front, as in the case of firefighters’ vehicles.

Figure 4 shows the linear meters of fire that can be arrested by using the firefighting system. For example, approximately 70–75 linear meters of active front can be extinguished with 120 drones each carrying $20 \mathrm{L}$ or with 80 drones carrying $30 \mathrm{L}$ (Figure 4a). These results show that a platform managing up to 120 drones is a valid alternative to current firefighting systems in the case of small or low-intensity fires. In a large wildland fire, the system can control a part of the front, e.g., to prevent advance in critical areas. The effectiveness can be further improved by the simultaneous use of multiple platforms that can attack the fire front from multiple sides (Figure 4f). Moreover, the effect of the platform can be directed to the fire front or to areas that have not yet caught fire thereby creating a firebreak without risk for firefighters who are not forced to approach the fire.

3.2. Cellular Automata Model for Studying the Effect of the UAV Platform on Fire Evolution

The CA model described in Section 2.6 has been applied to simulate the spread of forest fires in order to enable drone intervention to entirely or just partially suppress the fire. The environment is completely simulated and it is not based on a real case study. The territory consists of a small-scale surface area of about 40,000 square meters, essentially flat, characterized by vegetation types similar to those of the Mediterranean scrub. It is displayed as a grid of 2-m-long side cells created in the form of a matrix in MATLAB^® environment. Different matrices are used to characterize the parameters involved in fire: wind velocity and direction, vegetation density and type (grass and shrubs), and moisture content. All the parameters employed in the CA model are included in

Table 5. Values for CA model.

Values for the probability${\mathit{p}}_{\mathit{v}\mathit{e}\mathit{g}}$and parameter${\mathit{p}}_{\mathit{m}}$
	Grass	Shrub
$p_{veg}$	0.4	0.4
$M_d$	0.18	0.24
Values for the probability${\mathit{p}}_{\mathit{d}\mathit{e}\mathit{n}}$
Category	Density	$p_{den}$
	Sparse	−0.4
$p_{den}$	Normal	0
	Dense	0.3
Operational parameters for CA simulations
Parameter	Symbol	Value
Spread probability under no wind and flat terrain	$p_0$	0.6
Wind parameter 1	$c_1$	0.045
Wind parameter 2	$c_2$	0.131
Moisture parameter	$b$	0.111

. The probability values related to density and type of vegetation have been empirically computed by [61]. Other parameters, as constant fire propagation probability $p_0$, and wind coefficient $c_1$ and $c_2$, have been determined by [61] by performing multiple simulations with non-linear optimization technique. Random matrices are generated for the vegetation density and typology covering the entire cell grid.

To carry out the simulations, a platform managing $120$ drones each carrying $20$ L of extinguishing liquid was selected. The number $m_f$ of linear meters of active fire front that can be extinguished by using the platform is computed by Equation (22). Given both this value and the cell size, the number of cells $n_c$ where drones can spread the liquid is calculated in two different ways: if the front develops diagonally, $n_c$ is obtained by dividing $m_f$ with the length of the cell side $l=2$ multiplied by a factor equal to $\sqrt{2}$, i.e., applying the formula to calculate the diagonal of a square $\sqrt{2} \mathrm{l}$; otherwise $m_f$ is divided only by $l$.

After deciding the position of the platform (on the south side of the domain in the simulation), we faced the flames with a direct attack on both the head and the flank of the fire, as described in [70]. The state of $n_c$ contiguous cells of the fire front closer to the platform is set equal to $4$, i.e., in these cells there is a continuous flow of water that extinguishes the fire. With the intervention of drones, the total fire area varies in different ways depending on fire parameters. Specifically, both types of vegetation adopted in the model lead to the outbreak of a fire with low, but rapidly spreading flames. Furthermore, the higher the wind speed, the faster the front spreads, and the more water is needed to extinguish it, all other factors being equal.

Figure 5 shows the effects of the platform ($120$ drones each carrying $20$ L) impact on the evolution of a wildland fire. In particular, in Figure 5a the variation of the area in time without any extinguishing intervention and with the intervention of the firefighting method is depicted for wind speed of $10$, $20$, and $30{ \mathrm{km} \mathrm{h}}^{-1}$. Drones start to arrive 15 min after fire ignition and the moisture content is assumed to be $18\%$ for grassland and $24\%$ for shrubland. A platform is able to completely arrest the fire for wind speed of 10${ \mathrm{km} \mathrm{h}}^{-1}$. Figure 5b shows the variation of the area in time with wind speed fixed at $20{ \mathrm{km} \mathrm{h}}^{-1},$ compared with to the spread without any intervention. Drones start the intervention at times $t_a=10, 15, 20, 25 \min$. Finally, Figure 5c,d illustrate the fire evolution fronts without any extinction and with the intervention of drones at $t_a=15 \min$ (positioned along the blue line and corresponding to $n_c=31$ cells), respectively. Even if a single platform is not able to completely extinguish the fire in these conditions, it is nevertheless effective in containing its advance. The use of two platforms allows the complete extinction in that case.

The interaction between the action of drones and the fire front considered in the previous simulations does not take into account possible strategies aimed at maximizing the effect. As stated in Section 2.1, the volume of water transported by a drone is significantly limited compared to the volume of water carried by a firefighting aircraft, but drones can provide temporal continuity and uniformity of diffusion. The evaluation of a more precise interaction between the action of drones and the modification of the fire front requires an accurate study of how water modifies the fire parameters, considering its distribution, the pressure with which it is released, and whether it is atomized into droplets. The literature on this topic is limited and further research will be needed to determine how a constant flow of water (possibly atomized into droplets) modifies the fire front, even compared to current firefighting equipment. It may be necessary to adopt physical fire models, which can more accurately represent the effect of water on temperature, pyrolysis, etc. than the CA model. In this work, physical models were not chosen because of their dependence on many parameters whose values are determined by the specific scenario under consideration, while the purpose of this work is to study the effect of the drone system for a scenario as generic as possible.

As an example of a possible strategy, we assume that fire conditions need a $CF$ of $4 {\mathrm{L} \min }^{-1}{\mathrm{m}}^{-1}$. According to Figure 3a, such $\mathrm{CF}$ is required for example in a fire with wind speed of $18{ \mathrm{km} \mathrm{h}}^{-1}$, moisture content of $26\%$, and active flame depth of $2 \mathrm{m}$. We consider a scenario in which 12 drones carrying a payload of 20 L and completing a round trip in $\Delta t=6$ min. Such drones are capable of extinguish $10$ linear meters of fire front corresponding, for $\mathrm{D}=2$, to an area of $20{ \mathrm{m}}^2$. Indeed, by using Equation (24), we obtain:

$$n_r= \frac{ CF \Delta t m_r}{ L_d}= \frac{ 4 ·6 ·10}{ 20}=12$$

(30)

A potential approach to generate a rain effect could be to spray the 20 L of water carried by each drone for 30 s while it flies over 10 linear meters of front. Since a drone is over the area every 30 s, this leads to an essentially continuous flow of water. A very limited number of drones could then complement traditional firefighting resources. For example, they could be sent to either contain fires in areas that are dangerous or not easily accessible by ground firefighting crews, stop outbreaks that might restart burning overnight, or contain part of the front while waiting for aircraft to arrive.

4. Conclusions

We have estimated the impact of the use of a platform managing a variable number of drones able to spread water or other extinguishing liquid on a wildland fire. Assuming that the drone system meets the requirements (i)–(iii) stated in Section 2.1, we have estimated its effect on the propagation of a forest fire taking into account many factors including fire intensity, flame length, vegetation, moisture content, wind speed and direction, payload carried by each drone, time for each drone to reach the fire front. On the basis of the critical water flow computed as a function of the main parameters involved in the evolution of a fire, we have calculated the number of linear meters of active fire front that can be extinguished as these factors vary.

Then, we have used a fire propagation model to study the evolution of the fire as a result of the containment effect of the platforms. By means of the results of the analyses and graphs carried out in both approaches, we have shown that the drone system can furnish the flow of water required to fight low-intensity and limited extent forest fires or to complement the existing techniques. Practical implementation of the platform requires a high degree of technology and further research is needed to realize a system that meets the assumed requirements.

Since the extinguishing liquid is fractioned into multiple parts, unlike when using aircrafts, future work will investigate a control strategy to decide the part of the fire front where it is preferable to address the action of drones, also using different fire simulation models [71]. It would also be interesting to study the rain effect induced by drones in comparison to the impact produced by aircraft carrying the same amount of water. Furthermore, the studies on the mechanics of the platform-drone system will be investigated with regard to technical issues such as the reaction to wind turbulences and high flame temperatures. Although in this work we have dealt with drones with a maximum payload of 50 L, the formulas for estimating the number of linear meters of active fire front that can be extinguished are also valid for drones with much heavier payloads. The use of hybrid UAVs with considerably higher payloads (between 300 and 500 L) will be the subject of a future study.

5. Patents

The idea of the drone system described herein is the subject of the patent “Methods and apparatus for the employment of drones in firefighting activities” [72].