A Group Maintenance Method of Drone Swarm Considering System Mission Reliability
Abstract
1. Introduction
2. Preliminaries
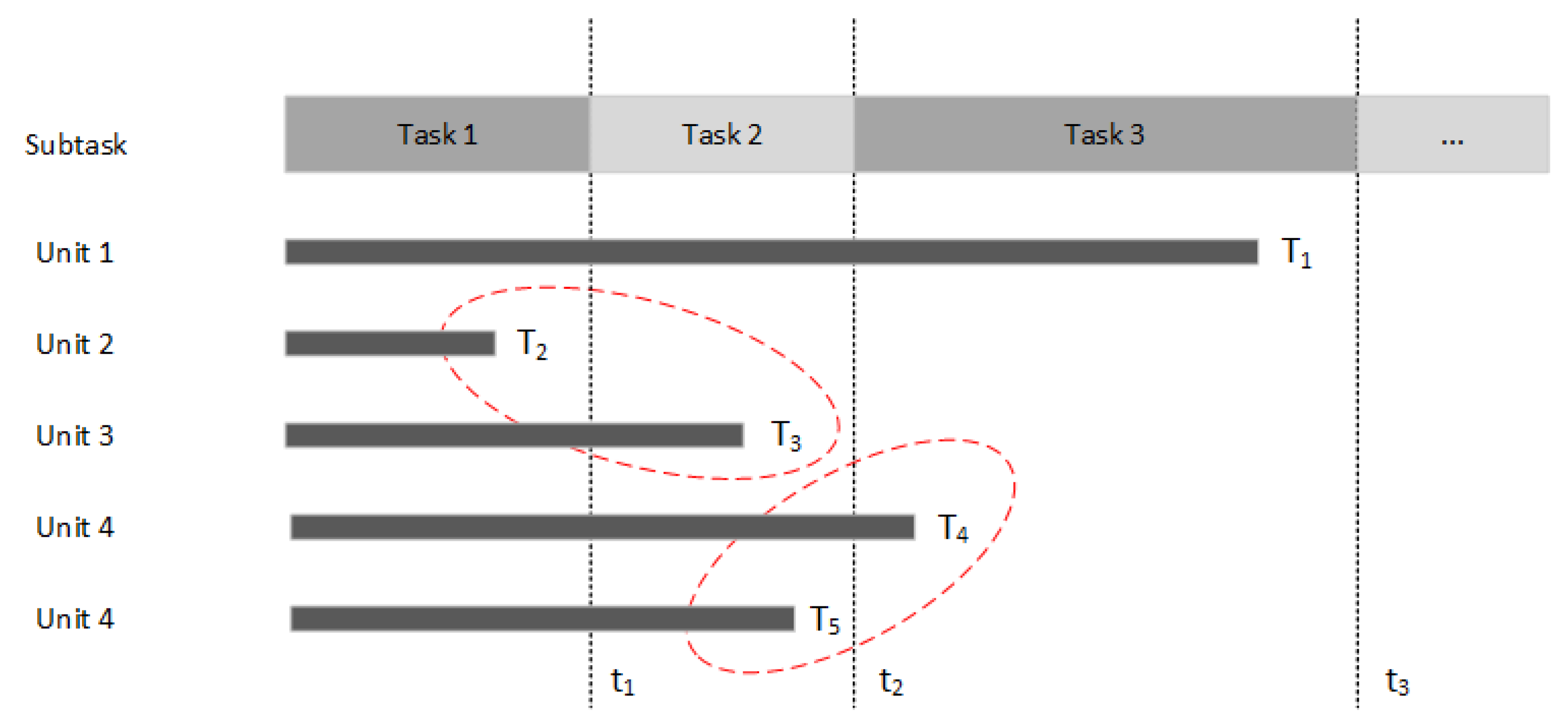
2.1. Mission Characteristics of Drone Swarm
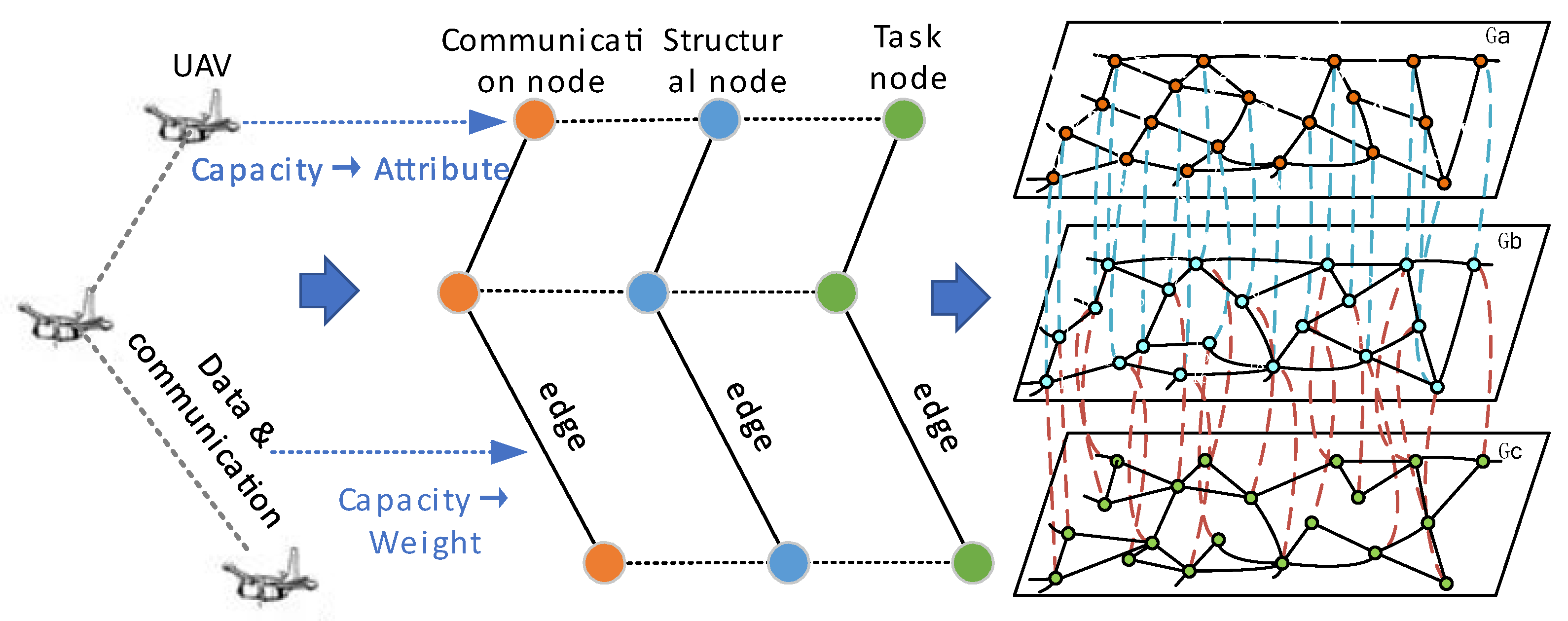
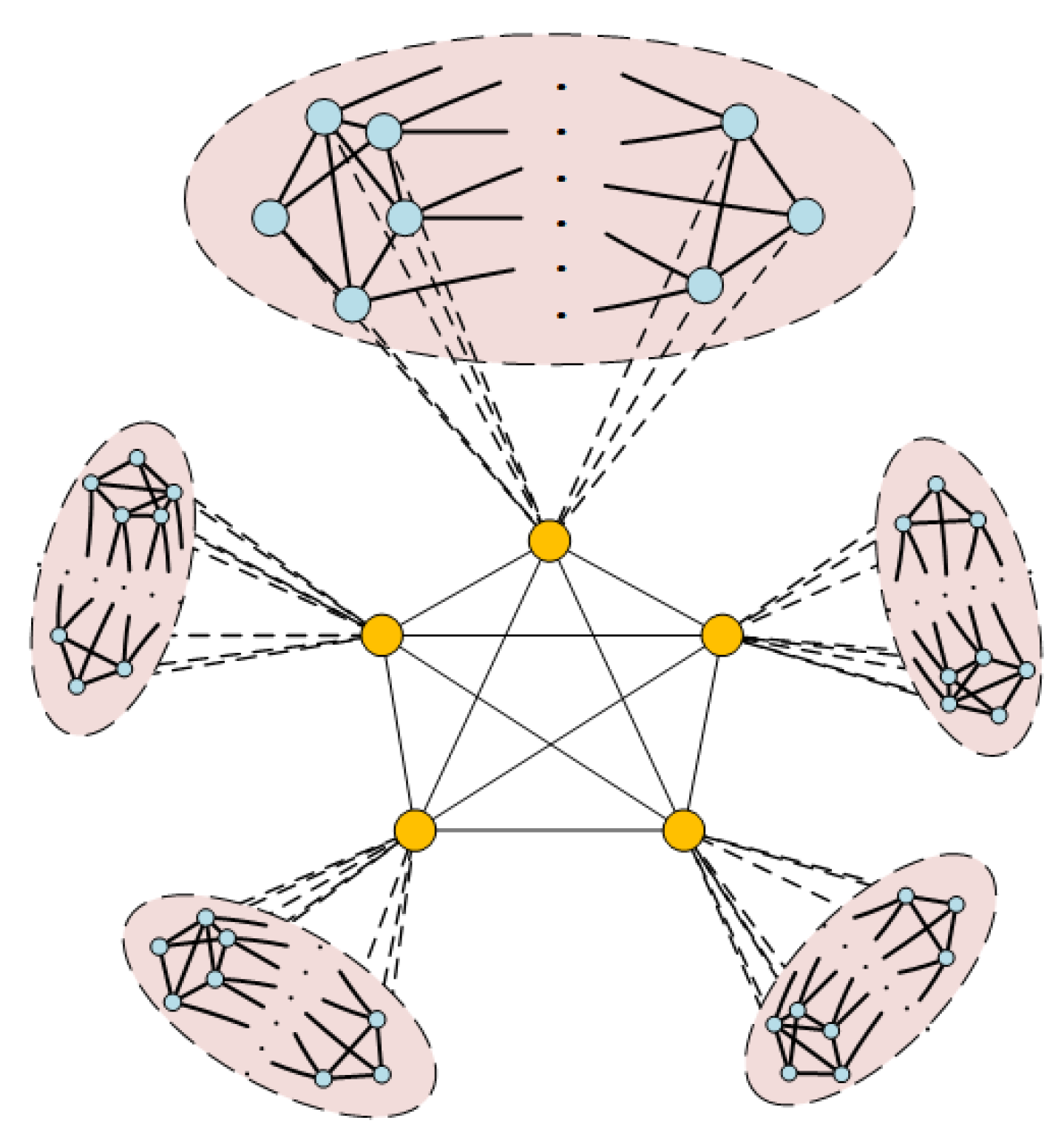
2.2. Complex Network Model of Swarm
2.3. Relationship between Swarm Maintenance and Network
2.4. Swarm Mission Reliability Evaluation Method
3. Swarm Maintenance Method
3.1. Basic Assumptions
3.2. Unit Reliability Prediction Based on Prevention
3.3. Maintenance Grouping Strategy and Cost
3.4. Mission Reliability Evaluation
3.5. Optimize Grouping Decision
4. Simulation Analysis
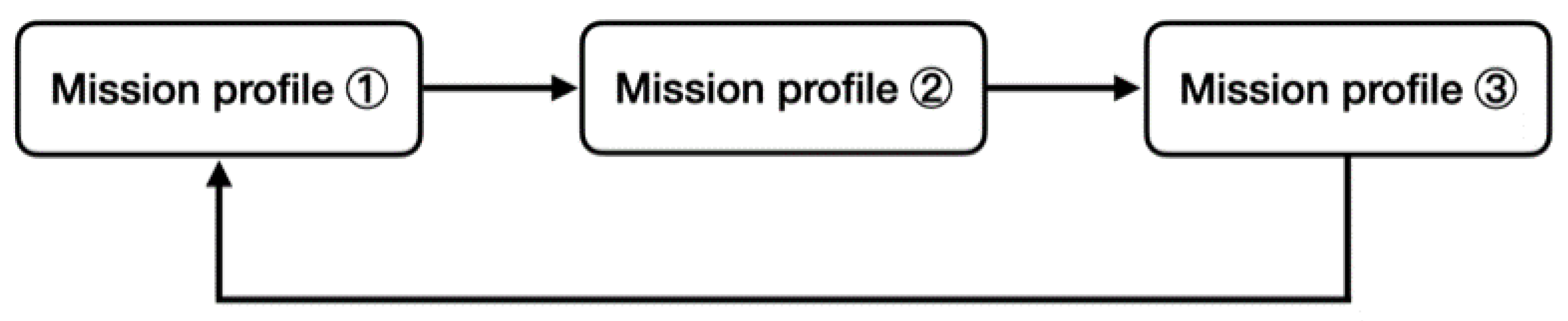
4.1. Maintenance Time and Grouping Strategy
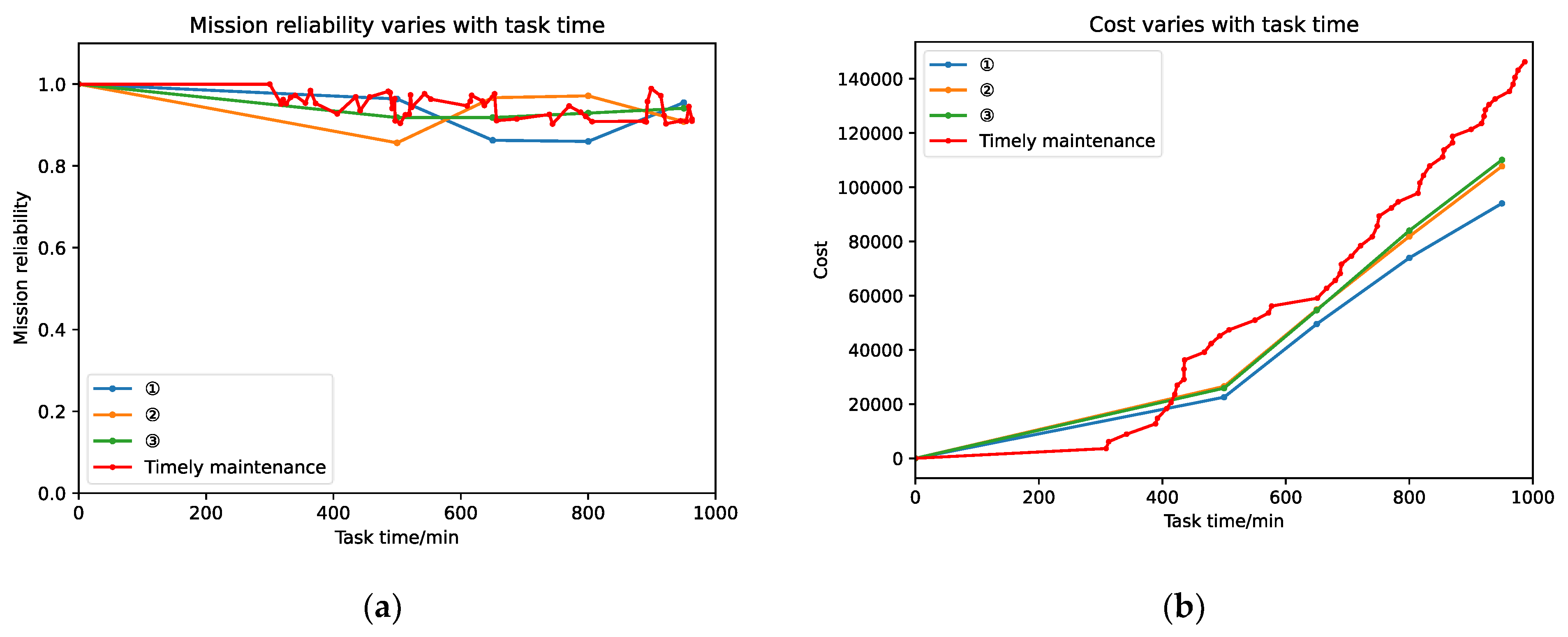
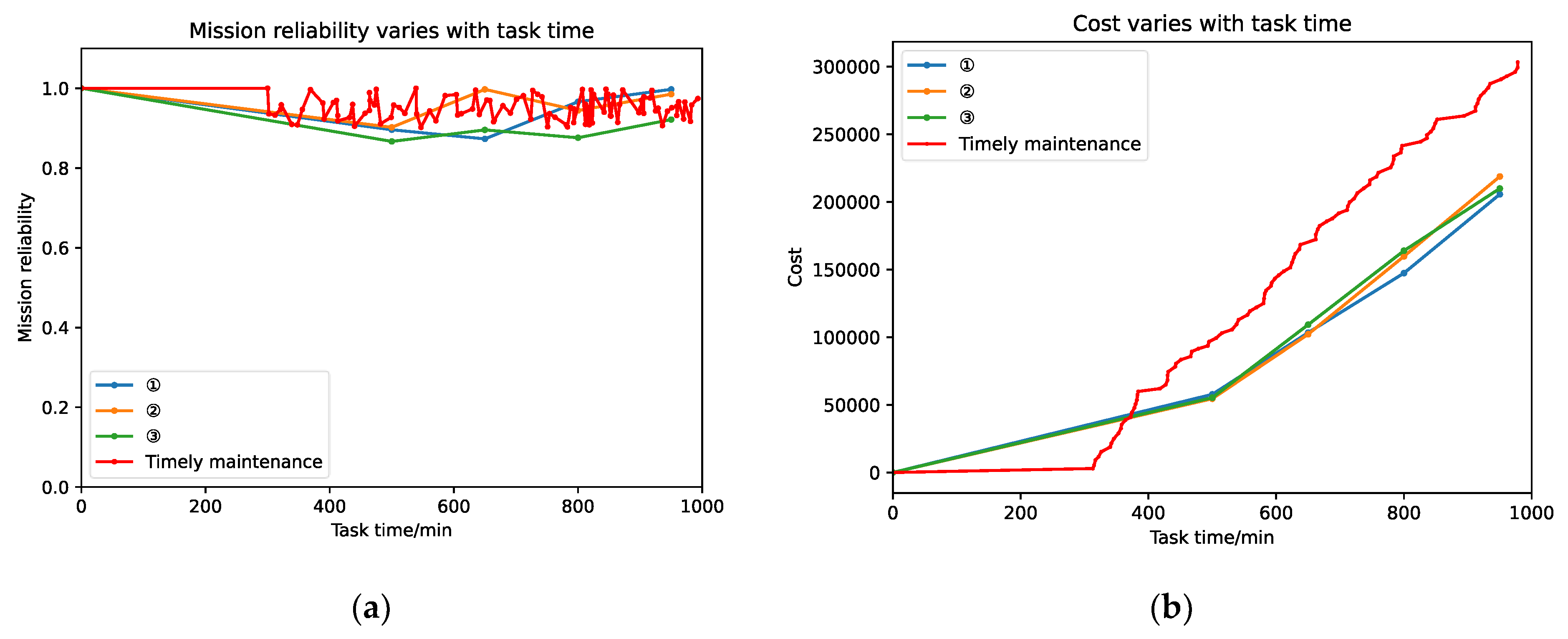
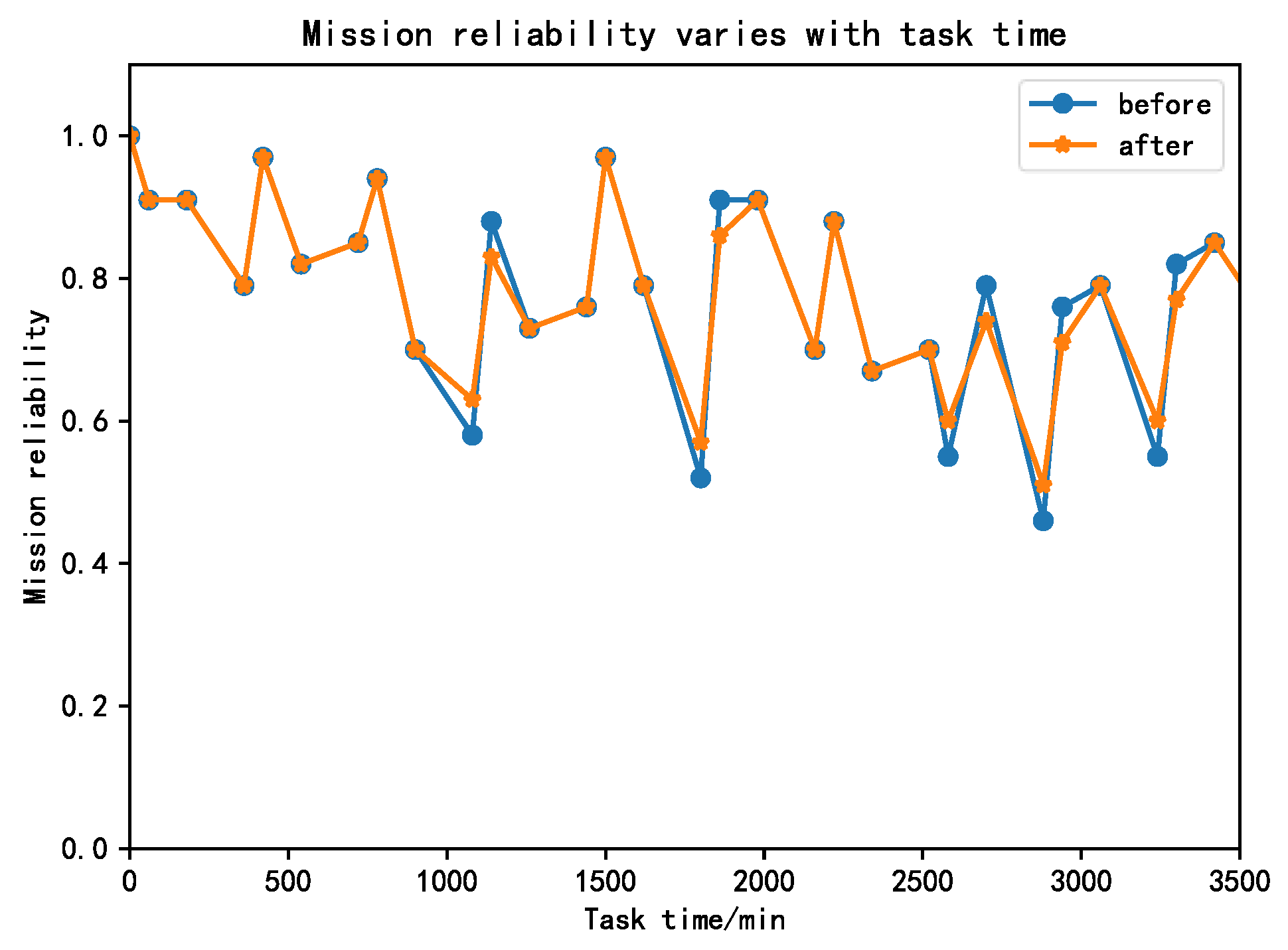
4.2. Mission Reliability and Cost of a Swarm System
4.3. Comparison Summary
- (1)
- In terms of system reliability: (a) As the scale of the swarm increases, the impact of node maintenance brought by timely maintenance strategy and group maintenance strategy on the reliability of swarm missions will gradually decrease. This is because there are many nodes, and the maintenance and removal of nodes have relatively little impact on the reliability of the remaining swarm missions; (b) The average mission reliability under the timely maintenance strategy is generally higher than that under any group maintenance. Because timely maintenance only repairs one node at a time, it has less impact on the reliability of the remaining swarm missions; (c) The reliability of system missions fluctuates under the timely maintenance strategy. Because the system is forced to be repaired during non-mission completion time and many repair opportunities, the system mission reliability fluctuates wildly. Still, the system mission reliability fluctuation will weaken with the expansion of the swarm scale.
- (2)
- In terms of maintenance costs: (a) Considering the cost of downtime, the maintenance cost of timely maintenance is far greater than the maintenance cost of group maintenance under any strategy. The cost has a specific impact, that is, the cost of maintenance in advance is reduced, whereas the cost of maintenance increases; (b) As the scale of the swarm continues to expand, the cost of timely maintenance is higher than the cost of any grouped maintenance. The scale has grown exponentially.
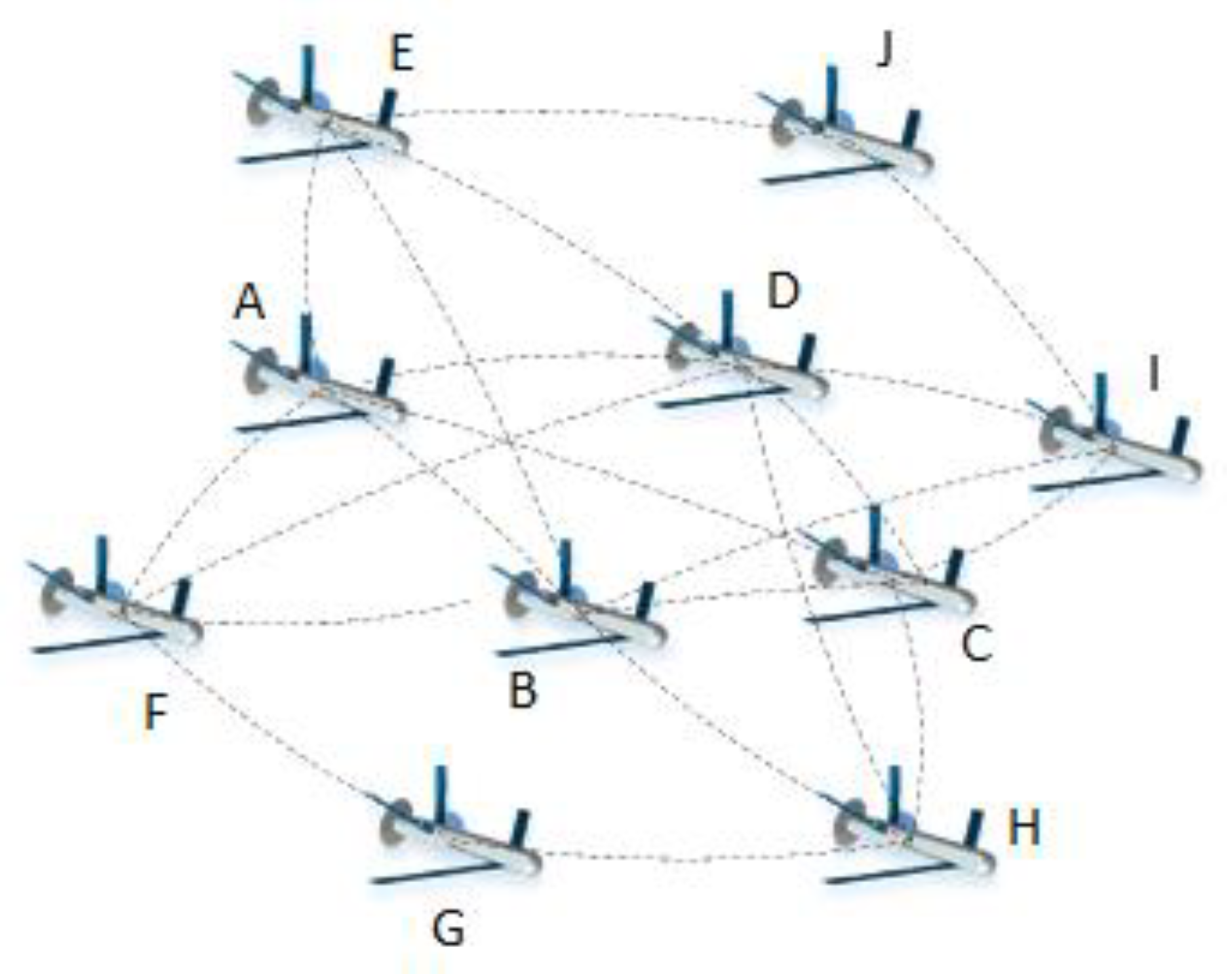
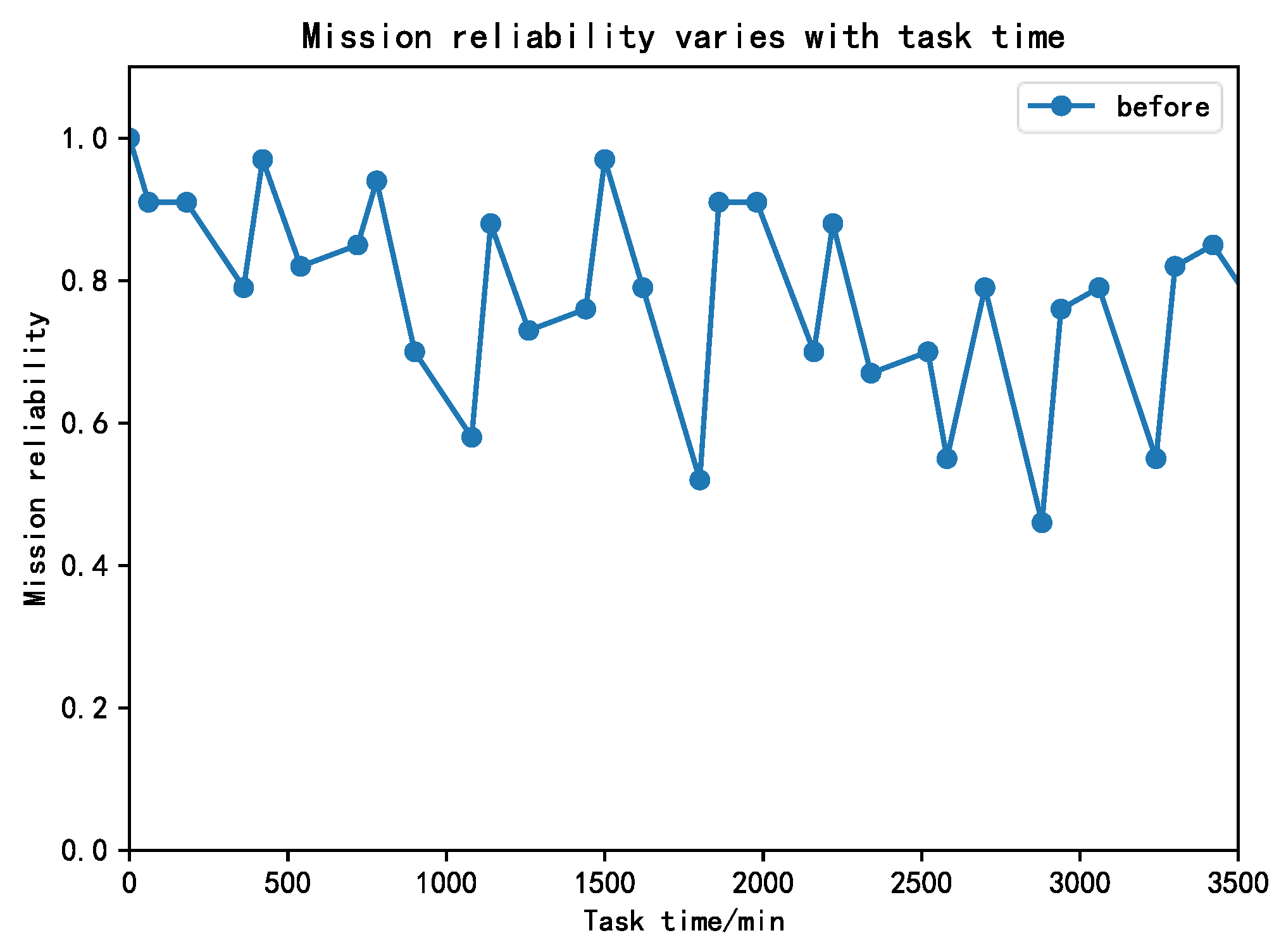
5. Case Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, W.; Li, M.; Alzahrani, B.; Alotaibi, R.; Barnawi, A.; Ai, Q. A Blockchain-Based Secure Crowd Monitoring System Using UAV Swarm. IEEE Netw. 2021, 35, 108–115. [Google Scholar] [CrossRef]
- He, D.; Yang, G.; Li, H.; Chan, S.; Cheng, Y.; Guizani, N. An Effective Countermeasure Against UAV Swarm Attack. IEEE Netw. 2021, 35, 380–385. [Google Scholar] [CrossRef]
- Xu, J.; Sun, K.; Xu, L. Integrated system health management-oriented maintenance decision-making for multi-state system based on data mining. Int. J. Syst. Sci. 2016, 47, 3287–3301. [Google Scholar] [CrossRef]
- Nzukam, C.; Voisin, A.; Levrat, E.; Sauter, D.; Iung, B. Opportunistic maintenance scheduling with stochastic opportunities duration in a predictive maintenance strategy. IFAC-PapersOnLine 2018, 51, 453–458. [Google Scholar] [CrossRef]
- Gonçalves, P.; Sobral, J.; Ferreira, L. Establishment of an initial maintenance program for UAVs based on reliability principles. Aircr. Eng. Aerosp. Technol. 2017, 89, 66–75. [Google Scholar] [CrossRef]
- Wang, H. A survey of maintenance policies of deteriorating systems. Eur. J. Oper. Res. 2002, 139, 469–489. [Google Scholar] [CrossRef]
- Gandhi, K.; Schmidt, B.; Ng, A.H.C. Towards data mining based decision support in manufacturing maintenance. Procedia CIRP 2018, 72, 261–265. [Google Scholar] [CrossRef]
- Batun, S.; Azizoğlu, M. Single machine scheduling with preventive maintenances. Int. J. Prod. Res. 2009, 47, 1753–1771. [Google Scholar] [CrossRef]
- Koochaki, J.; Bokhorst, J.C.; Wortmann, H.; Klingenberg, W. The influence of condition-based maintenance on workforce planning and maintenance scheduling. Int. J. Prod. Res. 2013, 51, 2339–2351. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Peng, R. An integrated preventive maintenance and production planning model with sequence-dependent setup costs and times. Qual. Reliab. Eng. Int. 2017, 33, 2451–2461. [Google Scholar] [CrossRef]
- Tian, Z.; Liao, H. Condition based maintenance optimization for multi-component systems using proportional hazards model. Reliab. Eng. Syst. Saf. 2011, 96, 581–589. [Google Scholar] [CrossRef]
- Martinod, R.M.; Bistorin, O.; Castañeda, L.F.; Rezg, N. Maintenance policy optimization for multi-component sys-tems considering degradation of components and imperfect maintenance actions. Comput. Ind. Eng. 2018, 124, 100–112. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, M. Research Progress on War Complex System of Systems Modeling Based on Complex Network. J. Syst. Simul. 2015, 27, 217–225. (In Chinese) [Google Scholar]
- Qu, X.; Liu, E.; Wang, R.; Ma, H. Complex Network Analysis of VANET Topology With Realistic Vehicular Traces. IEEE Trans. Veh. Technol. 2020, 69, 4426–4438. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, H.; Dang, W.; Li, Y.; Hong, X.; Liu, M.; Chen, G. Complex Network Analysis of Wire-Mesh Sensor Measurements for Characterizing Vertical Gas–Liquid Two-Phase Flows. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1134–1138. [Google Scholar] [CrossRef]
- Ren, W.; Wu, J.; Zhang, X.; Lai, R.; Chen, L. A Stochastic Model of Cascading Failure Dynamics in Communication Networks. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 632–636. [Google Scholar] [CrossRef]
- Zhao, Z. Study on the Network Traffic Abnormal Detection Based on EEMD. In Proceedings of the 2016 2nd International Conference on Advances in Mechanical Engineering and Industrial Informatics (AMEII 2016), Hangzhou, China, 9–10 April 2016. [Google Scholar]
- Yang, L.; Draief, M.; Yang, X. Heterogeneous virus propagation in networks: A theoretical study. Math. Methods Appl. Sci. 2017, 40, 1396–1413. [Google Scholar] [CrossRef]
- Duan, J.; Zheng, H. Vulnerability Analysis Method for Complex Networks Based on Node Importance. Control Eng. China 2020, 27, 692–696. (In Chinese) [Google Scholar]
- Cheng, C.; Bai, G.; Zhang, Y.-A.; Tao, J. Resilience evaluation for UAV swarm performing joint reconnaissance mission. Chaos 2019, 29, 053132. [Google Scholar] [CrossRef]
- Peng, C.; Huang, X.; Wu, Y.; Kang, J. Constrained Multi-Objective Optimization for UAV-Enabled Mobile Edge Computing: Offloading Optimization and Path Planning. IEEE Wirel. Commun. Lett. 2022, 11, 861–865. [Google Scholar] [CrossRef]
- Wang, L.; Lu, D.; Zhang, Y.; Wang, X. A Complex Network Theory-Based Modeling Framework for Unmanned Aerial Vehicle Swarm. Sensors 2018, 18, 3434. [Google Scholar] [CrossRef] [PubMed]
- Van Mieghem, P.; Doerr, C. A Framework for Computing Topological Network Robustness; Delft University of Technology: Delft, The Netherlands, 2010; pp. 1–11. [Google Scholar]









| Nodes | Life Distribution Model | Reliability Function | ||||
|---|---|---|---|---|---|---|
| A, B, C, D | Index distribution | 2840 | 150 | 26 | 150 | |
| E, F | normal distribution | 1200 | 150 | 3670 | 150 | |
| I, H | Weibull distribution | 960 | 150 | 7630 | 150 | |
| J, G | Inverse Gaussian distribution | 1984 | 150 | 18 | 150 | |
| Nodes | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| Actual maintenance time(min) | 584 | 603 | 536 | 555 | 689 | 720 | 930 | 496 | 523 | 871 |
| Maintenance Plan | 500 min | 650 min | 800 min | 950 min |
|---|---|---|---|---|
| ① | I, H, C | A, B, D | E, F | J, G |
| ② | I, H, D, C | B, A, E | F, J | G |
| ③ | I, H, D | A, B, C | E, F | J, G |
| Maintenance Strategy | Mission Reliability | Total Maintenance Cost ($) | |||
|---|---|---|---|---|---|
| 500 min | 650 min | 800 min | 950 min | ||
| ① | 0.803 | 0.735 | 0.892 | 0.933 | 23,620 |
| ② | 0.718 | 0.779 | 0.917 | 0.970 | 22,343 |
| ③ | 0.819 | 0.714 | 0.906 | 0.937 | 22,864 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Wang, L.; Wang, X. A Group Maintenance Method of Drone Swarm Considering System Mission Reliability. Drones 2022, 6, 269. https://doi.org/10.3390/drones6100269
Guo J, Wang L, Wang X. A Group Maintenance Method of Drone Swarm Considering System Mission Reliability. Drones. 2022; 6(10):269. https://doi.org/10.3390/drones6100269
Chicago/Turabian StyleGuo, Jinlong, Lizhi Wang, and Xiaohong Wang. 2022. "A Group Maintenance Method of Drone Swarm Considering System Mission Reliability" Drones 6, no. 10: 269. https://doi.org/10.3390/drones6100269
APA StyleGuo, J., Wang, L., & Wang, X. (2022). A Group Maintenance Method of Drone Swarm Considering System Mission Reliability. Drones, 6(10), 269. https://doi.org/10.3390/drones6100269





