Guidance, Navigation and Control System for Multi-Robot Network in Monitoring and Inspection Operations
Abstract
:1. Introduction
2. System Modeling and Description
2.1. Quadrotor Model
2.2. Wheeled Robot Model
3. Backstepping Controller
3.1. Quadrotor Control
3.2. Ground Robot Control
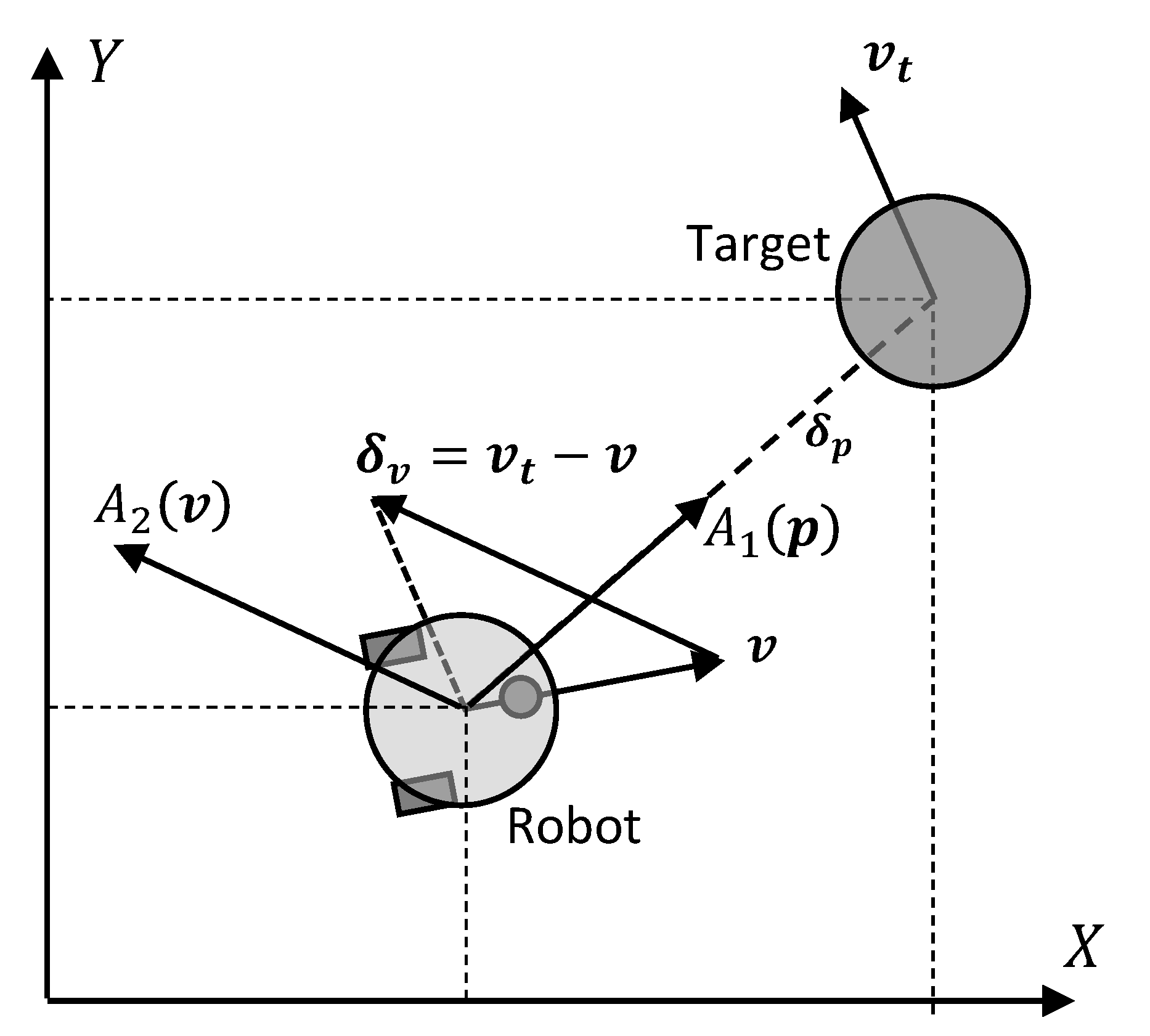
4. Motion Planning for Multi-Robot System
4.1. Potential Attractive Force
4.2. Potential Repulsive Force
5. Navigation System and State Estimations
5.1. Quadrotor State Estimations
5.2. Ground Robot State Estimation
6. Experimental Setup and Results
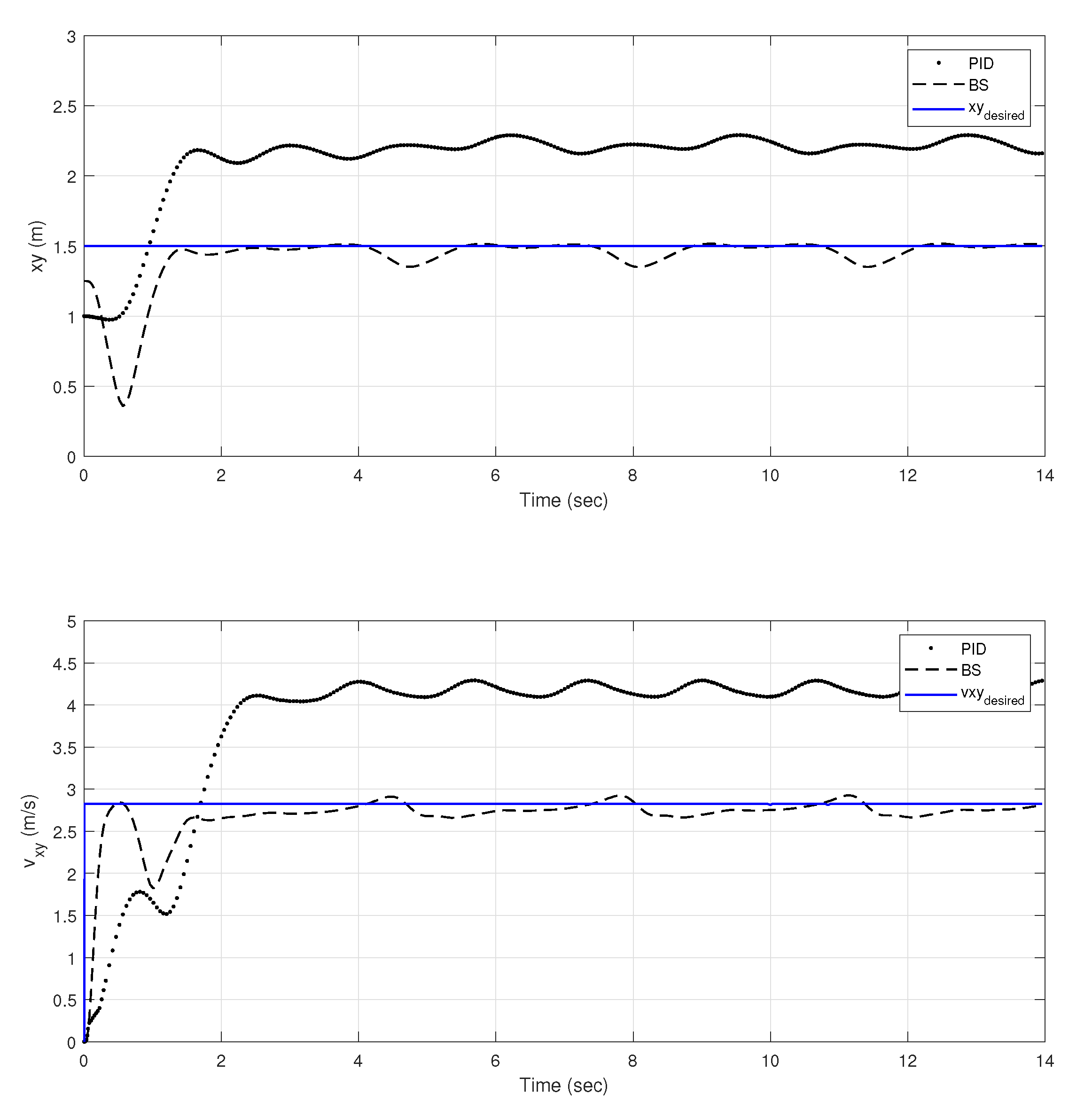
6.1. Backstepping and PID Comparison
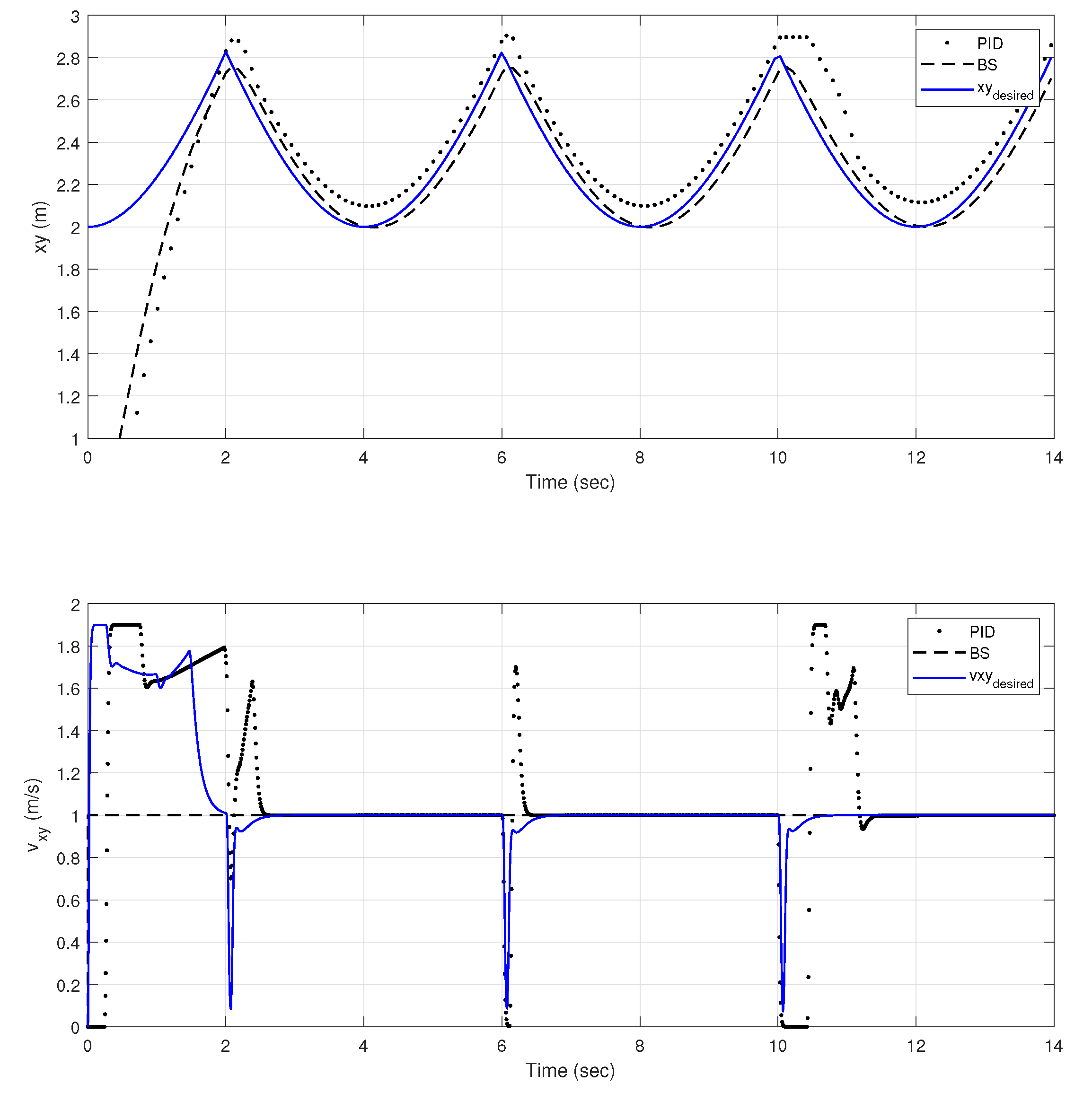
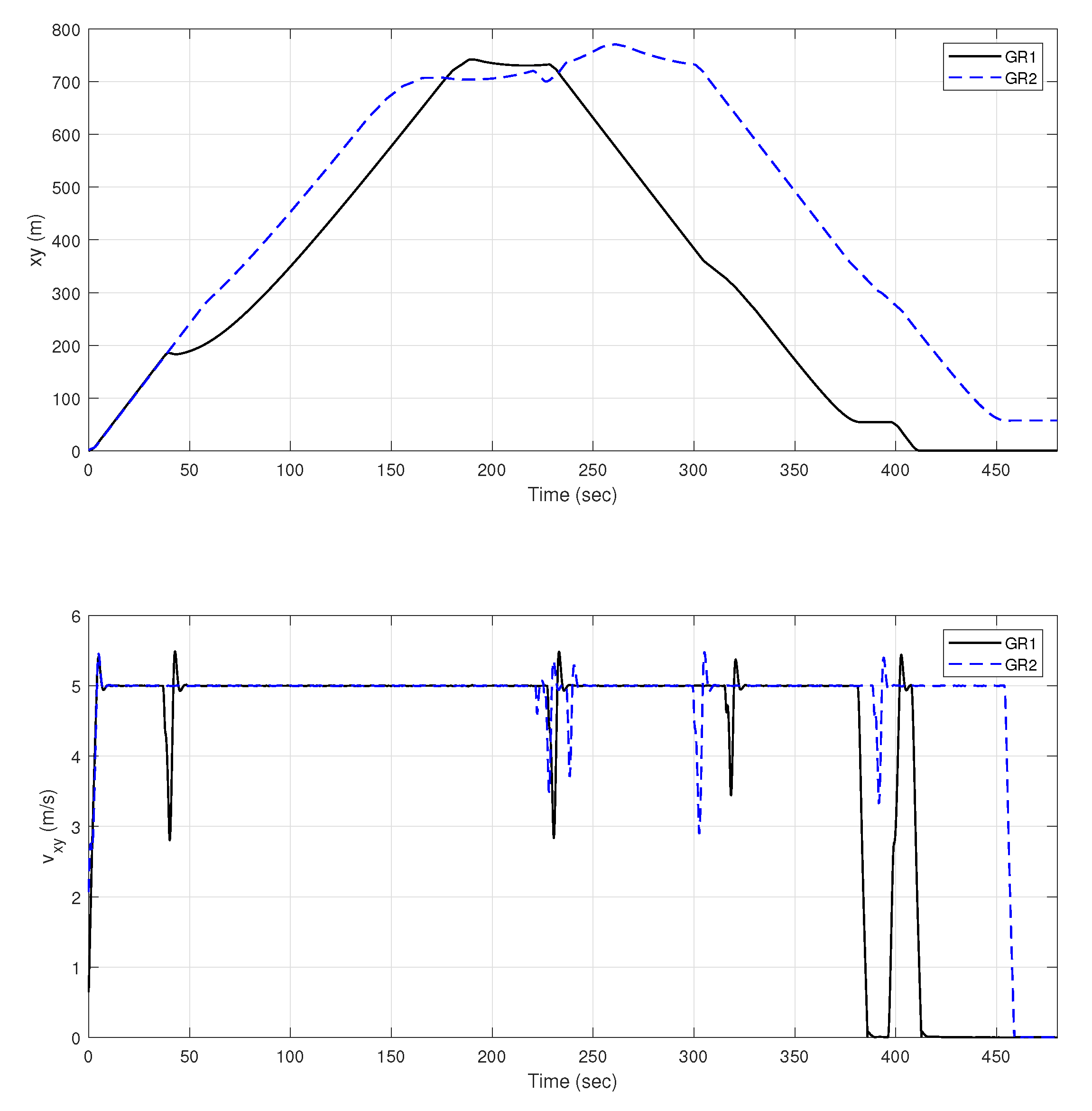
6.2. GNC System Performance
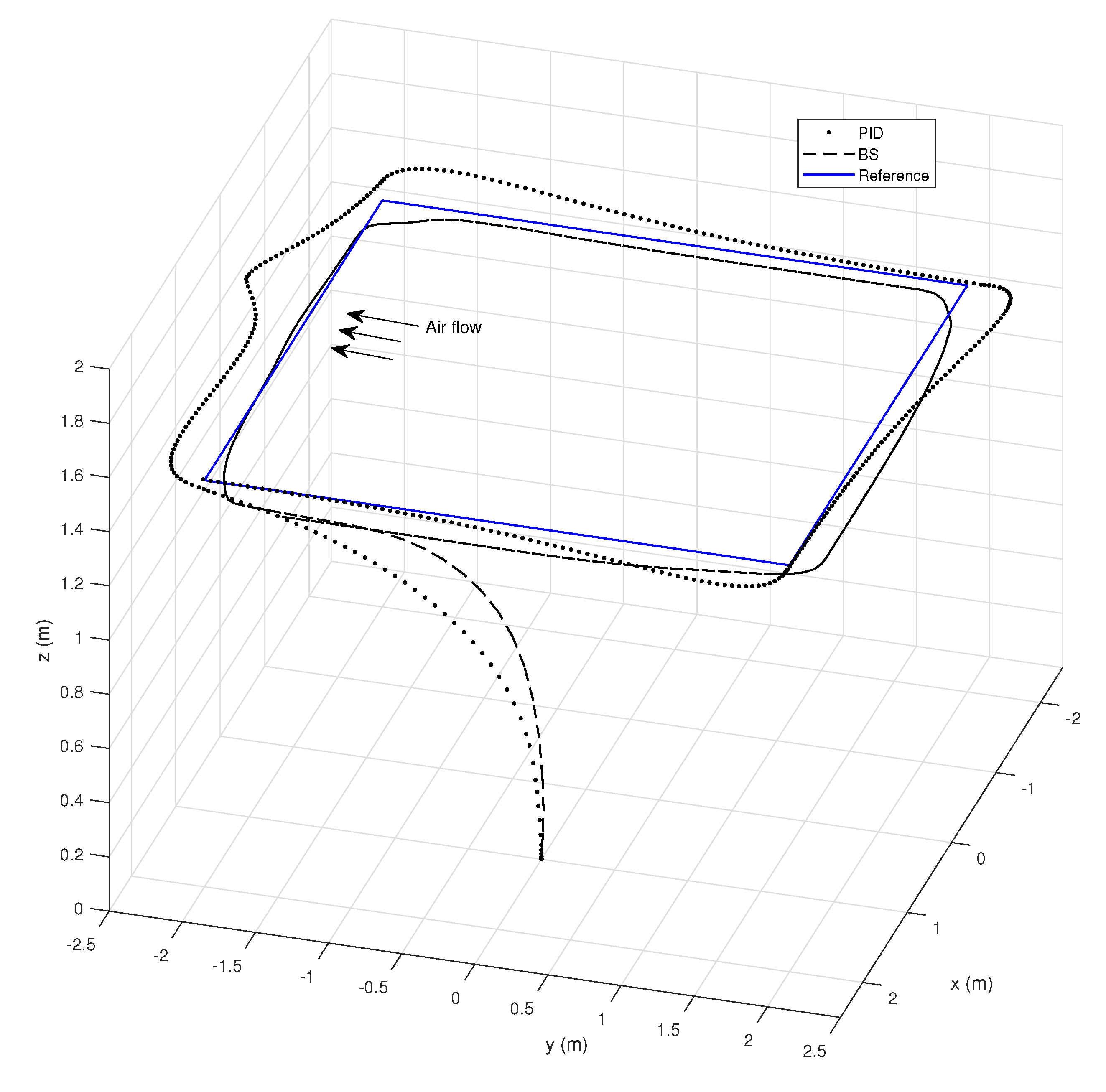
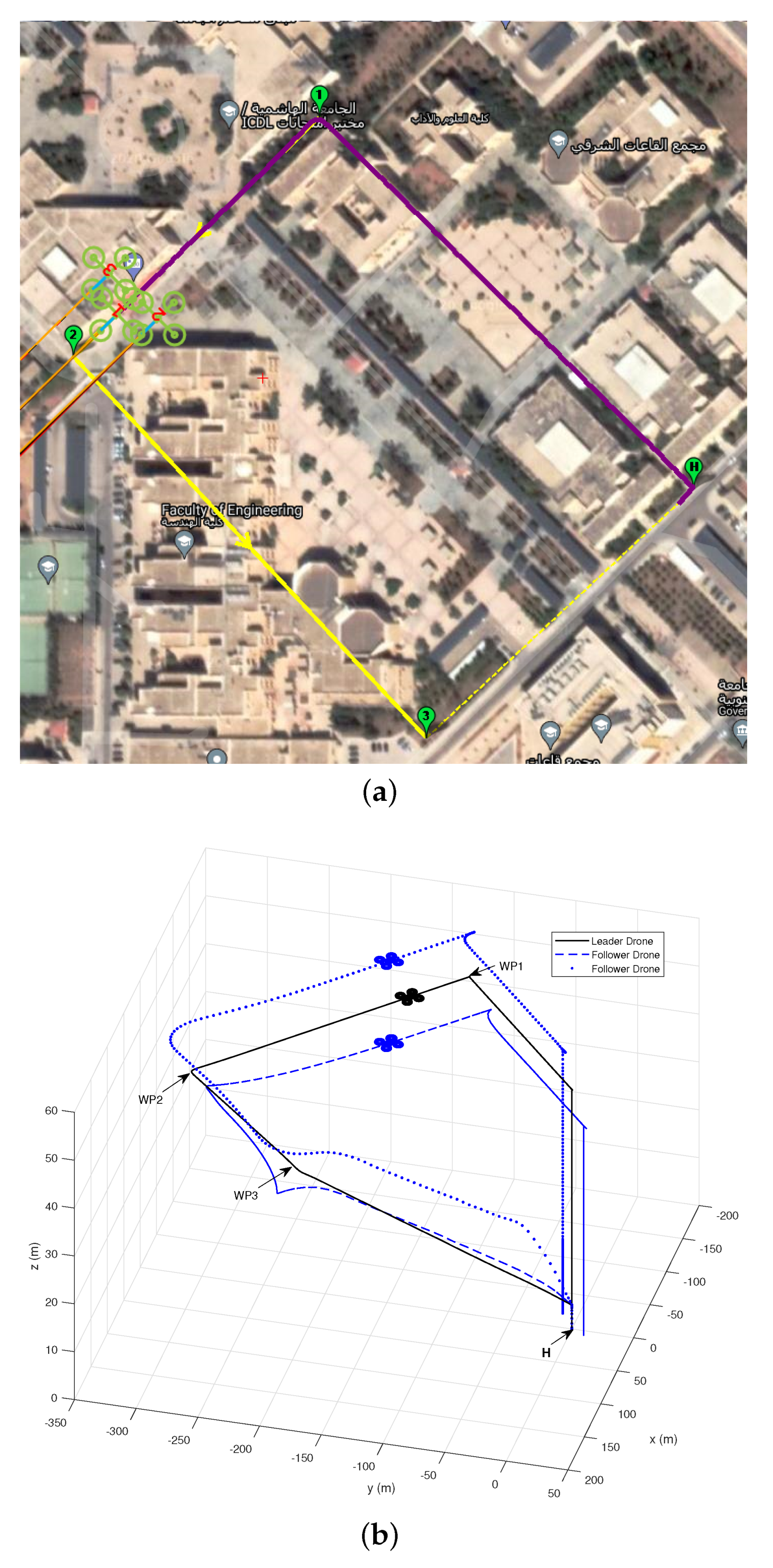
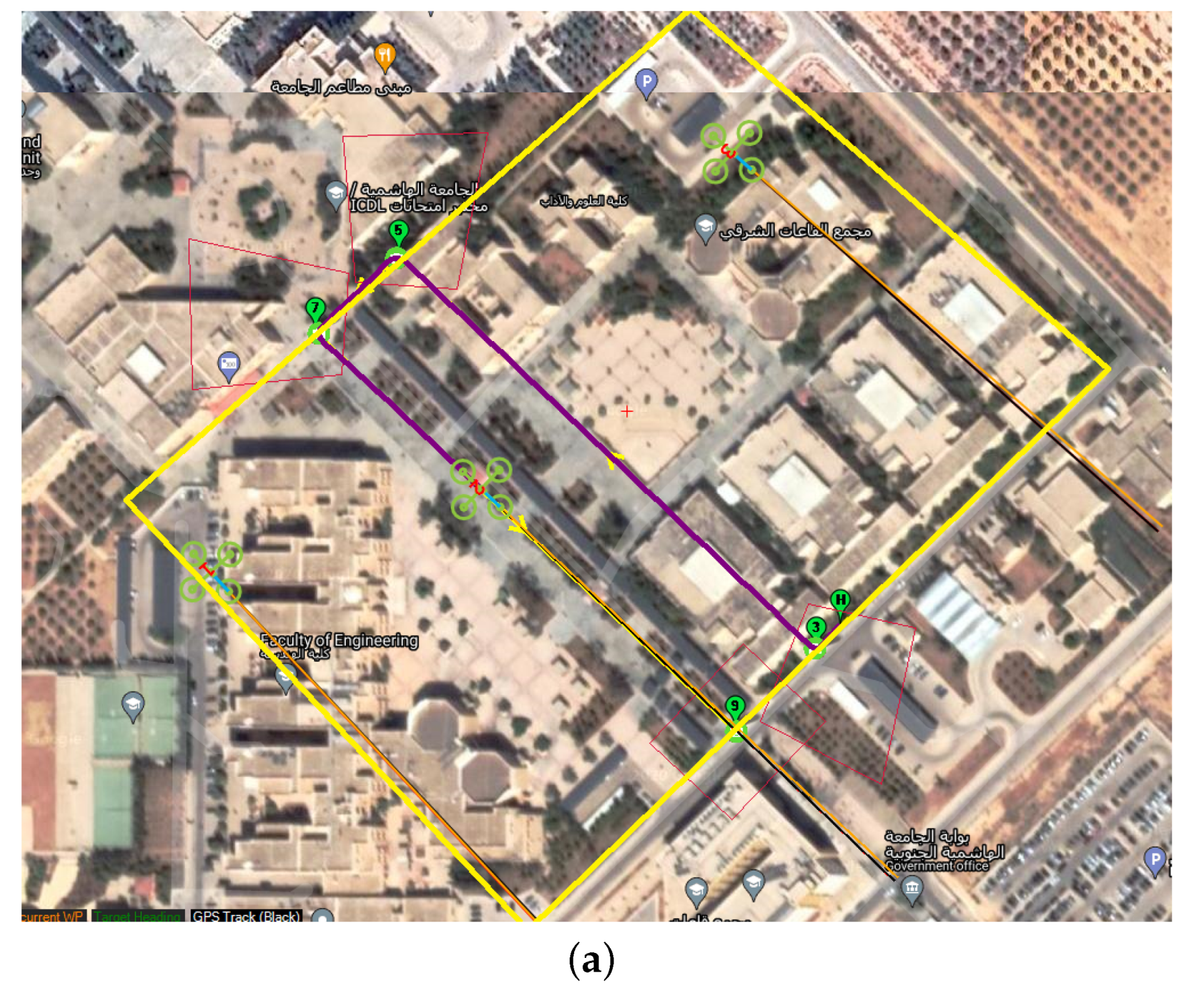
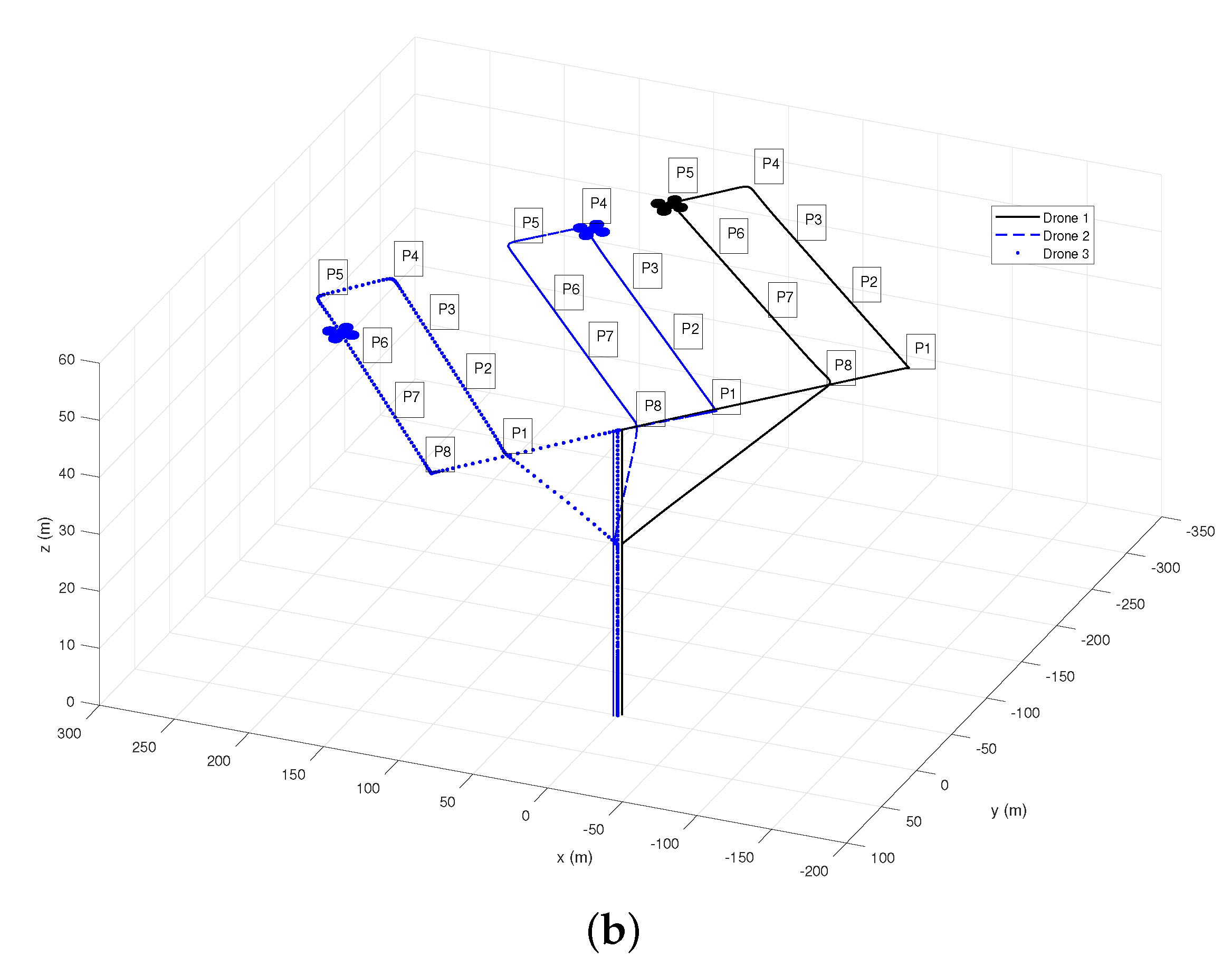
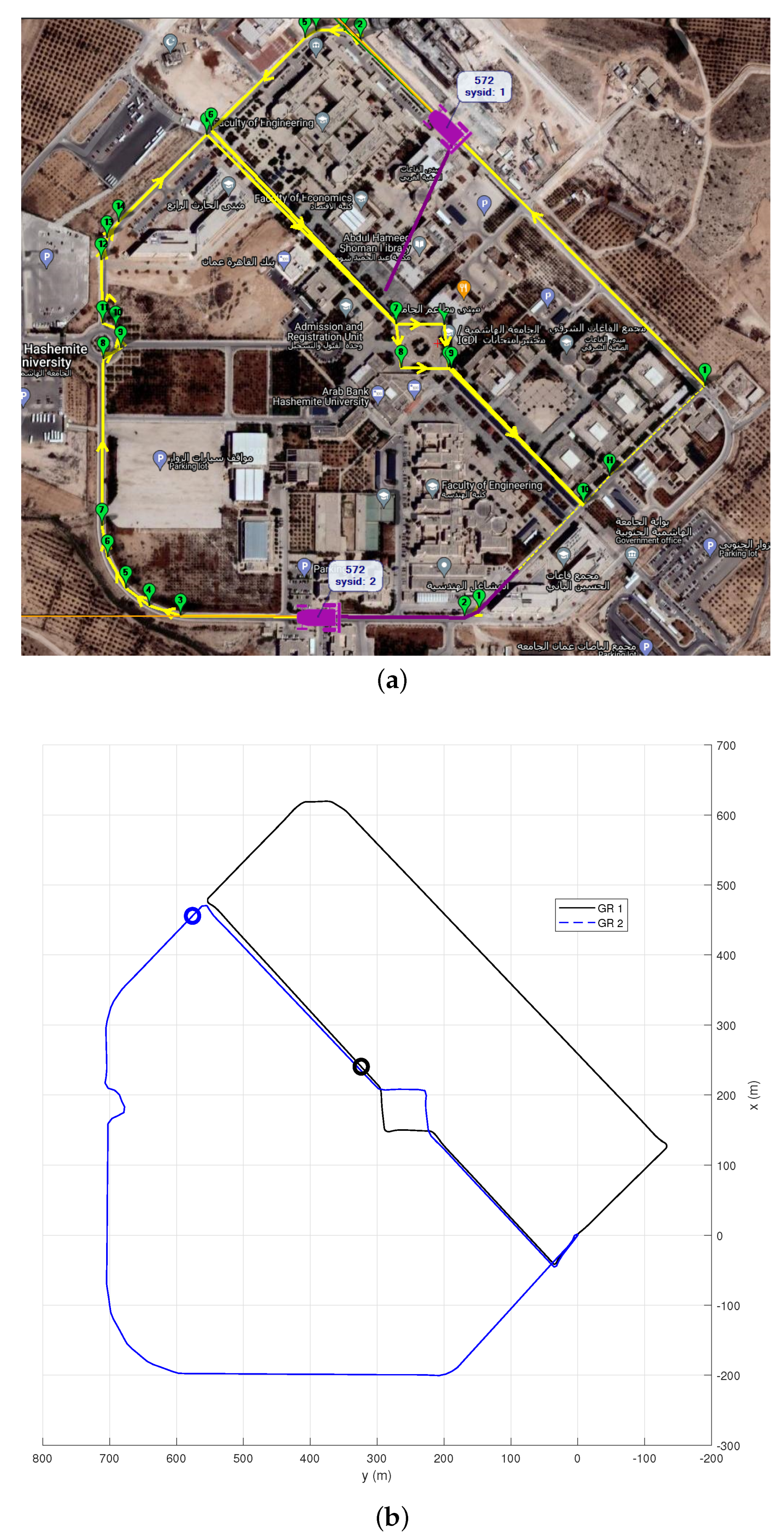
6.3. Outdoor Missions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- BaniHani, S.; Hayajneh, M.R.M.; Al-Jarrah, A.; Mutawe, S. New control approaches for trajectory tracking and motion planning of unmanned tracked robot. Adv. Electr. Electron. Eng. 2021, 19, 42–56. [Google Scholar] [CrossRef]
- Li, P.; Wu, X.; Shen, W.; Tong, W.; Guo, S. Collaboration of heterogeneous unmanned vehicles for smart cities. IEEE Netw. 2019, 33, 133–137. [Google Scholar] [CrossRef]
- Mohamed, N.; Al-Jaroodi, J.; Jawhar, I.; Idries, A.; Mohammed, F. Unmanned aerial vehicles applications in future smart cities. Technol. Forecast. Soc. Chang. 2020, 153, 119293. [Google Scholar] [CrossRef]
- Ju, C.; Son, H.I. Multiple UAV systems for agricultural applications: Control, implementation, and evaluation. Electronics 2018, 7, 162. [Google Scholar] [CrossRef] [Green Version]
- Mutawe, S.; Hayajneh, M.; BaniHani, S.; Al Qaderi, M. Simulation of Trajectory Tracking and Motion Coordination for Heterogeneous Multi-Robots System. Jordan J. Mech. Ind. Eng. 2021, 15, 337–345. [Google Scholar]
- Aminifar, F.; Rahmatian, F. Unmanned aerial vehicles in modern power systems: Technologies, use cases, outlooks, and challenges. IEEE Electrif. Mag. 2020, 8, 107–116. [Google Scholar] [CrossRef]
- Salahat, E.; Asselineau, C.A.; Coventry, J.; Mahony, R. Waypoint planning for autonomous aerial inspection of large-scale solar farms. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 763–769. [Google Scholar]
- Ismail, H.; Chikte, R.; Bandyopadhyay, A.; Al Jasmi, N. Autonomous detection of PV panels using a drone. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Salt Lake City, Utah, USA, 11–14 November 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59414, p. V004T05A051. [Google Scholar]
- Felsch, T.; Strauss, G.; Perez, C.; Rego, J.M.; Maurtua, I.; Susperregi, L.; Rodríguez, J.R. Robotized Inspection of Vertical Structures of a Solar Power Plant Using NDT Techniques. Robotics 2015, 4, 103–119. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.H.; Park, J.H. Developing inspection methodology of solar energy plants by thermal infrared sensor on board unmanned aerial vehicles. Energies 2019, 12, 2928. [Google Scholar] [CrossRef] [Green Version]
- Rezk, M.; Aljasmi, N.; Salim, R.; Ismail, H.; Nikolakakos, I. Autonomous PV Panel Inspection with Geotagging Capabilities Using Drone. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Virtual, Online, 1–5 November 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85611, p. V07AT07A040. [Google Scholar]
- Franko, J.; Du, S.; Kallweit, S.; Duelberg, E.; Engemann, H. Design of a multi-robot system for wind turbine maintenance. Energies 2020, 13, 2552. [Google Scholar] [CrossRef]
- Iyer, S.; Velmurugan, T.; Gandomi, A.H.; Noor Mohammed, V.; Saravanan, K.; Nandakumar, S. Structural health monitoring of railway tracks using IoT-based multi-robot system. Neural Comput. Appl. 2021, 33, 5897–5915. [Google Scholar] [CrossRef]
- Roy, S.; Vo, T.; Hernandez, S.; Lehrmann, A.; Ali, A.; Kalafatis, S. IoT Security and Computation Management on a Multi-Robot System for Rescue Operations Based on a Cloud Framework. Sensors 2022, 22, 5569. [Google Scholar] [CrossRef]
- Kendoul, F. Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems. J. Field Robot. 2012, 29, 315–378. [Google Scholar] [CrossRef]
- Verma, J.K.; Ranga, V. Multi-robot coordination analysis, taxonomy, challenges and future scope. J. Intell. Robot. Syst. 2021, 102, 1–36. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Jouandeau, N.; Cherif, A.A. A survey and analysis of multi-robot coordination. Int. J. Adv. Robot. Syst. 2013, 10, 399. [Google Scholar] [CrossRef]
- Zhilenkov, A.A.; Chernyi, S.G.; Sokolov, S.S.; Nyrkov, A.P. Intelligent autonomous navigation system for UAV in randomly changing environmental conditions. J. Intell. Fuzzy Syst. 2020, 38, 6619–6625. [Google Scholar] [CrossRef]
- Huang, L.; Song, J.; Zhang, C.; Cai, G. Design and performance analysis of landmark-based INS/Vision Navigation System for UAV. Optik 2018, 172, 484–493. [Google Scholar] [CrossRef]
- Qiu, Z.; Lin, D.; Jin, R.; Lv, J.; Zheng, Z. A Global ArUco-Based Lidar Navigation System for UAV Navigation in GNSS-Denied Environments. Aerospace 2022, 9, 456. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S.; Ju, C.; Son, H.I. Unmanned aerial vehicles in agriculture: A review of perspective of platform, control, and applications. IEEE Access 2019, 7, 105100–105115. [Google Scholar] [CrossRef]
- Tzafestas, S.G. Mobile robot control and navigation: A global overview. J. Intell. Robot. Syst. 2018, 91, 35–58. [Google Scholar] [CrossRef]
- Cabecinhas, D.; Cunha, R.; Silvestre, C. A globally stabilizing path following controller for rotorcraft with wind disturbance rejection. IEEE Trans. Control Syst. Technol. 2014, 23, 708–714. [Google Scholar] [CrossRef]
- Mutawe, S.; Hayajneh, M.; BaniHani, S. Robust Path Following Controllers for Quadrotor and Ground Robot. In Proceedings of the 2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Kuala Lumpur, Malaysia, 12–13 June 2021; pp. 1–6. [Google Scholar]
- Kim, A.R.; Keshmiri, S.; Blevins, A.; Shukla, D.; Huang, W. Control of multi-agent collaborative fixed-wing UASs in unstructured environment. J. Intell. Robot. Syst. 2020, 97, 205–225. [Google Scholar] [CrossRef]
- Elkaim, G.H.; Lie, F.A.P.; Gebre-Egziabher, D. Principles of guidance, navigation, and control of UAVs. In Handbook of Unmanned Aerial Vehicles; Springer: Berlin/Heidelberg, Germany, 2015; pp. 347–380. [Google Scholar]
- Edlerman, E.; Linker, R. Autonomous multi-robot system for use in vineyards and orchards. In Proceedings of the 2019 27th Mediterranean Conference on Control and Automation (MED), Akko, Israel, 1–4 July 2019; pp. 274–279. [Google Scholar]
- Singh, Y.; Bibuli, M.; Zereik, E.; Sharma, S.; Khan, A.; Sutton, R. A novel double layered hybrid multi-robot framework for guidance and navigation of unmanned surface vehicles in a practical maritime environment. J. Mar. Sci. Eng. 2020, 8, 624. [Google Scholar] [CrossRef]
- Al-Fetyani, M.; Hayajneh, M.; Alsharkawi, A. Design of an executable anfis-based control system to improve the attitude and altitude performances of a quadcopter drone. Int. J. Autom. Comput. 2021, 18, 124–140. [Google Scholar] [CrossRef]
- Kurak, S.; Hodzic, M. Control and estimation of a quadcopter dynamical model. Period. Eng. Nat. Sci. 2018, 6, 63–75. [Google Scholar] [CrossRef]
- Hayajneh, M. Experimental validation of integrated and robust control system for mobile robots. Int. J. Dyn. Control 2021, 9, 1491–1504. [Google Scholar] [CrossRef]
- Mutawe, S.; Hayajneh, M.; Al Momani, F. Accurate State Estimations and Velocity Drifting Compensations Using Complementary Filters for a Quadrotor in GPS-Drop Regions. Int. J. Eng. Appl. 2021, 9, 317–326. [Google Scholar] [CrossRef]









| Parameter | Description | Parameter | Description |
|---|---|---|---|
| controller gains | Saturation function | ||
| Desired path position as a function of | |||
| First and second partial derivatives of | |||
| Rotation matrix of Euler angles | Skew symmetric matrix |
| Parameter | v = 1 m/s | v = 3 m/s | v = 4 m/s | |||
|---|---|---|---|---|---|---|
| PID | BS | PID | BS | PID | BS | |
| 0.1074 | 0.0996 | 0.3712 | 0.1021 | 0.4900 | 0.1160 | |
| 0.1889 | 0.1189 | 0.4503 | 0.0839 | 1.1752 | 0.4881 | |
| 0.0707 | 0.0247 | 0.0475 | 0.0295 | 0.0754 | 0.0444 | |
| 0.0544 | 0.0415 | 0.0865 | 0.0824 | 0.0944 | 0.0997 | |
| Parameter | v = 1 m/s | v = 3 m/s | v = 4 m/s | |||
|---|---|---|---|---|---|---|
| PID | BS | PID | BS | PID | BS | |
| 0.0764 | 0.0198 | 0.2614 | 0.1106 | 0.4312 | 0.1995 | |
| 0.1796 | 0.0845 | 0.7109 | 0.3108 | 1.2450 | 0.6754 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayajneh, M.; Al Mahasneh, A. Guidance, Navigation and Control System for Multi-Robot Network in Monitoring and Inspection Operations. Drones 2022, 6, 332. https://doi.org/10.3390/drones6110332
Hayajneh M, Al Mahasneh A. Guidance, Navigation and Control System for Multi-Robot Network in Monitoring and Inspection Operations. Drones. 2022; 6(11):332. https://doi.org/10.3390/drones6110332
Chicago/Turabian StyleHayajneh, Mohammad, and Ahmad Al Mahasneh. 2022. "Guidance, Navigation and Control System for Multi-Robot Network in Monitoring and Inspection Operations" Drones 6, no. 11: 332. https://doi.org/10.3390/drones6110332
APA StyleHayajneh, M., & Al Mahasneh, A. (2022). Guidance, Navigation and Control System for Multi-Robot Network in Monitoring and Inspection Operations. Drones, 6(11), 332. https://doi.org/10.3390/drones6110332







