Prescribed Performance Rotating Formation Control of Multi-Spacecraft Systems with Uncertainties
Abstract
:1. Introduction
2. Preliminaries and Dynamics Model
2.1. Preliminaries
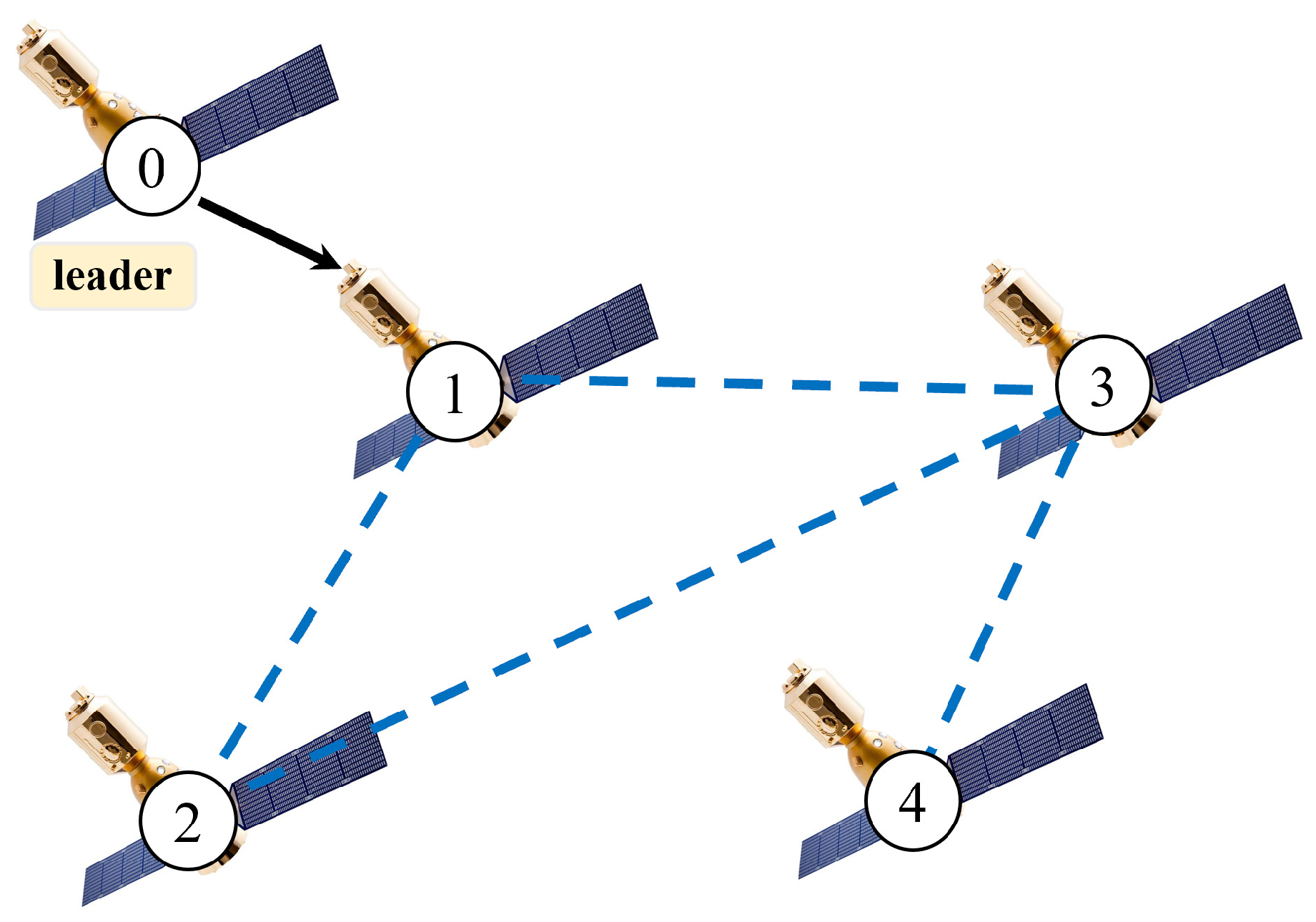
2.1.1. Graph Theory
2.1.2. Coordinate Frame
2.1.3. RBF Neural Network
2.1.4. Notions
2.2. Dynamics Model
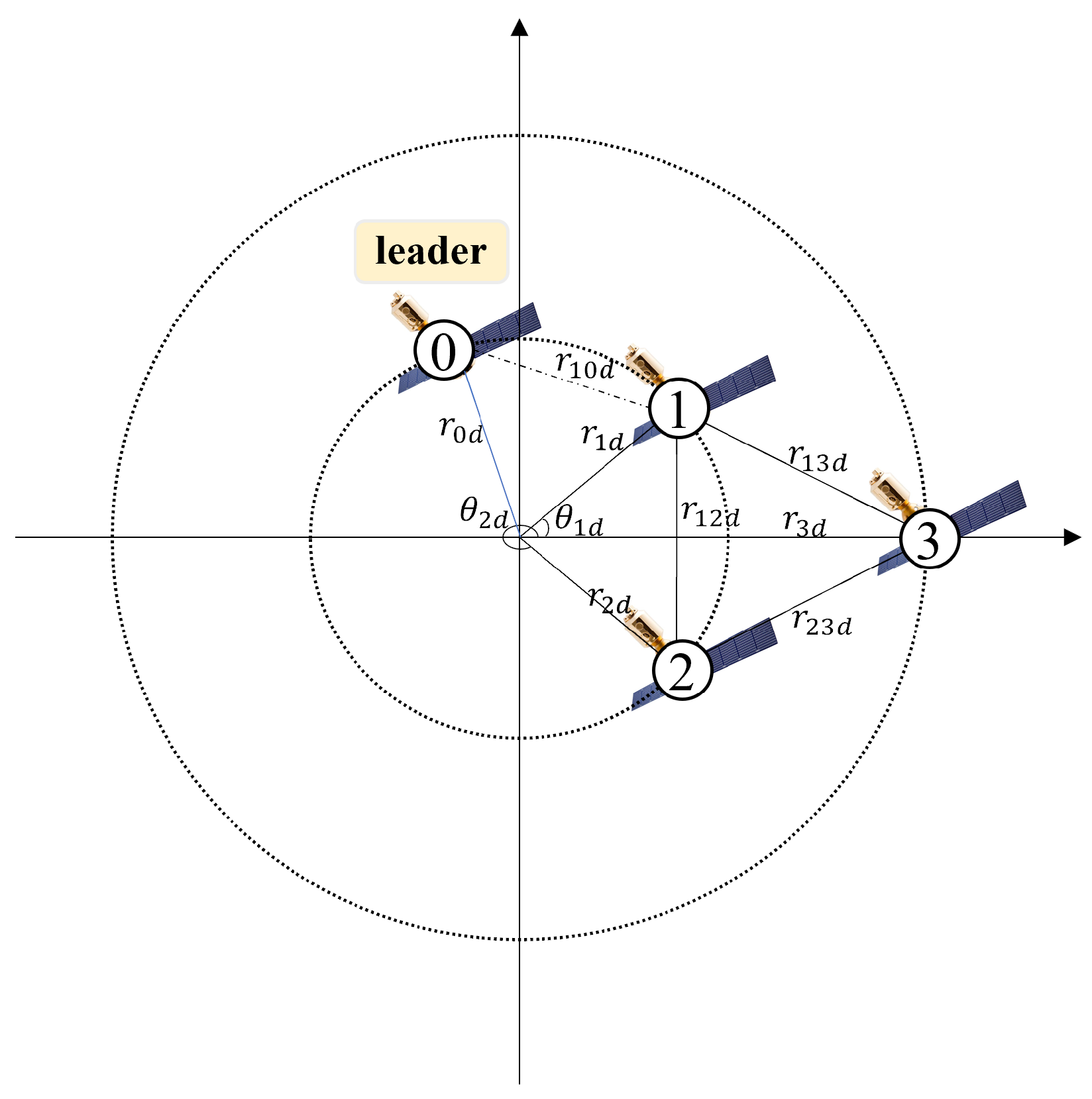
2.3. Problem Description
3. Main Results
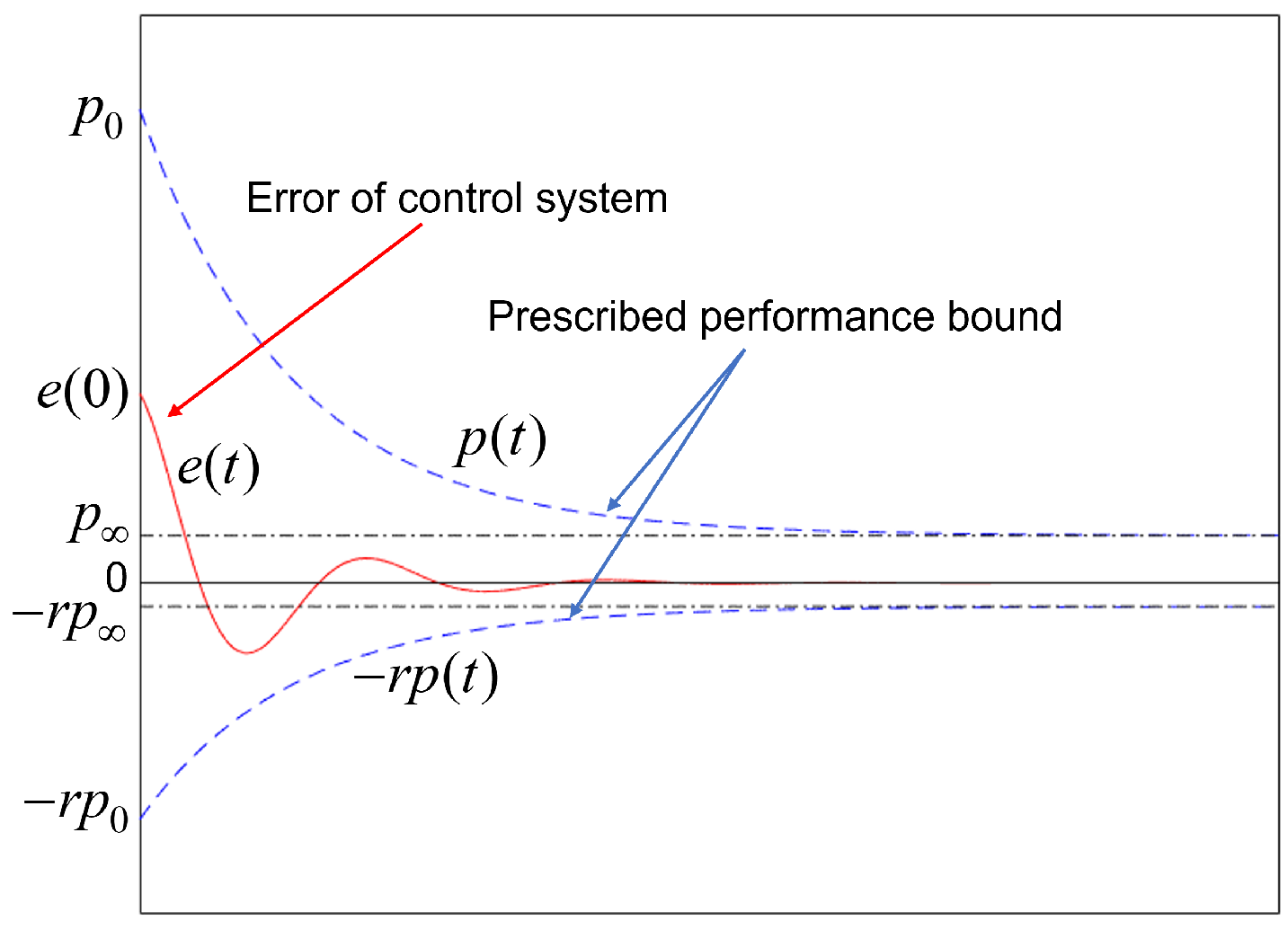
3.1. Controller Design
3.2. Stability Analysis
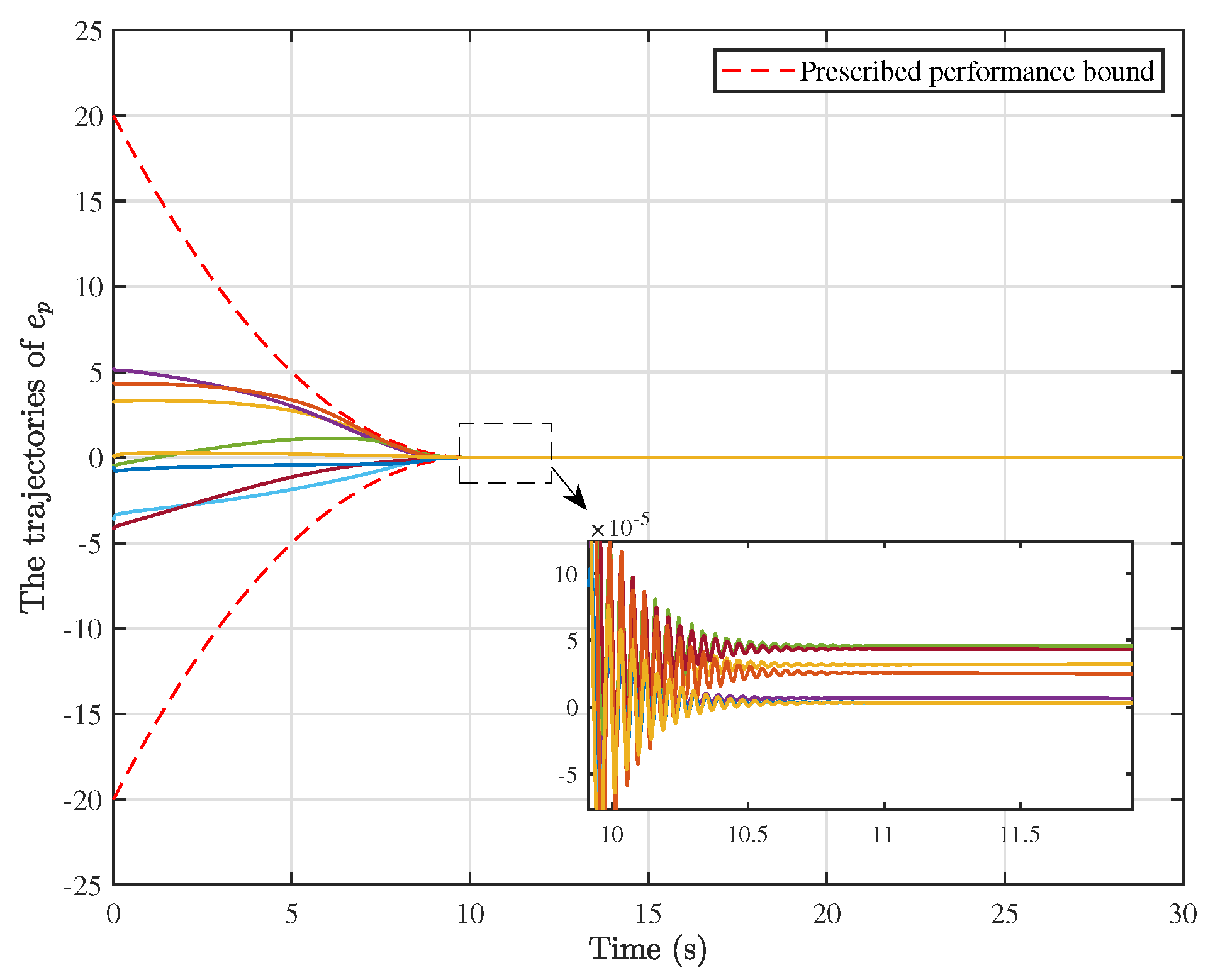
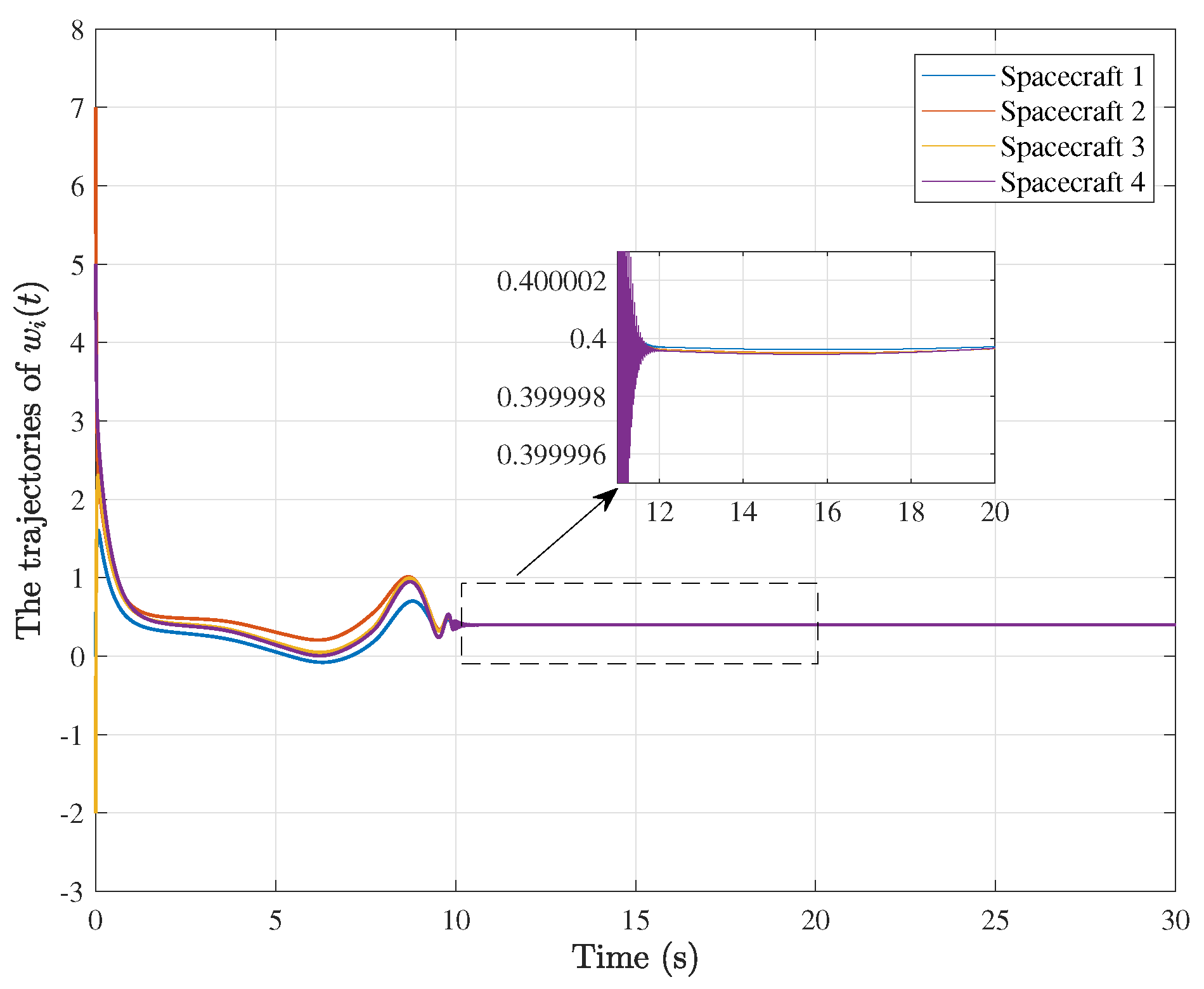
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Liu, C.; Sun, Z. Finite-time distributed hierarchical control for satellite cluster with collision avoidance. Aerosp. Sci. Technol. 2021, 114, 106750. [Google Scholar] [CrossRef]
- Hou, X.; Zhu, M.; Sun, L.; Ding, T.; Huang, Z.; Shi, Y.; Su, Y.; Li, L.; Chen, T.; Lee, C. Scalable self-attaching/assembling robotic cluster (S2A2RC) system enabled by triboelectric sensors for in-orbit spacecraft application. Nano Energy 2022, 93, 106894. [Google Scholar] [CrossRef]
- Wang, W.; Wu, D.; Lei, H.; Baoyin, H. Fuel-Optimal Spacecraft Cluster Flight Around an Ellipsoidal Asteroid. J. Guid. Control. Dyn. 2021, 44, 1875–1882. [Google Scholar] [CrossRef]
- Blackwell, W.J.; Braun, S.; Bennartz, R.; Velden, C.; DeMaria, M.; Atlas, R.; Dunion, J.; Marks, F.; Rogers, R.; Annane, B.; et al. An overview of the TROPICS NASA earth venture mission. Q. J. R. Meteorol. Soc. 2018, 144, 16–26. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.; Jia, Y. Distributed rotating formation control of multi-agent systems. Syst. Control Lett. 2010, 59, 587–595. [Google Scholar] [CrossRef]
- Lin, P.; Qin, K.; Li, Z.; Ren, W. Collective rotating motions of second-order multi-agent systems in three-dimensional space. Syst. Control Lett. 2011, 60, 365–372. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Q. Rotating consensus and tracking of second-order multi-agent systems in 3-D under directed interaction topologies. In Proceedings of the 2015 19th International Conference on System Theory, Control and Computing (ICSTCC), Cheile Gradistei, Romania, 14–16 October 2015; pp. 26–31. [Google Scholar]
- Li, P.; Qin, K.; Shi, M. Distributed robust H∞ rotating consensus control for directed networks of second-order agents with mixed uncertainties and time-delay. Neurocomputing 2015, 148, 332–339. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Y.; Lin, P.; Ren, W. Distributed rotating consensus of second-order multi-agent systems with nonuniform delays. Syst. Control Lett. 2018, 117, 18–22. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.; Hu, W. Distributed rotating formation control of second-order leader-following multi-agent systems with nonuniform delays. J. Frankl. Inst. 2019, 356, 3090–3101. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, W. Rotating Consensus of Second-Order Multi-Agent Systems with Signed Directed Graphs. IFAC-PapersOnLine 2020, 53, 2994–2998. [Google Scholar] [CrossRef]
- Ding, R.; Hu, W.; Yang, Y. Rotating consensus control of double-integrator multi-agent systems with event-based communication. Sci. China Inf. Sci. 2020, 63, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Lin, Y.; Zhong, Y. Multi-target Rotating Encirclement Formations of Second-order Multi-agent Systems with Communication Noises. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 1915–1919. [Google Scholar]
- Zhang, H.; Li, Z.; Wang, W.; Wang, H.; Zhang, Y. Mission Planning for Optical Satellite’s Constant Surveillance to Geostationary Spacecraft. 2021. Web. 20 September 2022. Available online: https://assets.researchsquare.com/files/rs-409796/v1_covered.pdf?c=1631862779 (accessed on 1 November 2022).
- Zhang, H.; Li, Z.; Wang, W.; Wang, H.; Zhang, Y. Trajectory Planning for Optical Satellite’s Continuous Surveillance of Geostationary Spacecraft. IEEE Access 2021, 9, 114282–114293. [Google Scholar] [CrossRef]
- Si-wei, C.; Jing, C.; Lin-Cheng, S.; Yu, L. A two-level resource organization and optimization framework via optimization and agent negotiation for multi-satellite reconnaissance and surveillance system. In Proceedings of the 2010 the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; Volume 3, pp. 397–401. [Google Scholar]
- Maheshwarappa, M.R.; Bowyer, M.; Bridges, C.P. Software defined radio (SDR) architecture to support multi-satellite communications. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–10. [Google Scholar]
- Liu, Y.; Dang, P.; Tang, X.; Mu, J.; Feng, Z. Performance analysis of LYSO–SiPM detection module for X-ray communication during spacecraft reentry blackout. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2021, 1013, 165673. [Google Scholar] [CrossRef]
- Tang, X.; Ye, D.; Huang, L.; Sun, Z.; Sun, J. Pursuit-evasion game switching strategies for spacecraft with incomplete-information. Aerosp. Sci. Technol. 2021, 119, 107112. [Google Scholar] [CrossRef]
- Lang, X.; de Ruiter, A. Non-cooperative differential game based output feedback control for spacecraft attitude regulation. Acta Astronaut. 2022, 193, 370–380. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, Q.; Li, H.; Lu, R. Adaptive prescribed performance control of a flexible-joint robotic manipulator with dynamic uncertainties. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef] [PubMed]
- Mehdifar, F.; Bechlioulis, C.P.; Hashemzadeh, F.; Baradarannia, M. Prescribed performance distance-based formation control of multi-agent systems. Automatica 2020, 119, 109086. [Google Scholar] [CrossRef]
- Liang, H.; Fu, Y.; Gao, J.; Cao, H. Finite-time velocity-observed based adaptive output-feedback trajectory tracking formation control for underactuated unmanned underwater vehicles with prescribed transient performance. Ocean Eng. 2021, 233, 109071. [Google Scholar] [CrossRef]
- Chen, G.; Yao, D.; Zhou, Q.; Li, H.; Lu, R. Distributed event-triggered formation control of USVs with prescribed performance. J. Syst. Sci. Complex. 2022, 35, 820–838. [Google Scholar] [CrossRef]
- Hu, Y.; Geng, Y.; Wu, B.; Wang, D. Model-free prescribed performance control for spacecraft attitude tracking. IEEE Trans. Control Syst. Technol. 2020, 29, 165–179. [Google Scholar] [CrossRef]
- Luo, J.; Yin, Z.; Wei, C.; Yuan, J. Low-complexity prescribed performance control for spacecraft attitude stabilization and tracking. Aerosp. Sci. Technol. 2018, 74, 173–183. [Google Scholar] [CrossRef]
- Zhao, D.; Jin, K.; Wei, C. On Novel Adaptive Coordinated Control for Spacecraft Formation: An Adjustable Performance Approach. IEEE Access 2021, 9, 96799–96813. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y.; Krstic, M. Collectively rotating formation and containment deployment of multiagent systems: A polar coordinate-based finite time approach. IEEE Trans. Cybern. 2016, 47, 2161–2172. [Google Scholar] [CrossRef] [PubMed]
- Zong, G.; Wang, Y.; Karimi, H.R.; Shi, K. Observer-based adaptive neural tracking control for a class of nonlinear systems with prescribed performance and input dead-zone constraints. Neural Netw. 2022, 147, 126–135. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Dai, S.; Dong, C. Adaptive synchronization control of uncertain multiple USVs with prescribed performance and preserved connectivity. Sci. China Inf. Sci. 2022, 65, 1–2. [Google Scholar] [CrossRef]
- Godsil, C.; Royle, G.F. Algebraic Graph Theory; Springer Science & Business Media: Cham, Switzerland, 2001; Volume 207. [Google Scholar]
- Zhou, Q.; Zhao, S.; Li, H.; Lu, R.; Wu, C. Adaptive neural network tracking control for robotic manipulators with dead zone. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3611–3620. [Google Scholar] [CrossRef]
- Li, Y.X.; Yang, G.H. Adaptive neural control of pure-feedback nonlinear systems with event-triggered communications. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 6242–6251. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.H.; Yang, G.H. Event-triggered adaptive output feedback control for a class of uncertain nonlinear systems with actuator failures. IEEE Trans. Cybern. 2018, 50, 201–210. [Google Scholar] [CrossRef]
- Liu, W.; Geng, Y.; Wu, B.; Wang, D. Neural-network-based adaptive event-triggered control for spacecraft attitude tracking. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 4015–4024. [Google Scholar] [CrossRef] [PubMed]
- Ge, S.S.; Wang, C. Adaptive NN control of uncertain nonlinear pure-feedback systems. Automatica 2002, 38, 671–682. [Google Scholar] [CrossRef]
- Shi, L.; Cheng, Y.; Shao, J.; Sheng, H.; Liu, Q. Cucker-Smale flocking over cooperation-competition networks. Automatica 2022, 135, 109988. [Google Scholar] [CrossRef]
- Shi, L.; Zheng, W.X.; Shao, J.; Cheng, Y. Sub-super-stochastic matrix with applications to bipartite tracking control over signed networks. SIAM J. Control Optim. 2021, 59, 4563–4589. [Google Scholar] [CrossRef]
- Zhang, C.H.; Yang, G.H. Event-triggered practical finite-time output feedback stabilization of a class of uncertain nonlinear systems. Int. J. Robust Nonlinear Control 2019, 29, 3078–3092. [Google Scholar] [CrossRef]
- Polycarpou, M.M. Stable adaptive neural control scheme for nonlinear systems. IEEE Trans. Autom. Control 1996, 41, 447–451. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Prescribed performance adaptive control of SISO feedback linearizable systems with disturbances. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 1035–1040. [Google Scholar]
- Karayiannidis, Y.; Doulgeri, Z. Model-free robot joint position regulation and tracking with prescribed performance guarantees. Robot. Auton. Syst. 2012, 60, 214–226. [Google Scholar] [CrossRef]
- Zhou, Z.G.; Zhang, Y.A.; Shi, X.N.; Zhou, D. Robust attitude tracking for rigid spacecraft with prescribed transient performance. Int. J. Control 2017, 90, 2471–2479. [Google Scholar] [CrossRef]
- Na, J.; Huang, Y.; Wu, X.; Gao, G.; Herrmann, G.; Jiang, J.Z. Active adaptive estimation and control for vehicle suspensions with prescribed performance. IEEE Trans. Control Syst. Technol. 2017, 26, 2063–2077. [Google Scholar] [CrossRef]


| Spacecraft Number | Initial States () | Derivative of the Initial States () | Desired States () |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
| Spacecraft | Limited | Practical | Desired |
|---|---|---|---|
| Number | Overshot | Overshot | Steady-State Error |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| Spacecraft | Practical | Desired Convergence | Practical |
| Number | Steady-State Error | Time (s) | Convergence Time (s) |
| 1 | 10 | ||
| 2 | 10 | ||
| 3 | 10 | ||
| 4 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Qin, K.; Li, W.; Shi, M.; Lin, B.; Cao, L. Prescribed Performance Rotating Formation Control of Multi-Spacecraft Systems with Uncertainties. Drones 2022, 6, 348. https://doi.org/10.3390/drones6110348
Liu Y, Qin K, Li W, Shi M, Lin B, Cao L. Prescribed Performance Rotating Formation Control of Multi-Spacecraft Systems with Uncertainties. Drones. 2022; 6(11):348. https://doi.org/10.3390/drones6110348
Chicago/Turabian StyleLiu, Yan, Kaiyu Qin, Weihao Li, Mengji Shi, Boxian Lin, and Lu Cao. 2022. "Prescribed Performance Rotating Formation Control of Multi-Spacecraft Systems with Uncertainties" Drones 6, no. 11: 348. https://doi.org/10.3390/drones6110348
APA StyleLiu, Y., Qin, K., Li, W., Shi, M., Lin, B., & Cao, L. (2022). Prescribed Performance Rotating Formation Control of Multi-Spacecraft Systems with Uncertainties. Drones, 6(11), 348. https://doi.org/10.3390/drones6110348





