Trajectory Optimization of a Subsonic Unpowered Gliding Vehicle Using Control Vector Parameterization
Abstract
1. Introduction
- Fluctuations caused by flight transition are minimized using a non-uniform CVP approach, and damped and steady gliding flight is achieved to maximize the gliding range;
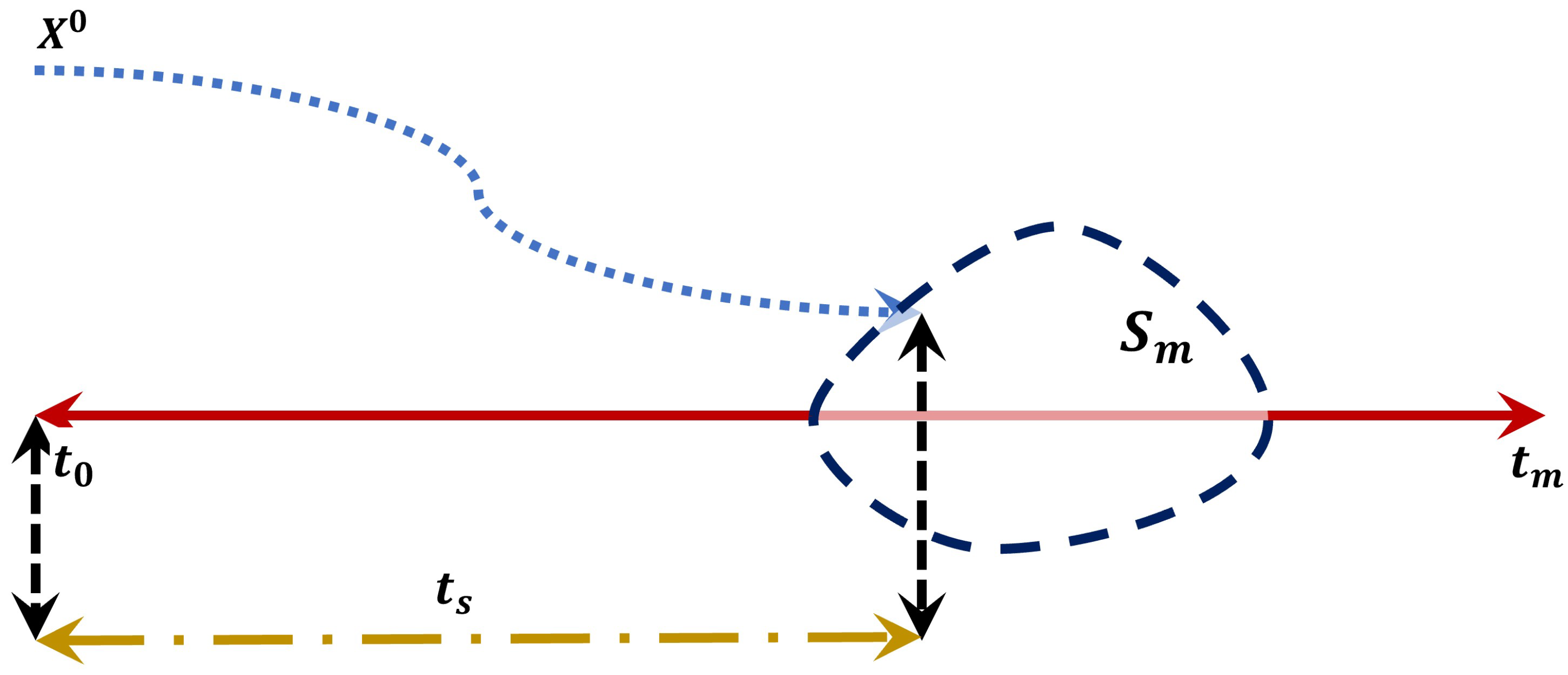
- By defining the maximum stoppable time with the height as the stopping constraint, the complexity of the optimization problem is decreased;
- The results of the non-uniform CVP approach are compared with those of the uniform CVP approach and those of the maximum step input.
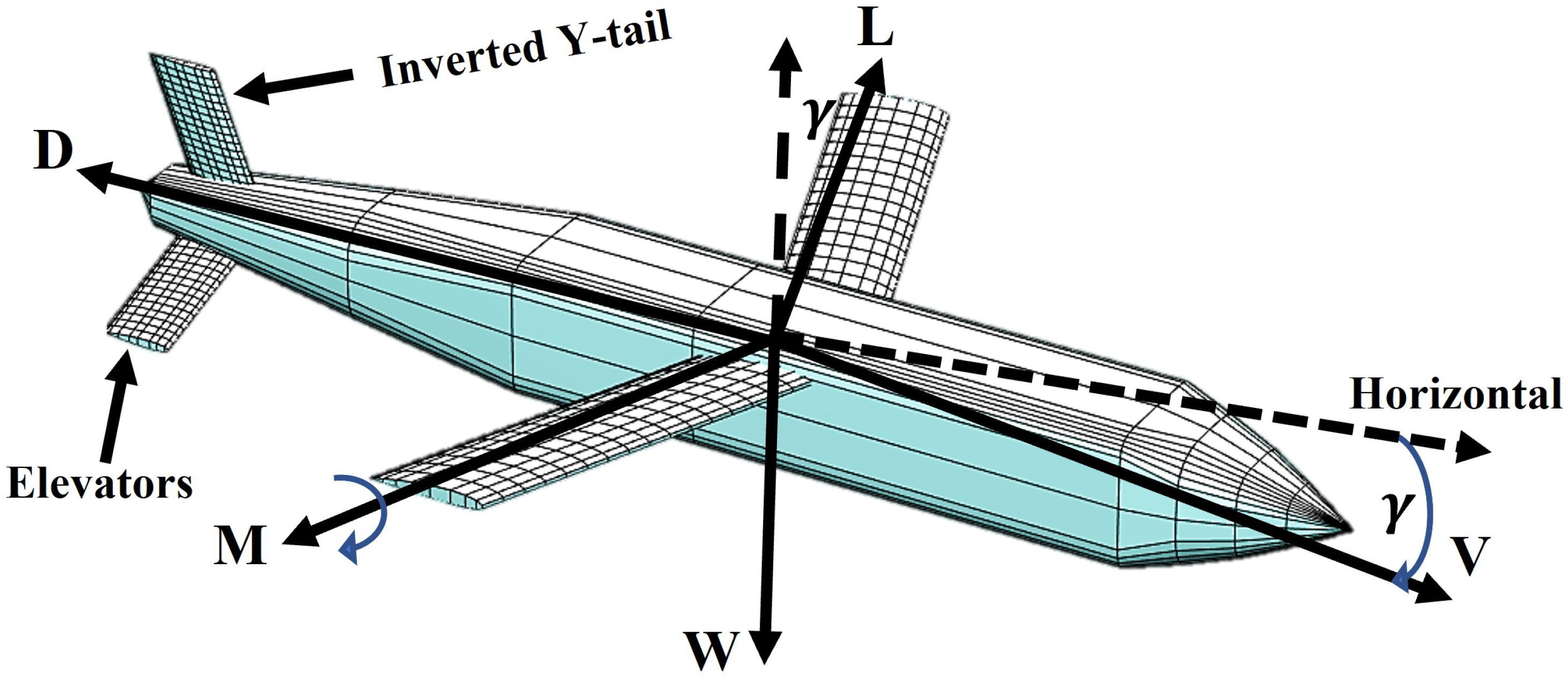
2. SUGV Modeling Overview
- A constant mass and gravity field;
- Rigid body dynamics;
- Non-rotating and flat earth.
2.1. Longitudinal Dynamics
2.2. Aerodynamic Forces and Moments
3. Problem Description
3.1. Performance Index
3.2. Constraints
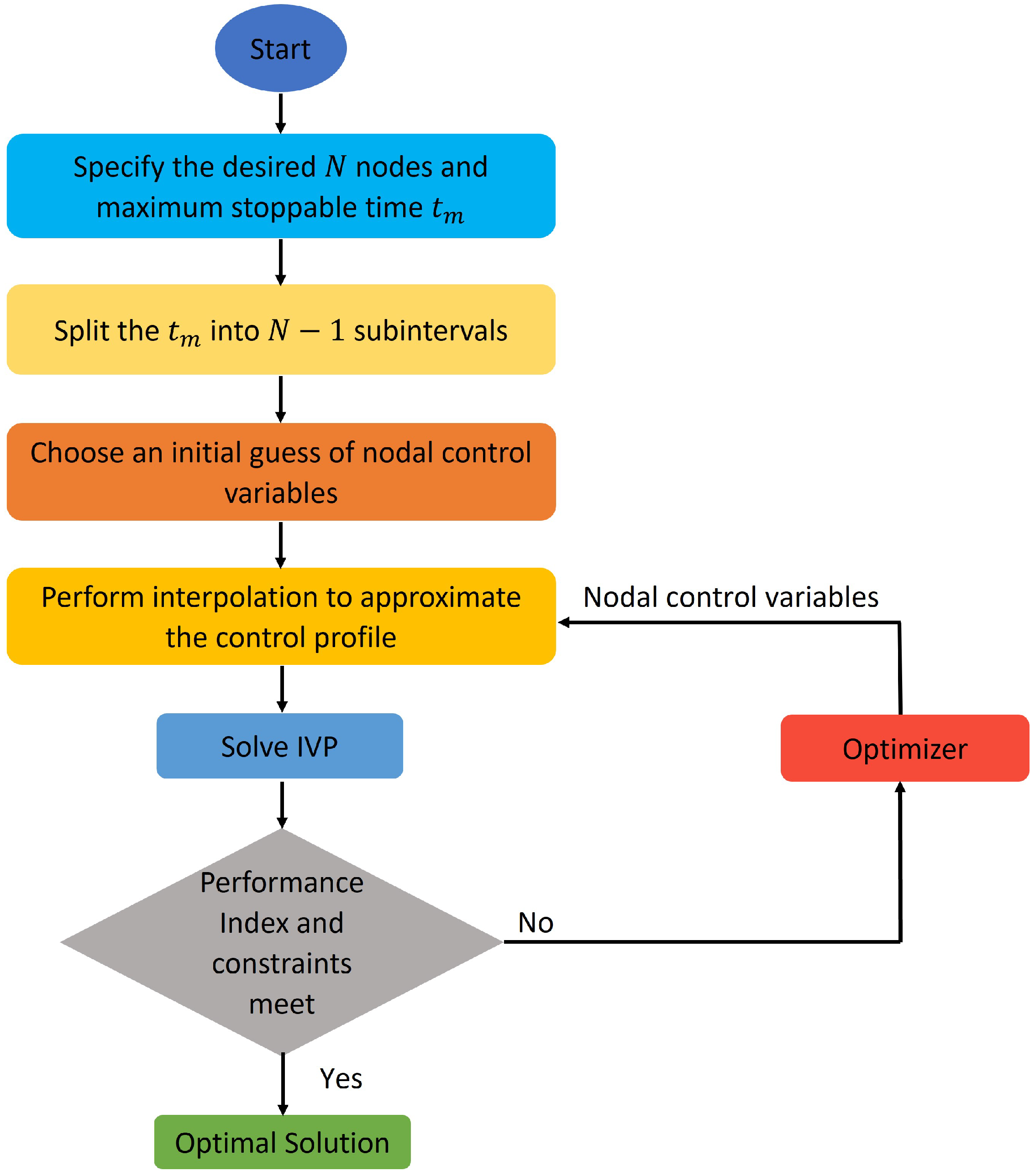
4. Control Vector Parameterization
- (i)
- Specify the desired number of nodes and split the supplied time vector into subintervals:The nodal time may be uniform or non-uniform.
- (ii)
- At each node, make an initial guess for the control variable. The following control vvector (CV) u(t) is expressed aswhere is a nodal control variable.
- (iii)
- Use an interpolation polynomial to approximate the CV profile.
- (iv)
- Solve the IVP by considering the approximated CV profile.
- (v)
- Compute the performance index as well as the constraints. If the performance index and constraints are satisfied, then the output will be the optimal solution; otherwise, proceed to step (iii) after optimizing the nodal control variables with any suitable optimizer.
4.1. Uniform CVP
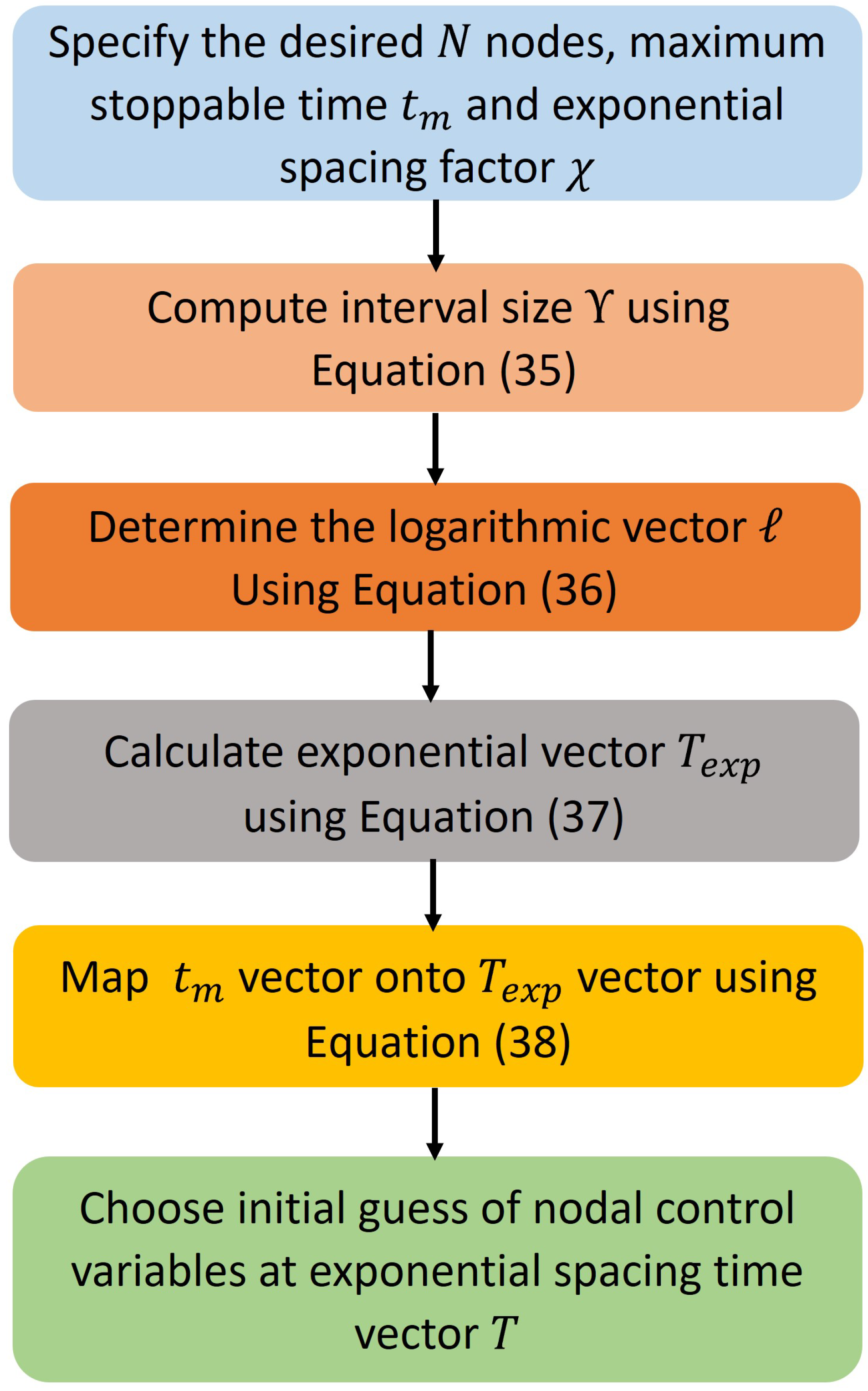
4.2. Non-Uniform CVP
5. Simulation Results
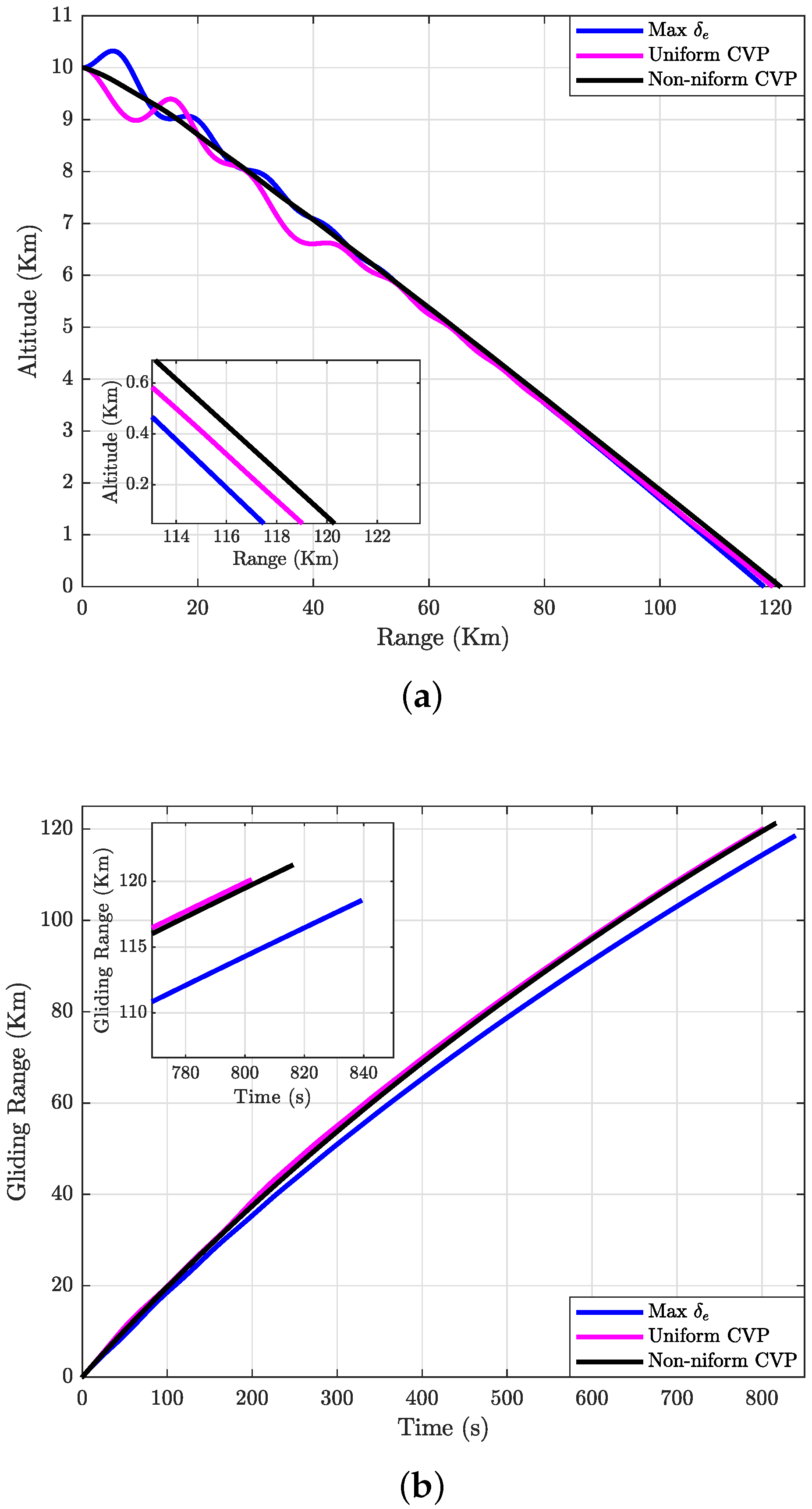
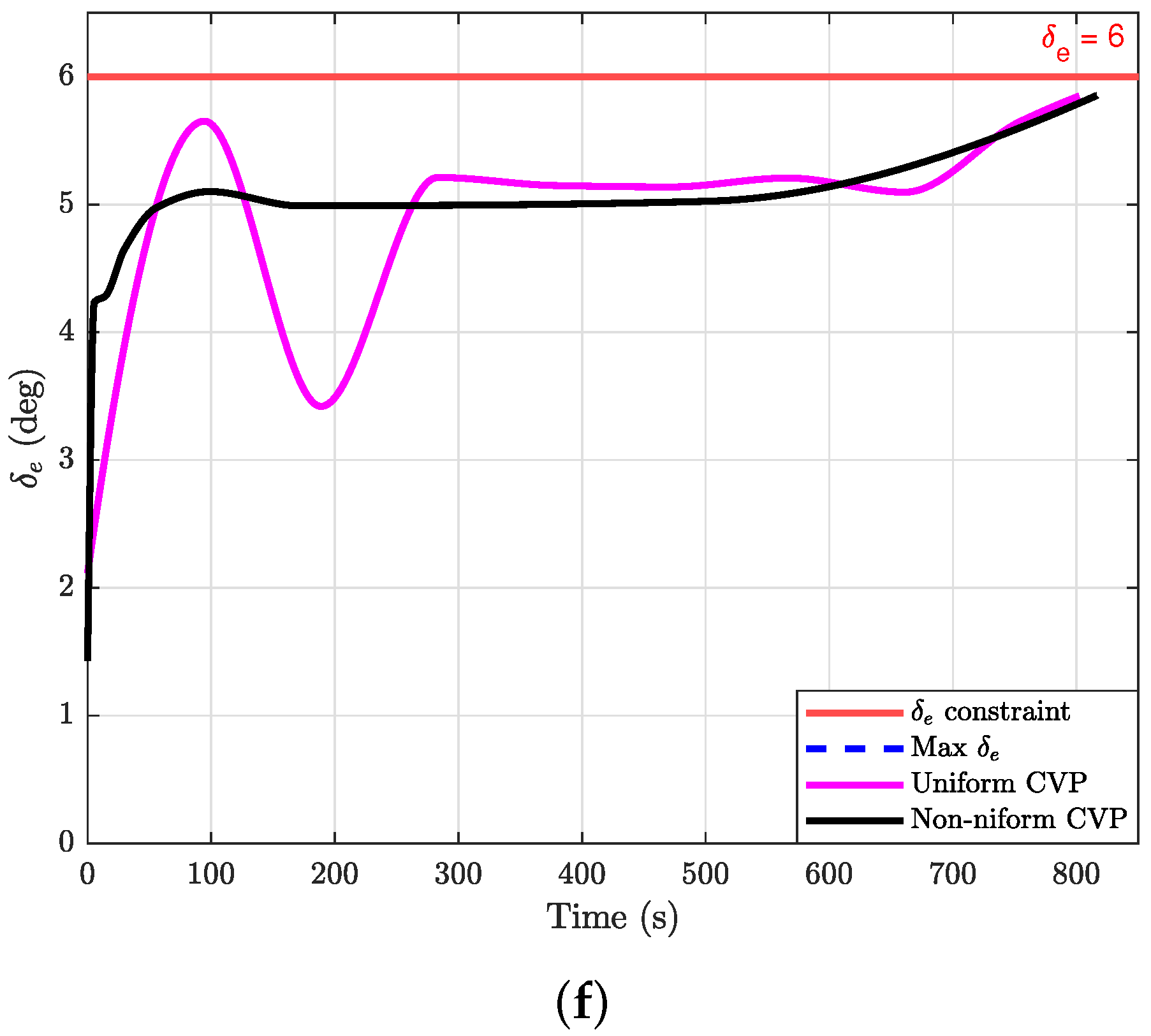
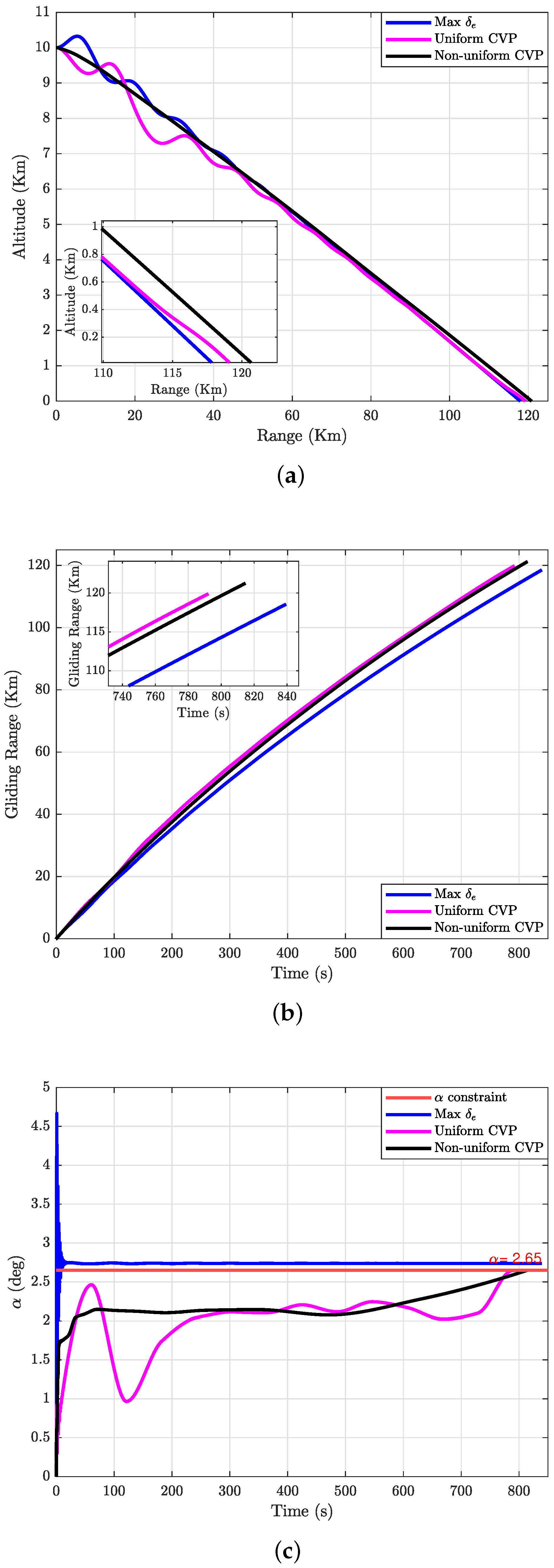
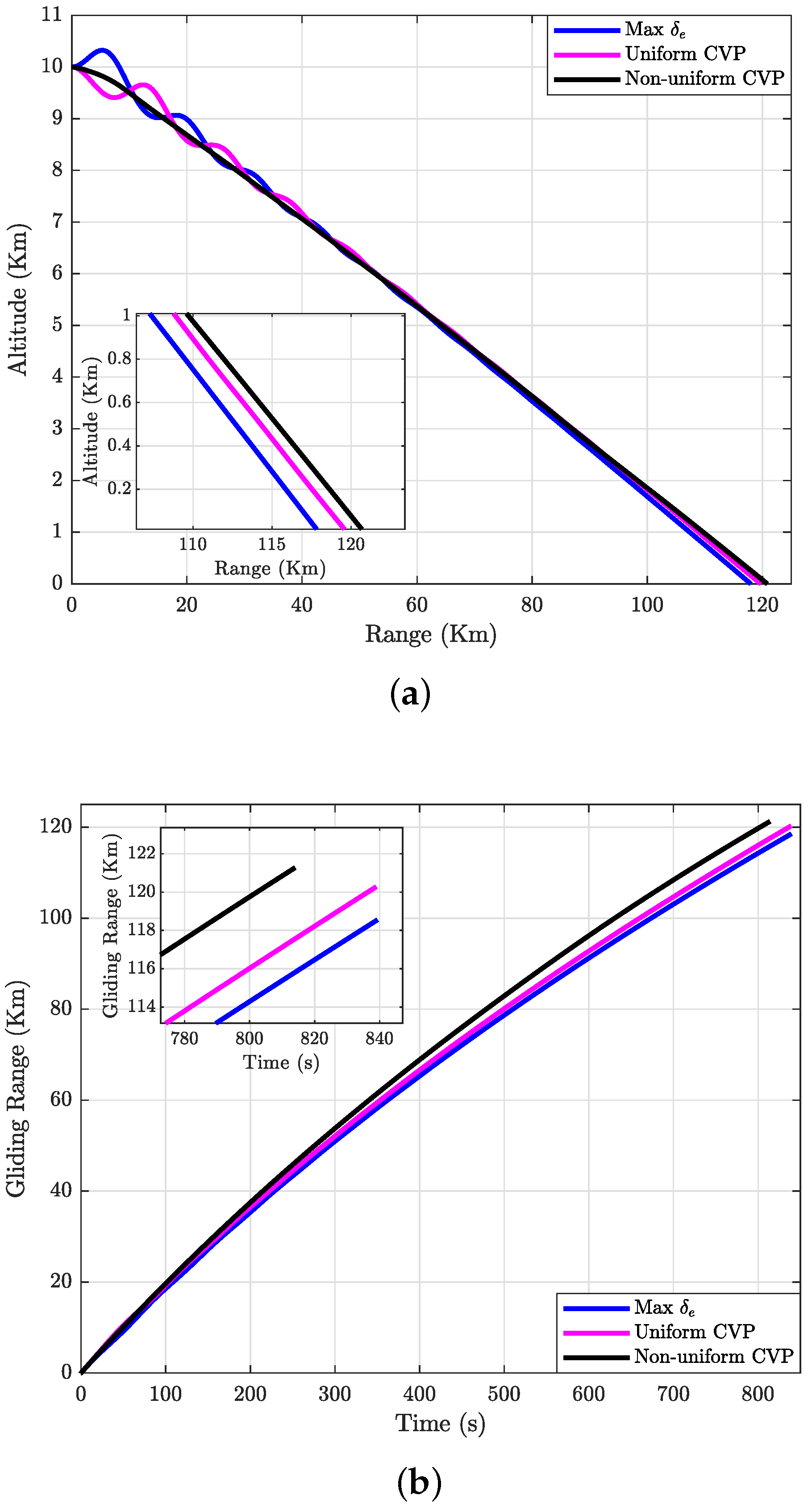
5.1. Case 1: N = 10
5.2. Case 2: N = 15
5.3. Case 3: N = 20
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoffren, J.; Raivio, T. Optimal maneuvering after engine failure. In Proceedings of the Atmospheric Flight Mechanics Conference, Boston, MA, USA, 10–12 August 2000. [Google Scholar]
- Rivas, D.; Franco, A.; Valenzuela, A. Optimization of unpowered descents for commercial aircraft. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011. [Google Scholar]
- Wu, H.; Cho, N.C.; Bouadi, H.; Zhong, L.; Mora-Camino, F. Dynamic programming for trajectory optimization of engine-out transportation aircraft. In Proceedings of the 2012, 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012. [Google Scholar]
- Tola, C.; Beyazpinar, P.; Akin, D. Analysis of range extension process for outdated ballistic munitions ejected from an accelerator launcher concept. J. Aviat. 2021, 5, 90–100. [Google Scholar] [CrossRef]
- Elsherbiny, A.; Bayoumy, A.; Elshabka, A.; Abdelrahman, M. Aerodynamic design optimization of range extension kit of a subsonic flying body. J. Eng. Sci. Mil. Technol. 2017, 17, 1–20. [Google Scholar] [CrossRef]
- Mir, I.; Akhtar, S.; Eisa, S.A.; Maqsood, A. Guidance and control of standoff air-to-surface carrier vehicle. Aeronaut. J. 2019, 123, 283–309. [Google Scholar] [CrossRef]
- Turco, K.T. Development of the Joint Stand Off Weapon (JSOW) Moving Target Capability: AGM-154 Block Three Program. Master’s Thesis, University of Tennessee, Knoxville, NT, USA, 2006. [Google Scholar]
- Pullat, S.; Pushparaj, A. Evolution of Smart Weapons; National Institute of Advanced Studies: Bengaluru, India, 2019; pp. 1–28. [Google Scholar]
- Sheu, D.; Chen, Y.-M.; Chang, Y.-J.; Chern, J.-S. Optimal glide for maximum range. In Proceedings of the 23rd Atmospheric Flight Mechanics Conference, Boston, MA, USA, 10–12 August 1998. [Google Scholar]
- Sheu, D.; Chen, Y.-M.; Chern, J.-S. Optimal three-dimensional glide for maximum reachable domain. In Proceedings of the 24th Atmospheric Flight Mechanics Conference, Portland, OR, USA, 9–11 August 1999. [Google Scholar]
- Chern, J.-S.; Ma, D.-M.; Vinh, N. Analytical solution for horizontal gliding flight. In Proceedings of the Atmospheric Flight Mechanics Conference, Hampton, VA, USA, 10–12 August 2000. [Google Scholar]
- Kim, Y.; Kim, G.H.; Choi, J.-H. Optimal guidance for range maximization of guided projectile: The effects of autopilot delay and fin deployment timing on the flight range. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019. [Google Scholar]
- Yu, W.; Chen, W. Guidance scheme for glide range maximization of a hypersonic vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2011. [Google Scholar]
- Phillips, C.P. Guidance algorithm for range maximization and time-of-flight control of a guided projectile. J. Guid. Control Dyn. 2008, 31, 1447–1455. [Google Scholar] [CrossRef]
- Zhang, D.-C.; Xia, Q.-L.; Wen, Q.-Q.; Zhou, G.-Q. An approximate optimal maximum range guidance scheme for subsonic unpowered gliding vehicles. Int. Aerosp. Eng. 2015, 2015, 1–8. [Google Scholar] [CrossRef]
- Yuan, Y.B.; Zhang, K.; Xue, X.D. Optimization of glide trajectory of guided bombs using a Radau pseudo-spectral method. Acta Armamentarii. 2014, 35, 1179–1186. [Google Scholar]
- Guo, K.; Xiong, F. Notice of retraction gliding trajectory optimization based on hp-adaptive pseudospectral method. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Chengdu, China, 15–18 July 2013. [Google Scholar]
- Qiu, W.; Jia, Q.; Meng, X.; Sun, Y. Maximum range trajectory optimization for a boost-glide vehicle using adaptive mesh refinement pseudospectral methods. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2017, 231, 1171–1182. [Google Scholar] [CrossRef]
- Gao, C.; Jiang, C.; Jing, W. Optimization of projectile state and trajectory of reentry body considering attainment of carrying aircraft. J. Syst. Eng. Electron. 2017, 28, 137–144. [Google Scholar] [CrossRef]
- Xiao, L.; Lv, L.; Liu, P.; Liu, X.; Huang, G. A novel adaptive Gauss pseudospectral method for nonlinear optimal control of constrained hypersonic re-entry vehicle problem. Int. J. Adapt. Control Signal Process. 2018, 32, 1243–1258. [Google Scholar] [CrossRef]
- An, K.; Guo, Z.-Y.; Xu, X.-P.; Huang, W. A framework of trajectory design and optimization for the hypersonic gliding vehicle. Aerosp. Sci. Technol. 2020, 106, 106110. [Google Scholar] [CrossRef]
- Shapira, I.; Ben-Asher, J. Range maximization for emergency landing after engine cutoff. J. Aircr. 2005, 42, 1296–1306. [Google Scholar] [CrossRef]
- Fang, X.; Wan, N.; Jafarnejadsani, H.; Sun, D.; Holzapfel, F.; Hovakimyan, N. Emergency landing trajectory optimization for fixed-wing UAV under engine failure. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Harada, M.; Bollino, K. Optimal trajectory of a glider in ground effect and wind shear. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, Monterey, CA, USA, 5–8 August 2005. [Google Scholar]
- BenAsher, J.; Dekel, K.M. Pseudo-spectral-method based optimal glide in the event of engine Cut-off. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar]
- Franco, A.; Rivas, D.; Valenzuela, A. Optimization of unpowered descents of commercial aircraft in altitude-dependent winds. J. Aircr. 2012, 49, 1460–1470. [Google Scholar] [CrossRef]
- Nevrekar, A.; Striz, A.; Vedula, P. Maximum range glide of a supersonic aircraft in the presence of wind. In Proceedings of the 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN, USA, 17–19 September 2012. [Google Scholar]
- Segal, D.; Bar-Gill, A.; Shimkin, N. Max-range glides in engine cutoff emergencies under severe wind. J. Guid. Control Dyn. 2019, 42, 1822–1835. [Google Scholar] [CrossRef]
- Bryson, J.; Vasile, J.D.; Celmins, I.; Fresconi, F. Approach for understanding range extension of gliding indirect fire munitions. In Proceedings of the 2018 Atmospheric Flight Mechanics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Vasile, J.D.; Bryson, J.; Gruenwald, B.C.; Fairfax, L.; Strohm, L.; Fresconi, F. A multi-disciplinary approach to design long range guided projectiles. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Elsherbiny, A.M.; Aly, A.M.; Elshabka, A.; Abdelrahman, M. Modeling, simulation and hyprid optimization method as design tools for range extension kit of a subsonic flying body. In Proceedings of the 2018 AIAA Modeling and Simulation Technologies Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Vasile, J.D.; Bryson, J.; Fresconi, F. Aerodynamic design optimization of long range projectiles using missile DATCOM. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Gaudet, B.; Drozd, K.; Furfaro, R. Adaptive approach phase guidance for a hypersonic glider via reinforcement meta learning. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Din, A.F.U.; Akhtar, S.; Maqsood, A.; Habib, M.; Mir, I. Modified model free dynamic programming: An augmented approach for unmanned aerial vehicle. Appl. Intell. 2022, 52, 1–21. [Google Scholar] [CrossRef]
- Din, A.F.U.; Mir, I.; Gul, F.; Nasar, A.; Rustom, M.; Abualigah, L. Reinforced learning-based robust control design for unmanned aerial vehicle. Arab. J. Sci. Eng. 2022, 47, 1–16. [Google Scholar] [CrossRef]
- Din, A.F.u.; Mir, I.; Gul, F.; Mir, S.; Saeed, N.; Althobaiti, T.; Abbas, S.M.; Abualigah, L. Deep Reinforcement Learning for integrated non-linear control of autonomous UAVs. Processes 2022, 10, 1307. [Google Scholar] [CrossRef]
- Hull, D.G. Conversion of optimal control problems into parameter optimization problems. J. Guid. Control Dyn. 1997, 20, 57–60. [Google Scholar] [CrossRef]
- Liu, H.; Teng, H.; Qiu, G.; Liu, P.; Yang, J. Gaussian discretization-based non-uniform control vector parameterization for terminal constrained hypersonic unmanned system trajectory optimization. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020. [Google Scholar]
- Guo, J.; Li, B.; Ji, Y. A control parametrization based path planning method for the quad-rotor uavs. J. Ind. Manag. Optim. 2022, 18, 1079. [Google Scholar] [CrossRef]
- Zhong, W.; Lin, Q.; Loxton, R.; Teo, K.L. Optimal train control via switched system dynamic optimization. Optim. Methods Softw. 2021, 36, 602–626. [Google Scholar] [CrossRef]
- Liu, P.; Hu, Q.; Li, L.; Liu, M.; Chen, X.; Piao, C.; Liu, X. Fast control parameterization optimal control with improved Polak-Ribière-Polyak conjugate gradient implementation for industrial dynamic processes. ISA Trans. 2022, 123, 188–199. [Google Scholar] [CrossRef]
- Hong, L.; Mo, Y.; Bao, D.; Gong, R. Chaos elite Harris hawk optimization algorithm to solve chemical dynamic optimization problems. IEEE Access 2022, 10, 65833–65853. [Google Scholar] [CrossRef]
- Jin, L.; Yin, Y.; Loxton, R.; Lin, Q.; Liu, F.; Teo, K.L. Optimal control of nonlinear Markov jump systems by control parametrisation technique. IET Control Theory Appl. 2022, 16, 1–9. [Google Scholar] [CrossRef]
- Liu, R.; Mo, Y.; Lu, Y.; Lyu, Y.; Zhang, Y.; Guo, H. Swarm-intelligence optimization method for dynamic optimization problem. Mathematics 2022, 10, 1803. [Google Scholar] [CrossRef]
- Zhang, Y.; Mo, Y. Dynamic optimization of chemical processes based on modified sailfish optimizer combined with an equal division method. Processes 2021, 9, 1806. [Google Scholar] [CrossRef]
- Xu, L.; Mo, Y.; Lu, Y.; Li, J. Improved seagull optimization algorithm combined with an unequal division method to solve dynamic optimization problems. Processes 2021, 9, 1037. [Google Scholar] [CrossRef]
- Lyu, Y.; Mo, Y.; Lu, Y.; Liu, R. Enhanced beetle antennae algorithm for chemical dynamic optimization problems’ non-fixed points discrete solution. Processes 2022, 10, 148. [Google Scholar] [CrossRef]
- Chen, X.; Du, W.; Tianfield, H.; Qi, R.; He, W.; Qian, F. Dynamic optimization of industrial processes with nonuniform discretization-based control vector parameterization. IEEE Trans. Autom. Sci. Eng. 2014, 11, 1289–1299. [Google Scholar] [CrossRef]
- Liu, P.; Liu, X.; Wang, P.; Li, G.; Xiao, L.; Yan, J.; Ren, Z. Control variable parameterisation with penalty approach for hypersonic vehicle reentry optimisation. Int. J. Control 2019, 92, 2015–2024. [Google Scholar] [CrossRef]
- Teo, K.L.; Jepps, G.; Moore, E.J.; Hayes, S. A computational method for free time optimal control problems, with application to maximizing the range of an aircraft-like projectile. J. Aust. Math. Soc. Series B Appl. Math. 1987, 28, 393–413. [Google Scholar] [CrossRef][Green Version]
- Liu, H.; Liu, P.; Liu, X.; Huang, H. Adaptive control arc length-based time grid refinement control parameterisation method for unmanned hypersonic vehicle reentry trajectory optimisation. Int. J. Control 2022, 95, 1–11. [Google Scholar] [CrossRef]
- Hui, X.; Guangbin, C.; Shengxiu, Z.; Xiaogang, Y.; Mingzhe, H. Hypersonic reentry trajectory optimization by using improved sparrow search algorithm and control parametrization method. Adv. Space Res. 2022, 69, 2512–2524. [Google Scholar] [CrossRef]
- Lin, Q.; Loxton, R.; Teo, K.L.; Wu, Y.H. Optimal control problems with stopping constraints. J. Glob. Optim. 2015, 63, 835–861. [Google Scholar] [CrossRef][Green Version]
- Lin, Q.; Loxton, R.; Teo, K.L.; Wu, Y.H. Optimal control computation for nonlinear systems with state-dependent stopping criteria. Automatica 2012, 48, 2116–2129. [Google Scholar] [CrossRef][Green Version]
- Clancy, L.J. Aerodynamics; Longman: London, UK, 1986. [Google Scholar]





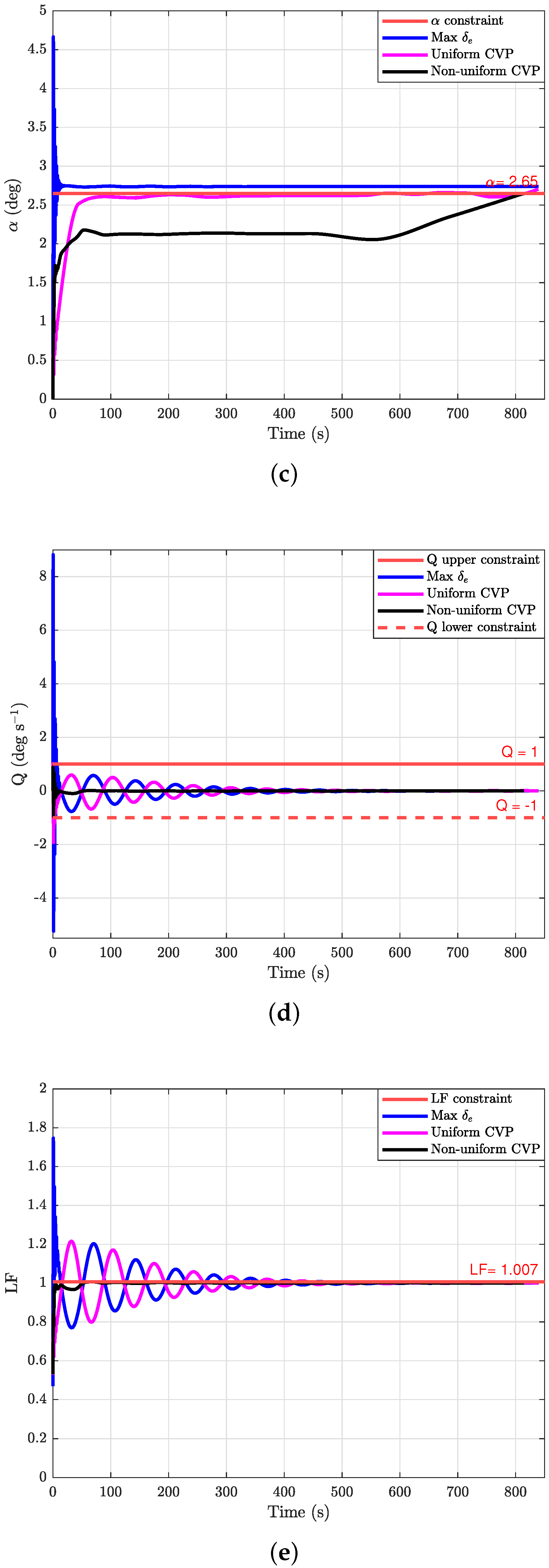
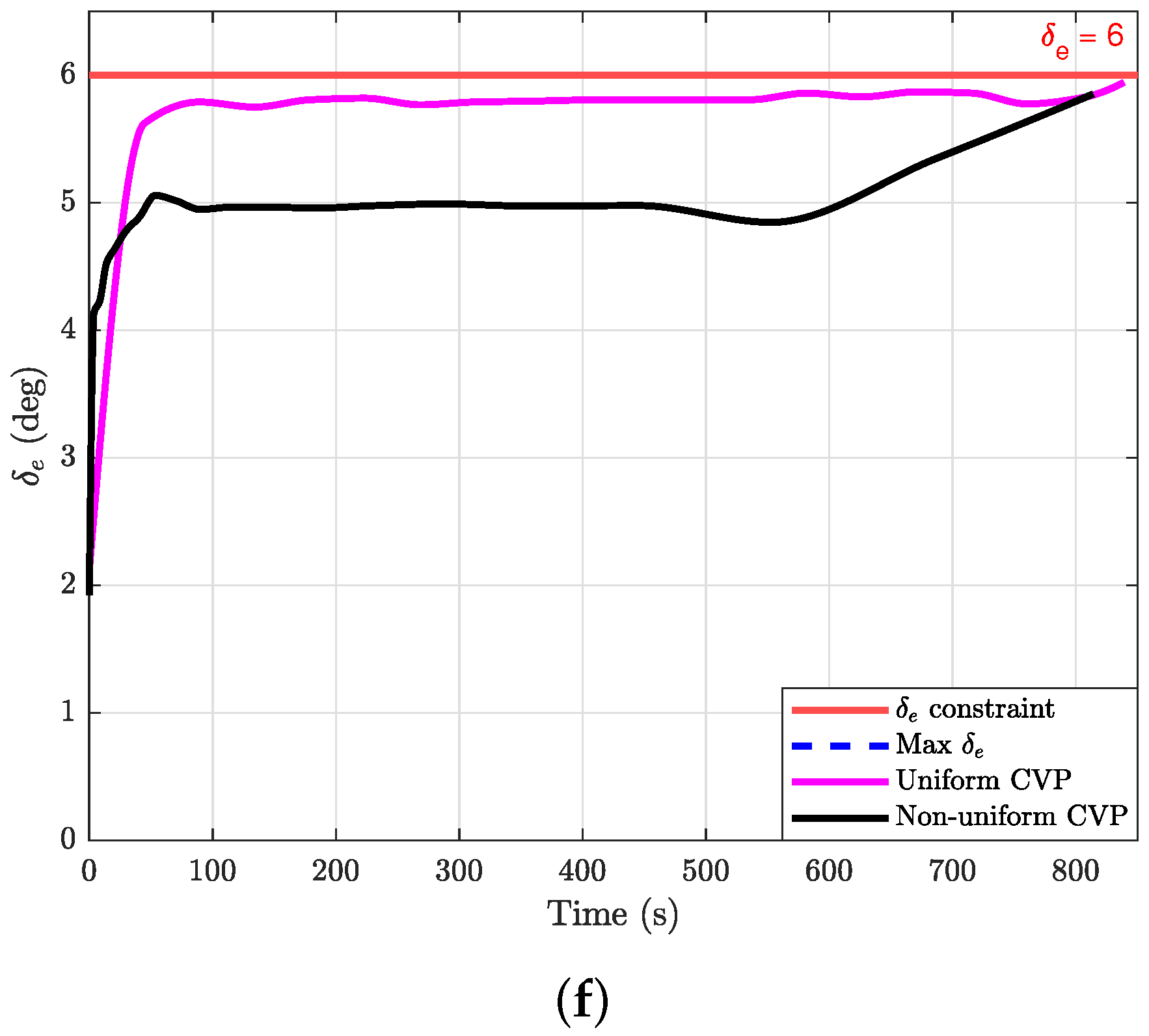
| States | Dispersion Points |
|---|---|
| V | 0.72 Ma |
| 0 deg | |
| Q | 0 deg s−1 |
| 0 deg | |
| R | 0 km |
| h | 10 km |
| Angle of Attack (deg) | Pitch Rate (deg s−1) | Load Factor | Elevator Deflection (deg) |
|---|---|---|---|
| LF |
| Constraints | Max | Uniform CVP | Non-Uniform CVP | ||||
|---|---|---|---|---|---|---|---|
| N = 10 | N = 15 | N = 20 | N = 10 | N = 15 | N = 20 | ||
| (deg) | 4.6652 | 2.6480 | 2.6467 | 2.7040 | 2.6499 | 2.6500 | 2.6498 |
| QL (deg s−1) | –5.2350 | –1.9868 | –1.9298 | –1.9269 | –1.0000 | –0.9302 | –0.9387 |
| QU (deg s−1) | 8.8224 | 1.0000 | 0.9761 | 1.0191 | 0.2654 | 0.3114 | 0.8970 |
| LF | 1.7466 | 1.2591 | 1.2199 | 1.2155 | 1.0069 | 1.0064 | 1.0063 |
| (deg) | 6.0000 | 5.8487 | 5.8464 | 5.9430 | 5.8522 | 5.8524 | 5.8521 |
| Stopping Values | Max | Uniform CVP | Non-Uniform CVP | ||||
|---|---|---|---|---|---|---|---|
| N = 10 | N = 15 | N = 20 | N = 10 | N = 15 | N = 20 | ||
| (s) | 839.351 | 802.215 | 792.177 | 838.989 | 816.190 | 814.735 | 814.023 |
| (km) | 118.556 | 120.141 | 119.901 | 120.282 | 121.250 | 121.259 | 121.278 |
| (km) | 117.993 | 119.553 | 119.260 | 119.758 | 120.831 | 120.840 | 120.856 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, A.; Rehman, F.u.; Bhatti, A.I. Trajectory Optimization of a Subsonic Unpowered Gliding Vehicle Using Control Vector Parameterization. Drones 2022, 6, 360. https://doi.org/10.3390/drones6110360
Mahmood A, Rehman Fu, Bhatti AI. Trajectory Optimization of a Subsonic Unpowered Gliding Vehicle Using Control Vector Parameterization. Drones. 2022; 6(11):360. https://doi.org/10.3390/drones6110360
Chicago/Turabian StyleMahmood, Ahmad, Fazal ur Rehman, and Aamer Iqbal Bhatti. 2022. "Trajectory Optimization of a Subsonic Unpowered Gliding Vehicle Using Control Vector Parameterization" Drones 6, no. 11: 360. https://doi.org/10.3390/drones6110360
APA StyleMahmood, A., Rehman, F. u., & Bhatti, A. I. (2022). Trajectory Optimization of a Subsonic Unpowered Gliding Vehicle Using Control Vector Parameterization. Drones, 6(11), 360. https://doi.org/10.3390/drones6110360





